
Мы уже начали разбираться с пределами и их решением. Продолжим по горячим следам и разберемся с решением пределов по правилу Лопиталя. Этому простому правилу по силам помочь Вам выбраться из коварных и сложных ловушек, которые преподаватели так любят использовать в примерах на контрольных по высшей математике и матанализу. Решение правилом Лопиталя – простое и быстрое. Главное – уметь дифференцировать.
Правило Лопиталя: история и определение
На самом деле это не совсем правило Лопиталя, а правило Лопиталя-Бернулли. Сформулировал его швейцарский математик Иоганн Бернулли, а француз Гийом Лопиталь впервые опубликовал в своем учебнике бесконечно малых в славном 1696 году. Представляете, как людям приходилось решать пределы с раскрытием неопределенностей до того, как это случилось? Мы – нет.
Кстати, о том, какой вклад внес в науку сын Иоганна Бернулли, читайте в статье про течение жидкостей и уравнение Бернулли.

Прежде чем приступать к разбору правила Лопиталя, рекомендуем прочитать вводную статью про пределы в математике и методы их решений. Часто в заданиях встречается формулировка: найти предел, не используя правило Лопиталя. О приемах, которые помогут Вам в этом, также читайте в нашей статье.
Если имеешь дело с пределами дроби двух функций, будь готов: скоро встретишься с неопределенностью вида 0/0 или бесконечность/бесконечность. Как это понимать? В числителе и знаменателе выражения стремятся к нулю или бесконечности. Что делать с таким пределом, на первый взгляд – совершенно непонятно. Однако если применить правило Лопиталя и немного подумать, все становится на свои места.
Но сформулируем правило Лопиталя-Бернулли. Если быть совершенно точными, оно выражается теоремой. Правило Лопиталя, определение:
Если две функции дифференцируемы в окрестности точки x=a обращаются в нуль в этой точке, и существует предел отношения производных этих функций, то при х стремящемся к а существует предел отношения самих функций, равный пределу отношения производных.
Запишем формулу, и все сразу станет проще. Правило Лопиталя, формула:
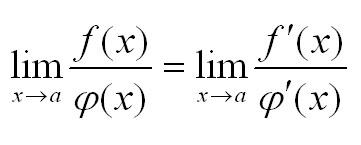
Так как нас интересует практическая сторона вопроса, не будем приводить здесь доказательство этой теоремы. Вам придется или поверить нам на слово, или найти его в любом учебнике по математическому анализу и убедится, что теорема верна.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Раскрытие неопределенностей по правилу Лопиталя
В раскрытии каких неопределенностей может помочь правило Лопиталя? Ранее мы говорили в основном о неопределенности 0/0. Однако это далеко не единственная неопределенность, с которой можно встретиться. Вот другие виды неопределенностей:
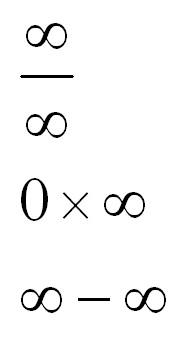
Рассмотрим преобразования, с помощью которых можно привести эти неопределенности к виду 0/0 или бесконечность/бесконечность. После преобразования можно будет применять правило Лопиталя-Бернулли и щелкать примеры как орешки.

Неопределенность вида бесконечность/бесконечность сводится к неопределенность вида 0/0 простым преобразованием:
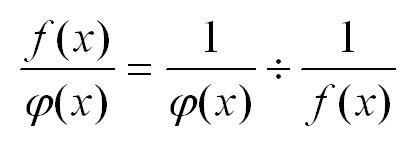
Пусть есть произведение двух функций, одна из которых первая стремиться к нулю, а вторая – к бесконечности. Применяем преобразование, и произведение нуля и бесконечности превращается в неопределенность 0/0:
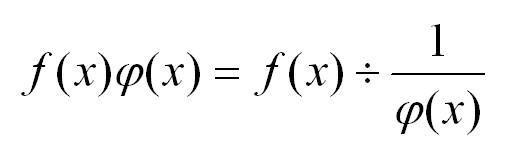
Для нахождения пределов с неопределенностями типа бесконечность минус бесконечность используем следующее преобразование, приводящее к неопределенности 0/0:
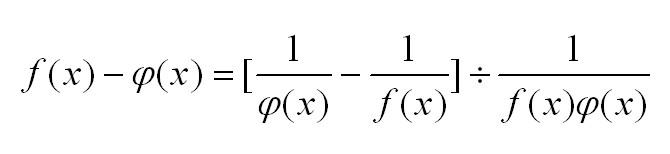
Для того чтобы пользоваться правилом Лопиталя, нужно уметь брать производные. Приведем ниже таблицу производных элементарных функций, которой Вы сможете пользоваться при решении примеров, а также правила вычисления производных сложных функций:

Теперь перейдем к примерам.
Пример 1
Найти предел по правилу Лопиталя:
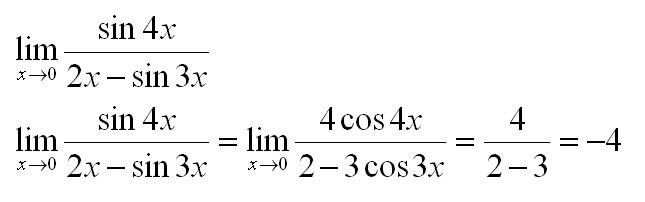
Пример 2
Вычислить с использованием правила Лопиталя:
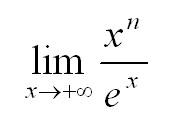
Важный момент! Если предел вторых и последующих производных функций существует при х стремящемся к а, то правило Лопиталя можно применять несколько раз.
Найдем предел (n – натуральное число). Для этого применим правило Лопиталя n раз:
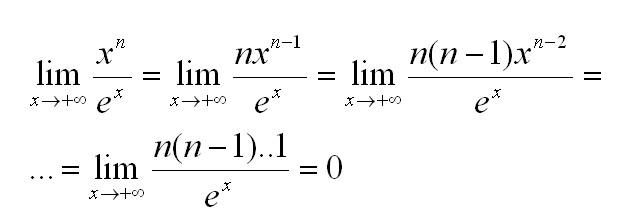
Желаем удачи в освоении математического анализа. А если Вам понадобится найти предел используя правило Лопиталя, написать реферат по правилу Лопиталя, вычислить корни дифференциального уравнения или даже рассчитать тензор инерции тела, обращайтесь к нашим авторам. Они с радостью помогут разобраться в тонкостях решения.
Назначение сервиса. Данный сервис предназначен для решения пределов, используя правило Лопиталя. Результаты вычисления оформляются в формате Word (см. пример).
Это поле предназначено для ввода числителя дроби.
Правила ввода функций:
Например, x2+3x, записываем как x^2+3*x; ln(1+sin2x) ≡ ln(1+sin(x)^2)
Это поле предназначено для ввода знаменателя дроби. Если знаменатель отсутствует, можно оставить это поле пустым или указать 1.
Правила ввода функций:
Пример. Найти 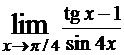 .
.
Решение.Сначала убедимся, что правило Лопиталя применить можно. Действительно, величины, стоящие в числителе и знаменателе при x → π/4 являются бесконечно малыми, то есть имеем неопределенность вида 0/0, следовательно можно воспользоваться правилом Лопиталя:
Пусть дана функция
y=f(x);
производная от этой функции
y′=f′(x).
Производная от этой производной
называется производной
второго порядка
функции y=f(x),
которая обозначается как y“
или f“(x)=![]() .
.
Аналогично
определяются производные более высокого
порядка f
(n)(x)=![]() .
.
Правила Лопиталя
Первое правило.
Неопределенность
![]() .
.
Если
![]() ,
,
то![]() .
.
Второе правило.
Неопределенность
![]() .
.
Если
![]() ,
,
то![]() .
.
Неопределенности
вида 0∞; ∞-∞; 1∞;00
сводятся к неопределенностям
![]() ,
,![]() путем алгебраических преобразований.
путем алгебраических преобразований.
______________
4.5.1. Найти производные
второго порядка:
а)
y=cos2x;
б)
y=arctgx2 ;
в)
![]() ;
;
г)
![]() ;
;
д)![]() .
.
4.5.2. Найти f‘(0),
f“(0),
f“‘(0)
если f(x)=e2xsin3x.
4.5.3. Вывести формулу
для производной n
– го порядка для функций:
а) y=xm;
б) у=ах.
Ответ: а) у
(n)=m(m–1)…(m–n+1)xm–n.
б) y(n)=ax(lna)n.
4.5.4. Найти пределы:
а)
![]() ;
;
б)![]() ;
;
в)
![]() ;
;
г)![]() ;
;
д)
![]() ;
;
е)![]() ;
;
ж)
![]() ;
;
з)![]() ;
;
и)
![]() ;
;
к)![]() .
.
Ответ: а)
![]() ;
;
б) 1; в) ∞; г) 1/2; д) 1; е)1; ж) 1; з)0; и) 1; к)1.
_________________
4.5.5. Найти производные
второго порядка:
а) у=(х2-10х+5)5;
б) y=sin2x;
в)
![]() ;
;
г)у=ln(x3-2x2+4).
4.5.6. Найти выражение
для n-й
производной следующих функций:
а) у=3х;
б) у=cosx;
в) y=sin2x.
4.5.7. Найти пределы:
а)
![]() ; б)
; б)![]() ;
;
в)
![]() ;
;
г)![]() ;
;
д)
![]() ;
;
е) ;
;
ж)
![]() ;
;
з)![]() ;
;
и)
![]() ;
;
к)![]() .
.
Ответ: а) 1; б) 0; в)0;
г)10; д) -1/3; е)∞; ж) -1; з) 1; и) 1; к)1.
§4.6. Монотонность функций. Экстремумы. Наибольшее и наименьшее значения функции на отрезке
Функция f(x)
называется возрастающей
в точке х0,
если в некоторой
– окрестности этой точки f(x0–h)<f(x0)<f(x0+h).
Убывающей
– если f(x0+h)<f(x0)<f(x0–h),
где 0<h<.
Функция f(x)
называется возрастающей
на отрезке [a,b],
если для любых х1
и х2
этого отрезка из неравенства х1>х2
следует неравенство f(х1)>f(х2).
Если же из неравенства х1>х2
следует, что f(х1)<f(х2),
то функция f(x)
– убывающая на отрезке [a,b].
Можно сформулировать
достаточные признаки возрастания и
убывания функции y=f(x)
Если y‘>0
для всех х[a,b],
то функция возрастает на [a,b];
при y‘<0
для х[a,b],
то функция на [a,b]
убывает.
Функция f(x)
может иметь экстремум лишь в тех точках,
в которых f‘(x)=0
или не существует. Такие точки называются
критическими, или стационарными, или
подозрительными на экстремум. Равенство
нулю первой производной данной функции
является необходимым условием
существования экстремума.
В качестве
достаточного условия существования
экстремума в критической точке х0
можно принять смену знака первой
производной при переходе через критическую
точку, при этом, если знак меняется с +
на -, то в точке х0
– максимум, если с – на + , то в точке х0
– минимум.
Если производная
y‘
знак не меняет при переходе через точку,
подозрительную на экстремум, то экстремума
в этой точке нет.
Для отыскания
наибольшего и наименьшего значений
функций у=f(x)
на отрезке
[a,b]
необходимо найти критические точки,
принадлежащие [a,b].
Вычислить значения функции в этих
критических точках и на концах отрезка.
Из всех найденных значений выбираем
наибольшее и наименьшее.
__________________
4.6.1. Найти интервалы
монотонности следующих функций:
а) у=2-3х+х3;
б) у=хе-х;
в) у=(х-2)2(х+2);
г) y=ln(x2-2x+4).
Ответ: а) (-∞;-1)(1;∞)
– возрастает; (-1;1) – убывает;
б) (-∞;1) –
возрастает; (1;∞) – убывает;
в) (-∞;-1)(1;∞)
– возрастает; (-1;1) – убывает;
г) (-∞;1) –
убывает; (1;∞) – возрастает;
4.6.2. Найти экстремумы
функций:
а)
![]() ;
;
б)y=ln(x2+1);
в)
![]() ;
;
г)у=(х-1)6/7.
Ответ: а) уmin=y(0)=0;
ymax=![]() ;
;
б)
уmin=y(0)=0;
в)
уmax=y(1)=![]() ;
;
ymin=![]() ;
;
г)
уmin=y(1)=0.
4.6.3. Найти наибольшее
и наименьшее значения функций на заданном
отрезке:
а) у=х4+2х2+5,
х[-2,2];
б)
![]() ,х[-6,8];
,х[-6,8];
в)
![]() ,х[0,4];
,х[0,4];
г) y=2tgx–tg2x,
х[0,π/2].
Ответ: а) 29,5; б) 10;
6; в) 3/5; -1; г) унаиб=1.
_______________
4.6.4. Найти интервалы
монотонности следующих функций:
а) у=(2-х)(х+1)2;
б) у=х3-6х+5;
в) у=х+е-х;
г) y=xlnx.
Ответ: а) (-∞;-1)(1;∞)
– убывает; (-1;1) – возрастает;
б) (-∞;-2)(2;∞)
– возрастает; (-2;2) – убывает;
в) (-∞;0) –
возрастает; (0;∞) – убывает;
г) (0;1/е)
– убывает; (1/е;∞)
– возрастает.
4.6.5. Найти экстремумы
функций:
а)
![]() ;
;
б)![]() .
.
Ответ:
а)
ymax=y(11/4)=13/4;
б)
ymin=y(e)=e.
4.6.6. Найти наибольшее
и наименьшее значения функций на отрезке:
а)
![]() ,х[0,4];
,х[0,4];
б)
![]() ,х[0,1];
,х[0,1];
в)
![]() ,х[0,1].
,х[0,1].
Ответ: а) 8;0; б) 1;
3/5; в) π/4; 0.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В задачах на пределы можно столкнуться с ситуациями, разрешить которые достаточно просто, используя правило Лопиталя. Относительно простая закономерность является очень полезной, когда требуется найти ответ к заданию по математике или математическому анализу. При этом важно владеть навыками дифференцирования.
Правило Лопиталя — в чем суть, понятие
Название этой закономерности не совсем соответствует действительности. Было бы правильнее говорить «правило Лопиталя — Бернулли». Первая подробная формулировка была представлена швейцарским математиком Иоганном Бернулли. Французский ученый Гийом Лопиталь впервые опубликовал это правило в издании собственного учебника в 1696 году.
Правило Лопиталя позволяет существенно упростить некоторые расчеты предела отношения (displaystyle frac{f(x)}{g(x)}) при (xrightarrow a) в том случае, когда (f) и (g) одновременно представляют собой бесконечно малые, либо бесконечно большие величины. С помощью выведенной закономерности допустимо осуществлять замену предела отношения функции, используя предел отношения их производных.
Доказательство 1 и 2 правила Лопиталя, вывод теоремы
Теорема 1
Допустим, что функции (f(x)) и (g(x)) дифференцируются на промежутке ((a,b)):
(lim_{xrightarrow a+0}f(x)=0)
(lim_{xrightarrow a+0}g(x)=0)
(g'(x)neq 0 ) для всех ( xin(a,b))
Тогда имеет место конечный и бесконечный:
(lim_{xrightarrow a+0}frac{f'(x)}{g'(x)}=A)
Таким образом, также существует и равен A:
(displaystylelim_{xrightarrow a+0}frac{f(x)}{g(x)})
Можно сделать вывод:
(lim_{xrightarrow a+0}frac{f(x)}{g(x)}=lim_{xrightarrow a+0}frac{f'(x)}{g'(x)})(lim_{xrightarrow a+0}frac{f(x)}{g(x)}=lim_{xrightarrow a+0}frac{f'(x)}{g'(x)})
Докажем данную теорию.
Допустим, что (xin(a,b))
Следует доопределить функции (f(x)) и (g(x)) в точке a, имея в виду, что:
(f(a)=g(a)=0)
Таким образом, из условий функций следует, что (f) и (g) непрерывны на отрезке [a,x]. По теореме Коши имеется точка (xiin (a,x)), такая, что:
(frac{f(x)}{g(x)}=frac{f(x)-f(a)}{g(x)-g(a)}=frac{f'(xi)}{g'(xi)})
В том случае, когда (xrightarrow a+0), можно определить, что (xirightarrow a+0). Зная, что существует (displaystyle lim_{xrightarrow a+0}frac{f'(xi)}{g'(xi)}=A), можно сделать вывод о справедливости утверждения (eqref).
Теорема, доказательства которой представлены путем соответствующих изменений ее условий, работает, когда (xrightarrow a-0) и (xrightarrow a). Точка a в данном случае является конечной.
Теорема 1 остается справедливой в таких ситуациях, когда (a=+infty) или (a=-infty), а также:
(displaystyle lim_{xrightarrow +infty}f(x)=lim_{xrightarrow +infty} g(x)=0)
( g'(x)neq 0) при (x > x_0)и существует (displaystyle lim_{xrightarrow +infty}frac{f'(x)}{g'(x)}=A)
В этом случае (displaystyle lim_{xrightarrow +infty}frac{f(x)}{g(x)}=A)
Доказательство данного утверждения выполнено с помощью замены переменного (displaystyle x=frac{1}{t}) и Теоремы 1.
Теорема 2
Допустим, что функции (f(x)) и (g(x)) дифференцируются при (x > alpha) и (g'(x)neq 0) при (x > alpha)
(lim_{xrightarrow+infty}f(x)=infty,quad lim_{xrightarrow +infty}g(x)=infty)
и существует конечный:
(lim_{xrightarrow +infty}frac{f'(x)}{g'(x)}=A)
В таком случае, существует (displaystyle lim_{xrightarrow +infty}frac{f(x)}{g(x)}), равный A.
Таким образом:
(lim_{xrightarrow +infty}frac{f(x)}{g(x)}=lim_{xrightarrow +infty}frac{f'(x)}{g'(x)} )
Доказательство
Зная, что:
(existsalpha_{1} > alpha: forall x > alpha_{1}rightarrow |f(x)| > 1)
( |g(x)| > 1)
Исходя из записанного выражения, получим, что (f(x)neq 0) и ( g(x)neq 0) при (x > alpha_1).
Согласно определению, для заданного числа (varepsilon > 0) можно вычислить (delta=delta_1(varepsilon)geq alpha_1) такое, что для всех (t > delta_{1}) выполняется неравенство:
(A-frac{varepsilon}{2} < frac{f'(t)}{g'(t)} < A+frac{varepsilon}{2})
Определив (x_{0} > delta_{1}) на рисунке, выберем число (delta_{2} > x_{0}) такое, чтобы при всех (x > delta_{2}) выполнялись неравенства:
(left|frac{f(x_{0})}{f(x)}right| < frac{1}{2},quad left|frac{g(x_{0})}{g(x)}right| < frac{1}{2})
В качестве доказательства выражения нужно определить, что существует (delta) такое, при котором, если все (x > delta), выполняется неравенство:
(A-varepsilon < frac{f(x)}{g(x)} < A+varepsilon)
Число (delta) будет выбрано ниже. Учитывая, что (x > delta), можно применить к функциям (f) и (g) на интервале ([x_0,x]) теорему Коши о среднем. Согласно данному утверждению, должна существовать точка (xiin [x_{0},x]) такая, при которой:
(frac{f(x)-f(x_{0})}{g(x)-g(x_{0})}=frac{f'(xi)}{g'(xi)})
Преобразуем левую часть равенства:
(frac{f(x)-f(x_{0})}{g(x)-g(x_{0})}=frac{f(x)}{g(x)}(varphi(x))^{-1})
где (varphi(x)=frac{1-g(x_0)/g(x)}{1-f(x_0)/f(x)}=1+beta(x)).
Можно заметить, что (beta(x)rightarrow 0) при (xrightarrow +infty).
Таким образом:
(forall varepsilon > 0 existsdeltageqdelta_{2}: forall x > deltarightarrow|beta(x)| < frac{varepsilon/2}{|A|+varepsilon/2})
Исходя из того, что (xi > x_{0} > delta_{1}) и вышеуказанных выражений, следует, что для всех (x > delta_{2}) выполняется неравенство:
(A-frac{varepsilon}{2} < frac{f(x)}{g(x)}(varphi(x))^{-1} < A+frac{varepsilon}{2})
Когда (x > delta), получаем (phi(x) > 0.)
Таким образом, выведенное неравенство равносильно следующему:
((A-frac{varepsilon}{2})(1+beta(x)) < frac{f(x)}{g(x)} < (A+frac{varepsilon}{2})(1+beta(x)))
Исходя из этого утверждения, можно записать:
((A-frac{varepsilon}{2})(1+beta(x))=A-frac{varepsilon}{2}+left(A-frac{varepsilon}{2}right)beta(x)geq A-frac{varepsilon}{2}-left(|A|+frac{varepsilon}{2}right)|beta(x)| > A-frac{varepsilon}{2}-frac{varepsilon}{2}=A-varepsilon)
Аналогичным способом можно определить:
(left(A+frac{varepsilon}{2}right)(1+beta(x)) leq A+frac{varepsilon}{2}+left(|A|+frac{varepsilon}{2}right)|beta(x)| < A+varepsilon)
Получим, что для всех (x > delta) справедливо выведенное в теореме неравенство.
Теорема 2 работает при условии, что (A=+infty) или (A=-infty).
Теорема справедлива и в тех случаях, когда (xrightarrow a (xrightarrow a-0, xrightarrow a+0)), где a является конечной точкой.
Исходя из теорем 1 и 2, правило Лопиталя можно применять для раскрытия неопределенностей вида (displaystyle frac{0}{0}) или (displaystyle frac{infty}{infty}).
Неопределенности видов (0cdot infty, infty-infty, 0^{0}, infty^{0}, 1^{infty}) нередко удается преобразить в неопределенности типа (displaystyle frac{0}{0}) или (displaystyle frac{infty}{infty}), используя при этом различные преобразования.
Правило Лопиталя для вычисления пределов
Решить пределы можно различными методами и формулами. Наиболее быстрый и простой способ, а также универсальный — это правило Лопиталя. Умение искать производные разных функций позволит использовать данную закономерность наиболее эффективно. Можно сформулировать правило Лопиталя при следующих условиях:
- (lim limits_{x to a} f(x) = lim limits_{x to a} g(x) = 0 text{ или } infty)
- имеются (f'(a) text{ и } g'(a))
- (g'(x)neq0)
- присутствует (lim limits_{x to a} frac{f(x)}{g(x)})
В таком случае:
(lim limits_{x to a} frac{f(x)}{g(x)} = lim limits_{x to a} frac{f'(x)}{g'(x)})
Последовательность решения:
- нужно подставить точку x в предел;
- в том случае, когда получается (frac{0}{0} text{ или } frac{infty}{infty}), можно определить производную числителя и знаменателя;
- далее следует подставить точку x в записанный предел и рассчитать его. При получении неопределенности следует повторить пункты 2 и 3.
Раскрытие неопределенностей по правилу Лопиталя
В том случае, когда функции (f(x)) и (g(x)) дифференцируются в точке a, при этом (f(a)=g(a)=0) и (g'(a)neq 0), то, применяя к функциям (f) и (g) локальную формулу Тейлора при (n=1), получаем:
(f(x)=f'(a)(x-a)+o((x-a)))
(g(x)=g'(a)(x-a)+o((x-a)))
Таким образом:
(lim_{xrightarrow a}frac{f(x)}{g(x)}=frac{f'(a)}{g'(a)})
Аналогичным методом можно определить, что, при условии (f^{(n)}a) и (g^{(n)}a), получим:
(f(a)=f'(a)=ldots =f^{(n-1)}(a)=0)
(g(a)=g'(a)=ldots =g^{(n-1)}(a)=0)
Учитывая, что (g^{(n)}(a)neq 0), можно записать выражение:
(lim_{xrightarrow a}frac{f(x)}{g(x)}=displaystylelim_{xrightarrow a}frac{displaystyle frac{f^{(n)}(a)}{n!}(x-a)^{n}+o((x-a)^n)}{displaystyle frac{g^{(n)}(a)}{n!}(x-a)^{n}+o((x-a)^n)}=frac{f^{(n)}(a)}{g^{(n)}(a)})
Правило Лопиталя применимо в случае неопределенностей типа (0 cdot infty, infty – infty, 0^0, 1^{infty}, infty^0.)
Первую и вторую неопределенности (0 cdot infty) и (infty – infty) достаточно просто преобразовать в (largefrac{0}{0}normalsize) или (largefrac{infty}{infty}normalsize) по средствам алгебраических операций. А неопределенности (0^0, 1^{infty}) и (infty^0) можно свести к типу (0 cdot infty), используя соотношение:
(f{left( x right)^{gleft( x right)}} = {e^{gleft( x right)ln fleft( x right)}})
Формула и примеры решений
Правило Лопиталя: в том случае, когда две функции дифференцируемы в окрестности точки x=a, обращаются в нуль в этой точке, и существует предел отношения производных этих функций, то при х, которое стремится к а, существует предел отношения самих функций, который соотвесттвует пределу отношения производных.
Формула имеет следующий вид:
(lim_{xrightarrow a}frac{f(x)}{varphi (x)}=lim_{xrightarrow a}frac{f^{,}(x)}{varphi^{,} (x)})
Задача 1
Требуется найти предел:
(limlimits_{x to -1} frac{x^2-1}{x^3+x+2})
Решение
(lim limits_{x to -1} frac{x^2-1}{x^3+x+2} = frac{0}{0})
В полученной неопределенности (frac{0}{0}) можно заменить (х) точкой (x = -1). Данный вывод говорит о необходимости применения формулы расчета предела. Получим:
(lim limits_{x to -1} frac{(x^2-1)’}{(x^3+x+2)’} =lim limits_{x to -1} frac{2x}{3x^2+1})
Далее необходимо вновь рассчитать предел с помощью подстановки (x=-1) в последний предел. Таким образом:
(frac{2 cdot (-1)}{3 cdot (-1)^2+1} = frac{-2}{4} = -frac{1}{2})
Ответ: (limlimits_{x to -1} frac{x^2-1}{x^3+x+2} = -frac{1}{2})
Задача 2
Требуется вычислить предел, используя правило Лопиталя:
(lim limits_{x to infty} frac{ln x}{x})
Решение
Алгоритм вычислений стандартный:
(lim limits_{x to infty} frac{ln x}{x} = frac{infty}{infty} = lim limits_{x to infty} frac{(ln x)’}{(x)’}=lim limits_{x to infty} frac{frac{1}{x}}{1}=lim limits_{x to infty} frac{1}{x} = frac{1}{infty} = 0)
Ответ: (lim limits_{x to infty} frac{ln x}{x} = 0)
Задача 3
Необходимо предоставить решение предела с помощью формулы Лопиталя:
(lim limits_{x to 0} frac{cos x – 1}{x^2})
Решение
(lim limits_{xto 0} frac{cos x-1}{x^2} = frac{0}{0} = lim limits_{x to 0} frac{(cos x-1)’}{(x^2)’} =lim limits_{x to 0} frac{-sin x}{2x} = frac{0}{0}=lim limits_{x to 0} frac{(-sin x)’}{(2x)’} =lim limits_{x to 0} frac{-cos x}{2}=)
( = frac{-cos 0}{2} = -frac{1}{2})
Ответ: (lim limits_{x to 0} frac{cos x – 1}{x^2} = -frac{1}{2})
Задача 4
Нужно решить предел:
(lim limits_{xto 0} frac{sin 2x-e^{5x}+1}{x-cos x+1})
Решение
(lim limits_{xto 0} frac{sin 2x-e^{5x}+1}{x-cos x+1} = frac{0}{0}=lim limits_{xto 0} frac{(sin 2x-e^{5x}+1)’}{(x-cos x+1)’} =lim limits_{xto 0} frac{(sin 2x)’-(e^{5x})’+(1)’}{(x)’-(cos x)’+(1)’}=lim limits_{xto 0} frac{2cos 2x-5e^{5x}}{1+sin x} =)
(=frac{2cos0-5e^0}{1+sin 0}=frac{2cdot 1-5cdot 1}{1+0} = frac{-3}{1} = -3)
Ответ: (lim limits_{xto 0} frac{sin 2x-e^{5x}+1}{x-cos x+1} = -3)
Правилом Лопиталя допустимо пользоваться при решении задач с односторонними пределами. Можно сказать, что эта методика является наиболее эффективной для раскрытия неопределенностей вида (frac{0}{0}) и (frac{infty}{infty}) в том случае, когда необходимо вычислить предел. Смысл правила заключается в том, что предел отношения функций равен пределу отношений производных от этих функций. Если в процессе освоения этой и других подобных тем возникли сложности, всегда можно обратиться за помощью к сервису Феникс.Хелп.
Преподаватель который помогает студентам и школьникам в учёбе.
Правило Лопиталя – определение и вычисление с примерами решения
Содержание:
Правило Лопиталя
Теорема 13.1 (правило Лопиталя). Пусть функции y=f(x) и y=g(x):
1) дифференцируемы в некоторой окрестности 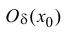
1. Если в п. 4 теоремы 13.1
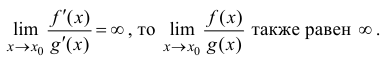
2. Аналогичная теорема верна и для односторонних пределов.
Теорема 13.2. Пусть M>0 и функции y=f(x) и y=g(x):
1) дифференцируемы при 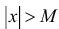 ;
;
2) 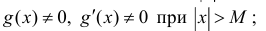
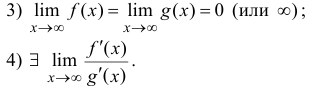
Тогда
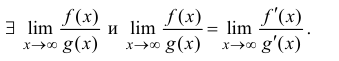
Доказательство
Пусть 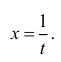 Рассмотрим функции
Рассмотрим функции 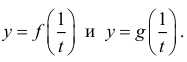
Тогда условия 1) –3) теоремы 13.1 выполнены в окрестности  .
.
Проверим условие 4):
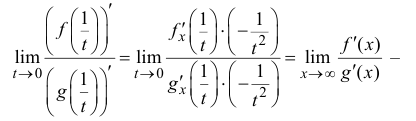
предел существует, поэтому по теореме 13.1
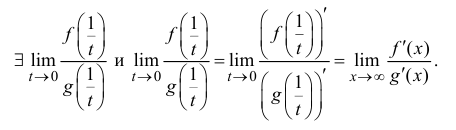
Тогда
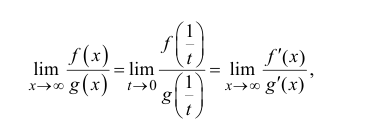
что и требовалось доказать.
ПустьM>0. Функции 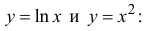
1) непрерывны и имеют производные при x> M;
2) 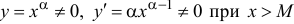 ;
;
3) 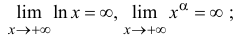
4)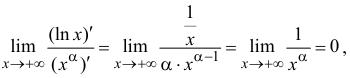 поэтому по теореме 13.2
поэтому по теореме 13.2
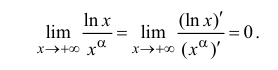
П р и м е р 13.2
Найти 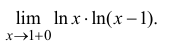
Р е ш е н и е
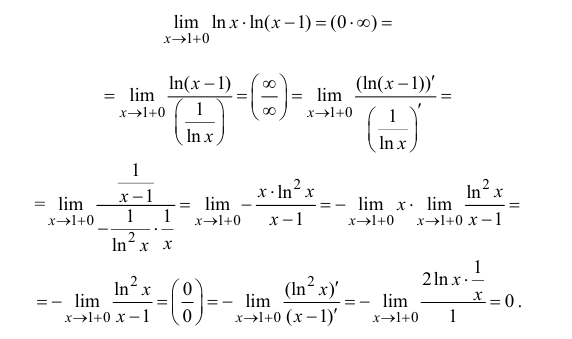
П р и м е р 13.3
Найти 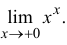
Р е ш е н и е
Имеем неопределенность вида 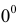 .
.
Преобразуем функцию 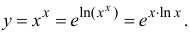
Найдем
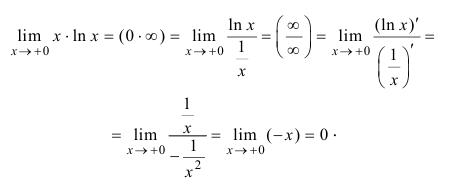
Поэтому
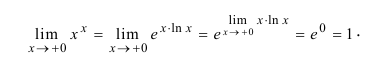
П р и м е р 13.4
Найти 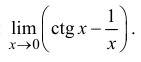
Р е ш е н и е
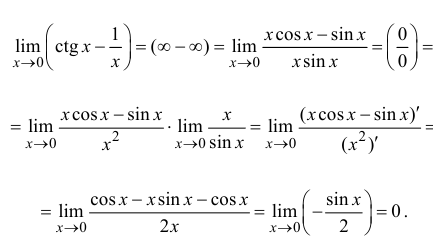
Если в условии теоремы 13.1 предположить дополнительно, что функции 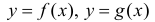 дифференцируемы в точке
дифференцируемы в точке 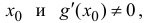 тогда формула (13.1) перепишется в виде
тогда формула (13.1) перепишется в виде
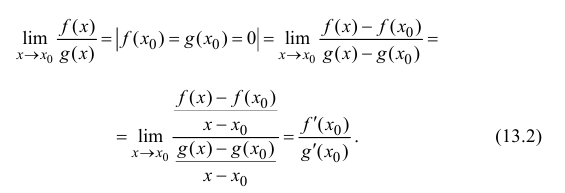
Геометрически это значит, что предел при 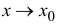 отношения значений функций
отношения значений функций 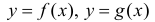 равен отношению угловых коэффициентов касательных к этим функциям в точке
равен отношению угловых коэффициентов касательных к этим функциям в точке 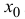 .
.
П р и м е р 13.5
Найти 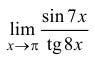 (см. пример 4.2).
(см. пример 4.2).
Р е ш е н и е
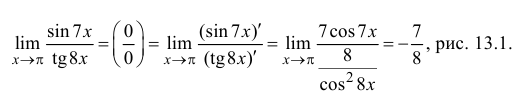
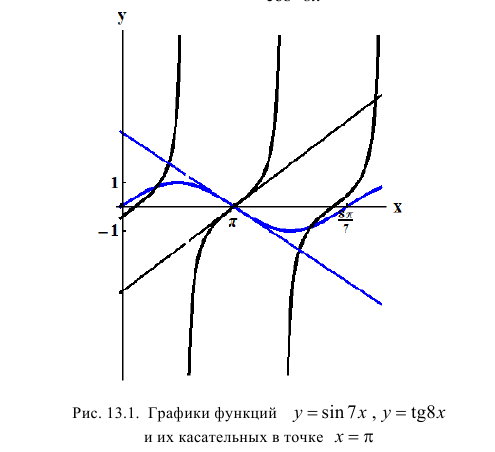
——-
Правило Лопиталя
Теорема 8.1. Пусть
1) функции 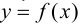 и
и 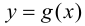 определены и непрерывны в проколотой окрестности
определены и непрерывны в проколотой окрестности 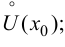
2) существуют конечные производные 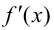 и
и 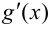 в
в 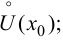
3) 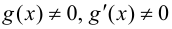 в
в 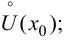
4) 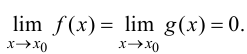
Тогда если существует 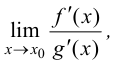 то существует
то существует 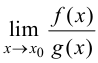 и имеет место равенство
и имеет место равенство
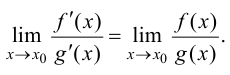
Доказательство.
Доопределим функции 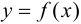 и
и 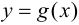 в точке
в точке 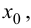 полагая
полагая
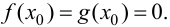
Тогда функции 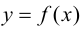 и
и 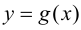 непрерывны в точке
непрерывны в точке 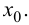 Используя теорему Коши (теорема 7.3), получим
Используя теорему Коши (теорема 7.3), получим
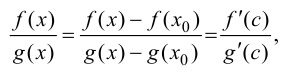
где точка 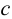 будет удовлетворять условиям
будет удовлетворять условиям 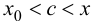 или
или 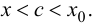 Если
Если 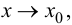 то
то 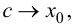 поэтому, согласно условию теоремы,
поэтому, согласно условию теоремы,
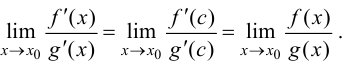
Теорема 8.1 формулирует правило раскрытия неопределенности типа 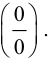
Замечание 8.1. Если производные 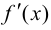 и
и 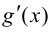 удовлетворяют тем же требованиям, что и сами функции
удовлетворяют тем же требованиям, что и сами функции 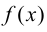 и
и 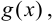 то правило Лопиталя можно применять повторно. При этом получаем
то правило Лопиталя можно применять повторно. При этом получаем
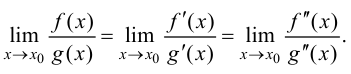
- Заказать решение задач по высшей математике
Пример 8.1. Найти предел 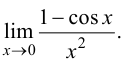
Решение.
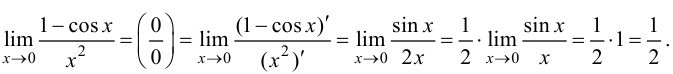
Ответ: 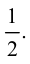
Пример 8.2. Найти предел 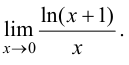
Решение.
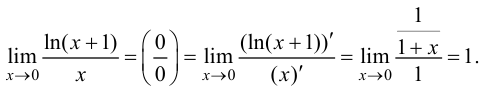
Ответ: 1
Пример 8.3. Найти предел 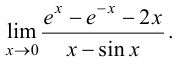
Решение.
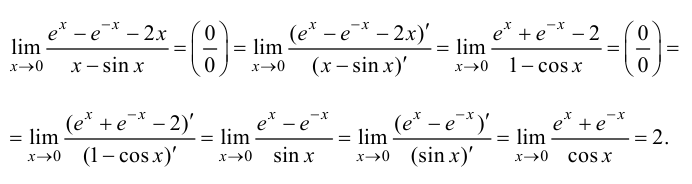
Ответ: 2.
Теорема 8.2*. Пусть
1) функции 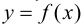 и
и 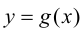 определены и непрерывны в проколотой окрестности
определены и непрерывны в проколотой окрестности 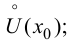
2) существуют конечные производные 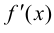 и
и 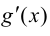 в
в 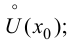
3) 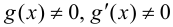 в
в 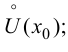
4) 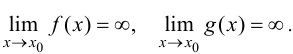
Тогда, если существует 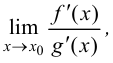 то существует
то существует 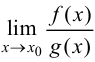
и имеет место равенство
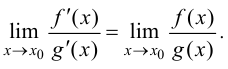
Теорема 8.2 формулирует правило раскрытия неопределенности
типа 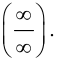
Замечание 8.2. Правило Лопиталя справедливо и в случаях 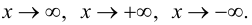
Пример 8.4. Найти предел 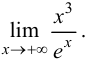
Решение.
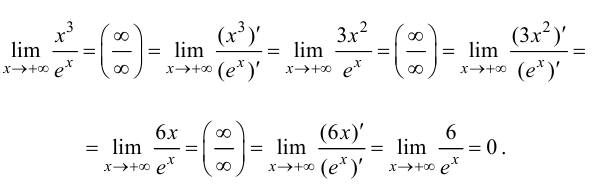
Ответ: 0.
Пример 8.5. Найти предел 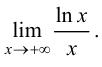
Решение.
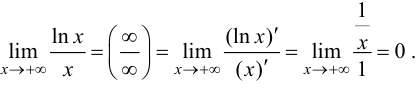
Ответ: 0.
Пример 8.6. Найти предел 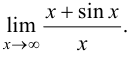
Решение.
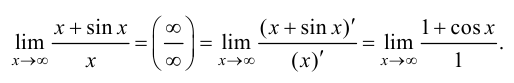
Полученный предел не существует, так как при 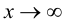 функция
функция 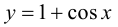 не стремится ни к какому предельному значению, а колеблется между 0 и 2. Правило Лопиталя не дает результатов. Рассмотрим другой подход к вычислению предела.
не стремится ни к какому предельному значению, а колеблется между 0 и 2. Правило Лопиталя не дает результатов. Рассмотрим другой подход к вычислению предела.
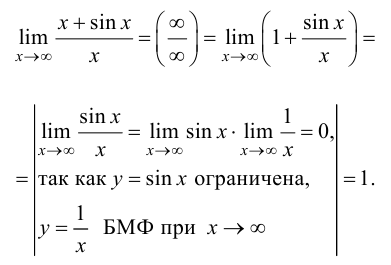
Ответ: 1.
Заметим, что правило Лопиталя дает также возможность раскрыть неопределенности типа 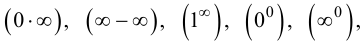 предварительно приведя их к виду
предварительно приведя их к виду 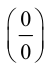 или
или 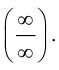
Пример 8.7. Найти предел 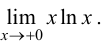
Решение.
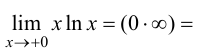
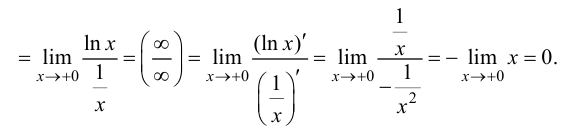
Ответ: 0.
Пример 8.8. Найти предел 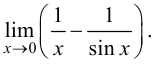
Решение.
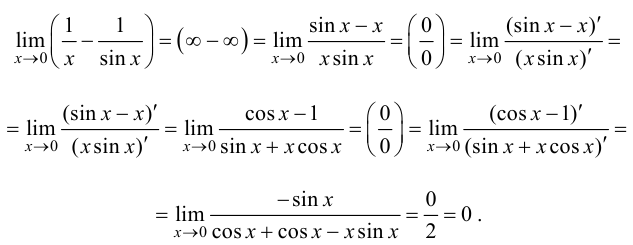
Ответ: 0.
Пример 8.9. Найти предел 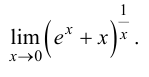
Решение.
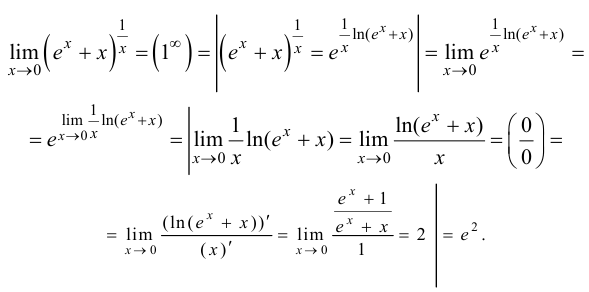
Ответ: 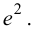
Пример 8.10. Найти предел 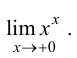
Решение.
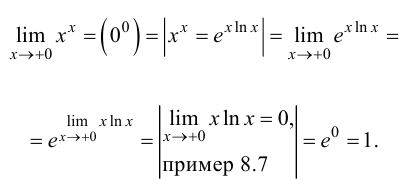
Ответ: 1.
- Вычисления в Mathematica с примерами
- Рациональная дробь
- Функция в математике
- Наибольшее и наименьшее значения функции
- Тригонометрические функции произвольного угла
- Теоремы синусов и косинусов
- Система показательных уравнений
- Непрерывные функции и их свойства

