Частные производные
Частной производной по x функции z = f(x,y) в точке A(x0,y0) называется предел отношения частного приращения по x функции в точке A к приращению ∆x при стремлении ∆x к нулю.
Частные производные функции z(x,y) находятся по следующим формулам:
Вторые частные производные функции z(x,y) находятся по формулам:
Смешанные частные производные функции z(x,y) находятся по формулам:
Назначение сервиса. Сервис используется для нахождения частных производных функции (см. пример). Решение производится в онлайн режиме и оформляется в формате Word.
- Решение онлайн
- Видеоинструкция
- Также решают
Правила ввода функции, заданной в явном виде
Примеры
x2+xy ≡ x^2+x*y.
cos2(2x+y) ≡ (cos(2*x+y))^2
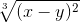
Правила ввода функции, заданной в неявном виде
- Все переменные выражаются через x,y,z
Примеры
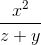
cos2(2x+zy) ≡ (cos(2*x+z*y))^2
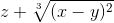
Частные производные используются, например, при нахождении полного дифференциала и экстремумов функции.
Частные производные функции нескольких переменных
Ели одному из аргументов функции z = f(x,y) придать приращение, а другой аргумент не изменять, то функция получит частное приращение по одному из аргументов: Δxz=f(x+Δx,y)-f(x,y) – это частное приращение функции z по аргументу x; Δyz=f(x,y+Δy)-f(x,y) – это частное приращение функции z по аргументу у.
Частной производной функции нескольких переменных по одному из её аргументов называется предел отношения частного приращения функции по этому аргументу к соответствующему приращению аргумента при условии, что приращение аргумента стремится к нулю:
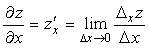
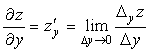
Чтобы вычислить частную производную ФНП по одному из её аргументов, нужно все другие её аргументы считать постоянными и проводить дифференцирование по правилам дифференцирования функции одного аргумента.
Пример 1. z=2x5+3x2y+y2–4x+5y-1
Пример 2. Найти частные производные функции z = f(x;y) в точке A(x0;y0).
Находим частные производные:
Найдем частные производные в точке А(1;1)
Находим вторые частные производные:

Найдем смешанные частные производные:
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Частные производные
Частные производные применяются в заданиях с функциями нескольких переменных. Правила нахождения точно такие же как и для функций одной переменной, с разницей лишь в том, что одну из переменных нужно считать в момент дифференцирования константой (постоянным числом).
Формула
Частные производные для функции двух переменных $ z(x,y) $ записываются в следующем виде $ z’_x, z’_y $ и находятся по формулам:
Частные производные первого порядка
$$ z’_x = frac{partial z}{partial x} $$
$$ z’_y = frac{partial z}{partial y} $$
Частные производные второго порядка
$$ z”_{xx} = frac{partial^2 z}{partial x partial x} $$
$$ z”_{yy} = frac{partial^2 z}{partial y partial y} $$
Смешанная производная
$$ z”_{xy} = frac{partial^2 z}{partial x partial y} $$
$$ z”_{yx} = frac{partial^2 z}{partial y partial x} $$
Частная производная сложной функции
а) Пусть $ z (t) = f( x(t), y(t) ) $, тогда производная сложной функции определяется по формуле:
$$ frac{dz}{dt} = frac{partial z}{partial x} cdot frac{dx}{dt} + frac{partial z}{partial y} cdot frac{dy}{dt} $$
б) Пусть $ z (u,v) = z(x(u,v),y(u,v)) $, тогда частные производные функции находится по формуле:
$$ frac{partial z}{partial u} = frac{partial z}{partial x} cdot frac{partial x}{partial u} + frac{partial z}{partial y} cdot frac{partial y}{partial u} $$
$$ frac{partial z}{partial v} = frac{partial z}{partial x} cdot frac{partial x}{partial v} + frac{partial z}{partial y} cdot frac{partial y}{partial v} $$
Частные производные неявно заданной функции
а) Пусть $ F(x,y(x)) = 0 $, тогда $$ frac{dy}{dx} = -frac{f’_x}{f’_y} $$
б) Пусть $ F(x,y,z)=0 $, тогда $$ z’_x = – frac{F’_x}{F’_z}; z’_y = – frac{F’_y}{F’_z} $$
Примеры решений
| Пример 1 |
| Найти частные производные первого порядка $ z (x,y) = x^2 – y^2 + 4xy + 10 $ |
| Решение |
|
Для нахождения частной производной по $ x $ будем считать $ y $ постоянной величиной (числом): $$ z’_x = (x^2-y^2+4xy+10)’_x = 2x – 0 + 4y + 0 = 2x+4y $$ Для нахождения частной производной функции по $ y $ определим $ y $ константой: $$ z’_y = (x^2-y^2+4xy+10)’_y = -2y+4x $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ z’_x = 2x+4y; z’_y = -2y+4x $$ |
| Пример 2 |
| Найти частные производные функции второго порядка $ z = e^{xy} $ |
| Решение |
|
Сперва нужно найти первый производные, а затем зная их можно найти производные второго порядка. Полагаем $ y $ константой: $$ z’_x = (e^{xy})’_x = e^{xy} cdot (xy)’_x = ye^{xy} $$ Положим теперь $ x $ постоянной величиной: $$ z’_y = (e^{xy})’_y = e^{xy} cdot (xy)’_y = xe^{xy} $$ Зная первые производные аналогично находим вторые. Устанавливаем $ y $ постоянной: $$ z”_{xx} = (z’_x)’_x = (ye^{xy})’_x = (y)’_x e^{xy} + y(e^{xy})’_x = 0 + ye^{xy}cdot (xy)’_x = y^2e^{xy} $$ Задаем $ x $ постоянной: $$ z”_{yy} = (z’_y)’_y = (xe^{xy})’_y = (x)’_y e^{xy} + x(e^{xy})’_y = 0 + x^2e^{xy} = x^2e^{xy} $$ Теперь осталось найти смешанную производную. Можно продифференцировать $ z’_x $ по $ y $, а можно $ z’_y $ по $ x $, так как по теореме $ z”_{xy} = z”_{yx} $ $$ z”_{xy} = (z’_x)’_y = (ye^{xy})’_y = (y)’_y e^{xy} + y (e^{xy})’_y = ye^{xy}cdot (xy)’_y = yxe^{xy} $$ |
| Ответ |
| $$ z’_x = ye^{xy}; z’_y = xe^{xy}; z”_{xy} = yxe^{xy} $$ |
| Пример 3 |
| Найти частную производную сложной функции $ z = x^2 + y^2, x = sin t, y = t^3 $ |
| Решение |
|
Находим $ frac{partial z}{partial x} $: $$ frac{partial z}{partial x} = (x^2+y^2)’_x = 2x $$ Находим $ frac{partial z}{partial y} $: $$ frac{partial z}{partial y} = (x^2+y^2)’_y = 2y $$ Теперь ищем $ frac{dx}{dt} $ и $ frac{dy}{dt} $: $$ frac{dx}{dt} = frac{d(sin t)}{dt} = cos t $$ $$ frac{dy}{dt} = frac{d(t^3)}{dt} = 3t^2 $$ Подставляем всё это в формулу и записываем ответ: $$ frac{dz}{dt} = frac{partial z}{partial x} cdot frac{dx}{dt} + frac{partial z}{partial y} cdot frac{dy}{dt} $$ $$ frac{dz}{dt} = 2x cdot cos t + 2y cdot 3t^2 $$ |
| Ответ |
| $$ frac{dz}{dt} = 2x cdot cos t + 2y cdot 3t^2 $$ |
| Пример 4 |
| Пусть $ 3x^3z – 2z^2 + 3yz^2-4x+z-5 = 0 $ задаёт неявную функцию $ F(x,y,z) = 0 $. Найти частные производные первого порядка. |
| Решение |
|
Записываем функцию в формате: $ F(x,y,z) = 3x^3z – 2z^2 + 3yz^2-4x+z-5 = 0 $ и находим производные: $$ z’_x (y,z – const) = (x^3 z – 2z^2 + 3yz^2-4x+z-5)’_x = 3 x^2 z – 4 $$ $$ z’_y (x,y – const) = (x^3 z – 2z^2 + 3yz^2-4x+z-5)’_y = 3z^2 $$ |
| Ответ |
| $$ z’_x = 3x^2 z – 4; z’_y = 3z^2; $$ |
Данный онлайн калькулятор предназначен для решения частных производных первого и второго порядков.
Частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Следовательно, частные производные находятся так же, как и производные функций одной переменной. Частная производная это обобщенное понятие производной, когда в функции содержится несколько переменных.
Калькулятор поможет найти частные производные функции онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step.
: x^a
модуль x: abs(x)
Для того, чтобы найти производную функции
нужно написать в строке: f[x], x. Если Вам требуется
найти производную n-го порядка, то следует написать: f[x], {x, n}. В
том случае, если Вам требуется найти частную производную функции 
— интересующая Вас переменная. Если нужно найти частную производную по
некоторой переменной порядка n, то следует ввести: f[x, y, z,…,t], {j,
n}, где 
Важно подчеркнуть, что калькулятор выдает пошаговое нахождение
производной при нажатии на «Show Steps» в правом верхнем углу
выдаваемого ей ответа.
- Примеры
- x*E^x, x;
- x^3*E^x, {x,17};
- x^3*y^2*Sin[x+y], x;
- x^3*y^2*Sin[x+y], y,
- x/(x+y^4), {x,6}.
Понятие частной производной применимо только к функциям многих переменных. Рассмотрим функцию двух переменных
z=f(x,y).
Частные производные по переменным
и
записываются в виде
∂z∂x
и
∂z∂y
соответственно. Сами частные производные
∂z∂x
и
∂z∂y
также являются функциями двух переменных:
∂z∂xpx,y
и
∂z∂yqx,y
, поэтому от них тоже можно взять производные:
∂p∂x∂∂x∂z∂x∂2z∂x2
∂q∂y∂∂y∂z∂y∂2z∂y2
∂p∂y∂∂y∂z∂x∂2z∂x∂y
∂q∂x∂∂x∂z∂y∂2z∂y∂x
Производные
∂2z∂x2
и
∂2z∂y2
– являются вторыми частными производными функции
по переменным
и
соответственно. Производные
∂2z∂x∂y
и
∂2z∂y∂x
– называются смешанными производными функции
по переменным
,
и
,
соответственно. При условии, что функция
и её смешанные производные
∂2z∂x∂y
и
∂2z∂y∂x
определены в некоторой окрестности точки
M(x0,y0)
и непрерывны в этой точке, выполняется равенство:
∂2z∂x∂y∂2z∂y∂x
По аналогии, можно ввести производные более высоких порядков, например, запись
∂5z∂x2∂y3
означает, что мы должны продифференцировать функцию
по переменной
два раза, а затем по переменной
три раза, т.е. фактически:
∂5z∂x2∂y3∂3∂y3∂2z∂x2∂∂y∂∂y∂∂y∂∂x∂z∂x
Иногда, для обозначения частных производных некоторой функции
z=f(x,y)
используют запись вида:
fx‘(x,y)
и
fy‘(x,y),
указывая переменную по которой происходит дифференцирование. Таким образом можно обозначать и смешанные производные:
fxy”(x,y)
и
fyx”(x,y)
а также вторые производные и производные более высокого порядка:
fxx”(x,y)
и
fxxy”’(x,y)
соответственно. Следующие обозначения эквиваленты:
В нашем онлайн калькуляторе для обозначения частных производных используются символы:
∂z∂x
;
∂z∂y
;
∂5z∂x2∂y3
.
Пример подробного решения, выдаваемого нашим онлайн сервисом, можно посмотреть
здесь.
Частной
производной по x
функции z = f(x,y)
в точке M0(x0,y0)
называется предел
,
если
этот предел существует.
Обозначается эта частная производная
любым из следующих символов:
;
;
.
Частная
производная по x
есть обычная производная от функции
z = f(x,y),
рассматриваемой как функция только от
переменной x
при фиксированном значении переменной
y.
Совершенно
аналогично можно определить частную
производную по y
функции z = f(x,y)
в точке M0(x0,y0):
=
.

В
пространстве XYZ
условие y = y0
описывает плоскость P,
перпендикулярную оси OY
и пересекающую эту ось в точке y0.
Плоскость P пересекается
с графиком функции z = f(x,y),
вдоль некоторой линии L,
как показано на рисунке
1. Тангенс угла между плоскостью XOY
и касательной к линии
L в точке с координатами
x0,y0
равен частной производной по x
функции z = f(x,y)
в этой точке. В этом
состоит геометрический смысл частной
производной.
Аналогичное
заключение можно сделать относительно
частной производной по y.
Приведем
примеры вычисления частных производных.
Как говорилось выше, для вычисления
частной производной по x
функции z = f(x,y)
нужно положить переменную y
равной константе, а при нахождении
частной производной по y
нужно считать константой переменную
x.
Примеры.
1.
.
2.
Если
частные производные функции z = f(x,y)
существуют на некотором множестве, а
точка, в которой вычисляются частные
производные, несущественна, то пользуются
более короткими обозначениями:
.
Сами
частные производные могут являться
функциями от нескольких переменных на
некотором множестве. У этих функций
тоже могут существовать частные
производные по x
и по y.
Они называются вторыми
частными производными
или частными производными
второго порядка и
обозначаются zxx, zyy, zxy
или
.
Согласно определению
;
.
Последняя частная производная второго
порядка называется смешанной. Смешанная
частная производная второго порядка,
вообще говоря, зависит от того, в какой
последовательности берутся переменные,
по которым вычисляется производная.
Так, производная zxy = (zx
)y
может не быть равной zyx = (zy
)x.
Однако существует теорема, утверждающая,
что если смешанные
частные производные второго порядка
непрерывны, то они не зависят от того,
в какой последовательности вычислялись
частные производные по x
и по y.
(Рекомендуем читателю самому убедиться
в справедливости этой теоремы для
функций, рассмотренных в приведенных
выше примерах 1 и 2.)
Отметим
очень важное отличие функции двух
переменных от функции одной переменной.
Из существования первых частных
производных в точке не следует
непрерывность функции в этой точке.
Рассмотрим, например, функцию
.
График
этой функции во всех точках, не
принадлежащих осям координат OX
и OY,
представляет собой плоскость, параллельную
плоскости XOY,
поднятую на 1. Сами эти оси координат
также принадлежат графику рассматриваемой
функции. Очевидно, что в точке (0,0) функция
имеет частные производные по обоим
аргументам, обе равные нулю. Очевидно
также, что в любой окрестности точки
(0,0) можно найти точку M
такую, что f(M) = 1,
в то время как f(0, 0) = 0.
Это означает существование разрыва
функции в точке (0,0). (Пример взят из книги
О.С.Ивашева-Мусатова “Начала математического
анализа”).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
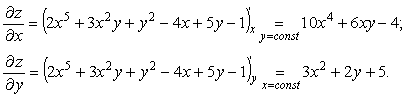

 : x^a
: x^a
