Как найти производную разницы

Производная разности

Определение

Производная разности двух функций равна разности производных каждой из функций: $$ (u-v)’ = (u)’ – (v)’ $$

Эта формула также распространяется на количество функций более двух, например:

$$ (u+v+g)’ = (u)’ + (v)’ + (g)’ $$

Пример 1

Найти производную разности функций $ y = x^4 – 2x^3 – 6 $

Решение

Производная разности равна разности производных: $$ y’ = (x^4 – 2x^3 – 6)’ = (x^4)’ – (2x^3)’ – (6)’ $$ Производные первого и второго слагаемых следует найти по правилу $ (x^p)’ = px^{p-1} $: $$ (x^4)’ = 4x^{4-1} = 4x^3 $$ $$ (2x^3)’ = 2 cdot 3 x^{3-1} = 6x^2 $$ Производная константы равна нулю: $$ (6)’ = 0 $$ Тогда продолжая решение примера: $$ y’ = (x^4 – 2x^3 – 6)’ = (x^4)’ – (2x^3)’ – (6)’ = $$ $$ = 4x^3 – 6x^2 – 0 = 4x^3 – 6x^2 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ y’ = 4x^3 – 6x^2 $$

Пример 2

Найти производную разности двух функций: $ y = sin x – ln 3x – sqrt{2x} $

Решение

Производная от $ sin x $ присутствует в таблице производных: $$ (sin x)’ = cos x $$ Для натурального логарифма есть правило $ (ln x)’ = frac{1}{x} $. Но так как выражение, стоящее под знаком логарифма отличается от $ x $, поэтому нужно ещё дробь домножить на производную от внутренней функции $ 3x $: $$ (ln 3x)’ = frac{1}{3x} cdot (3x)’ = frac{1}{3x} cdot 3 = frac{1}{x} $$ Третья функция является сложной, поэтому сначала находим производную от внешней части, затем от внутренней и перемножаем их: $$ (sqrt{2x})’ = frac{1}{2sqrt{2x}} cdot (2x)’ = frac{1}{2sqrt{2x}} cdot 2 = frac{1}{sqrt{2x}} $$ Подставляем все производные в исходную задачу: $$ y’ = (sin x – ln 3x – sqrt{2x})’ = (sin x)’ – (ln 3x)’ – (sqrt{2x})’ = $$ $$ = cos x – frac{1}{x} – frac{1}{sqrt{2x}} $$

Ответ

$$ y’ = cos x – frac{1}{x} – frac{1}{sqrt{2x}} $$

Правила вычисления производных

7 апреля 2011

• Скачать все правила

Если следовать определению, то производная функции в точке — это предел отношения приращения функции Δy к приращению аргумента Δx:

Вроде бы все понятно. Но попробуйте посчитать по этой формуле, скажем, производную функции f(x) = x
² + (2x + 3) · e

^x
· sin x. Если все делать по определению, то через пару страниц вычислений вы просто уснете. Поэтому существуют более простые и эффективные способы.

Для начала заметим, что из всего многообразия функций можно выделить так называемые элементарные функции. Это относительно простые выражения, производные которых давно вычислены и занесены в таблицу. Такие функции достаточно просто запомнить — вместе с их производными.

Производные элементарных функций

Элементарные функции — это все, что перечислено ниже. Производные этих функций надо знать наизусть. Тем более что заучить их совсем несложно — на то они и элементарные.

Итак, производные элементарных функций:

Название	Функция	Производная
Константа	f(x) = C, C ∈ R	0 (да-да, ноль!)
Степень с рациональным показателем	f(x) = x n	n · x n − 1
Синус	f(x) = sin x	cos x
Косинус	f(x) = cos x	− sin x (минус синус)
Тангенс	f(x) = tg x	1/cos2 x
Котангенс	f(x) = ctg x	− 1/sin2 x
Натуральный логарифм	f(x) = ln x	1/x
Произвольный логарифм	f(x) = log a x	1/(x · ln a)
Показательная функция	f(x) = e x	e x (ничего не изменилось)

Если элементарную функцию умножить на произвольную постоянную, то производная новой функции тоже легко считается:

(C · f)’ = C · f ’.

В общем, константы можно выносить за знак производной. Например:

(2x
³)’ = 2 · (x
³)’ = 2 · 3x
² = 6x
².

Очевидно, элементарные функции можно складывать друг с другом, умножать, делить — и многое другое. Так появятся новые функции, уже не особо элементарные, но тоже дифференцируемые по определенным правилам. Эти правила рассмотрены ниже.

Производная суммы и разности

Пусть даны функции f(x) и g(x), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций:

1. (f + g)’ = f ’ + g ’
2. (f − g)’ = f ’ − g ’

Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, (f + g + h)’ = f ’ + g ’ + h ’.

Строго говоря, в алгебре не существует понятия «вычитание». Есть понятие «отрицательный элемент». Поэтому разность f − g можно переписать как сумму f + (−1) · g, и тогда останется лишь одна формула — производная суммы.

Задача. Найти производные функций: f(x) = x
² + sin x; g(x) = x
⁴ + 2x
² − 3.

Функция f(x) — это сумма двух элементарных функций, поэтому:

f ’(x) = (x
² + sin x)’ = (x
²)’ + (sin x)’ = 2x + cos x;

Аналогично рассуждаем для функции g(x). Только там уже три слагаемых (с точки зрения алгебры):

g ’(x) = (x
⁴ + 2x
² − 3)’ = (x
⁴ + 2x
² + (−3))’ = (x
⁴)’ + (2x
²)’ + (−3)’ = 4x
³ + 4x + 0 = 4x · (x
² + 1).

Ответ:
f ’(x) = 2x + cos x;
g ’(x) = 4x · (x
² + 1).

Производная произведения

Математика — наука логичная, поэтому многие считают, что если производная суммы равна сумме производных, то производная произведения strike“>равна произведению производных. А вот фиг вам! Производная произведения считается совсем по другой формуле. А именно:

(f · g) ’ = f ’ · g + f · g ’

Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.

Задача. Найти производные функций: f(x) = x
³ · cos x; g(x) = (x
² + 7x − 7) · e

^x
.

Функция f(x) представляет собой произведение двух элементарных функций, поэтому все просто:

f ’(x) = (x
³ · cos x)’ = (x
³)’ · cos x + x
³ · (cos x)’ = 3x
² · cos x + x
³ · (− sin x) = x
² · (3cos x − x · sin x)

У функции g(x) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g(x) представляет собой многочлен, и его производная — это производная суммы. Имеем:

g ’(x) = ((x
² + 7x − 7) · e

^x
)’ = (x
² + 7x − 7)’ · e

^x
+ (x
² + 7x − 7) · (e

^x
)’ = (2x + 7) · e

^x
+ (x
² + 7x − 7) · e

^x
= e

^x
· (2x + 7 + x
² + 7x −7) = (x
² + 9x) · e

^x
= x(x + 9) · e

^x
.

Ответ:
f ’(x) = x
² · (3cos x − x · sin x);
g ’(x) = x(x + 9) · e

^x
.

Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию. А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.

Производная частного

Если есть две функции f(x) и g(x), причем g(x) ≠ 0 на интересующем нас множестве, можно определить новую функцию h(x) = f(x)/g(x). Для такой функции тоже можно найти производную:

Неслабо, да? Откуда взялся минус? Почему g
²? А вот так! Это одна из самых сложных формул — без бутылки не разберешься. Поэтому лучше изучать ее на конкретных примерах.

Задача. Найти производные функций:

В числителе и знаменателе каждой дроби стоят элементарные функции, поэтому все, что нам нужно — это формула производной частного:

По традиции, разложим числитель на множители — это значительно упростит ответ:

Ответ:

Производная сложной функции

Сложная функция — это не обязательно формула длиной в полкилометра. Например, достаточно взять функцию f(x) = sin x и заменить переменную x, скажем, на x
² + ln x. Получится f(x) = sin (x
² + ln x) — это и есть сложная функция. У нее тоже есть производная, однако найти ее по правилам, рассмотренным выше, не получится.

Как быть? В таких случаях помогает замена переменной и формула производной сложной функции:

f ’(x) = f ’(t) · t ’, если x заменяется на t(x).

Как правило, с пониманием этой формулы дело обстоит еще более печально, чем с производной частного. Поэтому ее тоже лучше объяснить на конкретных примерах, с подробным описанием каждого шага.

Задача. Найти производные функций: f(x) = e
^{2x + 3}; g(x) = sin (x
² + ln x)

Заметим, что если в функции f(x) вместо выражения 2x + 3 будет просто x, то получится элементарная функция f(x) = e

^x
. Поэтому делаем замену: пусть 2x + 3 = t, f(x) = f(t) = e

^t
. Ищем производную сложной функции по формуле:

f ’(x) = f ’(t) · t ’ = (e

^t
)’ · t ’ = e

^t
· t ’

А теперь — внимание! Выполняем обратную замену: t = 2x + 3. Получим:

f ’(x) = e

^t
· t ’ = e
^{2x + 3} · (2x + 3)’ = e
^{2x + 3} · 2 = 2 · e
^{2x + 3}

Теперь разберемся с функцией g(x). Очевидно, надо заменить x
² + ln x = t. Имеем:

g ’(x) = g ’(t) · t ’ = (sin t)’ · t ’ = cos t · t ’

Обратная замена: t = x
² + ln x. Тогда:

g ’(x) = cos (x
² + ln x) · (x
² + ln x)’ = cos (x
² + ln x) · (2x + 1/x).

Вот и все! Как видно из последнего выражения, вся задача свелась к вычислению производной суммы.

Ответ:
f ’(x) = 2 · e
^{2x + 3};
g ’(x) = (2x + 1/x) · cos (x
² + ln x).

Очень часто на своих уроках вместо термина «производная» я использую слово «штрих». Например, штрих от суммы равен сумме штрихов. Так понятнее? Ну, вот и хорошо.

Таким образом, вычисление производной сводится к избавлению от этих самых штрихов по правилам, рассмотренным выше. В качестве последнего примера вернемся к производной степени с рациональным показателем:

(x

ⁿ
)’ = n · x

^{n − 1}

Немногие знают, что в роли n вполне может выступать дробное число. Например, корень — это x
^0,5. А что, если под корнем будет стоять что-нибудь навороченное? Снова получится сложная функция — такие конструкции любят давать на контрольных работах и экзаменах.

Задача. Найти производную функции:

Для начала перепишем корень в виде степени с рациональным показателем:

f(x) = (x
² + 8x − 7)^0,5.

Теперь делаем замену: пусть x
² + 8x − 7 = t. Находим производную по формуле:

f ’(x) = f ’(t) · t ’ = (t
^0,5)’ · t ’ = 0,5 · t
^−0,5 · t ’.

Делаем обратную замену: t = x
² + 8x − 7. Имеем:

f ’(x) = 0,5 · (x
² + 8x − 7)^−0,5 · (x
² + 8x − 7)’ = 0,5 · (2x + 8) · (x
² + 8x − 7)^−0,5.

Наконец, возвращаемся к корням:

Ответ:

Смотрите также:

1. Вводный урок по вычислению производных степенной функции
2. Уравнение касательной к графику функции
3. Тест к параграфу «Что такое логарифм» (легкий)
4. Комбинаторика в задаче B6: легкий тест
5. Задача B2: лекарство и таблетки
6. Задача B4 про шерсть и свитер

Содержание:

• Формула
• Примеры вычисления производной разности функций

Формула

Производная разности равна разности производных.

Примеры вычисления производной разности функций

Читать дальше: производная произведения (u*v)’.

Нахождение
производной функции непосредственно
по определению часто связано с
определенными трудностями. На практике
функции дифференцируют с помощью ряда
правил и формул.

Пусть
функции u=u(х) и ν=ν(х) – две дифференцируемые
в некотором интервале (a;b) функции.

Теорема
20.2 .
Производная суммы (разности) двух функций
равна сумме (разности) производных этих
функций: (u±ν)’=u’±ν’.

Обозначим
у=u±ν. По определению производной и
основным теоремам о пределах получаем:

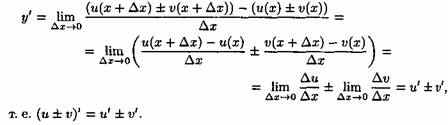
Теорема
справедлива для любого конечного числа
слагаемых.

Теорема
20.3 .
Производная произведения двух функций
равна произведению производной первого
сомножителя на второй плюс произведение
первого сомножителя на производную
второго: (u•ν)’=u’ν+v’u.

т.
е. (u•ν)’=u’•ν+u•ν‘.

При
доказательстве теоремы использовалась
теорема о связи непрерывности и
дифференцируемости: так как функции
u=u(х) и ν=ν(х) дифференцируемы, то они и
непрерывны, поэтому ∆ν→0 и ∆u→0 при
∆х→0.

Можно
показать, что:

а) 
(с•u)’=с•u’, где с = const; 

б) 
(u•ν•w)’=u’v•w+u•v’•w+u•v•w’.  

Теорема
20.4. Производная
частного двух функций   
 если
ν(х)≠0 равна дроби, числитель которой
есть разность произведений знаменателя
дроби на производную числителя и
числителя дроби на производную
знаменателя, а знаменатель есть квадрат
прежнего знаменателя:

Пусть
у=u/v. Тогда

Следствие
20.1.

  

Следствие
20.2.

20.5. Производная сложной и обратной функций

Пусть
у=ƒ(и) и u=φ(х), тогда у=ƒ(φ(х)) — сложная
функция с промежуточным аргументом u и
независимым аргументом х.

Теорема
20.5 .
Если функция u=φ(х) имеет производную
u’_х в
точке х, а функция у=ƒ(u) имеет производную
у’_u в
соответствующей точке u=φ(х), то сложная
функция у=ƒ(φ(х)) имеет производную у’_х в
точке х, которая находится по формуле
у’_х=у’_u-u’_х.

По
условию

Отсюда,
по теореме о связи функции, ее предела
и бесконечно малой функции, имеем

∆у=у’_u•∆u+α*∆u,                                    
(20.6)

где
α→0 при ∆u→0.

Функция
u=φ(х) имеет производную в точке х:

этому

∆u=u¢ _х •∆х+ß•∆х,
где ß→0 при ∆х→0.

Подставив
значение ∆u в равенство (20.6), получим

Δy=y¢ _u(u’_х•∆х+ß*∆х)+а(u’_х•∆х+ß•∆х),

т.е.

∆у=у’u•u’_х•∆х+у’_u•ß•∆х+u’_х•а•∆х+α•ß•∆х.

Разделив
полученное равенство на ∆х и перейдя
к пределу при ∆х→О, получим у’_х=у’_u*u’_х.

Итак,
для нахождения производной сложной
функции надо производную данной функции
по промежуточному аргументу умножыть
на производную промежуточного аргумента
по независимому аргументу.

Это
правило остается в силе, если промежуточных
аргументов несколько. Так, если у=ƒ(u),
u=φ(ν), ν=g(х), то у’_х=у’_u•u’_ν•ν’_х.
Пусть у=ƒ(х) и х=φ(у) — взаимно обратные
функции.

Теорема
20.6 .
Если функция у=ƒ(х) строго монотонна на
интервале (a;b) и имеет неравную нулю
производную ƒ'(х) в произвольной точке
этого интервала, то обратная ей функция
х=φ(у) также имеет производную φ'(у) в
соответствующей точке, определяемую
равенством

Рассмотрим
обратную функцию х=φ(у). Дадим аргументу
у приращение ∆у¹ 0. Ему соответствует
приращение ∆х обратной функции, причем
∆х¹ 0 в силу строгой монотонности
функции у=ƒ(х). Поэтому можно записать

Если
∆у→0, то в силу непрерывности обратной
функции приращение ∆х→0. И так как

то
из (20.7) следуют равенства

Таким
образом, производная
обратной функции равна обратной величине
производной данной функции.

Правило
дифференцирования обратной функции
записывают так:

<<
Пример 20.3

 Найти
производную функции у=log₂³tg
x⁴.

Решение:
Данная функция является сложной. Ее
можно представить в виде цепочки
«простых» функций: у=u³,
где u=Iog₂z,
где z=tgq, где q=х⁴.
По правилу дифференцирования сложной
функции (у’_х=y’_u•u’_z•z’_q•q’_x)
получаем:

<<
Пример 20.4

 Пользуясь  
правилом   дифференцирования  
обратной функции, найти производную
у’_х для
функции  

Решение:
Обратная функция х=у³+1
имеет производную х’_y =3у².

Следовательно,

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #