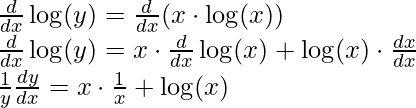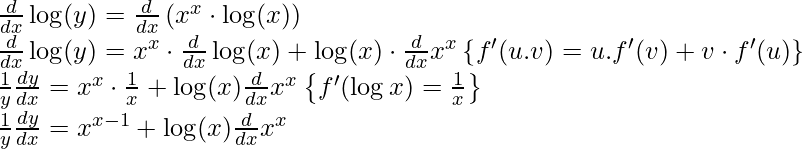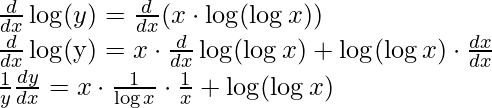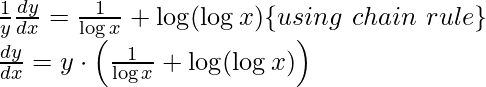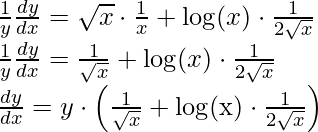Как найти производную с помощью логарифмического дифференцирования

Содержание:

Суть метода логарифмического дифференцирования
Производная показательно-степенной функции

Для функций вида $y(x)=frac{u_{1}(x) cdot u_{2}(x) cdot ldots cdot u_{k}(x)}{v_{1}(x) cdot v_{2}(x) cdot ldots cdot v_{m}(x)}$ для упрощения нахождения
производной рациональнее использовать логарифмическое дифференцирование.

Суть метода логарифмического дифференцирования

Суть такого дифференцирования заключается в следующем: вначале находится
логарифм заданной функции, а уже затем
вычисляется от него производная. Пусть задана некоторая функция
$y=f(x)$. Прологарифмируем левую и правую части данного выражения:

$$ln y=ln f(x)$$

Далее продифференцируем полученное равенство при условии, что
$y$ является функцией от $x$, то есть найдем
производную сложной функции:

$$(ln y)^{prime}=(ln f(x))^{prime} Rightarrow frac{1}{y} cdot y^{prime}=(ln f(x))^{prime}$$

А тогда, выражая искомую производную $y^{prime}$, в
результате имеем:

$$y^{prime}=y cdot(ln f(x))^{prime}$$

Пример

Задание. Найти производную функции
$y=frac{(x+2)^{2}(x-4) sqrt{x^{2}+1}}{(x-2)^{3}(x-4)^{5}}$

Решение. Если находить производную данной функции, используя
таблицу производных и
правила дифференцирования, то процесс будет очень трудоемким. Производную будем находить с помощью логарифмического
дифференцирования. Прологарифмируем левую и правую части заданной функции:

$$ln y=ln frac{(x+2)^{2}(x-4) sqrt{x^{2}+1}}{(x-2)^{3}(x-4)^{5}}$$

Используя свойства логарифмов, преобразуем правую часть полученного равенства к следующему виду:

$$begin{array}{c}
ln frac{(x+2)^{2}(x-4) sqrt{x^{2}+1}}{(x-2)^{3}(x-4)^{5}}= \
=ln left[(x+2)^{2}(x-4) sqrt{x^{2}+1}right]-ln left[(x-2)^{3}(x-4)^{5}right]= \
=ln (x+2)^{2}+ln (x-4)+ln sqrt{x^{2}+1}-ln (x-2)^{3}-ln (x-4)^{5}= \
=2 ln (x+2)+ln (x-4)+frac{1}{2} ln left(x^{2}+1right)-3 ln (x-2)-5 ln (x-4)= \
=2 ln (x+2)-4 ln (x-4)+frac{1}{2} ln left(x^{2}+1right)-3 ln (x-2)
end{array}$$
$$ln y=2 ln (x+2)-4 ln (x-4)+frac{1}{2} ln left(x^{2}+1right)-3 ln (x-2)$$

Дифференцируем левую и правую часть последнего равенства, не забывая, что
$y$ является функцией переменной
$x$:

$$begin{array}{c}
(ln y)^{prime}=left(2 ln (x+2)-4 ln (x-4)+frac{1}{2} ln left(x^{2}+1right)-3 ln (x-2)right)^{prime} \
frac{y^{prime}}{y}=(2 ln (x+2))^{prime}-(4 ln (x-4))^{prime}+left(frac{1}{2} ln left(x^{2}+1right)^{prime}-right. \
-(3 ln (x-2))^{prime}=2(ln (x+2))^{prime}-4(ln (x-4))^{prime}+frac{1}{2}left(ln left(x^{2}+1right)right)^{prime}- \
-3(ln (x-2))^{prime}=2 cdot frac{1}{x+2} cdot(x+2)^{prime}-4 cdot frac{1}{x-4} cdot(x-4)^{prime}+ \
+frac{1}{2} cdot frac{1}{x^{2}+1} cdotleft(x^{2}+1right)^{prime}-3 cdot frac{1}{x-2} cdot(x-2)^{prime}= \
=frac{2}{x+2}-frac{4}{x-4}+frac{x}{x^{2}+1}-frac{3}{x-2}
end{array}$$

Итак,

$$frac{y^{prime}}{y}=frac{2}{x+2}-frac{4}{x-4}+frac{x}{x^{2}+1}-frac{3}{x-2}$$

Отсюда

$$y^{prime}=yleft(frac{2}{x+2}-frac{4}{x-4}+frac{x}{x^{2}+1}-frac{3}{x-2}right)$$

Подставляя вместо функции $y$ ее выражение,
окончательно будем иметь, что

$$y^{prime}=frac{(x+2)^{2} sqrt{x^{2}+1}}{(x-2)^{3}(x-4)^{4}}left(frac{2}{x+2}-frac{4}{x-4}+frac{x}{x^{2}+1}-frac{3}{x-2}right)$$

Ответ. $y^{prime}=frac{(x+2)^{2} sqrt{x^{2}+1}}{(x-2)^{3}(x-4)^{4}}left(frac{2}{x+2}-frac{4}{x-4}+frac{x}{x^{2}+1}-frac{3}{x-2}right)$

Производная показательно-степенной функции

Рационально использовать логарифмическое дифференцирование и при нахождении
производной показательно-степенной
(или степенно-показательной) функции или “функции в степени функция”, то есть в случае, когда заданная функция имеет
вид $y(x)=u(x)^{v(x)}$. Логарифмируем левую и правую часть:

$$ln y(x)=ln u(x)^{v(x)}$$
$$ln y(x)=v(x) cdot ln u(x)$$

Тогда

$$(ln y(x))^{prime}=(v(x) cdot ln u(x))^{prime}$$

Производную в левой части равенства находим как производную сложной функции, а в правой – как производную произведения:

$$begin{array}{c}
frac{y^{prime}(x)}{y(x)}=v^{prime}(x) cdot ln u(x)+v(x) cdot frac{u^{prime}(x)}{u(x)} Rightarrow \
Rightarrow y^{prime}(x)=y(x) cdotleft(v^{prime}(x) cdot ln u(x)+v(x) cdot frac{u^{prime}(x)}{u(x)}right)
end{array}$$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти производную функции $y(x)=(sin x)^{x}$

Решение. Применим логарифмическое дифференцирование:

$$begin{array}{l}
ln y(x)=ln (sin x)^{x} \
ln y(x)=x ln (sin x)
end{array}$$

Тогда, продифференцировав левую и правую часть, будем иметь:

$$begin{array}{c}
(ln y(x))^{prime}=(x ln (sin x))^{prime} \
frac{y^{prime}(x)}{y(x)}=(x)^{prime} cdot ln sin x+x cdot(ln sin x)^{prime}= \
=1 cdot ln sin x+x cdot frac{1}{sin x} cdot(sin x)^{prime}=ln sin x+frac{x}{sin x} cdot cos x= \
=ln sin x+x cdot operatorname{ctg} x
end{array}$$

Отсюда получаем, что

$$y^{prime}(x)=y(x)(ln sin x+x operatorname{ctg} x)=(sin x)^{x} cdot(ln sin x+x operatorname{ctg} x)$$

Ответ. $y^{prime}(x)=(sin x)^{x} cdot(ln sin x+x operatorname{ctg} x)$

Читать дальше: производная степенно-показательной функции.

Источник

Простое объяснение принципов решения логарифмического дифференцирования и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения логарифмического дифференцирования

В некоторых случаях нахождение производной функции значительно упрощается, если сначала произвести логарифмирование исходной функции, а уже затем произвести дифференцирование. Такой приём носит название логарифмического дифференцирования.

Правило нахождения степенно-показательной функции

$(u^{v})' = u^{v}cdotln ucdot v' + vcdot u^{v - 1}cdot u'$

Таблица основных производных

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Подробнее

Примеры решения логарифмического дифференцирования

Задача

Найти производную функции $y = frac{(x^{2} + 2)cdotsqrt[4]{(x - 1)^{3}}cdot e^{x}}{(x + 5)^{3}}$ .

Решение

Найдём логарифм функции

$ln y = ln{x^{2} + 2} + frac{3}{4}ln(x - 1) + x - 3ln(x + 5)$ .

Дифференцируем это равенство по :

$frac{1}{y}y' = frac{1}{x^{2} + 2}cdot2x + frac{3}{4}cdotfrac{1}{x - 1} + 1 - 3cdotfrac{1}{x + 5}$

Выразим :

$y' = ycdotleft(frac{2x}{x^{2} + 2} + frac{3}{4(x - 1)} + 1 - frac{3}{x + 5}right) = frac{(x^{2} + 2)cdotsqrt[4]{(x - 1)^{3}}cdot e^{x}}{(x + 5)^{3}}cdotleft(frac{2x}{x^{2} + 2} + frac{3}{4(x - 1)} + 1 - frac{3}{x + 5}right)$

Ответ

$y' = frac{(x^{2} + 2)cdotsqrt[4]{(x - 1)^{3}}cdot e^{x}}{(x + 5)^{3}}cdotleft(frac{2x}{x^{2} + 2} + frac{3}{4(x - 1)} + 1 - frac{3}{x + 5}right)$

Задача

Найти производную функции $y = (sin2x)^{x^{2} + 1}$ .

Решение

Используя формулу $(u^{v})' = u^{v}cdotln ucdot v' + vcdot u^{v - 1}cdot u'$ , получаем:

$y' = (sin2x)^{x^{2} + 1}cdotlnsin2xcdot2x + (x^{2} + 1)cdot(sin2x)^{x^{2}}cdotcos2xcdot2$

Ответ

$y' = (sin2x)^{x^{2} + 1}cdotlnsin2xcdot2x + (x^{2} + 1)cdot(sin2x)^{x^{2}}cdotcos2xcdot2$

Задача

Найти производную функции $y = lnfrac{x}{1 - x^{4}}$ .

Решение

Найдём логарифм функции

$[ln y = ln{x} - ln(1 - x^{4})]$

Дифференцируем это равенство по :

$[y' = frac{1}{x} - frac{1}{1 - x^{4}}(1 - x^{4})' = frac{1}{x} + frac{4x^{3}}{1 - x^{4}} = frac{1 + 3x^{4}}{x(1 - x^{4})}]$

Ответ

$y' = frac{1 + 3x^{4}}{x(1 - x^{4})}$

Задача

Найти производную функции

$[y = lnfrac{x}{sqrt{1 + x^{2}}}]$

Решение

Найдём логарифм функции

$[ln y = ln{x} - frac{1}{2}ln(1 + x^{2})]$

Дифференцируем это равенство по :

$[y' = frac{1}{x} - frac{1}{2}frac{1}{1 + x^{2}}cdot2x = frac{1}{x(1 + x^{2})}]$

Ответ

$[y' = frac{1}{x(1 + x^{2})}]$

Задача

Найти производную функции

$[y = lnfrac{1 + x}{1 - x}]$

Решение

Найдём логарифм функции

Дифференцируем это равенство по :

$[y' = frac{1}{1 + x}cdot(1 + x)' - frac{1}{1 - x}cdot(1 - x)' = frac{1}{1 + x} + frac{1}{1 - x} = frac{2}{1 - x^{2}}]$

Ответ

$[y' = frac{2}{1 - x^{2}}]$

Задача

Найти производную функции $y = (x + 5)^{2}(2x - 7)^{3}(x - 2)(x + 3)$ .

Решение

Найдём логарифм функции

Дифференцируем это равенство по :

$[frac{1}{y}y' = frac{2}{x + 5} + frac{3}{2x - 7}cdot2 + frac{1}{x - 2} + frac{1}{x + 3}]$

Выразим :

$[y' = ycdotleft(frac{2}{x + 5} + frac{3}{2x - 7}cdot2 + frac{1}{x - 2} + frac{1}{x + 3}right) =]$

$[= (x + 5)^{2}(2x - 7)^{3}(x - 2)(x + 3)cdotleft(frac{2}{x + 5} + frac{3}{2x - 7}cdot2 + frac{1}{x - 2} + frac{1}{x + 3}right)]$

Ответ

$[y' = (x + 5)^{2}(2x - 7)^{3}(x - 2)(x + 3)cdotleft(frac{2}{x + 5} + frac{3}{2x - 7}cdot2 + frac{1}{x - 2} + frac{1}{x + 3}right)]$

Задача

Найти производную функции

$[y = frac{sqrt[4]{x^{2} + 7x - 8}cdotsqrt[6]{x^{4} - 1}}{sqrt[3]{x^{3} - 3x^{2} + x - 4}}]$

Решение

Найдём логарифм функции

$[ln y = frac{1}{4}cdotfrac{1}{x^{2} + 7x - 8}(2x + 7) + frac{1}{6}cdotfrac{1}{x^{4} - 1}4x^{3} -]$

$[-frac{1}{3}cdotfrac{1}{x^{3} - 3x^{2} + x - 4}cdot(3x^{2} - 6x +1)]$

Дифференцируем это равенство по :

$[frac{1}{y}y' = frac{1}{4}cdotfrac{1}{x^{2} + 7x - 8}(2x + 7) + frac{1}{6}cdotfrac{1}{x^{4} - 1}4x^{3} -]$

$[-frac{1}{3}cdotfrac{1}{x^{3} - 3x^{2} + x - 4}cdot(3x^{2} - 6x + 1)]$

Выразим :

$[y' = ycdotfrac{1}{4}cdotfrac{1}{x^{2} + 7x - 8}(2x + 7) + frac{1}{6}cdotfrac{1}{x^{4} - 1}4x^{3} -]$

$[-frac{1}{3}cdotfrac{1}{x^{3} - 3x^{2} + x - 4}cdot(3x^{2} - 6x + 1) =]$

$[y' = frac{sqrt[4]{x^{2} + 7x - 8}cdotsqrt[6]{x^{4} - 1}}{sqrt[3]{x^{3} - 3x^{2} + x - 4}}ast]$

$[ast(frac{1}{4}cdotfrac{1}{x^{2} + 7x - 8}(2x + 7) + frac{1}{6}cdotfrac{1}{x^{4} - 1}4x^{3} -]$

$[-frac{1}{3}cdotfrac{1}{x^{3} - 3x^{2} + x - 4}cdot(3x^{2} - 6x + 1))]$

Ответ

$[y' = frac{sqrt[4]{x^{2} + 7x - 8}cdotsqrt[6]{x^{4} - 1}}{sqrt[3]{x^{3} - 3x^{2} + x - 4}}ast]$

$[ast(frac{1}{4}cdotfrac{1}{x^{2} + 7x - 8}(2x + 7) + frac{1}{6}cdotfrac{1}{x^{4} - 1}4x^{3} -]$

$[-frac{1}{3}cdotfrac{1}{x^{3} - 3x^{2} + x - 4}cdot(3x^{2} - 6x + 1))]$

Задача

Найти производную функции

$[y = x^{x}, (x > 0)]$

Решение

Возьмём натуральные логарифмы от обеих частей равенства, получим:

Дифференцируем это равенство по :

$[frac{1}{y}y' = ln x + frac{1}{x}]$

$[frac{1}{y}y' = ln x + 1]$

Выразим :

$[y' = ycdot(ln x + 1) = x^{x}cdot(ln x + 1)]$

Ответ

$[y' = x^{x}cdot(ln x + 1)]$

Задача

Найти производную функции

$[y = (sin x)^{cos x}, (pi < x > 0)]$

Решение

Возьмём натуральные логарифмы от обеих частей равенства, получим:

Дифференцируем это равенство по :

$[frac{1}{y}y' = -sin xcdotlnsin x + cos xcdotfrac{1}{sin x}cdotcos x]$

Выразим :

$[y' = ycdot(-sin xcdotlnsin x + cos xcdotfrac{1}{sin x}cdotcos x) =]$

$[= (sin x)^{cos x}cdot(-sin xcdotlnsin x + cos xcdotfrac{1}{sin x}cdotcos x) =]$

$[= (sin x)^{cos x}cdotleft(-sin xcdotlncos x + frac{cos^{2}x}{sin x}right)]$

Ответ

$[y' = (sin x)^{cos x}cdotleft(-sin xcdotlncos x + frac{cos^{2}x}{sin x}right)]$

Задача

Найти производную функции

$[y = sqrt{frac{ax + b}{cx + d}}]$

Решение

Найдём логарифм функции

$[ln y = frac{1}{2}left[ln(ax + b) - ln(cx + d)right]]$

Дифференцируем это равенство по :

$[frac{1}{y}y' = frac{1}{2}cdotleft[frac{1}{ax + b}cdot a - frac{1}{cx + d}cdot cright]]$

Выразим :

$[y' = ycdotfrac{1}{2}cdotleft[frac{1}{ax + b}cdot a - frac{1}{cx + d}cdot cright] =]$

$[y' = sqrt{frac{ax + b}{cx + d}}cdotfrac{1}{2}cdotleft[frac{1}{ax + b}cdot a - frac{1}{cx + d}cdot cright] =]$

$[y' = frac{ad - bc}{2(ax + b)(cx + d)}cdotsqrt{{frac{ax + b}{cx + d}}}]$

Ответ

$[y' = frac{ad - bc}{2(ax + b)(cx + d)}cdotsqrt{{frac{ax + b}{cx + d}}}]$

Источник

Когда нам нужно выполнить дифференцирование показательно степенной функции вида y=(f(x))g(x) или преобразовать громоздкое выражение с дробями, можно использовать логарифмическую производную. В рамках этого материала мы приведем несколько примеров применения этой формулы.

Чтобы понять эту тему, необходимо знать, как пользоваться таблицей производных, быть знакомым с основными правилами дифференцирования и представлять себе, что такое производная сложной функции.

Как вывести формулу логарифмической производной

Для получения этой формулы нужно сначала произвести логарифмирование по основанию e, а затем упростить получившуюся функцию, применив основные свойства логарифма. После этого надо вычислить производную неявно заданной функции:

y=f(x)ln y=ln(f(x))(ln y)’=(ln(f(x)))’1y·y’=(ln(f(x)))’⇒y’=y·(ln(f(x)))’

Примеры использования формулы

Покажем на примере, как это делается.

Пример 1

Вычислить производную показательно степенной функции переменной x в степени x.

Решение

Проводим логарифмирование по указанному основанию и получаем ln y=ln xx. С учетом свойств логарифма это можно выразить как ln y=x·ln x. Теперь дифференцируем левую и правую части равенства и получаем результат:

ln y=x·ln xln y’=x·ln x’1y·y’=x’·ln x+·ln x’⇒y’=y·1·ln x+x·1x=y·(ln x+1)=xx·(ln x+1)

Ответ: xx’=xx·(ln x+1)

Такую задачу можно решить и другим способом, без логарифмической производной. Сначала нам надо преобразовать исходное выражение так, чтобы перейти от дифференцирования показательно степенной функции к вычислению производной сложной функции, например:

y=xx=eln xx=ex·ln x⇒y’=(ex·ln x)’=ex·ln x·x·ln x’=xx·x’·ln x+x·(ln x)’==xx·1·ln x+x·1x=xx·ln x+1

Рассмотрим еще одну задачу.

Пример 2

Вычислите производную функции y=x2+13×3·sin x.

Решение

Исходная функция представлена в виде дроби, значит, мы можем решить задачу с помощью дифференцирования. Однако эта функция довольно сложная, значит, преобразований потребуется много. Значит, нам лучше использовать здесь логарифмическую производную y’=y·ln(f(x))’. Поясним, почему такое вычисление удобнее.

Начнем с нахождения ln(f(x)). Для дальнейшего преобразования нам потребуются следующие свойства логарифма:

логарифм дроби можно представить в виде разности логарифмов;
логарифм произведения можно представить в виде суммы;
если у выражения под логарифмом есть степень, мы можем вынести ее в качестве коэффициента.

Преобразуем выражение:

ln(f(x))=ln(x2+1)13×3·sin x12=ln(x2+1)13-ln(x3·sin x)12==13ln(x2+1)-32ln x-12ln sin x

В итоге у нас получилось достаточно простое выражение, производную которого вычислить несложно:

(ln(f(x)))’=13ln(x2+1)-32ln x-12ln sin x’==13ln(x2+1)’-32ln x’-12ln sin x’==13(ln(x2+1))’-32(ln x)’-12(ln sin x)’==13·1×2+1·x2+1′-32·1x-12·1sin x·(sin x)’==13·2xx2+1-32x-cos x2 sin x

Теперь то, что у нас получилось, нужно подставить в формулу логарифмической производной.

Ответ: y’=y·ln(f(x))’=x2+13×3·sin x·13·2xx2+1-32x-cos x2 sin x

Чтобы закрепить материал, изучите еще пару следующих примеров. Здесь будут приведены только вычисления с минимумом комментариев.

Пример 3

Дана показательно степенная функция y=(x2+x+1)x3. Вычислите ее производную.

Решение:

y’=y·(ln(f(x)))’=(x2+x+1)x3·ln(x2+x+1)x3’==(x2+x+1)x3·x3·(x2+x+1)’==(x2+x+1)x3·x3’·ln(x2+x+1)+x3ln(x2+x+1)’==(x2+x+1)x3·3×2·ln(x2+x+1)+x3·1×2+x+1·x2+x+1’==(x2+x+1)x3·3×2·ln(x2+x+1)+x32x+1×2+x+1==(x2+x+1)x3·3×2·ln(x2+x+1)+2×4+x3x2+x+1

Ответ: y’=y·(ln(f(x)))’=(x2+x+1)x3·3×2·ln(x2+x+1)+2×4+x3x2+x+1

Пример 4

Вычислите производную выражения y=x2+13·x+1·x3+14×2+2x+2.

Решение

Применяем формулу логарифмической производной.

y’=y·lnx2+13·x+1·x3+14×2+2x+2’==y·lnx2+13+lnx+1+lnx3+14-lnx2+2x+2’==y·13ln(x2+1)+12lnx+1+14ln(x3+1)-12ln(x2+2x+2)’==y·(x2+1)’3(x2+1)+x+1’2(x+1)+(x3+1)’4×3+1-x2+2x+2’2×2+2x+2==x2+13·x+1·x3+14×2+2x+2·2×3(x2+1)+12(x+1)+3×24(x3+1)-2x+22(x2+2x+2)

Ответ:

y’=x2+13·x+1·x3+14×2+2x+2·2×3(x2+1)+12(x+1)+3×24(x3+1)-2x+22(x2+2x+2).

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Пусть функция
дифференцируема в точкеxи принимает в этой точке положительное
значение. Тогда в окрестности этой точки
существует функцияЭту функцию можно рассматривать как
сложную функцию аргументаxс промежуточным аргументомy.
Продифференцируем эту функцию:

.
Из этого соотношения можно выразить
производную:.
Такая операция нахождения производной
после предварительного логарифмирования
называется логарифмическим
дифференцированием. Существуют функции,
производную которых можно найти только
таким способом. К числу этих функций
относится степенно-показательная
функция,
гдеи– дифференцируемые функции аргументаx. В качестве примера
найдём производную этой функции с
помощью логарифмического дифференцирования.

Прологарифмируем эту функцию:
.

Продифференцируем обе части полученного
равенства:
,
отсюда (т.к.)

Раскрыв скобки, получим окончательную
формулу

(13.1)

Рассмотрим пример конкретной функции.

Пример. Найти производную функции
.

Решение. Можно сразу воспользоваться
формулой (13.1), но можно выполнить
логарифмическое дифференцирование и
непосредственно:

Бывают случаи, когда применение
логарифмического дифференцирования
не необходимо, но целесообразно. Пусть,
например,
.
Конечно, в этом случае можно непосредственно
воспользоваться правилами вычисления
производной, но логарифмическое
дифференцирование упрощает выкладки:

§ 14. Односторонние производные

Производная есть предел разностного
отношения
,
причём этот предел не зависит от
характера стремленияк нулю (может быть как больше, так и меньше нуля,
то есть может стремиться к нулю как
справа, так и слева). Но в ряде случаев
функция может не иметь в заданной точке
производной, хотя в этой точке существует
предел отношенияпри условии, чтостремится к нулю только справа (правый
предел) или только слева (левый предел),
или же существует как правый, так и левый
предел, но они не равны друг другу.
Например, если функция определена на
отрезке, а за пределами этого отрезка
не определена, то на границах отрезка
могут существовать только односторонние
пределы. Такие односторонние пределы
называются односторонними производными.
А именно, если для рассматриваемой
функции в заданной точке существует
правый (левый) предел отношения,
то этот предел называется правой (левой)
производной. Правая производная функцииобозначается символом,
левая – символом.
То есть,.
Выше (см. § 7) уже говорилось о том, что
функцияy==не дифференцируема в точкеx= 0.
Однако в этой точке она имеет как правую,
так и левую производную. Действительно,,.

Если функция
имеет в точкеxпроизводную, то
очевидно, что она имеет в этой точке как
правую, так и левую производную, причём.

Верно и обратное утверждение: если
функция
имеет в точкеxравные между собой
правую и левую производную, то она имеет
в этой точке и производную, причём

§ 15. Производные высших порядков

Пусть функция y=f(x)имеет производную в каждой точке
некоторого интервала. Тогда на этом
интервале производная(x)
есть функция аргументаx. Может
случиться, что в некоторой точкеxэтого интервала функция(x)
в свою очередь имеет производную. Тогда
эту производную называют второй
производной, или производной 2-го порядка
функцииf(x)в точкеx, и обозначают одним из
символов

Предположив, что вторая производная
определена на некотором интервале, т.е.
является на этом интервале функцией
аргумента x, можно аналогичным
образом ввести понятие производной
3-го порядка. Рассуждая аналогичным
образом, можно затем ввести понятие
производной 4-го порядка и т.д. Предположим,
что понятие производной-го
порядка уже определено, и что эта
производная сама имеет производную.
Тогда можно ввести понятие производной-го
порядка от исходной функцииy=f(x),
определив её как производную от
производной-го
порядка. Производнуюn-го
порядка обозначают одним из символов

Пример. Найти производную 4-го порядка
от функции
.

Решение.
.

Источник

Logarithmic differentiation helps to find the derivatives of complicated functions, using the concept of logarithmic. Sometimes finding the differentiation of the function is very tough but differentiating the logarithm of the same function is very easy, then in such cases, the logarithmic differentiation formula is used.

In calculus, the differentiation of some complex functions is found first by taking log and then finding the logarithmic derivative of that function. In this article, we will learn about Logarithmic Differentiation in detail.

What is Logarithmic Differentiation?

Method of finding the derivative of a function by first taking the logarithm and then differentiating is called logarithmic differentiation. This method is specially used when the function is type y = f(x)^g(x). In this type of problem where y is a composite function, we first need to take a logarithm, making the function log (y) = g(x) log (f(x)). This creates a situation where the differentiation of the exponent function was quite tricky but after taking the log on both sides of the equation, we can easily differentiate it using logarithm properties and the chain rule. This method is also known as Composite exponential function differentiation. This approach allows us to calculate the derivative of complex exponential functions efficiently.

Logarithmic differentiation uses the chain rule of differentiation and is generally used to differentiate functions of form f(x)g(x), f(x)/g(x), f(x)^g(x), and others.

Read More: Laws of Logarithms

Logarithmic Differentiation Formula

Logarithmic differentiation of a function f(x) is found by dividing the differentiation of the function, by the function. The formula used is shown below,

d / dx [log f(x)] = f'(x) / f(x)

Logarithmic formulas are very useful in solving logarithmic differentiation. Some of the important logarithmic properties used are,

log XY = log X + log Y
log X/Y = log X – log Y
log X^Y = Y log X
log_YX = (log X) / (log Y)

Note: Logarithmic differentiation rules are only valid for the positive functions only because logarithm of negative function is undefined.

Applications of Log Differentiation

Log differentiation found its application while solving various differentiation problems. Various types of problems where Log Differentiation is used are discussed below,

Product of Functions (Product Rule)

The differentiation of any function which is a product of two functions can easily be calculated using logarithmic differentiation.

Suppose we have to find differentiation of f(x) where, f(x) = g(x) × h(x) then by using concept of logarithmic differentiation,

f(x) = g(x) × h(x)

Taking log on both sides,

log f(x) = log (g(x) × h(x))

log f(x) = log g(x) + log h(x) [Using property log (XY) = log (X) + log (Y)]

Differentiating both sides with respect to x,

d/dx [log f(x)] = d/dx [log g(x)] + d/dx [log h(x)]

f'(x)/f(x) = g'(x)/g(x) + h'(x)/h(x)

f'(x) = f(x) [g'(x)/g(x) + h'(x)/h(x)]

f'(x) = f(x) [(h(x)×g'(x) + g(x)×h'(x))/ (g(x)×h(x))]

f'(x) = g(x)×h(x) [h(x)×g'(x) + g(x)×h'(x)] / g(x)×h(x)

f'(x) = h(x)×g'(x) + g(x)×h'(x)

The result obtained above is the “Leibniz rule” and is commonly known as the “Product rule“.

Division of Functions (Quotient Rule)

The differentiation of any function which is in form of a division of two functions can easily be calculated using logarithmic differentiation.

Suppose one has to find the differentiation of f(x) where f(x) = g(x) / h(x) by using the concept of logarithmic. differentiation,

f(x) = g(x)/h(x)

Taking log on both sides,

log f(x) = log [g(x)/h(x)]

log f(x) = log g(x) – log h(x) [Using property log (X/Y) = log (X) – log (Y)]

Differentiating both sides with respect to x,

d/dx [log f(x)] = d/dx [log g(x)] – d/dx [log h(x)]

f'(x)/f(x) = g'(x)/g(x) – h'(x)/h(x)

f'(x) = f(x)[g'(x)/g(x) – h'(x)/h(x)]

f'(x) = f(x) [(g'(x)×h(x) – g(x)×h'(x))/(g(x)×h(x))]

f'(x) = g(x)/h(x) [g'(x)×h(x) – g(x)×h'(x)]/g(x)×h(x)

f'(x) = [g'(x)×h(x) – g(x)×h'(x)] / h²(x)

The result obtained above is commonly known as the “Quotient rule“.

Exponential Functions

The differentiation of any function which is in exponential form can easily be calculated using logarithmic differentiation.

Suppose we have to find differentiation of f(x) where, f(x) = g(x)^h(x) then by using concept of logarithmic differentiation,

f(x) = g(x)^h(x)

Taking log on both sides

log f(x) = log [g(x)^h(x)]

log f(x) = h(x) × log (g(x)) [Using property log (X^Y) = Ylog (X)]

Differentiating both sides with respect to x,

d/dx [log f(x)] = d/dx [h(x) × log g(x)]

f'(x)/f(x) = h(x) × d/dx log g(x) + log g(x) × d/dx h(x) [Using uv rule of differentiation]

f'(x)/f(x) = h(x) × g'(x)/g(x) + log g(x) × h'(x)

f'(x)/f(x) = [h(x) × g'(x) + g(x) × h'(x) × log g(x)] / g(x)

f'(x) = f(x) [h(x)×g'(x) + g(x)×h'(x)×log g(x)] / g(x)

f'(x) = g(x)^h(x)[h(x)×g'(x) + g(x)×h'(x)×log g(x)] / g(x)

f'(x) = g(x)^h(x)-1 [h(x)×g'(x) + g(x)×h'(x)×log g(x)]

Method to Solve Logarithmic Functions

The steps involved in differentiating a logarithmic function are summarized below,

Take log on both sides,
Use logarithmic properties to simplify the function,
Now differentiate the equation with respect to x,
Simplify the obtained equation,
Substitute back the value of y.

Following the above result one can easily find the differentiation of logarithmic functions.

Also, Check

Advanced Differentiation

Implicit Differentiation

Differentiation and Integration Formula

Solved Examples on Logarithmic Differentiation

Example 1: Find the derivative of x^x.

Solution:

Let y = x^x

Step 1: Taking log on both sides

log(y) = log(x^x)

Step 2: Use logarithmic property to simplify the equation

log(y) = x ⋅ log(x) [Using property log(a^b) = b⋅ log(a)]

Step 3: Now differentiate the equation with respect to x,

$frac{d}{d x} log (y)=frac{d}{d x}(x cdot log (x)) \ frac{d}{d x} log (y)=x cdot frac{d}{d x} log (x)+log (x) cdot frac{d x}{d x} \ frac{1}{y} frac{d y}{d x}=x cdot frac{1}{x}+log (x)$

Step 4: Simplify the obtained equation

$frac{d y}{d x}=y(1+log (x))$

Step 5: Substitute back the value of y

$frac{d y}{d x}=x^{x}(1+log (x))$

Example 2: Find the derivative of $x^{left(x^{x}right)}$ ?

Solution:

Given,

y = $x^{left(x^{x}right)}$

Step 1: Taking log on both sides,

log(y) = log( $x^{left(x^{x}right)}$ )

Step 2: Use logarithmic property to simplify the equation

log(y) = x^x⋅ log(x) [Using property log(a^b) = b⋅ log(a)]

Step 3: Differentiating both sides with respect to x,

$frac{d}{d x} log (y)=frac{d}{d x}left(x^{x} cdot log (x)right) \ frac{d}{d x} log (y)=x^{x} cdot frac{d}{d x} log (x)+log (x) cdot frac{d}{d x} x^{x}left{f^{prime}(u . v)=u . f^{prime}(v)+v cdot f^{prime}(u)right} \ frac{1}{y} frac{d y}{d x}=x^{x} cdot frac{1}{x}+log (x) frac{d}{d x} x^{x} left{f^{prime}(log x)=frac{1}{x}right}\ frac{1}{y} frac{d y}{d x}=x^{x-1}+log (x) frac{d}{d x} x^{x}$

Step 4: Simplify the obtained equation,

Since now we know the derivative of x^x, We will substitute here directly.

$frac{1}{y} frac{d y}{d x}=x^{x-1}+log x cdot x^{x}(1+log x) \ frac{d y}{d x}=yleft(x^{x-1}+log x cdot x^{x}(1+log x)right)$

Step 5: Substitute back the value of y

$frac{d y}{d x}=x^{left(x^{x}right)}left(x^{x-1}+log x cdot x^{x}(1+log x)right)$

Example 3: Find the derivative of y = (log x)^x.

Solution:

Given,

y = (logx)^x

Step 1: Taking log on both sides,

log(y) = log((logx)^x)

Step 2: Use logarithmic property to simplify the equation

log(y) = x ⋅ log(logx) [using property log(a^b) = b⋅ log(a)]

Step 3: Differentiating both sides with respect to x,

$frac{d}{d x} log (y)=frac{d}{d x}(x cdot log (log x)) \ frac{d}{d x} log (mathrm{y})=x cdot frac{d}{d x} log (log x)+log (log x) cdot frac{d x}{d x} \ frac{1}{y} frac{d y}{d x}=x cdot frac{1}{log x} cdot frac{1}{x}+log (log x)$

Step 4: Simplify the obtained equation,

$frac{1}{y} frac{d y}{d x}=frac{1}{log x}+log (log x) { using~chain~rule } \ frac{d y}{d x}=y cdotleft(frac{1}{log x}+log (log x)right)$

Step 5: Substitute back the value of y

$frac{d y}{d x}=(log x)^{x} cdotleft(frac{1}{log x}+log (log x)right)$

Example 4: Find the derivative of y = x^√x.

Solution:

Given,

y = x^√x

Step 1: Taking log on both sides,

log(y) = log(x^√x)

Step 2: Use logarithmic property to simplify the equation

log(y) = √x⋅ log(x) [using property log(a^b) = b⋅ log(a)]

Step 3: Differentiating both sides with respect to x,

$frac{d}{d x} log (y)=frac{d}{d x}(sqrt{x} cdot log (x))\ frac{d}{d x} log (mathrm{y})=sqrt{x} cdot frac{d}{d x} log (mathrm{x})+log (x) cdot frac{d sqrt{x}}{d x}$

Step 4: Simplify the obtained equation,

$frac{1}{y} frac{d y}{d x}=sqrt{x} cdot frac{1}{x}+log (x) cdot frac{1}{2 sqrt{x}} \ frac{1}{y} frac{d y}{d x}=frac{1}{sqrt{x}}+log (x) cdot frac{1}{2 sqrt{x}} \ frac{d y}{d x}=y cdotleft(frac{1}{sqrt{x}}+log (mathrm{x}) cdot frac{1}{2 sqrt{x}}right)$

Step 5: Substitute back the value of y

$frac{d y}{d x}=mathrm{x}^{sqrt{x}} cdotleft(frac{1}{sqrt{x}}+log (mathrm{x}) cdot frac{1}{2 sqrt{x}}right)$

FAQs on Logarithmic Differentiation

Question 1: What is the Formula of Logarithmic Differentiation?

Answer:

Logarithmic Differentiation of a function f(x) is found by dividing the differentiation of the function by the function itself. i.e.

d/dx [log f(x)] = f ‘(x)/f(x)

Logarithmic differentiation of a function is calculated using the chain rule of differentiation. These functions are also used to solve exponential functions.

Question 2: When Logarithmic Differentiation is used?

Answer:

Logarithmic differentiation is used when one need to find the differentiation of the complex function, such as, multiplication or division of two fucntions, a function in power of another function, etc. Logarithmic differentiation solves such types of complex functions very easily.

Question 3: What are the Examples of Log Differentiation?

Answer:

Logarithmic differentiation is used to solve different functions, such as, exponential e^{cos x}, product (x + 5)³ (x² + 2)³, exponent (cos x)^{sin x} , etc.

Question 4: What are the Different Rules of Logarithmic Differentiation?

Answer:

Logarithmic differentiation uses the following rules to obtain the differentiation of the complex functions, such as,

Product Rule

Quotient Rule

Exponential Rule

Источник

Суть метода логарифмического дифференцирования

Производная показательно-степенной функции

Алгоритм решения логарифмического дифференцирования

Примеры решения логарифмического дифференцирования

Как вывести формулу логарифмической производной

Примеры использования формулы

§ 14. Односторонние производные

§ 15. Производные высших порядков

What is Logarithmic Differentiation?

Logarithmic Differentiation Formula

Applications of Log Differentiation

Product of Functions (Product Rule)

Division of Functions (Quotient Rule)

Exponential Functions

Method to Solve Logarithmic Functions

Solved Examples on Logarithmic Differentiation

FAQs on Logarithmic Differentiation

Question 1: What is the Formula of Logarithmic Differentiation?

Question 2: When Logarithmic Differentiation is used?

Question 3: What are the Examples of Log Differentiation?

Question 4: What are the Different Rules of Logarithmic Differentiation?

Вам также может понравиться

Как найти перуанские рисунки на карте

Как найти номер двигателя на сонате

Как найти с какого номера мне звонили

Добавить комментарий Отменить ответ