Алгебра щедра. Зачастую она дает больше,
чем у нее спрашивают.
Ж.Даламбер
Межпредметные связи являются
дидактическим условием и средством глубокого и
всестороннего усвоения основ наук в школе.
Кроме того, они способствуют повышению научного
уровня знаний учащихся, развитию логического
мышления и их творческих способностей.
Реализация межпредметных связей устраняет
дублирование в изучении материала, экономит
время и создаёт благоприятные условия для
формирования общеучебных умений и навыков
учащихся.
Установление межпредметных связей в курсе
физики повышает эффективность политехнической и
практической направленности обучения.
В преподавании математики очень важна
мотивационная сторона. Математическая задача
воспринимается учащимися лучше, если она
возникает как бы у них на глазах, формулируется
после рассмотрения каких-то физических явлений
или технических проблем.
Сколько бы ни говорил учитель о роли практики в
прогрессе математики и о значении математики для
изучения физики, развития техники, но если он не
показывает, как физика влияет на развитие
математики и как математика помогает практике в
решении её проблем, то развитию
материалистического мировоззрения будет
нанесен серьёзный ущерб. Но для того, чтобы
показать, как математика помогает в решении её
проблем, нужны задачи, не придуманные в
методических целях, а возникающие на самом деле в
различных областях практической деятельности
человека
Исторические сведения
Дифференциальное исчисление было создано
Ньютоном и Лейбницем в конце 17 столетия на основе
двух задач:
- о разыскании касательной к произвольной линии;
- о разыскании скорости при произвольном законе
движения.
Еще раньше понятие производной встречалось в
работах итальянского математика Николо Тартальи
(около 1500 – 1557гг.) – здесь появилась касательная
в ходе изучения вопроса об угле наклона орудия,
при котором обеспечивается наибольшая дальность
полета снаряда.
В 17 веке на основе учения Г.Галилея о движении
активно развивалась кинематическая концепция
производной.
Посвящает целый трактат о роли производной в
математике известный учёный Галилео Галилей.
Различные изложения стали встречаться в работах
у Декарта, французского математика Роберваля,
английского ученого Л.Грегори. Большой вклад в
изучение дифференциального исчисления внесли
Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.
Термин «производная» является буквальным
переводом на русский французского слова derive,
которое ввел в1797 году Ж. Лагранж (1736-1813).
И.Ньютон называл производную функцию флюксией,
а саму функцию – флюентой.
Некоторые применения производной в физике
Производная — основное понятие
дифференциального исчисления, характеризующее скорость
изменения функции.
Определяется как предел отношения
приращения функции к приращению ее аргумента при
стремлении приращения аргумента к нулю, если
таковой предел существует.
Таким образом,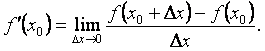 
Значит, чтобы вычислить производную функции f(x)
в точке x0 по определению, нужно:
Рассмотрим несколько физических задач, при
решении которых применяется эта схема.
Задача о мгновенной скорости. Механический
смысл производной
Напомним, как определялась скорость движения.
Материальная точка движется по координатной
прямой. Координата х этой точки есть известная
функция x(t) времени t. За промежуток
времени от t0 до t0 + 
перемещение точки
равно x(t0 + )
– x(t0) – а её средняя скорость такова: 
.
Обычно характер движения бывает таковым, что при
малых , средняя
скорость практически не меняется, т.е. движение с
большой степенью точности можно считать
равномерным. Другими словами, значение средней
скорости при 
стремится
к некоторому вполне определённому значению,
которое называют мгновенной скоростью v(t0)
материальной точки в момент времени t0.
Итак, 
Но по определению 
Поэтому считают, что мгновенная скорость в
момент времени t0 
Коротко говорят: производная координаты по
времени есть скорость. В этом состоит
механический смысл производной.
Аналогично рассуждая, получаем, что
производная от скорости по времени есть
ускорение, т.е. 
Задача о теплоемкости тела
Чтобы температура тела массой в 1г повысилась
от 0 градусов до t градусов, телу необходимо
сообщить определенное количество тепла Q.
Значит, Q есть функция температуры t, до
которой тело нагревается: Q = Q(t). Пусть
температура тела повысилась с t0 до t.
Количество тепла, затраченное для этого
нагревания, равно 
Отношение 
есть количество тепла, которое
необходимо в среднем для нагревания тела на 1
градус при изменении температуры на градусов. Это
отношение называется средней теплоёмкостью
данного тела и обозначается сср.
Т.к. средняя теплоёмкость не дает представления о
теплоёмкости для любого значения температуры Т,
то вводится понятие теплоёмкости при данной
температуре t0 (в данной точке t0).
Теплоемкостью при температуре t0 (в
данной точке) называется предел
Коротко говорят: производная от количества
тепла, получаемого телом, по температуре есть
теплоемкость.
Задача о линейной плотности стержня
Рассмотрим неоднородный стержень.
Стержень называют неоднородным, если на два
участка одинаковой длины приходятся различные
массы.
Для такого стержня встаёт вопрос о скорости
изменения массы в зависимости от его длины.
Средняя линейная плотность 
масса стержня есть функция
его длины х.
Таким образом, линейная плотность
неоднородного стержня в данной точке
определяется следующим образом: 
Коротко говорят: линейная плотность стержня в
точке есть производная массы по длине.
Рассматривая подобные задачи, можно получить
аналогичные выводы по многим физическим
процессам. Некоторые из них приведены в таблице.
|
Функция |
Формула |
Вывод |
| m(t) – зависимость массы расходуемого горючего от времени. |
 |
Производная массы по времени есть скорость расхода горючего. |
| T(t) – зависимость температуры нагреваемого тела от времени. |
 |
Производная температуры по времени есть скорость нагрева тела. |
| m(t) – зависимость массы при распаде радиоактивного вещества от времени. |
  |
Производная массы радиоактивного вещества по времени есть скорость радиоактивного распада. |
| q(t) – зависимость количества электричества, протекающего через проводник, от времени |
 |
Производная количества электричества по времени есть сила тока. |
| A(t) – зависимость работы от времени |  |
Производная работы по времени есть мощность. |
Практические задания:
№1.
Снаряд, вылетевший из пушки, движется по закону
x(t) = – 4t2 + 13t (м). Найти скорость снаряда в
конце 3 секунды.
№2.
Количество электричества, протекающего через
проводник, начиная с момента времени t = 0 c,
задаётся формулой q(t) = 2t2 + 3t + 1 (Кул) Найдите
силу тока в конце пятой секунды.
№3.
Количество тепла Q (Дж), необходимого для
нагревания 1 кг воды от 0o до toС,
определяется формулой Q(t) = t + 0,00002t2 + 0,0000003t3.
Вычислите теплоемкость воды, если t = 100o.
№4.
Тело движется прямолинейно по закону х(t) = 3 + 2t + t2
(м). Определите его скорость и ускорение в моменты
времени 1 с и 3 с.
№ 5.
Найдите величину силы F, действующей на точку
массой m, движущуюся по закону х(t) = t2 – 4t4
(м), при t = 3 с.
№ 6.
Тело, масса которого m = 0,5кг, движется
прямолинейно по закону х(t) = 2t2 + t – 3 (м).
Найдите кинетическую энергию тела через 7 с после
начала движения.
Заключение
Можно указать еще много задач из техники, для
решения которых также необходимо отыскивать
скорость изменения соответствующей функции.
Например, отыскание угловой скорости
вращающегося тела, линейный коэффициент
расширения тел при нагревании, скорость
химической реакции в данный момент времени.
Ввиду обилия задач, приводящих к вычислению
скорости изменения функции или, иначе, к
вычислению предела отношения приращения функции
к приращению аргумента, когда последнее
стремится к нулю, оказалось необходимым выделить
такой предел для произвольной функции и изучить
его основные свойства. Этот предел и назвали производной
функции.
Итак, на ряде примеров мы показали, как
различные физические процессы описываются с
помощью математических задач, каким образом
анализ решений позволяет делать выводы и
предсказания о ходе процессов.
Конечно, число примеров такого рода огромно, и
довольно большая часть из них вполне доступна
интересующимся учащимся.
“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать
материальную сторону жизни людей,
А математика способна достичь всех этих целей”.
Так сказал американский математик Морис
Клайн.
Список литературы :
- Абрамов А.Н., Виленкин Н.Я. и др. Избранные
вопросы математики. 10 класс. – М: Просвещение, 1980. - Виленкин Н.Я., Шибасов А.П. За страницами
учебника математики. – М: Просвещение,1996. - Доброхотова М.А., Сафонов А.Н. Функция, её
предел и производная. – М: Просвещение, 1969. - Колмогоров А.Н., Абрамов А.М. и др. Алгебра и
начала математического анализа. – М:
Просвещение, 2010. - Колосов А.А. Книга для внеклассного чтения
по математике. – М: Учпедгиз, 1963. - Фихтенгольц Г.М. Основы математического
анализа, ч.1 – М: Наука, 1955. - Яковлев Г.Н. Математика для техникумов.
Алгебра и начала анализа, ч.1 – М: Наука, 1987.
- Авторы
- Файлы
- Ключевые слова
- Литература
Родина Е.В.
1
Шунина А.А.
1
Савельева Е.В.
1
1 Ставропольский государственный аграрный университет
1. Письменный Д. Конспект лекций по высшей математике. – М.: Айрис-пресс, 2008.
2. Рольф М. 3000 конкурсных задач по математике. – М.: Айрис-пресс, 1998.
Производная – одно из фундаментальных понятий математики, это основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке).
Еще в древности был решен ряд задач дифференциального исчисления. Архимед, например, разработал способ проведения касательной, применимый для кривых. Само понятие производной возникло в XVII веке в связи с необходимостью решения физических, механических, математических задач, в первую очередь, следующих двух: определение скорости прямолинейного неравномерного движения и построение касательной к произвольной плоской кривой. Первой проблемой занимался великий Исаак Ньютон, второй проблемой – не менее великий Го́тфрид Лейбниц. Независимо друг от друга И. Ньютон и Г. Лейбниц разработали аппарат нахождения производной, которым мы и пользуемся в настоящее время. Благодаря дифференциальному исчислению, был решен целый ряд задач теоретической механики, физики и астрономии. Используя методы дифференциального исчисления, ученые предсказали возвращение кометы Галлея, что было большим триумфом науки XVIII в. Основные понятия дифференциального исчисления долгое время не были должным образом обоснованы. Однако в начале XIX в. французский математик О. Коши дал строгое построение дифференциального исчисления на основе понятия предела.
В наши дни производная играет одну из самых главных ролей в науке и технике: с помощью дифференциального исчисления находят решение большинства задач в различных областях научного познания.
В своей работе мы бы хотели подробнее рассмотреть приложение производной в технике: принцип ее работы, значение. В дальнейшем мы рассмотрим применение производной на примере нескольких задач, касающихся и нашей специальности «Электроэнергетика и электротехника». Очень важно знать, что производная показывает скорость изменения функции, или какого-либо процесса, величины как по времени, так и по другим параметрам.
Так как в практических приложениях обычно интересует не только сама функция, но и скорость ее изменения, то производная, будучи характеристикой скорости изменения, функции, имеет самые широкие практические применения в вопросах физики, химии, геометрии и т.д. Так, например: сила тока есть производная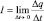 
, где Δq – положительный электрический заряд, переносимый через сечение проводника за время Δt. Примеры задач, в которых используют производную в различных дисциплинах специальности «Электроэнергетика и электротехника».
Количество электричества, протекающее через проводник, начиная с момента времени t = 0, задается формулой Q = 3t2 – 3t + 4 Определить силу тока в конце 6-й секунды.
Для нахождения силы тока используем известные формулы. Сила тока есть производная количества электричества по времени: следовательно, нужно найти производную функции Q = 3t2 – 3t + 4 и вычислить ее значение при t = 6 c. Имеем I = Q′ = 6t – 3, откуда при t = 6 получим I = 6⋅6 – 3 = 33 (A).
Задача о мгновенной величине тока. Обозначим через q = q(t) количество электричества, протекающее через поперечное сечение проводника за время t.
Пусть Δt – некоторый промежуток времени, Δq = q(t + Δt) – q(t) – количество электричества, протекающее через указанное сечение за промежуток времени от момента t до момента t + Δt. Тогда отношение называют средней силой тока. Мгновенной силой тока в момент времени t называется предел отношения приращения количества электричества Δq ко времени Δt, при условии, что Δt → 0.
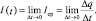
При изучении механического смысла производной пользуемся механическим истолкованием производной: скорость движения материальной точки в данный момент времени равна производной пути по времени, т.е.
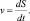
Ускорение движущегося тела представляет собой скорость изменения его скорости, т.е.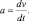 
Точка движется по окружности радиуса 4 м по закону S = 4,5t3, где S – путь в метрах, t – время в секундах. Найдем модуль ускорения 
точки в момент времени Т, когда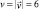 
м/с.
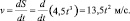
По условию v = 6 м/с, значит, 13,5t2 = 6, t2 = 6/13,5,, t2 = 60/135, t2 = 4/9.
Таким образом
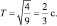
Касательное ускорение
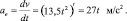
при t = T = 2/3 с; at = 27⋅2/3 = 18 м/с2.
Нормальное ускорение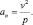 
Так как v = 6 м/с, p = r = 4 м то an = 62/4 = 9 м/с2.
Модуль полного ускорения точки:
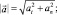
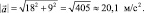
Умение дифференцировать позволяет исследовать различные функции. Используя задачи общетехнических и специальных дисциплин, мы формируем понимание глубокой общности в применении математического аппарата к широкому кругу разнообразных явлений природы
Мощность в переменном сопротивлении r2 определяется формулой P2 = IU – I2⋅r1, где r1 – const, v – const,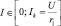 
. Определить, при каком значении тока I получается наибольшее значение мощности P2.
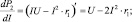
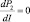при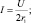 
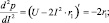–2r1 < 0.
Значит, наибольшее значение мощности P2 при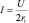 
.
В заключении хотелось бы сказать о том, что энергетика, безусловно, является одним из приоритетных направлений развития общества и государства. При этом развитие цивилизации неразрывно связано с увеличением электропотребления, что, к сожалению, приводит к истощению природных ресурсов. Главнейшей задачей человечества становится предотвращение глобальной проблемы – экологической катастрофы. Ученые всех стран на теории и практике пытаются найти решение. В своих опытах они полагаются на такие дисциплины, как физика, экология, математика (в частности, применение производной).
Задачи, рассмотренные в работе, применительно относятся к специальности: «Электроэнергетика и электротехника», так как позволяют узнать и применить производную в ее широком смысле.
В наше время, в связи с научно-техническим прогрессом, в частности с быстрой эволюцией вычислительных систем, дифференциальное исчисление становится все более актуальным в решении как простых, так и сверхсложных задач. Таким образом, производная играет исключительную роль в электроэнергетике. Благодаря приложению производной в электроэнергетике, становится возможным решение множества задач, касающихся таких тем, как «Применение альтернативных источников энергии», «Измерение физических величин: мощности тока, индуктивности, емкостного напряжения», «Влияние электроэнергетики на окружающую среду».
Библиографическая ссылка
Родина Е.В., Шунина А.А., Савельева Е.В. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ В ЭЛЕКТРОЭНЕРГЕТИКЕ // Современные наукоемкие технологии. – 2013. – № 6.
– С. 86-88;
URL: https://top-technologies.ru/ru/article/view?id=31995 (дата обращения: 15.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
а конкретно вопрос такой:
функция f(x) определяет число электрических зарядов, протекающих через поперечное сечение проводника за время x. Что в этом случае определяет производная f'(x)?
варианты
А – потенциал поперечного сечения проводника в момент времени x относительно нулевого потенциала;
Б – силу тока, проходящую через поперечное сечение проводника в момент времени x ;
В – среднее значение потенциала поперечного сечения проводника за время x относительно нулевого потенциала;
Г – среднее значение силы тока через поперечное сечение проводника в момент времени x
Что такое производная силы тока?
Знаток
(450),
закрыт
2 года назад
Собака Некрещённая ТРУША
Ученик
(103)
1 год назад
Сама по себе сила тока это производная от заряда по времени, то есть можно провести аналогию с кинематикой: заряд Q, который был передан за время t – это как путь S, пройденный за время t. Сила тока I = dQ/dt – скорость переноса заряда в данный момент времени dt, аналогия – механическая скорость v = dS/dt.
Ну тогда логично предположить, что производная от силы тока будет второй производной от заряда по времени, а значит она будет иметь физический смысл, аналогичный второй производной от расстояния по времени: d2S/dt2 = a.
То есть, вычислив производную от силы тока по времени, Вы сможете получить своеобразное “ускорение переноса электрического заряда”.
Ну или, если говорить проще, получите скорость изменения силы тока за единицу времени (о чем в этом треде несколько раз писали до меня)
В этой статье мы раскроем физический смысл понятия производной. Для этого рассмотрим пример, подтолкнувший Ньютона к созданию дифференциального и интегрального исчисления (вместе с Лейбницем, который подошел к этому вопросу с математической точки зрения).
Классическое определение производной
Рассмотрим функцию одной переменной y=f(x)y=f(x). Функция ff устанавливает зависимость между величинами xx и yy. Каждому значению независимой переменной xx ставится в соответствие определенное значение величины yy (yy есть функция от xx). Выберем теперь любое значение xx и обозначим его через x0x_0. Этому значению соответствует величина y0y_0: y0=f(x0)y_0=f(x_0). Придадим значению x0x_0 какое-то приращение ΔxDelta x и рассмотрим точку x0+Δxx_0+Delta x. Этой точке будет соответствовать величина f(x0+Δx)f(x_0+Delta x). Рассмотрим такое отношение:
f(x0+Δx)−f(x0)Δxfrac{f(x_0+Delta x)-f(x_0)}{Delta x}
Теперь нужно устремить приращение ΔxDelta x к нулю (перейти к пределу при Δx→0Delta xrightarrow 0) и мы получим значение производной функции f(x)f(x) в точке x0x_0:
f′(x0)=limΔx→0f(x0+Δx)−f(x0)Δx.f'(x_0)=displaystylelim_{Delta xto 0}frac{f(x_0+Delta x)-f(x_0)}{Delta x}.
Осталось сказать, что значение x0x_0 мы выбирали произвольно и на его месте могла быть любая другая точка. Так что можно убрать нулевой индекс возле x0x_0 и написать просто:
f′(x)=limΔx→0f(x+Δx)−f(x)Δx.f'(x)=displaystylelim_{Delta xto 0}frac{f(x+Delta x)-f(x)}{Delta x}.
Это и есть производная функции f(x)f(x) в любой точке xx. Такую формулу вы видите почти во всех учебниках по математическому анализу (другое название дифференциального и интегрального исчисления). Ее часто бывает удобно переписать в следующем виде:
f′(x)=dydxf'(x)=frac{dy}{dx},
где буква dd обозначает бесконечно малое приращение, а величины dydy и dxdx называют дифференциалами соответственно величин yy и xx.
Это отношение приращения функции к приращению аргумента (независимой переменной), при условии, что последнее стремится к нулю (становится сколь угодно малым).
Для тех, кто хоть немного представляет себе использование различных функций в физике, станет очевидным и физический смысл производной. Это просто скорость изменения какой то величины (функции).
Новый взгляд на понятие производной
Рассмотрим задачу, к которой приходят, как только начинают изучать физику. Это задача о движении тела и одной из главных его характеристик – скорости. Предположим (для простоты), что тело движется вдоль прямой и за время t=10t=10 с прошло расстояние l=50l=50 м. Что можно сказать о скорости vv данного тела? Простейшая формула физики говорит:
v=lt.v=frac{l}{t}.
В нашем случае получаем, что v=5v=5 м/c. Казалось бы, что такая простая задача может иметь общего с производной и функциями? Из формулы v=l/tv=l/t можно выразить путь, который тело, двигаясь со скоростью vv, проходит за время tt:
l=vt.l=vt.
Смотрите, у нас есть функция l=l(t)l=l(t) – зависимость пройденного пути от времени. Давайте теперь попробуем найти производную от этой функции по ее аргументу (то есть по времени). Найдем величину:
l′(t)=dldt=limΔt→0l(t+Δt)−l(t)Δt.displaystyle l'(t)=frac{dl}{dt}=lim_{Delta tto 0}frac{l(t+Delta t)-l(t)}{Delta t}.
Мы взяли и разделили приращение функции (бесконечно малого пути dldl, проходимого телом за бесконечно малое время dtdt) на приращение аргумента (время движения dtdt): разделили пройденное расстояние на время движения. Это и есть скорость движения. Мы даже видим, что размерность производной будет м/c. Таким образом, становится ясно, что производная действительно является скоростью изменения функции при изменении аргумента. В нашем случае в роли функции выступает путь, а в роли аргумента – время. Однако мы рассмотрели самый простой случай движения – с постоянной скоростью. Но самое интересное состоит в том, что какое бы сложное движение мы ни брали, его скорость всегда будет определяться как производная. Тут необходимо сделать некоторые обобщения. Например, если местоположение тела (материальной точки) задается радиус-вектором r(t){r}(t) как функция времени, то скорость этого тела v(t){v}(t) тоже будет вектором и по определению равна:
v(t)=dr(t)dt=limΔt→0r(t+Δt)−r(t)Δt.displaystyle {v}(t)=frac{d{r}(t)}{dt}=lim_{Delta tto 0}frac{{r}(t+Delta t)-{r}(t)}{Delta t}.
Этот пример можно было бы назвать самым типичным и наглядным для понимания физического смысла производной. Именно так и поступают многие авторы книг по математике и физике. Но существует масса других примеров. Производные встречаются на каждом шагу в разных разделах физики. Давайте рассмотрим еще некоторые из них. Просто для того, чтобы оценить всю важность понятия производной.
Другие примеры производных в физике
Вектор ускорения материальной точки – это производная от вектор-функции скорости точки по времени:
a=dfvdt{a}=frac{df{v}}{dt}
Плотность объемного тела определяется как производная от массы данного тела по объему, занимаемому этой массой:
ρ=dmdVrho=frac{dm}{dV}
Вектор силы, действующий на тело, равен производной от вектора импульса тела по времени:
F=dpdt{F}=frac{d{p}}{dt}
В этом утверждение состоит основной закон нерелятивистской динамики – второй закон Ньютона.
Мощность равна производной от работы по времени:
P=dAdtP=frac{dA}{dt}
Теплоемкость – это производная от количества теплоты по температуре:
C=dQdTC=frac{dQ}{dT}
Сила тока равна производной от заряда, проходящего в проводнике по времени:
I=dqdtI=frac{dq}{dt}
Как видите, производная – это очень важное и полезное понятие. Она позволяет формулировать многие физические утверждения и законы математически строго, точно, кратко и красиво.
