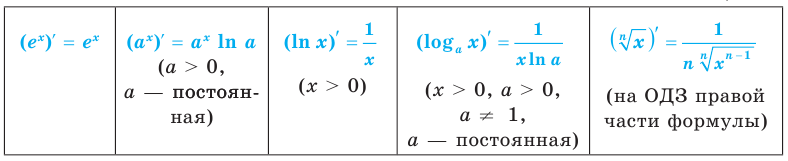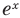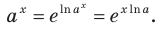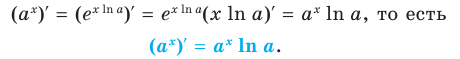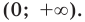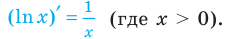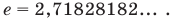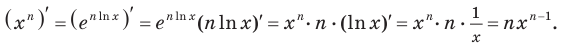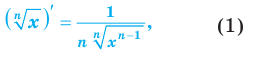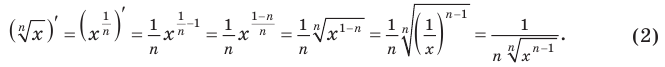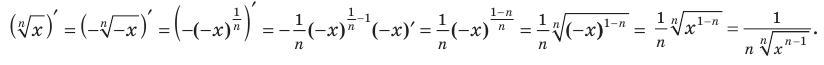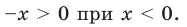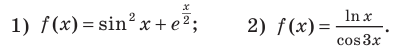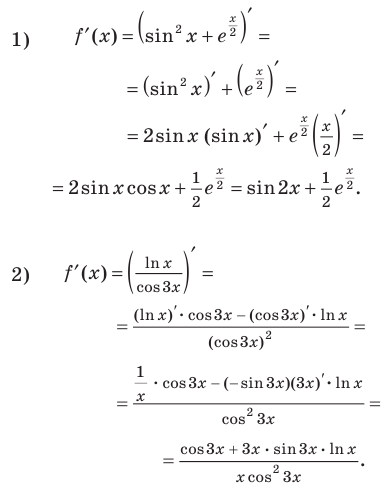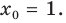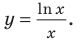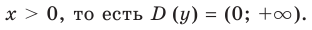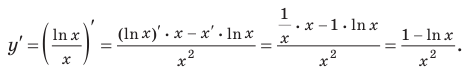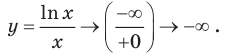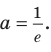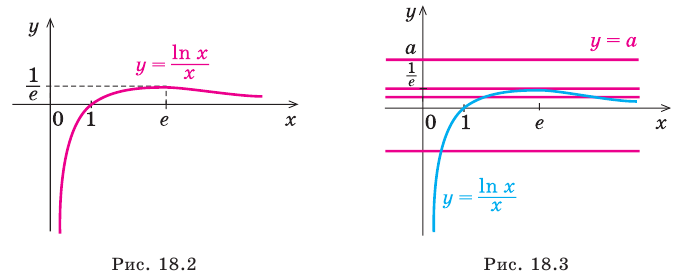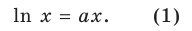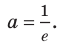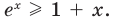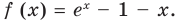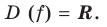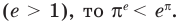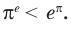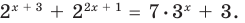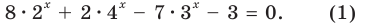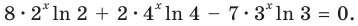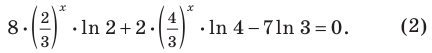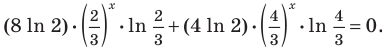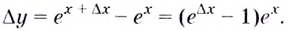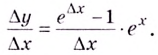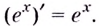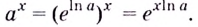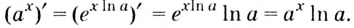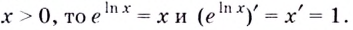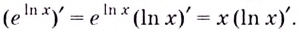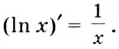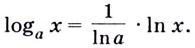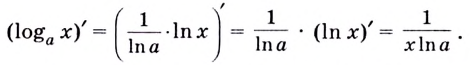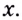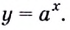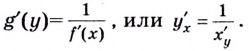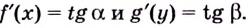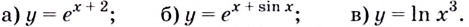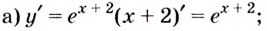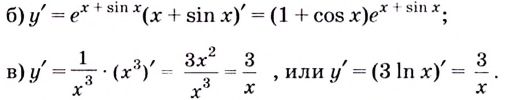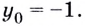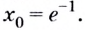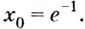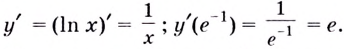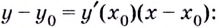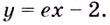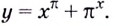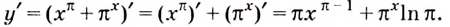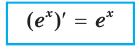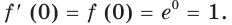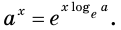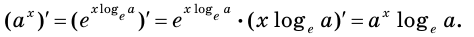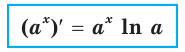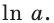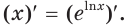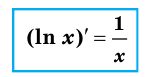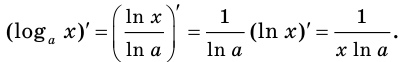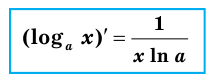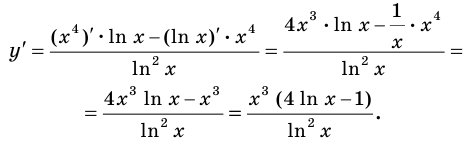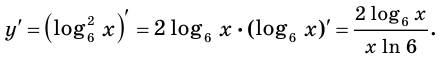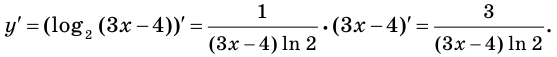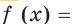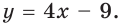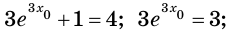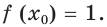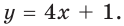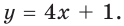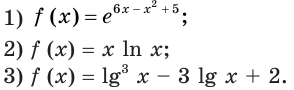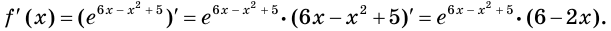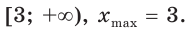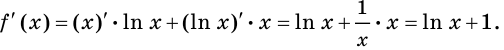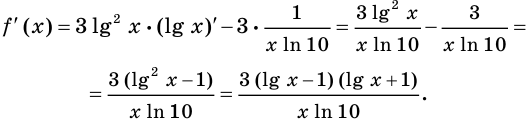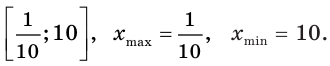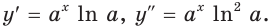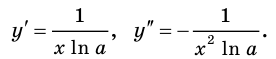Содержание:
- 1-ый способ
- 2-ой способ
- 3-ий способ
Определение
Степенно-показательной функцией (или показательно-степенной, или
функцией в степени функция) называется функция вида
$y(x)=u(x)^{v(x)}$
Рассмотрим способы нахождения ее производной.
1-ый способ
Применяя формулу:
$$left(u(x)^{v(x)}right)^{prime}=v(x) cdot u(x)^{v(x)-1} cdot u^{prime}(x)+u(x)^{v(x)} cdot ln u(x) cdot v^{prime}(x)$$
То есть вначале производная берется как от степенной функции, а потом как от показательной.
Замечание
Порядок следования слагаемых неважен: можно вначале взять производную от показательной функции, а
затем как от степенной, так как от перестановки слагаемых сумма не меняется:
$$left(u(x)^{v(x)}right)^{prime}=u(x)^{v(x)} cdot ln u(x) cdot v^{prime}(x)+v(x) cdot u(x)^{v(x)-1} cdot u^{prime}(x)$$
Пример
Задание. Найти производную функции
$y(x)=(operatorname{arctg} x)^{x}$
Решение. Применяем формулу. В рассматриваемом случае
$u(x)=operatorname{arctg} x, v(x)=x$
Тогда имеем:
$$begin{array}{c}
y^{prime}(x)=left((operatorname{arctg} x)^{x}right)^{prime}=x cdot(operatorname{arctg} x)^{x-1} cdot(operatorname{arctg} x)^{prime}+ \
+(operatorname{arctg} x)^{x} cdot ln operatorname{arctg} x cdot(x)^{prime}=x cdot(operatorname{arctg} x)^{x-1} cdot frac{1}{1+x^{2}}+ \
quad+(operatorname{arctg} x)^{x} cdot ln operatorname{arctg} x cdot 1= \
=frac{x(operatorname{arctg} x)^{x-1}}{1+x^{2}}+(operatorname{arctg} x)^{x} cdot ln operatorname{arctg} x= \
=(operatorname{arctg} x)^{x}left(frac{x}{operatorname{arctg} x cdotleft(1+x^{2}right)}+ln operatorname{arctg} xright)
end{array}$$
Ответ. $y^{prime}(x)=(operatorname{arctg} x)^{x}left(frac{x}{operatorname{arctg} x cdotleft(1+x^{2}right)}+ln operatorname{arctg} xright)$
2-ой способ
С помощью логарифмического дифференцирования:
$$begin{array}{c}
y(x)=u(x)^{v(x)} \
ln y(x)=ln u(x)^{v(x)} \
ln y(x)=v(x) cdot ln u(x) \
(ln y(x))^{prime}=(v(x) cdot ln u(x))^{prime} \
frac{y^{prime}(x)}{y(x)}=v^{prime}(x) cdot ln u(x)+v(x) cdot(ln u(x))^{prime} Rightarrow \
Rightarrow y^{prime}(x)=y(x)left[v^{prime}(x) cdot ln u(x)+v(x) cdot(ln u(x))^{prime}right]= \
=u(x)^{v(x)}left[v^{prime}(x) cdot ln u(x)+v(x) cdot(ln u(x))^{prime}right]
end{array}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти производную функции $y(x)=(operatorname{arctg} x)^{x}$ с помощью логарифмического дифференцирования.
Решение. Прологарифмируем левую и правую часть заданной функции, будем иметь:
$$ln y(x)=ln (operatorname{arctg} x)^{x}$$
По свойствам логарифмов в правой части полученного равенства степень подлогарифмической функции выносим перед логарифмом:
$$ln y(x)=x ln (operatorname{arctg} x)$$
Дифференцируем левую и правую часть равенства. Слева берем
производную как от сложной функции (так как
$y$ – это функция от переменной
$x$), а справа – как
производную произведения:
$$begin{array}{c}
(ln y(x))^{prime}=(x ln (operatorname{arctg} x))^{prime} \
frac{y^{prime}(x)}{y(x)}=(x)^{prime} cdot ln (operatorname{arctg} x)+x cdot(ln (operatorname{arctg} x))^{prime}= \
=1 cdot ln (operatorname{arctg} x)+x cdot frac{1}{operatorname{arctg} x} cdot(operatorname{arctg} x)^{prime}= \
=ln (operatorname{arctg} x)+frac{x}{operatorname{arctg} x} cdot frac{1}{1+x^{2}}=ln (operatorname{arctg} x)+frac{x}{operatorname{arctg} x cdotleft(1+x^{2}right)}
end{array}$$
А тогда
$$begin{array}{c}
y^{prime}(x)=y(x)left(ln (operatorname{arctg} x)+frac{x}{operatorname{arctg} x cdotleft(1+x^{2}right)}right)= \
=(operatorname{arctg} x)^{x}left(ln (operatorname{arctg} x)+frac{x}{operatorname{arctg} x cdotleft(1+x^{2}right)}right)
end{array}$$
Ответ. $y^{prime}(x)=(operatorname{arctg} x)^{x}left(ln (operatorname{arctg} x)+frac{x}{operatorname{arctg} x cdotleft(1+x^{2}right)}right)$
3-ий способ
Представим функцию $y(x)=u(x)^{v(x)}$ в следующем виде
(используются свойства логарифмов):
$$y(x)=u(x)^{v(x)}=e^{ln u(x)^{w(x)}}=e^{v(x) ln u(x)}$$
Тогда
$$begin{array}{c}
y^{prime}(x)=left(e^{v(x) ln u(x)}right)^{prime}=e^{v(x) ln u(x)} cdot(v(x) ln u(x))^{prime}= \
=e^{v(x) ln u(x)} cdotleft[v^{prime}(x) cdot ln u(x)+v(x) cdot(ln u(x))^{prime}right]= \
=u(x)^{v(x)} cdotleft[v^{prime}(x) cdot ln u(x)+v(x) cdot(ln u(x))^{prime}right]
end{array}$$
Пример
Задание. Найти производную функции $y(x)=(operatorname{arctg} x)^{x}$
Решение. Представляем функцию в следующем виде:
$$y(x)=(operatorname{arctg} x)^{x}=e^{ln (operatorname{arctg} x)^{x}}=e^{x ln (operatorname{arctg} x)}$$
Далее находим производную, от экспоненты берем производную как от сложной функции (см.
производные сложных функций):
$$y^{prime}(x)=left(e^{x ln operatorname{arctg} x}right)^{prime}=e^{x ln operatorname{arctg} x} cdot(x cdot ln operatorname{arctg} x)^{prime}=$$
$$=(operatorname{arctg} x)^{x}left[(x)^{prime} cdot ln operatorname{arctg} x+x cdot(ln operatorname{arctg} x)^{prime}right]=$$
$$=(operatorname{arctg} x)^{x}left[1 cdot ln operatorname{arctg} x+x cdot frac{1}{operatorname{arctg} x} cdot(operatorname{arctg} x)^{prime}right]=$$
$$=(operatorname{arctg} x)^{x}left[ln operatorname{arctg} x+frac{x}{operatorname{arctg} x} cdot frac{1}{1+x^{2}}right]=$$
$$=(operatorname{arctg} x)^{x}left[ln operatorname{arctg} x+frac{x}{operatorname{arctg} x cdotleft(1+x^{2}right)}right]$$
Ответ. $y^{prime}(x)=(operatorname{arctg} x)^{x}left(ln (operatorname{arctg} x)+frac{x}{operatorname{arctg} x cdotleft(1+x^{2}right)}right)$
Читать дальше: основные теоремы дифференциального исчисления.
В данной публикации мы рассмотрим, чему равна производная степенной функций (в т.ч. сложной), а также разберем примеры решения задач для закрепления изложенного материала.
-
Формула производной степенной функции
- Производная сложной степенной функции
- Примеры задач
Формула производной степенной функции
Для функции f(x) = x n, где n – действительное число, справедливо следующее выражение:
f ‘(x) = (x n)‘ = nx n-1
Т.е. производная степенной функции равняется произведению показателя степени на основание в степени, уменьшенной на единицу.
n – может быть как положительным, так и отрицательным числом (в т.ч. дробным):
Производная сложной степенной функции
В сложной функции вместо x представлено более сложное выражение. Производная такой функции определяется по формуле:
(y n)‘ = ny n-1 ⋅ y ‘
Примеры задач
Задание 1:
Вычислите производную функцию f(x) = x3/5.
Решение:
Согласно правилам дифференцирования константу в виде дроби можно вынести за знак производной:
Применив формулу производной, рассмотренную выше, получаем:
Задание 2:
Найдите производную функции f(x) = x2 + √x – 6.
Решение:
Первоначальный вид производной функции:
f ‘(x) = (x2 + √x – 6)‘.
С учетом правила дифференцирования суммы получаем:
f ‘(x) = (x2)‘ + (√x)‘ – (6)‘.
Остается только вычислить производные по отдельности:
(x2)‘ = 2x2-1 = 2x
(-6)‘ = 0 (производная константы равна нулю)
Таким образом получаем:
Как считать производную степенной функции
3 февраля 2015
Этим видео я начинаю длинную серию уроков, посвященную производным. Этот урок состоит из нескольких частей.
В первую очередь, я расскажу вам, что вообще такое производные и как их считать, но не мудреным академическим языком, а так, как я сам это понимаю и как объясняю своим ученикам. Во-вторых, мы рассмотрим простейшее правило для решения задач, в которых будем искать производные суммы, производные разности и производные степенной функции.
Мы рассмотрим более сложные комбинированные примеры, из которых вы, в частности, узнаете, что подобные задачи, содержащие корни и даже дроби, могут быть решены при использовании формулы производной степенной функции. Кроме того, конечно, будет множество задач и примеров решений самого разного уровня сложности.
Вообще, изначально я собирался записать коротенький 5-минутный ролик, но сами видите, что из этого получилось. Поэтому хватит лирики — приступаем к делу.
Что такое производная?
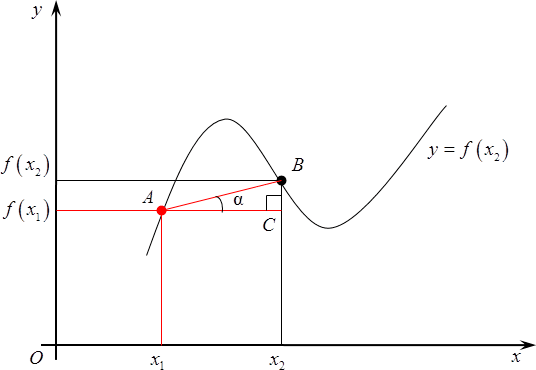
Итак, начнем издалека. Много лет назад, когда деревья были зеленее, а жизнь была веселее, математики задумались вот над чем: рассмотрим простую функцию, заданную своим графиком, назовем ее $y=fleft( x right)$. Разумеется, график существует не сам по себе, поэтому нужно провести оси $x$, а также ось $y$. А теперь давайте выберем любую точку на этом графике, абсолютно любую. Абсциссу назовем ${{x}_{1}}$, ордината, как не трудно догадаться, будет $fleft( {{x}_{1}} right)$.
Рассмотрим на том же графике еще одну точку. Не важно, какую, главное, чтобы она отличалась от первоначальной. У нее, опять же, есть абсцисса, назовем ее ${{x}_{2}}$, а также ордината — $fleft( {{x}_{2}} right)$.
Итак, мы получили две точки: у них разные абсциссы и, следовательно, разные значения функции, хотя последнее — необязательно. А вот что действительно важно, так это что, что из курса планиметрии нам известно: через две точки можно провести прямую и, причем, только одну. Вот давайте ее и проведем.
А теперь проведем через самую первую из них прямую, параллельную оси абсцисс. Получим прямоугольный треугольник. Давайте его обозначим $ABC$, прямой угол $C$. У этого треугольника возникает одно очень интересное свойство: дело в том, что угол$alpha $, на самом деле, равен углу, под которым пересекается прямая $AB$ с продолжением оси абсцисс. Судите сами:
- прямая $AC$параллельна оси $Ox$ по построению,
- прямая $AB$ пересекает $AC$ под $alpha $,
- следовательно, $AB$ пересекает $Ox$под тем же самым $alpha $.
Что мы можем сказать об $text{ }!!alpha!!text{ }$? Ничего конкретного, разве что в треугольнике $ABC$отношение катета $BC$ к катету $AC$ равно тангенсу этого самого угла. Так и запишем:
[tg=frac{BC}{AC}]
Разумеется, $AC$ в данном случае легко считается:
[AC={{x}_{2}}-{{x}_{1}}]
Точно также и $BC$:
[BC=fleft( {{x}_{2}} right)-fleft( {{x}_{1}} right)]
Другими словами, мы можем записать следующее:
[operatorname{tg}text{ }!!alpha!!text{ }=frac{fleft( {{x}_{2}} right)-fleft( {{x}_{1}} right)}{{{x}_{2}}-{{x}_{1}}}]
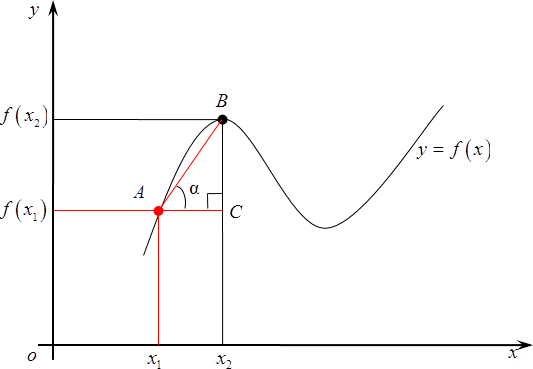
Теперь, когда мы все это выяснили, давайте вернемся к нашему графику и рассмотрим новую точку $B$. Сотрем старые значения и возьмем и возьмем $B$ где-нибудь поближе к ${{x}_{1}}$. Вновь обозначим ее абсциссу за ${{x}_{2}}$, а ординату — $fleft( {{x}_{2}} right)$.
Вновь рассмотрим наш маленький треугольник $ABC$и $text{ }!!alpha!!text{ }$ внутри него. Совершенно очевидно, что это будет уже совсем другой угол, тангенс будет также другим потому, что длины отрезков $AC$ и $BC$ существенно изменились, а формула для тангенса угла нисколько не поменялась — это по-прежнему соотношение между изменением функции и изменением аргумента.
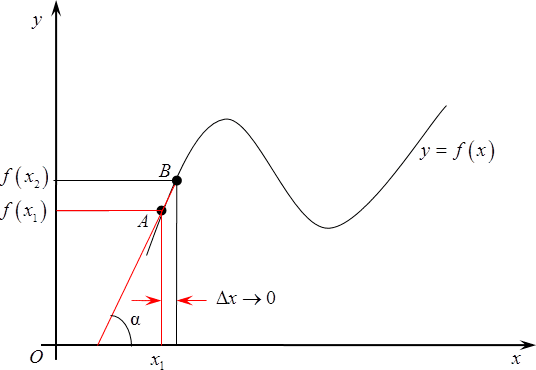
Наконец, продолжаем двигать $B$ все ближе к изначальной точке $A$, в результате треугольник еще уменьшится, а прямая, содержащая отрезок $AB$, все больше будет походить на касательную к графику функции.
В итоге, если продолжать сближение точек, т. е., уменьшать расстояние до нуля, то прямая $AB$, действительно, превратится в касательную к графику в данной точке, а $text{ }!!alpha!!text{ }$превратится из обычного элемента треугольника в угол между касательной к графику и положительным направлением оси $Ox$.
И вот тут мы плавно переходим к определению$f$, а именно, производной функции в точке ${{x}_{1}}$ называется тангенс угла $alpha $ между касательной к графику в точке ${{x}_{1}}$ и положительным направлением оси $Ox$:
[{f}’left( {{x}_{1}} right)=operatorname{tg}text{ }!!alpha!!text{ }]
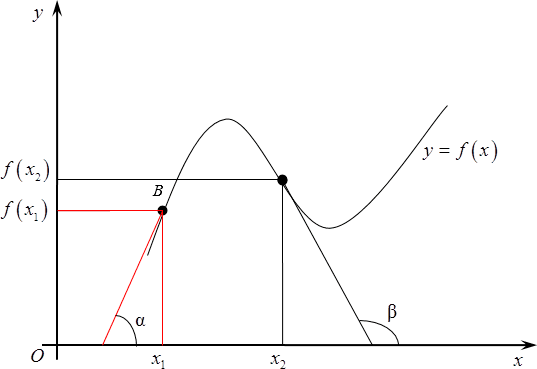
Возвращаясь к нашему графику, следует отметить, что в качестве ${{x}_{1}}$ можно выбрать любую точку на графике. Например, с тем же успехом мы могли снять штрих в точке, показанной на рисунке.
Угол между касательной и положительным направлением оси назовем $beta $. Соответственно, $f$ в ${{x}_{2}}$ будет равна тангенсу этого угла $beta $.
[{f}’left( {{x}_{2}} right)=tgtext{ }!!beta!!text{ }]
В каждой точке графика будет своя касательная, а, следовательно, свое значение функции. В каждом из этих случаев помимо точки, в которой мы ищем производную разности или суммы, или производную степенной функции, необходимо взять другую точку, находящуюся на некотором расстоянии от нее, а затем устремить эту точку к исходной и, разумеется, выяснить, как в процессе такого движения будет меняться тангенс угла наклона.
Производная степенной функции
К сожалению, подобное определение нас совершено не устраивает. Все эти формулы, картинки, углы не дают нам ни малейшего представления о том, как считать реальную производную в реальных задачах. Поэтому давайте немного отвлечемся от формального определения и рассмотрим более действенные формулы и приемы, с помощью которых уже можно решать настоящие задачи.
Начнем с самых простых конструкций, а именно, функций вида $y={{x}^{n}}$, т.е. степенных функций. В этом случае мы можем записать следующее: ${y}’=ncdot {{x}^{n-1}}$. Другими словами, степень, которая стояла в показателе, показывается в множителе спереди, а сам показатель уменьшается на единицу. Например:
[begin{align}& y={{x}^{2}} \& {y}’=2cdot {{x}^{2-1}}=2x \end{align}]
А вот другой вариант:
[begin{align}& y={{x}^{1}} \& {y}’={{left( x right)}^{prime }}=1cdot {{x}^{0}}=1cdot 1=1 \& {{left( x right)}^{prime }}=1 \end{align}]
Пользуясь этими простыми правилами, давайте попробуем снять штрих следующих примеров:
[fleft( x right)={{x}^{6}}]
Итак, мы получаем:
[{{left( {{x}^{6}} right)}^{prime }}=6cdot {{x}^{5}}=6{{x}^{5}}]
Теперь решим второе выражение:
[begin{align}& fleft( x right)={{x}^{100}} \& {{left( {{x}^{100}} right)}^{prime }}=100cdot {{x}^{99}}=100{{x}^{99}} \end{align}]
Разумеется, это были очень простые задачи. Однако реальные задачи более сложные и они не ограничиваются одними лишь степенями функции.
Итак, правило № 1 – если функция представлена в виде других двух, то производная этой суммы равна сумме производных:
[{{left( f+g right)}^{prime }}={f}’+{g}’]
Аналогично, производная разности двух функций равна разности производных:
[{{left( f-g right)}^{prime }}={f}’-{g}’]
Пример:
[{{left( {{x}^{2}}+x right)}^{prime }}={{left( {{x}^{2}} right)}^{prime }}+{{left( x right)}^{prime }}=2x+1]
Кроме того, есть еще одно важное правило: если перед некоторой $f$ стоит константа $c$, на которую эта функция умножается, то $f$ всей этой конструкции считается так:
[{{left( ccdot f right)}^{prime }}=ccdot {f}’]
Пример:
[{{left( 3{{x}^{3}} right)}^{prime }}=3{{left( {{x}^{3}} right)}^{prime }}=3cdot 3{{x}^{2}}=9{{x}^{2}}]
Наконец, еще одно очень важное правило: в задачах часто встречается отдельное слагаемое, которое вообще не содержит $x$. Например, мы можем наблюдать это в наших сегодняшних выражениях. Производная константы, т. е., числа, никак не зависящего от $x$, всегда равна нулю, причем совершенно неважно, чему равна константа $c$:
[{{left( c right)}^{prime }}=0]
Пример решения:
[{{left( 1001 right)}^{prime }}={{left( frac{1}{1000} right)}^{prime }}=0]
Еще раз ключевые моменты:
- Производная суммы двух функций всегда равна сумме производных: ${{left( f+g right)}^{prime }}={f}’+{g}’$;
- По аналогичным причинам производная разности двух функций равна разности двух производных: ${{left( f-g right)}^{prime }}={f}’-{g}’$;
- Если у функции присутствует множитель константа, то эту константу можно выносить за знак производной: ${{left( ccdot f right)}^{prime }}=ccdot {f}’$;
- Если вся функция представляет собой константу, то ее производная всегда ноль: ${{left( c right)}^{prime }}=0$.
Давайте посмотрим, как все это работает на реальных примерах. Итак:
[y={{x}^{5}}-3{{x}^{2}}+7]
Записываем:
[begin{align}& {{left( {{x}^{5}}-3{{x}^{2}}+7 right)}^{prime }}={{left( {{x}^{5}} right)}^{prime }}-{{left( 3{{x}^{2}} right)}^{prime }}+{7}’= \& =5{{x}^{4}}-3{{left( {{x}^{2}} right)}^{prime }}+0=5{{x}^{4}}-6x \end{align}]
В этом примере мы видим и производную суммы, и производную разности. Итого, производная равна $5{{x}^{4}}-6x$.
Переходим ко второй функции:
[fleft( x right)=3{{x}^{2}}-2x+2]
Записываем решение:
[begin{align}& {{left( 3{{x}^{2}}-2x+2 right)}^{prime }}={{left( 3{{x}^{2}} right)}^{prime }}-{{left( 2x right)}^{prime }}+{2}’= \& =3{{left( {{x}^{2}} right)}^{prime }}-2{x}’+0=3cdot 2x-2cdot 1=6x-2 \end{align}]
Вот мы и нашли ответ.
Переходим к третьей функции — она уже посерьезней:
[y=2{{x}^{3}}-3{{x}^{2}}+frac{1}{2}x-5]
Решаем:
[begin{align}& {{left( 2{{x}^{3}}-3{{x}^{2}}+frac{1}{2}x-5 right)}^{prime }}={{left( 2{{x}^{3}} right)}^{prime }}-{{left( 3{{x}^{2}} right)}^{prime }}+{{left( frac{1}{2}x right)}^{prime }}-{5}’= \& =2{{left( {{x}^{3}} right)}^{prime }}-3{{left( {{x}^{2}} right)}^{prime }}+frac{1}{2}cdot {x}’=2cdot 3{{x}^{2}}-3cdot 2x+frac{1}{2}cdot 1=6{{x}^{2}}-6x+frac{1}{2} \end{align}]
Ответ мы нашли.
Переходим к последнему выражению — самому сложному и самому длинному:
[y=6{{x}^{7}}-14{{x}^{3}}+4x+5,{{x}_{0}}=-1]
Итак, считаем:
[begin{align}& {{left( 6{{x}^{7}}-14{{x}^{3}}+4x+5 right)}^{prime }}={{left( 6{{x}^{7}} right)}^{prime }}-{{left( 14{{x}^{3}} right)}^{prime }}+{{left( 4x right)}^{prime }}+{5}’= \& =6cdot 7cdot {{x}^{6}}-14cdot 3{{x}^{2}}+4cdot 1+0=42{{x}^{6}}-42{{x}^{2}}+4 \end{align}]
Но на этом решение не заканчивается, потому что нас просят не просто снять штрих, а посчитать ее значение в конкретной точке, поэтому подставляем в выражение −1 вместо $x$:
[{y}’left( -1 right)=42cdot 1-42cdot 1+4=4]
Идем далее и переходим к еще более сложным и интересным примерам. Дело в том, что формула решения степенной производной ${{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}$ имеет еще более широкую область применения, чем обычно принято считать. С ее помощью можно решать примеры с дробями, корнями и т. д. Именно этим мы сейчас и займемся.
Для начала еще раз запишем формулу, которая поможет нам найти производную степенной функции:
[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]
А теперь внимание: до сих пор мы рассматривали в качестве $n$ лишь натуральные числа, однако ничего не мешаем рассмотреть дроби и даже отрицательные числа. Например, мы можем записать следующее:
[begin{align}& sqrt{x}={{x}^{frac{1}{2}}} \& {{left( sqrt{x} right)}^{prime }}={{left( {{x}^{frac{1}{2}}} right)}^{prime }}=frac{1}{2}cdot {{x}^{-frac{1}{2}}}=frac{1}{2}cdot frac{1}{sqrt{x}}=frac{1}{2sqrt{x}} \end{align}]
Ничего сложного, поэтому посмотрим, как эта формула поможет нам при решении более сложных задач. Итак, пример:
[y=sqrt{x}+sqrt[3]{x}+sqrt[4]{x}]
Записываем решение:
[begin{align}& left( sqrt{x}+sqrt[3]{x}+sqrt[4]{x} right)={{left( sqrt{x} right)}^{prime }}+{{left( sqrt[3]{x} right)}^{prime }}+{{left( sqrt[4]{x} right)}^{prime }} \& {{left( sqrt{x} right)}^{prime }}=frac{1}{2sqrt{x}} \& {{left( sqrt[3]{x} right)}^{prime }}={{left( {{x}^{frac{1}{3}}} right)}^{prime }}=frac{1}{3}cdot {{x}^{-frac{2}{3}}}=frac{1}{3}cdot frac{1}{sqrt[3]{{{x}^{2}}}} \& {{left( sqrt[4]{x} right)}^{prime }}={{left( {{x}^{frac{1}{4}}} right)}^{prime }}=frac{1}{4}{{x}^{-frac{3}{4}}}=frac{1}{4}cdot frac{1}{sqrt[4]{{{x}^{3}}}} \end{align}]
Возвращаемся к нашему примеру и записываем:
[{y}’=frac{1}{2sqrt{x}}+frac{1}{3sqrt[3]{{{x}^{2}}}}+frac{1}{4sqrt[4]{{{x}^{3}}}}]
Вот такое сложное решение.
Переходим ко второму примеру — здесь всего два слагаемых, но каждое из них содержит как классическую степень, так и корни.
[y={{x}^{3}}sqrt[3]{{{x}^{2}}}+{{x}^{7}}sqrt[3]{x}]
Сейчас мы узнаем, как найти производную степенной функции, которая, кроме того, содержит и корень:
[begin{align}& {{left( {{x}^{3}}sqrt[3]{{{x}^{2}}}+{{x}^{7}}sqrt[3]{x} right)}^{prime }}={{left( {{x}^{3}}cdot sqrt[3]{{{x}^{2}}} right)}^{prime }}={{left( {{x}^{3}}cdot {{x}^{frac{2}{3}}} right)}^{prime }}= \& ={{left( {{x}^{3+frac{2}{3}}} right)}^{prime }}={{left( {{x}^{frac{11}{3}}} right)}^{prime }}=frac{11}{3}cdot {{x}^{frac{8}{3}}}=frac{11}{3}cdot {{x}^{2frac{2}{3}}}=frac{11}{3}cdot {{x}^{2}}cdot sqrt[3]{{{x}^{2}}} \& {{left( {{x}^{7}}cdot sqrt[3]{x} right)}^{prime }}={{left( {{x}^{7}}cdot {{x}^{frac{1}{3}}} right)}^{prime }}={{left( {{x}^{7frac{1}{3}}} right)}^{prime }}=7frac{1}{3}cdot {{x}^{6frac{1}{3}}}=frac{22}{3}cdot {{x}^{6}}cdot sqrt[3]{x} \end{align}]
Оба слагаемых посчитаны, осталось записать окончательный ответ:
[{y}’=frac{11}{3}cdot {{x}^{2}}cdot sqrt[3]{{{x}^{2}}}+frac{22}{3}cdot {{x}^{6}}cdot sqrt[3]{x}]
Мы нашли ответ.
Производная дроби через степенную функцию
Но и на этом возможности формулы для решения производной степенной функции не заканчиваются. Дело в том, что с ее помощью можно считать не только примеры с корнями, но также и с дробями. Это как раз та редкая возможность, которая значительно упрощает решение таких примеров, но при этом зачастую игнорируется не только учениками, но и учителями.
Итак, сейчас мы попытаемся совместить сразу две формулы. С одной стороны, классическая производная степенной функции
[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]
С другой стороны мы знаем, что выражение вида $frac{1}{{{x}^{n}}}$ представимо в виде ${{x}^{-n}}$. Следовательно,
[left( frac{1}{{{x}^{n}}} right)’={{left( {{x}^{-n}} right)}^{prime }}=-ncdot {{x}^{-n-1}}=-frac{n}{{{x}^{n+1}}}]
Пример:
[{{left( frac{1}{x} right)}^{prime }}=left( {{x}^{-1}} right)=-1cdot {{x}^{-2}}=-frac{1}{{{x}^{2}}}]
Таким образом, производные простых дробей, где в числителе стоит константа, а в знаменателе — степень, также считаются с помощью классической формулы. Посмотрим, как это работает на практике.
Итак, первая функция:
[fleft( x right)=frac{1}{{{x}^{2}}}]
Считаем:
[{{left( frac{1}{{{x}^{2}}} right)}^{prime }}={{left( {{x}^{-2}} right)}^{prime }}=-2cdot {{x}^{-3}}=-frac{2}{{{x}^{3}}}]
Первый пример решен, переходим ко второму:
[y=frac{7}{4{{x}^{4}}}-frac{2}{3{{x}^{3}}}+frac{5}{2}{{x}^{2}}+2{{x}^{3}}-3{{x}^{4}}]
Решаем:
[begin{align}& {{left( frac{7}{4{{x}^{4}}}-frac{2}{3{{x}^{3}}}+frac{5}{2}{{x}^{2}}+2{{x}^{3}}-3{{x}^{4}} right)}^{prime }}= \& ={{left( frac{7}{4{{x}^{4}}} right)}^{prime }}-{{left( frac{2}{3{{x}^{3}}} right)}^{prime }}+{{left( 2{{x}^{3}} right)}^{prime }}-{{left( 3{{x}^{4}} right)}^{prime }} \& {{left( frac{7}{4{{x}^{4}}} right)}^{prime }}=frac{7}{4}{{left( frac{1}{{{x}^{4}}} right)}^{prime }}=frac{7}{4}cdot {{left( {{x}^{-4}} right)}^{prime }}=frac{7}{4}cdot left( -4 right)cdot {{x}^{-5}}=frac{-7}{{{x}^{5}}} \& {{left( frac{2}{3{{x}^{3}}} right)}^{prime }}=frac{2}{3}cdot {{left( frac{1}{{{x}^{3}}} right)}^{prime }}=frac{2}{3}cdot {{left( {{x}^{-3}} right)}^{prime }}=frac{2}{3}cdot left( -3 right)cdot {{x}^{-4}}=frac{-2}{{{x}^{4}}} \& {{left( frac{5}{2}{{x}^{2}} right)}^{prime }}=frac{5}{2}cdot 2x=5x \& {{left( 2{{x}^{3}} right)}^{prime }}=2cdot 3{{x}^{2}}=6{{x}^{2}} \& {{left( 3{{x}^{4}} right)}^{prime }}=3cdot 4{{x}^{3}}=12{{x}^{3}} \end{align}]…
Теперь собираем все эти слагаемые в единую формулу:
[{y}’=-frac{7}{{{x}^{5}}}+frac{2}{{{x}^{4}}}+5x+6{{x}^{2}}-12{{x}^{3}}]
Мы получили ответ.
Однако прежде чем двигаться дальше, хотел бы обратить ваше внимание на форму записи самих исходных выражений: в первом выражении мы записали $fleft( x right)=…$, во втором: $y=…$ Многие ученики теряются, когда видят разные формы записи. Чем отличаются $fleft( x right)$ и $y$? На самом деле, ничем. Это просто разные записи с одним и тем же смыслом. Просто когда мы говорим $fleft( x right)$, то речь идет, прежде всего, о функции, а когда речь идет об $y$, то чаще всего подразумевается график функции. В остальном же это одно и то же, т. е., производная в обоих случаях считается одинаково.
Сложные задачи с производными
В заключение хотелось бы рассмотреть пару сложных комбинированных задач, в которых используется сразу все то, что мы сегодня рассмотрели. В них нас ждут и корни, и дроби, и суммы. Однако сложными эти примеры будут лишь в рамках сегодняшнего видеоурока, потому что по-настоящему сложные функции производных будут ждать вас впереди.
Итак, заключительная часть сегодняшнего видеоурока, состоящая из двух комбинированных задач. Начнем с первой из них:
[y={{x}^{3}}-frac{1}{{{x}^{3}}}+sqrt[3]{x}]
Считаем:
[begin{align}& {{left( {{x}^{3}}-frac{1}{{{x}^{3}}}+sqrt[3]{x} right)}^{prime }}={{left( {{x}^{3}} right)}^{prime }}-{{left( frac{1}{{{x}^{3}}} right)}^{prime }}+left( sqrt[3]{x} right) \& {{left( {{x}^{3}} right)}^{prime }}=3{{x}^{2}} \& {{left( frac{1}{{{x}^{3}}} right)}^{prime }}={{left( {{x}^{-3}} right)}^{prime }}=-3cdot {{x}^{-4}}=-frac{3}{{{x}^{4}}} \& {{left( sqrt[3]{x} right)}^{prime }}={{left( {{x}^{frac{1}{3}}} right)}^{prime }}=frac{1}{3}cdot frac{1}{{{x}^{frac{2}{3}}}}=frac{1}{3sqrt[3]{{{x}^{2}}}} \end{align}]
Производная функции равна:
[{y}’=3{{x}^{2}}-frac{3}{{{x}^{4}}}+frac{1}{3sqrt[3]{{{x}^{2}}}}]
Первый пример решен. Рассмотрим вторую задачу:
[y=-frac{2}{{{x}^{4}}}+sqrt[4]{x}+frac{4}{xsqrt[4]{{{x}^{3}}}}]
Во втором примере действуем аналогично:
[{{left( -frac{2}{{{x}^{4}}}+sqrt[4]{x}+frac{4}{xsqrt[4]{{{x}^{3}}}} right)}^{prime }}={{left( -frac{2}{{{x}^{4}}} right)}^{prime }}+{{left( sqrt[4]{x} right)}^{prime }}+{{left( frac{4}{xcdot sqrt[4]{{{x}^{3}}}} right)}^{prime }}]
Посчитаем каждое слагаемое отдельно:
[begin{align}& {{left( -frac{2}{{{x}^{4}}} right)}^{prime }}=-2cdot {{left( {{x}^{-4}} right)}^{prime }}=-2cdot left( -4 right)cdot {{x}^{-5}}=frac{8}{{{x}^{5}}} \& {{left( sqrt[4]{x} right)}^{prime }}={{left( {{x}^{frac{1}{4}}} right)}^{prime }}=frac{1}{4}cdot {{x}^{-frac{3}{4}}}=frac{1}{4cdot {{x}^{frac{3}{4}}}}=frac{1}{4sqrt[4]{{{x}^{3}}}} \& {{left( frac{4}{xcdot sqrt[4]{{{x}^{3}}}} right)}^{prime }}={{left( frac{4}{xcdot {{x}^{frac{3}{4}}}} right)}^{prime }}={{left( frac{4}{{{x}^{1frac{3}{4}}}} right)}^{prime }}=4cdot {{left( {{x}^{-1frac{3}{4}}} right)}^{prime }}= \& =4cdot left( -1frac{3}{4} right)cdot {{x}^{-2frac{3}{4}}}=4cdot left( -frac{7}{4} right)cdot frac{1}{{{x}^{2frac{3}{4}}}}=frac{-7}{{{x}^{2}}cdot {{x}^{frac{3}{4}}}}=-frac{7}{{{x}^{2}}cdot sqrt[4]{{{x}^{3}}}} \end{align}]
Все слагаемые посчитаны. Теперь возвращаемся к исходной формуле и складываем вместе все три слагаемых. Получаем, что окончательный ответ будет таким:
[{y}’=frac{8}{{{x}^{5}}}+frac{1}{4sqrt[4]{{{x}^{3}}}}-frac{7}{{{x}^{2}}cdot sqrt[4]{{{x}^{3}}}}]
И на этом все. Это был первый наш урок. В следующих уроках мы рассмотрим более сложные конструкции, а также выясним, зачем вообще нужны производные.
Смотрите также:
- Производная произведения и частного
- Правила вычисления производных
- Теорема Виета
- Преобразование уравнений
- Тест по методу интервалов для строгих неравенств
- Тест по задачам B14: средний уровень, 2 вариант
Функции сложного вида не всегда подходят под определение сложной функции. Если имеется функция вида y=sin x-(2-3)·arctgxx57x10-17×3+x-11, то ее нельзя считать сложной в отличие от y=sin2 x.
Данная статья покажет понятие сложной функции и ее выявление. Поработаем с формулами нахождения производной с примерами решений в заключении. Применение таблицы производных и правила дифференцирования заметно уменьшают время для нахождения производной.
Основные определения
Сложной функцией считается такая функция, у которой аргумент также является функцией.
Обозначается это таким образом: f(g(x)). Имеем, что функция g(x) считается аргументом f(g(x)).
Если есть функция f и является функцией котангенса, тогда g(x) = lnx – это функция натурального логарифма. Получаем, что сложная функция f(g(x)) запишется как arctg(lnx). Или функция f, являющаяся функцией возведенной в 4 степень, где g(x)=x2+2x-3 считается целой рациональной функцией, получаем, что f(g(x))=(x2+2x-3)4.
Очевидно, что g(x) может быть сложной. Из примера y=sin2x+1×3-5 видно, что значение g имеет кубический корень с дробью. Данное выражение разрешено обозначать как y=f(f1(f2(x))). Откуда имеем, что f – это функция синуса, а f1 – функция, располагаемая под квадратным корнем, f2(x)=2x+1×3-5 – дробная рациональная функция.
Степень вложенности определено любым натуральным числом и записывается как y=f(f1(f2(f3(…(fn(x)))))).
Понятие композиция функции относится к количеству вложенных функций по условию задачи. Для решения используется формула нахождения производной сложной функции вида
(f(g(x)))’=f'(g(x))·g'(x)
Примеры
Найти производную сложной функции вида y=(2x+1)2.
Решение
По условию видно, что f является функцией возведения в квадрат, а g(x)=2x+1 считается линейной функцией.
Применим формулу производной для сложной функции и запишем:
f'(g(x))=((g(x))2)’=2·(g(x))2-1=2·g(x)=2·(2x+1);g'(x)=(2x+1)’=(2x)’+1’=2·x’+0=2·1·x1-1=2⇒(f(g(x)))’=f'(g(x))·g'(x)=2·(2x+1)·2=8x+4
Необходимо найти производную с упрощенным исходным видом функции. Получаем:
y=(2x+1)2=4×2+4x+1
Отсюда имеем, что
y’=(4×2+4x+1)’=(4×2)’+(4x)’+1’=4·(x2)’+4·(x)’+0==4·2·x2-1+4·1·x1-1=8x+4
Результаты совпали.
При решении задач такого вида важно понимать, где будет располагаться функция вида f и g(x).
Следует найти производные сложных функций вида y=sin2x и y=sin x2.
Решение
Первая запись функции говорит о том, что f является функцией возведения в квадрат, а g(x) – функцией синуса. Тогда получим, что
y’=(sin2x)’=2·sin2-1x·(sin x)’=2·sin x·cos x
Вторая запись показывает, что f является функцией синуса, а g(x)=x2 обозначаем степенную функцию. Отсюда следует, что произведение сложной функции запишем как
y’=(sin x2)’=cos(x2)·(x2)’=cos(x2)·2·x2-1=2·x·cos(x2)
Формула для производной y=f(f1(f2(f3(…(fn(x)))))) запишется как y’=f'(f1(f2(f3(…(fn(x))))))·f1′(f2(f3(…(fn(x)))))··f2′(f3(…(fn(x))))·…·fn'(x)
Найти производную функции y=sin(ln3 arctg(2x)).
Решение
Данный пример показывает сложность записи и определения расположения функций. Тогда y=f(f1(f2(f3(f4(x))))) обозначим, где f, f1, f2, f3, f4(x) является функцией синуса, функцией возведения в 3 степень, функцией с логарифмом и основанием е, функцией арктангенса и линейной.
Из формулы определения сложной функции имеем, что
y’=f'(f1(f2(f3(f4(x)))))·f1′(f2(f3(f4(x))))··f2′(f3(f4(x)))·f3′(f4(x))·f4′(x)
Получаем, что следует найти
- f'(f1(f2(f3(f4(x))))) в качестве производной синуса по таблице производных, тогда f'(f1(f2(f3(f4(x)))))=cos(ln3 arctg(2x)).
- f1′(f2(f3(f4(x)))) в качестве производной степенной функции, тогда f1′(f2(f3(f4(x))))=3·ln3-1arctg(2x)=3·ln2arctg(2x).
- f2′(f3(f4(x))) в качестве производной логарифмической, тогда f2′(f3(f4(x)))=1arctg(2x).
- f3′(f4(x)) в качестве производной арктангенса, тогда f3′(f4(x))=11+(2x)2=11+4×2.
- При нахождении производной f4(x)=2x произвести вынесение 2 за знак производной с применением формулы производной степенной функции с показателем, который равняется 1, тогда f4′(x)=(2x)’=2·x’=2·1·x1-1=2.
Производим объединение промежуточных результатов и получаем, что
y’=f'(f1(f2(f3(f4(x)))))·f1′(f2(f3(f4(x))))··f2′(f3(f4(x)))·f3′(f4(x))·f4′(x)==cos(ln3 arctg(2x))·3·ln2 arctg(2x)·1arctg(2x)·11+4×2·2==6·cos(ln3 arctg(2x))·ln2 arctg(2x)arctg(2x)·(1+4×2)
Разбор таких функций напоминает матрешки. Правила дифференцирования не всегда могут быть применены в явном виде при помощи таблицы производных. Зачастую нужно применять формулу нахождения производных сложных функций.
Существуют некоторые различия сложного вида от сложных функций. При явном умении это различать, нахождение производных будет давать особенно легко.
Необходимо рассмотреть на приведении подобного примера. Если имеется функция вида y=tg2x+3tgx+1, тогда ее можно рассмотреть в качестве сложной вида g(x)=tgx, f(g)=g2+3g+1. Очевидно, что необходимо применение формулы для сложной производной:
f'(g(x))=(g2(x)+3g(x)+1)’=(g2(x))’+(3g(x))’+1’==2·g2-1(x)+3·g'(x)+0=2g(x)+3·1·g1-1(x)==2g(x)+3=2tgx+3;g'(x)=(tgx)’=1cos2x⇒y’=(f(g(x)))’=f'(g(x))·g'(x)=(2tgx+3)·1cos2x=2tgx+3cos2x
Функция вида y=tgx2+3tgx+1 не считается сложной, так как имеет сумму tgx2, 3tgx и 1. Однако, tgx2 считается сложной функцией, то получаем степенную функцию вида g(x)=x2 и f, являющуюся функцией тангенса. Для этого следует продифференцировать по сумме. Получаем, что
y’=(tgx2+3tgx+1)’=(tgx2)’+(3tgx)’+1’==(tgx2)’+3·(tgx)’+0=(tgx2)’+3cos2x
Переходим к нахождению производной сложной функции (tgx2)’:
f'(g(x))=(tg(g(x)))’=1cos2g(x)=1cos2(x2)g'(x)=(x2)’=2·x2-1=2x⇒(tgx2)’=f'(g(x))·g'(x)=2xcos2(x2)
Получаем, что y’=(tgx2+3tgx+1)’=(tgx2)’+3cos2x=2xcos2(x2)+3cos2x
Функции сложного вида могут быть включены в состав сложных функций, причем сами сложные функции могут являться составными функции сложного вида.
Для примера рассмотрим сложную функцию вида y=log3x2+3cos3(2x+1)+7ex2+33+ln2x·(x2+1)
Данная функция может быть представлена в виде y=f(g(x)), где значение f является функцией логарифма по основанию 3, а g(x) считается суммой двух функций вида h(x)=x2+3cos3(2x+1)+7ex2+33 и k(x)=ln2x·(x2+1). Очевидно, что y=f(h(x)+k(x)).
Рассмотрим функцию h(x). Это отношение l(x)=x2+3cos3(2x+1)+7 к m(x)=ex2+33
Имеем, что l(x)=x2+3cos2(2x+1)+7=n(x)+p(x) является суммой двух функций n(x)=x2+7 и p(x)=3cos3(2x+1), где p(x)=3·p1(p2(p3(x))) является сложной функцией с числовым коэффициентом 3, а p1 – функцией возведения в куб, p2 функцией косинуса, p3(x)=2x+1 – линейной функцией.
Получили, что m(x)=ex2+33=q(x)+r(x) является суммой двух функций q(x)=ex2 и r(x)=33, где q(x)=q1(q2(x)) – сложная функция, q1 – функция с экспонентой, q2(x)=x2 – степенная функция.
Отсюда видно, что h(x)=l(x)m(x)=n(x)+p(x)q(x)+r(x)=n(x)+3·p1(p2(p3(x)))q1(q2(x))+r(x)
При переходе к выражению вида k(x)=ln2x·(x2+1)=s(x)·t(x) видно, что функция представлена в виде сложной s(x)=ln2x=s1(s2(x)) с целой рациональной t(x)=x2+1, где s1 является функцией возведения в квадрат, а s2(x)=ln x – логарифмической с основанием е.
Отсюда следует, что выражение примет вид k(x)=s(x)·t(x)=s1(s2(x))·t(x).
Тогда получим, что
y=log3x2+3cos3(2x+1)+7ex2+33+ln2 x·(x2+1)==fn(x)+3·p1(p2(p3(x)))q1(q2(x))=r(x)+s1(s2(x))·t(x)
По структурам функции стало явно, как и какие формулы необходимо применять для упрощения выражения при его дифференцировании. Для ознакомления подобных задач и и для понятия их решения необходимо обратиться к пункту дифференцирования функции, то есть нахождения ее производной.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Содержание:
Производные показательной и логарифмической функций:
Объяснение и обоснование
Чтобы обосновать формулы производных показательных и логарифмических функций, используем без доказательства свойство функции
При а > 0 по основному логарифмическому тождеству имеем
Тогда по правилу нахождения производной сложной функции:
По полученной формуле мы можем найти значение производной показательной функции для любого значения 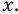
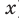
Для логарифмической функции сначала найдем производную функции 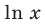
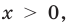
При 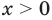
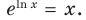
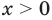
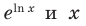
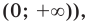
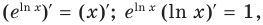
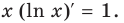
Поскольку 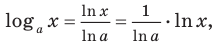
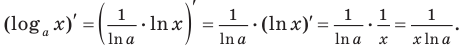
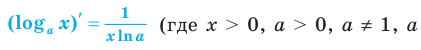
Замечание. Формула 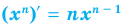
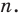
*Напомним , что 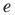
Если 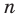
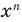
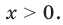
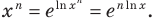
Следовательно, далее формулой 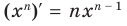
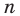
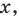
Опираясь на полученный результат, обоснуем также формулу
которую можно использовать при тех значениях 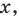
Если 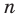
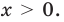
Если 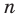
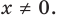

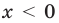
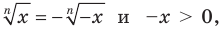
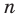
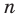
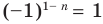
Следовательно, и для нечетного 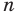
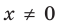
В последнем случае такие громоздкие преобразования пришлось вы- 1 полнить вследствие того, что при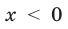
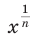
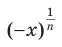
Примеры решения задач
Пример №1
Найдите производную функции:
Решение:
Комментарий:
Последовательно определяем, от какого выражения берется производная (ориентируясь на результат последнего действия). В задании 1 сначала берется производная суммы: 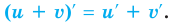
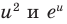
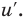
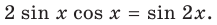
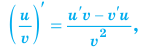

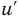
Пример №2
Найдите уравнение касательной к графику функции 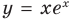
Решение:
Если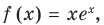
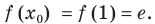
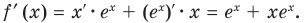
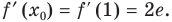
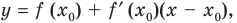
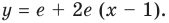
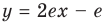
Комментарий:
Уравнение касательной к графику функции 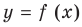
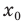
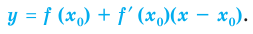
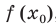
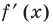
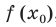
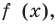
Пример №3
1) Постройте график функции 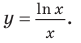
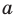
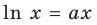
Комментарий:
Для выполнения задания 1 исследуем функцию 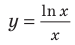
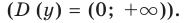
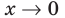
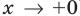
Тогда 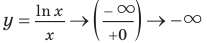
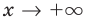
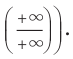
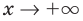
При выполнении задания 2 целесообразно использовать графическую иллюстрацию решения. Это можно сделать двумя способами:
Решение:
1) Исследуем функцию
1. Область определения:
2. Функция ни четная, ни нечетная, поскольку ее область определения не симметрична относительно точки 0. 3. Точки пересечения графика с осями координат. График не пересекает ось 
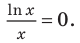

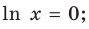
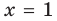
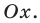
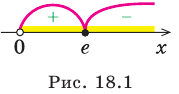
Производная существует на всей области определения функции 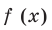
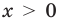
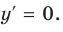
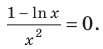
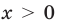
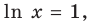
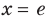
5. Отмечаем критические точки на области определения функции и находим знак 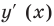
Составляем таблицу, в которой отмечаем промежутки возрастания, убывания и экстремумы функции.
6. Найдем координаты еще нескольких точек графика функции:
Заметим, что при 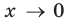

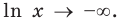
7. Используя результаты исследования, строим график функции 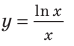
I способ решения задания 2
Область допустимых значений данного уравнения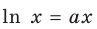
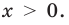
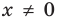
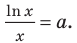
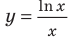
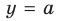
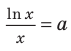

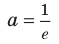
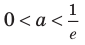
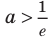
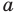
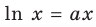
II способ решения задания 2
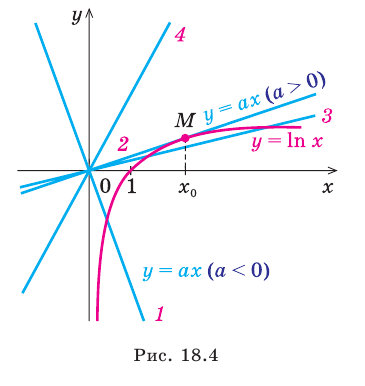
Рассмотрим графическую иллюстрацию (рис. 18.4) решения данного уравнения
Функция 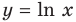
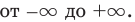
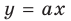
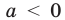
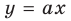
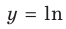
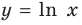
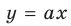
При 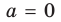
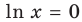
При 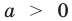
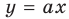
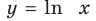
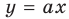
Тогда уравнение (1) будет иметь два корня. Если же прямая 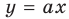
Выясним, когда прямая 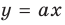
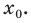
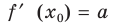
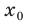
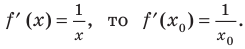
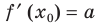
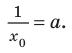
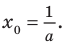
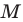
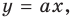
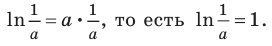
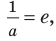
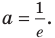
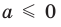
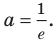
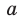
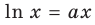
Пример №4
Докажите, что при всех действительных значениях 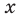
Решение:
Рассмотрим функцию
Область определения:
Производная 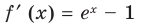
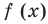
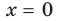
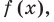
Как видим, непрерывная функция 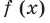
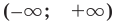
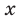
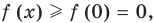

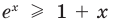
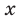
Комментарий:
Используем производную для доказательства данного неравенства. Для этого исследуем функцию 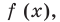
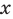
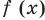
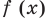
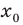
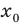
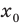
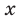

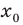
При доказательстве числовых неравенств или для сравнения двух чисел часто бывает удобно перейти к более общему функциональному неравенству
Пример №5
Сравните числа
Комментарий:
Чтобы составить план решения, можно рассуждать следующим образом. Мы не знаем, какое из данных чисел больше: 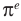
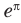

Затем заменим знак «
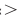
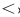




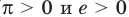
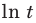
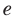
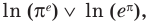

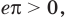
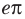
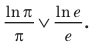
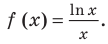
Далее, учитывая, что 
Решение:
Рассмотрим функцию 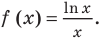
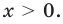
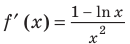
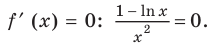
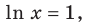
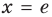
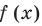
Функция 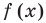
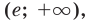
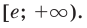

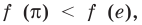
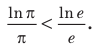
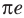
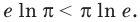
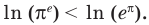
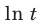
Ответ:
Пример №6
Решите уравнение
Комментарий:
Если попытаться применить к данному уравнению схему решения показательных уравнений (см. с. 178), то удается реализовать только первый ее пункт — избавиться от числовых слагаемых в показателях степеней. А привести все степени к одному основанию (с удобными показателями) или к двум основаниям так, чтобы получить однородное уравнение, или перенести все члены в одну сторону и разложить полученное выражение на множители — не удается. Попробуем применить свойства соответствующих функций. Но и на этом пути нам не удается использовать конечность ОДЗ (она бесконечна), оценку значений левой и правой частей уравнения (они обе в пределах от 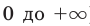
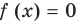
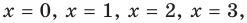
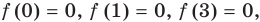
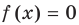
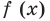
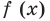
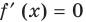
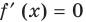
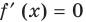
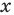
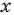
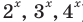
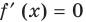
Решение:
Данное уравнение равносильно уравнению 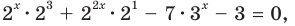
Обозначим 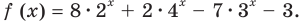
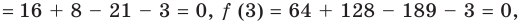
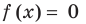
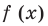
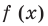
Производная 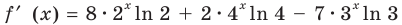
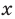
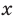
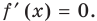
Поскольку 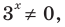
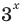
Чтобы доказать, что уравнение (2) имеет не больше двух корней, достаточно доказать, что функция 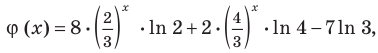
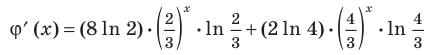
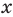
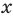
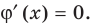
Поскольку 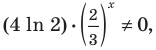
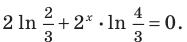
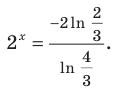
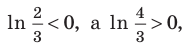
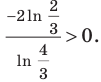
- Заказать решение задач по высшей математике
Производные показательной и логарифмической функций – формулы и доказательство
Докажем следующие формулы производных:
1. Пусть дана функция 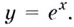
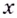
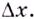
Следовательно,
Если 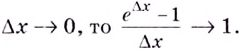
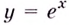
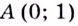
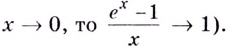
Если значение 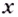
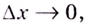
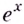
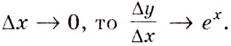
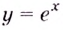
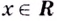
2.Как известно, при каждом 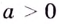
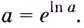
По теореме о производной сложной функции
Итак, формула 2 доказана.
3. Если
А по теореме о производной сложной функции
Следовательно, 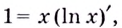
4. При каждом 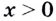
Следовательно,
По доказанным формулам можно находить производные любых показательных или логарифмических функций, а значит, и исследовать эти функции.
Обратите внимание! Если функция содержит логарифм сложного выражения, то прежде чем находить её производную, целесообразно это выражение прологарифмировать.
Пример №7
Найдите производную функции
Решение:
Теперь можно вывести формулу производной степенной функции 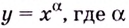
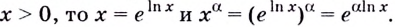
Итак, формула 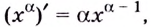
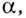
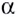
Формулу для нахождения производной логарифмической функции можно вывести иначе, используя тот факт, что функция 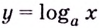
Выясним, как связаны между собой производные взаимно обратных функций.
Теорема. Если функция 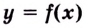
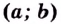
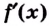
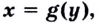
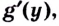
Обоснуем эти формулы, используя геометрический смысл производной.
Пусть 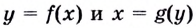
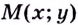
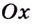
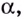
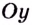
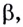
Поскольку 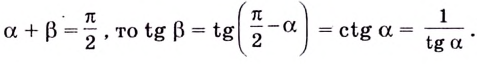
Строгое доказательство этой теоремы рассматривается в университетском курсе математического анализа.
Применим формулу 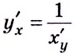
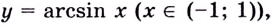
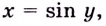
Получим:
Пример №8
Найдите производную функции:
Решение:
Пример №9
Запишите уравнение касательной к графику функции 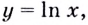
Решение:
Найдём абсциссу точки касания: 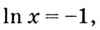
Найдём производную функции 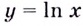
Уравнение касательной запишем в виде 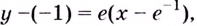
Пример №10
Найдите производную функции
Решение:
Заданная функция является суммой степенной и показательной функций. Для нахождения её производной воспользуемся соответствующими формулами:
Определение производной показательной и логарифмической функций
Существует ли функция, производная которой равна самой функции? Ответить на этот вопрос легко. Например, функция, которая является нулевой константой, обладает этим свойством.
А можно ли указать такую функцию 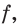
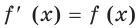
Оказывается, что среди показательных функций 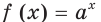
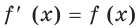
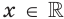
основанием степени, обозначают буквой 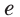
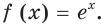
Установлено, что число 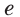
Функцию 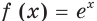
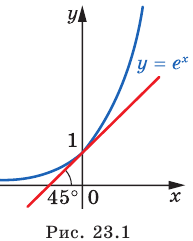
Отметим одну особенность графика экспоненты.
Имеем:
Следовательно, касательная к графику экспоненты в точке с абсциссой, равной нулю, имеет угловой коэффициент, равный 1. То есть эта касательная образует угол 45° с положительным направлением оси абсцисс (рис. 23.1).
Выведем формулу для нахождения производной показательной функции
Имеем: 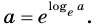
Пользуясь правилом вычисления производной сложной функции, запишем:
Логарифм по основанию 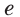
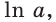
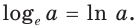
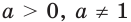
Эта формула показывает, что между значением производной показательной функции и соответствующим значением самой функции существует прямая пропорциональная зависимость. Коэффициент пропорциональности равен
В пункте 20 мы определили, что логарифмическая функция 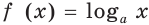
Для любого 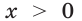
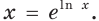
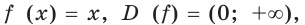
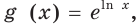
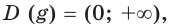
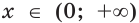
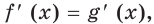
Левая часть этого равенства равна 1. В правой части получаем: 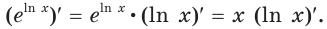
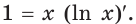
Имеем:
Следовательно,
Пример №11
Найдите производную функции:
Решение:
1) Применяя теорему о производной произведения двух функций, получаем:
2) Имеем:
3) Используя теорему о производной сложной функции, запишем:
4) Имеем:
5) Применив теорему о производной сложной функции, получаем:
6) Имеем:
Пример №12
Составьте уравнение касательной к графику функции 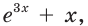
Решение:
Поскольку угловой коэффициент прямой 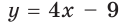
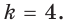
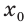
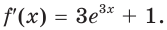
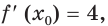
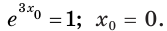
Тогда искомое уравнение имеет вид
Ответ:
Ответ: у = 4х + 1.
Пример №13
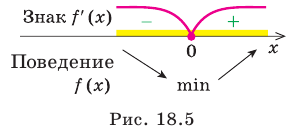
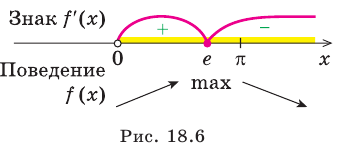
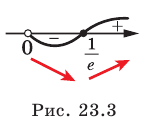
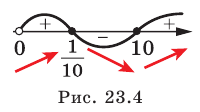
Найдите промежутки возрастания и убывания и точки экстремума функции:
Решение:
1) Имеем:
Исследовав знак производной функции 
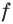
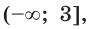
2) Имеем:
Исследуем знак 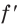
Имеем: 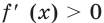
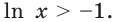
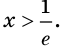
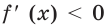
Получаем, что функция 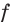
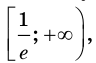
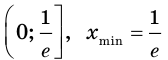
3) Имеем:
Тогда 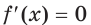
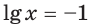
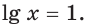
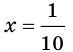
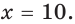
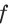
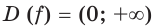
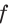
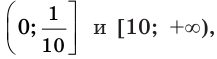
Пример №14
Докажите, что: 1) показательная функция 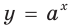
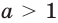
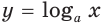
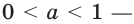
Решение:
1) Имеем:
Поскольку 
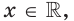
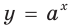
2) Запишем:
Если 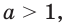
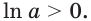
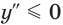
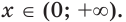
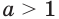
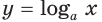
При 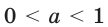
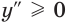
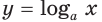
- Показательно-степенные уравнения и неравенства
- Показательные уравнения и неравенства
- Логарифмические уравнения и неравенства
- Степенная функция – определение и вычисление
- Дифференциальная геометрия
- Логарифмическая функция, её свойства и график
- Логарифмические выражения
- Показательная функция, её график и свойства