Алгебра и начала математического анализа, 11 класс
Урок №12. Производная степенной функции.
Перечень вопросов, рассматриваемых в теме:
- разбор понятия производной степенной функции;
- вычисление производной степенной функции;
- знакомство с правилами вычисления производных одночлена и многочлена.
Глоссарий по теме
Формула для вычисления производной степенной функции xn, где n – произвольное натуральное число, такова:
(xn) ‘ =nxn-1
Формула для вычисления производной степенной функции (kx+b)p:
((kx+b)p) ‘ = pk(kx+b)p
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Формула для вычисления производной степенной функции xn, где n – произвольное натуральное число, такова: (xn)’=nxn-1.
Нам уже известна формула производной функции х2: (x2)’=2x.
Пользуясь формулой дифференцирования произведения, получаем:
(x3) ‘ = (x2·x) ‘ = (x2) ‘ · x + x2 · (x) ‘ = 2x·x+x2·1 = 3x2;
(x4) ‘ = (x3·x) ‘ = (x3) ‘·x+x3·(x) ‘ = 3x2·x+x3·1 = 4x3.
Заметим, что
(x2) ‘ = 2x2-1
(x3) ‘ = 3x3-1
(x4)’=4x4-1
Т.е. для n, равного 2, 3 и 4, формула (1) доказана. Продолжая аналогичные рассуждения, нетрудно убедиться в справедливости формулы (1) для n, равного 5, 6 и т.д.
Пример 1.
Докажем что, 

Решение:
- представим
как х-1;
- воспользуемся формулой (1): (х-1)’=-1·x-1-1=-x-2;
- вернемся к первоначальному виду

В более сложных случаях, например, при нахождении производной функции (3х-1)7, можно воспользоваться следующей формулой:
((kx+b)p)’=pk(kx+b)p-1
Пример
Найдем производную функции (3х-1)7.
Решение:
воспользуемся формулой (2)
((3х-1)7)’=21(3x-1)6.
Примеры и разбор решения заданий тренировочного модуля
Пример 1
Вычислить f’(9), если 
Решение:


Пример 2
Доказать, что 
- x>0;
- x<0.
Доказательство:
- если x>0, то
и по формуле (1) получаем:

- если x<0, то
и по формуле (2) получаем:

Как считать производную степенной функции
3 февраля 2015
Этим видео я начинаю длинную серию уроков, посвященную производным. Этот урок состоит из нескольких частей.
В первую очередь, я расскажу вам, что вообще такое производные и как их считать, но не мудреным академическим языком, а так, как я сам это понимаю и как объясняю своим ученикам. Во-вторых, мы рассмотрим простейшее правило для решения задач, в которых будем искать производные суммы, производные разности и производные степенной функции.
Мы рассмотрим более сложные комбинированные примеры, из которых вы, в частности, узнаете, что подобные задачи, содержащие корни и даже дроби, могут быть решены при использовании формулы производной степенной функции. Кроме того, конечно, будет множество задач и примеров решений самого разного уровня сложности.
Вообще, изначально я собирался записать коротенький 5-минутный ролик, но сами видите, что из этого получилось. Поэтому хватит лирики — приступаем к делу.
Что такое производная?
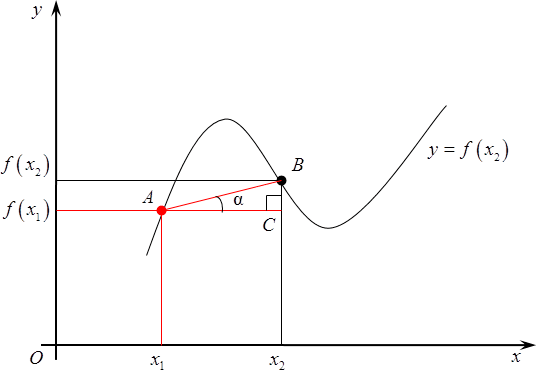
Итак, начнем издалека. Много лет назад, когда деревья были зеленее, а жизнь была веселее, математики задумались вот над чем: рассмотрим простую функцию, заданную своим графиком, назовем ее $y=fleft( x right)$. Разумеется, график существует не сам по себе, поэтому нужно провести оси $x$, а также ось $y$. А теперь давайте выберем любую точку на этом графике, абсолютно любую. Абсциссу назовем ${{x}_{1}}$, ордината, как не трудно догадаться, будет $fleft( {{x}_{1}} right)$.
Рассмотрим на том же графике еще одну точку. Не важно, какую, главное, чтобы она отличалась от первоначальной. У нее, опять же, есть абсцисса, назовем ее ${{x}_{2}}$, а также ордината — $fleft( {{x}_{2}} right)$.
Итак, мы получили две точки: у них разные абсциссы и, следовательно, разные значения функции, хотя последнее — необязательно. А вот что действительно важно, так это что, что из курса планиметрии нам известно: через две точки можно провести прямую и, причем, только одну. Вот давайте ее и проведем.
А теперь проведем через самую первую из них прямую, параллельную оси абсцисс. Получим прямоугольный треугольник. Давайте его обозначим $ABC$, прямой угол $C$. У этого треугольника возникает одно очень интересное свойство: дело в том, что угол$alpha $, на самом деле, равен углу, под которым пересекается прямая $AB$ с продолжением оси абсцисс. Судите сами:
- прямая $AC$параллельна оси $Ox$ по построению,
- прямая $AB$ пересекает $AC$ под $alpha $,
- следовательно, $AB$ пересекает $Ox$под тем же самым $alpha $.
Что мы можем сказать об $text{ }!!alpha!!text{ }$? Ничего конкретного, разве что в треугольнике $ABC$отношение катета $BC$ к катету $AC$ равно тангенсу этого самого угла. Так и запишем:
[tg=frac{BC}{AC}]
Разумеется, $AC$ в данном случае легко считается:
[AC={{x}_{2}}-{{x}_{1}}]
Точно также и $BC$:
[BC=fleft( {{x}_{2}} right)-fleft( {{x}_{1}} right)]
Другими словами, мы можем записать следующее:
[operatorname{tg}text{ }!!alpha!!text{ }=frac{fleft( {{x}_{2}} right)-fleft( {{x}_{1}} right)}{{{x}_{2}}-{{x}_{1}}}]
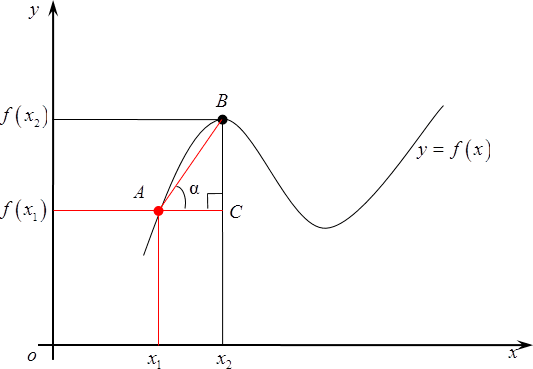
Теперь, когда мы все это выяснили, давайте вернемся к нашему графику и рассмотрим новую точку $B$. Сотрем старые значения и возьмем и возьмем $B$ где-нибудь поближе к ${{x}_{1}}$. Вновь обозначим ее абсциссу за ${{x}_{2}}$, а ординату — $fleft( {{x}_{2}} right)$.
Вновь рассмотрим наш маленький треугольник $ABC$и $text{ }!!alpha!!text{ }$ внутри него. Совершенно очевидно, что это будет уже совсем другой угол, тангенс будет также другим потому, что длины отрезков $AC$ и $BC$ существенно изменились, а формула для тангенса угла нисколько не поменялась — это по-прежнему соотношение между изменением функции и изменением аргумента.
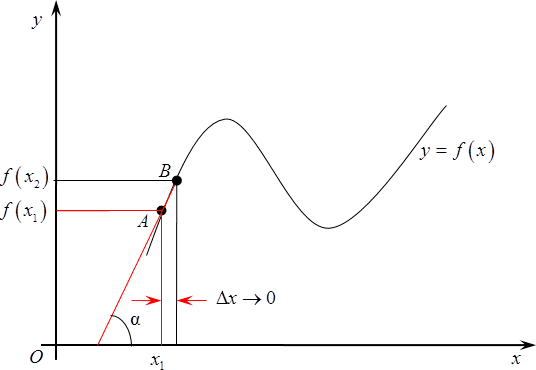
Наконец, продолжаем двигать $B$ все ближе к изначальной точке $A$, в результате треугольник еще уменьшится, а прямая, содержащая отрезок $AB$, все больше будет походить на касательную к графику функции.
В итоге, если продолжать сближение точек, т. е., уменьшать расстояние до нуля, то прямая $AB$, действительно, превратится в касательную к графику в данной точке, а $text{ }!!alpha!!text{ }$превратится из обычного элемента треугольника в угол между касательной к графику и положительным направлением оси $Ox$.
И вот тут мы плавно переходим к определению$f$, а именно, производной функции в точке ${{x}_{1}}$ называется тангенс угла $alpha $ между касательной к графику в точке ${{x}_{1}}$ и положительным направлением оси $Ox$:
[{f}’left( {{x}_{1}} right)=operatorname{tg}text{ }!!alpha!!text{ }]
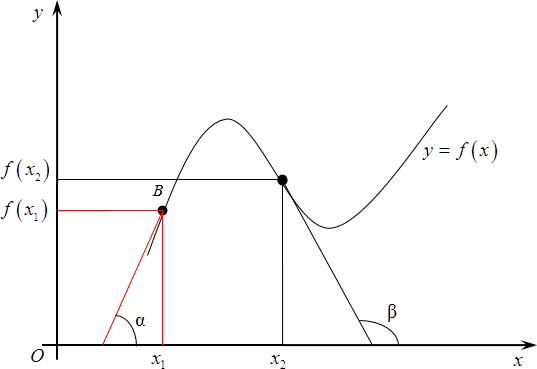
Возвращаясь к нашему графику, следует отметить, что в качестве ${{x}_{1}}$ можно выбрать любую точку на графике. Например, с тем же успехом мы могли снять штрих в точке, показанной на рисунке.
Угол между касательной и положительным направлением оси назовем $beta $. Соответственно, $f$ в ${{x}_{2}}$ будет равна тангенсу этого угла $beta $.
[{f}’left( {{x}_{2}} right)=tgtext{ }!!beta!!text{ }]
В каждой точке графика будет своя касательная, а, следовательно, свое значение функции. В каждом из этих случаев помимо точки, в которой мы ищем производную разности или суммы, или производную степенной функции, необходимо взять другую точку, находящуюся на некотором расстоянии от нее, а затем устремить эту точку к исходной и, разумеется, выяснить, как в процессе такого движения будет меняться тангенс угла наклона.
Производная степенной функции
К сожалению, подобное определение нас совершено не устраивает. Все эти формулы, картинки, углы не дают нам ни малейшего представления о том, как считать реальную производную в реальных задачах. Поэтому давайте немного отвлечемся от формального определения и рассмотрим более действенные формулы и приемы, с помощью которых уже можно решать настоящие задачи.
Начнем с самых простых конструкций, а именно, функций вида $y={{x}^{n}}$, т.е. степенных функций. В этом случае мы можем записать следующее: ${y}’=ncdot {{x}^{n-1}}$. Другими словами, степень, которая стояла в показателе, показывается в множителе спереди, а сам показатель уменьшается на единицу. Например:
[begin{align}& y={{x}^{2}} \& {y}’=2cdot {{x}^{2-1}}=2x \end{align}]
А вот другой вариант:
[begin{align}& y={{x}^{1}} \& {y}’={{left( x right)}^{prime }}=1cdot {{x}^{0}}=1cdot 1=1 \& {{left( x right)}^{prime }}=1 \end{align}]
Пользуясь этими простыми правилами, давайте попробуем снять штрих следующих примеров:
[fleft( x right)={{x}^{6}}]
Итак, мы получаем:
[{{left( {{x}^{6}} right)}^{prime }}=6cdot {{x}^{5}}=6{{x}^{5}}]
Теперь решим второе выражение:
[begin{align}& fleft( x right)={{x}^{100}} \& {{left( {{x}^{100}} right)}^{prime }}=100cdot {{x}^{99}}=100{{x}^{99}} \end{align}]
Разумеется, это были очень простые задачи. Однако реальные задачи более сложные и они не ограничиваются одними лишь степенями функции.
Итак, правило № 1 – если функция представлена в виде других двух, то производная этой суммы равна сумме производных:
[{{left( f+g right)}^{prime }}={f}’+{g}’]
Аналогично, производная разности двух функций равна разности производных:
[{{left( f-g right)}^{prime }}={f}’-{g}’]
Пример:
[{{left( {{x}^{2}}+x right)}^{prime }}={{left( {{x}^{2}} right)}^{prime }}+{{left( x right)}^{prime }}=2x+1]
Кроме того, есть еще одно важное правило: если перед некоторой $f$ стоит константа $c$, на которую эта функция умножается, то $f$ всей этой конструкции считается так:
[{{left( ccdot f right)}^{prime }}=ccdot {f}’]
Пример:
[{{left( 3{{x}^{3}} right)}^{prime }}=3{{left( {{x}^{3}} right)}^{prime }}=3cdot 3{{x}^{2}}=9{{x}^{2}}]
Наконец, еще одно очень важное правило: в задачах часто встречается отдельное слагаемое, которое вообще не содержит $x$. Например, мы можем наблюдать это в наших сегодняшних выражениях. Производная константы, т. е., числа, никак не зависящего от $x$, всегда равна нулю, причем совершенно неважно, чему равна константа $c$:
[{{left( c right)}^{prime }}=0]
Пример решения:
[{{left( 1001 right)}^{prime }}={{left( frac{1}{1000} right)}^{prime }}=0]
Еще раз ключевые моменты:
- Производная суммы двух функций всегда равна сумме производных: ${{left( f+g right)}^{prime }}={f}’+{g}’$;
- По аналогичным причинам производная разности двух функций равна разности двух производных: ${{left( f-g right)}^{prime }}={f}’-{g}’$;
- Если у функции присутствует множитель константа, то эту константу можно выносить за знак производной: ${{left( ccdot f right)}^{prime }}=ccdot {f}’$;
- Если вся функция представляет собой константу, то ее производная всегда ноль: ${{left( c right)}^{prime }}=0$.
Давайте посмотрим, как все это работает на реальных примерах. Итак:
[y={{x}^{5}}-3{{x}^{2}}+7]
Записываем:
[begin{align}& {{left( {{x}^{5}}-3{{x}^{2}}+7 right)}^{prime }}={{left( {{x}^{5}} right)}^{prime }}-{{left( 3{{x}^{2}} right)}^{prime }}+{7}’= \& =5{{x}^{4}}-3{{left( {{x}^{2}} right)}^{prime }}+0=5{{x}^{4}}-6x \end{align}]
В этом примере мы видим и производную суммы, и производную разности. Итого, производная равна $5{{x}^{4}}-6x$.
Переходим ко второй функции:
[fleft( x right)=3{{x}^{2}}-2x+2]
Записываем решение:
[begin{align}& {{left( 3{{x}^{2}}-2x+2 right)}^{prime }}={{left( 3{{x}^{2}} right)}^{prime }}-{{left( 2x right)}^{prime }}+{2}’= \& =3{{left( {{x}^{2}} right)}^{prime }}-2{x}’+0=3cdot 2x-2cdot 1=6x-2 \end{align}]
Вот мы и нашли ответ.
Переходим к третьей функции — она уже посерьезней:
[y=2{{x}^{3}}-3{{x}^{2}}+frac{1}{2}x-5]
Решаем:
[begin{align}& {{left( 2{{x}^{3}}-3{{x}^{2}}+frac{1}{2}x-5 right)}^{prime }}={{left( 2{{x}^{3}} right)}^{prime }}-{{left( 3{{x}^{2}} right)}^{prime }}+{{left( frac{1}{2}x right)}^{prime }}-{5}’= \& =2{{left( {{x}^{3}} right)}^{prime }}-3{{left( {{x}^{2}} right)}^{prime }}+frac{1}{2}cdot {x}’=2cdot 3{{x}^{2}}-3cdot 2x+frac{1}{2}cdot 1=6{{x}^{2}}-6x+frac{1}{2} \end{align}]
Ответ мы нашли.
Переходим к последнему выражению — самому сложному и самому длинному:
[y=6{{x}^{7}}-14{{x}^{3}}+4x+5,{{x}_{0}}=-1]
Итак, считаем:
[begin{align}& {{left( 6{{x}^{7}}-14{{x}^{3}}+4x+5 right)}^{prime }}={{left( 6{{x}^{7}} right)}^{prime }}-{{left( 14{{x}^{3}} right)}^{prime }}+{{left( 4x right)}^{prime }}+{5}’= \& =6cdot 7cdot {{x}^{6}}-14cdot 3{{x}^{2}}+4cdot 1+0=42{{x}^{6}}-42{{x}^{2}}+4 \end{align}]
Но на этом решение не заканчивается, потому что нас просят не просто снять штрих, а посчитать ее значение в конкретной точке, поэтому подставляем в выражение −1 вместо $x$:
[{y}’left( -1 right)=42cdot 1-42cdot 1+4=4]
Идем далее и переходим к еще более сложным и интересным примерам. Дело в том, что формула решения степенной производной ${{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}$ имеет еще более широкую область применения, чем обычно принято считать. С ее помощью можно решать примеры с дробями, корнями и т. д. Именно этим мы сейчас и займемся.
Для начала еще раз запишем формулу, которая поможет нам найти производную степенной функции:
[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]
А теперь внимание: до сих пор мы рассматривали в качестве $n$ лишь натуральные числа, однако ничего не мешаем рассмотреть дроби и даже отрицательные числа. Например, мы можем записать следующее:
[begin{align}& sqrt{x}={{x}^{frac{1}{2}}} \& {{left( sqrt{x} right)}^{prime }}={{left( {{x}^{frac{1}{2}}} right)}^{prime }}=frac{1}{2}cdot {{x}^{-frac{1}{2}}}=frac{1}{2}cdot frac{1}{sqrt{x}}=frac{1}{2sqrt{x}} \end{align}]
Ничего сложного, поэтому посмотрим, как эта формула поможет нам при решении более сложных задач. Итак, пример:
[y=sqrt{x}+sqrt[3]{x}+sqrt[4]{x}]
Записываем решение:
[begin{align}& left( sqrt{x}+sqrt[3]{x}+sqrt[4]{x} right)={{left( sqrt{x} right)}^{prime }}+{{left( sqrt[3]{x} right)}^{prime }}+{{left( sqrt[4]{x} right)}^{prime }} \& {{left( sqrt{x} right)}^{prime }}=frac{1}{2sqrt{x}} \& {{left( sqrt[3]{x} right)}^{prime }}={{left( {{x}^{frac{1}{3}}} right)}^{prime }}=frac{1}{3}cdot {{x}^{-frac{2}{3}}}=frac{1}{3}cdot frac{1}{sqrt[3]{{{x}^{2}}}} \& {{left( sqrt[4]{x} right)}^{prime }}={{left( {{x}^{frac{1}{4}}} right)}^{prime }}=frac{1}{4}{{x}^{-frac{3}{4}}}=frac{1}{4}cdot frac{1}{sqrt[4]{{{x}^{3}}}} \end{align}]
Возвращаемся к нашему примеру и записываем:
[{y}’=frac{1}{2sqrt{x}}+frac{1}{3sqrt[3]{{{x}^{2}}}}+frac{1}{4sqrt[4]{{{x}^{3}}}}]
Вот такое сложное решение.
Переходим ко второму примеру — здесь всего два слагаемых, но каждое из них содержит как классическую степень, так и корни.
[y={{x}^{3}}sqrt[3]{{{x}^{2}}}+{{x}^{7}}sqrt[3]{x}]
Сейчас мы узнаем, как найти производную степенной функции, которая, кроме того, содержит и корень:
[begin{align}& {{left( {{x}^{3}}sqrt[3]{{{x}^{2}}}+{{x}^{7}}sqrt[3]{x} right)}^{prime }}={{left( {{x}^{3}}cdot sqrt[3]{{{x}^{2}}} right)}^{prime }}={{left( {{x}^{3}}cdot {{x}^{frac{2}{3}}} right)}^{prime }}= \& ={{left( {{x}^{3+frac{2}{3}}} right)}^{prime }}={{left( {{x}^{frac{11}{3}}} right)}^{prime }}=frac{11}{3}cdot {{x}^{frac{8}{3}}}=frac{11}{3}cdot {{x}^{2frac{2}{3}}}=frac{11}{3}cdot {{x}^{2}}cdot sqrt[3]{{{x}^{2}}} \& {{left( {{x}^{7}}cdot sqrt[3]{x} right)}^{prime }}={{left( {{x}^{7}}cdot {{x}^{frac{1}{3}}} right)}^{prime }}={{left( {{x}^{7frac{1}{3}}} right)}^{prime }}=7frac{1}{3}cdot {{x}^{6frac{1}{3}}}=frac{22}{3}cdot {{x}^{6}}cdot sqrt[3]{x} \end{align}]
Оба слагаемых посчитаны, осталось записать окончательный ответ:
[{y}’=frac{11}{3}cdot {{x}^{2}}cdot sqrt[3]{{{x}^{2}}}+frac{22}{3}cdot {{x}^{6}}cdot sqrt[3]{x}]
Мы нашли ответ.
Производная дроби через степенную функцию
Но и на этом возможности формулы для решения производной степенной функции не заканчиваются. Дело в том, что с ее помощью можно считать не только примеры с корнями, но также и с дробями. Это как раз та редкая возможность, которая значительно упрощает решение таких примеров, но при этом зачастую игнорируется не только учениками, но и учителями.
Итак, сейчас мы попытаемся совместить сразу две формулы. С одной стороны, классическая производная степенной функции
[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]
С другой стороны мы знаем, что выражение вида $frac{1}{{{x}^{n}}}$ представимо в виде ${{x}^{-n}}$. Следовательно,
[left( frac{1}{{{x}^{n}}} right)’={{left( {{x}^{-n}} right)}^{prime }}=-ncdot {{x}^{-n-1}}=-frac{n}{{{x}^{n+1}}}]
Пример:
[{{left( frac{1}{x} right)}^{prime }}=left( {{x}^{-1}} right)=-1cdot {{x}^{-2}}=-frac{1}{{{x}^{2}}}]
Таким образом, производные простых дробей, где в числителе стоит константа, а в знаменателе — степень, также считаются с помощью классической формулы. Посмотрим, как это работает на практике.
Итак, первая функция:
[fleft( x right)=frac{1}{{{x}^{2}}}]
Считаем:
[{{left( frac{1}{{{x}^{2}}} right)}^{prime }}={{left( {{x}^{-2}} right)}^{prime }}=-2cdot {{x}^{-3}}=-frac{2}{{{x}^{3}}}]
Первый пример решен, переходим ко второму:
[y=frac{7}{4{{x}^{4}}}-frac{2}{3{{x}^{3}}}+frac{5}{2}{{x}^{2}}+2{{x}^{3}}-3{{x}^{4}}]
Решаем:
[begin{align}& {{left( frac{7}{4{{x}^{4}}}-frac{2}{3{{x}^{3}}}+frac{5}{2}{{x}^{2}}+2{{x}^{3}}-3{{x}^{4}} right)}^{prime }}= \& ={{left( frac{7}{4{{x}^{4}}} right)}^{prime }}-{{left( frac{2}{3{{x}^{3}}} right)}^{prime }}+{{left( 2{{x}^{3}} right)}^{prime }}-{{left( 3{{x}^{4}} right)}^{prime }} \& {{left( frac{7}{4{{x}^{4}}} right)}^{prime }}=frac{7}{4}{{left( frac{1}{{{x}^{4}}} right)}^{prime }}=frac{7}{4}cdot {{left( {{x}^{-4}} right)}^{prime }}=frac{7}{4}cdot left( -4 right)cdot {{x}^{-5}}=frac{-7}{{{x}^{5}}} \& {{left( frac{2}{3{{x}^{3}}} right)}^{prime }}=frac{2}{3}cdot {{left( frac{1}{{{x}^{3}}} right)}^{prime }}=frac{2}{3}cdot {{left( {{x}^{-3}} right)}^{prime }}=frac{2}{3}cdot left( -3 right)cdot {{x}^{-4}}=frac{-2}{{{x}^{4}}} \& {{left( frac{5}{2}{{x}^{2}} right)}^{prime }}=frac{5}{2}cdot 2x=5x \& {{left( 2{{x}^{3}} right)}^{prime }}=2cdot 3{{x}^{2}}=6{{x}^{2}} \& {{left( 3{{x}^{4}} right)}^{prime }}=3cdot 4{{x}^{3}}=12{{x}^{3}} \end{align}]…
Теперь собираем все эти слагаемые в единую формулу:
[{y}’=-frac{7}{{{x}^{5}}}+frac{2}{{{x}^{4}}}+5x+6{{x}^{2}}-12{{x}^{3}}]
Мы получили ответ.
Однако прежде чем двигаться дальше, хотел бы обратить ваше внимание на форму записи самих исходных выражений: в первом выражении мы записали $fleft( x right)=…$, во втором: $y=…$ Многие ученики теряются, когда видят разные формы записи. Чем отличаются $fleft( x right)$ и $y$? На самом деле, ничем. Это просто разные записи с одним и тем же смыслом. Просто когда мы говорим $fleft( x right)$, то речь идет, прежде всего, о функции, а когда речь идет об $y$, то чаще всего подразумевается график функции. В остальном же это одно и то же, т. е., производная в обоих случаях считается одинаково.
Сложные задачи с производными
В заключение хотелось бы рассмотреть пару сложных комбинированных задач, в которых используется сразу все то, что мы сегодня рассмотрели. В них нас ждут и корни, и дроби, и суммы. Однако сложными эти примеры будут лишь в рамках сегодняшнего видеоурока, потому что по-настоящему сложные функции производных будут ждать вас впереди.
Итак, заключительная часть сегодняшнего видеоурока, состоящая из двух комбинированных задач. Начнем с первой из них:
[y={{x}^{3}}-frac{1}{{{x}^{3}}}+sqrt[3]{x}]
Считаем:
[begin{align}& {{left( {{x}^{3}}-frac{1}{{{x}^{3}}}+sqrt[3]{x} right)}^{prime }}={{left( {{x}^{3}} right)}^{prime }}-{{left( frac{1}{{{x}^{3}}} right)}^{prime }}+left( sqrt[3]{x} right) \& {{left( {{x}^{3}} right)}^{prime }}=3{{x}^{2}} \& {{left( frac{1}{{{x}^{3}}} right)}^{prime }}={{left( {{x}^{-3}} right)}^{prime }}=-3cdot {{x}^{-4}}=-frac{3}{{{x}^{4}}} \& {{left( sqrt[3]{x} right)}^{prime }}={{left( {{x}^{frac{1}{3}}} right)}^{prime }}=frac{1}{3}cdot frac{1}{{{x}^{frac{2}{3}}}}=frac{1}{3sqrt[3]{{{x}^{2}}}} \end{align}]
Производная функции равна:
[{y}’=3{{x}^{2}}-frac{3}{{{x}^{4}}}+frac{1}{3sqrt[3]{{{x}^{2}}}}]
Первый пример решен. Рассмотрим вторую задачу:
[y=-frac{2}{{{x}^{4}}}+sqrt[4]{x}+frac{4}{xsqrt[4]{{{x}^{3}}}}]
Во втором примере действуем аналогично:
[{{left( -frac{2}{{{x}^{4}}}+sqrt[4]{x}+frac{4}{xsqrt[4]{{{x}^{3}}}} right)}^{prime }}={{left( -frac{2}{{{x}^{4}}} right)}^{prime }}+{{left( sqrt[4]{x} right)}^{prime }}+{{left( frac{4}{xcdot sqrt[4]{{{x}^{3}}}} right)}^{prime }}]
Посчитаем каждое слагаемое отдельно:
[begin{align}& {{left( -frac{2}{{{x}^{4}}} right)}^{prime }}=-2cdot {{left( {{x}^{-4}} right)}^{prime }}=-2cdot left( -4 right)cdot {{x}^{-5}}=frac{8}{{{x}^{5}}} \& {{left( sqrt[4]{x} right)}^{prime }}={{left( {{x}^{frac{1}{4}}} right)}^{prime }}=frac{1}{4}cdot {{x}^{-frac{3}{4}}}=frac{1}{4cdot {{x}^{frac{3}{4}}}}=frac{1}{4sqrt[4]{{{x}^{3}}}} \& {{left( frac{4}{xcdot sqrt[4]{{{x}^{3}}}} right)}^{prime }}={{left( frac{4}{xcdot {{x}^{frac{3}{4}}}} right)}^{prime }}={{left( frac{4}{{{x}^{1frac{3}{4}}}} right)}^{prime }}=4cdot {{left( {{x}^{-1frac{3}{4}}} right)}^{prime }}= \& =4cdot left( -1frac{3}{4} right)cdot {{x}^{-2frac{3}{4}}}=4cdot left( -frac{7}{4} right)cdot frac{1}{{{x}^{2frac{3}{4}}}}=frac{-7}{{{x}^{2}}cdot {{x}^{frac{3}{4}}}}=-frac{7}{{{x}^{2}}cdot sqrt[4]{{{x}^{3}}}} \end{align}]
Все слагаемые посчитаны. Теперь возвращаемся к исходной формуле и складываем вместе все три слагаемых. Получаем, что окончательный ответ будет таким:
[{y}’=frac{8}{{{x}^{5}}}+frac{1}{4sqrt[4]{{{x}^{3}}}}-frac{7}{{{x}^{2}}cdot sqrt[4]{{{x}^{3}}}}]
И на этом все. Это был первый наш урок. В следующих уроках мы рассмотрим более сложные конструкции, а также выясним, зачем вообще нужны производные.
Смотрите также:
- Производная произведения и частного
- Правила вычисления производных
- Теорема Виета
- Преобразование уравнений
- Тест по методу интервалов для строгих неравенств
- Тест по задачам B14: средний уровень, 2 вариант
В данной публикации мы рассмотрим, чему равна производная степенной функций (в т.ч. сложной), а также разберем примеры решения задач для закрепления изложенного материала.
-
Формула производной степенной функции
- Производная сложной степенной функции
- Примеры задач
Формула производной степенной функции
Для функции f(x) = x n, где n – действительное число, справедливо следующее выражение:
f ‘(x) = (x n)‘ = nx n-1
Т.е. производная степенной функции равняется произведению показателя степени на основание в степени, уменьшенной на единицу.
n – может быть как положительным, так и отрицательным числом (в т.ч. дробным):
Производная сложной степенной функции
В сложной функции вместо x представлено более сложное выражение. Производная такой функции определяется по формуле:
(y n)‘ = ny n-1 ⋅ y ‘
Примеры задач
Задание 1:
Вычислите производную функцию f(x) = x3/5.
Решение:
Согласно правилам дифференцирования константу в виде дроби можно вынести за знак производной:
Применив формулу производной, рассмотренную выше, получаем:
Задание 2:
Найдите производную функции f(x) = x2 + √x – 6.
Решение:
Первоначальный вид производной функции:
f ‘(x) = (x2 + √x – 6)‘.
С учетом правила дифференцирования суммы получаем:
f ‘(x) = (x2)‘ + (√x)‘ – (6)‘.
Остается только вычислить производные по отдельности:
(x2)‘ = 2x2-1 = 2x
(-6)‘ = 0 (производная константы равна нулю)
Таким образом получаем:
Содержание:
- 1-ый способ
- 2-ой способ
- 3-ий способ
Определение
Степенно-показательной функцией (или показательно-степенной, или
функцией в степени функция) называется функция вида
$y(x)=u(x)^{v(x)}$
Рассмотрим способы нахождения ее производной.
1-ый способ
Применяя формулу:
$$left(u(x)^{v(x)}right)^{prime}=v(x) cdot u(x)^{v(x)-1} cdot u^{prime}(x)+u(x)^{v(x)} cdot ln u(x) cdot v^{prime}(x)$$
То есть вначале производная берется как от степенной функции, а потом как от показательной.
Замечание
Порядок следования слагаемых неважен: можно вначале взять производную от показательной функции, а
затем как от степенной, так как от перестановки слагаемых сумма не меняется:
$$left(u(x)^{v(x)}right)^{prime}=u(x)^{v(x)} cdot ln u(x) cdot v^{prime}(x)+v(x) cdot u(x)^{v(x)-1} cdot u^{prime}(x)$$
Пример
Задание. Найти производную функции
$y(x)=(operatorname{arctg} x)^{x}$
Решение. Применяем формулу. В рассматриваемом случае
$u(x)=operatorname{arctg} x, v(x)=x$
Тогда имеем:
$$begin{array}{c}
y^{prime}(x)=left((operatorname{arctg} x)^{x}right)^{prime}=x cdot(operatorname{arctg} x)^{x-1} cdot(operatorname{arctg} x)^{prime}+ \
+(operatorname{arctg} x)^{x} cdot ln operatorname{arctg} x cdot(x)^{prime}=x cdot(operatorname{arctg} x)^{x-1} cdot frac{1}{1+x^{2}}+ \
quad+(operatorname{arctg} x)^{x} cdot ln operatorname{arctg} x cdot 1= \
=frac{x(operatorname{arctg} x)^{x-1}}{1+x^{2}}+(operatorname{arctg} x)^{x} cdot ln operatorname{arctg} x= \
=(operatorname{arctg} x)^{x}left(frac{x}{operatorname{arctg} x cdotleft(1+x^{2}right)}+ln operatorname{arctg} xright)
end{array}$$
Ответ. $y^{prime}(x)=(operatorname{arctg} x)^{x}left(frac{x}{operatorname{arctg} x cdotleft(1+x^{2}right)}+ln operatorname{arctg} xright)$
2-ой способ
С помощью логарифмического дифференцирования:
$$begin{array}{c}
y(x)=u(x)^{v(x)} \
ln y(x)=ln u(x)^{v(x)} \
ln y(x)=v(x) cdot ln u(x) \
(ln y(x))^{prime}=(v(x) cdot ln u(x))^{prime} \
frac{y^{prime}(x)}{y(x)}=v^{prime}(x) cdot ln u(x)+v(x) cdot(ln u(x))^{prime} Rightarrow \
Rightarrow y^{prime}(x)=y(x)left[v^{prime}(x) cdot ln u(x)+v(x) cdot(ln u(x))^{prime}right]= \
=u(x)^{v(x)}left[v^{prime}(x) cdot ln u(x)+v(x) cdot(ln u(x))^{prime}right]
end{array}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти производную функции $y(x)=(operatorname{arctg} x)^{x}$ с помощью логарифмического дифференцирования.
Решение. Прологарифмируем левую и правую часть заданной функции, будем иметь:
$$ln y(x)=ln (operatorname{arctg} x)^{x}$$
По свойствам логарифмов в правой части полученного равенства степень подлогарифмической функции выносим перед логарифмом:
$$ln y(x)=x ln (operatorname{arctg} x)$$
Дифференцируем левую и правую часть равенства. Слева берем
производную как от сложной функции (так как
$y$ – это функция от переменной
$x$), а справа – как
производную произведения:
$$begin{array}{c}
(ln y(x))^{prime}=(x ln (operatorname{arctg} x))^{prime} \
frac{y^{prime}(x)}{y(x)}=(x)^{prime} cdot ln (operatorname{arctg} x)+x cdot(ln (operatorname{arctg} x))^{prime}= \
=1 cdot ln (operatorname{arctg} x)+x cdot frac{1}{operatorname{arctg} x} cdot(operatorname{arctg} x)^{prime}= \
=ln (operatorname{arctg} x)+frac{x}{operatorname{arctg} x} cdot frac{1}{1+x^{2}}=ln (operatorname{arctg} x)+frac{x}{operatorname{arctg} x cdotleft(1+x^{2}right)}
end{array}$$
А тогда
$$begin{array}{c}
y^{prime}(x)=y(x)left(ln (operatorname{arctg} x)+frac{x}{operatorname{arctg} x cdotleft(1+x^{2}right)}right)= \
=(operatorname{arctg} x)^{x}left(ln (operatorname{arctg} x)+frac{x}{operatorname{arctg} x cdotleft(1+x^{2}right)}right)
end{array}$$
Ответ. $y^{prime}(x)=(operatorname{arctg} x)^{x}left(ln (operatorname{arctg} x)+frac{x}{operatorname{arctg} x cdotleft(1+x^{2}right)}right)$
3-ий способ
Представим функцию $y(x)=u(x)^{v(x)}$ в следующем виде
(используются свойства логарифмов):
$$y(x)=u(x)^{v(x)}=e^{ln u(x)^{w(x)}}=e^{v(x) ln u(x)}$$
Тогда
$$begin{array}{c}
y^{prime}(x)=left(e^{v(x) ln u(x)}right)^{prime}=e^{v(x) ln u(x)} cdot(v(x) ln u(x))^{prime}= \
=e^{v(x) ln u(x)} cdotleft[v^{prime}(x) cdot ln u(x)+v(x) cdot(ln u(x))^{prime}right]= \
=u(x)^{v(x)} cdotleft[v^{prime}(x) cdot ln u(x)+v(x) cdot(ln u(x))^{prime}right]
end{array}$$
Пример
Задание. Найти производную функции $y(x)=(operatorname{arctg} x)^{x}$
Решение. Представляем функцию в следующем виде:
$$y(x)=(operatorname{arctg} x)^{x}=e^{ln (operatorname{arctg} x)^{x}}=e^{x ln (operatorname{arctg} x)}$$
Далее находим производную, от экспоненты берем производную как от сложной функции (см.
производные сложных функций):
$$y^{prime}(x)=left(e^{x ln operatorname{arctg} x}right)^{prime}=e^{x ln operatorname{arctg} x} cdot(x cdot ln operatorname{arctg} x)^{prime}=$$
$$=(operatorname{arctg} x)^{x}left[(x)^{prime} cdot ln operatorname{arctg} x+x cdot(ln operatorname{arctg} x)^{prime}right]=$$
$$=(operatorname{arctg} x)^{x}left[1 cdot ln operatorname{arctg} x+x cdot frac{1}{operatorname{arctg} x} cdot(operatorname{arctg} x)^{prime}right]=$$
$$=(operatorname{arctg} x)^{x}left[ln operatorname{arctg} x+frac{x}{operatorname{arctg} x} cdot frac{1}{1+x^{2}}right]=$$
$$=(operatorname{arctg} x)^{x}left[ln operatorname{arctg} x+frac{x}{operatorname{arctg} x cdotleft(1+x^{2}right)}right]$$
Ответ. $y^{prime}(x)=(operatorname{arctg} x)^{x}left(ln (operatorname{arctg} x)+frac{x}{operatorname{arctg} x cdotleft(1+x^{2}right)}right)$
Читать дальше: основные теоремы дифференциального исчисления.
Приведем сводную таблицу для удобства и наглядности при изучении темы.
|
Константа y=C (C)’=0 Степенная функция y=xp (xp)’=p·xp-1 |
Показательная функция y=ax (ax)’=ax·ln a В частности, при a=e имеем y=ex (ex)’=ex |
|
Логарифмическая функция (logax)’=1x·ln a В частности, при a=e имеем y=ln x (ln x)’=1x |
Тригонометрические функции (sin x)’=cos x(cos x)’=-sin x(tgx)’=1cos2x(ctgx)’=-1sin2x |
|
Обратные тригонометрические функции (arcsin x)’=11-x2(arccos x)’=-11-x2(arctg x)’=11+x2(arcctg x)’=-11+x2 |
Гиперболические функции (shx)’=chx(chx)’=shx(thx)’=1ch2x(cthx)’=-1sh2x |
Разберем, каким образом были получены формулы указанной таблицы или, иначе говоря, докажем вывод формул производных для каждого вида функций.
Производная постоянной
Для того, чтобы вывести данную формулу, возьмем за основу определение производной функции в точке. Используем x0=x, где x принимает значение любого действительного числа, или, иначе говоря, x является любым числом из области определения функции f(x)=C. Составим запись предела отношения приращения функции к приращению аргумента при ∆x→0:
lim∆x→0∆f(x)∆x=lim∆x→0C-C∆x=lim∆x→00∆x=0
Обратите внимание, что под знак предела попадает выражение 0∆x. Оно не есть неопределенность «ноль делить на ноль», поскольку в числителе записана не бесконечно малая величина, а именно нуль. Иначе говоря, приращение постоянной функции всегда есть нуль.
Итак, производная постоянной функции f(x)=C равна нулю на всей области определения.
Даны постоянные функции:
f1(x)=3,f2(x)=a, a∈R,f3(x)=4.13722,f4(x)=0,f5(x)=-87
Необходимо найти их производные.
Решение
Опишем заданные условия. В первой функции мы видим производную натурального числа 3. В следующем примере необходимо брать производную от а, где а – любое действительное число. Третий пример задает нам производную иррационального числа 4.13722, четвертый – производную нуля (нуль – целое число). Наконец, в пятом случае имеем производную рациональной дроби -87.
Ответ: производные заданных функций есть нуль при любом действительном x (на всей области определения)
f1′(x)=(3)’=0,f2′(x)=(a)’=0, a∈R,f3′(x)=4.13722’=0,f4′(x)=0’=0,f5′(x)=-87’=0
Производная степенной функции
Переходим к степенной функции и формуле ее производной, имеющей вид: (xp)’=p·xp-1, где показатель степени p является любым действительным числом.
Приведем доказательство формулы, когда показатель степени – натуральное число: p=1, 2, 3, …
Вновь опираемся на определение производной. Составим запись предела отношения приращения степенной функции к приращению аргумента:
(xp)’=lim∆x→0=∆(xp)∆x=lim∆x→0(x+∆x)p-xp∆x
Чтобы упростить выражение в числителе, используем формулу бинома Ньютона:
(x+∆x)p-xp=Cp0+xp+Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+…++Cpp-1·x·(∆x)p-1+Cpp·(∆x)p-xp==Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+…+Cpp-1·x·(∆x)p-1+Cpp·(∆x)p
Таким образом:
(xp)’=lim∆x→0∆(xp)∆x=lim∆x→0(x+∆x)p-xp∆x==lim∆x→0(Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+…+Cpp-1·x·(∆x)p-1+Cpp·(∆x)p)∆x==lim∆x→0(Cp1·xp-1+Cp2·xp-2·∆x+…+Cpp-1·x·(∆x)p-2+Cpp·(∆x)p-1)==Cp1·xp-1+0+0+…+0=p!1!·(p-1)!·xp-1=p·xp-1
Так, мы доказали формулу производной степенной функции, когда показатель степени – натуральное число.
Чтобы привести доказательство для случая, когда p – любое действительное число, отличное от нуля, используем логарифмическую производную (здесь следует понимать отличие от производной логарифмической функции). Чтобы иметь более полное понимание желательно изучить производную логарифмической функции и дополнительно разобраться с производной неявно заданной функции и производной сложной функции.
Рассмотрим два случая: когда x положительны и когда x отрицательны.
Итак, x>0. Тогда: xp>0. Логарифмируем равенство y=xp по основанию e и применим свойство логарифма:
y=xpln y=ln xpln y=p·ln x
На данном этапе получили неявно заданную функцию. Определим ее производную:
(ln y)’=(p·ln x)1y·y’=p·1x⇒y’=p·yx=p·xpx=p·xp-1
Теперь рассматриваем случай, когда x – отрицательное число.
Если показатель p есть четное число, то степенная функция определяется и при x<0, причем является четной: y(x)=-y((-x)p)’=-p·(-x)p-1·(-x)’==p·(-x)p-1=p·xp-1
Тогда xp<0 и возможно составить доказательство, используя логарифмическую производную.
Если p есть нечетное число, тогда степенная функция определена и при x<0, причем является нечетной: y(x)=-y(-x)=-(-x)p. Тогда xp<0, а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:
y'(x)=(-(-x)p)’=-((-x)p)’=-p·(-x)p-1·(-x)’==p·(-x)p-1=p·xp-1
Последний переход возможен в силу того, что если p – нечетное число, то p-1 либо четное число, либо нуль (при p=1), поэтому, при отрицательных x верно равенство (-x)p-1=xp-1.
Итак, мы доказали формулу производной степенной функции при любом действительном p.
Даны функции:
f1(x)=1×23,f2(x)=x2-14,f3(x)=1xlog712
Определите их производные.
Решение
Часть заданных функций преобразуем в табличный вид y=xp, опираясь на свойства степени, а затем используем формулу:
f1(x)=1×23=x-23⇒f1′(x)=-23·x-23-1=-23·x-53f2′(x)=x2-14=2-14·x2-14-1=2-14·x2-54f3(x)=1xlog712=x-log712⇒f3′(x)=-log712·x-log712-1=-log712·x-log712-log77=-log712·x-log784
Производная показательной функции
Выведем формулу производной, взяв за основу определение:
(ax)’=lim∆x→0ax+∆x-ax∆x=lim∆x→0ax(a∆x-1)∆x=ax·lim∆x→0a∆x-1∆x=00
Мы получили неопределенность. Чтобы раскрыть ее, запишем новую переменную z=a∆x-1 (z→0 при ∆x→0). В таком случае a∆x=z+1⇒∆x=loga(z+1)=ln(z+1)ln a. Для последнего перехода использована формула перехода к новому основанию логарифма.
Осуществим подстановку в исходный предел:
(ax)’=ax·lim∆x→0a∆x-1∆x=ax·ln a·lim∆x→011z·ln(z+1)==ax·ln a·lim∆x→01ln(z+1)1z=ax·ln a·1lnlim∆x→0(z+1)1z
Вспомним второй замечательный предел и тогда получим формулу производной показательной функции:
(ax)’=ax·ln a·1lnlimz→0(z+1)1z=ax·ln a·1ln e=ax·ln a
Даны показательные функции:
f1(x)=23x,f2(x)=53x,f3(x)=1(e)x
Необходимо найти их производные.
Решение
Используем формулу производной показательной функции и свойства логарифма:
f1′(x)=23x’=23x·ln23=23x·(ln 2-ln 3)f2′(x)=53x’=53x·ln 513=13·53x·ln 5f3′(x)=1(e)x’=1ex’=1ex·ln1e=1ex·ln e-1=-1ex
Производная логарифмической функции
Приведем доказательство формулы производной логарифмической функции для любых x в области определения и любых допустимых значениях основания а логарифма. Опираясь на определение производной, получим:
(logax)’=lim∆x→0loga(x+∆x)-logax∆x=lim∆x→0logax+∆xx∆x==lim∆x→01∆x·loga1+∆xx=lim∆x→0loga1+∆xx1∆x==lim∆x→0loga1+∆xx1∆x·xx=lim∆x→01x·loga1+∆xxx∆x==1x·logalim∆x→01+∆xxx∆x=1x·logae=1x·ln eln a=1x·ln a
Из указанной цепочки равенств видно, что преобразования строились на основе свойства логарифма. Равенство lim∆x→01+∆xxx∆x=e является верным в соответствии со вторым замечательным пределом.
Заданы логарифмические функции:
f1(x)=logln3 x,f2(x)=ln x
Необходимо вычислить их производные.
Решение
Применим выведенную формулу:
f1′(x)=(logln3 x)’=1x·ln(ln 3);f2′(x)=(ln x)’=1x·ln e=1x
Итак, производная натурального логарифма есть единица, деленная на x.
Производные тригонометрических функций
Используем некоторые тригонометрические формулы и первый замечательный предел, чтобы вывести формулу производной тригонометрической функции.
Согласно определению производной функции синуса, получим:
(sin x)’=lim∆x→0sin (x+∆x)-sin x∆x
Формула разности синусов позволит нам произвести следующие действия:
(sin x)’=lim∆x→0sin (x+∆x)-sin x∆x==lim∆x→02·sin x+∆x-x2·cosx+∆x+x2∆x==lim∆x→0sin ∆x2·cosx+∆x2∆x2==cosx+02·lim∆x→0sin ∆x2∆x2
Наконец, используем первый замечательный предел:
sin’ x=cos x+02·lim∆x→0sin∆x2∆x2=cos x
Итак, производной функции sin x будет cos x.
Совершенно также докажем формулу производной косинуса:
cos’ x=lim∆x→0cos (x+∆x)-cos x∆x==lim∆x→0-2·sin x+∆x-x2·sinx+∆x+x2∆x==-lim∆x→0sin∆x2·sinx+∆x2∆x2==-sinx+02·lim∆x→0sin∆x2∆x2=-sin x
Т.е. производной функции cos x будет –sin x.
Формулы производных тангенса и котангенса выведем на основе правил дифференцирования:
tg’x=sin xcos x’=sin’ x·cos x-sin x·cos’ xcos2 x==cos x·cos x-sin x·(-sin x)cos2 x=sin2 x+cos2 xcos2 x=1cos2 xctg’x=cos xsin x’=cos’x·sin x-cos x·sin’xsin2 x==-sin x·sin x-cos x·cos xsin2 x=-sin2 x+cos2 xsin2 x=-1sin2 x
Производные обратных тригонометрических функций
Раздел о производной обратных функций дает исчерпывающую информацию о доказательстве формул производных арксинуса, арккосинуса, арктангенса и арккотангенса, поэтому дублировать материал здесь не будем.
Производные гиперболических функций
Вывод формул производных гиперболического синуса, косинуса, тангенса и котангенса осуществим при помощи правила дифференцирования и формулы производной показательной функции:
sh’x=ex-e-x2’=12ex’-e-x’==12ex–e-x=ex+e-x2=chxch’x=ex+e-x2’=12ex’+e-x’==12ex+-e-x=ex-e-x2=shxth’x=shxchx’=sh’x·chx-shx·ch’xch2x=ch2x-sh2xch2x=1ch2xcth’x=chxshx’=ch’x·shx-chx·sh’xsh2x=sh2x-ch2xsh2x=-1sh2x
Рекомендуется выучить формулы из таблицы производных: они не столь сложны для запоминания, но экономят много времени, когда необходимо решать задачи дифференцирования.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
 как х-1;
как х-1; и по формуле (1) получаем:
и по формуле (1) получаем: и по формуле (2) получаем:
и по формуле (2) получаем: