Как найти производную суммы произведения частного

Нахождение
производной функции непосредственно
по определению часто связано с
определенными трудностями. На практике
функции дифференцируют с помощью ряда
правил и формул.

Пусть
функции u=u(х) и ν=ν(х) – две дифференцируемые
в некотором интервале (a;b) функции.

Теорема
20.2 .
Производная суммы (разности) двух функций
равна сумме (разности) производных этих
функций: (u±ν)’=u’±ν’.

Обозначим
у=u±ν. По определению производной и
основным теоремам о пределах получаем:

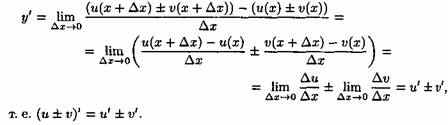
Теорема
справедлива для любого конечного числа
слагаемых.

Теорема
20.3 .
Производная произведения двух функций
равна произведению производной первого
сомножителя на второй плюс произведение
первого сомножителя на производную
второго: (u•ν)’=u’ν+v’u.

т.
е. (u•ν)’=u’•ν+u•ν‘.

При
доказательстве теоремы использовалась
теорема о связи непрерывности и
дифференцируемости: так как функции
u=u(х) и ν=ν(х) дифференцируемы, то они и
непрерывны, поэтому ∆ν→0 и ∆u→0 при
∆х→0.

Можно
показать, что:

а) 
(с•u)’=с•u’, где с = const; 

б) 
(u•ν•w)’=u’v•w+u•v’•w+u•v•w’.  

Теорема
20.4. Производная
частного двух функций   
 если
ν(х)≠0 равна дроби, числитель которой
есть разность произведений знаменателя
дроби на производную числителя и
числителя дроби на производную
знаменателя, а знаменатель есть квадрат
прежнего знаменателя:

Пусть
у=u/v. Тогда

Следствие
20.1.

  

Следствие
20.2.

20.5. Производная сложной и обратной функций

Пусть
у=ƒ(и) и u=φ(х), тогда у=ƒ(φ(х)) — сложная
функция с промежуточным аргументом u и
независимым аргументом х.

Теорема
20.5 .
Если функция u=φ(х) имеет производную
u’_х в
точке х, а функция у=ƒ(u) имеет производную
у’_u в
соответствующей точке u=φ(х), то сложная
функция у=ƒ(φ(х)) имеет производную у’_х в
точке х, которая находится по формуле
у’_х=у’_u-u’_х.

По
условию

Отсюда,
по теореме о связи функции, ее предела
и бесконечно малой функции, имеем

∆у=у’_u•∆u+α*∆u,                                    
(20.6)

где
α→0 при ∆u→0.

Функция
u=φ(х) имеет производную в точке х:

этому

∆u=u¢ _х •∆х+ß•∆х,
где ß→0 при ∆х→0.

Подставив
значение ∆u в равенство (20.6), получим

Δy=y¢ _u(u’_х•∆х+ß*∆х)+а(u’_х•∆х+ß•∆х),

т.е.

∆у=у’u•u’_х•∆х+у’_u•ß•∆х+u’_х•а•∆х+α•ß•∆х.

Разделив
полученное равенство на ∆х и перейдя
к пределу при ∆х→О, получим у’_х=у’_u*u’_х.

Итак,
для нахождения производной сложной
функции надо производную данной функции
по промежуточному аргументу умножыть
на производную промежуточного аргумента
по независимому аргументу.

Это
правило остается в силе, если промежуточных
аргументов несколько. Так, если у=ƒ(u),
u=φ(ν), ν=g(х), то у’_х=у’_u•u’_ν•ν’_х.
Пусть у=ƒ(х) и х=φ(у) — взаимно обратные
функции.

Теорема
20.6 .
Если функция у=ƒ(х) строго монотонна на
интервале (a;b) и имеет неравную нулю
производную ƒ'(х) в произвольной точке
этого интервала, то обратная ей функция
х=φ(у) также имеет производную φ'(у) в
соответствующей точке, определяемую
равенством

Рассмотрим
обратную функцию х=φ(у). Дадим аргументу
у приращение ∆у¹ 0. Ему соответствует
приращение ∆х обратной функции, причем
∆х¹ 0 в силу строгой монотонности
функции у=ƒ(х). Поэтому можно записать

Если
∆у→0, то в силу непрерывности обратной
функции приращение ∆х→0. И так как

то
из (20.7) следуют равенства

Таким
образом, производная
обратной функции равна обратной величине
производной данной функции.

Правило
дифференцирования обратной функции
записывают так:

<<
Пример 20.3

 Найти
производную функции у=log₂³tg
x⁴.

Решение:
Данная функция является сложной. Ее
можно представить в виде цепочки
«простых» функций: у=u³,
где u=Iog₂z,
где z=tgq, где q=х⁴.
По правилу дифференцирования сложной
функции (у’_х=y’_u•u’_z•z’_q•q’_x)
получаем:

<<
Пример 20.4

 Пользуясь  
правилом   дифференцирования  
обратной функции, найти производную
у’_х для
функции  

Решение:
Обратная функция х=у³+1
имеет производную х’_y =3у².

Следовательно,

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Чтобы успешно решать задачи на дифференцирование, нужно уметь находить разные виды производных. Данная статья посвящена основным правилам дифференцирования, которые постоянно используются на практике. С помощью самого определения производной функции мы сформулируем доказательства всех этих правил и подробно рассмотрим несколько примеров, чтобы понять, как они применяются при решении задач.

Условимся заранее, что все функции f(x) и g(x), упомянутые здесь, будем считать дифференцируемыми на промежутке x, иными словами, для любого x0=x∈X будет справедливо равенство f'(x)=lim∆x→0∆f(x)∆x, g'(x)=lim∆x→0∆g(x)∆x. Здесь ∆f(x)=f(x+∆x)-f(x), ∆g(x)=g(x+∆x)-g(x) считаются приращениями указанных функций. Также это можно записать как f(x+∆x)=f(x)+∆f(x), g(x+∆x)=g(x)+∆g(x).

Разберем все эти случаи по порядку.

C·f(x)’=C·f'(x), C∈R(f(x)±g(x))’=f'(x)±g'(x)(f(x)·g(x))’=f'(x)·g(x)+f(x)·g'(x)f(x)g(x)’=f'(x)·g(x)-f(x)·g'(x)g2(x)

Как вынести постоянный множитель за знак производной

Этим мы доказали первое правило дифференцирования. Разберем задачу на его применение. 

Это самый простой пример. На практике чаще всего приходится предварительно преобразовывать дифференцируемую функцию, чтобы увидеть нужное значение в таблице производных и применить соответствующее правило.

Как вычислить производную суммы и производную разности

Чтобы доказать второе правило дифференцирования f(x)±g(x)’=f'(x)±g'(x), нам нужно вспомнить определение производной, а также одно из свойств, которым обладает предел непрерывной функции.

f(x)±g(x)’=lim∆x→0∆(f(x)±g(x))∆x==lim∆x→0fx+∆x±gx+∆x-(f(x)±g(x))∆x==lim∆x→0f(x+∆x)-f(x)±(g(x+∆x)-g(x))∆x==lim∆x→0f(x+∆x)-f(x)∆x±lim∆x→0g(x+∆x)-g(x)∆x==lim∆x→0∆f(x)∆x±lim∆x→0∆g(x)∆x=f'(x)±g'(x)

Как вычислить производную произведения функций

Правило дифференцирования произведения двух функций выглядит следующим образом: fx·g(x)’=f'(x)·g(x)’+f(x)·g'(x)

Попробуем доказать его.  

Теперь разберем, что нужно делать в случае, когда производную нужно найти для произведения трех функций. По той же схеме решаются задачи с произведениями четырех, пяти и большего количества функций.

Из этого примера видно, что иногда приходится применять несколько правил дифференцирования подряд для вычисления нужного результата. Это не так сложно, как кажется, главное – соблюдать нужную последовательность действий.

Как вычислить производную частного двух функций (дробного выражения с функциями)

Данное правило выглядит следующим образом: f(x)g(x)’=f'(x)·g(x)-f(x)·g'(x)g2(x).

Докажем его.  

Возьмем задачу на применение всех изученных правил.

В задачах, которые мы разобрали в этой статье, использовались только основные элементарные функции, которые были связаны между собой знаками простых арифметических действий. Они нагляднее всего иллюстрируют правила дифференцирования. Однако возможно их применение и к более сложным функциям.

После того, как мы разберем, что такое производная сложной функции, мы сможете проводить дифференцирование выражений любой сложности.

Макеты страниц

Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Геометрический и физический смысл производной

Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:

Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.

Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:

Нам нужно найти скорость в момент времени t=2c. Вычислим производную:

Правила нахождения производных

Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.

Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правило первое: выносим константу

Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте.

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

Решение:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Решение:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.

Правило четвертое: производная частного двух функций

Формула для определения производной от частного двух функций:

Пример:

Решение:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.

Лекция
3. Производная суммы, разности, произведения и
частного функций

Производные
основных элементарных функций.

План

1. Производная
степенной функции.

2. Правила дифференцирования. Производная сложной функции.

3. Производные
основных элементарных функций.

4. Таблица
производных

5. Решение задач.

 (Учебник: Ш.А.
Алимов Алгебра и начала математического анализа 10-11 класс глава VIII §45, §46, §47, стр. 236-238, стр. 240-242, стр. 245-249)

1. Производная
степенной функции.

Итак, на предыдущих
занятиях нами были получены следующие формулы производных:

.

Четыре последние
формулы являются формулами производной степенной функции  для . Их можно записать так:

,

.

Вообще, справедлива
формула производной степенной функции для любого действительного показателя:

.                                   (1)

Эта формула
применима при тех значениях x, при которых её правая часть
имеет смысл.

Например, .

Пример 1

Вычислить , если .

Решение

.

Ответ:

Пользуясь формулами
 и , можно найти производные степенной и линейной функций, например .

В более сложных
случаях, например при нахождении производной функции , можно воспользоваться следующей формулой: .             (2)

По формуле (2) при k = 3, b = -1, p = 7 имеем .

2. Правила дифференцирования. Производная сложной функции.

При вычислении
производной используются следующие правила дифференцирования суммы,
произведения и частного:

1. Производная суммы равна сумме производных:

                                 (3)

Подробно это
свойство производной формулируется так: если каждая из функций  и  имеет производную, то их сумма также имеет производную и справедлива
формула (3).

Производная суммы
нескольких функций равна сумме производных этих функций, производная разности
равна разности производных.

Пример 2

Найдите производную
функции:

1) ;        2) .

Решение

1) ;

2) .

Ответ: 1) ; 2) .

2. Постоянный множитель можно вынести за знак производной:

                        (4)

Пример 3

Вычислить .

Решение

,

.

Ответ: -9

3. Производная
произведения:

                     (5)

Пример 3

Найдите производную функции , если .

Решение

По формуле (5) находим .

Ответ:

4. Производная
частного:

                      (6)

Формулы (5) и (6)
справедливы при условии, что функции  и  имеют производную в точке x, причём в раенстве (6)
.

Пример 4

Найдите производную
функции .

Решение

Обозначим . По формуле (6) находим .

Ответ:

Производная сложной функции.

Рассмотрим функция . Эту функцию можно рассматривать как сложную функцию , где , т.е. как функцию , аргумент которой также является функцией . Иными словами, сложная функция – это функция от функции . Производная сложной функции находится по формуле , где , т.е. по формуле

.                          (7)

Рассмотрим примеры.

1) Пусть .

Здесь .

По формуле (7)
находим .

2) Пусть . Здесь . По формуле (7) находим
.

3. Производные
основных элементарных функций.

Элементарными
функциями нвзывают степенную, показательную,
логарифмическую и тригонометрические функции, а также из различные комбинации.
При решении многих практических задач часто приходится находить производные
таких функций.

Например,
напряжение в цепи переменного тока выражается формулой ; для нахождения силы тока  нужно уметь находить производную , так как .

1) Производная
показательной функции.

Показательная
функция , где , определена на всей числовой прямой и имеет производную в каждой её
точке. Любую показательную функцию можно выразить через показательную функцию с
основанием e по формуле ,      (8)

так как . В курсе высшей математики доказывается, что функция  обладает замечательным свойством: её производная также равна , т.е.

                         (9)

Применяя правило
дифференцирования сложной функции, получаем

                                   (10)

Например, .

Пример 5

Найдите производную
функции , где .

Решение

Используя формулы
(8) и (10), находим .

Итак,                                              (11)

Ответ:

Например, .

2) Производная
логарифмической функции.

Логарифмическую
функцию  с любым основанием  можно выразить через логарифмическую функцию с основанием e
с помощью формулы перехода

.                              (12)

Производная функции
 выражается формулой .                   (13)

Применяя правило дифференцирования
сложной функции, получаем

.                                    (14)

Например, .

Пример 6

Найти производную
функции , где .

Решение

Используя формулы
(12) и (13), находим

.

Итак, .                                     (15)

Ответ:

3) Производные
тригонометрических функций.

Справедливы
следующие формулы:

; .                  (16)

Применяя правило
дифференцирования сложной функции, имеем следующие формулы

,

.

Например, ,

.

Пример 7

Найдите производную
функции .

Решение

Используя правило
дифференцирования частного и формулы (16), находим

.

Итак, .                                     (17)

Ответ:

Пример 8

Найдите производную
функции:

1) ;

2) ;

3) .

Решение

1) ;

2) ;

3) .

Пример 9

Найдите значение x, при которых значение производной функции  равно нулю; положительно; отрицательно.

Решение

Найдем производную .

Заметим, что
равенство  справедливо при тех значениях x, при которых обе
части имеют смысл, т.е. при .

Выражение  равно нулю при , положительно на промежутках
 ; отрицательно на промежутках .

Так как , то  только при ;  при ;  при
.

Ответ:  при ;  при ;  при .

5. Задания для самостоятельного решения.

Задача 1

Вычислите
производную  при данном значении аргумента x:

.

Задача 2

Вычислите
производную  при данном значении аргумента x:

.

Задача 3

Найдите , если: .

Задача 4

Вычислите
производную  при данном значении аргумента x: .

Задача 5

Найдите производную
функции .

В ответе укажите
номер правильного ответа.

1.                  2.                   3.                 4.

Задача 6

Найдите , если .

Задача 7

Найти значение
производной функции  в точке :

.

Задача 8

Выяснить, при каких
значениях x значение производной функции
 равно нулю (.

Если у вас
получилось больше одного значения, перечислите их через точку с запятой (;) без
пробелов в порядке возрастания.

Задача 9

Найдите значение
производной функции  в точке .

Задача 10

Найдите значение
производной функции  в точке .