Как найти производную тангенса по формуле

Производная тангенса

Определение

Производная тангенса равна единице деленной на квадрат косинуса того же самого аргумента: $$ (tg x)’ = frac{1}{cos^2 x} $$

Данную формулу легко вывести, если знать, что по тригонометрической формуле: $$ tg x = frac{sin x}{cos x} $$

А производные синуса и косинуса:

$$ (sin x)’ = cos x $$ $$ (cos x)’ = -sin x $$

Тогда по правилу производной дроби находим:

$$ (tg x)’ = bigg (frac{sin x}{cos x} bigg )’ = frac{(sin x)’ cdot cos x – sin x cdot (cos x)’}{cos^2 x} = $$

Выполняем упрощение числителя с учетом тождества $ sin^2 x + cos^2 x = 1 $:

$$ = frac{cos x cdot cos x – sin x cdot (-sin x)}{cos^2 x} = frac{cos^2 x + sin^2 x}{cos^2 x} = frac{1}{cos^2 x} $$

Пример 1

Найти производную тангенса сложной функции: $ y = tg 2x $

Решение

Производная тангенса равна отношению единицы и квадрата косинуса одно и того же аргумента. Так как функция сложная, то еще нужно домножить на производную аргумента тангенса: $$ y’ = (tg 2x)’ = frac{1}{cos 2x} cdot (2x)’ = frac{1}{cos 2x} cdot 2 = frac{2}{cos 2x} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ y’ = frac{2}{cos 2x} $$

Пример 2

Чему равна производная от тангенса в квадрате? $ y = tg^2 x $

Решение

Тангенс представлен степенной функцией, поэтому берем производную по правилу $ (x^p)’ = px^{p-1} $, а затем умножаем на производную тангенса: $$ y’ = (tg^2 x)’ = 2tg x cdot (tg x)’ = $$ $$ = 2tg x cdot frac{1}{cos^2 x} = 2frac{tg x}{cos^2 x} = 2 frac{sin x}{cos^3 x} $$

Ответ

$$ y’ = 2frac{sin x}{cos^3 x} $$

Производные тригонометрических функций

1. Производная синуса
2. Производная косинуса
3. Производная тангенса и котангенса
4. Примеры

п.1. Производная синуса

Найдем производную функции (f(x)=sin⁡x) по общему алгоритму.
Пусть (triangle x) – некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=sin⁡(x+triangle x)-sin⁡x=\ =2sin⁡frac{x+triangle x-x}{2}cosfrac{x+triangle x+x}{2}=2sinfrac{triangle x}{2}cosfrac{2x+triangle x}{2} end{gather*} Используем первый замечательный предел (см. §39 данного справочника): begin{gather*} lim_{xrightarrow 0}frac{sinx}{x}=1 end{gather*} Ищем производную: begin{gather*} f'(x)=lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{2sinfrac{triangle x}{2}cosfrac{2x+triangle x}{2}}{triangle x}=underbrace{left(lim_{triangle xrightarrow 0}frac{sinfrac{triangle x}{2}}{frac{triangle x}{2}}right)}_{=1}cdot lim_{triangle xrightarrow 0}cosfrac{2x+triangle x}{2}=\ =1cdot cosfrac{2x+0}{2}=cos x end{gather*} Или: ((sinx)’=cos x)

Для любого действительного x: $$ (sinx)’=cos x $$

Например:
((x^2sinx)’=(x^2)’cdot sinx+x^2cdot (sinx)’=2xsinx+x^2cosx)

п.2. Производная косинуса

Найдем производную функции (f(x)=cos⁡x) по общему алгоритму.
Пусть (triangle x) – некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=cos⁡(x+triangle x)-cos⁡x=\ =-2sin⁡frac{x+triangle x-x}{2}sin{x+triangle x+x}{2}=-2sinfrac{triangle x}{2}sinfrac{2x+triangle x}{2} end{gather*} Как и для производной синуса, используем первый замечательный предел. Ищем производную: begin{gather*} f'(x)=lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{-2sinfrac{triangle x}{2}sinfrac{2x+triangle x}{2}}{triangle x}=underbrace{-left(lim_{triangle xrightarrow 0}frac{sinfrac{triangle x}{2}}{frac{triangle x}{2}}right)}_{=1}cdot lim_{triangle xrightarrow 0}sinfrac{2x+triangle x}{2}=\ =-1cdot sinfrac{2x+0}{2}=-sinx end{gather*} Или: ((cosx)’=-sinx)

Для любого действительного x: $$ (cosx)’=-sinx $$

Например:
((sqrt{x}cosx)’=(sqrt{x})’cdot cosx+sqrt{x}cdot (cosx)’=frac{1}{2sqrt{x}}cosx-sqrt{x}sinx )

п.3. Производная тангенса и котангенса

Производные от тангенса и котангенса найдем с помощью формулы производной частного двух функций (см. §43 данного справочника). begin{gather*} (tgx)’=left(frac{sinx}{cosx}right)’=frac{(sinx)’cosx-sinx(cosx)’}{cos^2x}=\ =frac{cosxcosx-sinx(-sinx)}{cos^2x}=frac{cos^2x+sin^2x}{cos^2x}=frac{1}{cos^2x} end{gather*} Аналогично: begin{gather*} (ctgx)’=left(frac{cosx}{sinx}right)’=frac{(cosx)’sinx-cosx(sinx)’}{sin^2x}=\ =frac{sinx(-sinx)-cosxcosx}{sin^2x}=frac{-sin^2x-cos^2x}{sin^2x}=-frac{sin^2x+cos^2x}{sin^2x}=-frac{1}{sin^2x} end{gather*}
Как видно из результатов, производные тангенса и котангенса имеют те же ограничения по ОДЗ, что и сами функции.

begin{gather*} (tgx)’=frac{1}{cos^2x}, xnefracpi 2+pi k\ (ctgx)’=-frac{1}{sin^2x}, xnepi k end{gather*}

Например:
( left(frac{tgx}{x}right)’=frac{(tgx)’cdot x-tgxcdot(x)’}{x^2}=frac{frac{x}{cos^2x}-tgx}{x^2}=frac{x-tgxcdot cos^2x}{x^2cos^2x}=frac{x-sinxcosx}{x^2cos^2x} )

п.4. Примеры

Пример 1. Найдите производную:
a) ( f(x)=2sinx-5x ) begin{gather*} f'(x)=2cdot sin’x-5cdot x’=2cosx-5 end{gather*}

б) ( f(x)=3sqrt{x}ctgx ) begin{gather*} f'(x)=3left((sqrt{x})’cdot ctgx+sqrt{x}(ctgx)’right)=3left(frac{ctgx}{2sqrt{x}}-frac{sqrt{x}}{sin^2x}right) end{gather*}

в) ( f(x)=9cosx-3tgx ) begin{gather*} f'(x)=9cdot cos’x-3cdot tg’x=-9sinx-frac{3}{cos^2x} end{gather*}

г) ( f(x)=frac{2x}{sinx} ) begin{gather*} f'(x)=2frac{(x)’cdot sinx-xcdot sin’x}{sin^2x}=frac{2(sinx-xcosx)}{sin^2x} end{gather*}

Пример 2. Найдите значение производной в данной точке:
a) ( f(x)=sinx+cosx, x_0=fracpi 4 ) begin{gather*} f'(x)=sin’x+cos’x=cosx-sinx\ f'(fracpi 4)=cosfracpi 4-sinfracpi 4=frac{sqrt{2}}{2}-frac{sqrt{2}}{2}=0 end{gather*}

б) ( f(x)=tgx-5cosx, x_0=pi ) begin{gather*} f'(x)=tg’x-5cos’x=frac{1}{cos^2x}+5sinx\ f'(pi)=frac{1}{cos^2pi}+5sinpi=1+0=1 end{gather*}

в) ( f(x)=sinxcosx, x_0=frac{pi}{12} ) begin{gather*} f'(x)=sin’xcosx+sinxcos’x=cos^2x-sin^2x=cos2x\ f’left(frac{pi}{12}right)=cosleft(2cdotfrac{pi}{12}right)=cosfracpi 6=frac{sqrt{3}}{2} end{gather*}

г) ( f(x)=frac{x}{cosx}, x_0=pi ) begin{gather*} f'(x)=frac{x’cdot cosx-xcos’x}{cos^2x}=frac{cosx+xsinx}{cos^2x}\ f'(pi)=frac{cospi+pi sinpi}{cos^2pi}=frac{-1+picdot 0}{(-1)^2}=-1 end{gather*}

Пример 3. Решите уравнение:
a) ( y’cdot y+y^2=0), если (y=3cosx)
(y’=3cdot cos’x=-3sinx)
Подставляем: begin{gather*} -3sinxcdot 3cosx+(3cosx)^2=0\ -9sincosx+9cos^2x=0\ 9cosx(cosx-sinx)=0 end{gather*} Уравнение: begin{gather*} left[ begin{array}{l} cosx=0\ cosx-sinx=0 |:cosx end{array} right. Rightarrow left[ begin{array}{l} x=fracpi 2+pi k\ 1-tgx=0 end{array} right. Rightarrow left[ begin{array}{l} x=fracpi 2+pi k\ tgx=1 end{array} right. Rightarrow left[ begin{array}{l} x=fracpi 2+pi k\ x=fracpi 4+pi k end{array} right. end{gather*} Ответ: (left{fracpi 2+pi k; x=fracpi 4+pi kright})

б) ( (y’)^2+y^2=1), если (y=1-cosx)
(y’=1′-cos’x=0+sinx=sinx)
Подставляем: begin{gather*} sin^2x+(1-cosx)^2=1\ sin^2x+1-2cosx+cos^2x=1\ 1-2cosx=0\ cosx=frac12\ x=pmfracpi 3+2pi k end{gather*} Ответ: (left{pmfracpi 3+2pi kright})

Рейтинг пользователей

Содержание:

• Формула
• Примеры вычисления производной тангенса

Формула

Производная от тангенса равна единице, деленной на косинус в квадрате.

Если под тангенсом находится сложная функция $u=u(x)$,
то производная исходной функции будет равна:

$$(operatorname{tg} u)^{prime}=frac{1}{cos ^{2} u} cdot u^{prime}$$

Примеры вычисления производной тангенса

Читать дальше: производная котангенса (ctgx)’.

Что такое производная тангенса

Производная тангенса рассчитывается, как отношение единицы к квадрату косинуса аналогичного аргумента.

Формула для данного определения будет записана, таким образом:

((tg x)’ = frac{1}{cos^2 x})

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Вывод данной закономерности достаточно просто представить, зная смысл тригонометрического уравнения следующего порядка:

(tg x = frac{sin x}{cos x})

Производные геометрических определений синуса и косинуса соответствуют значениям:

((sin x)’ = cos x)

((cos x)’ = -sin x)

Исходя из правила производной дроби, можно определить, что:

((tg x)’ = bigg (frac{sin x}{cos x} bigg )’ = frac{(sin x)’ cdot cos x – sin x cdot (cos x)’}{cos^2 x})

Следует принять во внимание тождество:

(sin^2 x + cos^2 x = 1)

Далее можно упростить числитель с учетом вышеуказанного уравнения:

(frac{cos x cdot cos x – sin x cdot (-sin x)}{cos^2 x} = frac{cos^2 x + sin^2 x}{cos^2 x} = frac{1}{cos^2 x})

Таким образом, записано доказательство определения.

Производная от тангенса в квадрате

Сформулируем выражение производной тангенса угла, обратного котангенсу:

(tan ^{2}(x))

Выполним замену:

(u=tan (x))

Исходя из составного правила, применим: (u ^{2}) получим (2u) 

Далее, руководствуясь правилами, выполним умножение на выражение:

(frac{d}{dx}tan (x))

Вычислим производную:

(frac{d}{dx}tan (x)=frac{1}{cos^2 (x)})

(frac{2 tan (x)}{cos^2( x)} (sin ^{2}(x)+cos ^{2}(x)))

Можно упростить полученное выражение и записать ответ:

(frac{2 tan (x)}{cos^2( x)})

Производная от тангенса в кубе

Запишем выражение:

(tan ^{3}(x))

Первая производная степени будет записана таким образом:

((3tan ^{2}(x)+3) tan ^{2}(x))

Выполним замену:

(u=tan(x))

Исходя из правила, применим: (u ^{3}) получим (3u^{2})

Действие, обратное возведению числа в степень, является извлечением корня.

Далее, руководствуясь правилами, выполним умножение на выражение:

(frac{d}{dx}tan (x))

Плюс нужно переписать функции, чтобы выполнить дифференцирование:

(tan (x)=frac{sin (x)}{cos(x)})

Согласно правилу производной частного:

(frac{d}{dx}frac{f(x)}{g(x)}=frac{-f(x)frac{d}{dx}g(x)+g(x)frac{d}{dx}f(x)}{g^{2}(x)})

Учитывая, что:

(f(x)= sin (x))

(g(x)= cos(x))

С целью определения (frac{d}{dx} f(x)) необходимо записать, что производная синуса равна косинусу:

(frac{d}{dx} sin (x)= cos(x))

Найти (frac{d}{dx} g(x)) можно, если вспомнить, что производная косинуса является отрицательным синусом:

(frac{d}{dx} cos(x) = -sin (x))

Далее следует использовать правило производной деления:

(frac{sin ^{2}(x)+cos ^{2}(x)}{cos^{2}(x)})

С помощью применения последовательности правил можно записать уравнение:

(frac{3(sin ^{2}(x)+cos ^{2}(x))tan ^{2}(x)}{cos^{2}(x)})

После упрощения получим ответ:

(frac{3tan ^{2}(x)}{cos^{2}(x)})

Примеры решения задач по теме «Производная тангенса»

Необходимо определить производную тангенса этой функции.

Решение:

Учитывая, что по определению производная тангенса представляет собой единицу, деленную на косинус в квадрате одного и того же аргумента. В связи с тем, что в условии записана сложная функция, следует дополнительно выполнить умножение на производную аргумента тангенса. В результате получим выражение:(y’ = (tg 2x)’ = frac{1}{cos 2x} cdot (2x)’ = frac{1}{cos 2x} cdot 2 = frac{2}{cos 2x}

).

Ответ: (y’ = frac{2}{cos 2x})

Решение:

Тангенс в данном случае представляет собой степенную функцию. Исходя из этого условия, следует взять производную по правилу:

((x^p)’ = px^{p-1})

Далее можно умножить выражение на производную тангенса:(y’ = (tg^2 x)’ = 2tg x cdot (tg x)’ =2tg x cdot frac{1}{cos^2 x} = 2frac{tg x}{cos^2 x} = 2 frac{sinx}{cos^3 x}

).

Ответ: (y’ = 2frac{sin x}{cos^3 x})

Что такое тангенс

Тангенс некоторого угла (alpha), который меньше девяносто градусов, представляет собой отношение противоположного катета а к прилегающему катету b в треугольной геометрической фигуре с прямым углом.

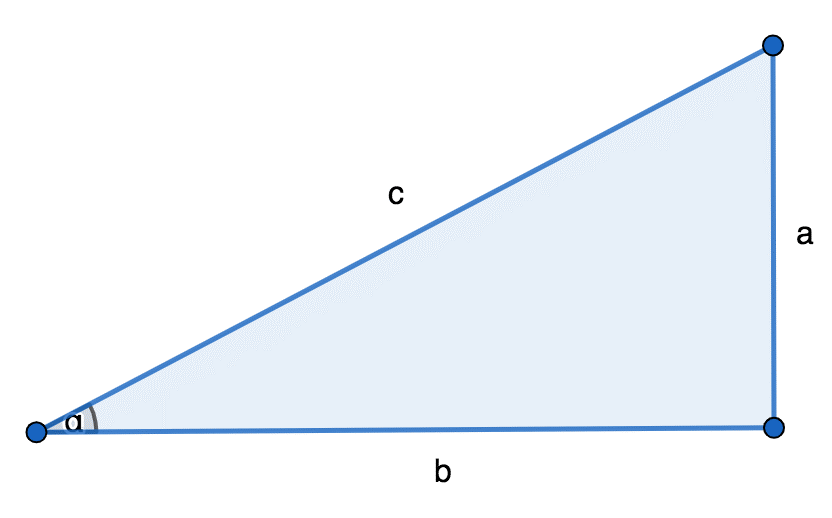
Источник: microexcel.ru

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Записанное определение целесообразно выразить с помощью формулы:

(tanalpha = frac{a}{b})

В качестве обозначения тангенса какого-либо угла используют выражения: tg или tan.

Воспользуемся формулой для вычисления тангенса угла, подставим известные значения и выполним математические операции:

(tanalpha = frac{a}{b} = frac{3}{4} = 0,75)

Тогда получим, что:

(tanalpha = 0,75)

В процессе поисков ответов на примеры из тригонометрии обычно возникает необходимость в построении графиков функций. Поиск переменных графическим методом является одним из наиболее точных и эффективных способов. Представим на координатной плоскости тригонометрическую функцию y = tg (x).

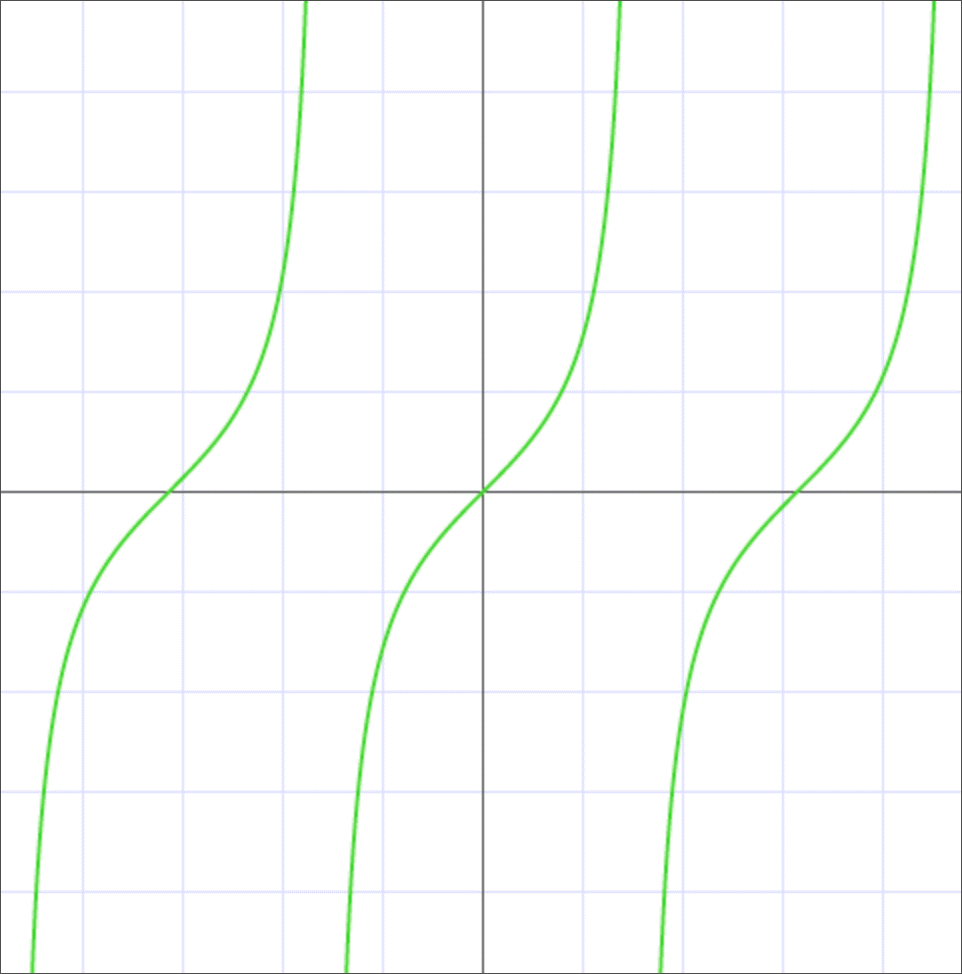
Источник: microexcel.ru

Что такое производная tgx

Производная тригонометрической функции тангенс вычисляется как частное от деления единицы на косинус во второй степени аналогичного аргумента, то есть:  ((tg x)’ = frac{1}{cos^2 x})

Прийти к такому выводу можно путем поэтапного доказательства. В первую очередь целесообразно представить тангенс через синус и косинус. На этот случай имеется справедливое тригонометрическое тождество. Запишем соотношение:

(tg x = frac{sin x}{cos x})

Далее необходимо вычислить, чему равна производная от косинуса и синуса. Запишем выражения ниже:

((sin x)’ = cos x)

((cos x)’ = -sin x)

Известно, что для определения производной от дробного числа проще всего воспользоваться специальным правилом. Тогда расчеты значительно упрощаются. Найдем производную:

( (tg x)’ = bigg (frac{sin x}{cos x} bigg )’ = frac{(sin x)’ cdot cos x – sin x cdot (cos x)’}{cos^2 x} = (tgx))

Упростим выражение, которое записано на месте числителя. При этом важно обратиться к справедливому равенству:

(sin^2 x + cos^2 x = 1sin)

Запишем порядок вычислений:

(frac{cos x cdot cos x – sin x cdot (-sin x)}{cos^2 x} = frac{cos^2 x + sin^2 x}{cos^2 x} = frac{1}{cos^2 x})

Производная tgx 2

Производную тригонометрической функции тангенса допустимо возводить во вторую степень. Однако в этом случае нет необходимости выполнять громоздкие вычисления, перемножая сложные выражения между собой. Достаточно применить в расчетах более простую формулу.

На первом этапе запишем соотношение, подходящее для расчета производной тангенса некоторого угла, который является обратным для котангенса:

(tan ^{2}(x))

Если заменить тангенс переменной, получим:

(u=tan (x))

Затем , прибегая к составному правилу, запишем:

(u ^{2}) получим 2u

На следующем шаге целесообразно вычислить произведение:

(frac{d}{dx}tan (x))

Найдем, чему соответствует производная:

(frac{d}{dx}tan (x)=frac{1}{cos^2 (x)})

(frac{2 tan (x)}{cos^2( x)} (sin ^{2}(x)+cos ^{2}(x)))

Соотношение, которое получилось в итоге, стоит упростить:

(frac{2 tan (x)}{cos^2( x)})

В результате, доказано равенство:

(tan ^{2}(x) = frac{2 tan (x)}{cos^2( x)})

Производная от тангенса в кубе

Аналогично путем поэтапных вычислений и математических преобразований можно найти значение производной от тригонометрической функции тангенса в третьей степени, то есть в кубе:

(tan ^{3}(x))

Определим, как рассчитать первую производную степени. С этой целью можно воспользоваться следующим выражением:

((3tan ^{2}(x)+3) tan ^{2}(x))

Как и в предыдущем примере при вычислении производной квадрата тангенса, в данном случае целесообразно прибегнуть к замене:

(u=tan(x))

В результате, из (u ^{3}) получим (3u^{2}). Известно, что для поиска степени некоторого числа предусмотрена обратная операция, которая заключается в извлечении корня. Затем с помощью уже знакомых правил найдем произведение:

(frac{d}{dx}tan (x))

При выполнении дифференцирования проще всего изменить вид записи функций:

(tan (x)=frac{sin (x)}{cos(x)})

Заметим, что здесь можно воспользоваться правилом производной от деления. Выполним необходимые преобразования:

(frac{d}{dx}frac{f(x)}{g(x)}=frac{-f(x)frac{d}{dx}g(x)+g(x)frac{d}{dx}f(x)}{g^{2}(x)})

Далее потребуется учитывать следующее условие:

(f(x)= sin (x))

(g(x)= cos(x))

Попробуем рассчитать, чему равно такое выражение:

(frac{d}{dx} f(x))

В процессе важно учитывать следующее справедливое равенство:

(frac{d}{dx} sin (x)= cos(x))

Вычислить значение выражения (frac{d}{dx} g(x)) несложно, если знать об отрицательном значении синуса при определении производной косинуса:

(frac{d}{dx} cos(x) = -sin (x))

Затем целесообразно применить в процессе вычислений закономерность производной от частного:

(frac{sin ^{2}(x)+cos ^{2}(x)}{cos^{2}(x)})

Путем применения в данной ситуации рассмотренных ранее правил выполним все нужные преобразования:

(frac{3(sin ^{2}(x)+cos ^{2}(x))tan ^{2}(x)}{cos^{2}(x)})

Полученное выражение несложно упростить. В итоге получим:

(frac{3tan ^{2}(x)}{cos^{2}(x)})

Запишем окончательную формулу:

(tan ^{3}(x))

Примеры решения задач

Решение

Из определения производной тангенса известно, что при вычислении искомого значения требуется разделить единицу на косинус во второй степени от аналогичного аргумента. Заметим, по условию задачи дана сложная функция. По этой причине на втором этапе дополнительно умножим значение на производную аргумента тангенса. С учетом всех преобразований получим:

(y’ = (tg 2x)’ = frac{1}{cos 2x} cdot (2x)’ = frac{1}{cos 2x} cdot 2 = frac{2}{cos 2x})

Ответ: (y’ = frac{2}{cos 2x}).

Решение

В этом случае целесообразно воспользоваться следующей справедливой закономерностью:

((x^p)’ = px^{p-1})

Далее можно найти произведение:

(y’ = (tg^2 x)’ = 2tg x cdot (tg x)’ = 2tg x cdot frac{1}{cos^2 x} = 2frac{tg x}{cos^2 x} = 2 frac{sin x}{cos^3 x})

Ответ: (y’ = 2frac{sin x}{cos^3 x}).