Как найти производную второго порядка для функции - Сайт, где вы сможете решить свои вопросы

Вторая производная или производная второго порядка функции является производной от производной от . Грубо говоря, вторая производная измеряет, как изменяется скорость изменения самой величины; например, вторая производная положения объекта по времени — это мгновенное ускорение объекта или скорость изменения скорости объекта по времени. В нотации Лейбница:

${displaystyle mathbf {a} ={frac {dmathbf {v} }{dt}}={frac {d^{2}{boldsymbol {x}}}{dt^{2}}},}$

где — ускорение, — скорость, — время, — положение объекта, d — мгновенная «дельта» или изменение. Последнее выражение ${displaystyle {tfrac {d^{2}{boldsymbol {x}}}{dt^{2}}}}$ является второй производной положения (x) по времени.

На графике функции вторая производная соответствует кривизне или выпуклости графика. График функции с положительной второй производной на некотором участке является выпуклым вниз на этом участке, в то время как график функции с отрицательной второй производной на некотором участке изгибается в противоположную сторону на этом участке.

Обозначение[править | править код]

Вторая производная функции f(x) обычно обозначается f''(x) ^[1]^[2]. То есть:

При использовании нотации Лейбница, частная вторая производная зависимой переменной по независимой переменной записывается как:

${displaystyle {frac {d^{2}y}{dx^{2}}}.}$

Данное обозначение получено из следующей формулы:

${displaystyle {frac {d^{2}y}{dx^{2}}},=,{frac {d}{dx}}left({frac {dy}{dx}}right).}$

Вторая производная степенной функции[править | править код]

Взяв два раза производную, получается формула второй производной:

${displaystyle {frac {d^{2}}{dx^{2}}}left[x^{n}right]={frac {d}{dx}}{frac {d}{dx}}left[x^{n}right]={frac {d}{dx}}left[nx^{n-1}right]=n{frac {d}{dx}}left[x^{n-1}right]=n(n-1)x^{n-2}.}$

Пример[править | править код]

Дана функция

производная от — функция

${displaystyle f^{prime }(x)=3x^{2}.}$

Вторая производная от является производной от ${displaystyle f^{prime }}$ , а именно

${displaystyle f^{prime prime }(x)=left(f'left(xright)right)'=6x.}$

Вторая производная на графике[править | править код]

Выпуклость[править | править код]

Вторая производная функции может использоваться для определения выпуклости/вогнутости графика ^[2]. Функция, вторая производная которой положительна, будет выпуклой вниз (также называется вогнутой вверх), что означает, что касательная будет лежать ниже графика функции. Точно так же функция, у которой вторая производная отрицательна, будет выпукла вверх (также называется просто вогнутой вниз), а её касательные линии будут лежать над графиком функции.

Точки перегиба[править | править код]

Если вторая производная функции меняет знак, то график функции меняется с выпуклого вверх на выпуклый вниз или наоборот. Точка, в которой график уже не выпуклый вверх, но еще не выпуклый вниз, называется точкой перегиба. Если вторая производная непрерывна, она принимает нулевое значение в любой точке перегиба, однако стоит учитывать, что не каждая точка, в которой вторая производная равна нулю, обязательно является точкой перегиба.

Исследование стационарных точек[править | править код]

Связь второй производной и графика можно использовать для проверки того, является ли стационарная точка функции (то есть точка, где f'(x)=0 ) локальным максимумом или локальным минимумом. Более подробно:

Причину, по которой вторая производная дает такие результаты, можно понять с помощью аналогии с реальным миром. Рассмотрим транспортное средство, которое вначале движется вперед с большой скоростью, но с отрицательным ускорением. Ясно, что положение автомобиля в точке, где скорость достигает нуля, будет наибольшим расстоянием от начального положения — следующим шагом скорость станет отрицательной, и автомобиль начнет ехать в противоположную сторону. То же самое верно и для минимума, когда транспортное средство сначала имеет отрицательную скорость, но положительное ускорение.

Предел[править | править код]

Можно записать вторую производную при помощи всего одного предела:

${displaystyle f''(x)=lim _{hto 0}{frac {f(x+h)-2f(x)+f(x-h)}{h^{2}}}.}$

Данный предел можно называть второй симметричной производной^[3]^[4]. Стоит обратить внимание, что вторая симметричная производная может существовать, даже если (обычная) вторая производная не существует.

Правую часть выражения можно записать в виде разностного отношения разностных отношений:

${displaystyle {frac {f(x+h)-2f(x)+f(x-h)}{h^{2}}}={frac {{frac {f(x+h)-f(x)}{h}}-{frac {f(x)-f(x-h)}{h}}}{h}}.}$

Этот предел можно рассматривать как непрерывную версию второй конечной разности^[en] для последовательностей.

Однако существование указанного выше предела не означает, что функция имеет вторую производную. Приведенный выше предел просто дает возможность вычислить вторую производную, но не дает представления о ее существовании. Контрпримером является функция , которая определяется как:

${displaystyle operatorname {sgn}(x)={begin{cases}-1, x<0\0, x=0\1, x>0end{cases}}}$

Функция разрывна в нуле, поэтому вторая производная для x=0 не существует. Но вышеуказанный предел существует для x=0 :

${displaystyle {begin{aligned}lim _{hto 0}{frac {operatorname {sgn}(0+h)-2operatorname {sgn}(0)+operatorname {sgn}(0-h)}{h^{2}}}&=lim _{hto 0}{frac {operatorname {sgn}(h)-2cdot 0+operatorname {sgn}(-h)}{h^{2}}}\&=lim _{hto 0}{frac {operatorname {sgn}(h)+(-operatorname {sgn}(h))}{h^{2}}}=lim _{hto 0}{frac {0}{h^{2}}}=0.end{aligned}}}$

Квадратичная аппроксимация[править | править код]

Так же, как первая производная связана с линейной аппроксимацией, вторая производная связана с квадратичной аппроксимацией для функции . Эта квадратичная функция, первые и вторые производные которой такие же, как у в данной точке. Формула квадратичного приближения функции вокруг точки x=a имеет вид

${displaystyle f(x)approx f(a)+f'(a)(x-a)+{tfrac {1}{2}}f''(a)(x-a)^{2}.}$

Эта квадратичная аппроксимация представляет собой ряд Тейлора второго порядка для функции с центром в точке x = a.

Собственные значения и собственные векторы второй производной[править | править код]

Для многих краевых задач можно получить явные формулы для собственных значений и собственных векторов оператора второй производной. Например, если предположить, что и заданы однородные граничные условия Дирихле (то есть ), то собственные значения ${displaystyle lambda _{j}=-{tfrac {j^{2}pi ^{2}}{L^{2}}}}$ и соответствующие собственные векторы (также называемые собственными функциями) равны ${displaystyle v_{j}(x)={sqrt {tfrac {2}{L}}}sin left({tfrac {jpi x}{L}}right)}$ . Здесь ${displaystyle v''_{j}(x)=lambda _{j}v_{j}(x),,j=1,ldots ,infty .}$

Для других известных случаев см. собственные значения и собственные векторы второй производной^[en].

Обобщение на более высокие измерения[править | править код]

Гессиан[править | править код]

Вторая производная обобщается на более высокие измерения с помощью понятия вторых частных производных. Для функции ${displaystyle f:mathbb {R} ^{3}rightarrow mathbb {R} }$ есть три частные производные второго порядка:

${displaystyle {frac {partial ^{2}f}{partial x^{2}}},;{frac {partial ^{2}f}{partial y^{2}}},{text{ и }}{frac {partial ^{2}f}{partial z^{2}}}}$

и смешанные частные производные:

${displaystyle {frac {partial ^{2}f}{partial x,partial y}},;{frac {partial ^{2}f}{partial x,partial z}},{text{ и }}{frac {partial ^{2}f}{partial y,partial z}}.}$

Если все эти производные непрерывны, то можно составить из них симметричную матрицу, известную как матрица Гессе. Собственные значения этой матрицы можно использовать для реализации многомерного аналога проверки второй производной.

Другим распространенным обобщением второй производной является лапласиан. Это дифференциальный оператор $nabla ^{2}$ (или же Delta ), определяется как:

${displaystyle nabla ^{2}f={frac {partial ^{2}f}{partial x^{2}}}+{frac {partial ^{2}f}{partial y^{2}}}+{frac {partial ^{2}f}{partial z^{2}}}.}$

Лапласиан функции равен дивергенции градиента и следу матрицы Гессе.

См. также[править | править код]

Конечная разность, используемая для аппроксимации второй производной
Проверка на точку перегиба^[en]
Равенство смешанных производных

Примечания[править | править код]

↑ Content – The second derivative. amsi.org.au. Дата обращения: 16 сентября 2020. Архивировано 24 марта 2022 года.
↑ ¹ ² Second Derivatives (амер. англ.) (недоступная ссылка — история). Math24. Дата обращения: 16 сентября 2020.
↑ A. Zygmund. Trigonometric Series. — Cambridge University Press, 2002. — P. 22–23. — ISBN 978-0-521-89053-3.
↑ Thomson. Symmetric Properties of Real Functions. — Marcel Dekker, 1994. — ISBN 0-8247-9230-0.

Литература[править | править код]

Печатные ресурсы[править | править код]

Anton, Howard; Bivens, Irl & Davis, Stephen (February 2, 2005), Calculus: Early Transcendentals Single and Multivariable (8th ed.), New York: Wiley, ISBN 978-0-471-47244-5
Apostol, Tom M. (June 1967), Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra (2nd ed.), Wiley, ISBN 978-0-471-00005-1, <https://archive.org/details/calculus01apos>
Apostol, Tom M. (June 1969), Calculus, Vol. 2: Multi-Variable Calculus and Linear Algebra with Applications (2nd ed.), Wiley, ISBN 978-0-471-00007-5, <https://archive.org/details/calculus01apos>
Eves, Howard (January 2, 1990), An Introduction to the History of Mathematics (6th ed.), Brooks Cole, ISBN 978-0-03-029558-4
Larson, Ron; Hostetler, Robert P. & Edwards, Bruce H. (February 28, 2006), Calculus: Early Transcendental Functions (4th ed.), Houghton Mifflin Company, ISBN 978-0-618-60624-5
Spivak, Michael (September 1994), Calculus (3rd ed.), Publish or Perish, ISBN 978-0-914098-89-8
Stewart, James (December 24, 2002), Calculus (5th ed.), Brooks Cole, ISBN 978-0-534-39339-7, <https://archive.org/details/calculus0000stew>
Thompson, Silvanus P. (September 8, 1998), Calculus Made Easy^[en] (Revised, Updated, Expanded ed.), New York: St. Martin’s Press, ISBN 978-0-312-18548-0

Книги, доступные в интернете[править | править код]

Crowell, Benjamin (2003), Calculus, <http://www.lightandmatter.com/calc/>
Garrett, Paul (2004), Notes on First-Year Calculus, <http://www.math.umn.edu/~garrett/calculus/>
Hussain, Faraz (2006), Understanding Calculus, <http://www.understandingcalculus.com/>
Keisler, H. Jerome (2000), Elementary Calculus: An Approach Using Infinitesimals, <http://www.math.wisc.edu/~keisler/calc.html>
Mauch, Sean (2004), Unabridged Version of Sean’s Applied Math Book, <http://www.its.caltech.edu/~sean/book/unabridged.html>
Sloughter, Dan (2000), Difference Equations to Differential Equations, <http://synechism.org/drupal/de2de/>
Strang, Gilbert (1991), Calculus, <http://ocw.mit.edu/ans7870/resources/Strang/strangtext.htm>
Stroyan, Keith D. (1997), A Brief Introduction to Infinitesimal Calculus, <http://www.math.uiowa.edu/~stroyan/InfsmlCalculus/InfsmlCalc.htm>
Wikibooks, Calculus, <http://en.wikibooks.org/wiki/Calculus>

Ссылки[править | править код]

Дискретная вторая производная от неравномерно расположенных точек

Источник

Производные различных порядков

Наталья Игоревна Восковская

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Производные различных порядков — производные первого и высших порядков.

Дифференцируя производную первого порядка f`(x) мы получим производную от производной — производную второго порядка.

Определение

Производная от производной второго порядка называется производной третьего порядка, а производная n-го порядка называется производной от производной n-1го порядка.

Производная второго порядка обозначается y” или f”(x). Таким образом, дифференцируя функцию, n-раз получим производную вида f n(x).

Формула дифференцирования второго порядка

Формула дифференцирования второго порядка имеет вид:

[f”(x)=frac{d^{2} y}{dx^{2} } =mathop{lim }limits_{xto x0} frac{f'(x)-f'(x_{0} )}{x-x_{0} } =left(f'(x)right){{‘} } ]

Производная n-го порядка равна нулю, если степень меньше порядка производной. Например, пятая производная функции y = 5×2 равна нулю

Таблица производных высших порядков

Пример 1

Найдем производную первого порядка сложной функции по формуле произведения:

[left[f(x)cdot g(x)right]{{‘} } =f(x)’cdot g(x)+f(x)cdot g(x)’]

[y’=left[xcdot ln (2x+1)right]{{‘} } =x’cdot ln (2x+1)+xcdot left(ln (2x+1)right){{‘} } =1cdot ln (2x+1)+xcdot left(ln (2x+1)right){{‘} } =]

[y’=ln (2x+1)+xcdot left(ln (2x+1)right){{‘} } =ln (2x+1)+xcdot frac{1}{2x+1} cdot (2x+1)’=]

[=ln (2x+1)+2xcdot frac{1}{2x+1} =ln (2x+1)+frac{2x}{2x+1} ]

Найдем производную второго порядка для выражения

[y”=left(ln (2x+1)+frac{2x}{2x+1} right){{‘} } =ln (2x+1)’+left(frac{2x}{2x+1} right){{‘} } =frac{1}{2x+1} cdot (2x+1)’+frac{2x’cdot (2x+1)-2xcdot (2x+1)’}{left(2x+1right)^{2} } =]

[y”=frac{2}{2x+1} +frac{2(2x+1)-2xcdot 2}{left(2x+1right)^{2} } =frac{2}{2x+1} +frac{2((2x+1)-2x)}{left(2x+1right)^{2} } =frac{2}{2x+1} +frac{2}{left(2x+1right)^{2} } =]

Упростим выражение

[y”=frac{2left(2x+1right)}{left(2x+1right)^{2} } +frac{2}{left(2x+1right)^{2} } =frac{2left(2x+1right)+2}{left(2x+1right)^{2} } =frac{4x+4}{left(2x+1right)^{2} } ]

«Производные различных порядков» 👇

Пример 2

Найти производную четвертого порядка

[y=x^{5} -x^{4} +3x^{3} ]

Решение.

Найдем производную первого порядка

[y’=left(x^{5} -x^{4} +3x^{3} right){{‘} } =5x^{4} -4x^{3} +3cdot 3x^{2} =5x^{4} -4x^{3} +9x^{2} ]

Найдем производную второго порядка

[y”=left(5x^{4} -4x^{3} +9x^{2} right){{‘} } =20x^{3} -12x^{2} +18x]

Найдем производную третьего порядка

[y”’=left(20x^{3} -12x^{2} +18xright){{‘} } =60x^{2} -24x+18]

Найдем производную четвертого порядка

[y””=left(60x^{2} -24x+18right){{‘} } =120x-24]

Пример 3

Найти производную четвертого порядка функции

[y=frac{x^{2} +5x^{3} }{18} ]

Решение: Самая большая степень составного неизвестного равна 3, что меньше степени производной, а значит производная четвертого порядка равна 0.

Пример 4

Найти производную 13 порядка функции

[y=sin x]

Решение.

Найдем производную первого порядка

[y’=sin’x=cos x=sin (x+frac{pi }{2} )]

Найдем производную второго порядка

[y”=cos’x=-sin x=sin (x+2frac{pi }{2} )]

Найдем производную третьего порядка

[y”’=-sin’x=-cos x=sin (x+3frac{pi }{2} )]

Найдем производную четвертого порядка

[y^{(4)} =-cos x’=sin x=sin (x+4frac{pi }{2} )]

Таким образом:

[y^{(n)} =sin (x+frac{ncdot pi }{2} ),nin N]

Найдем производную 13 порядка:

[y^{(13)} =sin (x+frac{13cdot pi }{2} )=cos x]

Пример 5

Вычислить производную четвертой степени функции $x^{8}$

Решение.

Вычисления производим по формуле нахождения производной высшего порядка

[left(x^{p} right)^{(n)} =p(p-1)(p-2)…(p-n+1)x^{p-n} ]

где p = 8, n = 4

[left(x^{8} right)^{(4)} =8(8-1)(8-2)(8-4+1)x^{8-4} =8cdot 7cdot 6cdot 5cdot x^{4} =1680x^{4} ]

[left(x^{8} right)^{(4)} =1680x^{4} ]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 15.12.2022

Источник

Чтобы понять частные производные, сначала нужно разобраться с обычными. И не нужно ничего искать: в нашей отдельной статье мы уже подготовили все для того, чтобы у вас это получилось. А сейчас речь пойдет о частных производных.

Добро пожаловать на наш телеграм-канал за полезной рассылкой и актуальными студенческими новостями.

Функция двух и более переменных

Прежде чем говорить о частных производных, нужно затронуть понятие функции нескольких переменных, без которого нет смысла в частной производной. В школе мы привыкли иметь дело с функциями одной переменной:

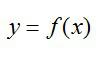
Производными таких функций мы и считали раньше. График функции одной переменной представляет собой линию на плоскости: прямую, параболу, гиперболу и т.д.

А что, если добавить еще одну переменную? Получится такая функция:

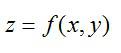
Это – функция двух независимых переменных x и y. График такой функции представляет собой поверхность в трехмерном пространстве: шар, гиперболоид, параболоид или еще какой-нибудь сферический конь в вакууме. Частные производные функции z по иксу и игреку соответственно записываются так:

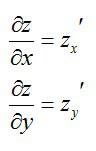
Существуют также функции трех и более переменных. Правда, график такой функции нарисовать невозможно: для этого понадобилось бы как минимум четырехмерное пространство, которое невозможно изобразить.

Частная производная первого порядка

Запоминаем главное правило:

При вычислении частной производной по одной из переменных, вторая переменная принимается за константу. В остальном правила вычисления производной не меняются.

То есть, частная производная по сути ничем не отличается от обычной. Так что, держите перед глазами таблицу производных элементарных функций и правила вычисления обычных производных. Рассмотрим пример, чтобы стало совсем понятно. Допустим, нужно вычислить частные производные первого порядка следующей функции:

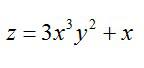
Сначала возьмем частную производную по иксу, считая игрек обычным числом:

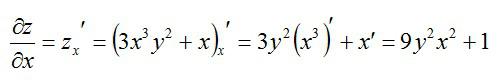
Теперь считаем частную производную по игреку, принимая икс за константу:

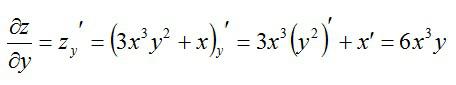
Как видите, ничего сложного в этом нет, а успех с более сложными примерами – лишь дело практики.

Частная производная второго порядка

Как находится частная производная второго порядка? Так же, как и первого. Чтобы найти частные производные второго порядка, нужно просто взять производную от производной первого порядка. Вернемся к примеру выше и посчитаем частные производные второго порядка.

По иксу:

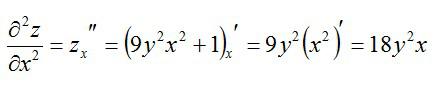
По игреку:

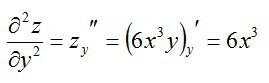
Частные производные третьего и высших порядков не отличаются по принципу вычисления. Систематизируем правила:

При дифференцировании по одной независимой переменной, вторая принимается за константу.
Производная второго порядка – это производная от производной первого порядка. Третьего порядка – производная от производной второго порядка и т.д.

Частные производные и полный дифференциал функции

Частый вопрос в практических заданиях – нахождение полного дифференциала функции. Для функции нескольких переменных полный дифференциал определяется, как главная линейная часть малого полного приращения функции относительно приращений аргументов.

Определение звучит громоздко, но с буквами все проще. Полный дифференциал первого порядка функции нескольких переменных выглядит так:

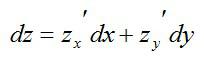
Зная, как считаются частные производные, нет никакой проблемы вычислить и полный дифференциал.

Частные производные – не такая уж и бесполезная тема. Например, дифференциальные уравнения в частных производных второго порядка широко используются для математического описания реальных физических процессов.

Здесь мы дали лишь общее, поверхностное представление о частных производных первого и второго порядка. Вас интересует эта тема или остались конкретные вопросы? Задавайте их в комментариях и обращайтесь к экспертам профессионального студенческого сервиса за квалифицированной и скорой помощью в учебе. С нами вы не останетесь один на один с проблемой!

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Вторая производная

Всё
очень просто. Вторая производная –
это производная
от первой производной:

Стандартные
обозначения второй производной:
,
или
(дробь
читается так: «дэ два игрек по дэ икс
квадрат»). Чаще всего вторую производную
обозначают первыми двумя вариантами.
Но третий вариант тоже встречается,
причем, его очень любят включать в
условия контрольных заданий, например:
«Найдите
функции…».
А студент сидит и битый час чешет репу,
что это вообще такое.

Рассмотрим
простейший пример. Найдем вторую
производную от функции
.

Для того чтобы
найти вторую производную, как многие
догадались, нужно сначала найти первую
производную:

Теперь находим
вторую производную:

Готово.

Рассмотрим более
содержательные примеры.

Пример 11

Найти
вторую производную функции

Найдем
первую производную:

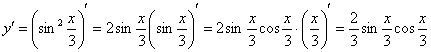
На
каждом шаге всегда смотрим, нельзя ли
что-нибудь упростить? Сейчас нам предстоит
дифференцировать произведение двух
функций, и мы избавимся от этой
неприятности, применив
известную тригонометрическую
формулу
.
Точнее говоря, использовать формулу
будем в обратном направлении:
:

Находим
вторую производную:

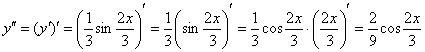
Готово.

Можно
было пойти другим путём – понизить
степень функции еще перед дифференцированием,
используя формулу
:

Если интересно,
возьмите первую и вторую производные
снова. Результаты, естественно, совпадут.

Отмечу,
что понижение степени бывает очень
выгодно при нахождении частных
производных функции.
Здесь же оба способа решения будут
примерно одинаковой длины и сложности.

Как и
для первой производной, можно
рассмотреть задачу
нахождения второй производной в точке.

Например:
Вычислим значение найденной второй
производной в точке
:

Необходимость
находить вторую производную и вторую
производную в точке возникает при
исследовании графика функции на
выпуклость/вогнутость и перегибы.

Пример 12

Найти
вторую производную функции
.
Найти

Это пример для
самостоятельного решения.

Аналогично можно
найти третью производную, а также
производные более высоких порядков.
Такие задания встречаются, но встречаются
значительно реже.

Решения
и ответы:

Пример
2: Найдем производную:

Вычислим
значение функции в точке
:

Пример
4: Найдем производную:

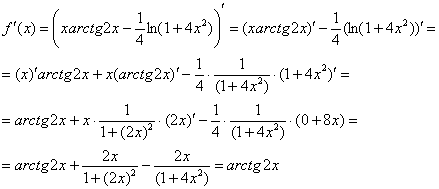
Вычислим
производную в заданной точке:

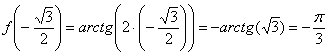
Пример
6: Уравнение касательной составим по
формуле

1)
Вычислим значение функции в точке
:

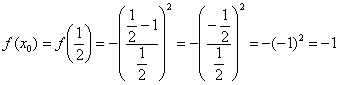
2)
Найдем производную. Перед дифференцированием
функцию выгодно упростить:

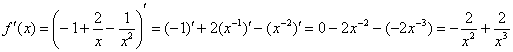
3)
Вычислим значение производной в
точке
:

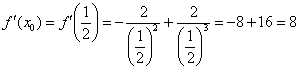
4)
Подставим значения
,
и
в
формулу
:

Пример
8: Преобразуем функцию:

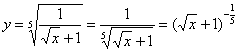
Найдем
производную:

Запишем
дифференциал:

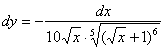
Пример
10: Найдем производную:

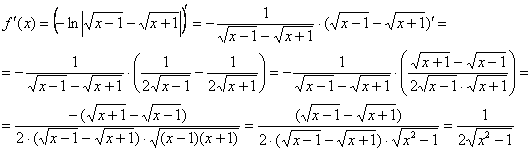
Запишем
дифференциал:

Вычислим
дифференциал в точке
:

Пример
12: Найдем первую производную:

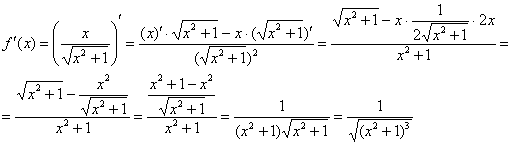
Найдем
вторую производную:

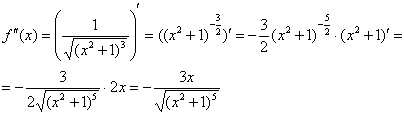
Вычислим:

4. 2.Частные производные. Примеры решений

На
данном уроке мы познакомимся с понятием
функции двух переменных, а также подробно
рассмотрим наиболее распространенное
задание – нахождение частных
производныхпервого
и второго порядка, полного дифференциала
функции. Студенты-заочники, как правило,
сталкиваются с частными производными
на 1 курсе во 2 семестре. Причем, по моим
наблюдениям, задание на нахождение
частных производных практически всегда
встречается на экзамене.

Для
эффективного изучения нижеизложенного
материала Вам необходимо уметь
более или менее уверенно находить
«обычные» производные функции одной
переменной. Научиться правильно
обращаться с производными можно на
уроках Как
найти производную? иПроизводная
сложной функции.
Также нам потребуется таблица производных
элементарных функций и правил
дифференцирования, удобнее всего, если
она будет под рукой в распечатанном
виде. Раздобыть справочный материал
можно на страницеМатематические
формулы и таблицы.

Начнем
с самого понятия функции двух переменных,
я постараюсь ограничиться минимумом
теории, так как сайт имеет практическую
направленность. Функция двух переменных
обычно записывается как
,
при этом переменные
,
называются независимыми
переменными или аргументами.

Пример:
–
функция двух переменных.

Иногда
используют запись
.
Также встречаются задания, где вместо
буквы
используется
буква
.

Полезно
знать геометрический смысл функций.
Функции одной переменной
соответствует
определенная линия на плоскости,
например,
–
всем знакомая школьная парабола. Любая
функция двух переменных
с
геометрической точки зрения представляет
собой поверхность в трехмерном
пространстве (плоскости, цилиндры, шары,
параболоиды и т.д.). Но, собственно, это
уже аналитическая геометрия, а у нас на
повестке дня математический анализ.

Переходим
к вопросу нахождения частных производных
первого и второго порядков. Должен
сообщить хорошую новость для тех, кто
выпил несколько чашек кофе и настроился
на невообразимо трудный материал: частные
производные – это почти то же самое,
что и «обычные» производные функции
одной переменной.

Для
частных производных справедливы все
правила дифференцирования и таблица
производных элементарных функций. Есть
только пара небольших отличий, с которыми
мы познакомимся прямо сейчас.

Пример 1

Найти
частные производные первого и второго
порядка функции

Сначала найдем
частные производные первого порядка.
Их две.

Обозначения:

или
–
частная производная по «икс»

или
–
частная производная по «игрек»

Начнем
с
. Когда
мы находим частную производную по «икс»,
то переменная
считается
константой (постоянным числом).

Решаем. На данном
уроке я буду приводить полное решение
сразу, а комментарии давать ниже.

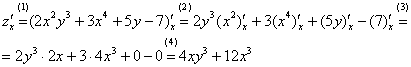
Комментарии к
выполненным действиям:

(1)
Первое, что мы делаем при нахождении
частной производной – заключаем всю функцию
в скобки под штрих с
подстрочным индексом.

Внимание,
важно! Подстрочные
индексы НЕ ТЕРЯЕМ по ходу решения. В
данном случае, если Вы где-нибудь
нарисуете «штрих» без
,
то преподаватель, как минимум, может
поставить рядом с заданием
(сразу
откусить часть балла за невнимательность).

Далее данный шаг
комментироваться не будет, все сделанные
замечания справедливы для любого примера
по рассматриваемой теме.

(2)
Используем правила дифференцирования
,
.
Для простого примера, как этот, оба
правила вполне можно применить на одном
шаге. Обратите внимание на первое
слагаемое: так как
считается
константой, а любую константу можно
вынести за знак производной,
то
мы
выносим за скобки. То есть в данной
ситуации
ничем
не лучше обычного числа. Теперь посмотрим
на третье слагаемое
:
здесь, наоборот, выносить нечего. Так
как
константа,
то
–
тоже константа, и в этом смысле она ничем
не лучше последнего слагаемого –
«семерки».

(3)
Используем табличные производные
и
.

(4) Упрощаем, или,
как я люблю говорить, «причесываем»
ответ.

Теперь
. Когда
мы находим частную производную по
«игрек», то переменная
считается
константой (постоянным числом).

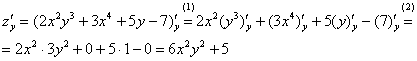
(1)
Используем те же правила дифференцирования
,
.
В первом слагаемом выносим константу
за
знак производной, во втором слагаемом
ничего вынести нельзя поскольку
–
уже константа.

(2)
Используем таблицу производным
элементарных функций. Мысленно
поменяем в таблице все «иксы» на «игреки».
То есть данная таблица рАвно справедлива
и для
(да
и вообще почти для любой буквы). В
частности, используемые нами формулы
выглядят так:
и
.

Итак, частные
производные первого порядка найдены

Подведем итог, чем
же отличается нахождение частных
производных от нахождения «обычных»
производных функции одной переменной:

1)
Когда мы находим частную
производную
, переменная
считается
константой.

2)
Когда мы находим частную
производную
, переменная
считается
константой.

3)
Правила и таблица производных элементарных
функций справедливы и применимы для
любой переменной (
,
либо
какой-нибудь другой), по которой ведется
дифференцирование.

Шаг второй. Находим
частные производные второго порядка.
Их четыре.

Обозначения:

или
–
вторая производная по «икс»

или
–
вторая производная по
«игрек»

или
– смешанная производная
«икс по игрек»

или
– смешанная производная
«игрек по икс»

В
понятии второй производной нет ничего
сложного. Говоря простым языком, вторая
производная – это производная от первой
производной.

Для
наглядности я перепишу уже найденные
частные производные первого порядка:

Сначала
найдем смешанные производные:

Как
видите, всё просто: берем частную
производную
и
дифференцируем ее еще раз, но в данном
случае – уже по «игрек».

Аналогично:

Для
практических примеров справедливо
следующее равенство:

Таким образом,
через смешанные производные второго
порядка очень удобно проверить, а
правильно ли мы нашли частные производные
первого порядка.

Находим
вторую производную по «икс».

Никаких
изобретений, берем
и
дифференцируем её по «икс» еще раз:

Аналогично:

Следует
отметить, что при нахождении
,
нужно
проявить повышенное
внимание, так как
никаких чудесных равенств для проверки
не существует.

Пример 2

Найти
частные производные первого и второго
порядка функции

Это
пример для самостоятельного решения
(ответ в конце урока). Если возникли
трудности с дифференцированием корней,
рекомендую ознакомиться уроком Как
найти производную?

При определенном
опыте частные производные из примеров
№№1,2 будут решаться Вами устно.

Переходим к более
сложным примерам.

Пример 3

Найти
частные производные первого порядка
функции
.
Проверить, что
.
Записать полный дифференциал первого
порядка
.

Решение:
Находим частные производные первого
порядка:

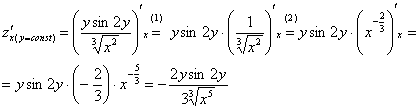
Обратите
внимание на подстрочный индекс:
,
рядом с «иксом» не возбраняется в скобках
записывать, что
–
константа. Данная пометка может быть
очень полезна для начинающих, чтобы
легче было ориентироваться в решении.

Дальнейшие
комментарии:

(1)
Выносим все константы за знак производной.
В данном случае
и
,
а, значит, и их произведение
считается
постоянным числом.

(2) Не забываем, как
правильно дифференцировать корни.

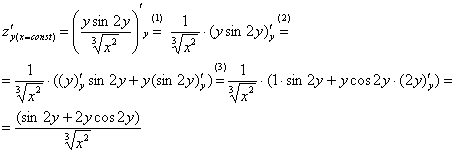
(1)
Выносим все константы за знак производной,
в данной случае константой является

(2) Под
штрихом у нас осталось произведение
двух функций, следовательно, нужно
использовать правило дифференцирования
произведения
.

(3) Не
забываем, что

– это сложная функция (хотя и простейшая
из сложных). Используем соответствующее
правило:

Теперь находим
смешанные производные второго порядка:

,
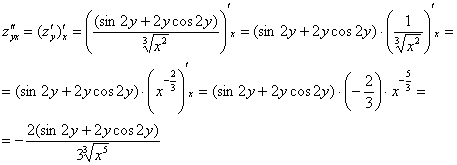
значит, все вычисления выполнены верно.

Запишем
полный дифференциал
.
В контексте рассматриваемого задания
не имеет смысла рассказывать, что такое
полный дифференциал функции двух
переменных. Важно, что этот самый
дифференциал очень часто требуется
записать в практических задачах.

Полный
дифференциал первого порядка функции
двух переменных имеет вид:

В данном случае:

То
есть, в формулу нужно просто подставить
уже найденные частные производные
первого порядка. Значки дифференциалов
и
в
этой и похожих ситуациях по возможности
лучше записывать в числителях:

Пример 4

Это пример для
самостоятельного решения. Полное решение
и образец оформления задачи – в конце
урока.

Рассмотрим серию
примеров, включающих в себя сложные
функции.

Пример 5

Найти
частные производные первого порядка
функции

.

Записать
полный дифференциал
.

Решение:

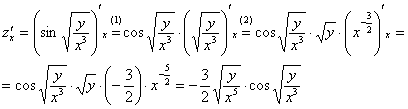
(1)
Применяем правило дифференцирования
сложной функции
.
С урока Производная
сложной функции
следует помнить
очень важный момент: когда мы по таблице
превращаем синус (внешнюю функцию) в
косинус, то вложение

(внутренняя
функция) у нас не
меняется.

(2)
Здесь используем свойство корней:

,
выносим константу

за знак производной, а корень

представляем в нужном для дифференцирования
виде.

Аналогично:

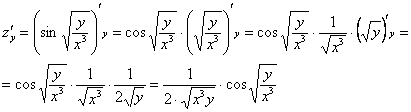
Запишем
полный дифференциал первого порядка:

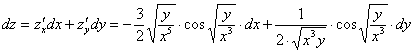
Пример 6

Найти
частные производные первого порядка
функции
.

Записать
полный дифференциал
.

Это пример для
самостоятельного решения (ответ в конце
урока). Полное решение не привожу, так
как оно достаточно простое

Довольно часто
все вышерассмотренные правила применяются
в комбинации.

Пример 7

Найти
частные производные первого порядка
функции
.

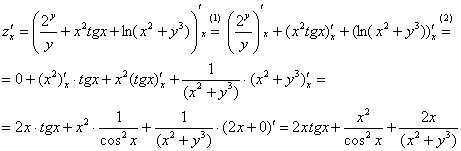
(1) Используем
правило дифференцирования суммы

(2)
Первое слагаемое в данном случае
считается константой, поскольку в
выражении

нет ничего, зависящего от «икс» – только
«игреки».

(Знаете,
всегда приятно, когда дробь удается
превратить в ноль).

Для
второго слагаемого применяем правило
дифференцирования произведения. Кстати,
в этом смысле ничего бы не изменилось,
если бы вместо

была дана функция

– важно, что здесь произведение
двух функций, КАЖДАЯ
из которых зависит от
«икс»,
а поэтому, нужно использовать правило
дифференцирования произведения. Для
третьего слагаемого применяем правило
дифференцирования сложной функции.

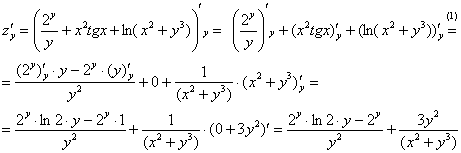
(1) В
первом слагаемом и в числителе и в
знаменателе содержится «игрек»,
следовательно, нужно использовать
правило дифференцирования частного:
.
Второе слагаемое зависит ТОЛЬКО от
«икс», значит,
считается
константой и превращается в ноль. Для
третьего слагаемого используем правило
дифференцирования сложной функции.

Для тех читателей,
которые мужественно добрались почти
до конца урока, расскажу старый
мехматовский анекдот для разрядки:

Однажды
в пространстве функций появилась злобная
производная и как пошла всех
дифференцировать. Все функции разбегаются
кто куда, никому не хочется превращаться!
И только одна функция никуда не убегает.
Подходит к ней производная и спрашивает:

– А
почему это ты от меня никуда не убегаешь?

– Ха.
А мне всё равно, ведь я «е в степени икс»,
и ты со мной ничего не сделаешь!

На
что злобная производная с коварной
улыбкой отвечает:

– Вот
здесь ты ошибаешься, я тебя продифференцирую
по «игрек», так что быть тебе нулем.

(Кто
понял анекдот, тот освоил производные,
минимум, на «тройку»).

Пример 8

Найти
частные производные первого порядка
функции

.

Это пример для
самостоятельного решения. Полное решение
и образец оформления задачи – в конце
урока.

Ну вот почти и всё.
Напоследок не могу не обрадовать
любителей математики еще одним примером.
Дело даже не в любителях, у всех разный
уровень математической подготовки –
встречаются люди (и не так уж редко),
которые любят потягаться с заданиями
посложнее. Хотя, последний на данном
уроке пример не столько сложный, сколько
громоздкий с точки зрения вычислений.

Пример 9

Дана
функция двух переменных
.
Найти все частные производные первого
и второго порядков.

Это пример для
самостоятельного решения. Полное решение
и образец оформления где-то рядом.

Ответы:

Пример
2:

,

,

,

Пример
4: Ссылка для просмотра ниже.

Пример
6:

,

,

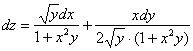
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.02.20157.31 Mб91.rtf
#
#
#
#
#
#
#
#
#
#

Источник

Производная второго порядка

Содержание:

Производная второго порядка
Производная второго порядка. Пройденный путь, скорость, ускорение
Задача пример №101
Задача пример №102

Производная второго порядка

Производная второго порядка. Пройденный путь, скорость, ускорение

Пусть для функции на заданном промежутке существует производная . Если функция является дифференцируемой функцией, то ее производная для функции называется производной второго порядка и обозначается как .

Известно, что производная показывает мгновенное изменение. Мгновенное изменение пройденного пути в зависимости от времени является скоростью. Отсюда становится ясным физический смысл производной. При прямолинейном движении по закону , мгновенная скорость равна производной функции :

Скорость также изменяется в зависимости от времени. Изменение скорости выражается новой величиной, называемой ускорением. Вообще, находя производную функции зависимости пройденного пути от времени, находят функцию скорости. Находя производную от функции скорости получаем ускорение. Т.е. получая два раза подряд производную от функции пройденного пути можно найти ускорение:

Из физики известно, что и скорость, и ускорение являются векторными величинами. Если скорость и ускорение имеют одинаковые знаки, то движение ускоренное, если знаки разные, то движение замедленное. Производная второго порядка используется для решения ряда экономических задач, в том числе задач, моделирующих реальные жизненные ситуации. Умение приблизительно определить является ли скорость изменения положительной или отрицательной имеет важное практическое значение.

Задача пример №101

Найдите производную второго порядка у.

а) b)

Решение: a) находим производную первого порядка

находим производную второго порядка

находим производную первого порядка, используя правило дифференцирования производной сложной функции

находим производную второго порядка

Задача пример №102

Для функции пройденного пути , зависящей от времени ( время в сек., расстояние в м, ), исследуйте связь между функциями расстояния, скорости и ускорения.

Решение:

Из графика видно, что угловой коэффициент касательной функции в точках и равен нулю. Т.е. функция производной в соответствующих точках обнуляется.

В интервалах (0; 2) и (6; 8) угловой коэффициент касательной к графику функции положителен и функция также положительна (расположена выше оси ). В интервале (2;6) угловой коэффициент касательной отрицателен и функция также отрицательна (расположена ниже оси ).

Из графика функции видно, что в угловой коэффициент касательной равен нулю. Эта точка является точкой пересечения графика функции a(t) с осью абсцисс.

На интервале [0; 4) угловой коэффициент касательной к графику функции v(t) отрицателен, а на интервале (4; 8) угловой коэффициент положителен и функция на интервале [0; 4) принимает отрицательные значения; а на интервале (4; 8) – положительные значения.

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:

Другие темы которые вам помогут понять математику:

Производная сложной функции

Решение задач с применением производной

Производные показательной и логарифмической функций

Производные тригонометрических функций

Лекции:

Метод Жордана Гаусса
Некоторые простые неявные функции
Рациональные числа
Предел числовой последовательности
Пересекающиеся прямые
Метод интервалов
Обратная матрица примеры решения
Дифференцирование функций, заданных неявно и параметрически
Полярная система координат: примеры решения
Сходимость функционального ряда

Источник

Обозначение[править | править код]

Вторая производная степенной функции[править | править код]

Пример[править | править код]

Вторая производная на графике[править | править код]

Выпуклость[править | править код]

Точки перегиба[править | править код]

Исследование стационарных точек[править | править код]

Предел[править | править код]

Квадратичная аппроксимация[править | править код]

Собственные значения и собственные векторы второй производной[править | править код]

Обобщение на более высокие измерения[править | править код]

Гессиан[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Печатные ресурсы[править | править код]

Книги, доступные в интернете[править | править код]

Ссылки[править | править код]

Производные различных порядков

Формула дифференцирования второго порядка

Таблица производных высших порядков

Функция двух и более переменных

Частная производная первого порядка

Частная производная второго порядка

Частные производные и полный дифференциал функции

Вторая производная

4. 2.Частные производные. Примеры решений

Производная второго порядка

Производная второго порядка

Производная второго порядка. Пройденный путь, скорость, ускорение

Задача пример №101

Задача пример №102

Вам также может понравиться

Как найти гта сан андреас в стиме

Как на узи найти подключичную артерию

E01 стиральная машина как исправить

Добавить комментарий Отменить ответ