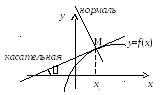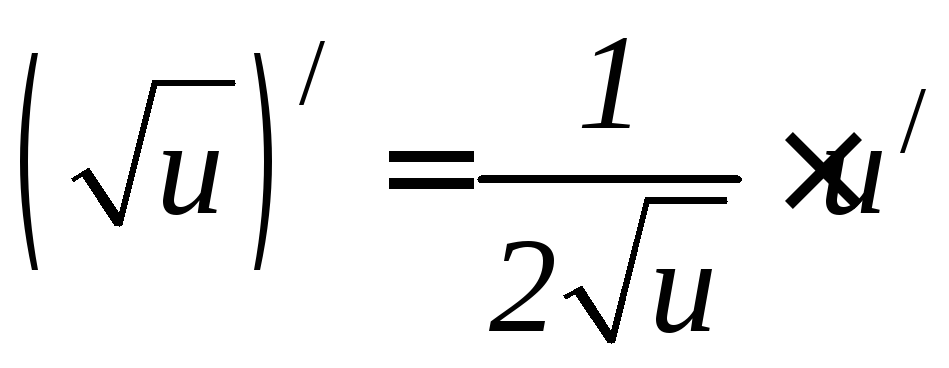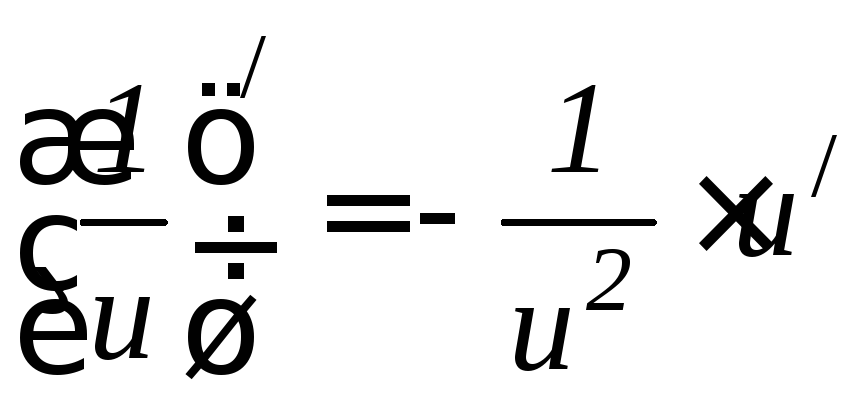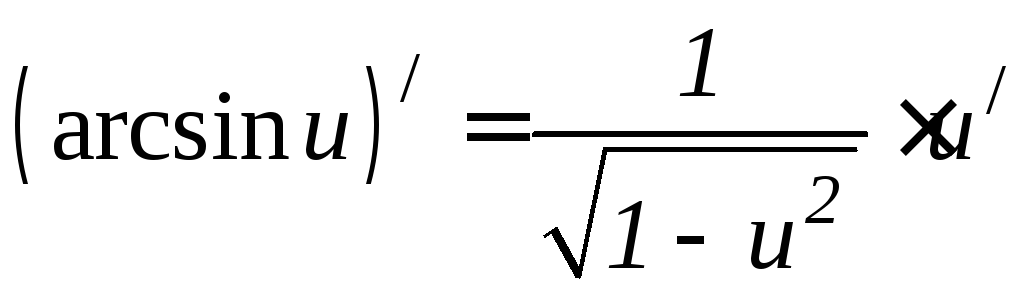-
Производная функции
6.1 Дифференцирование функций, заданных явно
Производной
функцииy=f(x)
в точкеx0называется предел отношения приращения
функции в этой точке к приращению
аргумента, когда последнее стремится
к нулю. Производная функцииy=f(x)
обозначается черезy/,
илиf /(x).
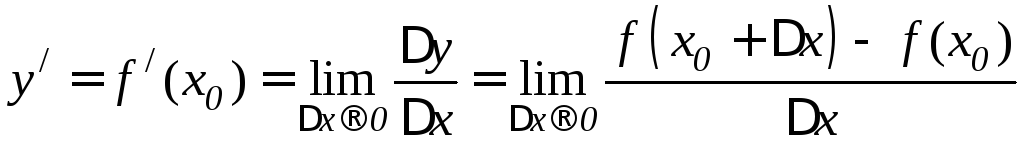
Операция
нахождения производной f
/(x) от
функцииf(x)
называетсядифференцированием
этой функции.
Геометрически
значение производной функции y=f(x)
в точкеx=x0равно тангенсу угла, образованного
положительным направлением осиОхи касательной, проведенной к графику
функции в точке с абсциссойx0,
то естьf /(
x0)=tg
(рис 6.1).
|
Число k В |
Рис |
![]() –уравнение касательной,
–уравнение касательной,
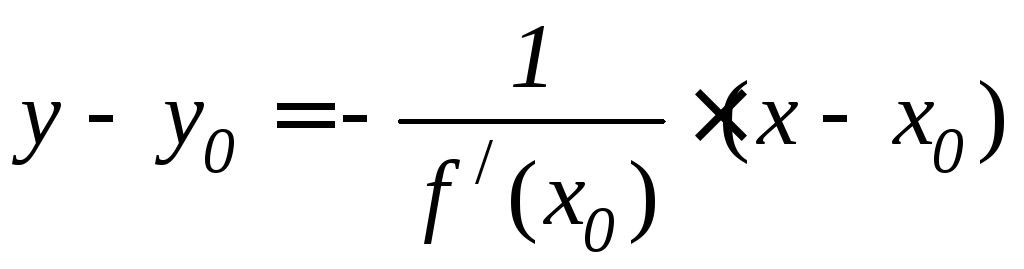 –уравнение нормали.
–уравнение нормали.
Если
функция y=f(x)
описывает какой–либо физический
процесс, то производнаяy/есть скорость протекания этого процесса.
В этом состоит физический смысл
производной.
Основные правила дифференцирования.
Пусть
даны функции, имеющие производные
u=u(x)
и v=v(x),
c=const
|
6.1 6.2 6.3 |
6.4 6.5 |
6.6
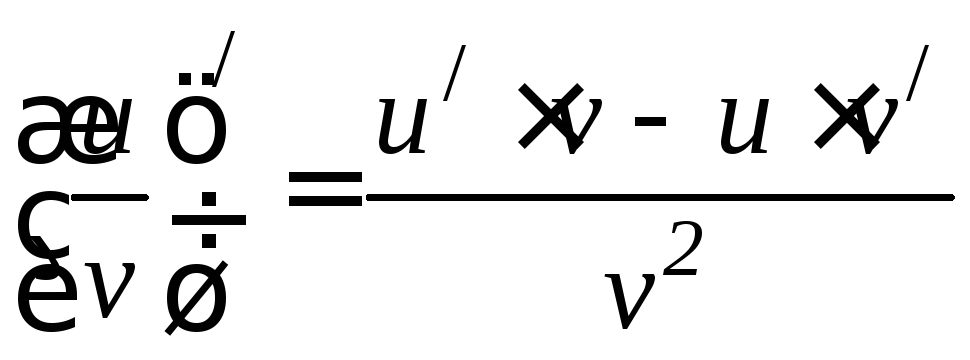
6.7
если
дана сложная функция y=f(u),
где u=u(x),
то есть y=f[u(x)],
где функции
f(u)
и u(x)
имеют производные, то
![]() (правило дифференцирования сложной
(правило дифференцирования сложной
функции).
Основные формулы дифференцирования.
|
6.8 6.9 6.10 6.11 6.12 6.13 6.14 6.15 6.16 6.17 |
6.18 6.19 6.20 6.21 6.22 6.23 6.24 6.25 6.26 |
Пример
1. Найти
производную функции
![]() .
.
Решение.
Дифференцируем как сумму по формулам
6.4, 6.1, 6.3 правил дифференцирования и
применяем формулу 6.8
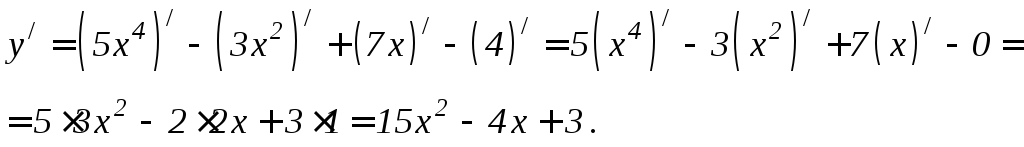
Пример
2. Найти
y// функции
 .
.
Решение.
Дифференцируем как частное по формуле
6.5 правил дифференцирования и применяем
формулы 6.2, 6.1 и 6.8
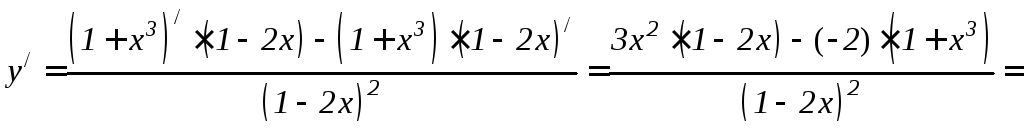
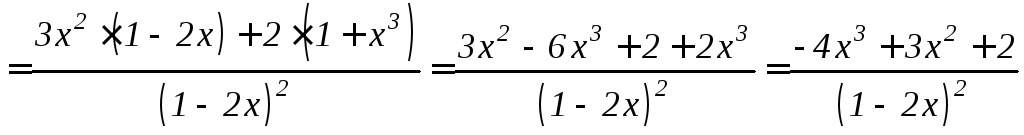 .
.
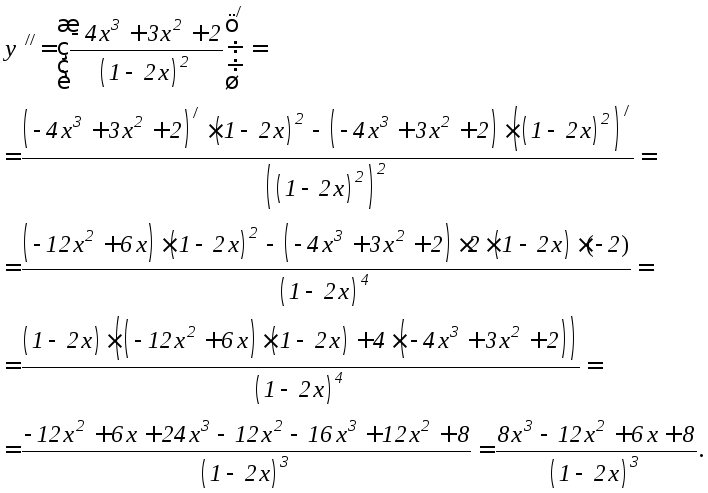
Пример
3. Найти y/функции
![]() .
.
Решение.
Дифференцируем, применяя формулы
производной сложной функции и формулы
6.8 и 6.12
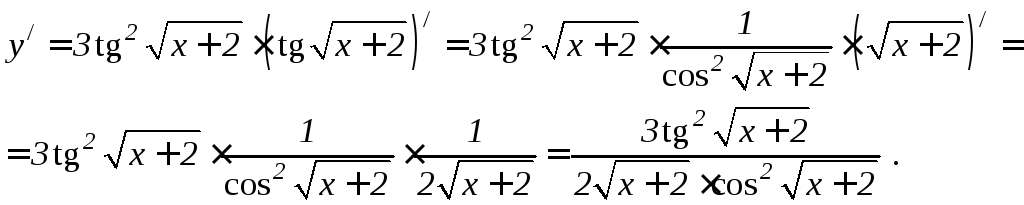
Пример
4. Найти
y/функции
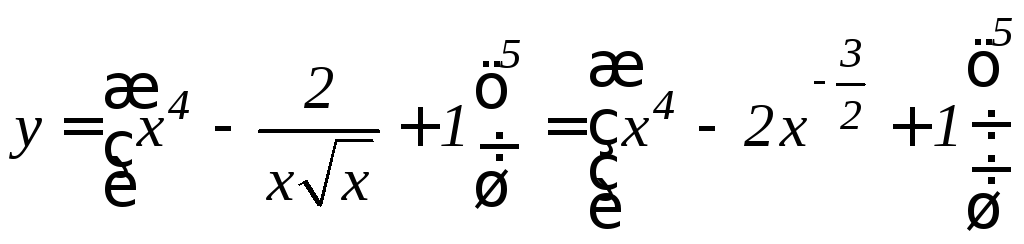 .
.
Решение. Вводим
сначала дробные и отрицательные
показатели, затем дифференцируем,
применяя формулы 6.3, 6.2 и 6.1 и формулу
6.8
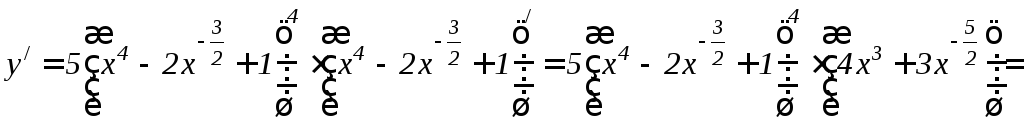
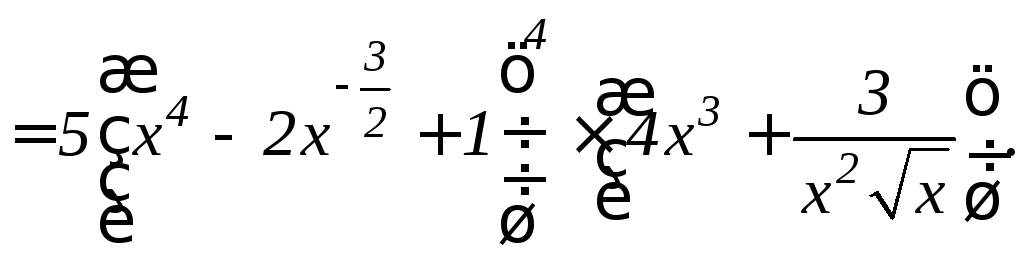
Пример
5. Найти
y/функции
![]() .
.
Решение.
Применяем сначала формулу 6.3, а для
второго слагаемого формулу 6.4. Затем
используем формулы 6.9, 6.14, 6.8 и 6.15
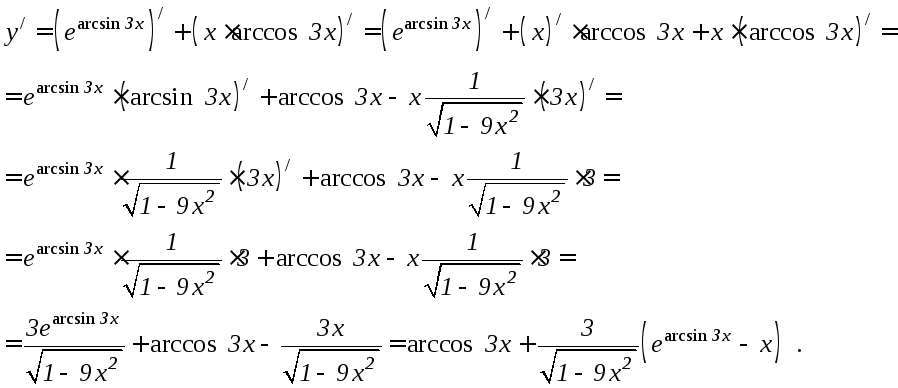
Логарифмический
метод.
Иногда,
прежде чем находить производную от
заданного выражения, лучше выражение
преобразовать так, чтобы процесс
дифференцирования упрощался. Во многих
случаях оказывается выгодным, прежде
чем дифференцировать заданную функцию,
взять ее логарифм, определить затем
производную от этого логарифма и по
производной от логарифма отыскать
производную от заданной функции. Такой
прием называется способом логарифмического
дифференцирования.
Метод
логарифмического дифференцирования
позволяет находить производные от
сложной функции вида
![]() ,
,
гдеu,v–
функции аргументаx.
Действительно, логарифмируя обе части
исходного равенства, получаем
![]() .
.
Дифференцируя последнее
равенство, имеем
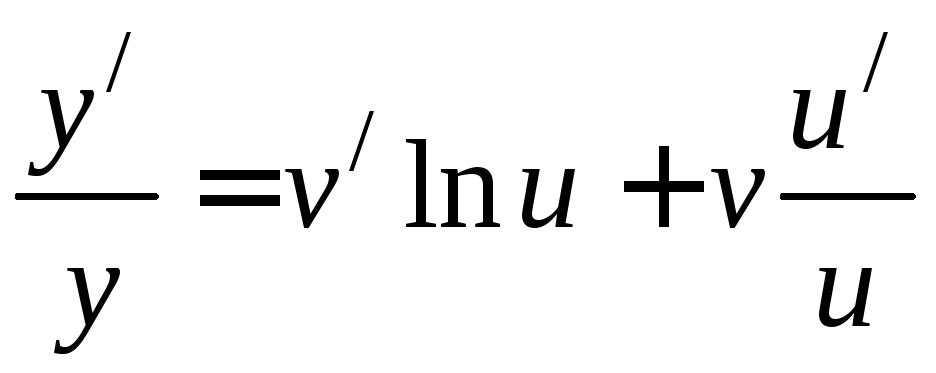 .
.
Умножая обе части
равенства на y и
заменяя затемy
черезuv,
окончательно получаем
![]() .
.
Пример 6. Найтиy/, если![]() .
.
Решение. Здесь
основание и показатель степени зависят
отx. Логарифмируя,
получим
![]() (так как
(так как![]() ).
).
Продифференцируем
обе части последнего равенства по x.
Так какyявляется
функцией отx, тоlny есть сложная функцияxи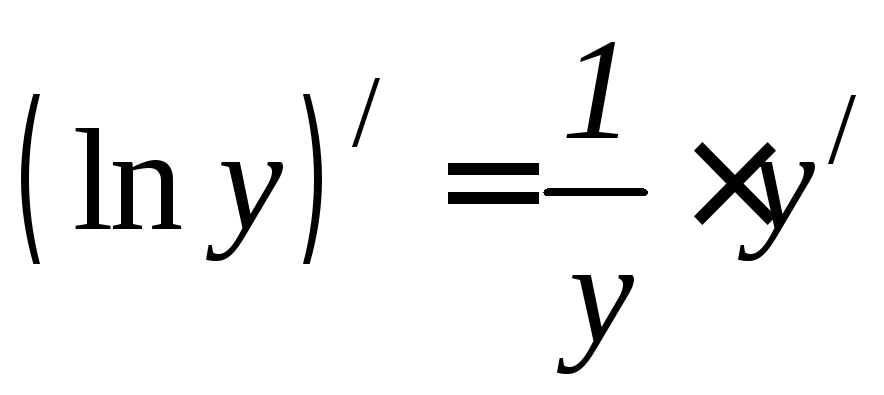 .
.
Следовательно,
![]()
или
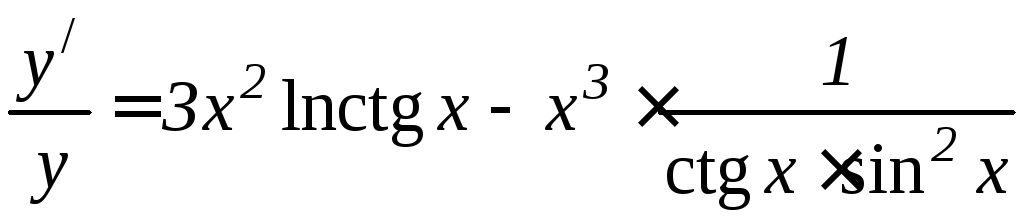 .
.
Умножив последнее
равенство на y,
получим
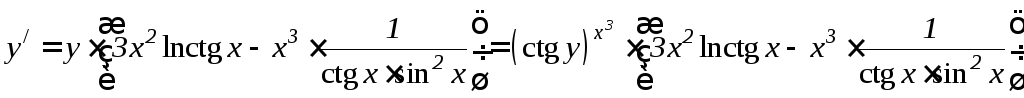 .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
15.02.2015565.25 Кб167 .doc
- #
- #

Производные высших порядков явно заданной функции
Производная 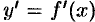 функции
функции 
есть также функция от 
и называется производной первого порядка.
Если функция 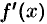 дифференцируема, то ее производная называется производной второго порядка и обозначается
дифференцируема, то ее производная называется производной второго порядка и обозначается 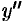 (или
(или 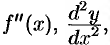
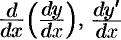 ) . Итак,
) . Итак, 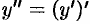 .
.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается 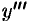 ( или
( или 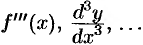 ), Итак,
), Итак, 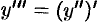 .
.
Производной 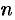 -го порядка (или
-го порядка (или 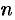 -й производной) называется производная от производной (
-й производной) называется производная от производной (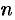 -1) порядка:
-1) порядка:
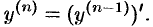
Производные порядка выше первого называются производными высших порядков.
Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (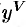 или
или 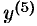 — производная пятого порядка).
— производная пятого порядка).
Пример №23.1.
Найти производную 13-го порядка функции 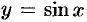 .
.
Решение:
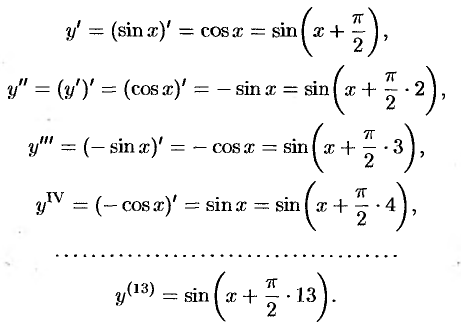
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:

Производная функции
Производной функции y=f(x) в точке x0 называется конечный предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (см. пример).
Если необходимо найти производные функции нескольких переменных z=f(x,y), то можно воспользоваться данным онлайн-калькулятором. Решение оформляется в формате Word.
- Решение онлайн
- Видеоинструкция
- Также решают
Правила ввода функции, заданной в явном виде
Примеры
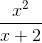 ≡ x^2/(x+2)
≡ x^2/(x+2)
cos2(2x+π) ≡ (cos(2*x+pi))^2
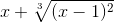 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3)
Правила ввода функции, заданной в неявном виде
Примеры
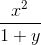 ≡ x^2/(1+y)
≡ x^2/(1+y)
cos2(2x+y) ≡ (cos(2*x+y))^2
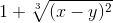 ≡ 1+(x-y)^(2/3)
≡ 1+(x-y)^(2/3)
Если функция задана в виде y2-x=cos(y), то ее необходимо записать так: y^2-x-cos(y).
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
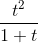 ≡ t^2/(1+t)
≡ t^2/(1+t)
cos2(t) ≡ cos(t)^2
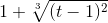 ≡ 1+(t-1)^(2/3)
≡ 1+(t-1)^(2/3)
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
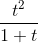 ≡ t^2/(1+t)
≡ t^2/(1+t)
cos2(t) ≡ cos(t)^2
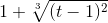 ≡ 1+(t-1)^(2/3)
≡ 1+(t-1)^(2/3)
Как найти производную, исходяя из ее определения?
Правила нахождения производных
Пример 1. Найти производную функции y=cos4x.
Решение.
Внешней функцией здесь служит степенная функция: cos(x) возводится в четвертую степень. Дифференцируя эту степенную функцию по промежуточному аргументу cos(x), получим
(cos4x)′cos x = 4cos4-1x = 4cos3x
но промежуточный аргумент cos(x) – функция независимой переменной х; поэтому надо полученный результат умножить на производную от cos(x) по независимой переменной х . Таким образом, получим
y′x = (cos4x)′cos x·(cosx)′x = 4·cos3x·(-sin x) = -4·cos3x·sin x
При дифференцировании функций нет необходимости в таких подробных записях. Результат следует писать сразу, представляя последовательно в уме промежуточные аргументы.
Пример 2. Найти производную функции
![]() .
.

 .
.
В некоторых случаях, если, например, нужно найти производную функции y = (u(x))v(x), или функции, заданной в виде произведения большого числа сомножителей, используется так называемый способ логарифмического дифференцирования.
Пример 3. Найти производную функции
 .
.
Решение.
Применим метод логарифмического дифференцирования. Рассмотрим функцию

Учитывая, что  , будем иметь
, будем иметь

Но  , откуда
, откуда
 .
.
Пример 4. Найти производную функции y=xex
Решение.
![]()
 ;
;
 .
.
Прикладное использование производной
Вычисление производной первого и второго порядка используется во многих прикладных задачах. Рассмотрим наиболее распространенные из них.
- Нахождение экстремумов функции одной переменной осуществляют приравниванием к нулю производной:
f'(x)=0. Этот этап является основным для построения графика функции методом дифференциального исчисления. - Значение производной в точке x0 позволяет находить уравнение касательной к графику функции.
- Отношение производных позволяет вычислять пределы по правилу Лопиталя.
- В математической статистике плотность распределения f(x) определяют как производную от функции распределения F(x).
- При отыскании частного решения линейного дифференциального уравнения требуется вычислять производную в точке.
- В методе Ньютона с помощью производной отделяют корни нелинейных уравнений.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Явные и неявные
В этой статье мы познакомимся с неявными функциями и техникой их дифференцирования. Вспомним для начала, как выглядят функции, заданные явно. Это “обычные” функции вида y=f(x)y=f(x), с которыми вы уже имели дело и умеете вычислять их производные. Запись y=f(x)y=f(x) обозначает, что мы функцию yy смогли выразить (явно представить) через её аргумент xx. З неявными функциями дело обстоит иначе. Здесь мы не можем “перетащить” yy в левую сторону выражения, а все что содержит xx — в правую. Такие функциональные зависимости в общем виде можно записать так:
F(x,y)=0F(x, y)=0
Эта запись означает, что величины xx и yy как-то связанны между собой, но ничего не говорится о том, как yy выражается через xx (и можно ли это вообще сделать). Одну и ту же функцию (но не каждую) можно записать как в явном так и в неявном виде. Например, неявно заданную функцию F(x,y)=3xy+5xF(x, y)=3xy+frac{5}{x} можно записать явно: y(x)=−53x2y(x)=-frac{5}{3x^2}. В этом случае нам удалось выразить yy через xx. Или, если:
F(x,y)=x2+y2−1=0F(x, y)=x^2+y^2-1=0
то
y=±1−x2y=pm sqrt{1-x^2}
Здесь функция получилась многозадачной (именно двузначной, отвечающей двум знакам), но это не страшно. Мы все-равно представили yy как выражение зависящее от xx. В правой стороне у нас присутствует только xx.
Но существуют случаи, когда этого сделать нельзя. Можно навести множество примеров таких функций. Например:
F(x,y)=ylnx+eyy2F(x, y)=yln x+e^yy^2
Ну попробуйте выразить отсюда yy через xx. То есть запишите эту функцию в виде y=f(x)y=f(x). Вот вам и пример неявной заданной функции. Ещё пример:
F(x,y)=xsinx+ysiny−12F(x, y)=xsin x+ysin y-12
Здесь, мы хотя и не можем выразить yy через xx, но мы все-равно можем считать yy функцией от аргумента xx. Так как каждому значению xx будут соответствовать какие-то значения yy.
Естественно, возникает вопрос о дифференцировании подобных функций. Вы уже понимаете, что эта операция очень важна, и было бы тяжело поверить, что математики ничего не придумали на этот счет.
Дифференцирование неявно заданных функций
Оказывается, что для того чтобы посчитать производную от yy по xx нам не обязательно решать уравнение:
F(x,y)=0F(x, y)=0
Теоретически можно доказать (пользуюсь определением производной, производя предельный переход и т. д.), что:
dydx=−∂F(x,y)∂x∂F(x,y)∂yfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}
Обозначение ∂partial обозначает частную производную. Мы здесь имеем дело с двумя переменными xx и yy и берем производные от функции F(x,y)F(x, y) по этим величинам. Так, выражение:
∂F(x,y)∂xfrac{partial F(x, y)}{partial x}
говорит, что берется производная от F(x,y)F(x, y) по xx, при этом величина yy считается постоянной. Следует обратить внимание на знак “минус” перед дробью, а также на то, что мы не можем сократить числитель и знаменатель на ∂F(x,y)partial F(x, y), так как производные берутся по разным величинам. Вооружившись этой главной формулой вычисления производных от неявных функций, перейдем к разбору нескольких примеров.
Примеры
F(x,y)=x2+y2−1F(x, y)=x^2+y^2-1
∂F(x,y)∂x=2x, ∂F(x,y)∂y=2yfrac{partial F(x, y)}{partial x}=2x, frac{partial F(x, y)}{partial y}=2y
dydx=−∂F(x,y)∂x∂F(x,y)∂y=−2x2y=−xyfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{2x}{2y}=-frac{x}{y}
F(x,y)=xsinx+ysiny−12F(x, y)=xsin x+ysin y-12
∂F(x,y)∂x=sinx+xcosx, ∂F(x,y)∂y=siny+ycosyfrac{partial F(x, y)}{partial x}=sin x+x cos x, frac{partial F(x, y)}{partial y}=sin y+y cos y
dydx=−∂F(x,y)∂x∂F(x,y)∂y=−sinx+xcosxsiny+ycosyfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{sin x+xcos x}{sin y+ycos y}
- F(x,y)=3xy+5xF(x, y)=3xy+frac{5}{x}
∂F(x,y)∂x=3y−5×2, ∂F(x,y)∂y=3xfrac{partial F(x, y)}{partial x}=3y-frac{5}{x^2}, frac{partial F(x, y)}{partial y}=3x
dydx=−∂F(x,y)∂x∂F(x,y)∂y=−3y−5x23x=−3yx2−53x3frac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{3y-frac{5}{x^2}}{3x}=-frac{3yx^2-5}{3x^3}
Но здесь мы можем выразить yy через xx явно:
y=−53x2y=-frac{5}{3x^2}
Подставим это выражение в формулу для производной выше:
dydx=103x3frac{dy}{dx}=frac{10}{3x^3}
А теперь поступим так, как будто нам с самого начала была известна явная зависимость y=f(x)y=f(x). То есть продифференцируем функцию y(x)=−53x2y(x)=-frac{5}{3x^2} по xx:
dydx=ddx(−53×2)=−53(−2)1×3=103x3frac{dy}{dx}=frac{d}{dx}Big(-frac{5}{3x^2}Big)=-frac{5}{3}(-2)frac{1}{x^3}=frac{10}{3x^3}
Получили то же самое. Значит мы все сделали правильно.