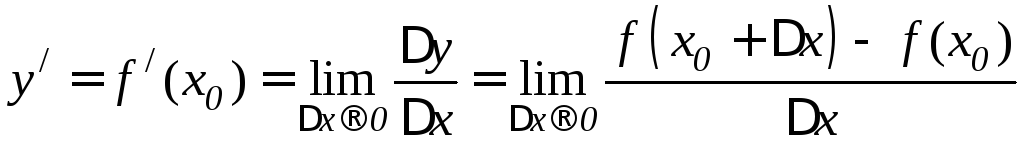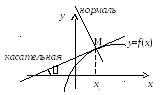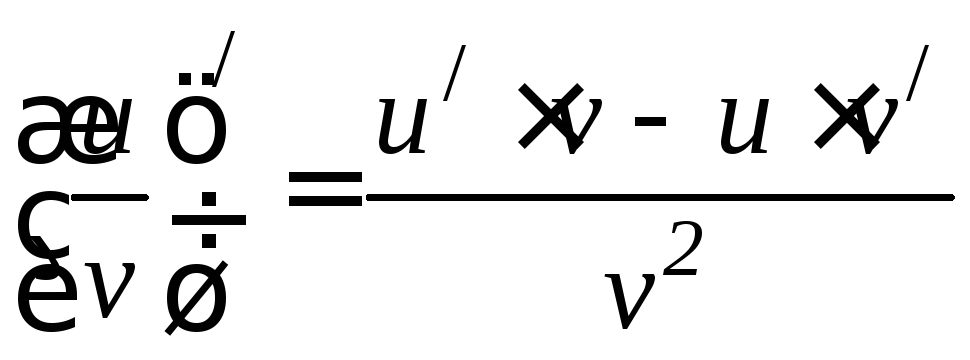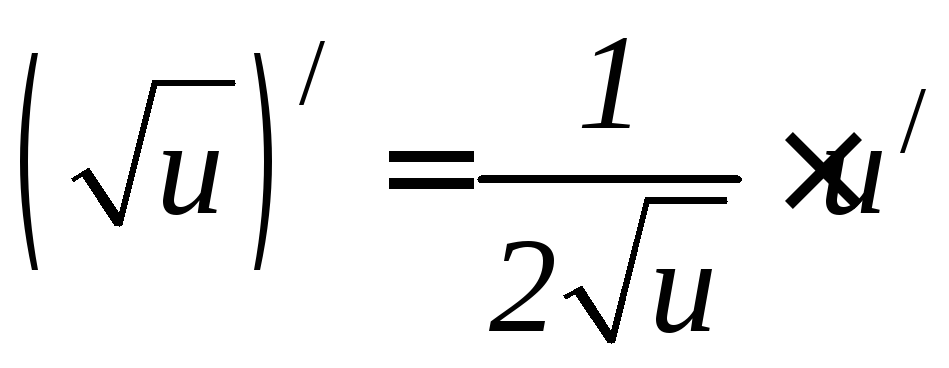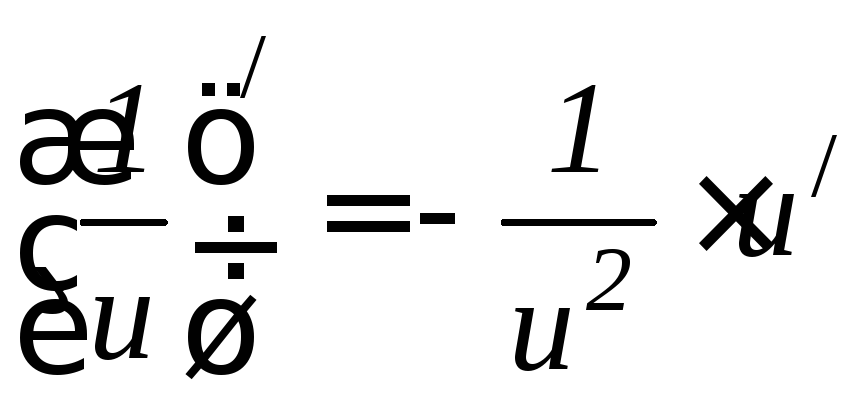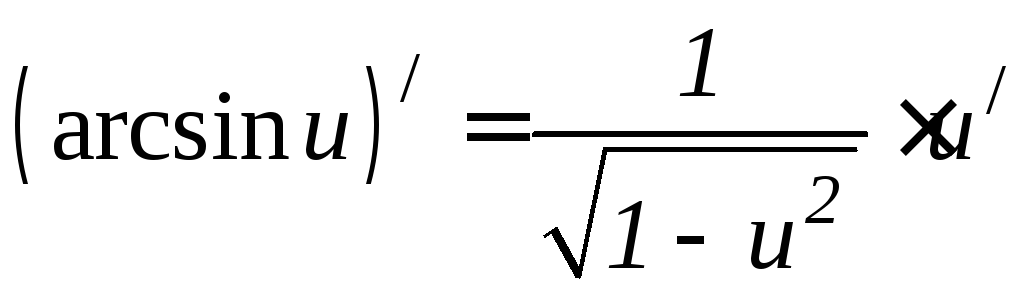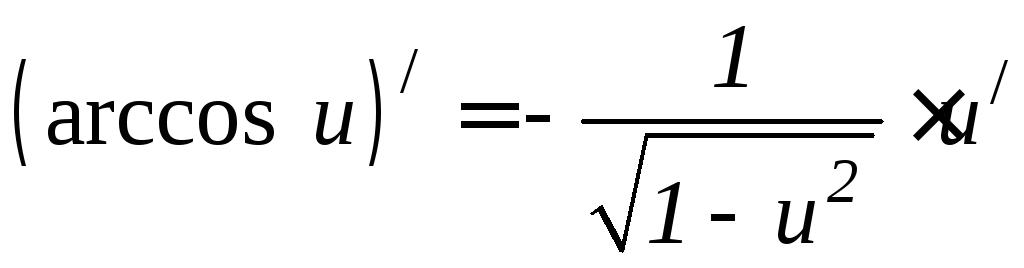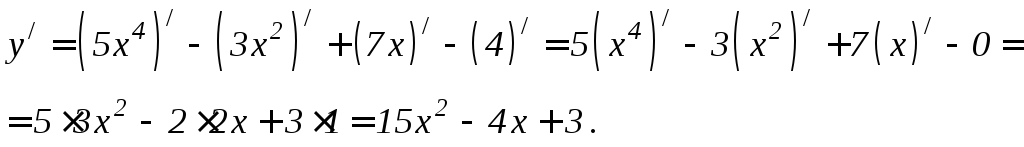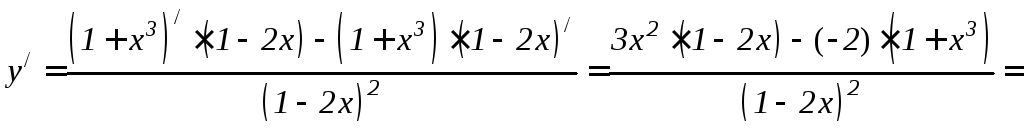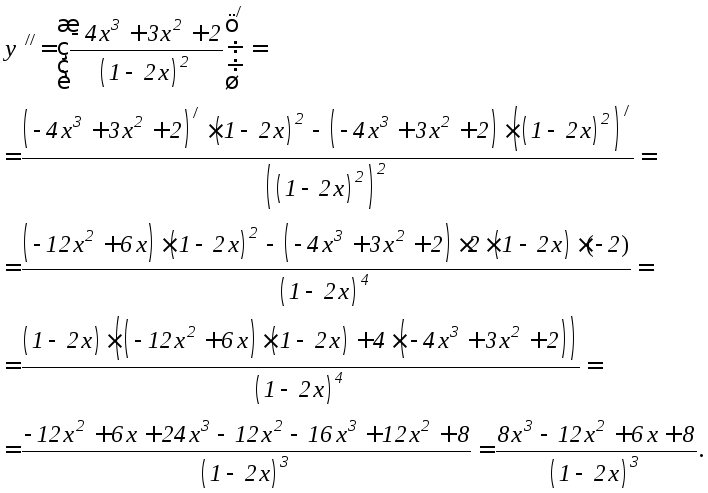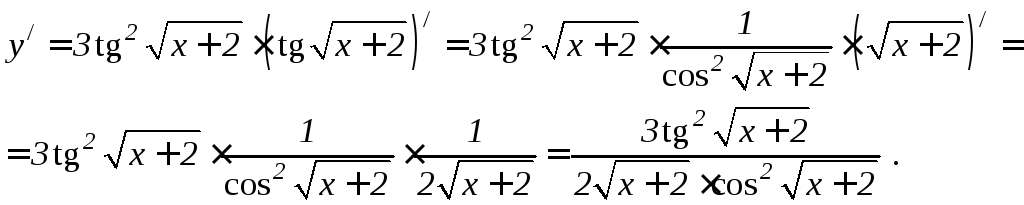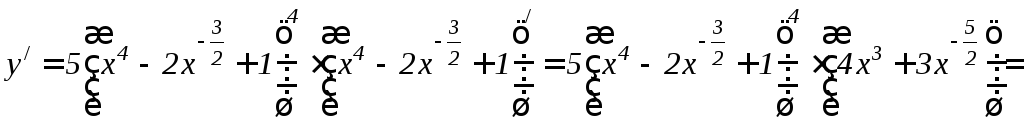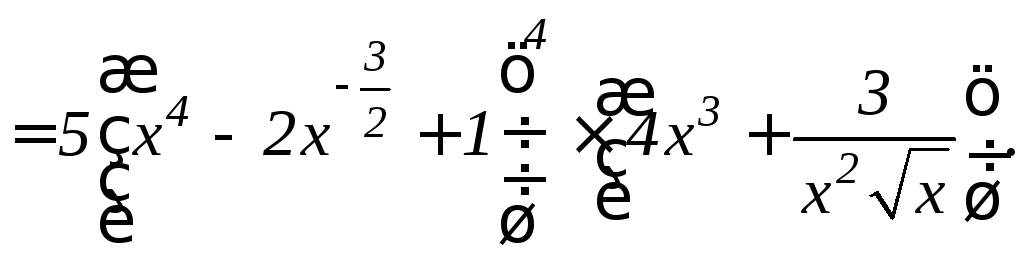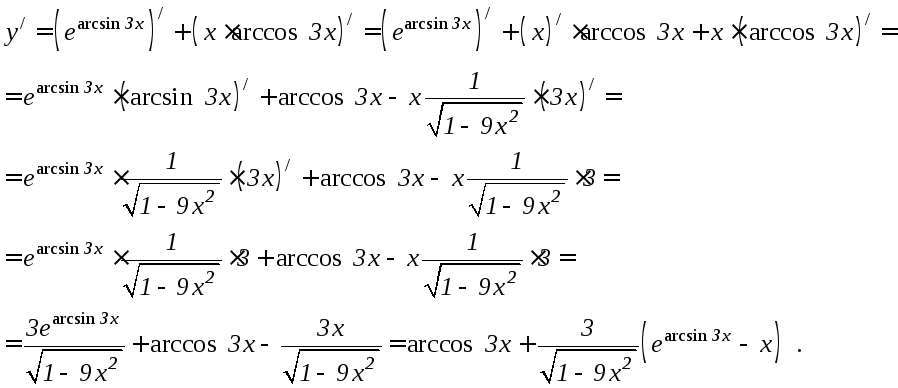-
Производная функции
6.1 Дифференцирование функций, заданных явно
Производной
функцииy=f(x)
в точкеx0называется предел отношения приращения
функции в этой точке к приращению
аргумента, когда последнее стремится
к нулю. Производная функцииy=f(x)
обозначается черезy/,
илиf /(x).
Операция
нахождения производной f
/(x) от
функцииf(x)
называетсядифференцированием
этой функции.
Геометрически
значение производной функции y=f(x)
в точкеx=x0равно тангенсу угла, образованного
положительным направлением осиОхи касательной, проведенной к графику
функции в точке с абсциссойx0,
то естьf /(
x0)=tg
(рис 6.1).
|
Число k В |
Рис |
–уравнение касательной,
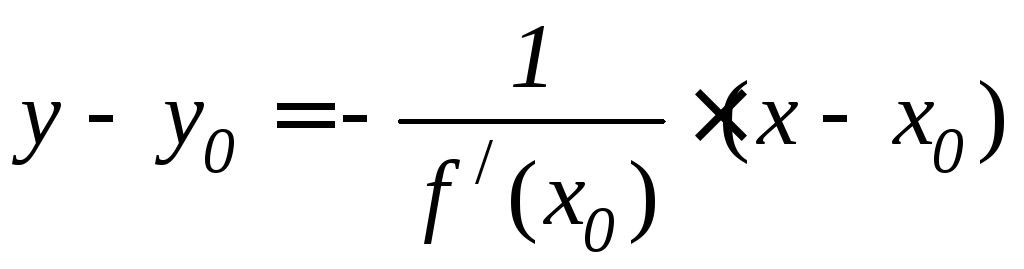
Если
функция y=f(x)
описывает какой–либо физический
процесс, то производнаяy/есть скорость протекания этого процесса.
В этом состоит физический смысл
производной.
Основные правила дифференцирования.
Пусть
даны функции, имеющие производные
u=u(x)
и v=v(x),
c=const
|
6.1 6.2 6.3 |
6.4 6.5 |
6.6
6.7
если
дана сложная функция y=f(u),
где u=u(x),
то есть y=f[u(x)],
где функции
f(u)
и u(x)
имеют производные, то
(правило дифференцирования сложной
функции).
Основные формулы дифференцирования.
|
6.8 6.9 6.10 6.11 6.12 6.13 6.14 6.15 6.16 6.17 |
6.18 6.19 6.20 6.21 6.22 6.23 6.24 6.25 6.26 |
Пример
1. Найти
производную функции
.
Решение.
Дифференцируем как сумму по формулам
6.4, 6.1, 6.3 правил дифференцирования и
применяем формулу 6.8
Пример
2. Найти
y// функции

Решение.
Дифференцируем как частное по формуле
6.5 правил дифференцирования и применяем
формулы 6.2, 6.1 и 6.8
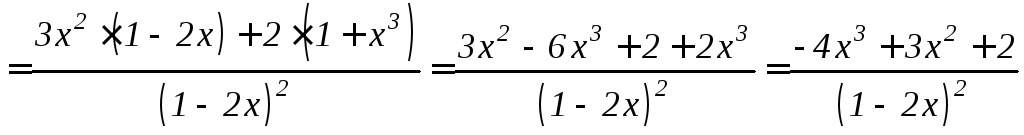
Пример
3. Найти y/функции
.
Решение.
Дифференцируем, применяя формулы
производной сложной функции и формулы
6.8 и 6.12
Пример
4. Найти
y/функции
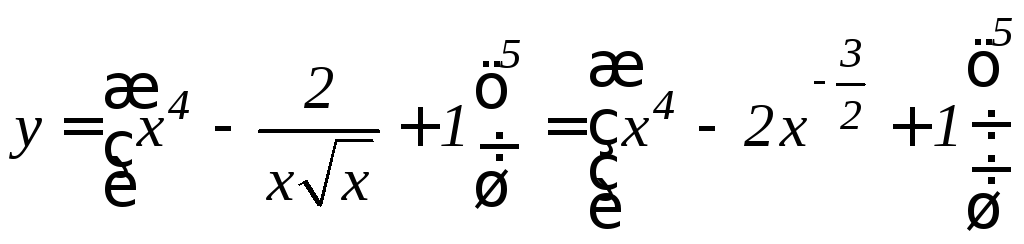
Решение. Вводим
сначала дробные и отрицательные
показатели, затем дифференцируем,
применяя формулы 6.3, 6.2 и 6.1 и формулу
6.8
Пример
5. Найти
y/функции
.
Решение.
Применяем сначала формулу 6.3, а для
второго слагаемого формулу 6.4. Затем
используем формулы 6.9, 6.14, 6.8 и 6.15
Логарифмический
метод.
Иногда,
прежде чем находить производную от
заданного выражения, лучше выражение
преобразовать так, чтобы процесс
дифференцирования упрощался. Во многих
случаях оказывается выгодным, прежде
чем дифференцировать заданную функцию,
взять ее логарифм, определить затем
производную от этого логарифма и по
производной от логарифма отыскать
производную от заданной функции. Такой
прием называется способом логарифмического
дифференцирования.
Метод
логарифмического дифференцирования
позволяет находить производные от
сложной функции вида
,
гдеu,v–
функции аргументаx.
Действительно, логарифмируя обе части
исходного равенства, получаем
.
Дифференцируя последнее
равенство, имеем
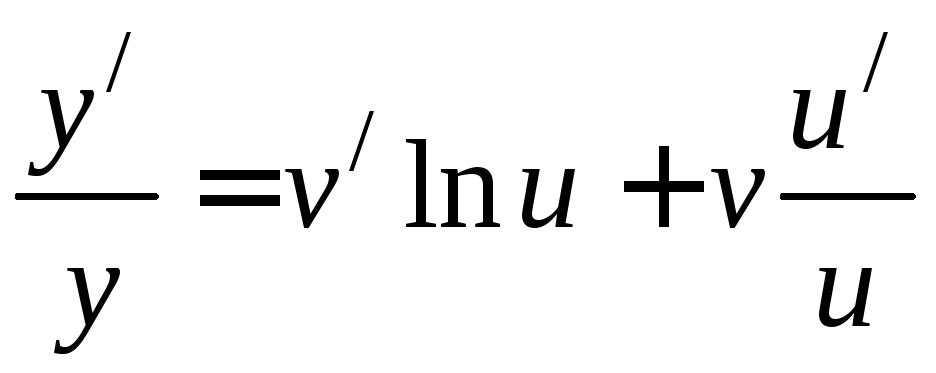
Умножая обе части
равенства на y и
заменяя затемy
черезuv,
окончательно получаем
.
Пример 6. Найтиy/, если.
Решение. Здесь
основание и показатель степени зависят
отx. Логарифмируя,
получим
(так как
).
Продифференцируем
обе части последнего равенства по x.
Так какyявляется
функцией отx, тоlny есть сложная функцияxи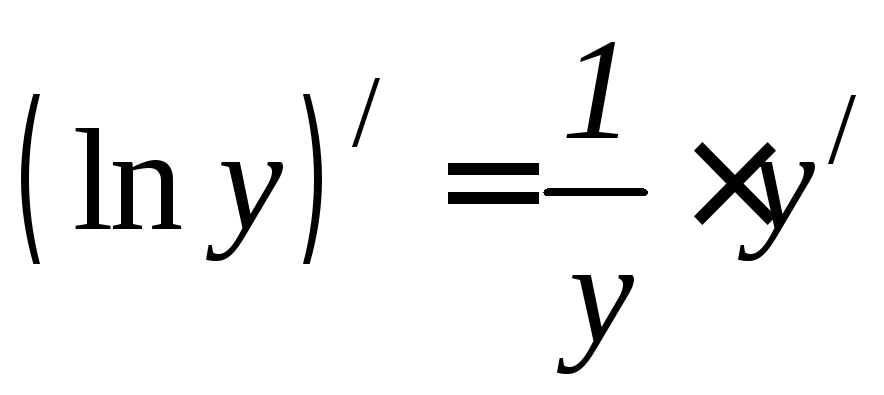
Следовательно,
или
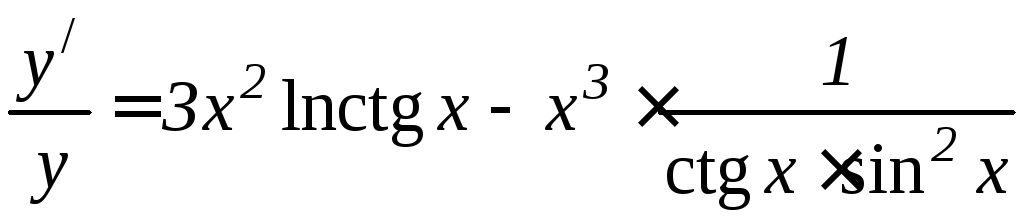
Умножив последнее
равенство на y,
получим
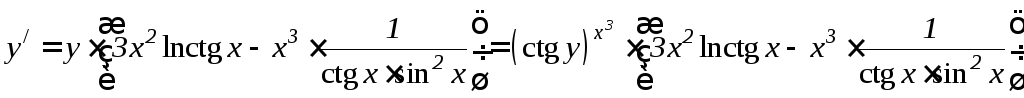
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
15.02.2015565.25 Кб167 .doc
- #
- #
(схема 30)
При дифференцировании различают функции по способу их задания: явные, неявные и параметрические.
Пусть явно задана функция y=f (x). Функция,
зависящая непосредственно от переменной x, называется
простой.
Рассмотрим для простой функции точку x, принадлежащую ее области определения. Дадим
приращение аргументу ∆x в точке x. Функция
получит при этом соответствующее (3.9) приращение ∆y=f(x+∆x)–f(x).
Производной функции y=f (x) по переменной x в некоторой точке называется предел отношения
приращения функции к приращению аргумента, когда
последнее стремится к нулю, то есть

Функция, имеющая в точке конечную производную,
называется дифференцируемой в этой точке. Процесс нахождения производной называется
дифференцированием и обозначается 
Производная
характеризует скорость изменения функции в достаточно малой окрестности заданной
точки.
Приведем таблицу производных основных элементарных
функций (без доказательства), которые рассматриваются нами как функции простые
и явно заданные.
Теорема 3.9. Если функция
дифференцируема в некоторой точке, то она в этой точке непрерывна
Следствие. В точках разрыва функция производной не имеет
Существуют такие точки, в которых функция непрерывна,
но не дифференцируема. Так, функция y=|x| в точке x=0 непрерывна, но производной не имеет, так как в этой
точке к графику функции можно провести бесконечное множество
касательных (рис. 3.6). Такие точки называются угловыми или точками излома функции. Данный случай показывает, что обратное утверждение к
теореме 3.9 неверно.
Среди явных
функций особое место занимают обратные функции, производная
которых находится с помощью следующей теоремы.
Теорема 3.10. Если
строго монотонная функция y=f (x) дифференцируема на некотором интервале Х, причем ее производная не
обращается в нуль на Х, то обратная к ней функция x=φ(y) также
дифференцируема на этом интервале, при этом:

Доказательство. Дадим функции
y=f (x) в точке x бесконечно малое приращение аргумента ∆x→0, функция при этом получит соответствующее приращение
∆y. Так как по условию теоремы функция
дифференцируема в каждой точке интервала Х, то в каждой точке этого
интервала функция непрерывна (по теореме 3.9). Следовательно, по определению
непрерывности функции выполняется: 
при ∆x→0; ∆y→0.
По
определению производной можно записать:

Среди явных функций выделяют класс сложных функций.
Функция называется
сложной, если она представляет собой композицию нескольких функций: y=f (φ(x)). Функция f называется внешней, а φ – внутренней функцией, выступающей в качестве
независимого переменного.
Теорема 3.11.
Чтобы
продифференцировать сложную
функцию необходимо сначала продифференцировать внешнюю функцию по внутренней,
считая внутреннюю функцию независимой переменной, затем
продифференцировать внутреннюю функцию по независимому переменному и результаты
дифференцирования перемножить, то есть

Пример 3.8. Найти
производную функции .
Решение. Согласно формуле (3.31) и с учетом табли
(3.17), (3.19), (3.29) имеем:

К явным функциям можно отнести функции, заданные
параметрически, вида:
где t –
параметр. Производную такой функции несложно получить:

Пример 3.9. Найти
производную функции 
Решение. Согласно
формуле (3.32) и с учетом табличных формул (3.18), (3.19) имеем:
Примечание. Функция,
заданная в примере 3.9, представляет собой параметрическое уравнение окружности
радиуса a. Действительно, возведем оба уравнения в квадрат и сложим
их почленно, получим:

Помимо таблицы производных
имеют место правила дифференцирования.
Теорема 3.12. Производная суммы двух дифференцируемых функций равна сумме
производных этих функций:

Данная теорема может быть обобщена для произвольного
конечного числа функций-слагаемых.
Пример 3.10.
Найти производную функции
Решение. Согласно
формулам (3.33) и (3.31) и с учетом табличных формул (3.17), (3.20), (3.23) имеем:

Теорема 3.13. Производная произведения двух дифференцируемых функций равна
произведению производной первой функции-сомножителя на вторую функцию плюс
произведение первой функции на производную
второй функции–сомножителя, то есть

Пример 3.11.
Найти производную функции 
Решение. Согласно формуле (3.34) и с учетом табличных формул
(3.22), (3.24) имеем:
Теорема 3.14.
Производная частного двух функций
равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а
числитель есть разность между
произведением знаменателя на производную числителя и произведением
числителя на производную знаменателя, то есть

Пример 3.12.
Найти производную функции
Решение. Согласно формуле (3.35) и с учетом табличных формул
(3.17), (3.29) имеем:

Все рассмотренные выше при дифференцировании функции
были заданы в явном виде, то есть уравнением y=f (x),
разрешенным относительно y.
Функция называется неявно заданной, если она
имеет вид F (x;y)=0.
Неявный способ задания к свойствам функции отношения не имеет. В этом случае
любое выражение, содержащее переменную y, нужно
рассматривать как функцию сложную. Следовательно, при нахождении производной неявных функций следует применять теорему о
дифференцировании сложной функции. В процессе отыскания 
содержащие 

множитель. Слагаемые, не содержащие 
относительно искомой 
Пример 3.13.
Найти производную неявной
функции 
Решение. Согласно формуле (3.31) дифференцирования сложной функции и (3.34) производной
произведения, с учетом табличных формул (3.17) и (3.18)
имеем:
Иногда для упрощения процесса дифференцирования
громоздких функций применяют их предварительное логарифмирование (логарифмическое
дифференцирование). Данный метод целесообразен в тех случаях, когда
функция представляет собой произведение и (или) частное различных функций,
таких как показательные и степенные выражения (особенно иррациональные).
Логарифмическое дифференцирование используется также для нахождения производных
показательно-степенных функций, которые без предварительного логарифмирования
вообще не дифференцируются. При использовании данного метода в левой части получают производную от натурального
логарифма y, которая равна 
условию функцию.
Пример 3.14.
Найти производную функции 
Решение.
Прологарифмируем заданную функцию 
По свойству логарифма степени имеем:
(3.31) дифференцирования сложной функции
и (3.34) производной произведения, с учетом табличных формул (3.19) и (3.29)
можно записать

После умножения обеих частей последнего равенства на y
окончательно получим:
производную заданной функции найти невозможно, так как нельзя обосновать
использование формул дифференцирования (3.17) или (3.22)
Пусть функция y=f (x)
дифференцируема в некоторой текущей точке x и при этом 
записать: 

Дифференциалом функции y=f (x) в точке x называется главная часть приращения этой
функции, равная произведению производной функции на приращение аргумента:

Найдем дифференциал независимой переменной x, то есть
дифференциал функции y=x. Так
как 
функции может быть записана в виде:

Если в формуле
(3.36) отбросить бесконечно малую величину α∙∆x, то
получим приближенное равенство


(3.39)
Формула (3.39) применяется для вычисления приближенных
значений функций.
Пример
3.15. Вычислить приближенно значение 
Решение.
Рассмотрим функцию 
имеем:

Так как x+∆x=0,95, то при x=1 и ∆x=-0,05
получаем:
Процесс дифференцирования может быть многократным. Производная от первой
производной называется второй производной функции или производной 2-го порядка.
Производная от последней, в свою очередь, является производной 3-го порядка и
так далее. Производная функции n-го порядка 
порядка заданной функции, то есть

Производная функции
Производной функции y=f(x) в точке x0 называется конечный предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (см. пример).
Если необходимо найти производные функции нескольких переменных z=f(x,y), то можно воспользоваться данным онлайн-калькулятором. Решение оформляется в формате Word.
- Решение онлайн
- Видеоинструкция
- Также решают
Правила ввода функции, заданной в явном виде
Примеры
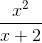
cos2(2x+π) ≡ (cos(2*x+pi))^2
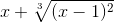
Правила ввода функции, заданной в неявном виде
Примеры
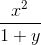
cos2(2x+y) ≡ (cos(2*x+y))^2
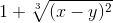
Если функция задана в виде y2-x=cos(y), то ее необходимо записать так: y^2-x-cos(y).
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
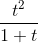
cos2(t) ≡ cos(t)^2
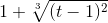
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
Примеры
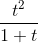
cos2(t) ≡ cos(t)^2
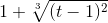
Как найти производную, исходяя из ее определения?
Правила нахождения производных
Пример 1. Найти производную функции y=cos4x.
Решение.
Внешней функцией здесь служит степенная функция: cos(x) возводится в четвертую степень. Дифференцируя эту степенную функцию по промежуточному аргументу cos(x), получим
(cos4x)′cos x = 4cos4-1x = 4cos3x
но промежуточный аргумент cos(x) – функция независимой переменной х; поэтому надо полученный результат умножить на производную от cos(x) по независимой переменной х . Таким образом, получим
y′x = (cos4x)′cos x·(cosx)′x = 4·cos3x·(-sin x) = -4·cos3x·sin x
При дифференцировании функций нет необходимости в таких подробных записях. Результат следует писать сразу, представляя последовательно в уме промежуточные аргументы.
Пример 2. Найти производную функции
.

В некоторых случаях, если, например, нужно найти производную функции y = (u(x))v(x), или функции, заданной в виде произведения большого числа сомножителей, используется так называемый способ логарифмического дифференцирования.
Пример 3. Найти производную функции

Решение.
Применим метод логарифмического дифференцирования. Рассмотрим функцию
Учитывая, что 
Но 

Пример 4. Найти производную функции y=xex
Решение.


Прикладное использование производной
Вычисление производной первого и второго порядка используется во многих прикладных задачах. Рассмотрим наиболее распространенные из них.
- Нахождение экстремумов функции одной переменной осуществляют приравниванием к нулю производной:
f'(x)=0. Этот этап является основным для построения графика функции методом дифференциального исчисления. - Значение производной в точке x0 позволяет находить уравнение касательной к графику функции.
- Отношение производных позволяет вычислять пределы по правилу Лопиталя.
- В математической статистике плотность распределения f(x) определяют как производную от функции распределения F(x).
- При отыскании частного решения линейного дифференциального уравнения требуется вычислять производную в точке.
- В методе Ньютона с помощью производной отделяют корни нелинейных уравнений.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Загрузить PDF
Загрузить PDF
Производную функции можно использовать для того, чтобы получить полезную информацию о графике, например, узнать положение максимумов, минимумов, пиков, впадин и характер наклона. Вы даже можете использовать их для построения на графике сложных уравнений без применения графического калькулятора! К сожалению, нахождение производной может быть утомительной задачей, но эта статья поможет вам узнать некоторые приемы и ловкости.
Шаги
-
1
Ознакомьтесь с формой обозначения производной. Следующие две формы обозначения являются наиболее распространенными, однако на Википедии можно найти огромное количество других here.
- Обозначение Лейбница. Это обозначение является наиболее распространенным в случаях, когда функция включает y и x. dy/dx буквально означает “производная y по отношению к x.” Удобно представить производную в виде отношения бесконечно малых разностей Δy/Δx. Это объяснение является следствием определения производной через предел: limh->0 (f(x+h)-f(x))/h. Используя данное обозначение для второй производной, вы должны написать: d2y/dx2.
- Обозначение Лагранжа. Производную функции можно также записать как f'(x). Это обозначение читается как “f штрих от x”. Это обозначение короче обозначения Лейбница, оно полезно при рассмотрении производной как функции. Чтобы образовать производные высших порядков, просто добавляйте к “f” новые ” ‘ “. Так, вторая производная будет иметь вид f”(x).
-
2
Выясните, что такое производная и зачем она нужна. Во-первых, для нахождения наклона прямой зависимости, берутся две точки на прямой, и их координаты подставляются в уравнение (y2 – y1)/(x2 – x1). Тем не менее, это может быть использовано только для линейных зависимостей. Для квадратичных зависимостей и выше линия будет кривой, поэтому определение “разности” двух точек не может быть точным. Чтобы найти наклон касательной к криволинейному графику, берутся две точки, которые подставляются в стандартное уравнение определения наклона касательной к кривой: [f(x + dx) – f(x)]/dx. Dx означает “delta x,” являющуюся разностью между двумя x-координатами графика. Обратите внимание, что это выражение аналогично (y2 – y1)/(x2 – x1), просто в другой форме. Поскольку уже известно, что результат не будет точным, применяется косвенный подход. Чтобы найти наклон касательной в точке (x, f(x)), dx должно стремиться к 0, так что две выбранные точки сольются в одну. Впрочем, мы не можем делить на 0, поэтому, подставив оба значения координат точки, вы должны будете разложить выражение на множители и использовать другие методы для сокращения dx в нижней части выражения. Сделав это, примите dx = 0 и решите уравнение. Это и будет углом наклона в точке (x, f(x)). Производная выражения – это общее выражение для нахождения наклона любой касательной к графику. Это может казаться чрезвычайно сложным, но несколько примеров, приведенных ниже, помогут вам понять процесс нахождения производной.
Реклама
-
1
Используйте дифференцирование явных функций, когда ваше выражение уже имеет y, расположенный в одной его части.
-
2
Подставьте выражение в выражение [f(x + dx) – f(x)]/dx. Например, если ваше уравнение имеет вид y = x2, производная будет иметь вид [(x + dx)2 – x2]/dx.
-
3
Раскройте скобки, а затем вынесите dx за скобки, получив уравнение [dx(2x + dx)]/dx. Теперь вы можете сократить два dx в верхней и нижней частях дроби. В результате вы получите 2x + dx, и когда dx стремится к 0, то производная равна 2x. Это означает, что наклон любой касательной к графику y = x2 равен 2x. Просто подставьте значение x точки, в которой вы хотите найти наклон.
-
4
Изучите схемы нахождения производной функций подобного типа. Ниже приведены несколько из них.
- Производная степенной функции равна произведению показателя степени и основания в степени на единицу меньше. Например, производная x5 равна 5x4, а производная x3.5 равна 3.5x2.5. Если перед x уже есть число, просто умножьте его на степень. Например, производная 3x4 равна 12x3.
- Производная любого числа равна 0. Иначе говоря, производная 8 равна 0.
- Производная суммы – это сумма отдельных производных. Например, производная x3 + 3x2 равна 3x2 + 6x.
- Производная произведения – это произведение первого множителя на производную второго плюс произведение второго множителя на производную первого. Например, производная x3(2x + 1) равна x3(2) + (2x + 1)3x2, что равно 8x3 + 3x2.
- Производная дроби (скажем, f/g) – это [g(производная f) – f(производная g)]/g2. Например, производная (x2 + 2x – 21)/(x – 3) равна (x2 – 6x + 15)/(x – 3)2.
Реклама
-
1
Используйте дифференцирование неявно выраженных функций, когда в вашем выражении нельзя выделить y на одной из сторон. Даже если вы смогли записать его с y в одной части, вычисление dy/dx будет громоздким. Ниже приведены примеры нахождения производной для выражений такого типа.
-
2
В этом примере: x2y + 2y3 = 3x + 2y, замените y на f(x), чтобы запомнить, что y на самом деле – функция. Выражение примет вид x2f(x) + 2[f(x)]3 = 3x + 2f(x).
-
3
Чтобы найти производную этого выражения, продифференцируйте (умное слово, означающее найти производную) обе стороны уравнение по x. Выражение станет x2f'(x) + 2xf(x) + 6[f(x)]2f'(x) = 3 + 2f'(x).
-
4
Снова замените f(x) на y. Будьте внимательны и не сделайте того же для f'(x), отличающегося от f(x).
-
5
Найдите f'(x). Ответ на этот пример принимает вид (3 – 2xy)/(x2 + 6y2 – 2).
Реклама
-
1
Взять производную высшего порядка функции означает взять производную производной (в случае порядка, равного 2). Например, если вас просят взять производную третьего порядка, просто возьмите производную производной производной. Для некоторых выражений, производные высших порядков принимают нулевое значение.
-
1
Если y – это дифференцируемая функция z, а z – дифференцируемая функция x, y – это сложная функция x, а производная y по x (dy/dx) равна (dy/du)*(du/dx). Правило цепочки также относится к сложным степенным выражениям, например: (2x4 – x)3. Чтобы найти производную, просто примените правило произведения. Умножьте выражение на степень и уменьшите степень на единицу. Затем умножьте выражение на производную основания (в нашем случае оно равно 2x^4 – x). Ответ на этот пример выглядит так: 3(2x4 – x)2(8x3 – 1).
Реклама
Советы
- Когда вы видите, что вам нужно решить просто огромный пример – не волнуйтесь. Разбейте его на как можно больше мельчайших кусков, применяя правила произведения, дроби и т.д. После этого приступайте к дифференцированию отдельных частей.
- Потренируйтесь использовать правила произведения, дроби, цепочек и в особенности – дифференцирования функций в неявной форме, поскольку они являются очень сложной частью матанализа.
- Умейте пользоваться калькулятором; пробуйте использовать различные функции вашего калькулятора, чтобы узнать его возможности. Особенно полезно знать функции касательной и производной, если они есть в вашем калькуляторе.
- Запомните производные основных тригонометрических функций и то, как с ними обращаться.
Реклама
Предупреждения
- Не забудьте, что при использовании правила дроби перед f(производная g) ставится знак минус; это распространенная ошибка и забыв его, вы получите неправильный ответ.
Реклама
Об этой статье
Эту страницу просматривали 11 770 раз.