Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 августа 2017 года; проверки требуют 5 правок.
В теории вероятностей, производящая функция вероятностей дискретной случайной величины представляет собой степенной ряд функции вероятности случайной величины. Производящие функции вероятностей часто используются для краткого описания их последовательности вероятностей P(X=i) для случайного величины Х, с возможностью применить теорию степенных рядов с неотрицательными коэффициентами.
Определение[править | править код]
Одномерный случай[править | править код]
Если Х является дискретной случайной величиной, принимающей неотрицательные целочисленные значения {0,1, …}, тогда производящая функция вероятностей от случайной величины Х определяется как
где p – это функция вероятности от Х. Заметим, что индексы обозначения GX и pX часто используются, чтобы подчеркнуть, что они относятся к конкретной случайной величине Х и ее распределению. Степенной ряд абсолютно сходится, по крайней мере, для всех комплексных чисел z, |z| ≤ 1; во многих примерах радиус сходимости больше.,c
Многомерный случай[править | править код]
Если X = (X1,…,Xd) является дискретной случайной величиной, принимающей значения из d-мерной неотрицательной целочисленной решетки {0,1, …}d, тогда производящая функция вероятностей от Х определена как
где p – это функция вероятности от Х. Степенной ряд абсолютно сходится по крайней мере для всех комплексных векторов z = (z1,…,zd ) ∈ ℂd с максимумом {|z1|,…,|zd |} ≤ 1.)
Свойства[править | править код]
Степенные ряды[править | править код]
Производящие функции вероятностей подчиняются всем правилам степенных рядов с неотрицательными коэффициентами. В частности, G(1−) = 1, где G(1−) = limz→1G(z) снизу, поскольку сумма вероятностей должна равняться 1. Таким образом, радиус сходимости любой производящей функции вероятностей должен быть как минимум 1, по теореме Абеля для степенных рядов с неотрицательными коэффициентами.
Вероятности и ожидания[править | править код]
Следующие свойства позволяют сделать вывод о различных базовых величинах, связанных с 
1. Функция вероятности от 

2. Из свойства 1 следует, что если случайные величины 






3. Нормализация функции плотности может быть выражена в терминах производящей функции
-
- Математическое ожидание X задается как
-
- В более общем плане, k-ый факториальный момент,
от X задается как
-
- Таким образом, дисперсия Х задается как
4. 



Функции независимых случайных величин[править | править код]
Производящие функции вероятностей полезны в частности для работы с функциями независимых случайных величин. Например:
- Если X1, X2, …, Xn представляет собой последовательность независимых (и не обязательно одинаково распределенных) случайных величин, и
-
- где ai – константы, тогда производящая функция вероятностей определяется как
- Например, если
- тогда производящая функция вероятностей, GSn(z), определяется как
- Из этого также следует, что производящая функция разности двух независимых случайных переменных S = X1 − X2 определяется как
- Предположим, что N также является независимой, дискретной случайной величиной, принимающая неотрицательные целочисленные значения, с производящей функцией вероятностей GN. Если X1, X2, …, XN независимы и одинаково распределены с общей производящей функцией вероятностей GX, тогда
-
- Это можно увидеть, используя закон полного математического ожидания следующим образом:
- Этот последний факт полезен при изучении процессов Гальтона-Ватсона.
- Пусть снова N также является независимой, дискретной случайной величиной, принимающей неотрицательные целочисленные значения, с производящей функцией вероятностей GN и плотностью вероятности fi=P{N=i}. Если X1, X2, …, Xn независимы, но неодинаково распределенные случайные величины, где GXi обозначает производящую функцию вероятностей от Xi, тогда
-
- Для одинаково распределенных Xi это упрощает тождественность указанную ранее. В общем случае иногда полезно получить разложение SN с помощью производящих функций вероятностей.
Примеры[править | править код]
- Производящая функция вероятностей для постоянной случайной величины принимающей одно значение c (P(X=c) = 1) есть
- Производящая функция вероятностей для случайной величины с биномиальным распределением есть
-
- Очевидно, что это n-кратное произведение производящих функции случайной величины с распределением Бернулли с параметром p
- Таким образом производящая функция случайной величины бросания честной монеты
- Производящая функция вероятностей для случайной величины с отрицательным биномиальным распределением с вероятностью успеха p, проводимой до r-го успеха
-
- (Сходится при
)
- Очевидно, что это r-кратное произведение производящих функции случайных величин с геометрическим распределением с параметром (1-p)
- Производящая функция вероятностей для случайной величины с распределением Пуассона с параметром λ есть
Ссылки[править | править код]
- Johnson, N.L.; Kotz, S.; Kemp, A.W. (1993) Univariate Discrete distributions (2nd edition). Wiley. ISBN 0-471-54897-9 (Section 1.B9)
Производящая функция
Для случайной величины $xi$ производящая функция моментов (сокращенно ПФМ) определяется следующим образом:
$$
M_{xi}(t)=M[e^{txi}].
$$
Для дискретной случайной величины с законом вида $(x_i,p_i)$ ПФМ выражается как
$$M_{xi}(t)=M[e^{txi}]=sum_i e^{tx_i}cdot p_i.$$
Для непрерывной случайной величины с плотностью распределения $f(x)$:
$$M_{xi}(t)=M[e^{txi}]=int_{-infty}^{infty} e^{tx}cdot f(x),dx.$$
Производящая функция моментов — это двустороннее преобразование Лапласа от плотности распределения случайной
величины.
По известной ПФМ можно вычислять моменты случайной величины по формуле:
$$M[xi^n] = frac{d^n}{dx^n} M_{xi}(t)|_{t=0} $$
ПФМ однозначно определяет распределение случайной величины. ПФМ суммы независимых случайных величин равна произведению их проиводящих функций моментов. Производящая функция существует только в случае существования всех моментов, а характеристическая функция – всегда.
В этом разделе вы найдете примеры нахождения производящей функции для разных законов распределения, в том числе для заданных произвольно случайных величины (см. задачи 3 и 4), а также пример решения обратной задачи – по имеющейся производящей функции восстановить закон распределения случайной величины.
Полезная страница? Сохрани или расскажи друзьям
Примеры решений: производящая функция
Задача 1. Найти производящую функцию моментов для случайной величины, имеющей геометрическое распределение. Вычислить с помощью найденной функции математическое ожидание и дисперсию.
Задача 2. Найти производящую функцию моментов для случайной величины, имеющей распределение Пуассона с параметром $lambda$. Вычислить с помощью найденной функции математическое ожидание и дисперсию.
Задача 3. Дискретная случайная величина X имеет ряд распределения.
x=-2 x=0 x=2
1/4 1/2 1/4
Найти производящую функцию моментов случайной величины X и с ее помощью вычислить математическое ожидание и дисперсию.
Задача 4. Абсолютно непрерывная случайная величина имеет плотность распределения
$$
p(x)=
left{
begin{array}{l}
sin(x)/2, x in[0;pi],\
0, x notin[0;pi] \
end{array}
right.
$$
Найти производящую функцию моментов.
Задача 5. Задана производящая функция вероятностей $p(t)=t(pt+q)^n$. Найти ряд и функцию распределения соответствующей случайной величины.
Мы отлично умеем решать задачи по теории вероятностей
Производящие функции:
Пусть дискретная случайная величина Х имеет закон распределения 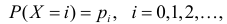
Функция
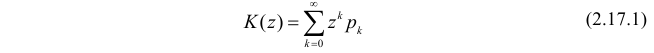
называется производящей функцией этого распределения.
Заметим, что 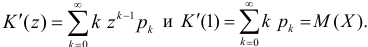
Напомним:
1) Начальным моментом порядка 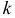 называется математическое ожидание
называется математическое ожидание 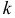 -й степени случайной величины
-й степени случайной величины

Само математическое ожидание является начальным моментом первого порядка.
2) Центральным моментом 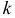 -го порядка называется математическое ожидание
-го порядка называется математическое ожидание 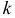 -й степени соответствующей центрированной случайной величины
-й степени соответствующей центрированной случайной величины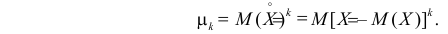
Дисперсия является центральным моментом второго порядка 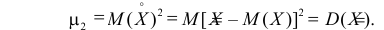
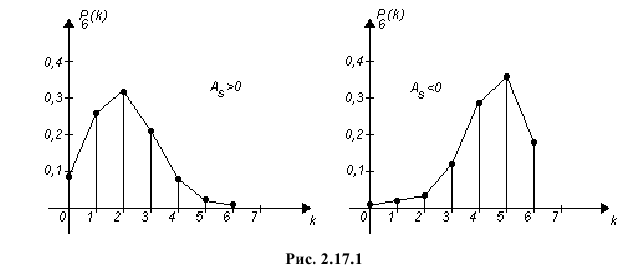
3) Асимметрией распределения называется отношение центрального момента третьего порядка к кубу среднего квадратического отклонения случайной величины: 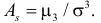
Если распределение симметрично, то 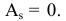 На рис. 2.17.1 слева (в качестве примера закона равпределения с положительной асимметрией) изображен многоугольник распределения для биномиального закона распределения при
На рис. 2.17.1 слева (в качестве примера закона равпределения с положительной асимметрией) изображен многоугольник распределения для биномиального закона распределения при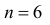 и
и 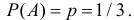 В правой части рис. 2.17.1 приведен пример закона распределения с отрицательной асимметрией (биномиальный закон при
В правой части рис. 2.17.1 приведен пример закона распределения с отрицательной асимметрией (биномиальный закон при 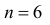 и
и 
4) Для нормального закона распределения 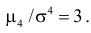 Безразмерный коэффициент
Безразмерный коэффициент 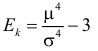 называется эксцессом. Этот коэффициент характеризует «островерхость» распределения в сравнении с нормальным законом распределения. Например, если говорить о функциях плотности вероятности, то при
называется эксцессом. Этот коэффициент характеризует «островерхость» распределения в сравнении с нормальным законом распределения. Например, если говорить о функциях плотности вероятности, то при 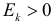 график функции плотности вероятности более островерхий, чем график кривой нормального распределения (см. левую часть рис 2.17.2). При
график функции плотности вероятности более островерхий, чем график кривой нормального распределения (см. левую часть рис 2.17.2). При 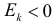 график плотности вероятности имеет более плоскую вершину, нежели нормальная кривая при тех же математическом ожидании и дисперсии (см. правую часть рис. 2.17.2).
график плотности вероятности имеет более плоскую вершину, нежели нормальная кривая при тех же математическом ожидании и дисперсии (см. правую часть рис. 2.17.2).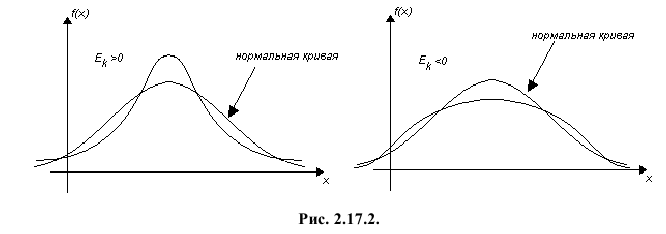
Через производящую функцию можно выразить и другие начальные и центральные моменты случайной величины. Выразим через производящую функцию, например, дисперсию. Так как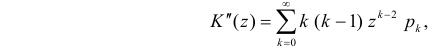
то
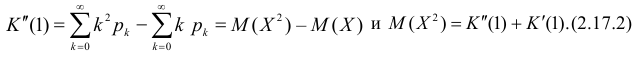
Сформируем в правой части последнего равенства дисперсию. Для этого прибавим и отнимем квадрат математического ожидания: 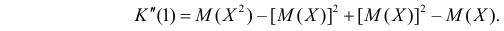
Величина 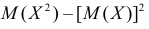 равна дисперсии. Поэтому
равна дисперсии. Поэтому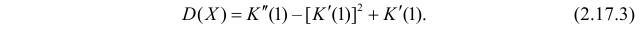
Аналогично
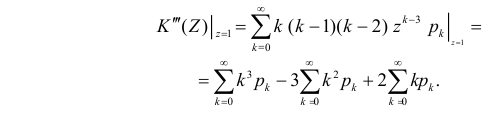
Итак, при z =1 имеем
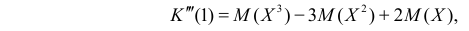
откуда
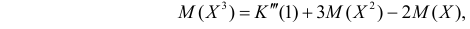
а с учетом (2.17.2) 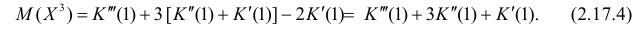
Пусть 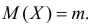 Рассмотрим модифицированную производящую функцию
Рассмотрим модифицированную производящую функцию 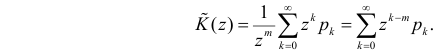
С помощью этой функции можно вычислять сразу центральные моменты случайной величины. Например
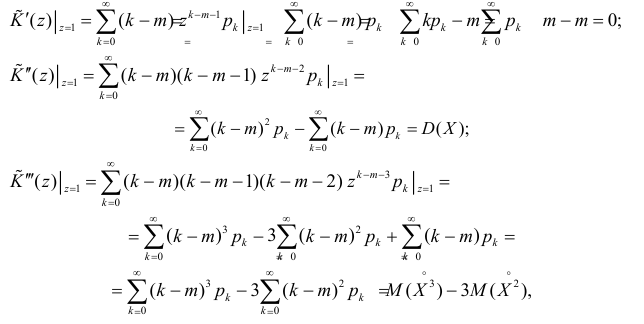
откуда
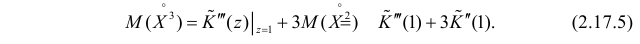
Пример:
Пусть Х имеет пуассоновский закон распределения: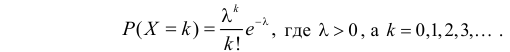
Требуется найти математическое ожидание, дисперсию и коэффициент асимметрии этой случайной величины.
Решение. Производящая функция пуассоновского распределения имеет вид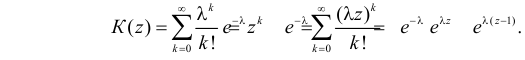
Заметим, что 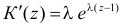 и
и  Поэтому
Поэтому 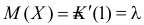 и, в соответствии с (2.17.3),
и, в соответствии с (2.17.3),
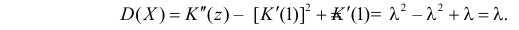
Для вычисления коэффициента асимметрии составим модифицированную производящую функцию. Так как 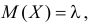 то
то 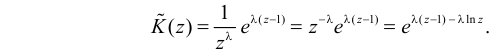
Тогда
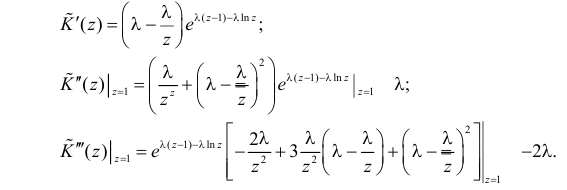
Поэтому по формуле (2.17.5) имеем 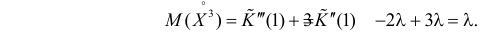
В итоге 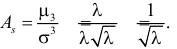
Ответ. 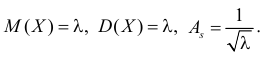
Пример:
Пусть Х имеет закон распределения
(Это частный случай отрицательного биномиального распределения или распределения Паскаля с параметрами 2 и 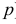 ). Требуется найти
). Требуется найти 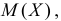
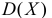 и коэффициент асимметрии
и коэффициент асимметрии 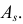
Решение. Составим производящую функцию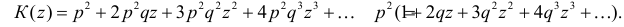
Для вычисления суммы ряда в скобке рассмотрим сумму ряда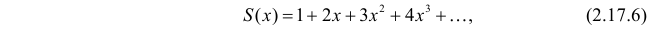
который абсолютно сходится при 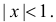 Легко видеть, что нас интересует
Легко видеть, что нас интересует 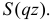 Проинтегрируем почленно ряд (2.17.6) внутри его области сходимости:
Проинтегрируем почленно ряд (2.17.6) внутри его области сходимости: 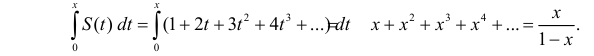
В последней строке мы воспользовались формулой суммы бесконечной убывающей прогрессии:
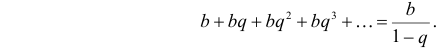
Отсюда 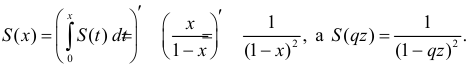 Откуда
Откуда 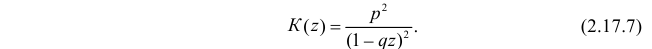
Воспользуемся теперь производящей функцией (2.17.7) для вычисления числовых характеристик случайной величины X:
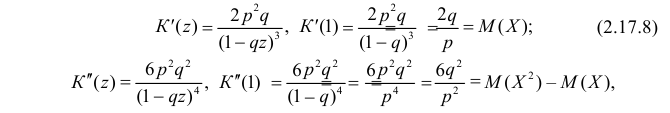
откуда следует, что 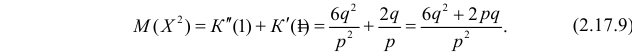
По формуле (2.17.3)
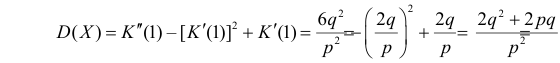
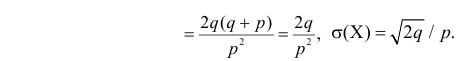
Далее
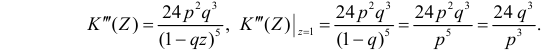
По формуле (2.17.4) вычисляем 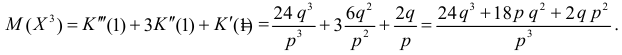
Так как
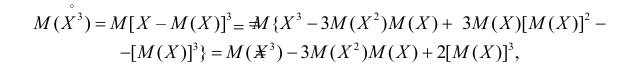
то с учетом (2.17.8) и (2.17.9) имеем
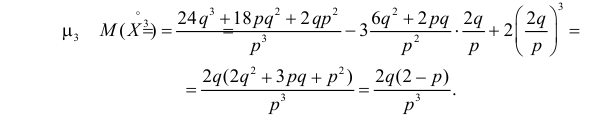
Учитывая это получаем значение коэффициента асимметрии 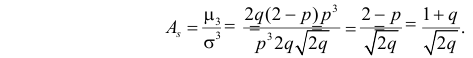
Ответ. 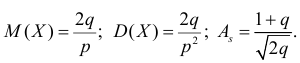
Преобразование Лапласа
Для непрерывной и неотрицательной случайной величины роль производящей функции может играть преобразование Лапласа.
Пусть Х – непрерывная, неотрицательная случайная величина с функцией распределения  . Тогда
. Тогда 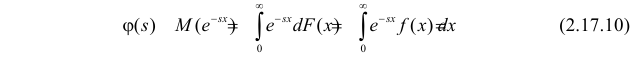
называется преобразованием Лапласа для этого распределения. (Фактически роль величины z в формуле (2.17.1) играет величина 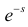 . Преимущество такого выбора состоит в том, что
. Преимущество такого выбора состоит в том, что  .)
.)
Отметим, что 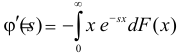 и
и 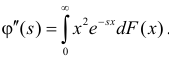 Поэтому
Поэтому 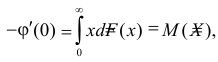 а
а 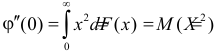 и
и 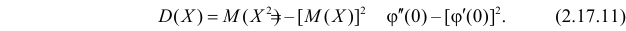
Производная любого порядка от преобразования Лапласа связана с начальными моментами случайной величины соотношением 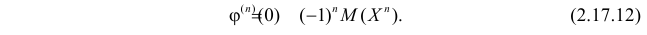
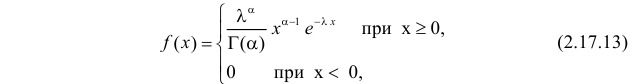
где 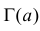 – так называемая гамма-функция Эйлера, которая при целых положительных a принимает значения
– так называемая гамма-функция Эйлера, которая при целых положительных a принимает значения 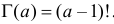
Пример:
Случайная величина X имеет функцию плотности вероятности
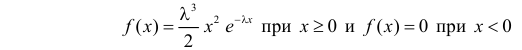
(гамма-распределение с параметрами 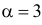 и
и 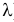 ). Требуется найти
). Требуется найти 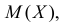
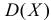 и коэффициент асимметрии
и коэффициент асимметрии 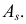
Решение. Соответствующее преобразование Лапласа имеет вид 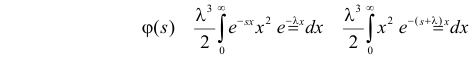
(интегрируем по частям)
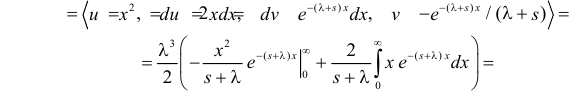
(первое слагаемое в скобке равно нулю, так как 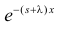 с увеличением
с увеличением 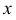 убывает быстрее, чем растет
убывает быстрее, чем растет 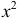 )
)
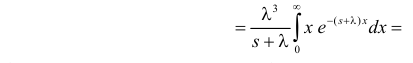
(интегрируем еще раз по частям)
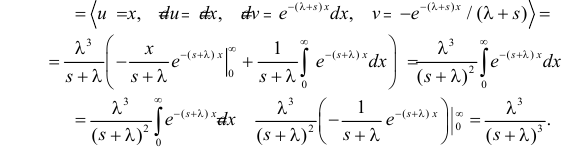
Вычислим начальные моменты распределения:


поэтому
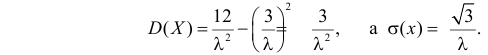
Далее
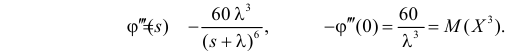
Вычислим центральный момент третьего порядка: 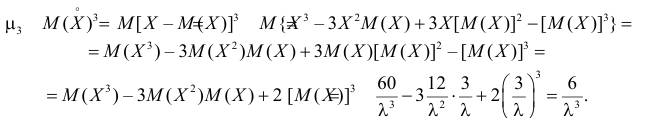
Поэтому
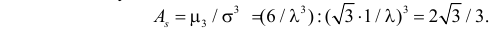
Ответ. 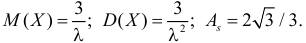
Пример:
Пусть 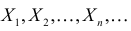 – последовательность независимых неотрицательных одинаково распределенных случайных величин с функцией плотности вероятности
– последовательность независимых неотрицательных одинаково распределенных случайных величин с функцией плотности вероятности 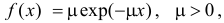
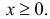 И пусть N – неотрицательная целочисленная случайная величина, независящая от величин
И пусть N – неотрицательная целочисленная случайная величина, независящая от величин 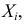 и имеющая пуассоновский закон распределения с параметром
и имеющая пуассоновский закон распределения с параметром 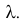 Для случайной величины
Для случайной величины 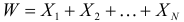 требуется найти
требуется найти 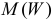 и
и 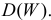
Решение. Производящая функция пуассоновского закона распределения равна 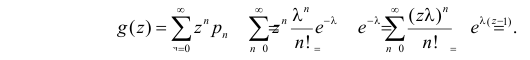
Преобразование Лапласа показательного распределения равно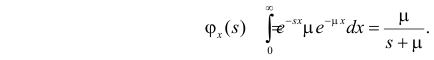
Поэтому по формуле (2.17.14) имеем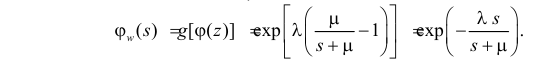
Так как 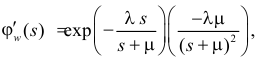 а
а 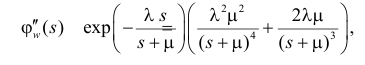
то
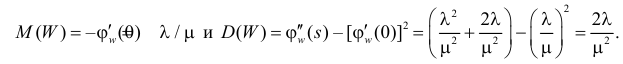
Ответ. 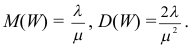
Характеристические функции
Замена z на 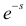 в определении производящей функции позволила рассматривать непрерывные неотрицательные величины. Выгода от такой замены состоит в мультипликативном свойстве:
в определении производящей функции позволила рассматривать непрерывные неотрицательные величины. Выгода от такой замены состоит в мультипликативном свойстве: 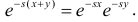 Таким же свойством обладает и показательная функция чисто мнимого аргумента, которая для действительных x определяется равенством:
Таким же свойством обладает и показательная функция чисто мнимого аргумента, которая для действительных x определяется равенством:

Характеристической функцией 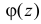 случайной величины X называется комплексно-значная функция, определенная при
случайной величины X называется комплексно-значная функция, определенная при 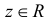 соотношением
соотношением
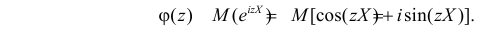
Если 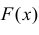 – функция распределения случайной величины X, то
– функция распределения случайной величины X, то 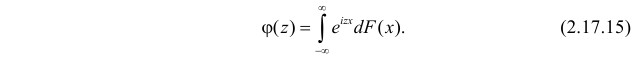
Существование интеграла, определяющего характеристическую функцию, вытекает из непрерывности функции 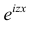 и ее ограниченности:
и ее ограниченности: 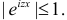 Для дискретной случайной величины X с возможными значениями
Для дискретной случайной величины X с возможными значениями 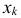 и их вероятностями
и их вероятностями 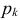 запись (2.17.15) расшифровывается как
запись (2.17.15) расшифровывается как 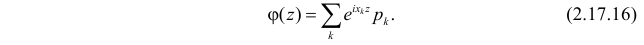
Для непрерывной случайной величины X с функцией плотности вероятности 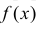
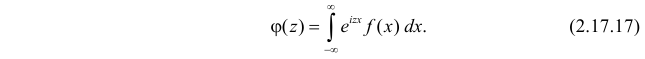
Пример:
Пусть случайная величина X имеет пуассоновский закон распределения, т.е.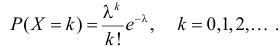 Тогда по формуле (2.17.11)
Тогда по формуле (2.17.11)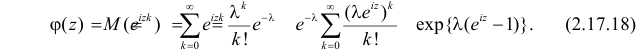
Пример:
Пусть 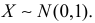 Тогда в соответствии с формулой (2.17.12)
Тогда в соответствии с формулой (2.17.12) 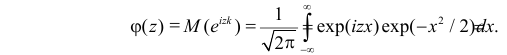
Вместо непосредственного вычисления интеграла, которое требует специальной математической техники, найдем его величину косвенным способом. Заметим, что
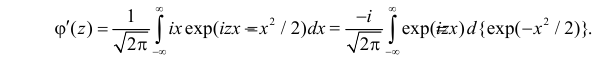
Полученный интеграл берем по частям, полагая 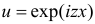 и
и 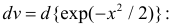
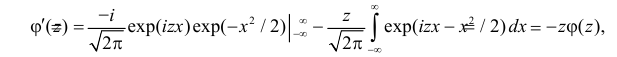
(первое слагаемое равно нулю так как 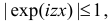 а
а 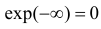 ).
).
В итоге для искомой характеристической функции получаем уравнение, которое при начальном условии 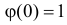 имеет решение
имеет решение 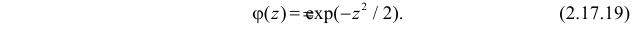
Подобным же образом можно показать, что закон распределения 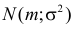 имеет характеристическую функцию
имеет характеристическую функцию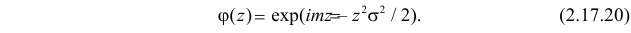
Свойства характеристических функций.
1. 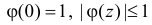 для всех вещественных
для всех вещественных 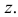
2. Если существует 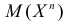 – момент порядка
– момент порядка 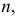 то функция
то функция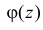 имеет
имеет 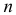 непрерывных производных и
непрерывных производных и

3. Пусть 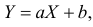 где
где 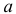 и
и 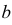 – постоянные величины, а X имеет характеристическую функцию
– постоянные величины, а X имеет характеристическую функцию 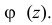 Тогда характеристическая функция случайной величины Y имеет вид
Тогда характеристическая функция случайной величины Y имеет вид 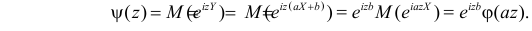
4. Характеристическая функция однозначно определяет распределение случайной величины.
5. Если X1 и X2 – независимые случайные величины, а 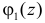 и
и 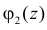 – их характеристические функции, то характеристическая функция суммы
– их характеристические функции, то характеристическая функция суммы 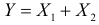 равна произведению характеристических функций слагаемых:
равна произведению характеристических функций слагаемых:
Это следует из того, что в силу независимости слагаемых 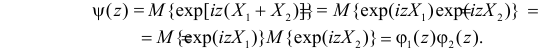
Можно показать, что для любого конечного числа независимых случайных величин 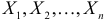 характеристическая функция их суммы
характеристическая функция их суммы 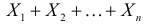 равна произведению характеристических функций слагаемых.
равна произведению характеристических функций слагаемых.
Пример:
Случайные величины X и Y независимы и имеют пуассоновские законы распределения с параметрами 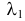 и
и 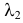 соответственно:
соответственно: 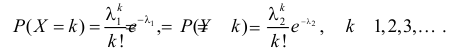
Требуется найти закон распределения случайной величины 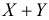 .
.
Решение. Согласно формуле (2.17.18) характеристические функции случайных величин X и Y имеют вид: 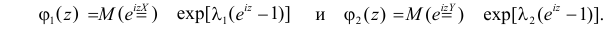
Сумме независимых случайных величин соответствует произведение характеристических функций слагаемых. Поэтому 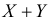 имеет характеристическую функцию
имеет характеристическую функцию 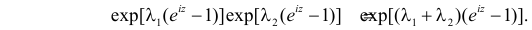
Ответ. 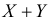 имеет пуассоновский закон распределения с параметром
имеет пуассоновский закон распределения с параметром 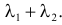
Полученный результат известен как факт устойчивости пуассоновского закона распределения. Этот результат можно обобщить на сумму любого конечного числа пуассоновских случайных величин.
Теорема. Если случайные величины Х1 и Х2 независимы и имеют соответственно нормальные законы распределения 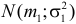 и
и 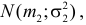 то их сумма
то их сумма 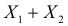 имеет тоже нормальный закон распределения
имеет тоже нормальный закон распределения

Доказательство. Пусть 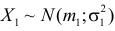 и
и 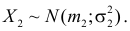 Их характеристические функции в соответствии с формулой (2.17.15) имеют вид
Их характеристические функции в соответствии с формулой (2.17.15) имеют вид 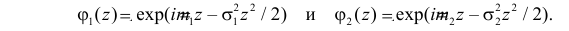
Тогда характеристическая функция суммы 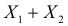 :
: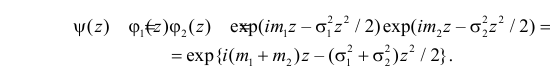
А это и означает, что 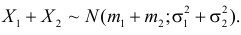
Пример:
Случайная величина 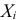 имеет закон распределения.
имеет закон распределения.
Требуется найти характеристическую функцию этой случайной величины. Используя свойства характеристических функций, найти характеристическую функцию случайной величины 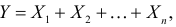 полагая слагаемые независимыми. Используя запись характеристической функции, найти
полагая слагаемые независимыми. Используя запись характеристической функции, найти 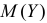 и
и 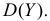
Решение. По формуле (2.17.16)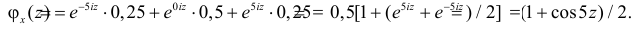
Поэтому характеристическая функция случайной величины Y имеет вид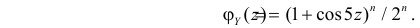
Для вычисления 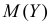 находим
находим 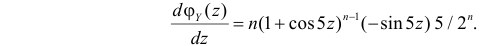
Последнее выражение при 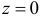 равно нулю. По свойству 2 это означает, что
равно нулю. По свойству 2 это означает, что 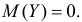 Так как вторая производная характеристической функции по z равна
Так как вторая производная характеристической функции по z равна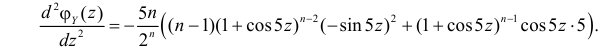
при 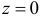 равна
равна 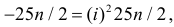 то из свойства 2 следует, что
то из свойства 2 следует, что 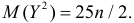 Поэтому
Поэтому
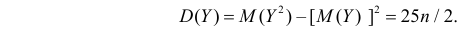
Ответ. 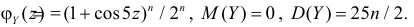
Пример:
Требуется найти характеристическую функцию случайной величины 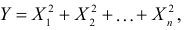 где все
где все 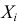 имеют закон распределения
имеют закон распределения 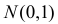 независимы в совокупности. С помощью характеристической функции найти
независимы в совокупности. С помощью характеристической функции найти 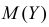 и
и 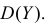
Решение. Найдем сначала характеристическую функцию для 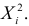 В соответствии с формулой (2.17.7)
В соответствии с формулой (2.17.7)
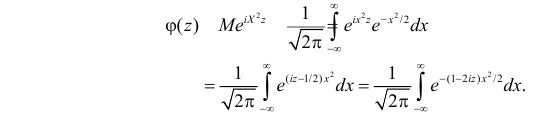
После замены переменных 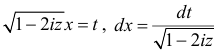 получаем
получаем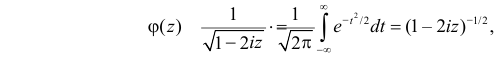
так как 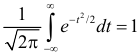 Из свойства 5 характеристических функций следует, что случайная величина
Из свойства 5 характеристических функций следует, что случайная величина 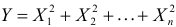 имеет характеристическую функцию
имеет характеристическую функцию
Для вычисления числовых характеристик случайной величины Y найдем сначала первую и вторую производные характеристической функции при 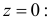
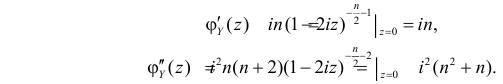
Это означает, что 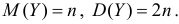
Ответ. 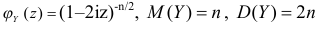
Пример:
Случайная величина Х имеет функцию плотности вероятности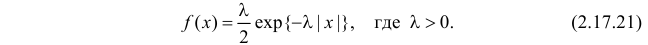
Требуется найти характеристическую функцию этой случайной величины и ее 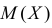 и
и 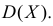 Требуется также найти характеристическую функцию случайной величины
Требуется также найти характеристическую функцию случайной величины 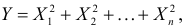 где величины
где величины 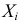 независимы и имеют распределение (2.17.21).
независимы и имеют распределение (2.17.21).
Решение. Найдем сначала характеристическую функцию: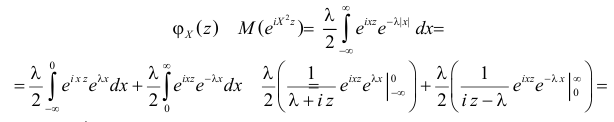
(так как 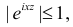 то равенство можно продолжить следующим образом)
то равенство можно продолжить следующим образом)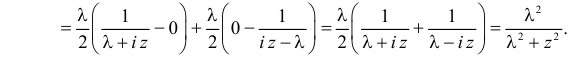
Тогда 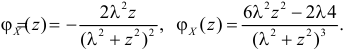 Откуда
Откуда 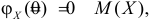
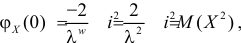 поэтому
поэтому 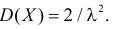
Характеристическая функция случайной величины 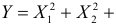
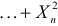 имеет вид:
имеет вид: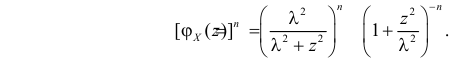
Ответ. 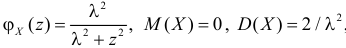
- Теоремы теории вероятностей
- Основные законы распределения дискретных случайных величин
- Непрерывные случайные величины
- Закон больших чисел
- Центральная предельная теорема
- Ковариация в теории вероятности
- Функциональные преобразования двухмерных случайных величин
- Правило «трех сигм» в теории вероятности
Содержание:
- Примеры с решением
- Биномиальный закон
- Геометрический закон
- Закон Пуассона
Мы видели, что дискретные случайные величины, рассмотренные в предыдущих параграфах, принимали только целые значения  Нахождение числовых характеристик таких величин упрощается, если рассмотреть производящие функции.
Нахождение числовых характеристик таких величин упрощается, если рассмотреть производящие функции.
Определение. Производящей функцией дискретной целочисленной случайной величины  с законом распределения
с законом распределения  называется функция, заданная степенным рядом
называется функция, заданная степенным рядом

Поскольку все коэффициенты этого ряда не превосходят 1, то сравнение с геометрической прогрессией показывает, что этот ряд сходится, по крайней мере, для значений  Из свойства закона распределения видно, что
Из свойства закона распределения видно, что  так что область сходимости ряда содержит точку
так что область сходимости ряда содержит точку 
Теорема 4.4. Производящая функция суммы независимых случайных величин  равна произведению производящих функций слагаемых
равна произведению производящих функций слагаемых

Доказательство. Имеем по определению

По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Примеры с решением
Пример 4.8.
Найти производящую функцию для биномиального закона.
Решение:
Если вспомнить, что формула Бернулли получается из разложения бинома, то легко сообразить, что

Можно также вспомнить, что случайная величина  распределенная по биномиальному закону, представляется в виде суммы
распределенная по биномиальному закону, представляется в виде суммы  независимых слагаемых – индикаторов появления события
независимых слагаемых – индикаторов появления события  Очевидно, что для одного слагаемого производящая функция равна
Очевидно, что для одного слагаемого производящая функция равна  Теперь осталось применить (4.23).
Теперь осталось применить (4.23).
Возможно вам будут полезны данные страницы:
Пример 4.9.
Найти производящую функцию для геометрического закона распределения.
Решение:
Имеем  поэтому
поэтому
 Данное равенство справедливо для всех значений
Данное равенство справедливо для всех значений  удовлетворяющих неравенству
удовлетворяющих неравенству  для которых мы применили формулу суммы бесконечно убывающей геометрической прогрессии. Таким образом,
для которых мы применили формулу суммы бесконечно убывающей геометрической прогрессии. Таким образом,

Пример 4.10.
Найти производящую функцию для распределения Пуассона.
Решение:
Для пуассоновского закона с параметром  имеем
имеем 

Поэтому

причем все ряды сходятся для любых значений аргумента  Окончательно
Окончательно

В качестве следствия получим теорему.
Теорема 4.5. Сумма независимых случайных величин, распределенных по закону Пуассона, распределена по тому же закону.
Доказательство. Пусть  – независимые случайные величины, распределенные по закону Пуассона с параметрами
– независимые случайные величины, распределенные по закону Пуассона с параметрами  Тогда их производящие функции находятся по формуле (4.26):
Тогда их производящие функции находятся по формуле (4.26):

а производящая функция суммы  находится согласно теореме 4.4
находится согласно теореме 4.4

Отсюда видно, что сумма будет распределена по закону Пуассона с параметром  что и требовалось доказать.
что и требовалось доказать.
Зная производящую функцию дискретной случайной величины  нетрудно найти ее математическое ожидание и дисперсию.
нетрудно найти ее математическое ожидание и дисперсию.
Теорема 4.6. Для дискретной случайной величины  с производящей функцией
с производящей функцией  выполняются следующие соотношения:
выполняются следующие соотношения:

Доказательство. Дифференцируя почленно ряд (4.22) два раза, имеем

Подставляя  получим
получим

откуда легко получить формулы (4.25), (4.26).
Комбинируя полученные выражения для производящих функций биномиального, геометрического и пуассоновского законов (4.23), (4.24), (4.25) с формулами (4.26), (4.27), теперь нетрудно найти основные числовые характеристики этих законов.
Биномиальный закон
Из выражения (4.23) для производящей функции получим

Подставляя  и учитывая, что
и учитывая, что  имеем
имеем

Используя формулы (4.26), (4.27), получим

откуда 
Геометрический закон
Дифференцируя два раза производящую функцию, имеем

Отсюда

откуда  что и требовалось.
что и требовалось.
Закон Пуассона
Имеем

поэтому  Подставляя найденные значения в формулы (4.26), (4.27), получим
Подставляя найденные значения в формулы (4.26), (4.27), получим 


Лекции:
- Комбинаторные задачи: пример решения
- Классическое определение вероятности
- Геометрическое определение вероятности
- Элементы комбинаторики
- Действии над событиями
- Количество сочетаний
- Число сочетаний: формула, расчет
- Сочетания с повторениями
- Комбинаторика формулы: основные элементы
- Элементы комбинаторики: примеры решения
Пусть
X
– целочисленная, неотрицательная
случайная величина с законом распределения
вероятностей:
![]() ,
,
k=0,1,2,…
.
Производящей
функцией случайной величины
X
называется неслучайная функция
![]() ,
,
определяемая при![]() равенством:
равенством:
 .
.
Производящая функция
![]() является аналитической внутри единичного
является аналитической внутри единичного
круга![]() и по ней закон распределения случайной
и по ней закон распределения случайной
величиныXоднозначно
определяется равенствами:
![]() ,
,
где
 ,k0.
,k0.
Величину MX(X-1)…(X–k+1)называютk-ым
факториальным моментом. Если
конеченk-ый факториальный
момент, то существует левосторонняя
производная![]() и
и
![]() .
.
В частности,
![]()
![]() ,
,
![]() .
.
Производящая функция
![]() суммы
суммы![]() независимых случайных величин равна
независимых случайных величин равна
произведению производящих функций
слагаемых:
![]() .
.
Характеристической функцией случайной
величиныХназывается
комплекснозначная неслучайная функция![]() вещественного аргументаt,
вещественного аргументаt,
определяемая равенством:
![]() .
.
Для дискретной случайной величины Х,
принимающей значения![]() с вероятностямиpk,
с вероятностямиpk,
характеристическая функция представляет
собой ряд Фурье:
![]() .
.
Если Х – непрерывная случайная
величина с плотностью вероятностей![]() ,
,
то характеристическая функция есть
преобразование Фурье плотности
вероятностей:
![]() .
.
Характеристическая функция обладает
следующими основными свойствами:
1.
![]() ,
,
![]() .
.
2.
![]() равномерно непрерывна на всей числовой
равномерно непрерывна на всей числовой
прямой.
3.
![]() .
.
В частности, вещественная характеристическая
функция является четной.
4.
![]() неотрицательно определена, т. е. для
неотрицательно определена, т. е. для
любого конечногоn1,
для любых комплексных чиселz1,…,znи любых действительных чиселt1,…,tn
спра-
ведливо
неравенство
![]() .
.
5. Если
![]()
–характеристическая функция случайной
величиныX,то
случайная величина![]() имеет характеристическую функцию
имеет характеристическую функцию![]() .
.
6. Характеристическая функция
![]() суммы
суммы![]() независимых случайных величин равна
независимых случайных величин равна
произведению характеристических функций
слагаемых:
![]() .
.
7. Если у случайной величины Хсуществует момент порядкаn,то характеристическая функция![]() имеетnнепрерывных
имеетnнепрерывных
производных и
![]() .
.
Функция распределения
![]() однозначно определяется своей
однозначно определяется своей
характеристической функцией![]() .Имеет место следующая формула обращения:
.Имеет место следующая формула обращения:

для
любых точек x
и y,
являющихся точками непрерывности
функции
![]() .
.
Если характеристическая функция
![]() абсолютно интегрируема, т.е.
абсолютно интегрируема, т.е. ,
,
то у случайной величины существует
плотность вероятностей![]() и
и
![]() .
.
Характеристической функцией
случайного вектора
![]() называется комплекснозначная неслучайная
называется комплекснозначная неслучайная
функцияn вещественных
переменных![]() ,
,
определяемая равенством:
 ,
,
где
![]() –
–
скалярное произведение векторов.
Пример 1. Найти производящую
функцию геометрической случайной
величины![]() с параметромр>0 и с ее помощью
с параметромр>0 и с ее помощью
найти![]() и
и![]() .
.
Решение. Геометрическая случайная
величина![]() принимает значения
принимает значения![]() с
с
вероятностями![]() .Поэтому
.Поэтому
производящая функции этой случайной
величины имеет вид:
 .
.
Найдем с помощью производящей функции
математическое ожидание и дисперсию
случайной величины
![]() .
.
 .
.

Отметим, что нахождение числовых
характеристик геометрической случайной
величины через производящую функцию
существенно проще, чем непосредственным
подсчетом.
Пример 2.Найти характеристическую
функцию случайной величины![]() ,
,
имеющей равномерное распределение на
отрезке![]() .
.
Решение. Случайная величина![]() имеет плотность вероятностей
имеет плотность вероятностей

Поэтому
 .
.
Пример
3.
Характеристическая функция непрерывной
случайной величины
![]() имеет вид
имеет вид![]() .
.
Найти плотность вероятностей этой
случайной величины.
Решение. Характеристическая
функция![]() является абсолютно интегрируемой.
является абсолютно интегрируемой.
Поэтому плотность вероятностей![]() случайной величины
случайной величины![]() существует и она представляет собой
существует и она представляет собой
обратное преобразование Фурье функции
![]() :
:

 –
–
закон распределения Коши.
Задачи
3.2.1.Найти производящую функцию
числа ”успехов”Хв схеме независимых
испытаний Бернулли и с её помощью найти![]() и
и![]() .
.
3.2.2.Найти производящую функцию
пуассоновской случайной величиныХ
и с её помощью найти![]() и
и![]() .
.
3.2.3.Пусть![]() и
и![]() – число испытаний в схеме Бернулли до
– число испытаний в схеме Бернулли до
появления первого иm-го
успеха соответственно. Найти производящие
функции величин![]() и
и![]() ,а также
,а также![]() ,
,![]() и
и![]() ,
,![]() .
.
3.2.4. Найти законы распределения,
которым соответствуют следующие
производящие функции:
а)
![]() ;
;
б) ;
;
в)
![]() ;
;
г) .
.
3.2.5.ПустьX –
неотрицательная целочисленная случайная
величина с производящей функциейp(z).Найти производящие функции случайных
величинX+1, 2Х и
3Х+2.
3.2.6.Пустьun– вероятность того, что число успехов
в последовательностиnиспытаний по схеме Бернулли чётно.
Доказать рекуррентную формулу:un
= qun-1
+ p(1-un-1).
Вывести отсюда производящую функцию,
а из неё точную формулу дляun
(u0 = 1).
3.2.7. Дискретная случайная величинаХможет принимать только два значения
–1 и 1 с равными вероятностями. Найти
характеристическую функцию данной
случайной величины.
3.2.8. Дискретная случайная величинаХимеет закон распределения:
|
X |
-2 |
0 |
2 |
|
|
1/4 |
1/2 |
1/4 |
Найти характеристическую функцию
случайной величины Хи с ее помощью
вычислить![]() .
.
3.2.9.Найти характеристическую функцию
числа ”успехов”Хв схеме Бернулли
и с её помощью найти![]() и
и![]() .
.
3.2.10.Найти характеристическую
функцию пуассоновской случайной величиныХи с её помощью найти![]() и
и![]() .
.
3.2.11.Найти характеристическую
функцию случайной величиныХ,
принимающей значения![]() (конечное или счетное множество) с
(конечное или счетное множество) с
вероятностями![]() .
.
3.2.12.Найти характеристические
функции следующих законов распределения:
а) равномерного на отрезке
![]() ;
;
б) показательного с параметром а>0;
в) нормального
![]() ;
;
г) закона Коши с плотностью вероятностей
![]() ;
;
д) закона распределения Лапласа с
плотностью вероятностей
![]() ;
;
е) χ2cn степенями свободы с плотностью
вероятностей

3.2.13.Случайная величинаXимеет плотность вероятностей:

Доказать, что характеристическая функция
случайной величины Xравна:
 .
.
3.2.14.Случайная величина Х имеет
плотность вероятностей:
![]() .
.
Доказать, что характеристическая функция
величины Xравна:
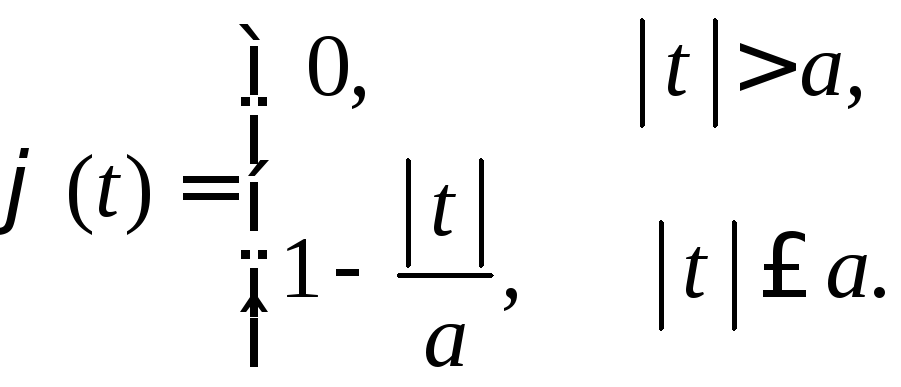
3.2.15.Найти характеристическую
функцию гамма-распределения![]() с
с
параметрами![]() ,
,
имеющего плотность вероятностей

3.2.16.Найти законы распределения,
соответствующие характеристическим
функциям:а)![]() в)
в)![]() ;г)
;г)
![]() ,где
,где![]() ,
,![]() .
.
3.2.17.Характеристическая функция
случайной величиныХимеет вид:![]() .
.
Найти закон распределения этой случайной
величины.
3.2.18.Найти плотности вероятностей
случайных величин, имеющих следующие
характеристические функции:
а)
![]()
б)
![]()
в)

г)
![]() .
.
3.2.19.Даны характеристические функции:
![]() ,
,
![]() .
.
Определить
соответствующие им плотности вероятностей.
3.2.20.С помощью характеристических
функций доказать, что:
а) сумма независимых пуассоновских
случайных величин имеет пуассоновское
распределение;
б) сумма независимых биномиальных
случайных величин, связанных со схемами
Бернулли с одинаковыми вероятностями
”успеха”, является биномиальной случайной
величиной;
в) сумма независимых нормально
распределенных случайных величин имеет
нормальное распределение;
г) сумма независимых случайных величин,
имеющих распределения Коши, также
распределена по закону Коши.
3.2.21. ВеличиныXиYнезависимы, одинаково
распределены и их характеристическая
функция равна(t).Найти характеристическую функцию
разности![]() .
.
3.2.22. Показать, что если(t)– характеристическая функция, то и![]() также является характеристической
также является характеристической
функцией.
3.2.23. Убедиться, что функция![]() является характеристической функцией
является характеристической функцией
и найти соответствующий ей закон
распределения.
3.2.24. Доказать, что при каждом
натуральномnфункция![]() является характеристической.
является характеристической.
3.2.25.Доказать, что функция при
при![]() ,
,
продолженная на всю числовую прямую с
периодом2а, является характеристической.
3.2.26.Являются ли характеристическими
следующие функции:
а)
![]() ;
;
б)![]() ;
;
в)![]() ;
;
г)![]() ;
;
д)
![]() ;
;
е)![]() ;
;
ж)![]() ?
?
3.2.27. Доказать, что функции
а)
![]()
б)

в)
![]()
г)

не
являются характеристическими.
3.2.28. Дать теоретико-вероятностную
интерпретацию равенства

3.2.29.Дать теоретико-вероятностную
интерпретацию равенства

3.2.30.Пусть![]() – независимые случайные величины,
– независимые случайные величины,
каждая из которых принимает значения
–1 и1с вероятностями1/2. Найти
характеристическую функцию случайной
величины ,
,
где![]() –
–
постоянные. Показать, что при![]() закон распределения случайной величины
закон распределения случайной величины![]() стремится при
стремится при![]() к равномерному закону распределения
к равномерному закону распределения
на отрезке![]() .
.
3.2.31.
Пусть X1,
X2,
X3
– независимые случайные величины,
имеющие стандартный нормальный закон
распределения
![]() .
.
Найти совместную характеристическую
функцию случайных величин![]()
и
![]() .
.
3.2.32.
Случайные величины
![]() имеют нормальное совместное распределение,
имеют нормальное совместное распределение,
причём![]() ,
,
![]() и
и
![]() ,
,
i,
k=![]() .
.
Найти: а)
![]() ;
;
б)![]() ;
;
в)![]() .
.
Соседние файлы в папке Sbornik_zadach
- #
- #
- #
- #
- #






![{displaystyle D(X)=G''(1^{-})+G'(1^{-})-[G'(1^{-})]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49b210d3c492a75a9339c371eea7ef5e6831732a)









![{displaystyle G(z)=[(1-p)+pz]^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad93fbb1208a6637ccd78540a9ddfc2e65a91ee2)



