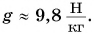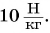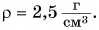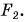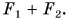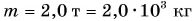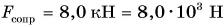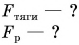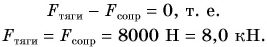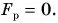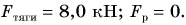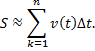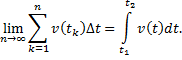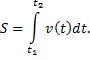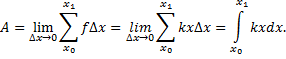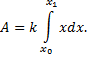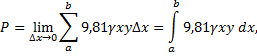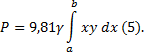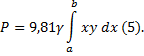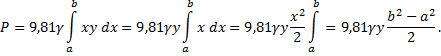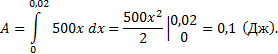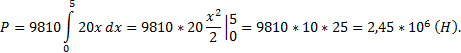Известна работа и сила , как найти путь s.
На этой странице вы найдете ответ на вопрос Известна работа и сила , как найти путь s?. Вопрос
соответствует категории Физика и уровню подготовки учащихся 5 – 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно
ознакомиться с вариантами ответов других посетителей страницы или обсудить с
ними интересующую тему. Здесь также можно воспользоваться «умным поиском»,
который покажет аналогичные вопросы в этой категории. Если ни один из
предложенных ответов не подходит, попробуйте самостоятельно сформулировать
вопрос иначе, нажав кнопку вверху страницы.
Содержание:
Движение и силы:
Вы уже знаете, каким сложным является хаотическое движение молекул. В повседневной жизни мы встречаемся с более простыми видами движения. Движутся люди, автомобили (рис. 76), самолеты, Солнце, Луна и другие тела. Окружающий нас мир немыслим без движения. Характеристики многих движений можно легко определить и описать с помощью несложных математических формул.
Как установить, движется или нет данное физическое тело? Рассмотрим пример. Вы стоите на остановке и вдали видите автобус (рис. 77). Движется он или нет? Несмотря на то что вращения колес не видно, вы уверенно определяете, что автобус движется. Изменяется с течением времени его положение относительно киоска, деревьев, домов, неподвижных относительно поверхности Земли. Точно так же мы судим о движении облаков и птиц в небе, рыб в аквариуме, футболистов на поле, поездов и любых других тел.
Изменение положения тела в пространстве относительно других тел с течением времени называется механическим движением. Следовательно, движение происходит в пространстве и во времени.
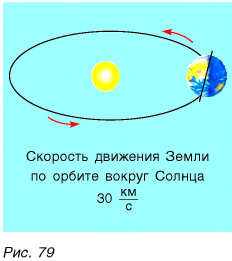
Рассмотрим еще один пример. Вы едете в электричке (рис. 78). Можно ли сказать, что, сидя в ней, вы находитесь в состоянии покоя? И да, и нет. Да — потому, что вы не движетесь по электричке, т. е. с течением времени ваше положение относительно электрички не меняется. Нет — потому, что вместе с электричкой вы движетесь относительно поверхности Земли. А если электричка остановилась? Теперь вы находитесь в состоянии покоя относительно электрички и поверхности Земли, но движетесь вместе с Землей вокруг Солнца (рис. 79), перемещаясь за каждую секунду примерно на 30 км относительно звезд.
Таким образом, покой и движение относительны. Относительны и характеристики движения. Это легко увидеть на опыте. Укрепите светоотражатель (фликер) на ободе колеса вашего велосипеда. Какова будет кривая, которую опишет фликер (ее называют траекторией) при движении колеса? Относительно вас или вашего друга, едущего рядом с вами, фликер будет двигаться по окружности. А стоящий человек, мимо которого вы проезжаете, увидит, что фликер описывает не окружность, а сложную кривую (рис. 80). Следовательно, траектория тоже относительна.
Главные выводы:
- Механическое движение — это изменение положения тела в пространстве относительно другого тела или тел с течением времени.
- Механическое движение и покой относительны.
Траектория, путь и время
Для решения научных и практических задач необходимо уметь описывать механическое движение тела или его частей, определять характеристики движения и устанавливать связи между ними.
Какими физическими величинами описывается механическое движение?
Проведите мелом по доске. Мел при движении описывает линию, которая хорошо видна на доске.
В голубом небе часто отчетливо видны белые следы позади летящих самолетов (рис. 81). Быстро мчащийся катер оставляет на поверхности воды пенистую дорожку (рис. 82).
Линия, которую описывает тело при своем движении, называется траекторией.
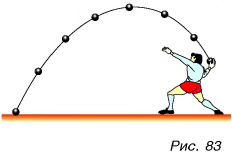
Мы привели примеры движений, когда траектория — видимая линия. Но чаще всего она невидима. Однако траекторию всегда можно изобразить, если отметить точками положения движущегося тела в различные моменты времени, а затем соединить эти точки. Несложно, например, представить траекторию летящего ядра (рис. 83).
Если траектория движения — прямая линия, движение называется прямолинейным. Например, такова траектория падающего с дерева яблока (рис. 84). Если же траектория — кривая линия, то движение называется криволинейным (см. рис. 83).
Длина той части траектории, которую описывает тело за данный промежуток времени, называется путем, пройденным телом за этот промежуток времени.
Обозначается путь обычно буквой s. Путь это физическая величина. Его можно измерить или вычислить по формуле. Единицей пути в СИ является 1 метр (1 м). На практике путь часто измеряют в кратных единицах — километрах — или в дольных — сантиметрах, миллиметрах, микрометрах.
А что такое промежуток времени? Допустим, вы отправляетесь в путешествие на поезде «Минск — Москва». Поставим вопрос: за какой промежуток времени поезд пройдет путь s = 212 км от Минска до Орши? Ответить на этот вопрос очень легко. Во-первых, нужно знать момент времени, когда поезд отправляется из Минска. Обозначим его буквой t с индексом 1, т. е. 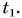
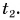
(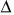
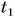
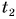
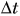
Для краткости вместо «промежуток времени» будем говорить «время».
Единицей времени в СИ является 1 секунда (1 с). Иногда удобнее использовать кратные единицы времени: минуту (мин) и час (ч). Существуют и такие единицы времени, как сутки (сут), год. Вы, конечно, знаете, что одни сутки равны 24 ч, 1 год равен 365 (366) сут.
Для измерения времени служат различные Рис. 87 приборы, например метроном (рис. 85), часы (рис. 86), секундомер (рис. 87).
Для практических целей полезно научиться отсчитывать про себя секунды, произнося числа через равные интервалы времени.
При прохождении лечебных процедур иногда необходимо фиксировать определенный промежуток времени, например 1 мин или 5 мин. В таких случаях удобно использовать песочные часы (рис. 88).
Для любознательных:
Для измерения пройденного пути в автомобилях имеется специальный прибор — одометр (от греч. «дорога» и «мера») (см. рис.). Одометр включает:
- датчик, фиксирующий обороты колеса;
- счетчик, подсчитывающий обороты;
- индикатор, фиксирующий путь, который проехал автомобиль.
Главные выводы:
- Траектория — линия, которую описывает тело при своем движении.
- Если траектория — прямая линия, то движение называется прямолинейным, если траектория — кривая линия, то движение криволинейное.
- Путь — длина той части траектории, которую описывает тело за данный промежуток времени.
Равномерное движение и скорость
Среди всего разнообразия движений тел наиболее просто описывается равномерное прямолинейное движение. Что представляет собой это движение? Как его охарактеризовать?
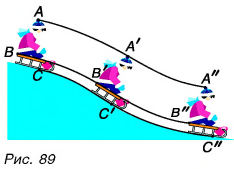
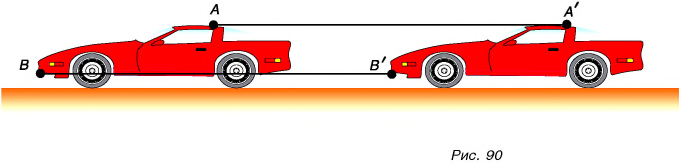
Рассмотрим пример. Девочка на санках спускается с горки. Понаблюдаем за движением нескольких точек, например А, B, С (рис. 89). Эти точки движутся совершенно одинаково, описывая равные траектории. Движение, при котором все точки тела описывают одинаковые по форме и равные по длине траектории, называется поступательным. А если тело движется поступательно, нужно ли изучать движение всего тела или достаточно изучить движение только одной его точки? Рис. 90 Ведь все точки (рис. 89, 90) движутся совершенно одинаково. В данном учебном пособии мы будем изучать движение тела, не рассматривая его форму, размеры, т. е. будем моделировать тело точкой.
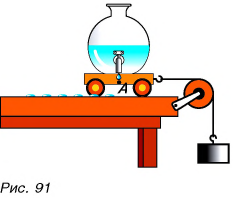
Как определить, какой путь пройдет тело при движении за данный промежуток времени? Пусть тележка (рис. 91) движется прямолинейно. Будем отмечать ее положения, точнее положения точки A, через равные промежутки времени. Это можно сделать, установив на тележке капельницу с вытекающими через равные промежутки времени, например через 2 с, каплями. Определим пути, проходимые тележкой за 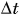
Подобрав груз, можно достичь того, что пути, пройденные тележкой за равные промежутки времени 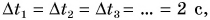
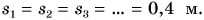
Движение, при котором тело за любые равные промежутки времени проходит равные пути, называется равномерным.
Найдем отношения путей к соответствующим промежуткам времени:
Величина 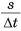
Тогда для равномерного прямолинейного движения можно записать формулу:
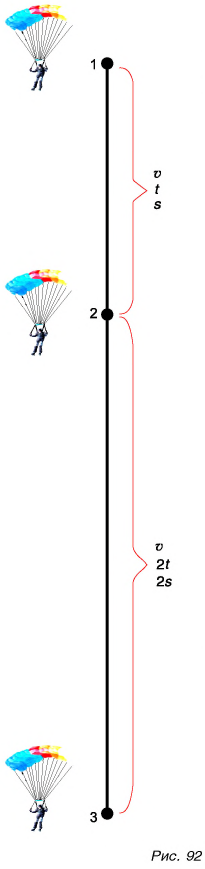
Из формулы (1) следует, что скорость равномерного прямолинейного движения есть физическая величина, равная отношению пути, пройденного телом, к промежутку времени.
Из формулы (1) легко найти путь, пройденный за любой промежуток времени, и промежуток времени:
На примере с капельницей вы убедились, что при равномерном прямолинейном движении скорость является постоянной величиной.
При равномерном прямолинейном движении с увеличением промежутка времени увеличивается путь (рис. 92), но скорость остается постоянной.
Значит, скорость является характеристикой движения. Теперь можно дать еще одно определение равномерного прямолинейного движения, используя его характеристику — скорость: равномерное прямолинейное движение — это движение но прямой с постоянной скоростью.
Единицей скорости в СИ является 1 метр в секунду 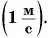
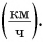
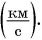
Пусть автомобиль движется но шоссе со скоростью 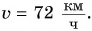
Скорость движения пешехода 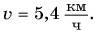
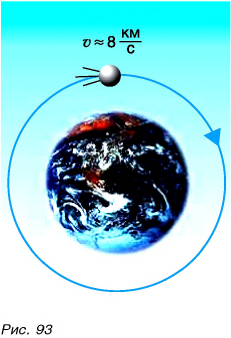
Максимальная скорость движения в природе — скорость распространения света в пустоте (рис. 94).
Она равна 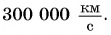
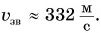
Из формулы 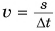
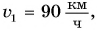
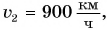
Таким образом, скорость характеризует быстроту движения, т. е. показывает, как быстро тело меняет свое положение в пространстве относительно других тел.
Главные выводы:
- Скорость — количественная характеристика быстроты движения.
- Определить скорость движения можно, разделив пройденный путь на затраченный промежуток времени.
- Если скорость постоянна, то движение равномерное.
Графики пути и скорости при равномерном прямолинейном движении
Можно ли выразить связь пути s и времени t не через формулы, а каким-либо другим способом? Для этого используются графики.
Поясним суть графического метода на конкретном примере. Пусть самолет движется равномерно и прямолинейно со скоростью 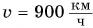
Путь s от начального момента времени 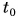
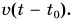
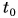
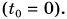
Найдем значения пути для различных значений промежутка времени и занесем их в таблицу 1.
Например, если t = 3ч, то
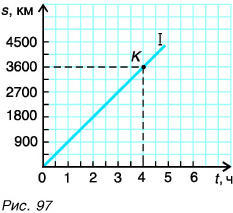
Теперь построим график зависимости пути от времени. По оси абсцисс в определенном масштабе (например, 1 см — 1 ч) будем откладывать промежутки времени движения, а по оси ординат (в масштабе 1 см — 900 км) — путь (рис. 97).
Прямая I выражает графическую зависимость пути от времени равномерного движения самолета. Эту прямую называют графиком пути. График пути напоминает известный вам из математики график функции 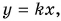
Ценность графика пути в том, что он, как и соотношение 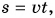
Например, нас интересует путь самолета за промежуток времени t = 4 ч. Для этого из точки на горизонтальной оси, соответствующей времени t = 4 ч (см. рис. 97), проводим перпендикуляр до пересечения с графиком (точка К). Из найденной точки К опускаем перпендикуляр на ось ординат и получаем ответ без вычислений. Путь s = 3600 км.
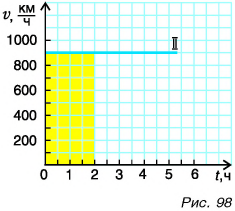
А что представляет собой график скорости? Он выражает зависимость скорости от времени. Так как скорость с течением времени не изменяется, то различным моментам времени соответствует одно и то же значение скорости. Составим таблицу 2 и построим прямую, выражающую зависимость скорости от времени, откладывая по оси абсцисс время, а по оси ординат — скорость (рис. 98).
График скорости равномерного прямолинейного движения — прямая, параллельная оси времени.
Прямая II изображает график скорости движения самолета. Что дает график скорости? Он не только показывает значение скорости, но и позволяет найти пройденный путь. Рассчитаем путь самолета за промежуток времени t = 2 ч. Согласно формуле 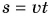
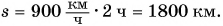
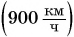
Для любознательных:
Площадью фигуры под графиком скорости определяется путь не только при равномерном прямолинейном, но и при любом другом движении. Например, путь за промежуток времени 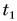
Главные выводы:
- График пути выражает зависимость пройденного пути от времени движения тела.
- Путь при равномерном прямолинейном движении можно определить по формуле
по графику пути или с помощью графика скорости.
Пример №1
Легковой и грузовой автомобили равномерно движутся в одном направлении но параллельным полосам прямолинейного участка
шоссе. Скорость движения легкового автомобиля 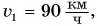
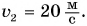
Запишем условие и выразим величины через основные единицы СИ.
Дано:
t = 3, 0 мин = 180 с
Решение:
Найдем путь, который проехал каждый из автомобилей за промежуток времени t:
Расстояние между автомобилями:
Подставим значения и вычислим:
Ответ:
Пример №2
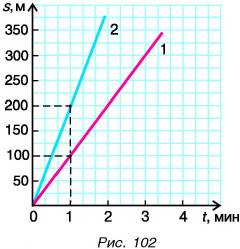
Графики зависимости пути от времени равномерных прямолинейных движений пешехода Димы (1) и велосипедиста Пети (2) представлены на рисунке 102. Во сколько раз отличаются скорости движения мальчиков?
Решение
Из графиков следует, что за промежуток времени t = 1 мин Дима прошел путь 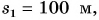
Скорость движения Димы:
Скорость движения Пети:
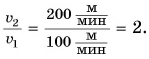
Отношение:
Ответ: скорость движения Пети на велосипеде в 2 раза больше скорости движения Димы пешком.
Этот же ответ можно было получить проще:
Из графика для одного и того же момента времени, например t = 1 мин (либо 2 мин и т. д.), определяем пути 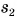
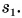
Неравномерное (переменное) движение. Средняя скорость
Проанализируйте движение автобуса. Он уменьшает скорость перед остановкой. Затем в течение какого-то промежутка времени стоит на остановке, т. е. его скорость равна нулю, после чего скорость увеличивается. Значит, скорость автобуса в процессе движения изменяется, т. е. является переменной величиной.
Движение, при котором скорость изменяется, называется неравномерным (переменным).
Практически все движения, наблюдаемые в природе и технике, — неравномерные. С изменяющейся скоростью движутся, например, люди, птицы (рис. 103), дельфины (рис. 104), поезда, падают предметы (рис. 105). Но как же тогда характеризовать это движение?
Неравномерное движение характеризуется средней скоростью. Как определить среднюю скорость? Рассмотрим пример. Вы едете на экскурсию в Брест поездом. Поезд проходит от Минска до Бреста путь s = 330 км. На прохождение этого пути затрачивается время t = 4,5 ч. В течение данного времени поезд стоит на станциях, движется то с увеличивающейся, то с уменьшающейся скоростью.
Среднюю скорость находят путем деления всего пути на весь промежуток времени, за который этот путь пройден. Обозначим среднюю скорость 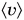
Тогда поезд «Минск — Брест» движется со средней скоростью
Вас не удивило, что мы использовали формулу равномерного движения? Да, действительно формально мы нашли среднюю скорость так, как будто поезд весь путь s = 330 км двигался равномерно с постоянной скоростью 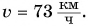
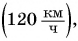
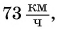
Для любознательных:
Средняя скорость дает лишь приблизительное представление о быстроте движения тела. Описание переменного движения более сложно по сравнению с описанием равномерного.
Например, если скорость поезда на участке разгона возрастает от О до 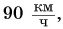
Главные выводы:
- Характеристикой неравномерного движения является средняя скорость.
- Для вычисления средней скорости нужно путь разделить на весь промежуток времени, затраченный на прохождение этого пути.
Пример №3
Катя прошла путь 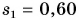
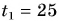
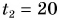
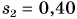
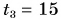
Дано:
Решение
Весь путь, который прошла Катя:
Весь затраченный промежуток времени:
Средняя скорость движения Кати:
Вычислим 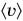
Ответ:
Пример №4
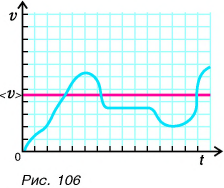
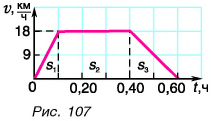
По графику скорости (рис. 107) определите путь и среднюю скорость движения велосипедиста за промежуток времени t = 0,60 ч.
Решение
Искомый путь численно равен площади фигуры под графиком скорости. Путь 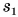
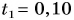
Аналогично можно найти пути 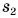
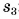
Весь путь:
Средняя скорость движения велосипедиста:
Ответ:
Почему изменяется скорость движения тела
Равномерное прямолинейное движение, т. е. движение с постоянной скоростью, — лишь модель реального движения. В жизни всякое движение (от движения огромных планет до движения невидимых частиц) чаще всего происходит с изменяющейся скоростью. Что является причиной изменения скорости?
Рассмотрим опыты. На столе лежит стальной шарик Он находится в состоянии покоя относительно стола. Чтобы заставить шарик двигаться, можно толкнуть его рукой или приблизить к нему магнит (рис. 111). В обоих случаях на шарик действуют другие тела (рука, магнит), что и является причиной изменения скорости движения шарика. А как долго шарик будет двигаться после толчка? Опыт показывает, что скорость движения шарика уменьшается, а через некоторое время его движение прекращается. Почему?
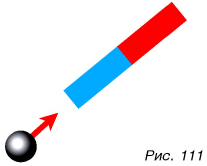
Проведем другой опыт. Три одинаковых шарика одновременно скатываются с одинаковой высоты (рис. 112). Дорожки, по которым затем о движутся шарики, отличаются: первая посыпана песком, вторая покрыта тканью, а третья — стеклом. Движение но третьей дорожке продолжается дольше, поскольку трение здесь наименьшее. Значит, причина прекращения движения шарика — трение между поверхностями шарика и стола и, конечно, сопротивление воздуха. А если бы мы смогли убрать эти причины, шарик двигался бы с постоянной скоростью сколько угодно долго.
Движение тела без действия на него других тел, как и покой, — его естественное состояние.
То, что тело остается в покое, если нет действия других тел, вполне понятно. Но как же тело может само но себе двигаться, если в повседневной жизни мы видим, что тело движется только тогда, когда Рис. 113 на него действует другое тело? Санки (рис. 113) надо тянуть за веревку, лодка плывет под действием весел (рис. 114). А были бы нужны веревка и весла, если бы не было сопротивления движению? Если бы вода не оказывала сопротивления движению, лодка после толчка двигалась бы бесконечно долго с постоянной скоростью.
Итак, если тело находится в состоянии покоя или в состоянии движения, то оно стремится сохранять это состояние (не изменять скорость), пока на него не подействуют другие тела.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения (сохранять свою скорость неизменной) при отсутствии действия на него других тел называется инерцией.
С инерцией нам приходится встречаться постоянно. При резком торможении автобуса пассажиры наклоняются вперед, так как продолжают двигаться по инерции. При резком разгоне автобуса они отклоняются назад. Почему? Л может ли автомобиль остановиться мгновенно? Нет. Как бы ни были сильны тормоза, инерция препятствует мгновенному торможению. Именно из-за инерции тормозной путь автомобиля тем больше, чем больше скорость его движения. Мы уверены, что, помня об инерции, вы не будете перебегать улицу перед движущимся транспортом и научите не делать этого своих младших братьев и сестер. А сколько неприятностей из-за инерции случается, пока мы учимся кататься на коньках!
Инерция может приносить человеку не только неприятности, но и огромную пользу. В водяных и паровых турбинах, а также в ветряных двигателях (рис. 115) используется инерция движения воды, пара, ветра. Инерция играет полезную роль при применении удара, от выколачивания пыли до насадки на рукоятку молотка. Космонавт благодаря инерции может выйти в открытый космос (рис. 116) и не отстать от корабля.
Для любознательных:
Древнегреческий философ Аристотель (IV в. до н. э.) считал, что только покой — естественное состояние тела, а движение — насильственное. Тело стремится к своему естественному состоянию, поэтому, если не поддерживать движение, оно прекращается.
Ошибка Аристотеля состояла в том, что он верил в инерцию покоя, но не понимал, что телам столь же свойственна инерция движения.
Спустя приблизительно 2000 лет после Аристотеля итальянский ученый Галилео Галилей смог вообразить идеализированный мир мир без трения. В результате он пришел к выводу о том, что движение тела без действия на него других тел, как и покой, является его естественным состоянием.
Главные выводы:
- Если на тело не действуют другие тела, то оно либо находится в состоянии покоя, либо движется равномерно и прямолинейно (по инерции).
- Изменить состояние покоя или движения тела можно только воздействием на него другого тела или тел.
Масса тела и плотность вещества
Одинаково ли легко изменить скорость различных тел? Мимо нас пролетает комар. Трудно ли изменить его скорость? Достаточно просто дунуть (рис. 117, а). А если проезжает груженый автомобиль МАЗ (рис. 117, б)? Инерция есть у всех тел, но это свойство проявляется у них в разной степени. Оно почти незаметно у комара, но очень заметно у автомобиля, для изменения скорости которого требуются большие и длительные воздействия.
Для характеристики инерции тела в физике используется физическая величина, называемая массой. Чем массивнее тело, тем труднее изменить его скорость, тем больше оно противится таким изменениям. Масса тела — мера его инерции. Иногда говорят: мера его инертности.
Обозначим массу тела буквой m. Основной единицей массы в СИ является 1 килограмм (1 кг). Полезно знать, что 1 л воды при комнатной температуре имеет массу, практически равную 1 кг. Соответственно, масса 1 мл равна 1 г. Обратите внимание! В килограммах измеряется единственная физическая величина — масса.
От чего зависит масса тела? Сравните разгон и торможение груженого и порожнего автомобилей. Понятно, что масса тела зависит от количества вещества в теле (от числа молекул). Дело в том, что массой (т. е. инерцией) обладает каждая молекула, поэтому массу всего тела можно рассматривать как сумму масс всех его молекул. Будут ли одинаковыми массы тел, если они содержат одинаковое число молекул? Да, если тела состоят из одного и того же вещества. Нет, если тела состоят из различных веществ (например, алюминиевая и золотая ложки). А теперь сравним массы разных веществ, имеющих одинаковый объем.
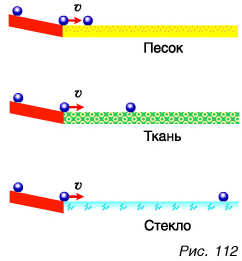
Задумайтесь над вопросом: какую тележку легче сдвинуть с места — нагруженную сухими дровами (рис. 118, а) или нагруженную камнями (рис. 118, б), имеющими равный с дровами объем? Конечно, тележку с дровами. Ее масса меньше. Значит, масса единицы объема дров и единицы объема камней разная.
Масса вещества, содержащегося в единице объема, называется плотностью вещества.
Чтобы найти плотность, необходимо массу вещества разделить на его объем. Плотность обозначается греческой буквой 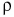
Единицей измерения плотности в СИ является 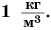
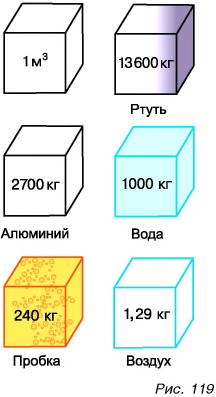
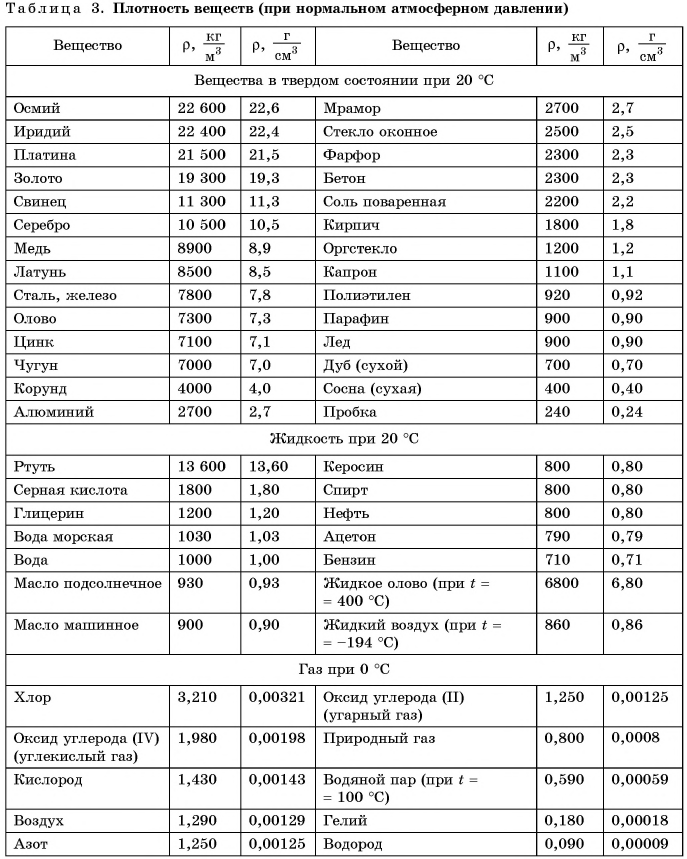
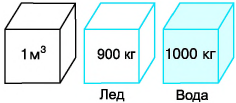
На рисунке 119 изображены массы известных вам веществ в объеме
У большинства веществ плотность в твердом состоянии больше, чем в жидком. Например, плотность олова в твердом состоянии 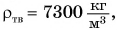
Плотность вещества в жидком состоянии больше, чем в газообразном. Чем это можно объяснить? Вспомните о различии в расстояниях между молекулами. Самые большие расстояния — между молекулами газа. Поэтому плотность сжиженного воздуха (при -194 °С) равна 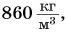
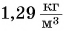
Зная плотность и объем тела, легко найти массу:
Формулу 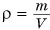
Для любознательных:
Твердое вещество, состоящее из молекул 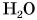
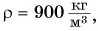
Вы заметили особенность? Плотность льда меньше плотности воды, что указывает на более плотную упаковку (т. е. меньшие промежутки) молекул в жидком состоянии вещества (вода), чем в твердом (лед).
Из всех видов деревьев наименьшей плотностью обладает древесина бальзового дерева 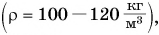
Средняя плотность Вселенной ничтожно мала 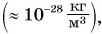
Главные выводы:
- Чем больше масса тела, тем труднее изменить скорость его движения.
- Плотность вещества показывает, какая масса вещества содержится в единице его объема.
- Плотность вещества в различных агрегатных состояниях разная.
- Тела, состоящие из разных веществ, характеризуются средней плотностью.
Пример №5
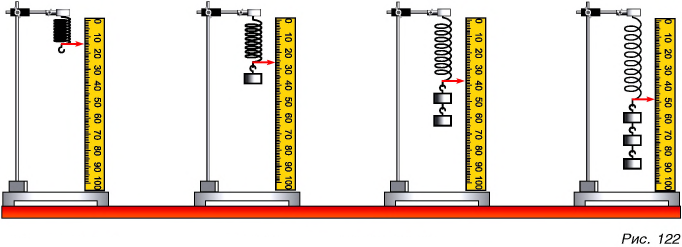
Средняя плотность тела человека примерно равна плотности воды. Зная свою массу, вычислите объем тела.
Дано:
Решение
Определим с помощью весов свою массу m. Например, m = 50 кг. Тогда объем тела
Ответ:
Сила
Изменить скорость движения тела можно воздействием на него другого тела. Чем больше это воздействие, тем сильнее изменяется скорость. Напрягая мышцы рук, вы увеличиваете скорость тележки. Ваш старший брат или отец может сильнее подействовать на тележку и увеличить скорость ее движения больше.
С помощью какой физической величины можно количественно определить, насколько сильно воздействует одно тело на другое, например человек на тележку? Такой величиной является сила.
Сила — количественная мера воздействия одного тела на другое.
В приведенном примере результатом воздействия является изменение скорости, значит, сила — причина изменения скорости движения тела.
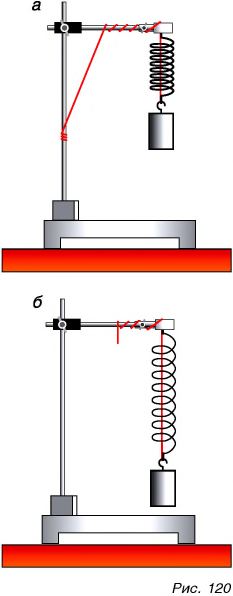
Однако действие одного тела на другое приводит не только к изменению скорости. Подействуем на пружину гирей (подвесим ее к пружине) (рис. 120, а). Действие гири на пружину вызывает ее удлинение (рис. 120, б). Гиря, стоящая на тонкой доске (рис. 121), прогибает ее. Сжимая пальцами ластик, вы изменяете его форму. В этих случаях действие одного тела на другое, т. е. сила, вызывает изменение размеров или формы тела.
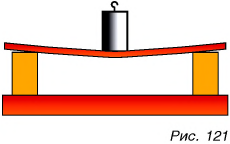
Изменение размеров или формы тела называется деформацией. Значит, сила является не только причиной изменения скорости, но и причиной деформации тела. Чем больше сила, тем больше деформация. Действительно, подействуйте на пружину более тяжелой гирей, т. е. большей силой, и растяжение пружины будет больше (рис. 122).
Сила не может существовать сама по себе. Если мы говорим, что на тело действует сила, это означает только то, что на тело действует другое тело.
Обычно силу обозначают буквой F и изображают в виде стрелки. Направление стрелки указывает направление действия силы. Начало стрелки совпадает с точкой приложения силы. Абсолютное число, выражающее длину стрелки, называют модулем силы.
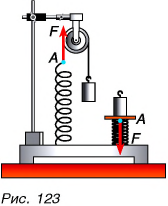
Итак, сила характеризуется модулем, направлением и точкой приложения. Пусть на одинаковые пружины действуют две одинаковые гири (рис. 123). Одна пружина растягивается под действием гири, другая — сжимается. Модули действующих на пружины сил одинаковы, но направления у сил разные.
На рисунке 124 изображены два тела (арбуз и яблоко), действующие на стол с одинаково направленными, но имеющими разные модули силами. Эти силы приложены к крышке стола в точках 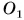
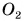
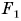
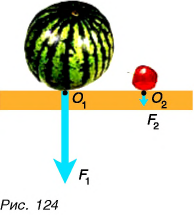
Чаще всего тело испытывает не одно, а сразу два или более действий, причем иногда противоположного направления. Как изменится скорость движения тела в этом случае? Если модули противоположно направленных сил равны, то, как и в математике при сложении равных но модулю, но противоположных но знаку чисел, мы получим в результате нуль. Такие силы мы будем называть компенсирующими друг друга. В этом случае, как и при отсутствии сил, скорость тела изменяться не будет. На рисунке 125 силы, приложенные к одному и тому же телу (ветке), компенсируют друг друга, и тело находится в состоянии покоя.
Для любознательных:
В повседневной жизни слово «сила» часто используется в сочетаниях «сила огня», «сила духа», «сила воли» и т. д. В физике слово «сила» употребляется только в смысле количественной меры такого воздействия, которое либо меняет скорость движения тела, либо деформирует его, либо вызывает то и другое одновременно. Действие даже самой малой силы обязательно приводит к тому или иному результату. От нажатия на стол пальцем крышка стола неизбежно прогнется, хотя это не всегда заметно.
Главные выводы:
- Сила является количественной мерой воздействия одного тела на другое.
- Сила является причиной изменения скорости движения тела и его деформации.
- Сила характеризуется модулем, направлением и точкой приложения.
Явление тяготения и сила тяжести
Посмотрите на глобус. Это модель Земли. Земля имеет форму, близкую к форме шара. Нам это кажется естественным. Но каково было недоумение людей, впервые услышавших об этом! Они никак не могли поверить, что люди, живущие на противоположной стороне Земли (рис. 126), не падают в бездну.
Почему люди одинаково устойчивы в любом месте Земли? Земля притягивает к себе все тела.
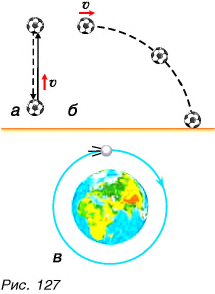
Если бы Земля не обладала притяжением, брошенные горизонтально или вверх тела, двигаясь но инерции, никогда не вернулись бы на Землю. Тем не менее мяч, брошенный вертикально вверх, возвращается обратно (рис. 127, а). Траектория мяча, брошенного горизонтально, но мере движения искривляется (рис. 127, б). Спутник движется вокруг Земли по круговой орбите (рис. 127, в). Искривление траектории мяча, спутника есть также результат притяжения этих тел к Земле.
Сила, с которой Земля притягивает к себе тело, называется силой тяжести.
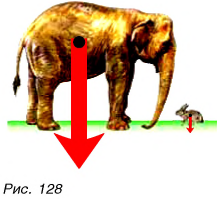
Зависит ли сила тяжести от массы тела? Конечно, да. Из жизненного опыта мы хорошо знаем, что, чем больше масса налитой в ведро воды, тем труднее его удерживать. Слона Земля притягивает гораздо сильнее, чем зайца (рис. 128).
Во сколько раз увеличивается масса тела, во столько раз возрастает сила тяжести 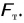
где 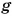
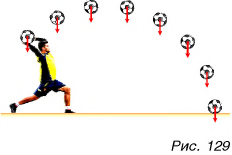
Сила тяжести направлена вертикально вниз (рис. 129) и приложена к центру однородного тела.
А обладают ли другие планеты притяжением, как Земля? Английский физик и математик Исаак Ньютон пришел к выводу, что притяжение свойственно всем планетам и вообще любому телу, обладающему массой, т. е. всем телам Вселенной. Поэтому явление взаимного притяжения тел названо всемирным тяготением.
Для любознательных:
Сила тяжести зависит не только от массы тела, которое притягивается, но и от массы того тела, которое притягивает (Земля, Луна и др.).
Все небесные тела притягивают к себе любые другие тела. Но так как массы и размеры небесных тел различны, то разной будет и действующая сила притяжения. Так, на Луне сила тяжести, действующая на тело, будет почти в 6 раз меньше, чем на Земле.
Масса Земли очень большая: 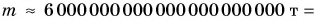
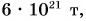
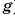
Еще сильнее притяжение Солнца, так как его масса примерно в 300 000 раз больше массы Земли. Именно поэтому Земля и другие планеты движутся вокруг Солнца.
Главные выводы:
- Все тела во Вселенной обладают свойством притягивать к себе другие тела.
- Сила, с которой Земля притягивает к себе тело, называется силой тяжести.
- Сила тяжести, действующая на тело, прямо пропорциональна его массе.
Пример №6
Плотность железного бруска в 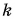
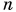
Дано:
Решение
Силы тяжести, действующие на бруски, равны:
Массы брусков равны:
Отношение сил:
Ответ:
Сила упругости
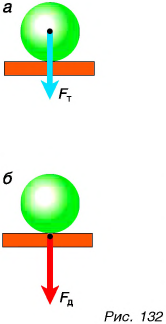
На горизонтальном столе лежит шар. Как и на всякое тело, на него действует сила тяжести 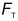
Из § 21 вы знаете, что приложенная к телу сила (даже очень большая) не вызывает изменения скорости движения тела, если она скомпенсирована (уравновешена) приложенной к нему противоположно направленной другой силой. Как возникает эта другая сила? В приведенном примере шар, притягиваясь Землей, давит на крышку стола. Сила давления 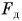
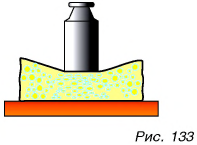
Вас. не должно удивлять утверждение, что любая, даже незначительная, сила давления (например, сила давления мухи, севшей на стол) вызывает деформацию. Деформации поверхности стола, на которую давит гиря, не видно. Но попробуйте положить под гирю поролон (рис. 133), и вы заметите его прогиб, т. е. деформация станет очевидной.
Вернемся к примеру с шаром. Деформированная опора, стремясь распрямиться, действует на шар с силой, направленной вверх (рис. 134), — силой упругости. Именно сила упругости 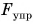
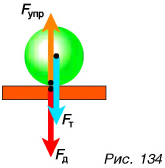
Проделаем еще один опыт. Подвесим шар к пружине, укрепленной на штативе. Шар, притягиваясь к Земле (рис. 135, а), движется и растягивает (деформирует) пружину. Деформирующая сила 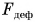
Как и в случае с лежащим шаром, сила упругости 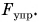
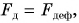
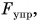
Итак, сила, действующая на тело со стороны деформированной опоры или подвеса, называется силой упругости.
Вы заметили закономерность? Сила упругости 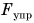
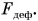
Для любознательных:
Иногда после действия большой деформирующей силы тело не возвращается к первоначальной форме. Например, покупая в магазине батон, вы определяете его свежесть, деформируя специальной ложкой. При действии на батон небольшой силы он после снятия воздействия восстанавливает форму, но если вы переусердствуете, нажимая ложкой, батон так и не сможет избавиться от своего непривлекательного деформированного вида.
Поскольку сила упругости возникает в ответ на воздействие (опора, подвес реагируют на воздействие), то силу упругости часто называют еще силой реакции.
Главные выводы:
- Сила упругости (сила реакции) возникает в ответ на действие деформирующей силы.
- Сила упругости приложена к телу, вызвавшему деформацию опоры или подвеса.
- Сила упругости противоположна деформирующей силе, но их модули равны.
Вес тела
При взаимодействии тел на каждое из них со стороны другого действует сила. Рассмотрим действие друг на друга тела и его горизонтальной опоры или тела и его вертикального подвеса.
На рисунке 140 представлены различные тела. Каждое из этих тел, притягиваясь к Земле, действует на опору или подвес с силой, которая вам хорошо знакома из предыдущего параграфа. Это сила давления на опору или сила натяжения подвеса. Иначе эту силу называют весом тела.
Почему тело действует на опору или подвес? Потому что его притягивает Земля. Неподвижные опора или подвес не позволяют телу падать и сами испытывают действие силы.
Вес — это сила, с которой тело вследствие притяжения Земли действует на опору или подвес.
Обозначим вес буквой Р и укажем вес каждого тела на рисунке 140. Вес мяча приложен к опоре (крышке стола), направлен вниз и является уже известной вам силой давления. Вес собаки приложен к земле в местах соприкосновения ее лап с землей и равен сумме четырех сил:
Определите сами и изобразите вес всех ос шальных тел, представленных на рисунке 140.
А теперь еще раз сравним силу тяжести и вес тела. У этих сил есть общее: они вызваны притяжением Земли. Эти силы очень часто (подчеркиваем — часто, но не всегда) численно равны друг другу. Но у силы тяжести и веса есть различия.
Во-первых, они приложены к разным телам: сила тяжести — к телу (шару), а вес. — к опоре или подвесу (крышке стола, нити) (рис. 141, а, б).
Во-вторых, сила тяжести в данном месте Земли имеет строго определенное значение 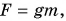
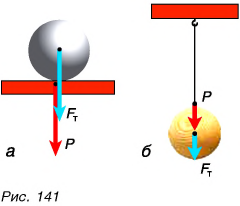
Докажем это с помощью опыта. Подвесим груз на пружине (рис. 142, а). Если мы будем равномерно поднимать и опускать этот груз, то удлинение пружины, а значит, и сила упругости и вес груза будут оставаться такими же, как в случае неподвижного груза. Но если мы неравномерно (с разгоном) опустим (рис. 142, б) или поднимем (рис. 142, в) груз в вертикальном направлении, то будут наблюдаться изменения в растяжении пружины, что указывает на изменения веса тела.
Для любознательных:
Вам известно, что действующая на тело сила тяжести на других планетах может быть как больше, так и меньше, чем на Земле. Значит, и вес тела на этих планетах будет другим.
А может ли тело вообще потерять вес? Космонавты и все тела в космическом корабле свободно парят, не оказывая действия на опору или подвес, т. е. их вес Р = 0. Это состояние тела называется невесомостью.
Невесомость можно создать и на Земле. Пустим свободно падать груз вместе с пружиной. Пружина не растягивается, а, значит, вес груза равен нулю. Это и есть невесомость.
Главные выводы:
- Вес тела — сила, приложенная к опоре или подвесу.
- Вес неподвижного или равномерно движущегося тела численно равен силе тяжести.
- Вес тела, движущегося неравномерно, может изменяться и быть больше силы тяжести, меньше и даже равным нулю.
Единица силы и измерение силы
Сила характеризуется числовым значением (модулем), направлением и точкой приложения. Чтобы определить числовое значение силы, нужно измерить силу, т. е. сравнить ее с другой силой, принятой в качестве единицы силы. Что принято за единицу силы?
Главный результат действия силы — изменение скорости движения тела, которая сама по себе никогда не изменяется. Исходя из этого, была выбрана в СИ единица силы — 1 ньютон (1 Н), названная в честь английского ученого Исаака Ньютона. Существуют кратные и дольные единицы силы: 1 кН = 1000 Н, 1 мН = 0,001 Н.
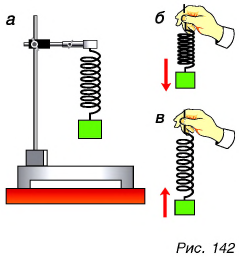
Сила, как вы знаете, может не только изменить скорость, но и вызвать деформацию тела. Пружина растягивается (рис. 143), потому что на нее действует вес груза, который притягивает Земля.
Какой массой должно обладать тело, чтобы действующая на него сила тяжести равнялась 1,0 И? Исследования показали, что с силой F = 1,0 Н Земля притягивает тело массой m = 0,102 кг.
Определим значение коэффициента 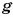
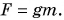
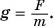
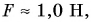
Значит, если масса тела равна 1,0 кг, то действующая на него сила тяжести 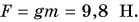
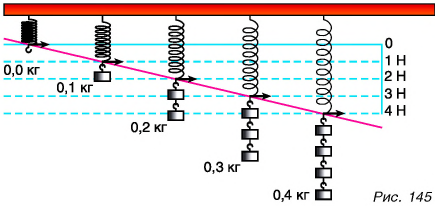
Как измерить силу? Для этого нужно создать измерительный прибор. Будем подвешивать к пружине сначала одну гирю массой m = 102 г = = 0,102 кг, затем две, три и т. д. Отметим метками положения указателя (рис. 145), напротив которых ставим значения 1 Н, 2 Н, 3 Н и т. д.
Пружина с указателем и шкалой представляет собой прибор для измерения сил — динамометр (от греч. dynamis — сила и metreo — измеряю) (рис. 146). Динамометром можно измерять не только вес тела, но и любые силы.
Динамометры бывают различных типов и размеров в зависимости от того, для измерения больших или малых сил они предназначены. Для измерения мускульной силы руки используют динамометр силомер (рис. 147, а). Определить силу тяги трактора позволяет тяговый динамо метр (рис. 147, б).
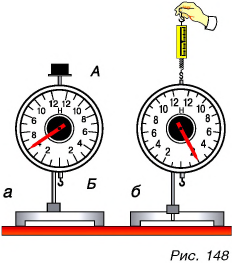
Для проведения различных исследований удобен динамометр с реечной передачей (рис. 148). Он позволяет измерять не только силу, направленную вниз, например создаваемую лежащим на опоре А телом (рис. 148, а), или вес подвешенного 1 к подвесу Б тела. Таким динамометром можно измерить и силу, направленную вверх (рис. 148, б).
Для любознательных:
Значение коэффициента 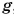
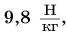
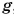
Для Луны этот коэффициент в б раз меньше, т. е. 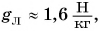
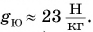
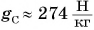
Главные выводы:
- В СИ единицей силы является 1 ньютон.
- Силу измеряют с помощью динамометра.
- С силой F = 1 Н Земля притягивает тело массой m = 0,102 кг.
- В формуле
силы тяжести, с которой Земля действует на тело, постоянный коэффициент
Пример №7
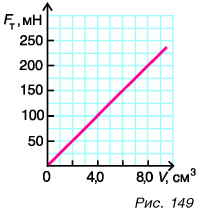
Зависимость силы тяжести, действующей на песок в песочных часах, от его объема представлена на рисунке 149. Определите плотность песка. Коэффициент 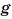
Решение
Плотность песка 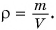
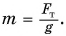
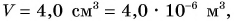
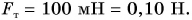
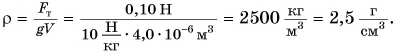
Ответ:
- Заказать решение задач по физике
Сложение сил и равнодействующая сила
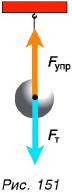
На любое тело действует хотя бы одна сила — сила тяжести. Но чаще всего на тело действует несколько сил. Например, на шарик (рис. 151) действуют Земля и нить (две силы). Каков результат их действия?
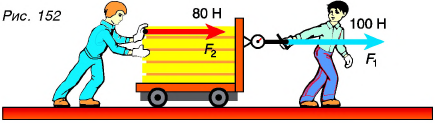
Решим такую задачу. Вы с другом перевозите на тележке груз, причем один из вас тянет тележку, прикладывая силу 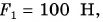
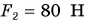
Эта сила 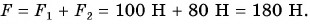
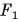
Сила, которая оказывает на тело такое же действие, как несколько одновременно действующих на него сил, называется равнодействующей этих сил.
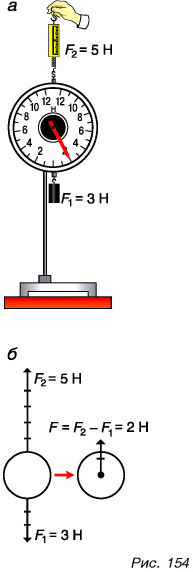
Как направлена равнодействующая? Проведем опыт. К нижнему крючку динамометра подвесим груз весом 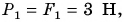
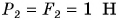
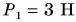
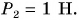
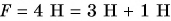
Модуль равнодействующей сил, действующих на тело в одном направлении но одной прямой, равен сумме модулей этих сил. Направление равнодействующей такое же, как и отдельных сил.
Изменим опыт: с помощью другого динамометра подействуем на данный динамометр вверх силой 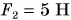
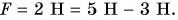
Значит, действие двух противоположно направленных сил можно заменить одной силой, модуль которой равен разности модулей двух приложенных сил и которая направлена в сторону большей силы (рис. 154, б).
А если силы 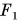
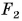
Ответим еще на один важный вопрос: как ведет себя тело при скомпенсированных силах, т. е. при нулевом значении равнодействующей?
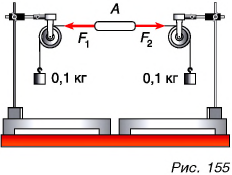
Проведем опыт. Возьмем пенопластовую пластинку А очень малой массы. Подействуем на пластинку одинаковыми по модулю силами упругости нитей 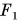
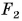
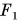
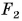
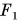
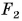
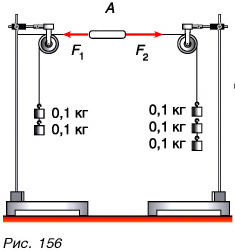
А если продолжить опыт и подвесить к одной нити два груза, а к другой — три? Пластинка придет в движение с увеличивающейся скоростью (рис. 156), ведь равнодействующая сил упругости нитей 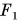
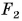
Внимание! Находить равнодействующую можно только для сил, приложенных к одному телу.
Для любознательных:
Если приложенные к телу силы действуют не вдоль одной прямой, то модуль равнодействующей силы не равен арифметической сумме этих сил. В показанном на рисунке опыте приложенные силы — 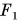
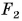
Главные выводы:
- Действие нескольких сил, приложенных к телу, можно заменить одной силой — их равнодействующей.
- Направление равнодействующей двух сил, действующих вдоль одной прямой, совпадает с направлением большей из них.
- Если равнодействующая сил, приложенных к телу, равна нулю, то оно либо покоится, либо движется равномерно и прямолинейно.
- Если равнодействующая всех сил, приложенных к телу, не равна нулю, скорость тела изменяется.
Пример №8
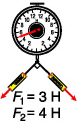
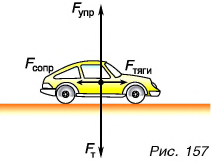
На автомобиль массой m = 2,0 т, движущийся равномерно по прямолинейному горизонтальному участку шоссе, действует сила сопротивления движению 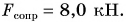
Дано:
Решение
Если автомобиль движется равномерно, то равнодействующая всех сил, приложенных к нему, равна нулю. На автомобиль действуют: сила тяжести 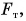
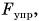
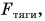
Изобразим 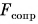
Аналогично 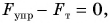
Ответ:
Трение и сила трения
Кто из вас не катался с горы на санках? Приобретя большую скорость, санки (рис. 158), выехав на горизонтальный участок, останавливаются. Почему? Вспомните, что действующая на тело сила может изменить скорость его движения. Этой силой является сила трения скольжения. А что нужно сделать, чтобы санки продолжали движение с той же скоростью? Необходимо скомпенсировать силу трения. Для этого следует тянуть санки горизонтально с силой, равной по модулю силе трения. От чего зависит сила трения?
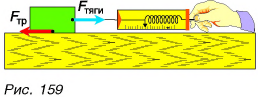
Проведем опыт. Будем с помощью динамометра равномерно перемещать брусок по горизонтальной поверхности стола (рис. 159). Динамометр показывает, что на брусок действует сила тяги, но скорость движения бруска не изменяется. Значит, на брусок действует еще одна сила компенсирующая сила. Этой силой является сила трения 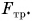
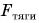
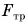
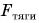
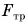
Итак, сила трения скольжения возникает при движении одного тела но поверхности другого и направлена в сторону, противоположную движению.
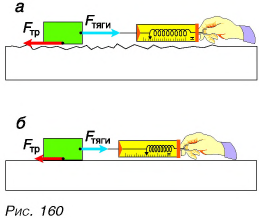
Почему возникает сила трения? Продолжим опыт. Будем равномерно перемещать брусок сначала по шероховатой, затем по обработанной поверхности доски. Сила тяги будет больше при движении по шероховатой поверхности (рис. 160, а). Значит, и модуль равной ей силы трения будет тем больше, чем более шероховатой, неровной окажется поверхность. При движении неровности цепляются друг за друга, деформируются, разрушаются. Это создает препятствия движению. А если бы поверхности были идеально гладкие, то возникла ли бы сила трения при движении одного тела по поверхности другого? Не спешите ответить «нет». При хорошо отполированных поверхностях расстояние между поверхностями тел или их участками при движении тел так мало, что станут существенными силы притяжения молекул поверхности одного тела к молекулам поверхности другого. Эти силы будут тормозить движение тел.
Значит, шероховатость поверхностей и силы притяжения между молекулами соприкасающихся поверхностей — причины возникновения сил трения.
Если при движении соприкасаются твердые поверхности тел, трение называют сухим.
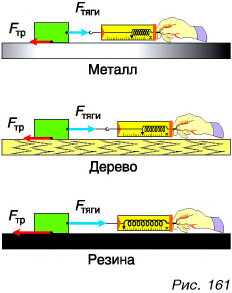
От чего еще зависит сила сухого трения? Дадим ответ, исходя из опыта. Будем равномерно двигать брусок по различным поверхностям: по металлической, деревянной, резиновой — с примерно одинаковым качеством обработки (рис. 161). Динамометр показывает различную силу тяги. Следовательно, силы трения дерева но металлу, дерева по дереву, дерева по резине будут различны. Наибольшая сила трения возникнет при движении по поверхности резины. Не случайно подошвы в спортивной обуви (рис. 162) делают резиновыми и рельефными.
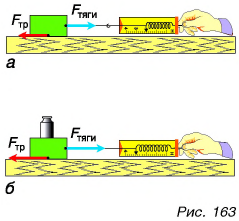
Поставим теперь на брусок гирю и сравним силы трения при равномерном движении ненагруженного бруска (рис. 163, а) и бруска с гирей (рис. 163, б). Видно, что во втором случае сила тяги, а значит, и сила трения увеличились. Но брусок с гирей с большей силой давит на поверхность, с которой соприкасается. Следовательно, сила трения тем больше, чем больше сила, прижимающая тело (брусок) к поверхности.
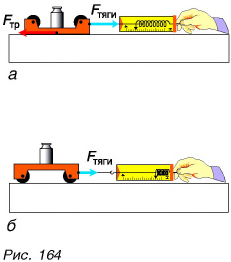
Как уменьшить трение? Здесь есть два пути. Первый — заменить трение скольжения трением качения. Проделаем такой опыт. Будем равномерно передвигать металлическую тележку по столу скольжением (рис. 164, а) и качением (рис. 164, б). Сила трения во втором случае значительно меньше, хотя материал поверхностей и прижимающая сила не изменяются. Значит, трение качения меньше трения скольжения. С тяжелым чемоданом справиться легко, если прикрепить к нему колеса.
Второй путь уменьшения трения скольжения — это смазывание трущихся поверхностей. Смазка (например, масло) заполняет все неровности трущихся поверхностей и располагается тонким слоем между ними так, что поверхности перестают касаться друг друга. При этом сухое трение заменяется трением слоев жидкости (масла), а оно в 8—10 раз меньше.
Опытный водитель никогда не отправится в далекий путь, не проверив, достаточно ли масла в двигателе машины. Объясните, зачем он это делает.
Для любознательных:
А знаете ли вы, что с помощью катков перемещают дома? Например, в городе Москве во время реконструкции улицы Тверской некоторые дома были передвинуты на другое место именно таким способом.
В машинах для замены трения скольжения трением качения используют шариковые и роликовые подшипники (см. рис.). Подшипники диаметром 1,5—2 мм применяют в точных измерительных приборах. Вращающийся вал машины или другого механизма не скользит но неподвижному вкладышу подшипника, а катится по нему на стальных шариках или роликах. Это снижает трение в 20—30 раз.
Главные выводы:
- Сила трения скольжения возникает при движении одного тела по поверхности другого.
- Сила трения скольжения направлена против движения.
- Сила трения зависит от свойств соприкасающихся поверхностей и силы, прижимающей тело к поверхности.
- Давление в физике
- Строение вещества в физике
- Физическое тело и вещество в физике
- Плотность и единицы плотности в физике
- Потенциальная энергия
- Кинетическая энергия
- Закон сохранения и превращения механической энергии
- Работа, мощность и энергия
Екатерина Владимировна Мосина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Ускорение тела, возникающее вследствие силы трения
Известно, что сила трения скольжения направлена в сторону, противоположную направлению относительной скорости движения трущихся тел.
Отсюда следует, что ускорение, которое такая сила сообщает движущемуся телу, тоже направлено против относительной скорости. А это значит, что действие силы трения приводит к уменьшению абсолютного значения скорости тела относительно того тела, по которому оно скользит.
Если на тело, которое скользит по неподвижной поверхности, никакие силы, кроме силы трения не действуют, то оно, в конце концов, останавливается. Рассмотри этот часто встречающийся случай.
Представим себе, что перед движущимся поездом неожиданно появилось некоторое препятствие и машинист отключил двигатель и включил тормоз. Начиная с это момента, на поезд действует только сила трения, так как сила тяжести скомпенсирована реакцией рельсов, а сила сопротивления воздуха мала. Через некоторое время $t$ поезд, пройдя расстояние $l$ – тормозной путь, остановится. Найдем время $t$, нужное для остановки, и расстояние $l$, которое поезд пройдет за это время.
Под действием сила трения $overline{F}_{mp} $поезд будет двигаться с ускорением, равным:
Выберем координатную ось $x$ так, чтобы ее положительное направление совпадало с направлением скорости движения поезда.
Рисунок 1.
Так как сила трения $overline{F}_{mp} $направлена в противоположном направлении, ее проекция на ось х отрицательна. Отрицательна и проекция вектора ускорения на ось $x$. Поэтому если абсолютное значение силы трения равно $left|overline{F}_{mp} right|$, то:
Но ускорение определяется также формулой:
где $v_{0} $- скорость поезда до начала торможения.
Время торможения при движении тела под действием силы трения
Так как нас интересует промежуток времени $t$ от начала торможения до остановки поезда, то конечная скорость $v=0$. Тогда:
«Движение тела под действием силы трения» 👇
Таким образом:
Получим выражения для времени торможения:
Нахождение пути, пройденного телом под действием силы трения
А теперь найдем тормозной путь $l$. Для этого воспользуемся формулой:
Так как $v=0$, то:
Так как $overline{a}=-frac{left|overline{F}_{mp} right|}{m} $, получим:
Из этой формулы видно, что пройденный до остановки путь пропорционален квадрату скорости. Если увеличить скорость вдвое, то потребуется вчетверо больший путь для остановки.
Пример 1
С какой скоростью двигался автомобиль, если после выключения двигателя он прошел до остановки путь равный $80$ м? Коэффициент трения принять равным $0,25$.
Дано: $l=80$м, $mu =0,25$.
Найти: $v$-?
Решение:
Воспользуемся раннее выведенными формулами для нахождения тормозного пути:
$l=frac{mv_{0}^{2} }{2overline{left|F_{mp} right|}} $. (1)
Так как $F_{mp} =mu mg$, подставим в формулу (1) и получим:
$l=frac{mv_{0}^{2} }{2mu mg} $. (2)
Выразив из формулы (2) $v_{0} $найдем величину искомой скорости:
$v_{0} =sqrt{2mu gl} =20$м/с
Ответ: Скорость автомобиля до выключения двигателя $v_{0} =20$ м/с.
Пример 2
Сноубордист массой $80$ кг, имеющий в конце спуска скорость $20$ м/с, останавливается через $40$ с после окончания спуска. Определите силу трения и коэффициент трения.
Дано: $m=80$кг, $v_{0} =20$м/с, $t=40$с.
Найти: $F_{mp} $, $mu $-?
Решение:
Уравнение движения сноубордиста будет иметь вид:
[ma=F_{mp} .]
Используя выражения для нахождения ускорения (конечная скорость $v=0$), получим:
[a=-frac{v_{0} }{t} .]
Тогда:
$F_{mp} =ma=-mfrac{v_{0} }{t} =40H$.
Так как сила трения $overline{F}_{mp} $равна $F_{mp} =mu Bg$, находим коэффициент трения $mu $:
[mu =frac{F_{mp} }{mg} =0,05.]
Ответ: $F_{mp} =40H$, $mu =0,05$.
Пример 3
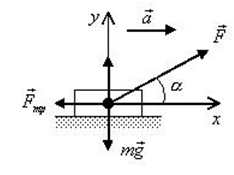
Сани массой $16$ кг перемещают по горизонтальной плоскости под действием силы $180 H$, направленной под углом $30^circ$ к горизонтали. Коэффициент терния саней о плоскость $0,5$. Определить ускорения, с которым движутся сани.
Дано: $m=16$кг, $F=180 H$, $alpha =30^circ$, $mu =0,5$.
Найти: $a$-?
Решение:
Рисунок 2.
Уравнение движения тела:
[moverline{a}=moverline{g}+overline{N}+overline{F}+overline{F}_{mp} .]
Выберем направление осей $x$ и $y$ и спроецируем на них силы и ускорение:
[begin{array}{l} {ma=Fcos alpha -F_{mp} } \ {0=-Bg+N+Fsin alpha } end{array}]
Поскольку $F_{mp} =mu N$, а из второго уравнения $N=mg-Fsin alpha $, то $F_{mp} =mu (mg-Fsin alpha )$. Тогда из первого уравнения ускорение:
$a=frac{1}{m} [Fcos alpha -mu (mg-Fsin alpha )]approx 7,6м/с^2$
Ответ: $a$=$7,6м/с^2$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Содержание:
- Определение и формула пути
- Виды движения и формулы длины пути
- Единицы измерения пути
- Примеры решения задач
Определение и формула пути
Линия, которую описывает материальная точка при своем движении, называется траекторией.
Определение
Длиной пути называют сумму длин всех участков траектории, которые прошла точка за рассматриваемый промежуток времени
от t1 до t2.
В том случае, если уравнения движения представлены в прямоугольной декартовой системе координат, то длина пути (s) определяется как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d x}{d t}right)^{2}+left(frac{d y}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}} d t(1)$$
В цилиндрических координатах длина пути может быть выражена как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d rho}{d t}right)^{2}+left(rho frac{d varphi}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}} d t(2)$$
В сферических координатах формулу длины пути запишем:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d r}{d t}right)^{2}+left(r frac{d theta}{d t}right)^{2}+left(r sin theta frac{d varphi}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{r})^{2}+(r dot{theta})^{2}+(r varphi sin theta)^{2}} d t(3)$$
Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t1 называют начальным положением.
Очень часто полагают t1=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).
Считают, что за промежуток времени $d t rightarrow 0$ материальная точка проходит путь ds,
который называют элементарным. При этом:
$$d s=|d bar{r}|=v d t$$
где $bar{r}$ – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
$$s=vleft(t_{2}-t_{1}right)(5)$$
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути
$Delta s$ на отрезке времени от
$t$ до
$t + Delta t$ находят как:
$$Delta s=langle vrangle Delta t(6)$$
где $langle vrangle$ – средняя путевая скорость. При равномерном движении
$langle vrangle = v$ .
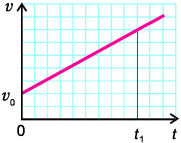
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:
$$s=v_{0} t+frac{a t^{2}}{2}(7)$$
где a – постоянное ускорение, v0 – начальная скорость движения.
Единицы измерения пути
Основной единицей измерения пути в системе СИ является: [s]=м
В СГС: [s]=см
Примеры решения задач
Пример
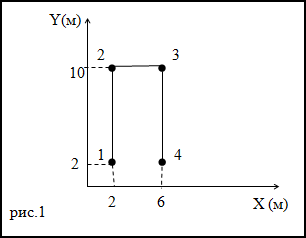
Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой,
чему равно перемещение, если точка двигалась 1-2-3-4.
Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:
$$6 – 2 = 4 (m)$$
Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:
$$8 + 4 + 8 = 20 (m)$$
Ответ. Путь равен 20 м, перемещение равно 4 м.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Уравнение движения материальной точки в прямоугольной декартовой системе координат представлено функцией:
x=-0,2t2 (м) . Какой путь пройдет материальная точка за 5 с?
Решение. Так как уравнение движения задано только одной координатой, то в качестве основы для решения
задачи примем формулу пути в виде:
$$s=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}} d t(2.1)$$
Подставим в (2.1) функцию x=-0,2t2, учтем, что $0 c leq t leq 5 c$ имеем:
$$s=int_{0}^{5} sqrt{left(-0,2 frac{dleft(t^{2}right)}{d t}right)^{2}} d t=0,left.4 cdot frac{t^{2}}{2}right|_{0} ^{5}=5(m)$$
Ответ. s=5м.
Читать дальше: Формула равноускоренного движения.
Цель урока:
- обобщить и закрепить ключевые задачи по теме;
- научиться работать с теоретическими вопросами
темы; - научиться применять интеграл к решению
физических задач.
План урока:
1. Схема решения задач на приложения
определенного интеграла
2. Нахождение пути, пройденного телом при
прямолинейном движении
3. Вычисление работы силы, произведенной при
прямолинейном движении тела
4. Вычисление работы, затраченной на растяжение
или сжатие пружины
5. Определение силы давления жидкости на
вертикально расположенную пластинку
Тип урока: интегрированный.
Воспитательная работа: расширение
кругозора и познавательной деятельности
учащихся, развитие логического мышления и умения
применять свои знания.
Техническое обеспечение:
интерактивная доска. Компьютер и диск.
Приложение: «Рапсодия
природы».
ХОД УРОКА
I. Организационный момент
II. Постановка цели урока
– Урок хотелось бы провести под девизом
Готфрида Вильгельма Лейбница – немецкого философа,
логика,
математика,
физика:
«Общее искусство знаков представляет чудесное
пособие, так как оно разгружает воображение…
Следует заботиться о том, чтобы обозначения были
удобны для открытий. Обозначения коротко
выражают и отображают сущность вещей. Тогда
поразительным образом сокращается работа
мысли».
III. Повторим основные понятия и
ответим на вопросы:
– Скажите основное определение интеграла?
– Что вы знаете о интеграле (свойства, теоремы)?
– Знаете ли вы какие-нибудь примеры задач с
применением интеграла?
IV. Объяснение нового материала
(рассмотрение теории):
1. Схема решения задач на приложения
определенного интеграла
С помощью определенного интеграла можно решать
различные задачи физики, механики и т. д., которые
трудно или невозможно решить методами
элементарной математики.
Так, понятие определенного интеграла
применяется при решении задач на вычисление
работы переменной силы, давления жидкости на
вертикальную поверхность, пути, пройденного
телом, имеющим переменную скорость, и ряд других.
Несмотря на разнообразие этих задач, они
объединяются одной и той же схемой рассуждений
при их решении. Искомая величина (путь, работа,
давление и т. д.) соответствует некоторому
промежутку изменения переменной величины,
которая является переменной интегрирования. Эту
переменную величину обозначают через Х, а
промежуток ее изменения – через [а, b].
Отрезок [a, b] разбивают на n равных частей, в
каждой из которых можно пренебречь изменением
переменной величины. Этого можно добиться при
увеличении числа разбиений отрезка. На каждой
такой части задачу решают по формулам для
постоянных величин.
Далее составляют сумму (интегральную сумму),
выражающую приближенное значение искомой
величины. Переходя к пределу при , находят искомую величину
I в виде интеграла
I = , где f(x)
– данная по условиям задачи функция (сила,
скорость и т. д.).
2. Нахождение пути, пройденного телом при
прямолинейном движении
Как известно, путь, пройденный телом при
равномерном движении за время t, вычисляется по
формуле S = vt.
Если тело движется неравномерно в одном
направлении и скорость его меняется в
зависимости от времени t, т. е. v = f(t), то для
нахождения пути, пройденного телом за время от до
, разделим этот
промежуток времени на n равных частей Δt. В каждой
из таких частей скорость можно считать
постоянной и равной значению скорости в конце
этого промежутка. Тогда пройденный телом путь
будет приблизительно равен сумме , т.е.

Если функция v(t) непрерывна, то
Итак,
3. Вычисление работы силы, произведенной
при прямолинейном движении тела
Пусть тело под действием силы F движется по
прямой s, а направление силы совпадает с
направлением движения. Необходимо найти работу,
произведенную силой F при перемещении тела из
положения a в положение b.
Если сила F постоянна, то работа находится по
формуле
(произведение силы на длину пути).
Пусть на тело, движущееся по прямой Ох,
действует сила F, которая изменяется в
зависимости от пройденного пути, т. е. . Для того чтобы найти
работу, совершаемую силой F на отрезке пути от а
до b, разделим этот отрезок на n равных частей
. Предположим,
что на каждой части сила сохраняет постоянное значение
Составим интегральную сумму, которая
приближенно равна значению произведенной
работы:
т.е. работа, совершенная этой силой на участке
от а до b, приближенно мала сумме:
Итак, работа переменной силы вычисляется по
формуле: 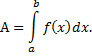
4. Вычисление работы, затраченной на
растяжение или сжатие пружины
Согласно закону Гука, сила F, необходимая для
растяжения или сжатия пружины, пропорциональна
величине растяжения или сжатия.
Пусть х – величина растяжения или сжатия
пружины. Тогда ,
где k – коэффициент пропорциональности,
зависящий от свойства пружины.
Работа на участке выразится формулой
, а вся затраченная работа
или
. Если
то погрешность величины
работы стремится к нулю.
Для нахождения истинной величины работы
следует перейти к пределу
Итак,
5. Определение силы давления жидкости на
вертикально расположенную пластинку
Из физики известно, что сила Р давления
жидкости на горизонтально расположенную
площадку S, глубина погружения которой равна h,
определяется по формуле:
, где
– плотность жидкости.
Выведем формулу для вычисления силы давления
жидкости на вертикально расположенную пластинку
произвольной формы, если ее верхний край
погружен на глубину a, а нижний – на глубину b.
Так как различные части вертикальной пластинки
находятся на разной глубине, то сила давления
жидкости на них неодинаковa. Для вывода формулы
нужно разделить пластинку на горизонтальных
полос одинаковой высоты . Каждую полосу приближенно
можно считать прямоугольником (рис.199).
По закону Паскаля сила давления жидкости на
такую полосу равна силе движения жидкости на
горизонтально расположенную пластинку той же
площади, погруженной на ту же глубину.
Тогда согласно формуле (4) сила давления на
полосу, находящуюся на расстоянии х от
поверхности, составит , где
– площадь полосы.
Составим интегральную сумму и найдем ее предел,
равный силе давления жидкости на всю пластинку:
т.е.
Если верхний край пластинки совпадает с
поверхностью жидкости, то а=0 и формула (5) примет
вид
Ширина каждой полосы зависит от формы
пластинки и является функцией глубины х
погружения данной полосы.
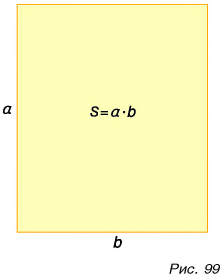
Для пластинки постоянной ширины формула (5)
упрощается, т.к. эту постоянную можно вынести за
знак интеграла:
V. Разбор задач по теме
1) Скорость движения материальной точки
задается формулой = (4
м/с.
Найти путь, пройденный точкой за первые 4с от
начала движения.
Решение:
2) Скорость движения изменяется по закону м/с . Найти длину
пути, пройденного телом за 3-ю секунду его
движения.
Решение:
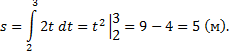
3) Скорость движения тела задана уравнением м/с. Определить
путь, пройденный телом от начала движения до
остановки.
Решение:
Скорость движение тела равна нулю в момент
начала его движения и остановки. Найдем момент
остановки тела, для чего приравняем скорость
нулю и решим уравнение относительно t; получим
Следовательно,
4) Тело брошено вертикально вверх со скоростью,
которая изменяется по закону м/с. Найти наибольшую высоту
подъема.
Решение:
Найдем время, в течении которого тело
поднималось вверх: 29,4–9,8t=0 (в момент наибольшего
подъема скорость равна нулю); t = 3 с. Поэтому
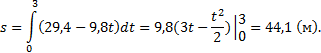
5) Какую работу совершает сила в 10Н при
растяжении пружины на 2 см?
Решение:
По закону Гука сила F, растягивающая пружину,
пропорциональна растяжению пружины , т.е. F = kx.
Используя условие, находим (Н/м), т.е. F = 500x. Получаем
6) Сила в 60Н растягивает пружину на 2 см.
Первоначальная длина пружины равна 14 см. Какую
работу нужно совершить, чтобы растянуть ее до 20
см?
Решение:
Имеем (H/м) и,
следовательно, F=3000x. Так как пружину требуется
растянуть на 0,06 (м), то
7) Определить силу давления воды на стенку
шлюза, длина которого 20 м, а высота 5 м (считая шлюз
доверху заполненным водой).
Здесь y = f(x) = 20, a = 0, b = 5 м, кг/
.
Находим
8) В воду опущена прямоугольная пластинка,
расположенная вертикально. Ее горизонтальная
сторона равна 1 м, вертикальная 2 м. Верхняя
сторона находится на глубине 0,5 м. Определить
силу давления воды на пластинку.
Решение:
Здесь y = 1, a = 0,5, b = 2 + 0,5 = 2,5 (м), = 1000 кг/
. Следовательно,
9) Скорость прямолинейного движения точки
задана уравнением . Найти уравнение движения точки.
Решение:
Известно, что скорость прямолинейного движения
тела равна производной пути s по времени t, т.е. , откуда ds = v dt.
Тогда имеем
Это искомое уравнение.
10) Скорость тела задана уравнением . Найти уравнение
движения, если за время тело прошло путь
.
Решение:
Имеем ds = v dt = (6+ 1) dt; тогда
Подставив в найденное уравнение начальные
условия s = 60 м, t = 3 c, получим
откуда С = 3.
Искомое уравнение примет вид
11) Тело движется со скоростью м/с. Найти закон движения s(t),
если в начальный момент тело находилось на
расстоянии 5 см от начала отсчета.
Решение:
Так как ds = v dt = (, то
Из условия следует, что если t = 0, то s = 5 см = 0,05 м.
подставив эти данные в полученное уравнение,
имеем откуда
0,05 = С.
Тогда искомое уравнение примет вид
12) Вычислить силу давления воды на плотину,
имеющую форму трапеции, у которой верхнее
основание, совпадающее с поверхностью воды,
имеет длину 10 м, нижнее основание 20 м, а высота 3 м.
Решение:
13) Цилиндрический стакан наполнен ртутью.
Вычислить силу давления ртути на боковую
поверхность стакана, если его высота 0,1 м, а
радиус основания 0,04 м. Плотность ртути равна 13600
кг/.
Решение:
Вычислим площадь круглой полоски
Элементарная сила давления составляет
Следовательно
VI. Самостоятельное решение задач на доске,
коллективный разбор решений задач:
- Скорость движения тела задана уравнением
. Найти уравнение
движения, если в начальный момент времени - Найти уравнение движения точки, если к моменту
начала отсчета она прошла путь, а его скорость задана
уравнением - Скорость движения тела пропорциональна
квадрату времени. Найти уравнение движения тела,
если известно, что за 3 с оно прошло 18 м. - Тело движется прямолинейно со скоростью
м/с. Найти путь,
пройденный телом за 5 с от начала движения. - Скорость движения тела изменяется по закону
м/с. Найти путь,
пройденный телом за 4 с от начала движения. - Найти путь пройденный телом за 10-ю секунду, зная,
что что скорость его прямолинейного движения
выражается формулойм/с.
- Найти путь, пройденный точкой от начала
движения до ее остановки, если скорость ее
прямолинейного движения изменяется по законум/с.
- Какую работу совершает сила в 8 Н при растяжении
пружины на 6 см? - Сила в 40 Н растягивает пружину на 0,04 м. Какую
работу надо совершить, чтобы растянуть пружину
на 0,02 м? - Вычислить силу давления воды на вертикальную
прямоугольную пластинку, основание которой 30 м, а
высота 10 м, причем верхний конец пластинки
совпадает с уровнем воды. - Вычислить силу давления воды на одну из стенок
аквариума, имеющего длину 30 см и высоту 20 см.
VII. Минутка релаксации
Запуск приложения «Минутка
релаксации»
VIII. Подведение итогов урока:
– Каким вопросам был посвящен урок?
– Чему научились на уроке?
– Какие теоретические факты обобщались на уроке?
– Какие рассмотренные задачи оказались наиболее
сложными? Почему?
Список литературы:
- Журнал «Потенциал»
- «Алгебра и начала анализа» 11 класс С.М.
Никольский, М.К. Потапов и др. - «Алгебра и математический анализ» Н.Я. Виленкин
и др. - «Учебник по математическому анализу» Град О.Г.,
Змеев О.А. - «Высшая математика: Учебник для вузов». В 3
томах. Бугров Я.С. Никольский С.М. - «Математический анализ». Е.Б. Боронина







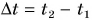




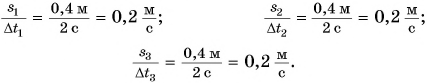
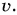


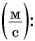
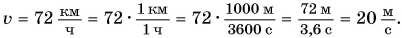
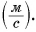

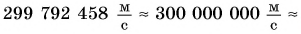

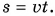

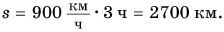

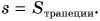
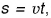 по графику пути или с помощью графика скорости.
по графику пути или с помощью графика скорости.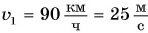
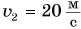
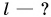

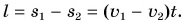
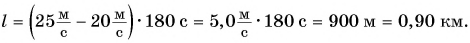
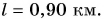
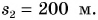
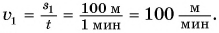
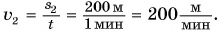
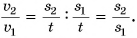
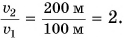



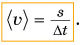

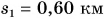
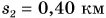
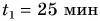
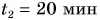
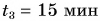
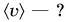
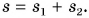
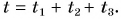
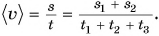
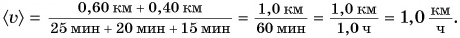
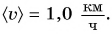
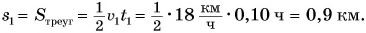
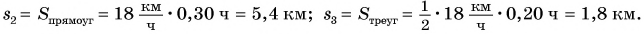
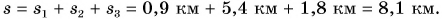
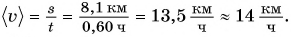





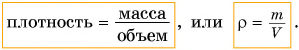
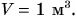
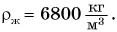
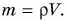
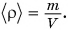
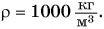
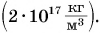
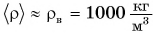

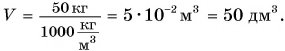
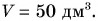
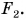

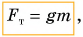
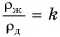
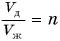
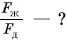
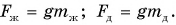
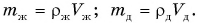
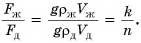
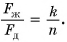
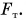


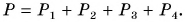
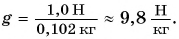
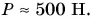



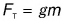 силы тяжести, с которой Земля действует на тело, постоянный коэффициент
силы тяжести, с которой Земля действует на тело, постоянный коэффициент