Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.
Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.
Возрастание и убывание функции на интервале
Функция y=f(x) будет возрастать на интервале x, когда при любых x1∈X и x2∈X , x2>x1неравенство f(x2)>f(x1) будет выполнимо. Иначе говоря, большему значению аргумента соответствует большее значение функции.
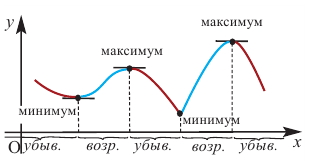
Функция y=f(x) считается убывающей на интервале x, когда при любых x1∈X, x2∈X, x2>x1 равенство f(x2)>f(x1) считается выполнимым. Иначе говоря, большему значению функции соответствует меньшее значение аргумента. Рассмотрим рисунок, приведенный ниже.

Замечание: Когда функция определенная и непрерывная в концах интервала возрастания и убывания, то есть (a;b), где х=а, х=b, точки включены в промежуток возрастания и убывания. Определению это не противоречит, значит, имеет место быть на промежутке x.
Основные свойства элементарных функций типа y=sinx – определенность и непрерывность при действительных значениях аргументах. Отсюда получаем, что возрастание синуса происходит на интервале -π2; π2, тогда возрастание на отрезке имеет вид -π2; π2.
Точки экстремума, экстремумы функции
Точка х0 называется точкой максимума для функции y=f(x), когда для всех значений x неравенство f(x0)≥f(x) является справедливым. Максимум функции – это значение функции в точке, причем обозначается ymax.
Точка х0 называется точкой минимума для функции y=f(x), когда для всех значений x неравенство f(x0)≤f(x) является справедливым. Минимум функции – это значение функции в точке, причем имеет обозначение вида ymin.
Окрестностями точки х0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.

Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.

Первый рисунок говорит о том, что необходимо найти наибольшее значение функции из отрезка [a;b]. Оно находится при помощи точек максимума и равняется максимальному значению функции, а второй рисунок больше походит на поиск точки максимума при х=b.
Достаточные условия возрастания и убывания функции
Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.
Первое достаточное условие экстремума
Пусть задана функция y=f(x), которая дифференцируема в ε окрестности точки x0, причем имеет непрерывность в заданной точке x0. Отсюда получаем, что
- когда f'(x)>0 с x∈(x0-ε; x0) и f'(x)<0 при x∈(x0; x0+ε), тогда x0 является точкой максимума;
- когда f'(x)<0 с x∈(x0-ε; x0) и f'(x)>0 при x∈(x0; x0+ε), тогда x0 является точкой минимума.
Иначе говоря, получим их условия постановки знака:
- когда функция непрерывна в точке x0, тогда имеет производную с меняющимся знаком, то есть с + на -, значит, точка называется максимумом;
- когда функция непрерывна в точке x0, тогда имеет производную с меняющимся знаком с – на +, значит, точка называется минимумом.
Алгоритм для нахождения точек экстремума
Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:
- найти область определения;
- найти производную функции на этой области;
- определить нули и точки, где функция не существует;
- определение знака производной на интервалах;
- выбрать точки, где функция меняет знак.
Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.
Найти точки максимума и минимума заданной функции y=2(x+1)2x-2.
Решение
Область определения данной функции – это все действительные числа кроме х=2. Для начала найдем производную функции и получим:
y’=2x+12x-2’=2·x+12’·(x-2)-(x+1)2·(x-2)'(x-2)2==2·2·(x+1)·(x+1)’·(x-2)-(x+1)2·1(x-2)2=2·2·(x+1)·(x-2)-(x+2)2(x-2)2==2·(x+1)·(x-5)(x-2)2
Отсюда видим, что нули функции – это х=-1, х=5, х=2, то есть каждую скобку необходимо приравнять к нулю. Отметим на числовой оси и получим:

Теперь определим знаки производной из каждого интервала. Необходимо выбрать точку, входящую в интервал, подставить в выражение. Например, точки х=-2, х=0, х=3, х=6.
Получаем, что
y'(-2)=2·(x+1)·(x-5)(x-2)2x=-2=2·(-2+1)·(-2-5)(-2-2)2=2·716=78>0, значит, интервал -∞; -1 имеет положительную производную. Аналогичным образом получаем, что
y'(0)=2·(0+1)·0-50-22=2·-54=-52<0y'(3)=2·(3+1)·(3-5)(3-2)2=2·-81=-16<0y'(6)=2·(6+1)·(6-5)(6-2)2=2·716=78>0
Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.
Получим, что в точке х=-1 функция будет непрерывна, значит, производная изменит знак с + на -. По первому признаку имеем, что х=-1 является точкой максимума, значит получаем
ymax=y(-1)=2·(x+1)2x-2x=-1=2·(-1+1)2-1-2=0
Точка х=5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид
ymin=y(5)=2·(x+1)2x-2x=5=2·(5+1)25-2=24
Графическое изображение

Ответ: ymax=y(-1)=0, ymin=y(5)=24.
Стоит обратить внимание на то, что использование первого достаточного признака экстремума не требует дифференцируемости функции с точке x0, этим и упрощает вычисление.
Найти точки максимума и минимума функции y=16×3=2×2+223x-8.
Решение.
Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:
-16×3-2×2-223x-8, x<016×3-2×2+223x-8, x≥0
После чего необходимо найти производную:
y’=16×3-2×2-223x-8′, x<016×3-2×2+223x-8′, x>0y’=-12×2-4x-223, x<012×2-4x+223, x>0
Точка х=0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:
lim y’x→0-0=lim yx→0-0-12×2-4x-223=-12·(0-0)2-4·(0-0)-223=-223lim y’x→0+0=lim yx→0-012×2-4x+223=12·(0+0)2-4·(0+0)+223=+223
Отсюда следует, что функция непрерывна в точке х=0, тогда вычисляем
lim yx→0-0=limx→0-0-16×3-2×2-223x-8==-16·(0-0)3-2·(0-0)2-223·(0-0)-8=-8lim yx→0+0=limx→0-016×3-2×2+223x-8==16·(0+0)3-2·(0+0)2+223·(0+0)-8=-8y(0)=16×3-2×2+223x-8x=0=16·03-2·02+223·0-8=-8
Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:
-12×2-4x-223, x<0D=(-4)2-4·-12·-223=43×1=4+432·-12=-4-233<0x2=4-432·-12=-4+233<0
12×2-4x+223, x>0D=(-4)2-4·12·223=43×3=4+432·12=4+233>0x4=4-432·12=4-233>0
Все полученные точки нужно отметить на прямой для определения знака каждого интервала. Поэтому необходимо вычислить производную в произвольных точках у каждого интервала. Например, у нас можно взять точки со значениями x=-6, x=-4, x=-1, x=1, x=4, x=6. Получим, что
y'(-6)=-12×2-4x-223x=-6=-12·-62-4·(-6)-223=-43<0y'(-4)=-12×2-4x-223x=-4=-12·(-4)2-4·(-4)-223=23>0y'(-1)=-12×2-4x-223x=-1=-12·(-1)2-4·(-1)-223=236<0y'(1)=12×2-4x+223x=1=12·12-4·1+223=236>0y'(4)=12×2-4x+223x=4=12·42-4·4+223=-23<0y'(6)=12×2-4x+223x=6=12·62-4·6+223=43>0
Изображение на прямой имеет вид

Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что
x=-4-233, x=0, x=4+233, тогда отсюда точки максимума имеют значениx=-4+233, x=4-233
Перейдем к вычислению минимумов:
ymin=y-4-233=16×3-22+223x-8x=-4-233=-8273ymin=y(0)=16×3-22+223x-8x=0=-8ymin=y4+233=16×3-22+223x-8x=4+233=-8273
Произведем вычисления максимумов функции. Получим, что
ymax=y-4+233=16×3-22+223x-8x=-4+233=8273ymax=y4-233=16×3-22+223x-8x=4-233=8273
Графическое изображение

Ответ:
ymin=y-4-233=-8273ymin=y(0)=-8ymin=y4+233=-8273ymax=y-4+233=8273ymax=y4-233=8273
Второй признак экстремума функции
Если задана функция f'(x0)=0, тогда при ее f”(x0)>0 получаем, что x0 является точкой минимума, если f”(x0)<0, то точкой максимума. Признак связан с нахождением производной в точке x0.
Найти максимумы и минимумы функции y=8xx+1.
Решение
Для начала находим область определения. Получаем, что
D(y): x≥0x≠-1⇔x≥0
Необходимо продифференцировать функцию, после чего получим
y’=8xx+1’=8·x’·(x+1)-x·(x+1)'(x+1)2==8·12x·(x+1)-x·1(x+1)2=4·x+1-2x(x+1)2·x=4·-x+1(x+1)2·x
При х=1 производная становится равной нулю, значит, точка является возможным экстремумом. Для уточнения необходимо найти вторую производную и вычислить значение при х=1. Получаем:
y”=4·-x+1(x+1)2·x’==4·(-x+1)’·(x+1)2·x-(-x+1)·x+12·x'(x+1)4·x==4·(-1)·(x+1)2·x-(-x+1)·x+12’·x+(x+1)2·x'(x+1)4·x==4·-(x+1)2x-(-x+1)·2x+1(x+1)’x+(x+1)22x(x+1)4·x==-(x+1)2x-(-x+1)·x+1·2x+x+12x(x+1)4·x==2·3×2-6x-1x+13·x3⇒y”(1)=2·3·12-6·1-1(1+1)3·(1)3=2·-48=-1<0
Значит, использовав 2 достаточное условие экстремума, получаем, что х=1 является точкой максимума. Иначе запись имеет вид ymax=y(1)=811+1=4.
Графическое изображение

Ответ: ymax=y(1)=4..
Третье достаточное условие экстремума
Функция y=f(x) имеет ее производную до n-го порядка в ε окрестности заданной точки x0 и производную до n+1-го порядка в точке x0. Тогда f'(x0)=f”(x0)=f”'(x0)=…=fn(x0)=0.
Отсюда следует, что когда n является четным числом, то x0 считается точкой перегиба, когда n является нечетным числом, то x0 точка экстремума, причем f(n+1)(x0)>0, тогда x0 является точкой минимума, f(n+1)(x0)<0, тогда x0 является точкой максимума.
Найти точки максимума и минимума функции yy=116(x+1)3(x-3)4.
Решение
Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что
y’=116x+13′(x-3)4+(x+1)3x-34’==116(3(x+1)2(x-3)4+(x+1)34(x-3)3)==116(x+1)2(x-3)3(3x-9+4x+4)=116(x+1)2(x-3)3(7x-5)
Данная производная обратится в ноль при x1=-1, x2=57, x3=3. То есть точки могут быть точками возможного экстремума. Необходимо применить третье достаточное условие экстремума. Нахождение второй производной позволяет в точности определить наличие максимума и минимума функции. Вычисление второй производной производится в точках ее возможного экстремума. Получаем, что
y”=116x+12(x-3)3(7x-5)’=18(x+1)(x-3)2(21×2-30x-3)y”(-1)=0y”57=-368642401<0y”(3)=0
Значит, что x2=57 является точкой максимума. Применив 3 достаточный признак, получаем, что при n=1 и f(n+1)57<0.
Необходимо определить характер точек x1=-1, x3=3. Для этого необходимо найти третью производную, вычислить значения в этих точках. Получаем, что
y”’=18(x+1)(x-3)2(21×2-30x-3)’==18(x-3)(105×3-225×2-45x+93)y”'(-1)=96≠0y”'(3)=0
Значит, x1=-1 является точкой перегиба функции, так как при n=2 и f(n+1)(-1)≠0. Необходимо исследовать точку x3=3. Для этого находим 4 производную и производим вычисления в этой точке:
y(4)=18(x-3)(105×3-225×2-45x+93)’==12(105×3-405×2+315x+57)y(4)(3)=96>0
Из выше решенного делаем вывод, что x3=3 является точкой минимума функции.
Графическое изображение

Ответ: x2=57 является точкой максимума, x3=3 – точкой минимума заданной функции.
Что такое возрастание функции
В начале прочитаем определение возрастания функции.
Запомните!
![]()
Функция « y(x) » называется возрастающей на некотором промежутке, если
для любых
« x1 » и « x2 »
принадлежащих данному промежутку, таких, что « x2 > x1 »
выполняется неравенство
« y( x2 ) > y( x1 )».
Определение сложно понять без наглядного примера.
Поэтому сразу перейдём к разбору задачи на возрастание функции.
По-другому можно сказать, что, если каждому бóльшему значению « x »
соответствует бóльшее значение « y », значит,
функция « y(x) » возрастает.
|
x2 > x1 |
Обязательное условие возрастания функции |
Давайте разберем определение возрастания функции на конкретном примере.
Разбор примера
Возрастающей или убывающей является функция « y = 9x − 4 » ?
Для начала определим
область определения функции
« y = 9x − 4 ».
y = 9x − 4
D(y): x ∈ R ,
то есть « x » —
любое действительное число.
Построим график функции
« y = 9x − 4 ».
Так как функция
« y = 9x − 4 »
линейная, ее график — прямая.
Используем правила построения графика линейной функции. Нам достаточно найти две точки, чтобы построить ее график.
Область определения функции
« y = 9x − 4 » — все действительные числа,
поэтому можно подставить любое число вместо « x » и вычислить « y » по
формуле функции
« y = 9x − 4 ». Например, возьмем
« x = 0 ».
x = 0
y(x) = 9x − 4
y(0) = 9 · 0 − 4 = −4
Для второй точки возьмем « x = 1 ».
x = 1
y(x) = 9x − 4
y(1) = 9 · 1 − 4 = 5
Отметим две полученные
точки «(0; −4)» и «(1; 5)» на
координатной плоскости
и проведем через них прямую.
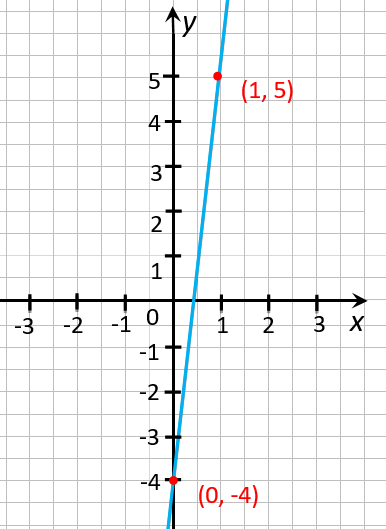
Докажем, что функция
« y = 9x − 4 » возрастает на всей своей области определения двумя способами: по ее графику и
аналитически
(по ее формуле).
Как определить по графику, что функция возрастает
По определению возрастания функции мы знаем, что
если « x » увеличивается,
то « y » тоже должен увеличиваться.
На рисунке ниже видно, что график функции « y = 9x − 4 »
«идет в гору». Другими словами, при увеличении « x »
↑ растет
значение « y » ↑.
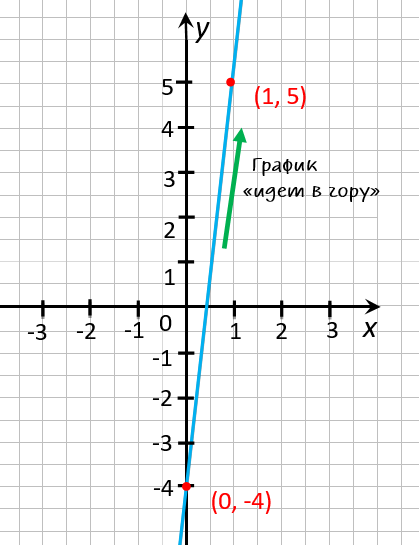
В этом можно убедиться, если взять две любые точки на графике. Например, точки, по
которым мы построили график функции. Назовем эти точки:
« (·)A » и « (·)B ».
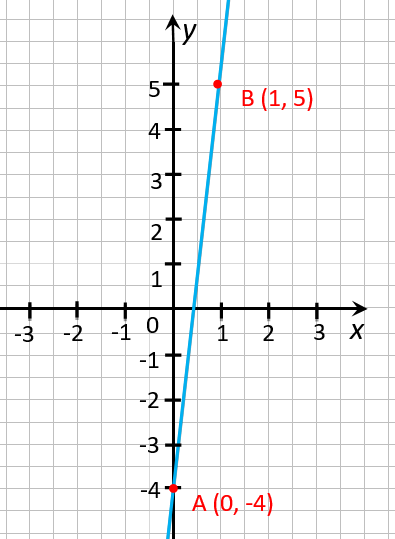
У первой точки « (·)A »
координаты:
x1 = 0 ; y1 = − 4
У второй точки « (·)B » координаты:
x2 = 1 ; y2 = 5
На примере точек « (·)A » и « (·)B » видно, что
при увеличении
« x ↑ ( x2 > x1 )»
растет
« y ↑ ( y2 > y1 ) ».
Поэтому график зрительно «идет в гору».
Как по формуле доказать, что функция возрастает
Вернёмся к нашей функции
« y = 9x − 4 ».
По графику мы поняли, что
функция « y = 9x − 4 » возрастает,
так как ее график «идет в гору».
Но как доказать по формуле, что функция
возрастает на всей своей области определения?
Запомните!
![]()
Функция возрастает на всей области определения, когда при
« x2 > x1 »
выполняется условие
« y( x2 ) > y( x1 ) ».
Формулировка выше не самая простая для понимания. Давайте разберем ее на практике.
По определению возрастания функции нам нужно доказать, что при
« x2 > x1 » увеличивается значение функции
« y( x2 ) > y( x1 ) ».
Но как нам найти значения функции
« y( x1 )» и
«y( x2 ) »?
Для нахождения « y( x1 )» и
«y( x2 ) »
достаточно подставить « x1 » и
« x2 » в исходную формулу « y = 9x − 4 ».
y( x1 ) = 9x1 − 4
y( x2 ) = 9x2 − 4
Теперь запишем обязательное условие возрастания функции.
|
x2 > x1 |
Обязательное условие возрастания функции |
Подставим в неравенство
« y( x2 ) >
y( x1 ) » полученные формулы
« y( x1 ) = 9x1 − 4» и
« y( x2 ) = 9x2 − 4 » .
y( x2 ) > y( x1 )
9x2 − 4 > 9x1 − 4
Упростим полученное
неравенство.
9x2 − 9x1 > − 4 + 4
9x2 − 9x1 > 0
Вынесем общий множитель
в левой части неравенства.
9(x2 − x1) > 0
Разделим левую и правую часть на «9».
При делении нуля на любое число получается ноль.
x2 − x1 > 0
x2 > x1
Мы доказали, что выполняется исходное условие возрастания функции «x2 > x1».
Отсюда следует, что функция
« y = 9x − 4 » возрастает на всей области определения.
В завершении вместо ответа следует написать фразу:
«Что и требовалось доказать».
Посмотрим другой пример, где требуется доказать, что функция возрастает.
Разбор примера
Доказать, что функция возрастает на всей области определения: y = 13x − 1
По аналогии с предыдущим примером составим неравенства, которые доказывают, что функция возрастает.
|
x2 > x1 |
Обязательное условие возрастания функции |
Вместо « y( x1 )» и
«y( x2 ) » запишем
формулу функции « y = 13x − 1 » и упростим полученное неравенство.
y( x2 ) > y( x1 )
13x2 − 1 > 13x1 − 1
13x2 − 13x1 > 1 − 1
13(x2 − x1) > 0 |: 13
>
x2 − x1 > 0
x2 > x1
Что и требовалось доказать.
Что такое убывание функции
Запомните!
![]()
Функция « y(x) » называется убывающей на некотором промежутке, если для любых
« x1 » и « x2 »
принадлежащих данному промежутку, таких,
что « x2 > x1 »
выполняется неравенство « y( x2 ) < y( x1 )».
|
x2 > x1 |
Обязательное условие убывания функции |
Как по графику понять, что функция убывает
Разбор примера
Доказать, что функция убывает на всей области определения: y = 1 − 3x
По определению убывания функции мы знаем, что,
если « x »
↑ растет, то
« y » ↓ должен уменьшаться.
Построим график функции
« y = 1 − 3x ». Ее график — прямая, поэтому нам будет достаточно двух точек.
Область определения функции
« y = 1 − 3x » — все действительные числа,
поэтому можно поставить любое число вместо « x » и вычислить « у » по
формуле функции
« y = 1 − 3x ». Например, возьмем
« x = 0 »
и « x = 1 ».
x = 0
y(x) = 1 − 3x
y(0) = 1 − 3 · 0 = 1
(·) А (0; 1)
x = 1
y(1) = 1 − 3x
y(1) = 1 − 3 · 1 = 1 − 3 = −2
(·) B (1; −2)
Построим график функции
« y = 1 − 3x » по полученным точкам
« (·)A » и « (·)B ».
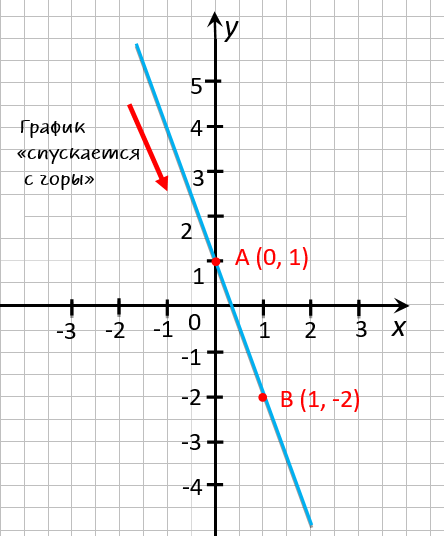
На графике функции видно, что зрительно график «спускается с горы», то есть функция убывает. Другими словами, при увеличении
« x »
↑ уменьшается
значение
« y » ↓.
Как по формуле доказать, что функция убывает
Вернёмся к нашей функции
« y = 1 − 3x ».
По ее графику мы поняли, что функция убывает, так как график «спускается с горы». Но как доказать по формуле,
что функция « y = 1 − 3x » убывает на всей области определения?
Запомните!
![]()
Чтобы доказать, что функция убывает требуется доказать, что при любых
« x2 > x1 » выполняется
« y( x2 ) < y( x1 ) ».
Давайте разберем на примере функции
« y = 1 − 3x ». Докажем, что она убывает
на всей своей области определения.
|
x2 > x1 |
Обязательное условие убывания функции |
Подставим « y( x1 )» и
«y( x2 ) » в
формулу функции « y = 1 − 3x » и упростим полученное неравенство.
y( x2 ) < y( x1 )
1 − 3x2 < 1 − 3x1
3x1 − 3x2 < 1 − 1
3(x1 − x2) < 0 | :3
<
x1 − x2 < 0
−x2 < −x1
Умножим на « −1 » левую и правую часть неравенства. При
умножении неравенства на отрицательное число знак неравенства поменяется на
противоположный.
−x2 < −x1 | · (−1)
x2 > x1
Что и требовалось доказать.
Как по графику функции определить
возрастание и убывание
Потренируемся только по графику функции определять промежутки возрастания и убывания функции.
Разбор примера
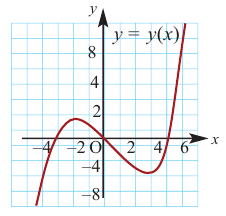
На рисунке ниже изображён график функции, определенной на множестве действительных чисел.
Используя график, найдите промежутки возрастания и промежутки убывания функции.
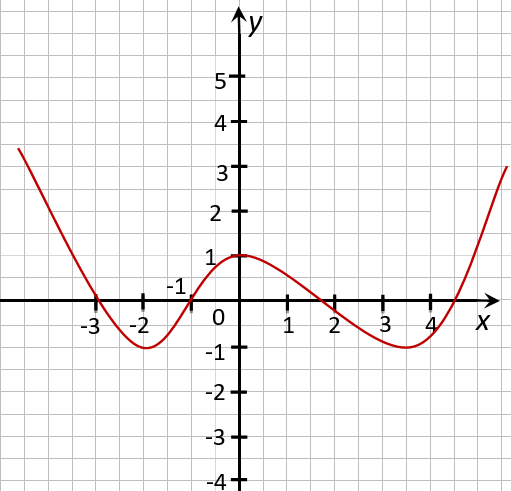
Отметим с помощью штриховых линий промежутки, где график функции убывает
(«спускается с горы») и где он возрастает («идет в гору»).
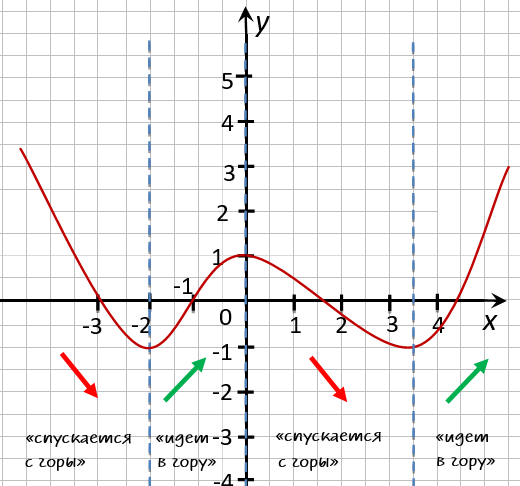
Запишем через знаки неравенств,
какие значения принимает « x » на полученных промежутках.
Обратите внимание, что во всех случаях при указании промежутков, мы указываем, что их
концы входят в промежуток, то есть используем знаки нестрогого неравенства.
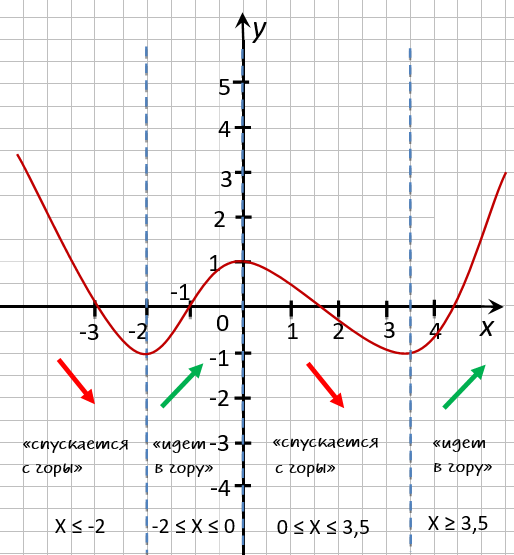
Остаётся записать полученные промежутки возрастания и убывания функции в ответ.
Ответ:
- функция убывает при
x ≤ −2; 0 ≤ x ≤ 3,5 - функция возрастает при
−2 ≤ x ≤ 0 ; x ≥ 3,5
Более грамотно будет записать ответ с помощью специальных
математических символов.
Ответ:
- функция убывает на промежутках
x ∈ (−∞ ; −2] ∪ [0; 3,5] - функция возрастает на промежутках x ∈ [−2 ; 0] ∪ [3,5 ; +∞]
При каких значениях
« m »
функция является убывающей или возрастающей
Ещё один тип заданий, в которых требуется определить,
при каких
« m » ( « а, b » или других буквах) функция убывает или возрастает.
Разбор примера
При каких значениях « m » функция
« y = mx − m − 3 + 2x » является убывающей?
Обратимся снова к определению убывания функции. Вспомним, как записать условия убывания функции с точки зрения формул.
|
x2 > x1 |
Обязательное условие убывания функции |
Запишем эти условия, используя формулу функции « y = mx − m − 3 + 2x », заданную в
задаче. Вместо
« x »
подставим « x1 » и « x2 ».
y( x2 ) < y( x1 )
mx2 − m − 3 + 2x2 < mx1 − m − 3 + 2x1
Упростим полученное неравенство. Перенесем из правой части все члены неравенства в левую часть с противоположными знаками.
mx2 − m − 3 + 2x2 − mx1
+ m
+ 3
− 2x1
< 0
Упростим полученное выражение. Некоторые члены неравенства взаимоуничтожатся.
mx2 − mx1
− m + m − 3 + 3 + 2x2 − 2x1
< 0
mx2 − mx1 + 2x2 − 2x1
< 0
Вынесем общие множители за скобки.
m( x2 − x1) + 2(x2 − x1)
< 0
Теперь
вынесем общий множитель
« ( x2 − x1 ) ».
( x2 − x1) (m + 2)
< 0
Вспомним обязательное условие убывания функции.
|
x2 > x1 |
Обязательное условие убывания функции |
Преобразуем исходное условие убывания функции « x2 > x1 ».
Перенесем все в левую часть.
x2 > x1
x2 − x1 > 0
По условию убывания функции
« x2 − x1 > 0 »,
значит, чтобы
произведение
«( x2 − x1) (m + 2)
» было меньше нуля, требуется, чтобы множитель «(m + 2)» был меньше нуля. Так как по
правилу знаков:
плюс на минус даёт минус.
| + | · | − | < 0 |
| (x2 − x1) | · | (m + 2) | < 0 |
Решим полученное неравенство.
m + 2 < 0
m < −2
Ответ: при «m < −2» функция
« y = mx − m − 3 + 2x »
является убывающей.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Алгебра и начала математического анализа, 11 класс
Урок №15. Возрастание и убывание функции.
Перечень вопросов, рассматриваемых в теме
1) Нахождение промежутков монотонности функции,
2) Определение алгоритма нахождения промежутков возрастания и убывания функции,
3) Решение задачи на нахождения промежутков возрастания и убывания функции
Глоссарий по теме
Алгоритм нахождения промежутков возрастания и убывания функции y = f(x)
- Найти D(f)
- Найти f‘(x).
- Определить, при каких значениях хf‘(x) ≥ 0 (на этих промежутках функция возрастает); при каких значениях х f‘(x) ≤ 0 (на этих промежутках функция убывает))
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
1. Функция y = f(x), определенная на промежутке Х, называется возрастающей на этом промежутке, если для любой пары чисел х1 и х2 из этого промежутка из неравенства х1< х2 следует неравенство f(x1) <f(x2)
2. Функция y = f(x), определенная на промежутке Х, называется убывающей на этом промежутке, если для любой пары чисел х1 и х2 из этого промежутка из неравенства х1< х2 следует неравенство f(x1) >f(x2)
Теоремы
- Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≥ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек),то функция y = f(x) возрастает на промежутке Х.
- Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≤ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек),то функция y = f(x) убывает на промежутке Х.
Примеры и разбор решения заданий тренировочного модуля
№1. Определите промежутки монотонности функции
у = -3х3 + 4х2 + х – 10.
Решение
1.Найдем область определения функции.
D(y) = 
2.Найдем производную функции.

y’ = (x – 1)(-9x – 1)
3.Определим, на каких промежутках производная положительна (на этих промежутках функция возрастает), на каких – отрицательна (на этих промежутках функция убывает).
Применим для этого метод интервалов. Для определения знака на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.

Так как на интервале  производная функции отрицательна, то на этом интервале функция убывает.
производная функции отрицательна, то на этом интервале функция убывает.
Так как на интервале  производная функции положительна, то на этом интервале функция возрастает.
производная функции положительна, то на этом интервале функция возрастает.
Так как на интервале  производная функции отрицательна, то на этом интервале функция убывает.
производная функции отрицательна, то на этом интервале функция убывает.
Так как в точках  функция непрерывна, то эти точки входят в промежутки возрастания и убывания данной функции.
функция непрерывна, то эти точки входят в промежутки возрастания и убывания данной функции.
Следовательно, функция возрастает на  ; функция убывает на
; функция убывает на  и на
и на  .
.
Ответ: Функция возрастает на 
Функция убывает на  и на
и на  .
.
№2. Определите промежутки монотонности функции
у = х5–5х4 +5х3 – 4.
Решение:
y‘ =
- Функция возрастает на
 ; функция убывает на
; функция убывает на  .
.
Ответ: Функция возрастает на  ;
;
функция убывает на  .
.
Исследовать функцию — это значит установить её свойства: указать её область определения и область значений; промежутки возрастания и убывания; промежутки, на которых функция приобретает положительные значения, на которых — отрицательные; выяснить, не является ли данная функция чётной или нечётной и т. д.
Содержание:
Что такое исследование функции
Одна из важных задач исследования функции — определение промежутков её возрастания и убывания. Как отмечалось, в тех точках, в которых функция возрастает, её производная (угловой коэффициент касательной) положительная, а в точках убывания функции её производная отрицательная {рис. 70).
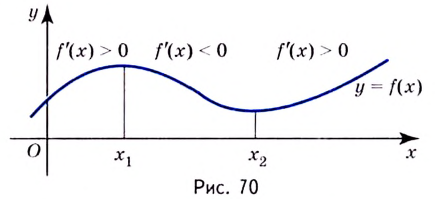
Правильными будут следующие утверждения.
- Если производная функции в каждой точке некоторого промежутка положительная, то функция на этом промежутке возрастает.
- Если производная в каждой точке промежутка отрицательная, то функция на этом промежутке убывает.
- Если производная в каждой точке промежутка тождественно равна нулю, то на этом промежутке функция постоянная.
Строгое доказательство этого утверждения достаточно громоздкое, поэтому мы его не приводим. Заметим только, что в нём выражается достаточный признак возрастания или убывания функции, но не необходимый. Поэтому функция может возрастать и на промежутке, в некоторых точках которого она не имеет производной. Например, функция 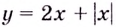
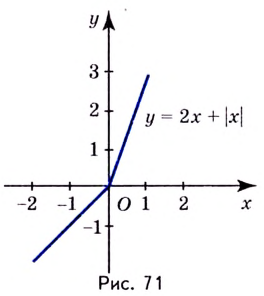
Из сказанного следует, что два соседних промежутка, на одном из которых функция возрастает, а на другом — убывает, могут разделяться только такой точкой, в которой производная функции равна нулю или не существует.
Внутренние точки области определения функции, в которых её производная равна нулю или не существует, называют критическими точками функции.
Следовательно, чтобы определить промежутки возрастания и убывания функции 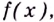 нужно решить неравенства
нужно решить неравенства 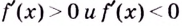 или найти все критические точки функции,разбить ими область определения функции на промежутки, а потом исследовать, на каких из них функция возрастает, а на каких — убывает.
или найти все критические точки функции,разбить ими область определения функции на промежутки, а потом исследовать, на каких из них функция возрастает, а на каких — убывает.
Пример:
Найдите промежутки возрастания и убывания функции 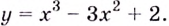
Решение:
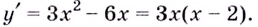
Уравнение 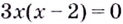 имеет корни
имеет корни 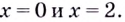 Это — критические точки. Область определения данной функции — множество
Это — критические точки. Область определения данной функции — множество 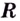 — они разбивают на три промежутка:
— они разбивают на три промежутка: 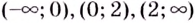 (рис. 72). Производная функции на этих промежутках имеет соответственно такие знаки:
(рис. 72). Производная функции на этих промежутках имеет соответственно такие знаки: 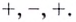 Следовательно, данная функция на промежутках
Следовательно, данная функция на промежутках 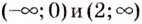 возрастает, а на
возрастает, а на 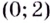 убывает.
убывает.
Замечание: Если функция непрерывна в каком-нибудь конце промежутка возрастания или убывания, то эту точку можно присоединить к рассматриваемому промежутку. Поскольку функция 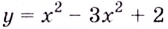 в точках 0 и 2 непрерывна, то можно утверждать, что она возрастает на промежутках
в точках 0 и 2 непрерывна, то можно утверждать, что она возрастает на промежутках 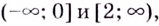 на
на 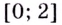 — убывает.
— убывает.
Пример:
Найдите промежутки убывания функции 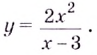
Решение:
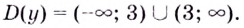
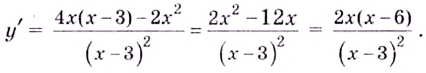
Критические точки: 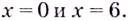 Они всю область определения функции разбивают на интервалы:
Они всю область определения функции разбивают на интервалы: 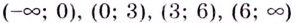 (рис. 73). Производная
(рис. 73). Производная 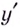 на этих промежутках имеет соответственно такие знаки:
на этих промежутках имеет соответственно такие знаки: 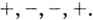 Следовательно, функция убывает на промежутках
Следовательно, функция убывает на промежутках 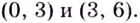 Поскольку в точках
Поскольку в точках 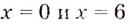 данная функция непрерывна, то ответ можно записать и так:
данная функция непрерывна, то ответ можно записать и так: 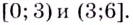
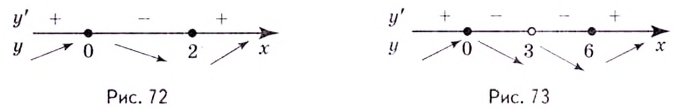
Пример:
Найдите критические точки функции 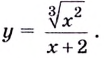
Решение:
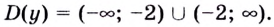 Найдем произвольную функции:
Найдем произвольную функции: 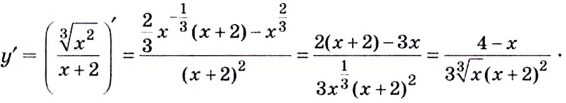
Найдём точки, в которых производная равна нулю или не существует: 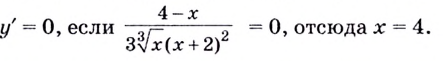
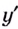 — не существует, если знаменатель равен нулю, отсюда
— не существует, если знаменатель равен нулю, отсюда 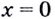 и
и 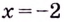 Точка
Точка  не входит в область определения функции. Следовательно, функция имеет две критические точки:
не входит в область определения функции. Следовательно, функция имеет две критические точки: 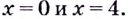
Ответ. 0 и 4.
Пример:
Докажите, что функция 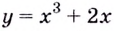 возрастает на
возрастает на 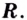
Решение:
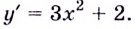 При любом значении
При любом значении 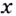 выражение
выражение 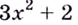 имеет положительное значение. Следовательно, данная функция возрастает на всей области определения, т.е. на множестве
имеет положительное значение. Следовательно, данная функция возрастает на всей области определения, т.е. на множестве 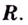
Пример:
Установите, на каком промежутке функция 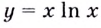 возрастает, а на каком убывает.
возрастает, а на каком убывает.
Решение:
Способ 1. 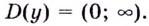 Найдём производную функции:
Найдём производную функции:
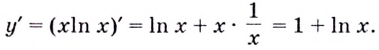
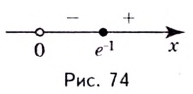
Найдём критические точки функции:
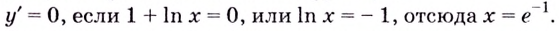
Эта точка разбивает область определения функции на два промежутка (рис. 74). Определим знак производной на каждом из них.
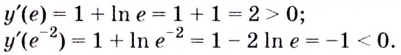
Следовательно, функция 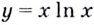 возрастает на промежутке
возрастает на промежутке 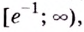 а убывает на
а убывает на 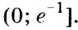
Способ 2. Решим неравенство 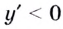 и
и 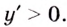
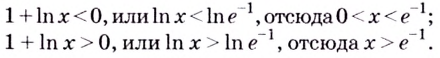
Ответ. Возрастает, если 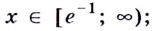 убывает если
убывает если 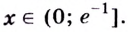
Применение второй производной к исследованию функций и построению их графиков
При помощи первой производной можно исследовать функцию на монотонность и экстремумы и схематично построить график. Оказывается, что поведение некоторых функций не всегда можно охарактеризовать, используя первую производную. Более детальное исследование проводится при помощи второй производной. Вспомним, что такое вторая производная.
Пусть функция 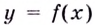 является дифференцируемой,
является дифференцируемой, 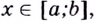 её производная
её производная 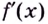 — функция, которая также дифференцируема. Тогда можно найти производную
— функция, которая также дифференцируема. Тогда можно найти производную 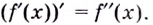 Это производная второго порядка, или вторая производная функции
Это производная второго порядка, или вторая производная функции 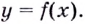
Например, найти производную 2-го порядка функции 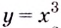
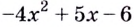 означает найти производную этой функции
означает найти производную этой функции 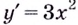
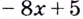 и полученную функцию продифференцировать:
и полученную функцию продифференцировать: 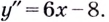
Кривая 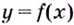 называется выпуклой на интервале
называется выпуклой на интервале 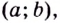 если все её точки, кроме точки касания, лежат ниже произвольной её касательной на этом интервале (на рис. 86 — 1).
если все её точки, кроме точки касания, лежат ниже произвольной её касательной на этом интервале (на рис. 86 — 1).
Кривая 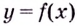 называется вогнутой на интервале
называется вогнутой на интервале 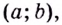 если все её точки, кроме точки касания, лежат выше произвольной её касательной на этом интервале (на рис. 86 — 2).
если все её точки, кроме точки касания, лежат выше произвольной её касательной на этом интервале (на рис. 86 — 2).
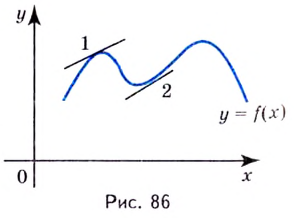
Точкой перегиба называется такая точка кривой, которая отделяет её выпуклую часть от вогнутой.
Интервалы выпуклости и вогнутости находят при помощи такой теоремы.
Теорема. Если вторая производная дважды дифференцируемой функции 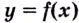 отрицательна
отрицательна 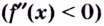 на интервале
на интервале 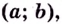 то кривая
то кривая 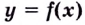 выпуклая на данном интервале; если вторая производная функции
выпуклая на данном интервале; если вторая производная функции 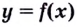 положительная
положительная 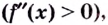 то кривая вогнутая на
то кривая вогнутая на 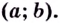
Из теоремы следует, что точками перегиба кривой 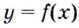 могут быть только точки, в которых вторая производная
могут быть только точки, в которых вторая производная 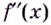 равна нулю или не существует. Такие точки называют критическими точками второго рода.
равна нулю или не существует. Такие точки называют критическими точками второго рода.
Установим до статочное условие существования точки перегиба.
Теорема. Пусть 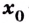 — критическая точка второго рода функции
— критическая точка второго рода функции 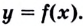 Если при переходе через точку
Если при переходе через точку 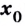 производная
производная 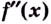 меняет знак, то точка
меняет знак, то точка 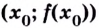 является точкой перегиба кривой
является точкой перегиба кривой 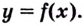
Для нахождения промежутков выпуклости и точек перегиба графика функции целесообразно пользоваться следующей схемой:
- найти область определения функции;
- найти критические точки второго рода;
- определить знак второй производной на образованных интервалах. Если
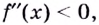 то кривая выпуклая; если
то кривая выпуклая; если 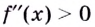 — кривая вогнутая;
— кривая вогнутая; - если производная
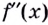 меняет знак при переходе через точку
меняет знак при переходе через точку 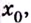 то точка
то точка 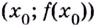 является точкой перегиба кривой
является точкой перегиба кривой 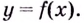
Пример №1
Найдите интервалы выпуклости, вогнутости и точки перегиба кривой 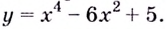
Решение:
1) Область определения функции: 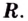
2) Найдём вторую производную: 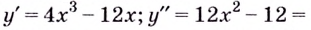
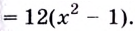 Критические точки второго рода:
Критические точки второго рода: 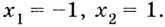 Других критических точек нет.
Других критических точек нет.
3) Разбиваем область определения на интервалы 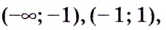
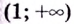 и определяем знак второй производной на каждом из них.
и определяем знак второй производной на каждом из них.
Если 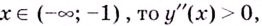 поэтому кривая вогнутая.
поэтому кривая вогнутая.
Если 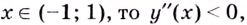 поэтому кривая выпуклая.
поэтому кривая выпуклая.
Если 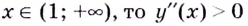 — кривая вогнутая.
— кривая вогнутая.
Следовательно, точки 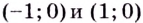 — точки перегиба кривой. Рассмотрим ещё один компонент в исследовании функций, благодаря которому упрощается построение некоторых графиков. Это асимптоты. В предыдущих параграфах рассматривались горизонтальные и вертикальные асимптоты. Повторим, расширим и обобщим это понятие. Асимптоты бывают вертикальные, наклонные и горизонтальные (рис. 87).
— точки перегиба кривой. Рассмотрим ещё один компонент в исследовании функций, благодаря которому упрощается построение некоторых графиков. Это асимптоты. В предыдущих параграфах рассматривались горизонтальные и вертикальные асимптоты. Повторим, расширим и обобщим это понятие. Асимптоты бывают вертикальные, наклонные и горизонтальные (рис. 87).
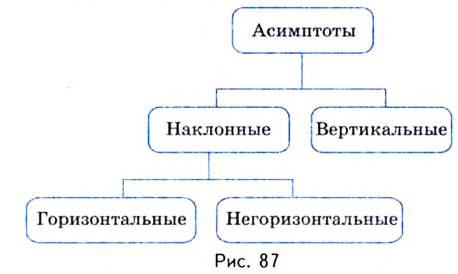
Напомним, что прямая 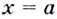 будет вертикальной асимптотой кривой
будет вертикальной асимптотой кривой 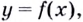 если при
если при 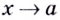 (справа или слева) значение функции
(справа или слева) значение функции 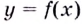 стремится к бесконечности, т.е. выполняется одно из условий:
стремится к бесконечности, т.е. выполняется одно из условий: 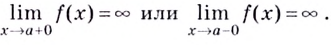
Уравнение наклонной асимптоты: 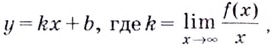
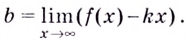
Если записанные пределы существуют, то существует наклонная асимптота; если хотя бы один из них не существует или равен 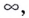 то кривая наклонной асимптоты не имеет.
то кривая наклонной асимптоты не имеет.
Если 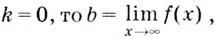 поэтому
поэтому 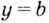 — уравнение горизонтальной асимптоты.
— уравнение горизонтальной асимптоты.
Замечание: Рассмотренные пределы могут быть односторонними, а под символом 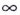 следует понимать и
следует понимать и 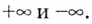 При этом указанные пределы могут быть разными при
При этом указанные пределы могут быть разными при 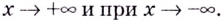
Пример №2
Найдите асимптоты кривых:
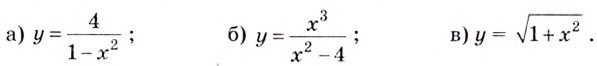
Решение:
а) 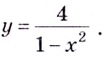 Найдём вертикальные асимптоты. Поскольку функция не определена в точках
Найдём вертикальные асимптоты. Поскольку функция не определена в точках 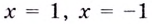 и
и 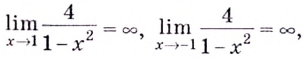 то прямые
то прямые 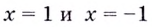 — вертикальные асимптоты.
— вертикальные асимптоты.
Найдём наклонную асимптоту: 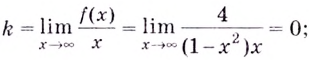
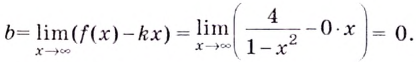 Кривая имеет горизонтальную асимптоту, её уравнение:
Кривая имеет горизонтальную асимптоту, её уравнение: 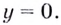
Следовательно, заданная кривая имеет три асимптоты: 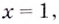
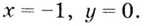
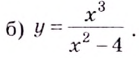 Найдем вертикальные асимптоты.
Найдем вертикальные асимптоты.
Поскольку функция не определена в точках 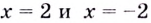 и
и 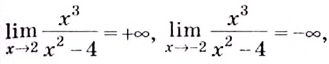 то прямые
то прямые 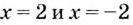 — вергикальные асимптоты.
— вергикальные асимптоты.
Для наклонной асимптоты 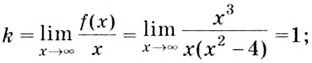
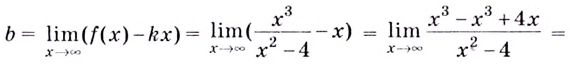
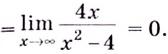
Значит прямая 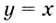 — наклонная асимптота. Горизонтальной асимптоты нет.
— наклонная асимптота. Горизонтальной асимптоты нет.
Итак, асимптоты кривой: 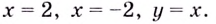
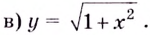 Будем искать наклонные асимптоты:
Будем искать наклонные асимптоты:
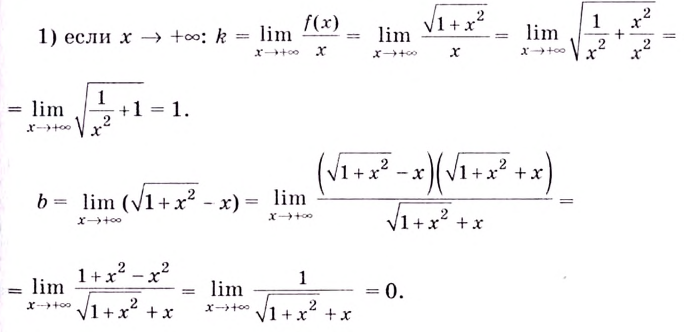
Следовательно, 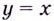 — наклонная асимптота, если
— наклонная асимптота, если 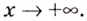
2) если 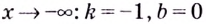 (проверьте самостоятельно), отсюда
(проверьте самостоятельно), отсюда  — наклонная асимптота, если
— наклонная асимптота, если 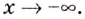
Следовательно, заданная кривая имеет две асимптоты: 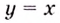
Определение точек перегиба, интервалов выпуклости и асимптот существенно помогает в построении графиков различных функций.
Нахождение промежутков возрастания и убывания функции
Интервалы возрастания и убывания функции
возрастающая функция
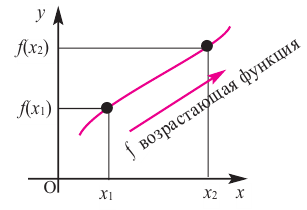
Если для любых 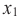 и
и 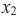 из некоторого промежутка области определения при
из некоторого промежутка области определения при 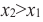 выполняется условие
выполняется условие 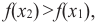 то на этом промежутке функция возрастающая.
то на этом промежутке функция возрастающая.
убывающая
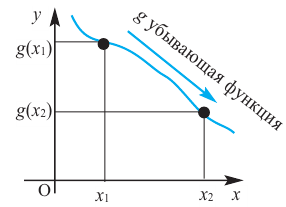
Если для любых 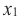 и
и 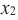 из некоторого промежутка области определения при
из некоторого промежутка области определения при 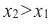 выполняется условие
выполняется условие 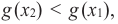 на этом промежутке функция убывающая.
на этом промежутке функция убывающая.
Связь промежутков возрастания и убывания функции с угловым коэффициентом секущей можно выразить следующим образом.
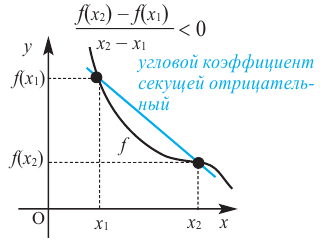
Если на заданном промежутке угловой коэффициент любой секущей положителен, то на этом промежутке функция  возрастает.
возрастает.
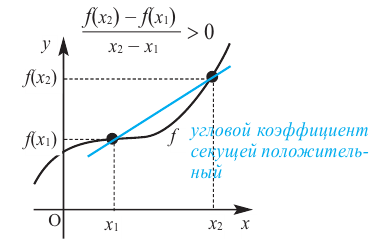
Если на заданном промежутке угловой коэффициент любой секущей отрицателен, то на этом промежутке функция  убывает.
убывает.
Промежутки возрастания и убывания функции
Пусть на определенном промежутке производная функции 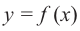 положительна, т. е.
положительна, т. е. 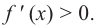 Так как
Так как 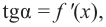 то угловой коэффициент касательной будет положительным. А это значит, что касательная с положительным направлением оси абсцисс образует острый угол и на заданном промежутке график “поднимается “, т. е. функция возрастает. Если
то угловой коэффициент касательной будет положительным. А это значит, что касательная с положительным направлением оси абсцисс образует острый угол и на заданном промежутке график “поднимается “, т. е. функция возрастает. Если 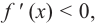 тогда касательная с положительным направлением оси абсцисс образует тупой угол, график “спускается”, т. е. функция убывает.
тогда касательная с положительным направлением оси абсцисс образует тупой угол, график “спускается”, т. е. функция убывает.
Теорема. Если функция 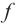 дифференцируема в каждой точке заданного промежутка, то:
дифференцируема в каждой точке заданного промежутка, то:
Примечание: если функция 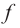 непрерывна в каком-либо из концов промежутка возрастания (убывания), то эту точку присоединяют к этому промежутку.
непрерывна в каком-либо из концов промежутка возрастания (убывания), то эту точку присоединяют к этому промежутку.
По графику функции 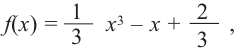 исследуйте промежутки возрастания и убывания функции.
исследуйте промежутки возрастания и убывания функции.
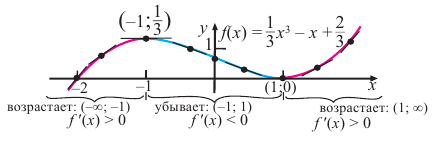
На интервалах 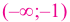 и
и 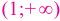 угловой коэффициент касательной положительный, поэтому на каждом из промежутков
угловой коэффициент касательной положительный, поэтому на каждом из промежутков 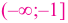 и
и 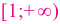 функция
функция 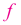 возрастает.
возрастает.
На интервале 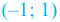 угловой коэффициент касательной отрицателен, поэтому на промежутке
угловой коэффициент касательной отрицателен, поэтому на промежутке 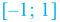 функция
функция 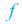 убывает.
убывает.
Пример №3
При помощи производной определите промежутки возрастания и убывания функции 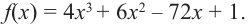
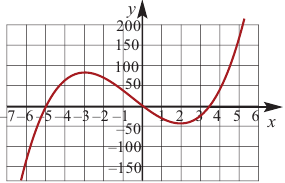
Решение: 1. Алгебраический метод.
Найдем производную функции
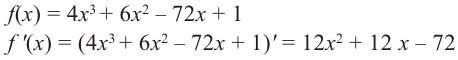
Функция 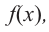 на промежутке удовлетворяющем неравенству
на промежутке удовлетворяющем неравенству 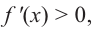 т. е.
т. е. 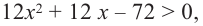 возрастает.
возрастает.
Для решения неравенства сначала надо решить соответствующее уравнение
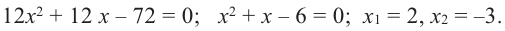
Значит, при 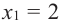 и
и 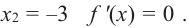 Точки
Точки 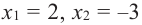 разбивают область определения функции на три интервала:
разбивают область определения функции на три интервала: 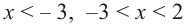 и
и 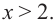 В каждом из интервалов выберем контрольную точку для проверки и установим знак производной.
В каждом из интервалов выберем контрольную точку для проверки и установим знак производной.

Из таблицы и непрерывности функции 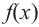 видно, что данная функция возрастает на промежутках
видно, что данная функция возрастает на промежутках 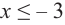 и
и 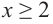 и убывает на промежутке
и убывает на промежутке 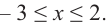 Из графика так же видно, что задания решение верно.
Из графика так же видно, что задания решение верно.
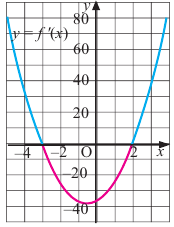
2. Промежутки возрастания и убывания функции можно определить но графику производной. На рисунке изображен график производной
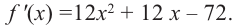
График производной 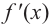 при
при 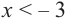 и
и 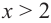 расположен выше оси
расположен выше оси 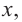 значит,
значит, 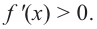 При
При 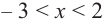 график производной расположен ниже оси
график производной расположен ниже оси 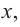 значит
значит 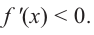 Так как функция
Так как функция 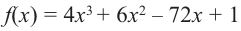 в точках
в точках 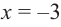 и
и 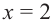 непрерывна, то на промежутках
непрерывна, то на промежутках 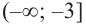 и
и 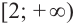 она возрастает, а на промежутке
она возрастает, а на промежутке 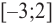 убывает.
убывает.
Пример №4
Изобразите схематично график непрерывной функции согласно еле дующим условиям:
a) при 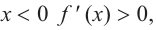 при
при 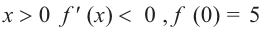
b) при 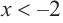 или
или 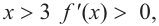 при
при 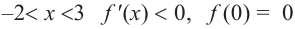
Решение:
а) при 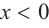 знак производной положительный:
знак производной положительный: 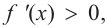 значит,
значит,
функция возрастает. При 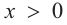 знак производной отрицательный:
знак производной отрицательный: 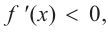 значит, функция убывает, при
значит, функция убывает, при 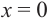 значение функции равно 5.
значение функции равно 5.
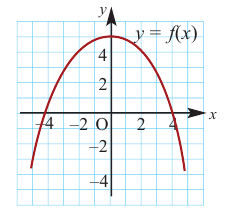
b) При 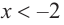 и
и 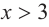 знак производной положительный:
знак производной положительный: 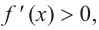 значит, функция возрастает. При
значит, функция возрастает. При 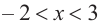 знак производной отрицательный:
знак производной отрицательный: 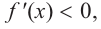 значит, функция убывает, при
значит, функция убывает, при 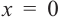 значение функции равно 0.
значение функции равно 0.
Критические точки и экстремумы функции
В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.
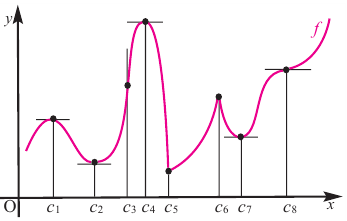
1. Для значений 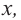 равных
равных 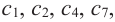
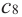 угловой коэффициент касательной к графику равен 0. Т. e.
угловой коэффициент касательной к графику равен 0. Т. e.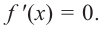 Эти точки являются критическими точками функции.
Эти точки являются критическими точками функции.
2. В точках 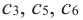 функция не имеет производной. Эти тоже критические точки функции.
функция не имеет производной. Эти тоже критические точки функции.
3. Для рассматриваемой нами функции критические точки 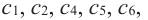
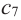 делят ее область определения на чередующиеся интервалы возрастания и убывания. Точки
делят ее область определения на чередующиеся интервалы возрастания и убывания. Точки 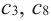 – критические точки, которые не изменяют возрастание и убывание (или наоборот).
– критические точки, которые не изменяют возрастание и убывание (или наоборот).
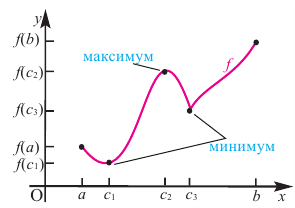
По графику видно, что в точках внутреннего экстремума(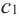 и
и 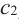 ) производная функции равна нулю, а в точке
) производная функции равна нулю, а в точке 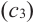 производная не существует. Точки, в которых производная функции равна нулю, также называются стационарными точками.
производная не существует. Точки, в которых производная функции равна нулю, также называются стационарными точками.
Теорема Ферма (Необходимое условие существовании экстремумов)
Во внутренних точках экстремума производная либо равна нулю, либо не существует.
Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке 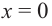 производная функции
производная функции 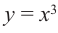 равна нулю, но эта точка не является ни точкой максимума, ни точкой минимума.
равна нулю, но эта точка не является ни точкой максимума, ни точкой минимума.
На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т. е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.
Достаточное условие существования экстремума
Пусть функция 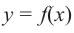 непрерывна на промежутке
непрерывна на промежутке 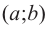 и
и 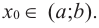 Если
Если 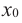 является критической точкой, в окрестности которой функция дифференцируема, то, если в этой окрестности:
является критической точкой, в окрестности которой функция дифференцируема, то, если в этой окрестности:
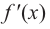 слева от точки
слева от точки 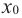 положительна, а справа – отрицательна, то точка
положительна, а справа – отрицательна, то точка 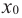 является точкой максимума.
является точкой максимума.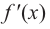 слева от
слева от 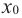 отрицательна, а справа – положительна, то точка
отрицательна, а справа – положительна, то точка 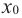 является точкой минимума
является точкой минимума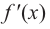 с каждой стороны от точки
с каждой стороны от точки 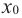 имеет одинаковые знаки, то точка
имеет одинаковые знаки, то точка 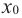 не является точкой экстремума.
не является точкой экстремума.
Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.
Соответствующие наибольшее и наименьшее значения функции 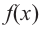 на отрезке
на отрезке 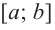 записываются как
записываются как 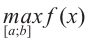 и
и 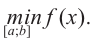
Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.
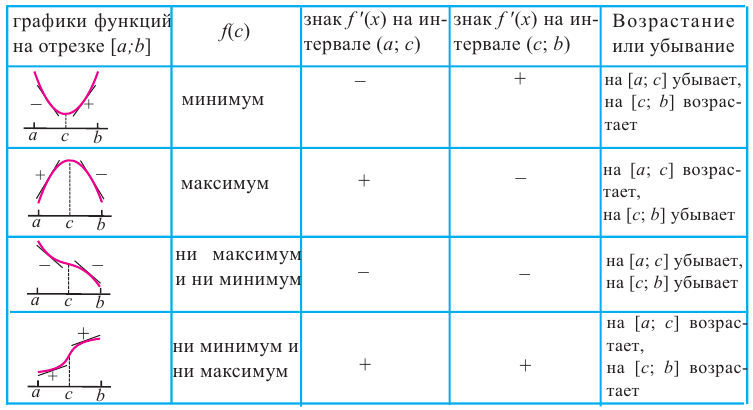
Пример №5
Для функции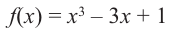 определите максимумы и минимумы и схематично изобразите график.
определите максимумы и минимумы и схематично изобразите график.
Решение: Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.
1. Производная функции: 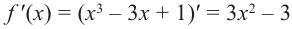
2. Критические точки функции: 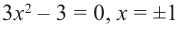
3. Точки 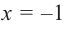 и
и 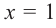 разбивают область определения функции на три промежутка.
разбивают область определения функции на три промежутка.
Проверим знак 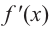 на интервалах, выбрав пробные точки:
на интервалах, выбрав пробные точки:
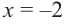 для интервала
для интервала 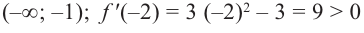
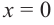 для интервала
для интервала 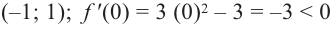
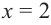 для интервала
для интервала 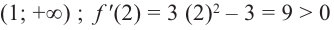
 При
При 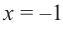 имеем
имеем 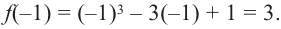
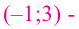 максимум
максимум
При 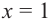 имеем
имеем 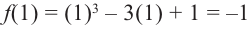
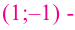 минимум
минимум
4. Используя полученные для функции 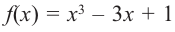 данные и найдя координаты нескольких дополнительных точек, построим график функции.
данные и найдя координаты нескольких дополнительных точек, построим график функции.

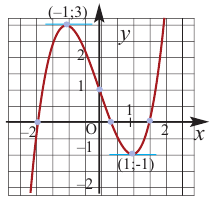
Пример №6
Найдите наибольшее и наименьшее значение функции 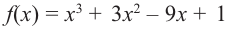 на отрезке
на отрезке 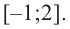
Решение: Сначала найдем критические точки.
Так как 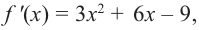 то критические точки можно найти из уравнения
то критические точки можно найти из уравнения 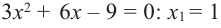 и
и 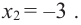 Критическая точка
Критическая точка 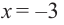 не принадлежит данному отрезку
не принадлежит данному отрезку 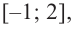 и поэтому мы ее не рассматриваем. Вычислим значение заданной функции в точке
и поэтому мы ее не рассматриваем. Вычислим значение заданной функции в точке 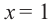 и на концах отрезка.
и на концах отрезка.
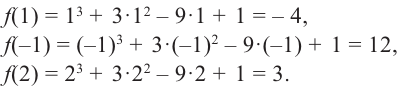
Из этих значений наименьшее – 4, наибольшее 12. Таким образом:
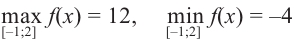
Пример №7
Найдите экстремумы функции 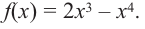
Решение: 1. Производная функции: 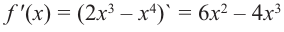
2. Критические точки: 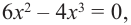
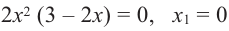 и
и 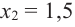
3. Интервалы, на которые критические точки делят область определения функции:
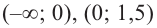 и
и 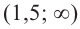
Проверим знак 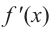 на интервалах, выбрав пробные точки.
на интервалах, выбрав пробные точки.
Для промежутка 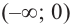 возьмем
возьмем 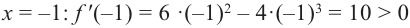
Для промежутка 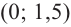 возьмем
возьмем 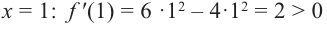
Для промежутка 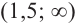 возьмем
возьмем 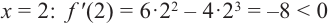

Используя полученную для функции 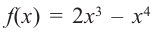 информацию и найдя значение функции еще в нескольких точках, можно построить график функции. При этом следует учитывать, что в точках с абсциссами
информацию и найдя значение функции еще в нескольких точках, можно построить график функции. При этом следует учитывать, что в точках с абсциссами 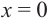 и
и 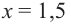 касательная к графику горизонтальна. Построение графика можно проверить при помощи графкалькулятора.
касательная к графику горизонтальна. Построение графика можно проверить при помощи графкалькулятора.
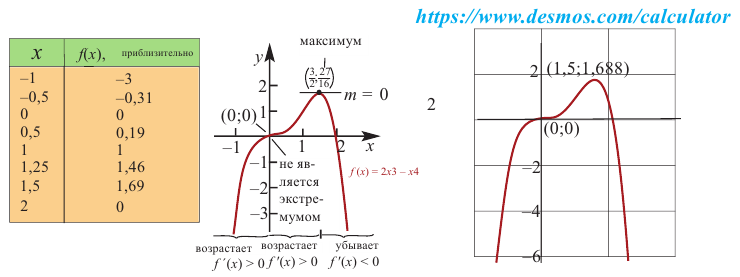
Пример №8
Найдите экстремумы функции 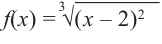
Решение: 1. Производная 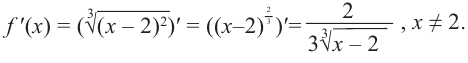
2. Критические точки: для этого надо решить уравнение 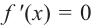 или найти точки, в которых производная не существует. В точке
или найти точки, в которых производная не существует. В точке 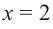 функция не имеет конечной производной. Однако точка
функция не имеет конечной производной. Однако точка 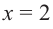 принадлежит области определения. Значит, точка
принадлежит области определения. Значит, точка 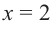 является критической точкой функции.
является критической точкой функции.
3. Промежутки, на которые критическая точка делит область определения функции: 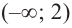 и
и 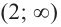
Определим знак 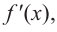 выбрав пробные точки для каждого промежутка:
выбрав пробные точки для каждого промежутка:
Для 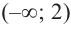 возьмем
возьмем 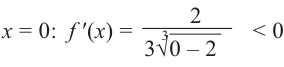
Для 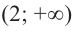 возьмем
возьмем 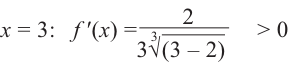

Пример №9
По графику функции производной 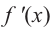 схематично изобразите график самой функции.
схематично изобразите график самой функции.
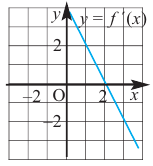
Решение:
Производная 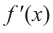 в точке
в точке 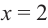 равна нулю, а при
равна нулю, а при 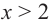 отрицательна, значит, на интервале
отрицательна, значит, на интервале 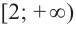 функция убывающая. При
функция убывающая. При 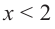 производная положительна, а это говорит о том, что функция/на промежутке
производная положительна, а это говорит о том, что функция/на промежутке 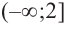 возрастает. Точкой перехода от возрастания к убыванию функции является точка
возрастает. Точкой перехода от возрастания к убыванию функции является точка  Соответствующий график представлен на рисунке.
Соответствующий график представлен на рисунке.
- Заказать решение задач по высшей математике
Построение графиков функции с помощью производной
Функция – многочлен определена и непрерывна на всей числовой оси.
Чтобы построить график функции- многочлен надо выполнить следующие шаги.
- Определите точки пересечения с осями координат.
- Найдите критические точки.
- Найдите промежутки возрастания и убывания функции.
- Найдите максимумы и минимумы.
- Постройте график.
Пример:
Постройте график функции 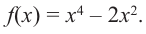
1) Точки пересечения с осями координат :
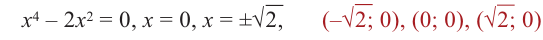
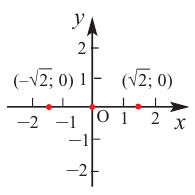
2) Критические точки ( точки, в которых производная равна нулю): 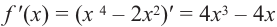
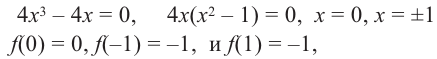
значит, точки 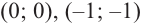 и
и 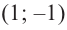 расположены на графике.
расположены на графике.
3) Промежутки возрастания и убывания. Экстремумы.
Критические точки 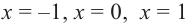 деляг область определения функции на четыре промежутка. Проверим знаки производной
деляг область определения функции на четыре промежутка. Проверим знаки производной 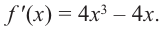

4) Используя полученную информацию, построим график функции.
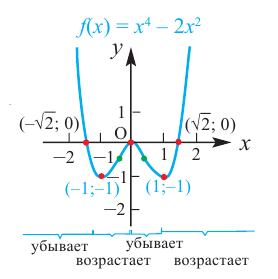
Чтобы построить график рациональной функции надо выполнить следующие шаги.
- Найдите область определения.
- Найдите асимптоты (если они есть).
- Определите точки пересечения с осями координат.
- Найдите критические точки.
- Найдите промежутки возрастания и убывания и экстремумы.
- Постройте график.
Пример:
Постройте график функции 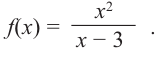
1) Область определения функции: 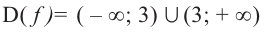
2) Асимптоты: 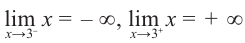
Прямая 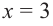 вертикальная асимптота функции.
вертикальная асимптота функции.
Так как степень многочлена в числителе больше степени многочлена в знаменателе, рациональная функция не имеет горизонтальной асимптоты. Однако, записав следующее: 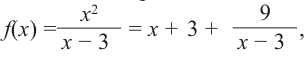
условии  имеем
имеем 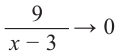 т. е. график функции
т. е. график функции 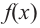 бесконечно приближается к прямой
бесконечно приближается к прямой 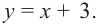 В этом случае прямая
В этом случае прямая 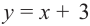 является наклонной асимптотой функции
является наклонной асимптотой функции 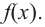 Вообще, если степень многочлена
Вообще, если степень многочлена 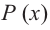 на 1 единицу больше степени многочлена
на 1 единицу больше степени многочлена 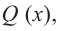 то рациональная функция
то рациональная функция 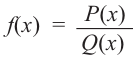 имеет наклонную асимптоту.
имеет наклонную асимптоту.
3) Точки пересечения с осями координат: 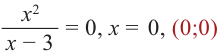
4) Критические точки:
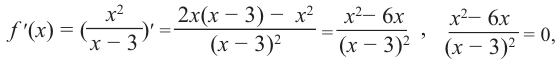
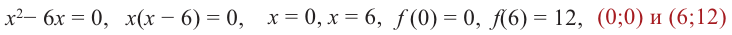
5) Промежутки возрастания и убывания: в точке 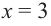 функция не определена, точки
функция не определена, точки 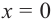 и
и 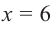 являются критическими точками функции. Определим знаки производной в каждом полученном интервале.
являются критическими точками функции. Определим знаки производной в каждом полученном интервале.

6) Построим график. Отметим на координатной плоскости точки 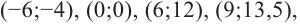 относящиеся к графику. Проведем вертикальную асимптоту
относящиеся к графику. Проведем вертикальную асимптоту 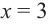 и наклонную асимптоту
и наклонную асимптоту 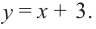 Используя полученные результаты, изобразим график функции.
Используя полученные результаты, изобразим график функции.
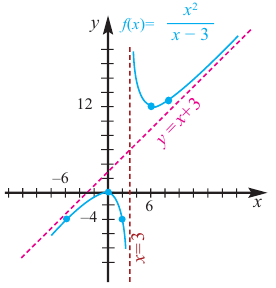
Обратите внимание! В области, близкой к точке 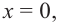 график функции ведет себя как парабола
график функции ведет себя как парабола 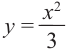
Задачи на экстремумы. Оптимизации
В реальной жизненной ситуации возникает необходимость выбора оптимального варианта и нахождения экстремумов определенной функции. Ежедневно, при решении проблем в различных областях, мы сталкиваемся с терминами наибольшая прибыль, наименьшие затраты, наибольшее напряжение, наибольший объем, наибольшая площадь и т.д. Большое экономическое значение в промышленности, при определении дизайна упаковки, имеет вопрос, как подобрать размеры упаковки с наименьшими затратами. Такого рода задания связаны с нахождением максимального или минимального значения величины. Задачи на нахождение максимального и минимального значения величины называются задачами на оптимизацию. Для решения данных задач применяется производная.
Замечание 1: На интервале 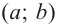 должны учитываться предельные значения функции на концах.
должны учитываться предельные значения функции на концах.
Замечание 2: В рассматриваемом интервале может быть одна стационарная точка: или точка максимума, или точка минимума. В этом случае, в точке максимума функция принимает наибольшее значение, а в точке минимума – наименьшее значение.
Пример 1. Максимальный объем. Фирма планирует выпуск коробки без крышки, с квадратным основанием и площадью поверхности 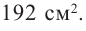 Найдите размеры коробки, при которых она будет иметь наибольший объем?
Найдите размеры коробки, при которых она будет иметь наибольший объем?
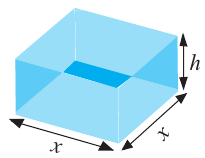
Решение:
Так как основанием коробки является квадрат, то ее объем можно вычислить по формуле 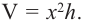 Используя другие данные задачи, выразим объем только через одну переменную
Используя другие данные задачи, выразим объем только через одну переменную 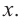 Вычислим площадь поверхности коробки. Она равна
Вычислим площадь поверхности коробки. Она равна 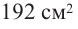 и состоит из 4 площадей боковых граней + площадь основания.
и состоит из 4 площадей боковых граней + площадь основания.
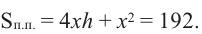
Тогда выразим 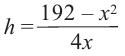 подставим в формулу
подставим в формулу 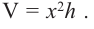 Зависимость объема коробки от переменной
Зависимость объема коробки от переменной 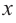 можно выразить следующим образом:
можно выразить следующим образом:
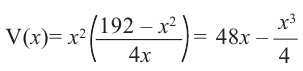
Теперь найдем область определения функции 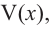 согласно условию задачи.
согласно условию задачи.
Понятно, что длина не может быть отрицательной, т. е. 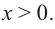 Площадь квадрата в основании коробки должна быть меньше 192, т. е.
Площадь квадрата в основании коробки должна быть меньше 192, т. е. 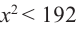
или 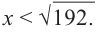 Значит,
Значит, 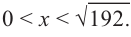
Найдем максимальное значение функции 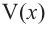 на интервале
на интервале 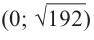
Для этого используем производную первого порядка:
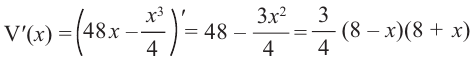
При 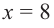 и
и 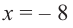 имеем, что
имеем, что 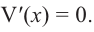
Однако. 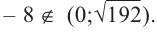 Значит, в рассматриваемом интервале критической точкой является
Значит, в рассматриваемом интервале критической точкой является 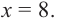
При 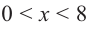 имеем
имеем 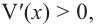 при
при 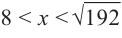 имеем
имеем 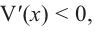 функция
функция
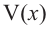 в точке
в точке 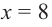 принимает максимальное значение.
принимает максимальное значение.
Если длина основания коробки будет 8 см, то высота будет равна
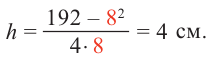
Значит, максимальный объем будет иметь коробка с размерами 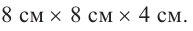
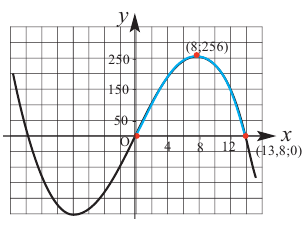
Построив при помощи графкалькулятора график функции 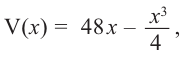 также можно увидеть, что при
также можно увидеть, что при 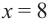 объем имеет максимальное значение. Постройте график функции при помощи производной и убедитесь в правильности решения.
объем имеет максимальное значение. Постройте график функции при помощи производной и убедитесь в правильности решения.
Пример 2. Минимальное потребление. Два столба высотой 4 м и 12 м находятся на расстоянии 12 м друг от друга. Самые высокие точки столбов соединены с металлической проволокой, каждая из которых, в свою очередь крепится на земле в одной точке. Выберите такую точку на земле, чтобы для крепления использовалось наименьшее количество проволоки.
Решение: 1) Изобразим рисунок, соответствующий условию задачи, и обозначим соответствующие данные на рисунке.
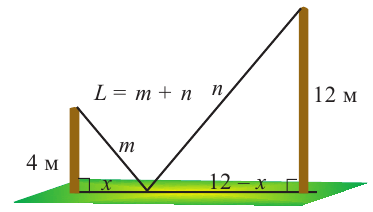
2) Аналитически выразим зависимость между переменными.
По теореме Пифагора:
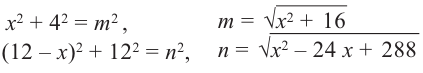
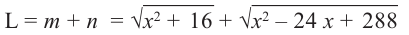
зависимость функции 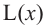 от переменной
от переменной 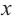 будет
будет
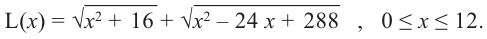
Производная функции 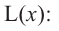
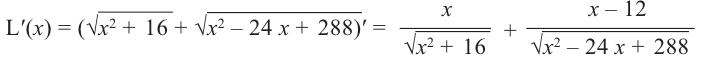
Найдем критические точки функции 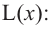
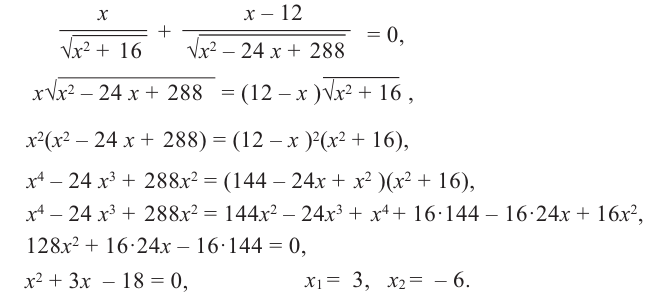
Сравнивая значения функции 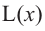 в точках
в точках 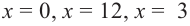 (это проверьте самостоятельно), получим, что наименьшее количество проволоки используется при
(это проверьте самостоятельно), получим, что наименьшее количество проволоки используется при 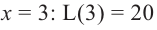 (метр)
(метр)
При решении задач на экстремумы обратите внимание на следующее!
1. Внимательно читайте условие. Сделайте соответствующий рисунок.
2. Задайте список соответствующих переменных и констант, которые менялись и оставались неизменными и какие единицы использовались. Если на рисунке есть размеры, обозначьте их.
3. Выберите соответствующий параметр 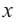 и выразите искомую величину функцией
и выразите искомую величину функцией 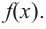 Найдите экстремумы данной функции.
Найдите экстремумы данной функции.
4. Полученные значения объясните экспериментально.
Пример: Минимальное потребление материала. Для мясных консервов планируется использовать банку в форме цилиндра объемом 250 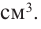
a) Каких размеров должна быть банка, чтобы для ее изготовления использовалось как можно меньше материала?
b) Для круглого основания используется материал, цена 1 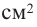 которого равна 0,05 гяпик, а для боковой поверхности используется материал цена 1
которого равна 0,05 гяпик, а для боковой поверхности используется материал цена 1 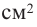 которого равна 0,12 гяпик. Какие размеры должна иметь банка, чтобы затраты на ее изготовление были минимальными?
которого равна 0,12 гяпик. Какие размеры должна иметь банка, чтобы затраты на ее изготовление были минимальными?
Решение: а) По условию задачи объем равен 250 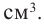 Эти данные дают нам возможность найти зависимость между
Эти данные дают нам возможность найти зависимость между 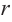 и
и 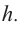
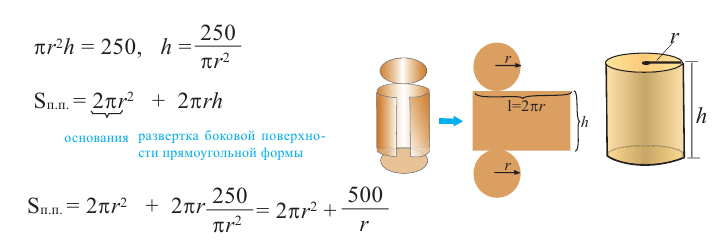
Для функции, выражающей площадь поверхности, область определения представляет собой незамкнутый интервал, и мы должны найти, при каком значении 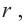 где
где 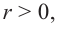 функция имеет наименьшее значение. Найдем производную функции
функция имеет наименьшее значение. Найдем производную функции 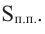
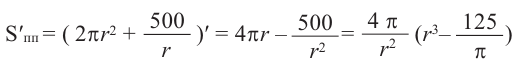 Критическая точка функции:
Критическая точка функции: 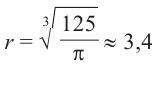 При
При 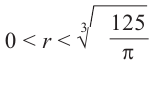 имеем
имеем 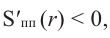 при
при 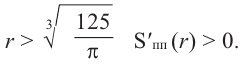
Значит, 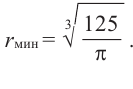
Подставим значение 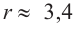 в формулу для высоты
в формулу для высоты 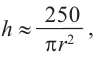 получим
получим 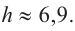
Итак, минимальные затраты на материал будет иметь банка цилиндрической формы с размерами 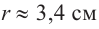 и
и 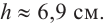
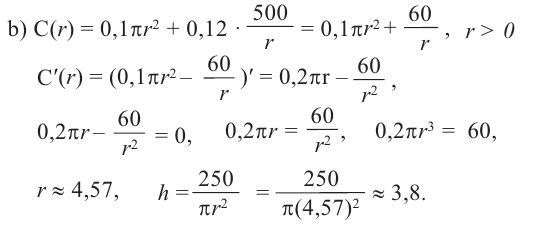
Размеры, при которых затраты на материал будут минимальными
- Приложения производной
- Производные высших порядков
- Дифференциал функции
- Дифференцируемые функции
- Касательная к графику функции и производная
- Предел и непрерывность функции
- Свойства функций, непрерывных в точке и на промежутке
- Предел функции на бесконечности
7. Взаимосвязь функции и ее производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Связь производной с возрастанием/убыванием функции
(blacktriangleright) Если производная положительна на промежутке ((a;b)), то функция на нем строго возрастает. (f'(x)>0
Longrightarrow f(x) uparrow)
Если производная отрицательна на промежутке ((a;b)), то функция на нем строго убывает. (f'(x)<0 Longrightarrow f(x) downarrow)
Заметим, что обратные утверждения неверны. То есть если функция строго возрастает на каком-то промежутке, то из этого не следует, что на всем этом промежутке ее производная будет положительной. Например:
функция (f(x)=x^3) на отрезке ([-1;1]) строго возрастает, но ее производная не положительна всюду: в точке (x=0) ее производная (f'(0)=0) (т.к. (f'(x)=3x^2)).
(blacktriangleright) Если функция не убывает (возрастает и/или константа) на промежутке ((a;b)), то на этом промежутке ее производная неотрицательна ((geq 0)). Верно и обратное утверждение.
(blacktriangleright) Если функция не возрастает (убывает и/или константа) на промежутке ((a;b)), то на этом промежутке ее производная неположительна ((leq 0)). Верно и обратное утверждение.
(blacktriangleright) В точках излома (на рисунке это точки (A) и (B)) производной не существует.
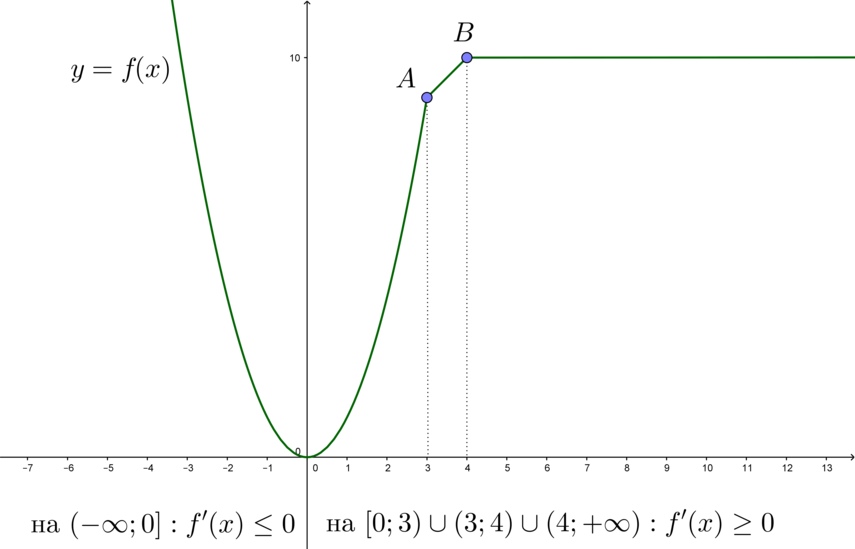
Заметим, что на промежутке ((4;+infty)) производная (f'(x)=0), т.к. на этом промежутке функция является константой ((f(x)=10)).
Пример: найдите количество точек, в которых производная равна нулю, если на рисунке дан график функции:
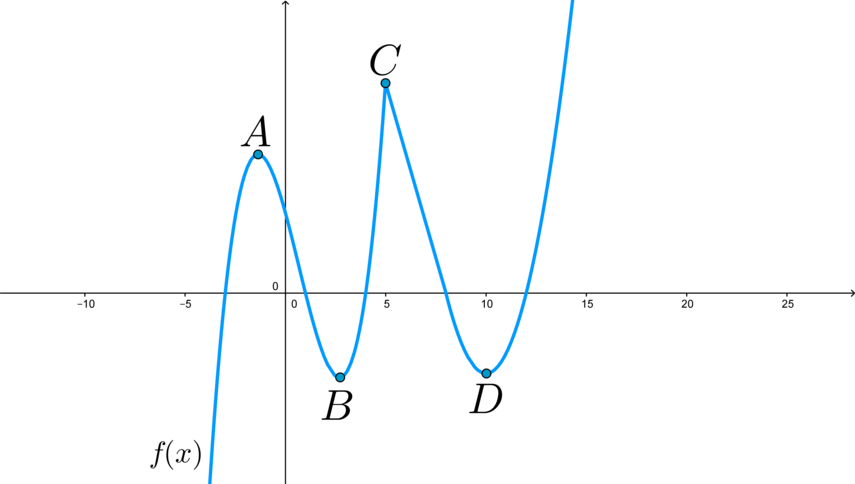
Производная равна нулю в точках (A,B,D), а в точке (C) она не существует, т.к. это точка излома.
Задание
1
#722
Уровень задания: Равен ЕГЭ
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-0,5; 4,3)). Определите количество целых точек (у которых координата – целое число), в которых производная функции положительна.
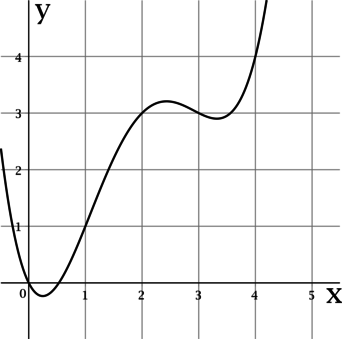
Для функции (f(x)), у которой производная в точке (x_0) существует, (f'(x_0) > 0) равносильно тому, что (f(x)) возрастает в (x_0).
На интервале ((-0,5; 4,3)) целыми являются точки (0), (1), (2), (3), (4). Среди этих точек (f(x)) возрастает только в (1), (2) и (4). Таким образом, производная функции (y = f(x)) положительна в (3) целых точках.
Ответ: 3
Задание
2
#723
Уровень задания: Равен ЕГЭ
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-0,5; 4,3)). Определите количество целых точек (у которых координата – целое число), в которых производная функции отрицательна.
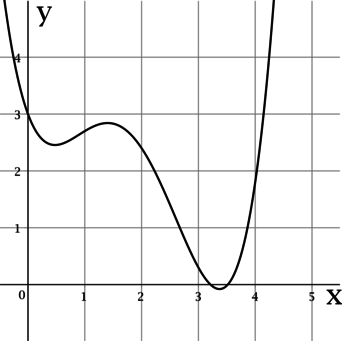
Для функции (f(x)), у которой производная в точке (x_0) имеет смысл, (f'(x_0) < 0) равносильно тому, что (f(x)) убывает в (x_0).
На интервале ((-0,5; 4,3)) целыми являются точки (0), (1), (2), (3), (4). Среди этих точек (f(x)) убывает только в (0), (2) и (3). Таким образом, производная функции (y = f(x)) отрицательна в (3) целых точках.
Ответ: 3
Задание
3
#724
Уровень задания: Равен ЕГЭ
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-0,5; 4,1)). Определите количество целых точек, в которых производная функции отрицательна.
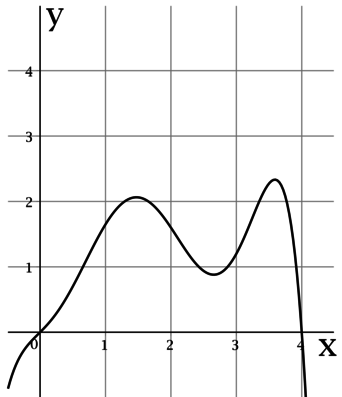
Для функции (f(x)), у которой производная в точке (x_0) имеет смысл, (f'(x_0) < 0) равносильно тому, что (f(x)) убывает в (x_0).
На интервале ((-0,5; 4,1)) целыми являются точки (0), (1), (2), (3), (4). Среди этих точек (f(x)) убывает только в (2) и (4). Таким образом, производная функции (y = f(x)) отрицательна в (2) целых точках.
Ответ: 2
Задание
4
#725
Уровень задания: Равен ЕГЭ
На рисунке изображен график (y = f'(x)) – производной функции (y = f(x)), определенной на интервале ((-0,6; 4,8)). Найдите промежутки возрастания функции (y = f(x)). В ответе укажите произведение целых точек, входящих в эти промежутки.
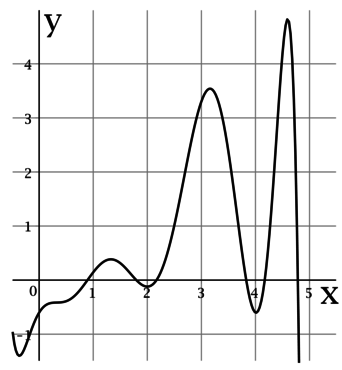
Для функции (f(x)), у которой производная в точке (x_0) имеет смысл, утверждение о том, что (f(x)) возрастает в (x_0) равносильно тому, что (f'(x_0) > 0).
На интервале ((-0,6; 4,8)) целыми являются точки (0), (1), (2), (3), (4). Среди этих точек (f'(x)) положительна только в (1) и (3). Таким образом, произведение целых точек, в которых функция возрастает, равно (3cdot 1 = 3).
Ответ: 3
Задание
5
#726
Уровень задания: Равен ЕГЭ
На рисунке изображен график (y = f'(x)) – производной функции (y = f(x)), определенной на интервале ((-1,5; 4,5)). Найдите промежутки возрастания функци (y = f(x)). В ответе укажите сумму целых точек, входящих в эти промежутки.
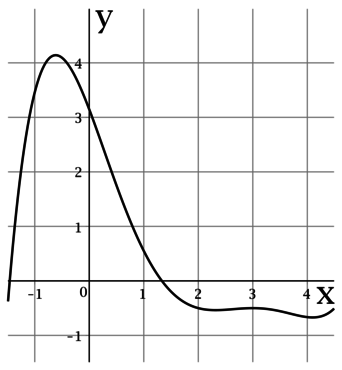
Для функции (f(x)), у которой производная в точке (x_0) имеет смысл, утверждение о том, что (f(x)) возрастает в (x_0) равносильно тому, что (f'(x_0) > 0).
На интервале ((-1,5; 4,5)) целыми являются точки (-1), (0), (1), (2), (3), (4). Среди этих точек (f'(x)) положительна только в (-1), (0) и (1). Таким образом, сумма целых точек, в которых функция возрастает, равна (-1 + 0 + 1 = 0).
Ответ: 0
Задание
6
#727
Уровень задания: Равен ЕГЭ
На рисунке изображен график (y = f'(x)) – производной функции (y = f(x)), определенной на интервале ((-1,5; 4,5)). Найдите промежутки убывания функции (y = f(x)). В ответе укажите количество целых точек, входящих в эти промежутки.
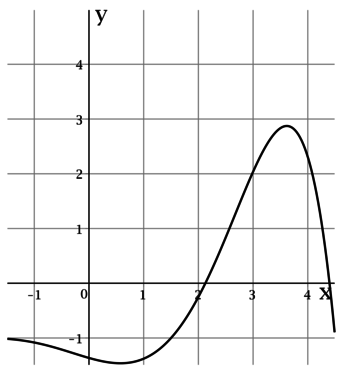
Для функции (f(x)), у которой производная в точке (x_0) имеет смысл, утверждение о том, что (f(x)) убывает в (x_0) равносильно тому, что (f'(x_0) < 0).
На интервале ((-1,5; 4,5)) целыми являются точки (-1), (0), (1), (2), (3), (4). Среди этих точек (f'(x)) отрицательна только в (-1), (0), (1) и (2). Таким образом, количество целых точек, в которых функция убывает, равно (4).
Ответ: 4
Задание
7
#728
Уровень задания: Равен ЕГЭ
На рисунке изображен график (y = f'(x)) – производной функции (y = f(x)), определенной на интервале ((-1,5; 4,6)). Найдите промежутки убывания функции (y = f(x)). В ответе укажите длину наибольшего из них.
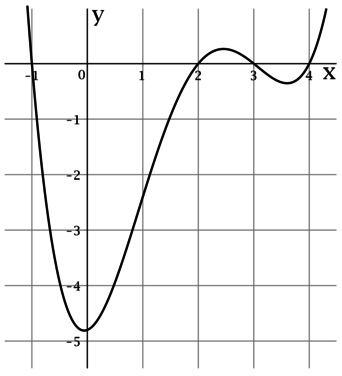
Для функции (f(x)), у которой производная в точке (x_0) имеет смысл, утверждение о том, что (f(x)) убывает в (x_0) равносильно тому, что (f'(x_0) < 0).
По рисунку видно, что (f'(x)) отрицательна на промежутках (-1 < x < 2) и (3 < x < 4), тогда (y = f(x)) убывает на промежутках (-1 < x < 2) и (3 < x < 4), из которых наибольшую длину, равную (3), имеет промежуток ((-1; 2)).
Ответ: 3
Выпускная работа в форме ЕГЭ для 11-классников обязательно содержит задания на вычисление пределов, промежутков убывания и возрастания производной функции, поиск точек экстремума и построение графиков. Хорошее знание этой темы позволяет правильно ответить на несколько вопросов экзамена и не испытывать затруднений в дальнейшем профессиональном обучении.
Основы дифференциального исчисления – одна из главных тем математики современной школы. Она изучает применение производной для исследования зависимостей переменных – именно через производную можно проанализировать возрастание и убывание функции без обращения к чертежу.
Комплексная подготовка выпускников к сдаче ЕГЭ на образовательном портале «Школково» поможет глубоко понять принципы дифференцирования – подробно разобраться в теории, изучить примеры решения типовых задач и попробовать свои силы в самостоятельной работе. Мы поможем вам ликвидировать пробелы в знаниях – уточнить представление о лексических понятиях темы и зависимостях величин. Ученики смогут повторить, как находить промежутки монотонности, что значит подъем или убывание производной функции на определенном отрезке, когда граничные точки включаются и не включаются в найденные интервалы.
Прежде чем начинать непосредственное решение тематических задач, мы рекомендуем сначала перейти к разделу «Теоретическая справка» и повторить определения понятий, правила и табличные формулы. Здесь же можно прочитать, как находить и записывать каждый промежуток возрастания и убывания функции на графике производной.
Все предлагаемые сведения излагаются в максимально доступной форме для понимания практически «с нуля». На сайте доступны материалы для восприятия и усвоения в нескольких различных формах – чтения, видеопросмотра и непосредственного тренинга под руководством опытных учителей. Профессиональные педагоги подробно расскажут, как найти промежутки возрастания и убывания производной функции аналитическими и графическими способами. В ходе вебинаров можно будет задать любой интересующий вопрос как по теории, так и по решению конкретных задач.
Вспомнив основные моменты темы, просмотрите примеры на возрастание производной функции, аналогичные заданиям экзаменационных вариантов. Для закрепления усвоенного загляните в «Каталог» – здесь вы найдете практические упражнения для самостоятельной работы. Задания в разделе подобраны разного уровня сложности с учетом наработки навыков. К каждому из них, например, на нахождение производной функции, прилагаются алгоритмы решений и правильные ответы.
Выбирая раздел «Конструктор», учащиеся смогут попрактиковаться в исследовании возрастания и убывания производной функции на реальных вариантах ЕГЭ, постоянно обновляемых с учетом последних изменений и нововведений.

УСТАЛ? Просто отдохни


