Загрузить PDF
Загрузить PDF
Линейная интерполяция (или просто интерполяция)[1]
— процесс нахождения промежуточных значений величины по ее известным значениям. Многие люди могут провести интерполяцию, полагаясь исключительно на интуицию, но в этой статье описан формализованный математический подход к проведению интерполяции.
Шаги
-
1
Определите величину, для которой вы хотите найти соответствующее значение. Интерполяция может быть проведена для вычисления логарифмов или тригонометрических функций или для вычисления соответствующего объема или давления газа при данной температуре.[2]
Научные калькуляторы в значительной степени заменили логарифмические и тригонометрические таблицы; поэтому в качестве примера проведения интерполяции мы вычислим давление газа при температуре, значение которой не указано в справочных таблицах (или на графиках).- В уравнении, которое мы выведем, «x» будет обозначать известную величину, а «у» — неизвестную величину (интерполированное значение). При построении графика эти значения откладываются соответственно их обозначениям — величина «x» — по оси X, величина «у» — по оси Y.
- В нашем примере под «x» будет подразумеваться температура газа, равная 37 °С.
-
2
В таблице или на графике найдите ближайшие значения, расположенные ниже и выше значения «x». В нашей справочной таблице не приведено давление газа при 37 °С, но приведены значения давления при 30 °С и при 40 °С. Давление газа при температуре 30 °С = 3 кПа, а давление газа при 40 °С = 5 кПа.
- Так как мы обозначили температуру в 37 °С как «x», то теперь обозначим температуру в 30 °С как x1, а температуру в 40 °С как x2.
- Так как мы обозначили неизвестное (интерполированное) давление газа как «у», то теперь обозначим давление в 3 кПа (при 30 °С) как у1, а давление в 5 кПа (при 40 °С) как у2.
- Так как мы обозначили температуру в 37 °С как «x», то теперь обозначим температуру в 30 °С как x1, а температуру в 40 °С как x2.
-
3
Найдем интерполированное значение. Уравнение для нахождения интерполированного значения можно записать в виде y = y1 + ((x – x1)/(x2 – x1) * (y2 – y1))[3]
- Подставим значения x, x1, x2 и получим: (37 – 30)/(40 – 30) = 7/10 = 0,7.
- Подставим значения у1, у2 и получим: (5 – 3) = 2.
- Умножив 0,7 на 2, получим 1,4. Сложим 1,4 и у1: 1,4 + 3 = 4,4 кПа. Проверим ответ: найденное значение 4,4 кПа лежит между 3 кПа (при 30 °С) и 5 кПа (при 40 °С), а так как 37 °С ближе к 40 °С, чем к 30 °С, то и окончательный результат (4,4 кПа) должен быть ближе к 5 кПа, чем к 3 кПа.
Реклама
- Подставим значения x, x1, x2 и получим: (37 – 30)/(40 – 30) = 7/10 = 0,7.
Советы
- Если вы умеете работать с графиками, вы можете сделать грубую интерполяцию, отложив известное значение по оси X и найдя соответствующее значение на оси Y.[4]
В приведенном выше примере можно построить график, на котором по оси X откладывается температура (в десятках градусов), а по оси Y — давление (в единицах кПа). На этом графике вы можете нанести точку 37 градусов, а затем найти точку на оси Y, соответствующую этой точке (она будет лежать между точками 4 и 5 кПа). Приведенное выше уравнение просто формализует процесс мышления и обеспечивает получение точного значения. - В отличие от интерполяции, экстраполяция позволяет вычислить приблизительные значения величины вне диапазона значений, приведенных в таблицах или отображенных на графиках.[5]
Реклама
Об этой статье
Эту страницу просматривали 98 044 раза.
Была ли эта статья полезной?
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 9 июля 2022 года; проверки требует 1 правка.
У этого термина существуют и другие значения, см. Интерполяция.
- О функции, см.: Интерполянт.
Интерполя́ция, интерполи́рование (от лат. inter–polis — «разглаженный, подновлённый, обновлённый; преобразованный») — в вычислительной математике нахождение неизвестных промежуточных значений некоторой функции, по имеющемуся дискретному набору её известных значений, определенным способом. Термин «интерполяция» впервые употребил Джон Валлис в своём трактате «Арифметика бесконечных» (1656).
В функциональном анализе интерполяция линейных операторов представляет собой раздел, рассматривающий банаховы пространства как элементы некоторой категории[1].
Многим из тех, кто сталкивается с научными и инженерными расчётами, часто приходится оперировать наборами значений, полученных опытным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.
Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить её значение в нескольких точках, а по ним построить, то есть интерполировать, более простую функцию. Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но в некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.
Следует также упомянуть и совершенно другую разновидность математической интерполяции, известную под названием «интерполяция операторов». К классическим работам по интерполяции операторов относятся теорема Рисса — Торина и теорема Марцинкевича[en], являющиеся основой для множества других работ.
Определения[править | править код]
Рассмотрим систему несовпадающих точек 



Задача интерполяции состоит в поиске такой функции 
</math>A(x)
Пример[править | править код]
1. Пусть мы имеем табличную функцию, наподобие описанной ниже, которая для нескольких значений 


|

|
|---|---|
| 0 | 0 |
| 1 | 0,8415 |
| 2 | 0,9093 |
| 3 | 0,1411 |
| 4 | −0,7568 |
| 5 | −0,9589 |
| 6 | −0,2794 |
Интерполяция помогает нам узнать, какое значение может иметь такая функция в точке, отличной от указанных точек (например, при x = 2,5).
К настоящему времени существует множество различных способов интерполяции. Выбор наиболее подходящего алгоритма зависит от ответов на вопросы: как точен выбираемый метод, каковы затраты на его использование, насколько гладкой является интерполяционная функция, какого количества точек данных она требует и т. п.
2. Найти промежуточное значение (способом линейной интерполяции).
| 6000 | 15.5 |
| 6378 | ? |
| 8000 | 19.2 |

Способы интерполяции[править | править код]
Интерполяция методом ближайшего соседа[править | править код]
Простейшим способом интерполяции является интерполяция методом ближайшего соседа.
Интерполяция многочленами[править | править код]
На практике чаще всего применяют интерполяцию многочленами. Это связано прежде всего с тем, что многочлены легко вычислять, легко аналитически находить их производные и множество многочленов плотно в пространстве непрерывных функций (теорема Вейерштрасса).
- Линейная интерполяция
- Интерполяционная формула Ньютона
- Метод конечных разностей
- ИМН-1 и ИМН-2
- Многочлен Лагранжа (интерполяционный многочлен)
- Схема Эйткена
- Сплайн-функция
- Кубический сплайн
Обратное интерполирование (вычисление x при заданной y)[править | править код]
- Полином Лагранжа
- Обратное интерполирование по формуле Ньютона
- Обратное интерполирование по формуле Гаусса
Интерполяция функции нескольких переменных[править | править код]
- Билинейная интерполяция
- Бикубическая интерполяция
Другие способы интерполяции[править | править код]
- Рациональная интерполяция
- Тригонометрическая интерполяция
Смежные концепции[править | править код]
- Экстраполяция — методы нахождения точек за пределами заданного интервала (продление кривой)
- Ретрополяция — методы нахождения по известным значениям переменной её неизвестных значений в начале динамического ряда.
- Аппроксимация — методы построения приближённых кривых
См. также[править | править код]
- Интерполяционные формулы
- Регрессия (математика)
- Метод наименьших квадратов
- Сглаживание данных эксперимента
Примечания[править | править код]
- ↑ Берг, 1980, с. 6—7.
Литература[править | править код]
- Й. Берг, Й. Лёфстрём. Интерполяционные пространства. Введение. — М.: Мир, 1980. — 264 с.
- Ибрагимов И. И. Методы интерполяций функций и некоторые их применения. — М.: Высшая школа, 1971. — 520 c.
- Уолш Дж. Л.[en] Интерполяция и аппроксимация рациональными функциями в комплексной области. — М.: Иностранная литература, 1961. — 508 c.
- Трибель Х. Теория интерполяции, функциональные пространства, дифференциальные операторы. — М.: Мир, 1980. — 664 c.
Интерполяция – это способ вычислить промежуточное значение функции по нескольким уже известным ее значениям.
Линейная интерполяция предполагает вычисление промежуточного значения функции по двум точкам (условно проведя прямую между ними).
Например, если известны значения функции в двух точках f(x1) и f(x2), то разумно предположить что значение в третьей точке, находящейся между первой и второй, можно найти графически, она лежит на отрезке, соединяющем x1 и x2.
$$ f(x) = f(x1)+(x-x1) frac{f(x2)-f(x1)}{x2-x1} $$
Если x лежит вне интервала (x1, x2), этот же процесс называется экстраполяция.
| x | f(x) | |
| x1 | ||
| x2 | ||
| x | 7.25 |
Подробный ход расчета
$$ f(5) = 9 + (5 – 4)frac {2 – 9}{8 – 4} = 7.25 $$
Интерполяция, интерполирование — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
Многим из тех, кто сталкивается с научными и инженерными расчётами, часто приходится оперировать наборами значений, полученных опытным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.
Проще говоря: способ приближенного вычисления значения величины, находящегося между двумя известными значениями.
Примечание! Для удобства можно воспользоваться другими удобными формами для рассчета:
– Линейная интерполяция по графику
– Двойная интерполяция
Это глава из книги Билла Джелена Гуру Excel расширяют горизонты: делайте невозможное с Microsoft Excel.
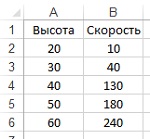
Задача: некоторые инженерные проблемы проектирования требуют использования таблиц для вычисления значений параметров. Поскольку таблицы являются дискретными, дизайнер использует линейную интерполяцию для получения промежуточного значения параметра. Таблица (рис. 1) включает высоту над землей (управляющий параметр) и скорость ветра (рассчитываемый параметр). Например, если надо найти скорость ветра, соответствующую высоте 47 метров, то следует применить формулу: 130 + (180 – 130) * 7 / (50 – 40) = 165 м/сек.
Рис. 1. Высота над землей (управляющий параметр) и скорость ветра (рассчитываемый параметр)
Скачать заметку в формате Word или pdf, примеры в формате Excel
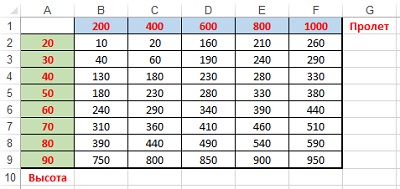
Как быть, если существует два управляющих параметра? Можно ли выполнить вычисления с помощью одной формулы? В таблице (рис. 2) показаны значения давления ветра для различных высот и величин пролета конструкций. Требуется вычислить давление ветра на высоте 25 метров и величине пролета 300 метров.
Рис. 2. Исходная таблица для интерполяции по двум управляющим параметрам
Решение: проблему решаем путем расширения метода, используемого для случая с одним управляющим параметром. Выполните следующие действия.
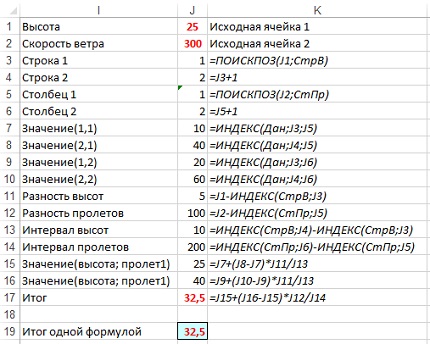
Начните с таблицы, изображенной на рис. 2. Добавьте исходные ячейки для высоты и пролета в J1 и J2 соответственно (рис. 3).
Рис. 3. Формулы в ячейках J3:J17 объясняют работу мегаформулы
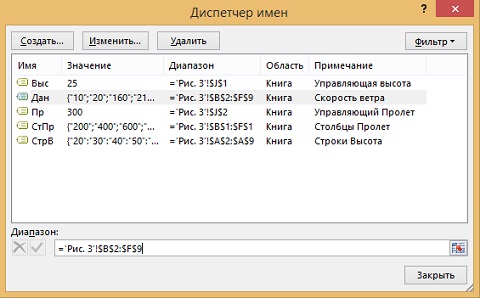
Для удобства использования формул определите имена (рис. 4).
Рис. 4. Определенные имена
Проследите за работой формулы последовательно переходя от ячейки J3 к ячейке J17.
Путем обратной последовательной подстановки соберите мегаформулу. Скопируйте текст формулы из ячейки J17 в J19. Замените в формуле ссылку на J15 на значение в ячейке J15: J7+(J8-J7)*J11/J13. И так далее. Получится формула, состоящая из 984 символов, которую невозможно воспринять в таком виде. Вы можете посмотреть на нее в приложенном Excel-файле. Не уверен, что такого рода мегаформулы полезны в использовании.
Резюме: линейная интерполяция используется для получения промежуточного значения параметра, если табличные значения заданы только для границ диапазонов; предложен метод расчета по двум управляющим параметрам.