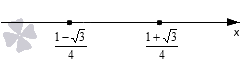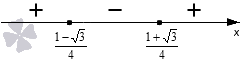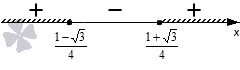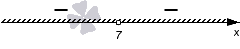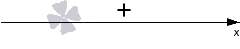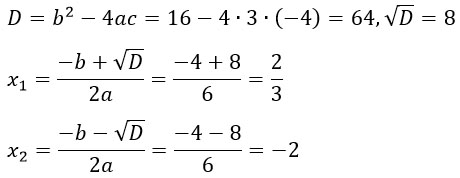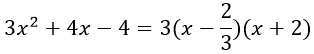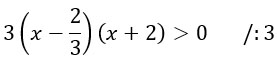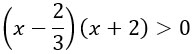Универсальным методом решения неравенств по праву считается метод интервалов. Именно его проще всего использовать для решения квадратных неравенств с одной переменной. В этом материале мы рассмотрим все аспекты применения метода интервалов для решения квадратных неравенств. Для облегчения усвоения материала мы рассмотрим большое количество примеров разной степени сложности.
Алгоритм применения метода интервалов
Рассмотрим алгоритм применения метода интервалов в адаптированном варианте, который пригоден для решения квадратных неравенств. Именно с таким вариантом метода интервалов знакомят учеников на уроках алгебры. Не будем усложнять задачу и мы.
Перейдем собственно к алгоритму.
У нас есть квадратный трехчлен a·x2+b·x+c из левой части квадратного неравенства. Находим нули из этого трехчлена.
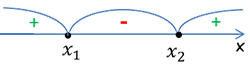
В системе координат изображаем координатную прямую. Отмечаем на ней корни. Для удобства можем ввести разные способы обозначения точек для строгих и нестрогих неравенств. Давайте договоримся, что «пустыми» точками мы будем отмечать координаты при решении строгого неравенства, а обычными точками – нестрогого. Отметив точки, мы получаем на координатной оси несколько промежутков.
Если на первом шаге мы нашли нули, то определяем знаки значений трехчлена для каждого из полученных промежутков. Если нули мы не получили, то производим это действие для всей числовой прямой. Отмечаем промежутки знаками «+» или «-».
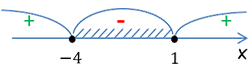
Дополнительно мы будем вводить штриховку в тех случаях, когда будем решать неравенства со знаками > или ≥ и < или ≤. В первом случае штриховка будет наноситься над промежутками, отмеченными «+», во втором над участками, отмеченными «-».
Отметив знаки значений трехчлена и нанеся штриховку над отрезками, мы получаем геометрический образ некоторого числового множества, которое фактически является решением неравенства. Нам остается лишь записать ответ.
Остановимся подробнее на третьем шаге алгоритма, который предполагает определение знака промежутка. Существует несколько подходов определения знаков. Рассмотрим их по порядку, начав с наиболее точного, хотя и не самого быстрого. Этот метод предполагает вычисление значений трехчлена в нескольких точках полученных промежутков.
Для примера возьмем трехчлен x2+4·x−5.
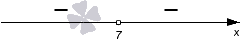
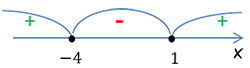
Корни этого трехчлена 1 и -5 разбивают координатную ось на три промежутка (−∞, −5), (−5, 1) и (1, +∞).
Начнем с промежутка (1, +∞). Для того, чтобы упростить себе задачу, примем х=2. Получаем 22+4·2−5=7.
7 – положительное число. Это значит, что значения данного квадратного трехчлена на интервале (1, +∞) положительные и его можно обозначить знаком «+».
Для определения знака промежутка (−5, 1) примем x=0. Имеем 02+4·0−5=−5. Ставим над интервалом знак «-».
Для промежутка (−∞, −5) возьмем x=−6, получаем (−6)2+4·(−6)−5=7. Отмечаем этот интервал знаком «+».
Намного быстрее определить знаки можно с учетом следующих фактов.
При положительном дискриминанте квадратный трехчлен с двумя корнями дает чередование знаков его значений на промежутках, на которые разбивается числовая ось корнями этого трехчлена. Это значит, что нам вовсе не обязательно определять знаки для каждого из интервалов. Достаточно провести вычисления для одного и проставить знаки для остальных, учитывая принцип чередования.
При желании, можно и вовсе обойтись без вычислений, сделав выводы о знаках по значению старшего коэффициента. Если a>0, то мы получаем последовательность знаков +, −, +, а если a<0 – то −, +, −.
У квадратных трехчленов с одним корнем, когда дискриминант равен нулю, мы получаем два промежутка на координатной оси с одинаковыми знаками. Это значит, что мы определяем знак для одного из промежутков и для второго ставим такой же.
Здесь также применим метод определения знака на основе значения коэффициента a: если a>0, то будет +, +, а если a<0, то −, −.
Если квадратный трехчлен не имеет корней, то знаки его значений для всей координатной прямой совпадают как со знаком старшего коэффициента a, так и со знаком свободного члена c.
Например, если мы возьмем квадратный трехчлен −4·x2−7, он не имеет корней (его дискриминант отрицательный). Коэффициент при x2 есть отрицательное число −4, и свободный член −7 тоже отрицателен. Это значит, что на промежутке (−∞, +∞) его значения отрицательны.
Примеры решения квадратных неравенств
Рассмотрим примеры решения квадратных неравенств с использованием рассмотренного выше алгоритма.
Решите неравенство 8·x2−4·x−1≥0.
Решение
Используем для решения неравенства метод интервалов. Для этого найдем корни квадратного трехчлена 8·x2−4·x−1. В связи с тем, что коэффициент при х четный, нам будет удобнее вычислить не дискриминант, а четвертую часть дискриминанта: D’=(−2)2−8·(−1)=12.
Дискриминант больше нуля. Это позволяет нам найти два корня квадратного трехчлена: x1=2-129, x1=1-34 и x2=2+128, x2=1+34. Отметим эти значения на числовой прямой. Так как уравнение нестрогое, то на графике мы используем обычные точки.
Теперь по методу интервалов определяем знаки трех полученных интервалов. Коэффициент при x2 равен 8, то есть, положителен, следовательно, последовательность знаков будет +, −, +.
Так как мы решаем неравенство со знаком ≥, то изображаем штриховку над промежутками со знаками плюс:
Запишем аналитически числовое множество по полученному графическому изображению. Мы можем сделать это двумя способами:
(-∞; 1-34]∪[1+34, +∞) или x≤1-34, x≥1+34.
Ответ: (-∞; 1-34]∪[1+34, +∞) или x≤1-34, x≥1+34.
Выполните решение квадратного неравенства -17·x2+2·x-7<0 методом интервалов.
Решение
Для начала найдем корни квадратного трехчлена из левой части неравенства:
D’=12–17·-7=0x0=-1-17×0=7
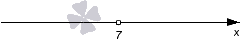
Это строгое неравенство, поэтому на графике используем «пустую» точку. С координатой 7.
Теперь нам нужно определить знаки на полученных промежутках (−∞, 7) и (7, +∞). Так как дискриминант квадратного трехчлена равен нулю, а старший коэффициент отрицательный, то мы проставляем знаки −, −:
Так как мы решаем неравенство со знаком <, то изображаем штриховку над интервалами со знаками минус:
В данном случае решениями являются оба промежутка (−∞, 7), (7, +∞).
Ответ: (−∞, 7)∪(7, +∞) или в другой записи x≠7.
Имеет ли квадратное неравенство x2+x+7<0 решения?
Решение
Найдем корни квадратного трехчлена из левой части неравенства. Для этого найдем дискриминант: D=12−4·1·7=1−28=−27. Дискриминант меньше нуля, значит, действительных корней нет.
Графическое изображение будет иметь вид числовой прямой без отмеченных на ней точек.
Определим знак значений квадратного трехчлена. При D<0 он совпадает со знаком коэффициента при x2, то есть, со знаком числа 1, оно положительное, следовательно, имеем знак +:
Штриховку мы могли бы нанести в данном случае над промежутками со знаком «-». Но таких промежутков у нас нет. Следовательно, чертеж сохраняет вот такой вид:
В результате вычислений мы получили пустое множество. Это значит, что данное квадратное неравенство решений не имеет.
Ответ: Нет.
Прежде чем разбираться, как решать квадратное неравенство,
давайте рассмотрим, какое неравенство называют квадратным.
Запомните!
Неравенство называют квадратным, если старшая (наибольшая) степень неизвестного «x»
равна двум.
Потренируемся определять тип неравенства на примерах.
| Неравенство | Тип |
|---|---|
|
x − 7 < 0
|
линейное |
| x2 + 5x ≥ 0 | квадратное |
| 2x − 7 > 5 | линейное |
| x2 + x − 12 ≤ 0 |
квадратное
|
Как решить квадратное неравенство
В предыдущих уроках мы разбирали, как решать
линейные неравенства.
Но в отличие от линейных неравенств квадратные решаются совсем иным образом.
Важно!
Решать квадратное неравенство таким же образом как и линейное нельзя!
Для решения квадратного неравенства используется специальный способ, который называется методом интервалов.
Что такое метод интервалов
Методом интервалов называют специальный способ решения квадратных неравенств. Ниже мы объясним, как использовать
этот метод и почему он получил такое название.
Запомните!
Чтобы решить квадратное неравенство методом интервалов нужно:
- перенести все члены неравенства в левую часть, так чтобы в правой остался только ноль;
- сделать так, чтобы при неизвестном «x2» стоял положительный коэффициент;
- приравнять левую часть неравенства к нулю и решить полученное квадратное уравнение;
- полученные корни уравнения разместить на числовой оси в порядке возрастания;
- нарисовать «арки» для интервалов. Справа налево,
начиная с «+», проставить чередуя знаки «+»
и «−»; - выбрать необходимые интервалы и записать их в ответ.
Мы понимаем, что правила, описанные выше, трудно воспринимать только в теории, поэтому сразу рассмотрим пример решения
квадратного неравенства по алгоритму выше.
Требуется решить квадратное неравенство.
x2 + x − 12 < 0
Итак, согласно п.1 мы должны перенести
все члены неравенства в левую часть, так чтобы в правой остался только ноль.
В заданном неравенстве
«x2 + x − 12 < 0» ничего дополнительно делать не требуется,
так как в правой части и так уже стоит ноль.
Переходим к п.2. Необходимо сделать так, чтобы перед «x2»
стоял положительный коэффициент. В неравенстве
«x2 + x − 12 < 0»
при «x2» стоит положительный коэффициент «1»,
значит, снова нам ничего делать не требуется.
Согласно п.3 приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение.
x2 + x − 12 = 0
x1;2 =
| −1 ± √12 − 4 · 1 · (−12) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
|
x1 = |
x2 = |
|
x1 = |
x2 = |
|
x1 = −4 |
x2 = 3 |
Теперь по п.4 отметим полученные корни на числовой оси в порядке возрастания.
Помните, что, исходя их того, какое перед нами неравенство (строгое или нестрогое) мы отмечаем точки на числовой оси
разным образом.
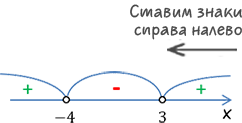
Теперь, как сказано в п.5, нарисуем «арки» над интервалами между отмеченными точками.
Проставим знаки внутри интервалов.
Справа налево чередуя, начиная с «+», отметим знаки.
Нам осталось только выполнить пункт 6, то есть выбрать нужные интервалы и записать их в ответ.
Вернемся к нашему неравенству.
Так как в нашем неравенстве
«x2 + x − 12 < 0»,
значит, нам требуются отрицательные интервалы.
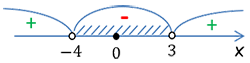
Заштрихуем все отрицательные области на числовой оси и выпишем их в ответ.
Отрицательным интервалом оказался лишь один, который находится между числами
«−4» и «3», поэтому
запишем его в ответ в виде двойного неравенства
−4 < x < 3.
Запишем полученный ответ квадратного неравенства.
Ответ: −4 < x < 3
Именно из-за того, что при решении квадратного неравенства мы рассматриваем интервалы между числами,
метод интервалов и получил свое название.
После получения ответа имеет смысл сделать его проверку, чтобы убедиться в правильности решения.
Выберем любое число, которое находится в заштрихованной области полученного ответа −4 < x < 3
и подставим его вместо «x» в исходное неравенство.
Если мы получим верное неравенство,
значит мы нашли ответ квадратного неравенства верно.
Возьмем, например, из интервала число «0». Подставим его в исходное неравенство
«x2 + x − 12 < 0».
x2 + x − 12 < 0
02 + 0 − 12 < 0
−12 < 0
(верно)
Мы получили верное неравенство при подстановке числа из области решений, значит ответ найден правильно.
Краткая запись решения методом интервалов
Сокращенно запись решения квадратного неравенства
«x2 + x − 12 < 0»
методом интервалов будет выглядеть так:
x2 + x − 12 < 0
x2 + x − 12 = 0
x1;2 =
| −1 ± √12 − 4 · 1 · (−12) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
|
x1 = |
x2 = |
|
x1 = |
x2 = |
|
x1 = −4 |
x2 = 3 |
Ответ: −4 < x < 3
Другие примеры решения квадратных неравенств
Рассмотрим решение других примеров квадратных неравенств. Требуется решить квадратное неравенство:
2x2 − x ≥ 0
В правой части неравенство уже стоит ноль. При «x2»
стоит «2» (положительный коэффициент), значит можно сразу переходить
к поиску корней.
2x2 − x ≥ 0
2x2 − x = 0
x1;2 =
| −(−1) ± √(−12) − 4 · 2 · 0 |
| 2 · 2 |
x1;2 =
x1;2 =
| x1 = |
x2 = |
| x1 = |
x2 = |
| x1 = |
x2 = 0 |
Ответ: x ≤ 0; x ≥
Рассмотрим пример, где перед «x2» в квадратном неравенстве стоит
отрицательный коэффициент.
−x2 − 3x + 4 ≥ 0
По п.2 общих правил решения методом интервалов нам нужно сделать так, чтобы
перед «x2» стоял положительный
коэффициент. Для этого умножим все неравенство на «−1».
−x2 − 3x + 4 ≥ 0 | ·(−1)
x2 + 3x − 4 ≤ 0
Можно переходить к п.4 и п.5. Приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение.
Затем расположим полученные корни на числовой оси и проведем между ними «арки».
x2 + 3x − 4 ≤ 0
x2 + 3x − 4 = 0
x1;2 =
| −3 ± √32 − 4 · 1 · (−4) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
|
x2 = |
x1 = |
|
x2 = |
x1 = |
| x2 = −4 | x1 = 1 |
Важно!
При определении того какие интервалы нам нужно брать в ответ, исходить нужно из самого последнего изменения неравенства
перед нахождением его корней.
В нашем случае самая последняя версия неравенства перед поиском корней уравнения это
«x2 + 3x − 4 ≤ 0».
Значит для ответа нужно выбирать интервалы со знаком «−».
Ответ: −4 ≤ x ≤ 1
К сожалению, при решении квадратного неравенства не всегда получаются два корня и все идет по общему плану выше.
Возможны случаи, когда получается один корень или даже ни одного корня.
Как решить квадратные неравенства в таких случаях, мы разберем в следующем уроке
«Квадратные неравенства
с одним корнем или без корней».
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
5 апреля 2019 в 8:15
Gulnara Muslimova
Профиль
Благодарили: 0
Сообщений: 1
Gulnara Muslimova
Профиль
Благодарили: 0
Сообщений: 1
Помогите решить неравенство (желательно подробно и с пояснениями):
(x2+3x+3)x^2 -1<(8x-3)x^2 -1
0
Спасибо
Ответить
6 апреля 2019 в 16:12
Ответ для Gulnara Muslimova
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Логарифмируем
ac < bc <=> c·ln(a/b) < 0
и метод интервалов.
0
Спасибо
Ответить
15 сентября 2018 в 22:11
Vlad Lukashenok
Профиль
Благодарили: 0
Сообщений: 1
Vlad Lukashenok
Профиль
Благодарили: 0
Сообщений: 1
Решите неравенство:
x · sin2(πx)>=0
0
Спасибо
Ответить
17 сентября 2018 в 23:05
Ответ для Vlad Lukashenok
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x = k ∈ Ζ; x > 0.
0
Спасибо
Ответить
2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.
Вывод: при х > 3 верно неравенство (х – 3) * (х – 2) > 0. Внесем эти данные в чертеж.
Исходное неравенство: (х – 3) * (х – 2) ≥ 0.
Если (х – 3) (х – 2) = 0 — при х1 = 3, х2 = 2.
Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.
Ответ: х ≤ 0, х ≥ 3.
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3
Решение квадратных неравенств методом интервалов
Универсальным методом решения неравенств по праву считается метод интервалов. Именно его проще всего использовать для решения квадратных неравенств с одной переменной. В этом материале мы рассмотрим все аспекты применения метода интервалов для решения квадратных неравенств. Для облегчения усвоения материала мы рассмотрим большое количество примеров разной степени сложности.
Алгоритм применения метода интервалов
Рассмотрим алгоритм применения метода интервалов в адаптированном варианте, который пригоден для решения квадратных неравенств. Именно с таким вариантом метода интервалов знакомят учеников на уроках алгебры. Не будем усложнять задачу и мы.
Перейдем собственно к алгоритму.
У нас есть квадратный трехчлен a · x 2 + b · x + c из левой части квадратного неравенства. Находим нули из этого трехчлена.
В системе координат изображаем координатную прямую. Отмечаем на ней корни. Для удобства можем ввести разные способы обозначения точек для строгих и нестрогих неравенств. Давайте договоримся, что «пустыми» точками мы будем отмечать координаты при решении строгого неравенства, а обычными точками – нестрогого. Отметив точки, мы получаем на координатной оси несколько промежутков.
Если на первом шаге мы нашли нули, то определяем знаки значений трехчлена для каждого из полученных промежутков. Если нули мы не получили, то производим это действие для всей числовой прямой. Отмечаем промежутки знаками « + » или « – ».
Дополнительно мы будем вводить штриховку в тех случаях, когда будем решать неравенства со знаками > или ≥ и или ≤ . В первом случае штриховка будет наноситься над промежутками, отмеченными « + », во втором над участками, отмеченными « – ».
Отметив знаки значений трехчлена и нанеся штриховку над отрезками, мы получаем геометрический образ некоторого числового множества, которое фактически является решением неравенства. Нам остается лишь записать ответ.
Остановимся подробнее на третьем шаге алгоритма, который предполагает определение знака промежутка. Существует несколько подходов определения знаков. Рассмотрим их по порядку, начав с наиболее точного, хотя и не самого быстрого. Этот метод предполагает вычисление значений трехчлена в нескольких точках полученных промежутков.
Для примера возьмем трехчлен x 2 + 4 · x − 5 .
Корни этого трехчлена 1 и – 5 разбивают координатную ось на три промежутка ( − ∞ , − 5 ) , ( − 5 , 1 ) и ( 1 , + ∞ ) .
Начнем с промежутка ( 1 , + ∞ ) . Для того, чтобы упростить себе задачу, примем х = 2 . Получаем 2 2 + 4 · 2 − 5 = 7 .
7 – положительное число. Это значит, что значения данного квадратного трехчлена на интервале ( 1 , + ∞ ) положительные и его можно обозначить знаком « + ».
Для определения знака промежутка ( − 5 , 1 ) примем x = 0 . Имеем 0 2 + 4 · 0 − 5 = − 5 . Ставим над интервалом знак « – ».
Для промежутка ( − ∞ , − 5 ) возьмем x = − 6 , получаем ( − 6 ) 2 + 4 · ( − 6 ) − 5 = 7 . Отмечаем этот интервал знаком « + ».
Намного быстрее определить знаки можно с учетом следующих фактов.
При положительном дискриминанте квадратный трехчлен с двумя корнями дает чередование знаков его значений на промежутках, на которые разбивается числовая ось корнями этого трехчлена. Это значит, что нам вовсе не обязательно определять знаки для каждого из интервалов. Достаточно провести вычисления для одного и проставить знаки для остальных, учитывая принцип чередования.
При желании, можно и вовсе обойтись без вычислений, сделав выводы о знаках по значению старшего коэффициента. Если a > 0 , то мы получаем последовательность знаков + , − , + , а если a 0 – то − , + , − .
У квадратных трехчленов с одним корнем, когда дискриминант равен нулю, мы получаем два промежутка на координатной оси с одинаковыми знаками. Это значит, что мы определяем знак для одного из промежутков и для второго ставим такой же.
Здесь также применим метод определения знака на основе значения коэффициента a : если a > 0 , то будет + , + , а если a 0 , то − , − .
Если квадратный трехчлен не имеет корней, то знаки его значений для всей координатной прямой совпадают как со знаком старшего коэффициента a , так и со знаком свободного члена c .
Например, если мы возьмем квадратный трехчлен − 4 · x 2 − 7 , он не имеет корней (его дискриминант отрицательный). Коэффициент при x 2 есть отрицательное число − 4 , и свободный член − 7 тоже отрицателен. Это значит, что на промежутке ( − ∞ , + ∞ ) его значения отрицательны.
Примеры решения квадратных неравенств
Рассмотрим примеры решения квадратных неравенств с использованием рассмотренного выше алгоритма.
Решите неравенство 8 · x 2 − 4 · x − 1 ≥ 0 .
Решение
Используем для решения неравенства метод интервалов. Для этого найдем корни квадратного трехчлена 8 · x 2 − 4 · x − 1 . В связи с тем, что коэффициент при х четный, нам будет удобнее вычислить не дискриминант, а четвертую часть дискриминанта: D ‘ = ( − 2 ) 2 − 8 · ( − 1 ) = 12 .
Дискриминант больше нуля. Это позволяет нам найти два корня квадратного трехчлена: x 1 = 2 – 12 9 , x 1 = 1 – 3 4 и x 2 = 2 + 12 8 , x 2 = 1 + 3 4 . Отметим эти значения на числовой прямой. Так как уравнение нестрогое, то на графике мы используем обычные точки.
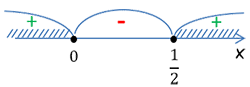
Теперь по методу интервалов определяем знаки трех полученных интервалов. Коэффициент при x 2 равен 8 , то есть, положителен, следовательно, последовательность знаков будет + , − , + .
Так как мы решаем неравенство со знаком ≥ , то изображаем штриховку над промежутками со знаками плюс:
Запишем аналитически числовое множество по полученному графическому изображению. Мы можем сделать это двумя способами:
( – ∞ ; 1 – 3 4 ] ∪ [ 1 + 3 4 , + ∞ ) или x ≤ 1 – 3 4 , x ≥ 1 + 3 4 .
Ответ: ( – ∞ ; 1 – 3 4 ] ∪ [ 1 + 3 4 , + ∞ ) или x ≤ 1 – 3 4 , x ≥ 1 + 3 4 .
Выполните решение квадратного неравенства – 1 7 · x 2 + 2 · x – 7 0 методом интервалов.
Решение
Для начала найдем корни квадратного трехчлена из левой части неравенства:
D ‘ = 1 2 – – 1 7 · – 7 = 0 x 0 = – 1 – 1 7 x 0 = 7
Это строгое неравенство, поэтому на графике используем «пустую» точку. С координатой 7 .
Теперь нам нужно определить знаки на полученных промежутках ( − ∞ , 7 ) и ( 7 , + ∞ ) . Так как дискриминант квадратного трехчлена равен нулю, а старший коэффициент отрицательный, то мы проставляем знаки − , − :
Так как мы решаем неравенство со знаком , то изображаем штриховку над интервалами со знаками минус:
В данном случае решениями являются оба промежутка ( − ∞ , 7 ) , ( 7 , + ∞ ) .
Ответ: ( − ∞ , 7 ) ∪ ( 7 , + ∞ ) или в другой записи x ≠ 7 .
Имеет ли квадратное неравенство x 2 + x + 7 0 решения?
Решение
Найдем корни квадратного трехчлена из левой части неравенства. Для этого найдем дискриминант: D = 1 2 − 4 · 1 · 7 = 1 − 28 = − 27 . Дискриминант меньше нуля, значит, действительных корней нет.
Графическое изображение будет иметь вид числовой прямой без отмеченных на ней точек.
Определим знак значений квадратного трехчлена. При D 0 он совпадает со знаком коэффициента при x 2 , то есть, со знаком числа 1 , оно положительное, следовательно, имеем знак + :
Штриховку мы могли бы нанести в данном случае над промежутками со знаком « – ». Но таких промежутков у нас нет. Следовательно, чертеж сохраняет вот такой вид:
В результате вычислений мы получили пустое множество. Это значит, что данное квадратное неравенство решений не имеет.
Квадратные неравенства
Чтобы решить квадратные неравенства вспомним, что такое квадратичная функция?
Квадратичная функция – это функция записанная формулой : y=ax 2 +bx+c, где x – независимая переменная, a, b и c – некоторые числа, при этом a≠0.
Графиком квадратичной функции является парабола.
В зависимости от значения a ветви графика направлены вверх или вниз:
- если a>0, то ветви параболы направлены вверх;
- если a 2 +bx+c=0
Квадратные неравенства имеют вид.
ax 2 +bx+c>0
ax 2 +bx+c 2 +bx+c≥0
ax 2 +bx+c≤0
Чтобы начать решать квадратные неравенства, необходимо знать как решаются квадратные уравнения?
А также для графического метода решения неравенства, необходимо знать алгоритм построения квадратичной функции или параболы?
Как решать квадратные неравенства?
Решение квадратных неравенств рассмотрим на примерах. Для начала разберем случаи, когда у квадратного уравнения дискриминант меньше нуля (нет корней).
Пример:
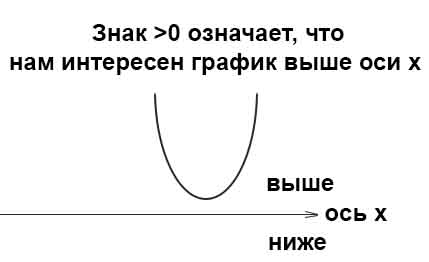
Дискриминант меньше нуля —236, следовательно у уравнения нет корней, а это значит, что весь график параболы находится выше оси х, потому что а=3>0 (ветви параболы смотрят вверх)
Можно проверить себя взяв любое число с числовой прямой, например число 1. Подставить число 1 вместо переменой х в неравенство 3x 2 +2x+20>0.
Получили верное неравенство 25>0, следовательно так как у нас нет корней уравнения нам подойдут все точки числовой прямой.
Пример:
Рассмотрим этот же пример со знаком неравенства меньше 0
3x 2 +2x+20 2 +2x+20=0
Дискриминант меньше нуля —236, следовательно у уравнения нет корней, значит парабола не пересекает ось x. Весь график параболы находится выше оси х, потому что а=3>0.
А знак уравнения меньше 2 +2x+20 2 +2•1+20 2 +x-2 2 +x-2=0
Дискриминант больше нуля, следовательно у уравнения два корня, значит парабола пересекает ось x в точка x=1 и x=-2. Ветви параболы смотрят вверх, потому что а=1>0.
Знак уравнения меньше 2 +x-2 2 +(-3)-2 2 +(0)-2 2 +(2)-2 2 +x-2>0
Дискриминант больше нуля, следовательно у уравнения два корня, значит парабола пересекает ось x в точка x=1 и x=-2. Ветви параболы смотрят вверх, потому что а=1>0.
Знак уравнения больше >0. Нам в ответ необходимо записать часть параболы, которая находится выше оси x. Визуально графически можно оценить по картинке, нам подходят интервалы (-∞;-2) и (1;+∞).

Первый участок (-∞;-2). На этом участке можно взять любое число меньше -2, например возьмем число -3 и подставим в неравенство x 2 +x-2 2 +(-3)-2>0
Получили верное неравенство 4>0, следовательно этот интервал (-∞; 2) подходит.
Второй участок (-2; 1). На этом участке можно взять число 0.
Получили неверное неравенство -2>0, следовательно этот интервал (-2; 1) не подходит.
Третий участок (1; +∞). На этом участке возьмем число 2.
Получили верное неравенство 4>0, следовательно этот интервал (1; +∞) подходит.
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/matematika/kvadratnye-neravenstva/reshenie-kvadratnyh-neravenstv-metodom-intervalov/
http://tutomath.ru/9-klass/kvadratnie-neravenstva.html
[/spoiler]
Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c < 0 a x 2 + b x + c ≤ 0 где a, b, c – некоторые числа, причем a ≠ 0, x – переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения.
Алгоритм решения квадратного неравенства методом интервалов
- Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 .
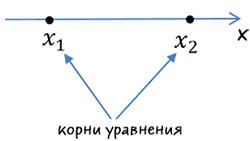
- Отметить на числовой прямой корни трехчлена.
Если знак неравенства строгий > , < , точки будут выколотые.
Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
- Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение a x 2 + b x + c вместо x.
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
- Выбрать подходящие интервалы (или интервал).
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.
- Записать ответ.
Примеры решения квадратных неравенств:
№1. Решить неравенство x 2 ≥ x + 12.
№2. Решить неравенство − 3 x − 2 ≥ x 2 .
№3. Решить неравенство 4 < x 2 + 3 x .
№4. Решить неравенство x 2 − 5 x < 6.
№5. Решить неравенство x 2 < 4.
№6. Решить неравенство x 2 + x ≥ 0.
Квадратные неравенства. Метод интервалов.
Квадратное неравенство – это неравенство вида ax2 + bx + c ν 0, где вместо ν может стоять любой из четырех знаков: <, ≤, >, ≥. Естественно, что а ≠ 0.
Чтобы воспользоваться методом интервалов при решении квадратных неравенств, надо уметь раскладывать квадратный трехчлен на множители. Посмотреть, как это делается, можно здесь.
Разберемся на примере. Пусть дано такое неравенство:
Чтобы разложить его на множители надо решить квадратное уравнение:
Решаем)
Корни уравнения найдены, теперь можем разложить квадратный трехчлен 3х2 + 4х – 4 на множители:
В исходном неравенстве заменяем левую часть на разложение. Тогда неравенство примет вид:
Разделив обе части на 3 получаем вот такую милашку:
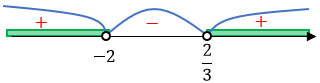
На числовой прямой отмечаем корни решенного нами ранее квадратного уравнения (можно сказать иначе: отмечаем такие числа, при которых левая часть неравенства обращается в ноль). Такими числами будут 2/3 и -2.
Далее определяем знаки трех получившихся промежутков.
Начинаем с правого. Возьмем любое число из промежутка (2/3; +∞); например, 1. Подставим его в левую часть неравенства и определим знак результата. Обе скобки получатся положительными, значит и весь результат будет положительный. Ставим плюс.
Из центрального промежутка (-2; 2/3) возьмем число 0. Подставляем и видим, что первая скобка отрицательная, вторая положительная. При умножении скобок с разными знаками результат получится отрицательный. Ставим минус.
И, наконец, из правого промежутка (-∞; -2) возьмем число -10. Подставляем… Обе скобки будут с отрицательными знаками, а при умножении они дадут положительный результат. Ставим плюс.
Смотрим на знак неравенства: >.
Выбираем положительные промежутки.
Ответ: (-∞; -2) ∪ (2/3; +∞).