В математике есть понятие нормированного пространства. По поводу ударения в слове “нормированное” существуют расхождения во мнениях. Пока я буду писать этот текст в своей голове буду делать ударение на букву и, если для вас этот вопрос принципиальный, то во время чтения вы можете делать ударение на вторую букву о. В конце концов, разговор у нас не лингвистический. Но вот если бы он был таким, можно было бы задаться вопросом от какого слово образовано это прилагательное и выяснить, что от глагола “нормировать”, т.е. устанавливать норму. Иными словами нормированное пространство это пространство на котором установлена норма. Интересно про какую норму вы сейчас подумали? На столько, что попрошу вас ответить на вопрос:
А теперь продолжим говорить, про ту норму о которой первым делом думают математики. Удивительно, но такое довольно серьезное понятие учащиеся российских школ проходят в шестом классе, когда начинают изучать отрицательные числа. Называют они его модулем и изучают, как вспомогательное понятие для вычислений. Но от этого оно не перестаёт быть менее важным. Помните, как определяется понятие модуля? Именно! Это расстояние. И да, можно сказать, что норма это расстояние. А нормированное пространство это пространство на котором задано расстояние, точнее способ находить расстояние, между элементами.
Пожалуй, тут у многих может возникнуть вопрос: “О каком расстоянии между математическими объектами можно говорить? ” Между городами понятно, даже между точками более-менее ясно. Но между функциями, числами или какими-нибудь матрицами? Не переживайте, нормой может быть всё что угодно, если оно удовлетворяет трём аксиомам нормы:
Если думать про норму, как про расстояние, эти аксиомы выглядят довольно логично.
В общем-то именно так развлекаются многие математики. Придумывают различные способы вычислять норму и смотрят к чему это может привести. Например, в 1897 Курт Гензель ввел понятие нормы для целых чисел.
Посчитаем с ее помощью расстояние между некоторыми числами:
Из определения видно, что это норма не может быть больше единицы. То есть, все целые числа лежат в круге с радиусом 1. Да, это те самые числа, которых бесконечно много. Но в p-адическом смысле все они довольно близки. р-адическую норму можно распространить и на рациональные числа:
Как видите рациональные числа выходят за пределы круга радиусом 1.
Внимание, сейчас будет сложная часть, рождение p-адических чисел. Как любое рождение оно требует усилий. Представьте, что вы выстроили целые числа в нумерованные последовательности, то есть каждому числу выдали номер и поставили в строй. Нас будут интересовать такие последовательности, для которых при достаточно больших номерах числах находятся очень близко друг к другу, в p-адическом смысле. Как очередь, у которой в начале люди стоят на расстоянии друг от друга, но потом всё ближе и ближе, а в какой-то момент сливаются в одну кучу. У таких последовательностей может быть предел, то есть каждое следующее число оказывается всё ближе к какому-то значению. Но предел не всегда принадлежит тому же множеству. Ведь все стремятся к идеалу, но часто он лежит за границей возможностей. Для чисел можно стереть эту границу, добавив все возможные пределы к множеству. Такая операция называется пополнением относительно нормирования. Если это p-адическое нормирование, то пределами будут p-адические числа.
Формально они представляют собой последовательности:
Похоже на сумму разрядных слагаемых, записанную справа налево. Над этими числами можно проводить операции сложения и умножения. Это выглядит довольно интересно, потому что производится в столбик, но справа налево.
Боюсь, к этому моменту у вас могло сложиться впечатления, что эти числа были придуманы исключительно для шокирования публики. Спешу вас разуверить. p-адические числа и p-адическая норма открыли совершенно новый взгляд на числа. Они наделили целые числа свойством непрерывности, что уже колоссально, но также нашли применение в решении задач теории чисел и теоретической физике. Для тех кто хочет подробностей, советую послушать лекции Конрада Кейта.
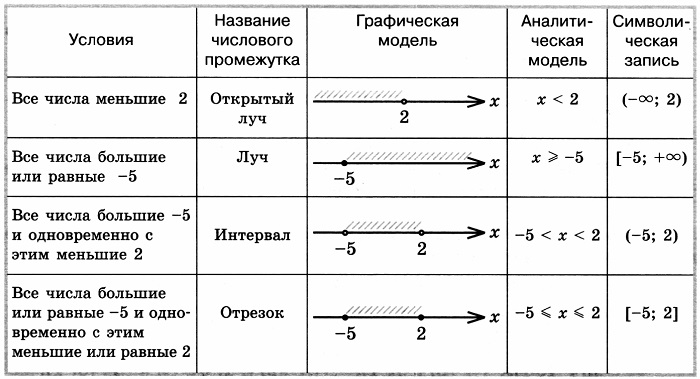
Среди множеств чисел имеются множества, где объектами выступают числовые промежутки. При указывании множества проще определить по промежутку. Поэтому записываем множества решений, используя числовые промежутки.
Данная статья дает ответы на вопросы о числовых промежутках, названиях, обозначениях, изображениях промежутков на координатной прямой, соответствии неравенств. В заключение будет рассмотрена таблица промежутков.
Виды числовых промежутков
Каждый числовой промежуток характеризуется:
- названием;
- наличием обычного или двойного неравенства;
- обозначением;
- геометрическим изображением на координатой прямой.
Числовой промежуток задается при помощи любых 3 способов из выше приведенного списка. То есть при использовании неравенства, обозначения, изображения на координатной прямой. Данный способ наиболее применимый.
Произведем описание числовых промежутков с выше указанными сторонами:
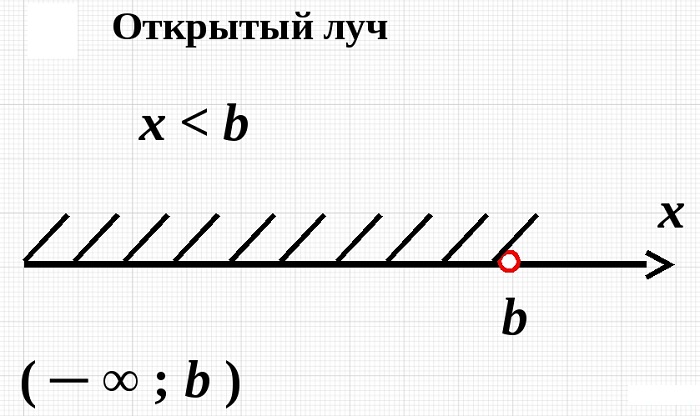
- Открытый числовой луч. Название связано с тем, что его опускают, оставляя открытым.
Этот промежуток имеет соответствующие неравенства x<a или x>a, где a является некоторым действительным числом. То есть на такое луче имеются все действительные числа, которые меньше a – (x<a) или больше a – (x>a).
Множество чисел, которые будут удовлетворять неравенству вида x<a обозначается виде промежутка (−∞, a), а для x>a, как (a, +∞).
Геометрический смыл отрытого луча рассматривает наличие числового промежутка. Между точками координатной прямой и ее числами имеется соответствие, благодаря которому прямую называем координатной. Если необходимо сравнить числа, то на координатной прямой большее число находится правее. Тогда неравенство вида x<a включает в себя точки, которые расположены левее, а для x>a – точки, которые правее. Само число не подходит для решения, поэтому на чертеже обозначают выколотой точкой. Промежуток, который необходим, выделяют при помощи штриховки. Рассмотрим рисунк, приведенный ниже.
Из вышеприведенного рисунка видно, что числовые промежутки соответствуют части прямой, то есть лучам с началом в a. Иначе говоря, называется лучами без начала. Поэтому он и получил название открытый числовой луч.
Рассмотрим несколько примеров.
При заданном строгом неравенстве x>−3 задается открытый луч. Эту запись можно представить в виде координат (−3, ∞) . То есть это все точки, лежащие правее, чем -3.
Если имеем неравенство вида x<2,3, то запись (−∞, 2,3) является аналогичной при задании открытого числового луча.
- Числовой луч. Геометрический смысл в том, что начало не отбрасывается, иначе говоря, луч оставляет за собой свою полноценность.
Его задание идет с помощью нестрогих неравенств вида x≤a или x≥a. Для такого вида приняты специальные обозначения вида (−∞, a] и [a, +∞), причем наличие квадратной скобки имеет значение того, что точка включена в решение или в множество. Рассмотрим рисунок, приведеный ниже.
Для наглядного примера зададим числовой луч.
Неравенство вида x≥5 соответствует записи [5, +∞), тогда получаем луч такого вида:
- Интервал. Задавание при помощи интервалов записывается при помощи двойных неравенств a<x<b, где а и b являются некоторыми действительными числами, где a меньше b, а x является переменной. На таком интервале имеется множество точек и чисел, которые больше a, но меньше b. Обозначение такого интервала принято записывать в виде (a, b). Наличие круглых скобок говорит о том, что число a и b не включены в это множество. Координатная прямая при изображении получает 2 выколотые точки.
Рассмотрим рисунок, приведенный ниже.
Пример интервала −1<x<3,5 говорит о том, что его можно записать в виде интервала (−1, 3,5). Изобразим на координатной прямой и рассмотрим.
- Числовой отрезок. Данный промежуток отличается тем, что он включает в себя граничные точки, тогда имеет запись вида a≤x≤b. Такое нестрогое неравенство говорит о том, что при записи в виде числового отрезка применяют квадратные скобки [a, b], значит, что точки включаются во множество и изображаются закрашенными.
Рассмотрев отрезок, получим , что его задание возможно при помощи двойного неравенства 2≤x≤3, которое изображаем в виде 2, 3. На координатной прямой данный точки будут включены в решение и закрашены.
- Полуинтервалы. Это промежуточные интервалы с включением приграничных точек. Они записываются при помощи двойных неравенств вида a<x≤b или a≤b<c, где (a, b] и [a, b). Изобразим на координатной прямой.
Если имеется полуинтервал (1, 3], тогда его обозначение можно в виде двойного неравенства 1<x≤3, при чем на координатной прямой изобразится с точками 1 и 3, где 1 будет исключена, то есть выколота на прямой.
Таблица числовых промежутков
Промежутки могут быть изображены в виде:
- открытого числового луча;
- числового луча;
- интервала;
- числового отрезка;
- полуинтервала.
Чтобы упростить процесс вычисления, необходимо пользоваться специальной таблицей, где имеются обозначения всех видов числовых промежутков прямой.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Числовые промежутки представляют собой множества чисел на координатной прямой. Это ось, на которой расположены точки или переменные, имеющие определенные координаты. Для нее важно начало отсчета, выбранный единичный отрезок и направление, чтобы обозначать положительные и отрицательные значения.
Знакомство с координатами и числами происходит на уроках математики в 6 классе, но некоторые понятия вводятся уже с 1 класса. Понятия и обозначения используются на протяжении всего курса алгебры и геометрии. Знакомство с азами в средней школе позволит легко справляться со сложными задачами в будущем. Со временем проводятся вычисления со множествами чисел, это касается их пересечения и объединения.
Виды числовых промежутков
На координатной прямой можно выделить несколько видов промежутков. При этом они зависят от одной или двух переменных, расположенных на оси. Они служат границами. Сама прямая имеет координаты (-∞; +∞), то есть от минус бесконечности до плюс бесконечности.
Промежутки позволяют находить значения числовых выражений даже для учащихся младших классов. Выбирается место отсчета и единичный отрезок, что характеризует любую координатную прямую.
Чтобы выполнить простое арифметическое действие, нужно нарисовать нужное число отрезков. Чтобы сложить «2» и «3», достаточно отмерить сначала два, затем три выбранных единицы и сосчитать полученный результат. Так наглядно представляются простые математические операции для младших школьников.
На координатную прямую можно нанести известные значения и сравнить их, обращая внимание на положение. Так дети наглядно представляют, какое число меньше, а какое больше.
Открытый числовой луч
Открытый луч – интервал с бесконечно большим числом точек. При объяснении понятие «числовой» часто опускается, при этом смысл не меняется.
Точки расположены по одну сторону от определенной переменной, признанной началом координат.
Находиться они могут как с правой, так и с левой стороны. При этом если за основу берется А, то множество обозначается следующим образом:
-
(-∞; А);
-
(А; +∞).
Таким образом указываются координаты. Читается как «от минус бесконечности до А» и «от А до плюс бесконечности».
Также можно охарактеризовать неравенством:
-
х < А;
-
х > А.
Знак зависит от расположения луча относительно А.
Замкнутый числовой луч
Замкнутый луч отличается от открытого тем, что к множеству относится А.
Также ему соответствует условие:
-
х ≤ А (значение меньше или равно А) или (-∞; А], то есть используются квадратные скобки;
-
х ≥ А (значение больше или равно А) или [А; +∞).
При графическом изображении А в этом случае закрашивается, на рисунке она черная.
Что касается открытого луча, то там А остается пустой, еще ее называют выколотой. Она связана с переменной строгим неравенством, не принадлежит к рассматриваемому множеству.
Числовой отрезок
Отрезок – замкнутый, закрытый промежуток или расстояние. Это множество переменных, расположенных на прямой между двумя точками, А и В. При этом они относятся к рассматриваемому множеству и называются концами.
При изображении они будут закрашены. Остальные точки отрезка считаются внутренними.
Обозначается отрезок, например, -7 ≤ х ≤ 3. Запись читается следующим образом: «отрезок от минус семи до трех».
Интервал
Интервал представляет собой открытый отрезок, от которого он отличается тем, что границы к нему не относятся. Интервалу принадлежат исключительно внутренние точки прямой, границы же будут выколоты.
Обозначается, например, 5 < х < 13. Читается запись как «интервал от пяти до тринадцати».
Полуинтервал
Полуинтервал – интервал, при этом одна из точек, его ограничивающих, входит в него. То есть он закрыт с одной стороны. При этом неважно, какая из границ будет принадлежать интервалу, а какая нет.
Обозначаются с помощью двойных неравенств, при этом они называются нестрогими, так как используются знаки «больше или равно» или «меньше или равно». Одна из точек на графике не будет закрашена.
Обозначение может выглядеть, например, так -2 ≤ х < 9, «полуинтервал от минус двух до девяти».
Таблица числовых промежутков
Все промежутки имеют обозначения и неравенства. Данные об этом собраны в таблице. Каждому виду соответствует графическое изображение.
Наглядное изображение поможет восприятию и закреплению материала.
Границы представлены а и b, они так и называются, граничными точками. При этом знаки ≥ и ≤ обозначаются квадратной скобкой. При графическом изображении такая граница закрашивается, это означает, что она входит в множество. Строгие неравенства соответствуют выколотым точкам на графиках.
Промежутки знакомят школьников с простыми неравенствами, строгими и нестрогими, которые необходимы для решения сложных математических задач.
Числовые промежутки
- Виды числовых промежутков
- Открытый и замкнутый луч
- Отрезок
- Интервал и полуинтервал
Числовые промежутки или просто промежутки — это числовые множества, которые можно изобразить на координатной прямой. К числовым промежуткам относятся лучи, отрезки, интервалы и полуинтервалы.
Виды числовых промежутков
| Название | Изображение | Неравенство | Обозначение |
|---|---|---|---|
| Открытый луч |  |
x > a | (a; +∞) |
 |
x < a | (-∞; a) | |
| Замкнутый луч |  |
x ⩾ a | [a; +∞) |
 |
x ⩽ a | (-∞; a] | |
| Отрезок |  |
a ⩽ x ⩽ b | [a; b] |
| Интервал |  |
a < x < b | (a; b) |
| Полуинтервал |  |
a < x ⩽ b | (a; b] |
 |
a ⩽ x < b | [a; b) |
В таблице a и b — это граничные точки, а x — переменная, которая может принимать координату любой точки, принадлежащей числовому промежутку.
Граничная точка — это точка, определяющая границу числового промежутка. Граничная точка может как принадлежать числовому промежутку, так и не принадлежать ему. На чертежах граничные точки, не принадлежащие рассматриваемому числовому промежутку, обозначают незакрашенным кругом, а принадлежащие — закрашенным кругом.
Открытый и замкнутый луч
Открытый луч — это множество точек прямой, лежащих по одну сторону от граничной точки, которая не входит в данное множество. Открытым луч называется именно из-за граничной точки, которая ему не принадлежит.
Рассмотрим множество точек координатной прямой, имеющих координату, большую 2, а, значит, расположенных правее точки 2:
Такое множество можно задать неравенством x > 2. Открытые лучи обозначаются с помощью круглых скобок — (2; +∞), данная запись читается так: открытый числовой луч от двух до плюс бесконечности
.
Множество, которому соответствует неравенство x < 2, можно обозначить (-∞; 2) или изобразить в виде луча, все точки которого лежат с левой стороны от точки 2:
Замкнутый луч — это множество точек прямой, лежащих по одну сторону от граничной точки, принадлежащей данному множеству. На чертежах граничные точки, принадлежащие рассматриваемому множеству, обозначаются закрашенным кругом.
Замкнутые числовые лучи задаются нестрогими неравенствами. Например, неравенства x ⩾ 2 и x ⩽ 2 можно изобразить так:
Обозначаются данные замкнутые лучи так: [2; +∞) и (-∞; 2], читается это так: числовой луч от двух до плюс бесконечности
и числовой луч от минус бесконечности до двух
. Квадратная скобка в обозначении показывает, что точка 2 принадлежит числовому промежутку.
Отрезок
Отрезок — это множество точек прямой, лежащих между двумя граничными точками, принадлежащими данному множеству. Такие множества задаются двойными нестрогими неравенствами.
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:
Множество точек, из которых состоит данный отрезок, можно задать двойным неравенством -2 ⩽ x ⩽ 3 или обозначить [-2; 3], такая запись читается так: отрезок от минус двух до трёх
.
Интервал и полуинтервал
Интервал — это множество точек прямой, лежащих между двумя граничными точками, не принадлежащими данному множеству. Такие множества задаются двойными строгими неравенствами.
Рассмотрим отрезок координатной прямой с концами в точках -2 и 3:
Множество точек, из которых состоит данный интервал, можно задать двойным неравенством -2 < x < 3 или обозначить (-2; 3). Такая запись читается так: интервал от минус двух до трёх
.
Полуинтервал — это множество точек прямой, лежащих между двумя граничными точками, одна из которых принадлежит множеству, а другая не принадлежит. Такие множества задаются двойными неравенствами:
Обозначаются данные полуинтервалы так: (-2; 3] и [-2; 3). Читается это так: полуинтервал от минус двух до трёх, включая 3
, и полуинтервал от минус двух до трёх, включая минус два
.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 декабря 2021 года; проверки требуют 6 правок.
У этого термина существуют и другие значения, см. Промежуток.
Промежуток[1], или, если более точно, промежуток числовой прямой, — это множество вещественных чисел — таких, что если некоторые два числа принадлежат этому множеству, то любое число, лежащее между ними, тоже принадлежит этому множеству[2]. С использованием логических символов это определение можно записать так:
- множество
является промежутком, только если
где 
Типы промежутков[править | править код]
Конечный промежуток[править | править код]
Конечный промежуток состоит из множества чисел, заключённых между двумя числами 


Замкнутый (закрытый) конечный промежуток[править | править код]
Если 

![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
В случае 
Открытый конечный промежуток[править | править код]
Если 


Для обозначения открытого промежутка вместо 
![{displaystyle ]a,b[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b51ec208e9582e11a4f340a42d4f17fb4748fcb)
Полузамкнутый (полуоткрытый) конечный промежуток[править | править код]
Промежутки
называются полусегментами (не дополненными до сегмента) или полуинтервалами.
Бесконечный промежуток[править | править код]
Бесконечные промежутки
и
с положительной или с отрицательной стороны не ограничены каким-либо вещественным числом. В этом случае удобно считать, что у этих промежутков одним из концов или обоими концами служат несобственные числа 



при этом из-за того, что 


Пустой промежуток[править | править код]
Пустое множество 
- где a < b.
Промежутки аффинно расширенной числовой прямой[править | править код]
Множество вещественных чисел 



При этом для любого вещественного числа 
Для расширенной числовой прямой тоже вводят понятия промежутков — отрезков, интервалов, полуинтервалов[1]. В отличие от соответствующих промежутков числовой прямой, они могут содержать элементы 
![(a, +infty] = (a, +infty) cup {{+infty}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2744315517be20cc64563ba44f7ab65bdb3344d0)
Терминология[править | править код]
В русском языке слова промежуток и интервал соответствуют одному английскому слову interval. В англоязычной литературе[4] и в переводах иностранных книг, а также в некоторых других книгах на русском языке используется следующая терминология:
— замкнутый интервал (англ. closed interval),
— открытый интервал (англ. open interval),
или
— полуоткрытый (или полузамкнутый) интервал (англ. half-open interval/half-closed interval).
То есть в такой терминологии они все называются интервалами, но только разного типа.
В более старой русскоязычной литературе[5] вместо «интервал» используется слово промежуток: замкнутый промежуток, открытый промежуток, полуоткрытый (или полузамкнутый) промежуток.
Однако, особенно в учебной литературе, где наибольшее количество теорем для функций на компактных множествах, для замкнутого промежутка предпочтительным считают использовать отдельное название в одно слово — сегмент[3] (термин «отрезок» имеет скорее геометрический оттенок, как и «промежуток числовой прямой»). В этом случае термин «интервал» закрепляется только за открытым промежутком.
См. также открытые и замкнутые множества.
Факты[править | править код]
Теорема о промежуточных значениях[править | править код]
Известная теорема Больцано — Коши о промежуточных значениях непрерывной функции гласит: образ любого промежутка при непрерывном отображении тоже является промежутком. У этой теоремы есть обобщение на случай произвольных топологических пространств: образ связного множества при непрерывном отображении связен. Числовые промежутки, и притом только они, как раз и являются связными подмножествами 
Операции с промежутками[править | править код]
На практике промежуток нередко характеризует интервал возможных значений (приближённо) измеренной величины. На множестве таких промежутков можно определить арифметические операции. Тогда результату вычислений над величинами можно сопоставить соответствующие вычисления над их интервалами, задающие в итоге интервал возможных значений для результата.
Мера[править | править код]
Промежутки числовой прямой, а также прямоугольники на плоскости, прямоугольные параллелепипеды в пространстве и т. п. являются одним из основных объектов, на которых основывается теория меры, поскольку они являются простейшими множествами, меру которых (длину, площадь, объем и т. п.) легко определить.
Обобщения[править | править код]
Связные множества[править | править код]
Обобщением промежутка числовой прямой является понятие связного топологического пространства. На числовой прямой всякое связное множество есть промежуток, и обратно, любой промежуток есть связное множество.
Также промежуток числовой прямой лежит в основе другого, более специального понятия линейной связности. Во множестве вещественных чисел 


Выпуклые множества[править | править код]
Другим обобщением понятия промежутка числовой прямой является понятие выпуклого множества.
Промежутки в частично упорядоченных множествах[править | править код]
В самом общем случае понятие промежутка можно ввести на любом множестве, на котором введено отношение порядка 
См. также[править | править код]
- Интервальная арифметика
- Отрезок
Примечания[править | править код]
- ↑ 1 2 3 Кудрявцев, Л. Д. Курс математического анализа. — 5-е изд. — М.: «Дрофа», 2003. — Т. 1. — С. 64—65. — 704 с. — ISBN 5-7107-4119-1.
- ↑ В ряде источников описывается как интервал; например, см. Интервал // Казахстан. Национальная энциклопедия. — Алматы: Қазақ энциклопедиясы, 2005. — Т. II. — ISBN 9965-9746-3-2. (CC BY-SA 3.0)
- ↑ 1 2 В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. I. — С. 53. — 672 с. — ISBN 5-482-00445-7. Архивная копия от 23 июня 2015 на Wayback Machine
- ↑ Гелбаум, Б., Олмстед, Дж. Контрпримеры в анализе = Counterexamples in Analysis. — М.: ЛКИ, 2007. — С. 17—18. — 258 с. — ISBN 978-5-382-00046-6.
- ↑ Фихтенгольц, Г. М. Основы математического анализа. — 7-е изд. — М.: «ФИЗМАТЛИТ», 2002. — Т. 1. — С. 35. — 416 с. — ISBN 5-9221-0196-X.






















![{displaystyle [a,b] {stackrel {text{def}}{=}} {xin mathbb {R} colon aleqslant xleqslant b}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c1bf5713da2592580171e198039b5ab9459deef)

![{displaystyle [a,b) {stackrel {text{def}}{=}} {xin mathbb {R} colon aleqslant x<b},quad (a,b] {stackrel {text{def}}{=}} {xin mathbb {R} colon a<xleqslant b}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/035fa2ecf5884a2c3986a09a996417c95bccdf19)


![{displaystyle [a,+infty ),quad (a,+infty ),quad (-infty ,b],quad (-infty ,b),quad (-infty ,+infty ),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b172bc8ecc11be3af5f260409cbbb1b03fea08b2)
![{displaystyle [b,a]=(b,a)=[b,a)=(b,a]=(a,a)=[a,a)=(a,a]=varnothing ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fff26c6e81f2c175be055610b7fa07bfaa044371)
![{displaystyle {overline {mathbb {R} }}=mathbb {R} cup {-infty ,+infty }=[-infty ,+infty ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e752a1488f9e5a72bf686b79d1cc41099e05a06)

![{displaystyle [a,b]={xin mathbb {R} colon aleqslant xleqslant b}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/380ad560c1428e1193da25128c3f384b471f85ce)


![{displaystyle (a,b]={xin mathbb {R} colon a<xleqslant b}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79fcac40034182c9d22041ccef012f55f48422ed)
