Мы продолжаем постигать основы академического рисунка. В статье «Основы академического рисунка. Начало.» мы смогли познакомиться с самыми азами рисунка карандашом, в этой статье я расскажу о том как определять пропорции предметов и зачем это нужно.
Что такое пропорции?
Из математики мы знаем, то пропорции это равенство двух отношений, 9:3=18:6 или 10:5=4:2 и так далее. В рисунке пропорции это ровно тоже самое, что и пропорции в математике, только выглядит это немного по другому. На рисунке изображены предметы разделённые на две группы. В каждой группе изображены предметы разных размеров, но имеющие одинаковые пропорции. Посмотрите на силуэты кувшинчиков: все изображенные на рисунке кувшины имеют одинаковые пропорции поэтому похожи как близнецы-братья.

Если на портрете человек получился очень похожим, значит художник правильно определил и передал в рисунке пропорции этого человека. Именно от правильности передачи пропорций и зависит будет ли похоже наше изображение на изображаемую натуру.
Вернёмся к нашей картинке и посмотрим на следующую группу предметов: это простые незатейливые прямоугольники и да, они хоть и все разного размера, но имеют одинаковые пропорции и поэтому очень похожи. Именно на прямоугольниках нагляднее всего видно что такое пропорции в рисунке. У прямоугольника есть длинная сторона и короткая сторона, длинна и ширина. У наших прямоугольников ширина (короткая сторона) укладывается в длине (длинной стороне) ровно два раза. То есть ширина в два раза меньше длинны. Допустим мы начертили прямоугольник со сторонами два сантиметра (короткая сторона) и четыре сантиметра (длинная сторона), также мы начертили прямоугольник со сторонами одиннадцать сантиметров и двадцать два сантиметра, потом начертили прямоугольник со сторонами три сантиметра семь миллиметров и семь сантиметров четыре миллиметра — все эти прямоугольники будут иметь одинаковые пропорции. У всех этих прямоугольников ширина ровно в два раза короче длинны, то есть если разделить длину на ширину получится одно и тоже число, в данном случае два (4:2=22:11=7,4:3,7=2). Мы можем взять прямоугольник со сторонами четыре сантиметра и семь сантиметров, а также прямоугольник со сторонами шесть сантиметров и десять с половиной сантиметров и опять у нас прямоугольники разного размера но с одинаковыми пропорциями. И хоть на этот раз при делении большей длинны на меньшую мы получим не два а другое число, это не имеет значения. Значение имеет то, что число в обеих случаях получается одинаковое (7:4=10,5:6), можете проверить.

Теперь разберем это на примере кувшинчиков. У кувшинчиков уже не две стороны как было у прямоугольников. Здесь мы имеем: высоту кувшинчика, ширину горлышка, высоту горлышка, высоту на которой находится самая широкая часть кувшина, ширина кувшина. Сравним между собой все части кувшина. Большой зелёный кувшин высотой 18 сантиметров, ширина горлышка у него 6 сантиметров, ширина самой широкой части кувшина 9 сантиметров и так далее. Если мы разделим высоту кувшинчика на ширину его горлышка, мы получим число три, если мы разделим высоту кувшинчика на ширину его самой широкой части мы получим число два. Сравним наш большой зелёный кувшин с маленьким красным. Высота маленького красненького кувшинчика 9 сантиметров, ширина горлышка 3 сантиметра, ширина самой широкой части кувшинчика 4,5 сантиметра. Разделив высоту маленького кувшинчика на ширину его горлышка мы получим число три, а разделив высоту на ширину самой широкой части получим число два. Всё точно также как и у большого зелёного кувшина, два наших кувшина имеют одинаковые пропорции. Пропорции — это соотношение всех частей предмета между собой. Предметы имеющие одинаковые соотношения частей, имеют одинаковые пропорции. Но что это мы всё про деление и числа? У нас ведь не урок математики? Можно описать пропорции кувшинов и по другому. Ширина горлышка имеющихся у нас кувшинов укладывается в высоте три раза, ширина самой широкой части кувшинов укладывается в их высоте ровно два раза, высота горлышка равна его ширине, ширина донышка в два раза меньше ширины горлышка и в три раза меньше ширины самой широкой части кувшинов. Всё это нам надо знать, чтобы точно изобразить объект на рисунке. Так как же нам измерить объекты, которые мы хотим нарисовать?
Визирование и измерение.
Метод, которым художники пользуются для определения пропорций, называется визирование. В академическом рисунке не пользуются линейками, транспортирами и другими приспособлениями. У художника есть универсальный инструмент для всех измерений — его карандаш. Мы уже знаем как, с помощью карандаша, можно измерять линии проведенные на листе бумаги, делить отрезки на равные части, проверять вертикальности и горизонтальность проведенных линий. Кто этого не знает, тот может прочитать статью «Основы академического рисунка. Начало». А теперь немного отвлечемся и разберёмся, что же такое на самом деле — измерение. Когда мы измеряем какой либо предмет или просто отрезок прямой, на самом деле мы сравниваем его длину (или ширину) с сантиметром или метром, или другой длинной принятой за единицу измерения. В метрах и сантиметрах мы измеряем не так давно. Раньше, когда сантиметров ещё не было, для измерений приходилось использовать другие вещи. Например в английской системе измерений есть такая единица измерения как фут. Сейчас принято — фут равен 30,48 сантиметрам, однако изначально фут это длинна человеческой стопы (собственно так слово «фут» и переводится на русский). Мы в детстве, ничего не зная о футах, часто пользовались такой единицей измерения, когда рисовали на асфальте «клеточки» для игры в «классики», просто проходя вдоль линии и ставя одну пяткой плотно к носку другой. Сами понимаете, что у единиц измерения подобных футу, есть серьёзный недостаток — у разных людей стопы немного различаются по длине. Поэтому и возникла необходимость в стандартизации системы измерений. Из всего этого, становится ясно, что измерять можно в чем угодно, хоть в попугаях. Кто не совсем понял, что такое измерение, может посмотреть замечательный мультфильм «Тридцать восемь попугаев».

А нам пора вернуться к постижению основ академического рисунка. И так перед нами предмет который нам предстоит нарисовать. С чего начать? Не торопитесь что то рисовать на чистом листе! Начать надо с того, что изучить натуру. Посмотрим на предмет. Это бутылка, бутылка довольно простой формы. Чтобы наш рисунок достоверно отображал натуру (то есть чтобы бутылка у нас получилась похожей), нам необходимо правильно определить пропорции. Для того, чтобы определить пропорции бутылки, нам необходимо её измерить. Мы не будем мереть бутылку линейкой, все измерения мы будем проводить карандашом, мало того, мы будем измерять бутылку на расстоянии. У бутылки есть высота всей бутылки, высота горлышка, высота «тела бутылки», ширина горлышка и ширина самой бутылки. Берём карандаш в правую руку (если Вы правша), то есть в ту руку которой Вы обычно рисуете. Вытягиваем руку перед собой и закрываем один глаз (всё равно какой). Следует четко, раз и навсегда запомнить — все измерения проводим только вытянутой рукой. Это очень важно, расстояние от глаза до карандаша, которым мы измеряем, всё время измерений должно оставаться одинаковым.

Длинна человеческой руки, как правило, не успевает измениться за пару часов (просто руки не растут так быстро) и поэтому расстояние от глаза до карандаша в нашей руке всегда одинаковое. Когда же мы сгибаем руку в локте, то нам будет очень трудно удерживать карандаш на одном и том же расстоянии от глаза, а это очень влияет на точность измерений. И так: мы закрыли один глаз и держим карандаш перед собой в вытянутой руке. Карандаш всегда держим перпендикулярно вытянутой руке. Острый кончик карандаша совмещаем с верхом бутылки и ногтем большего пальца, отмечаем место где начинается горлышко бутылки.

Теперь нам надо выяснить сколько раз высота горлышка помещается в высоте всей бутылки. Для этого, не меняя положения большого пальца на карандаше, перемещаем карандаш немного вниз, так что бы место на карандаше, отмеченное большим пальцем, совпало с донышком бутылки. Мысленно отмечаем точку на бутылке в которой находится сейчас кончик карандаша и перемещаем карандаш вверх так, чтобы точка отмеченная на карандаше большим пальцем, совпала с точкой мысленно нами отмеченной. Продолжаем перемещать карандаш таким образом вдоль бутылки пока бутылка «не закончится». Если Вы заметили, то в последний раз кончик карандаша оказался выше горлышка бутылки, не меняя положения большого пальца, отмечаем на карандаше точку совпадающую с концом горлышка бутылки и видим, что карандаш выходит за пределы бутылки как раз на две третьи того расстояния, которое мы на нём отметили. У нас получилось, что высота горлышка укладывается в высоте всей бутылки четыре раза полностью и одну треть. Теперь сравним ширину бутылки с высотой бутылки.

Опять берём карандаш на вытянутую руку, только теперь поворачиваем карандаш горизонтально, закрываем один глаз и совмещаем кончик карандаша с левым краем бутылки (если мы держим карандаш в правой руке), большим пальцем отмечаем на карандаше место, которое совпадает с правым краем бутылки. Разворачиваем карандаш вертикально, не меняя положения большого пальца, совмещаем место на карандаше, отмеченное большим пальцем, с нижним концом бутылке и проделываем тоже самое, что мы делали когда выясняли сколько раз высота горлышка умещается в высоте бутылки. Мы видим, что ширина бутылки умещается в высоте столько же раз, сколько в высоте бутылки умещается высота горлышка. Логично предположить, что ширина бутылки равна высоте горлышка. Сравниваем ширину бутылки с высотой горлышка. Измеряем ширину бутылки (как мы уже это делали ранее), разворачиваем карандаш вертикально, совмещаем место карандаша отмеченное большим пальцем с началом горлышка бутылки и видим, что кончик карандаша совпал с концом горлышка. Да, ширина бутылки равна высоте горлышка бутылки. Осталось определить ширину горлышка бутылки. Можно сравнить ширину горлышка с высотой всей бутылки, однако в этом нет необходимости, проще сравнить ширину горлышка с высотой горлышка или с шириной бутылки. Так будет проще и быстрее.

Измеряем ширину горлышка точно так же как измеряли ширину бутылки, поворачиваем карандаш вертикально и сравниваем ширину горлышка с высотой. Получается ширина горлышка помещается в высоте горлышка один и две третьи раза. Мы определили пропорции бутылки. Все измерения мы делали без непосредственного контакта с измеряемым объектом (так сказать дистанционно), это и называется визированием. Рисовать бутылку сейчас мы не будем, потому что для того чтобы грамотно нарисовать бутылку необходимо знать правила построения тел вращения, а об этом мы поговорим в следующий раз. Для начала мы потренируемся на плоских предметах.
Изображение плоских предметов.
Для начала нарисуем постановку из двух разделочных досок. Выполняя это несложное упражнение мы потренируемся в определении пропорций, а так же вспомним как проводить вертикальные и горизонтальные линии, откладывать расстояние без линейки и делить отрезки на части, опять же без линейки, используя только карандаш. Изображая что либо на плоскости листа мы создаём новый мир и первое что должны сделать — выбрать единицу измерения этого мира. Единицей измерения на нашем рисунке мы выбрали высоту желтой разделочной доски, именно с этим линейным размером мы и будем сравнивать все остальные линейные размеры на нашем рисунке. Надо запомнить и принять как данность, что вселенная нашего рисунка и вселенная постановки это две разные вселенные. И хоть мы и создаём копию нашей постановки, но переносить размеры на лист мы не можем, мы переносим только пропорции. То есть измерив (методом визирования) высоту желтой разделочной доски, мы не откладываем это же расстояние на листе бумаги (получится очень маленькое расстояние). На рисунке мы выбираем тот размер высоты предмета, который нам нужен по композиции. А потом мы все другие размеры определяем, сравнивая с этим самым выбранным размером (модулем). И так: мы приготовили себе рабочее место, поставили постановку, с чего начать? Начинать всегда следует с изучения натуры. Мы смотрим что из себя представляет постановка? В нашем случае это постановка из двух плоских предметов простой прямоугольной формы, расположены они к нам фронтально, таковы условия задачи. Для постановки я использовала две пластиковые разделочные доски разного размера и цвета. Но это могут быть и другие плоские прямоугольные предметы, например планшет и электронная книга.
Сначала нам надо определится с размерами всего нашего натюрморт. Берём карандаш и совмещаем кончик карандаша с левым краем желтой доски, а большим пальцем отмечаем то место с которым совпадает правый край зелёной доски. Разворачиваем карандаш вертикально и совмещаем место на карандаше отмеченное большим пальцем с нижним краем зелёной доски (поскольку именно на нижнем крае зелёной доски находятся самые нижние точки нашего натюрморта). Теперь смотрим, сравниваем ширину нашего натюрморта с его высотой. Мы видим, что кончик нашего карандаша не достаёт до самой высокой точки натюрморта (верхнего края желтой доски), значит общая высота натюрморта больше общей ширины натюрморта. Значит свой лист мы располагаем вертикально.

Приступаем к рисунку. Любой рисунок начинаем с компоновки в листе, от правильной композиции зависит весь рисунок. Намечаем в каких границах будет расположен наш натюрморт на листе. Изображение на листе не должно быть мелким и не должно упираться в край листа, лучше оставить больше места снизу листа чем сверху. Отмечаем нижний край желтой доски и её верхний край. Мы определились с высотой желтой доски, с этой высотой мы и будем сравнивать все остальные расстояния. Проводим линию обозначающую левый край желтой доски. Измеряем ширину желтой доски и сравниваем её с высотой (также как мы это делали с бутылкой). Ширина желтой доски умещается в её высоте один с половиной раза. Значит отмеченную на листе высоту мы делим на четыре равные части и откладываем вправо от линии, обозначающей левый край желтой доски, три четверти высоты желтой доски, намечаем контуры желтой доски. Мы видим, что у доски скруглённые края. Это определяет характер формы, поэтому скругляем края.

Теперь надо нарисовать отверстие в доске. Переключаем внимание на натуру и методом визирования измеряем сколько места занимает отверстие в ширине доски. Отверстие занимает половину ширины доски, при этом расположено оно строго по середине. Делим ширину доски на четыре части, отступаем одну четвертую от левого края и одну четвертую от правого края, отмечаем левый и правый край отверстия. Отверстие имеет полукруглую форму, от верхнего края доски отверстие располагается примерно на одной шестнадцатой части высоты доски, но такие не большие расстояния проще отмечать на глаз, так и делаем. Рисуем форму отверстия.

Переходим к рисованию зелёной доски. Маленькая зелёная доска стоит впереди желтой большой, поэтому на рисунке нижний край зелёной доски будет чуть-чуть ниже края желтой доски. Насколько ниже можно определить на глаз, а можно определить проведя мысленно линию от левого нижнего угла желтой доски к левому нижнему углу зеленой доски. Берём карандаш и подводим его под левые нижние углы досок, как бы соединяя эти углы карандашом, карандаш определит угол под которым пройдет линия соединяющая углы досок. Проводим эту линию на рисунке (линия эта вспомогательная и в конце мы её сотрём), но она поможет нам определить, где же будет нижний край зелёной доски по отношению к краю желтой доски. С нижним краем зелёной доски мы определились, теперь определяем высоту зелёной доски. Методом визирования сравниваем высоту зелёной доски с высотой желтой доски и выясняем, что высота зелёной доски помещается в высоте желтой один с половиной раза.

Получается высота зелёной доски равна ширине желтой доски. Откладываем от линии обозначающей нижний край зелёной доски вверх расстояние равное ширине желтой доски и проводим линию, которая обозначает высоту зелёной доски. Теперь нам надо определить ширину зелёной доски. На этот раз нам будет удобнее сравнить ширину зелёной доски с её же высотой, а не сравнивать ширину зелёной доски с высотой желтой доски. Так и поступим. Выясняем, что ширина зелёной доски умещается в её высоте один с половиной раза, то есть у зелёной доски такие же пропорции ка и у желтой. Следует обратить внимание ещё на один нюанс — расположена зелёная доска так, что она перекрывает часть жёлтой доски. Правый край желтой доски проходит как раз по середине зелёной доски. Расстояние равное трём четвертям высоты зелёной доски делим на две равные части, полученное в результате этого деления расстояние откладываем влево и вправо от правого края желтой доски (то есть от середины ширины зелёной доски). Проводим вертикальные линии и у нас получаются левый край и правый край зелёной доски. Скругляем края у получившегося прямоугольника.

Нам осталось нарисовать отверстие в зелёной доске. Если общие пропорции двух досок одинаковые, то пропорции у отверстий немного отличаются. Отверстие в желтой доске расположено по центру ширины и занимает половину ширины, при этом от краев доски отверстие удалено на одну четвертую. В зелёной доске отверстие тоже расположено строго посередине ширины, очень похоже по форме на отверстие в желтой доске, но занимает три пятые ширины зелёной доски и от краев удалено на расстояние в одну пятую ширины зелёной доски. Нам придётся разделить ширину зелёной доски на пять равных частей, отступить от краёв по одной пятой и нарисовать отверстие так же как мы рисовали его у желтой доски. Теперь нам осталось уточнить детали, стереть вспомогательные линии и заштриховать (то есть выполнить рисунок в тоне).

Это важно.
Мне очень часто приходится слышать жалобы на то, что рисовать всякие доски, бутылки и кувшины это скучно. «Мы не хотим рисовать кувшины — вдохновенно орут уверенные в себе Незнайки — мы хотим научится рисовать человека, а если мы всё время будем рисовать кувшины, мы не научимся рисовать людей».
Рисование кувшина (или разделочных досок) ничем не отличается от рисования человека, и это пожалуй, самый главный секрет реалистичного рисунка и рисунка вообще. Тот кто научился правильно рисовать кувшин, тот с лёгкостью нарисует и человека. А тот кто уверен, что для рисования человека нужны какие то особые знания и приёмы, отличные от тех которые нужны для рисования простых предметов, тот никогда не научится рисовать.
Всегда и во всём надо идти от простого к сложному и тогда всё получится. Посмотрите на два примера из математики: 123+65-5=183 и 28+66:3-10+8-45:(12-6+3)+199-36:(8+12-28:2)+(88-47)-15+7-167-3х10-4+81-5х7=131 Чем отличаются эти примеры? Первый пример проще, первый пример решается всего в два действия. А вот что бы решить второй пример придётся выполнить двадцать пять действий. В самом принципе решения этих примеров никакой ризницы нет, всего лишь количество действий. Также отличается и рисование кувшина от рисования человека. Если при рисовании кувшина мы решаем задачку в два или три действия, то при рисовании человека придется решать задачку даже не в двадцать пять, а в сотню действий. Конечно же решать сложные уравнения интереснее чем простенькие примеры, но начинать изучение математики лучше, всё таки, с простых примеров. Очень трудно справиться с делением и умножением если не освоил сложение и вычитание, невозможно научиться извлекать корни и возводить в степень не научившись делению и умножению. В рисунке как и в математике, чтобы добиться успеха необходимо идти от простого к сложному. Когда мы выполняем простые задания, похожие на только что выполненное нами (рисунок двух досок), меня часто спрашивают: зачем измерять предметы на расстоянии? Ведь можно же измерять эти самые доски линейкой, подойти и измерить. Да можно. Но ведь наша задача не измерить эти конкретные доски. Наша задача, на примере этих досок, научиться измерять на расстоянии любые предметы. Если мы будем рисовать девяти этажный дом, как мы будем определять пропорции и какой линейкой мерить? В прочим мы можем найти строительные чертежи этого дома и нам даже не надо будет что то измерять, все размеры там уже есть. Но мы же не чертёж дома делаем, а реалистичный рисунок. Глядя на дом, который решили изобразить, мы видим, что высота дальней стенки меньше высоты ближней, по крайней мере мы так это воспринимаем, а на чертежах это не отражено. Как же нам определить эту разность высот? Только с помощью визирования.

Посмотрим теперь на фотографию кубика: высота ближнего к нам ребра больше высоты ребер кубика, которые находятся от нас дальше, а если мы подойдём к кубику и измеряем их линейкой, то они будут все равны. То есть тот номер, который может прокатить с рисование плоских предметов фронтально к нам расположенных, при изображении объёмных предметов уже не прокатывает. Так и так нам необходимо учиться измерять на расстоянии (визировать), рисуя с натуры мы постепенно будем тренировать свой глазомер и вскоре сможем определять пропорции предметов на глаз, а визирование применять в основном для проверки. Возможно найдутся умники которые скажут: «а я сфотографирую предмет и на фотографии его измеряю и пропорции определю и срисую». Вот только тут сразу возникает вопрос — а зачем тебе тогда вообще рисовать этот предмет, если у тебя уже есть фотография? Я вовсе не против того, чтобы художники использовали в процессе работы фотографии. Если Вы, например, решили написать картину на историческую тему, то Вам придётся так или иначе использовать фотографии тех лет. Да и рисуя вполне современные сюжеты приходится пользоваться фотографиями. Создавая свои произведения художники используют фотографии как вспомогательный материал. Однако просто тупо перерисовывать фотографии не имеет никакого смысла. И тем более невозможно научиться рисовать срисовывая с фотографии. Конечно срисовывание с фотографий и копирование чужих рисунков может быть полезно для наработки кое каких навыков в рисовании, но это не заменит рисования с натуры. Я сравнивала рисунок с математикой, теперь сравню с физкультурой. Есть, например, такое упражнение как приседание, а есть отжимание, и то и другое упражнение полезно, но приседание нельзя заменить отжиманием, а отжимание приседанием потому, что эти упражнения направлены на разные группы мышц. А бывают упражнения комплексные, позволяющие эффективно тренировать максимальное количество мышц нашего организма. Рисование с натуры тренирует практически все «мышцы» нашего интеллекта, а так же мышцы отвечающие за мелкую моторику и цилиарную мышцу (которая отвечает за остроту зрения), перерисовка фотографии тренирует только мелкую моторику и глазомер (гораздо в меньшей степени, чем рисование с натуры). Рисуя с натуры мы на двухмерной плоскости создаем изображение трёхмерного пространства, решая задачу создания иллюзии трёхмерности. Срисовывая с фотографии мы срисовываем с двухмерного изображения, задача создания иллюзии трёхмерного пространства в этом случае уже решена фотоаппаратом (кстати, далеко не всегда удачно).
Если опять сравнить рисунок с математикой, то рисуя с натуры — мы решаем задачу, а рисуя с фотографии — списываем готовое решение. Можно ли научиться решать сложные уравнения списывая с доски готовое решение? Конечно нет! Научиться решать уравнения можно только решая их самостоятельно. Примерно также дело обстоит и в рисунке.
Рисунок объёмных предметов.
Пришло время потренироваться в рисовании объёмных предметов. Составим натюрморт и двух простых предметов, овощей или фруктов, у кого что окажется под рукой. Я предлагаю две луковицы. Любой рисунок начинаем с компоновки в листе, предметы располагаем по середине листа, не смещая их ни влево, ни вправо, не опуская слишком низко и не поднимая слишком высоко. Следим за тем чтобы предметы не получились слишком крупными (предметам не должно быть тесно в листе) и слишком мелкими (на листе не должно быть слишком много пустого места). Внимательно изучаем натуру.

Что мы имеем? Наша постановка состоит из двух предметов (двух луковиц) шаровидной формы, но и один, и другой предмет не является правильным шаром. По высоте обе луковицы одинаковы, ширина левой луковицы (которая лежит немного ближе к нам) чуть меньше её высоты, а у правой луковицы (находящейся чуть дальше от нас) ширина чуть больше её высоты. Расстояние между луковицами составляет примерно три четвертые высоты луковицы. Мы примерно определились где будут располагаться на листе наши луковицы, намечаем контуры левой луковицы, как мы определили, ширина этой луковицы чуть меньше её высоты. Теперь нам надо определить положение второй (правой) луковицы по отношению к первой (левой). Поскольку правая луковица лежит немного дальше от нас, то на листе она будет располагаться немного выше. Насколько? Можно конечно измерять насколько мы видим правую луковицу выше по отношению к левой, но можно поступить другим способом.

Подводим карандаш к нижним точкам луковиц, как бы соединяя эти точки между собой и смотрим под каким углом к горизонтали расположился карандаш. Под таким же углом проводим вспомогательную линию через нижнюю точку контура левой луковицы в право, на этой линии и будет лежать наша правая луковица. Теперь более точно определим местоположение правой луковицы. Визуально совмещаем карандаш с нижней точкой левой луковицы и верхней левой точкой правой луковицы, проводим линию под тем же углом. Визуально соединяем карандашом верхние точки луковиц и проводим на рисунке вспомогательную линию под тем же углом, что и карандаш. Эта линия окажется параллельна линии соединяющей нижние точки луковиц (это не удивительно, так как высота наших луковиц одинакова). С помощью вспомогательных линий мы точно определили местоположение второй луковицы, пропорции луковицы мы знаем (если нужно можно проверить ещё раз), рисуем контуры второй (правой) луковицы.

Теперь осталось наметить детали. У луковиц видны хвостики и корешки, расположены эти детали строго напротив друг друга, можно сказать на оси, проходящей через луковицу. Поводим ось на левой луковице, наклон определяем так же как определяли наклон вспомогательных линий когда находили местоположение правой луковицы. Определяем размер деталей по отношению к размеру предметов и рисуем детали (хвостики и корешки).

Нам осталось выполнить рисунок в тоне, то есть заштриховать предметы и фон так, чтобы предметы выглядели объёмными. До этого мы рисовали плоские предметы, а вот теперь нам предстоит показать объём. Для того, чтобы это сделать успешно нам надо познакомиться с такими понятиями как: свет, тень, блик, полутень, рефлекс, падающая тень, горизонтальная и вертикальная плоскость.

Предметы у нас шаровидной формы поэтому на их примере мы познакомимся с тем как распространяется свет и тень на предметах имеющих форму шара. Блик самое светлое место на предмете, на матовых (не блестящих) предметах блика мы можем и не увидеть. Но на наших луковицах блики хорошо видны. Свет — это освещенная часть предмета, она самая светлая после блика, но если блик всегда белый, то свет предмета всегда имеет цвет и тон. Свет постепенно переходит в полутень, а полутень переходит в собственную тень предмета. Если мы внимательно посмотрим на теневую часть предмета, то заметим, что на краю предмета тень высветляется, это рефлекс. На круглых предметах самая тёмная тень никогда не бывает на самом краю предмета, точно так же как и самое светлое место не бывает на краю предмета. На плоскость предметы отбрасывают тень, эта тень называется падающая, в отличие от собственной тени, которая находится на самом предмете. Под самим предметом падающая тень самая тёмная (и как правило темнее самого предмета), удаляясь от предмета падающая тень несколько высветляется.

Осталось поговорить о самой штриховке. В академическом рисунке нельзя графит растирать, некоторые любят это делать полагая, что это делает их рисунок лучше, однако это не так. Когда Вы станните самостоятельными художниками и будите создавать свои великие произведения, то Вам никто не сможет указывать как и чем вам рисовать, вы сможете растирать карандаш сколько угодно, называя это авторской техникой, но выполняя академический рисунок (особенно на экзамене по рисунку) не стоит так поступать. Растирание карандаша в академическом рисунке воспринимается как «неспортивное поведение», признаётся «непозволительным» и работа автор которой допустил такое «дисквалифицируется». Растирание применяется при работе мягкими материалами (углём, сангиной, соусом и т.д.). Как наносить штрих я уже рассказывала в статье «Основы академического рисунка. Начало». До настоящего момента нам приходилось штриховать плоские предметы расположенные к нам фронтально, теперь же мы перешли к рисованию объемных предметов лежащих на горизонтальной плоскости. Объёмные предметы штрихуют по форме предмета, как бы «ощупывая» предмет кончиком карандаша. Наносить штрих на предметы и на вертикальную плоскость можно в разных направлениях, главное чтобы на предметах штрих шел по форме. Горизонтальную плоскость тоже можно штриховать в любом направлении, кроме вертикального. Стоит заштриховать горизонтальную плоскость вертикальным штрихом и она «встанет стеной» и категорически откажется казаться горизонтальной, поэтому горизонтальную плоскость штрихуем под любым углом, горизонтально, но только не вертикально. Если хотите научиться рисовать , то изучите картинки приведенные в статье, но не срисовывайте их, поставите свои постановки и рисуйте с натуры. Только рисование с позволяет в совершенстве освоить рисунок и является мощным средством саморазвития.
§5 Пропорции
Мы признаем определенные пропорциональные отношения в построении фигуры человека, его окружения, архитектуры, как нечто должное. Эмоциональное начало художественного творчества проверяется точной наукой. Выдающиеся мастера былых эпох постоянно стремились проверить алгеброй гармонию, впрочем, математика античности, средневековья и Возрождения была лишена сухости и абстрактности.
Когда мы знакомимся с историей искусства, любуемся совершенными произведениями, например античной статуей или храмом, картинами Леонардо да Винчи, Рафаэля, Энгра, то нас поражает удивительная гармония, присущая им, которая во многом определяется таким эстетическим качеством, как пропорциональность целого и деталей. Слово «пропорция» в переводе с латыни обозначает «соотношение», «соразмерность». Сравнивая предметы, окружающие нас, по величине, высоте, ширине, объему мы можем сказать, что одни из них длинные, а другие короткие, высокие и низкие, широкие и узкие, большие и маленькие и т. д. Устанавливая соотношение между предметами и между частями формы отдельного предмета, мы выясняем их пропорциональные характеристики.

Пропорциями называются размерные соотношения элементов или частей формы между собой, а также между различными объектами.
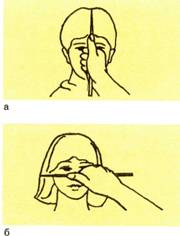
75. Измерение высоты (а) и ширины (б)
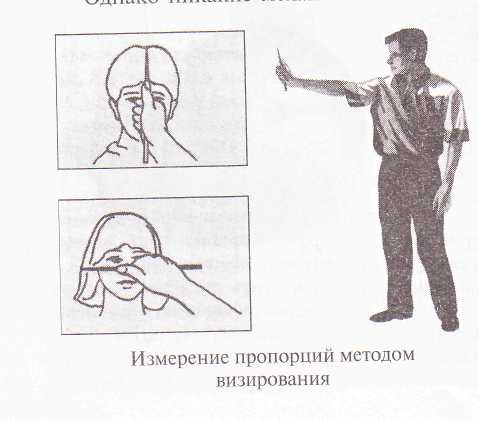
Проверять пропорции можно с помощью обычного карандаша или кисточки, при этом держать их следует на вытянутой руке.

76. Определение пропорций
Для удобства определения пропорций методом визирования можно прищурить один глаз. С помощью длины карандаша уточняют также степень наклона всей формы.
Пропорция – это гармонизация формы художественного произведения, пропорциональность – ее эстетическое качество. Соразмерность частей образует красоту формы. В основе определения пропорций лежит метод сравнения. Все эти свойства лежат и в основе грамотного рисунка. В художественной практике существует известный метод определения пропорций, называемый визированием.
Однако никакие механические способы определения пропорций не могут заменить развитого глазомера. Именно эту способность необходимо развивать в себе тренировкой.

Рисуя, нужно помнить, что мы изображаем предметы несколько меньшими их натуральной величины, поэтому необходимо придерживаться единого масштаба для определения пропорций всех объектов изображения, составляющих композицию. Таким образом, выдержать пропорции в рисунке – значит добиться соотношения величин всех частей предмета к целому в пределах выбранного формата листа.

Поиск пропорций в изображении фигуры человека является сложной задачей. Обратимся к истории, посмотрев, как решали ее художники разных эпох и разных культур.
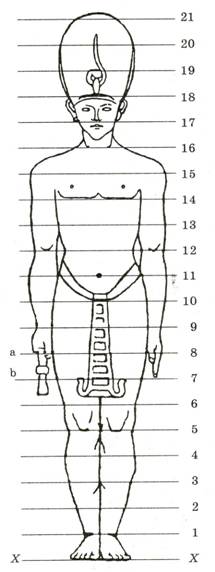
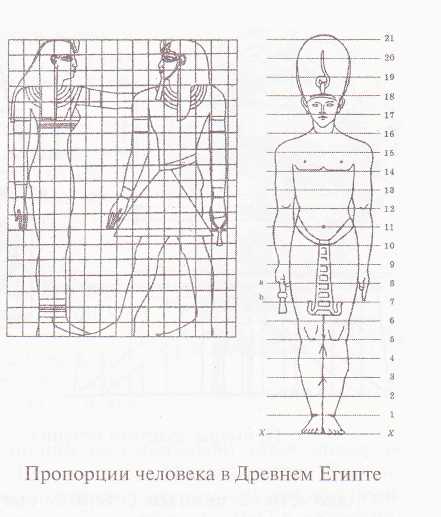
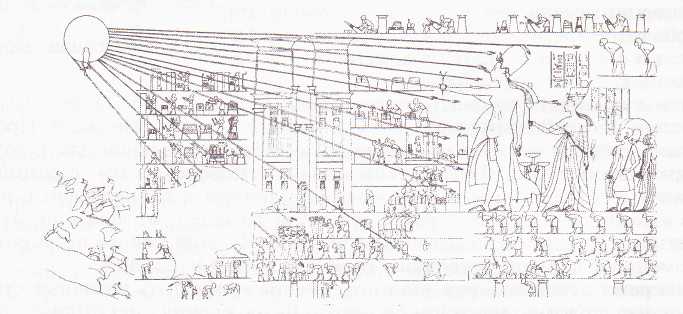
77. Композиция пропорций человека в Древнем Египте
Единицей измерения фигуры у древнеегипетских художников служила длина среднего пальца руки, вытянутой вдоль бедра.
В Древнем Египте для изображения человеческой фигуры был разработан специальный канон – то есть такая система пропорций человеческой фигуры, которая делила изображение на части и позволяла по части определить целое и по одной части тела определить другую. Известно, что египтяне положили в основу деления фигуры 21 1/4 части. В это число входили 19 равных частей разделения самой фигуры, а 2 1/4 части приходились на изображение традиционного головного убора (ил. 77), Египтяне пользовались и специальными сетками-таблицами, которые наносили на поверхность каменной плиты или стены для создания рельефа или росписи (ил. 34а).
На сохранившихся и дошедших до нас памятниках можно видеть, что горизонтальные и вертикальные линии делят рисунок в определенных местах, что соответствует членению фигур на части. Были установлены также определенные размеры для изображения сидящих фигур и изображения разных богов в соответствии с их иерархическим старшинством (одни должны быть выше, другие немного ниже). Детей изображали как взрослых, но значительно меньшими по размеру. Художнику необходимо было знать установленные каноном нормы и научиться вписывать в них изображения, пользуясь сеткой-таблицей. Единая система обучения и строгое соблюдение выработанных норм позволяли выполнять части одного произведения разными мастерами. Когда такие части составляли в единую композицию, то они точно сходились и не было нарушения пропорций.
Вся история учения о пропорциях связана с поисками законов гармонии и красоты. В Древней Греции систему идеальных пропорций человеческой фигуры создал скульптор Поликлет в V веке до н. э. Его теоретическое сочинение на эту тему называлось «Канон», а выражением в скульптуре этой системы явилась его статуя «Дорифор», что означает копьеносец. Мастер изобразил атлета-юношу, победителя в соревнованиях по метанию копья, в момент, когда после одержанной победы он совершает круг почета по стадиону и его приветствуют восторженные зрители.
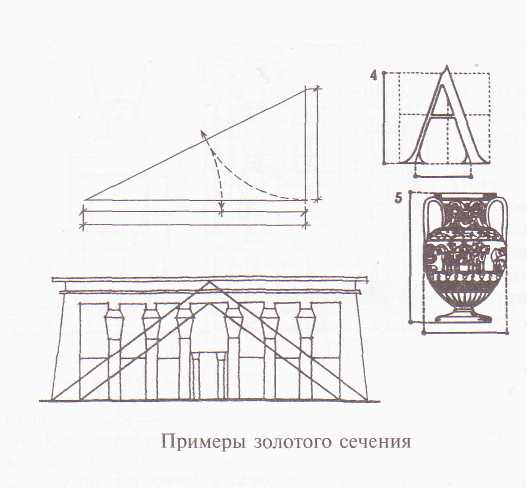
Открытие пропорций, полагают, принадлежит к заслугам древневосточной математики, античная же традиция связывает его с именем выдающегося философа и математика Пифагора, жившего в VI веке до н. э. Универсальный принцип гармонии и красоты в пропорциях получил название «золотое сечение», которое олицетворяло равновесие знания, чувств и силы. Золотое сечение возникает при делении отрезка на две неравные части таким образом, при котором весь отрезок относится к большей его части, как большая к меньшей (0,618).
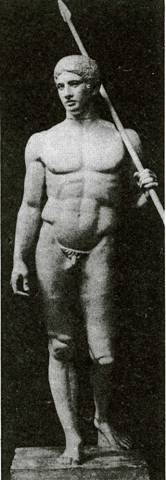
78. ПОЛИКЛЕТ. Дорифор
Поликлет создал новые членения пропорций человеческой фигуры, однако точных сведений о том, что именно было выбрано за единицу меры – величина ладони, ступни или высота головы,- не сохранилось.
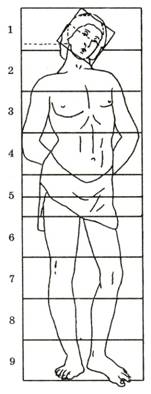
79. С. БОТТИЧЕЛЛИ. Канон пропорций
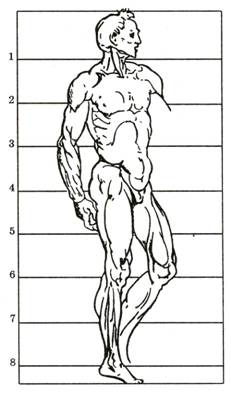
80. МИКЕЛАНДЖЕЛО. Пропорции фигуры человека
Знакомство с золотым сечением сыграло немалую роль в работе античных архитекторов, скульпторов и живописцев. Обучающимся рисунку будет интересно узнать правило, наглядно прослеживающееся в древнегреческих статуях: при делении туловища человека в соответствии с золотым сечением легко найти уровень пупа и локтя, при повторном делении двух отрезков в противоположных направлениях определяется высота колена и нижний уровень шеи.
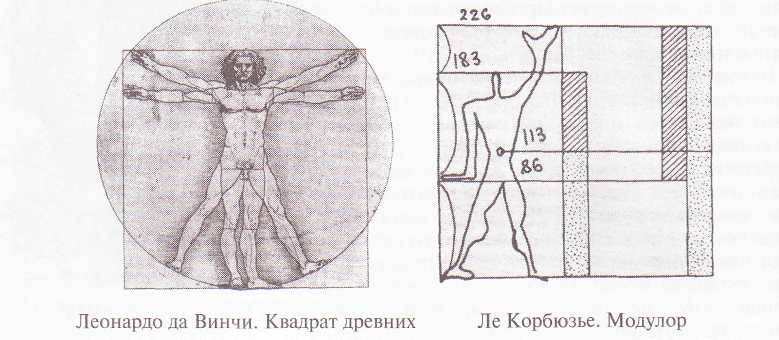
Примерами использования золотого сечения может быть античная голова Афродиты и любое из произведений художника Рафаэля. В поисках гармонии художники интуитивно всегда следовали этому принципу и в той или иной мере приближались к идеальным соотношениям, но теоретически принцип золотого сечения был сформулирован в эпоху Возрождения. Леонардо да Винчи, изучавший и глубоко анализировавший опыт древних, разрабатывая правила изображения человеческой фигуры, пытался на основе литературных сведений восстановить так называемый «квадрат древних». Он выполнил рисунок, в котором показана пропорциональная закономерность в соотношении частей тела человека.
Над выработкой канонов пропорций трудились такие знаменитые мастера эпохи Возрождения, как С. Боттичелли и Микеланджело. Проблема поиска системы идеальных пропорций остается актуальной и для художников и архитекторов XX века. Французский зодчий Jle Корбюзье в 1947 году разработал «Модулор» – систему деления человеческой фигуры на согласованные в золотом сечении отрезки от ступни до талии, от талии до затылка и от затылка до верха пальцев поднятой руки. На этой основе была создана школа модулей для архитектурного проектирования и дизайна.

Античное искусство установило идеальные пропорции и для головы человека, согласно которым она по вертикали от темени до конца подбородка делится на две равные части линией глазных впадин (ил. 83). Каждую из этих половин можно, в свою очередь, разделить на две равные части: верхнюю – линией волос, а нижнюю – основанием носа. Получается четыре равные части. Расстояние между глазами принимается равным ширине крыльев носа.
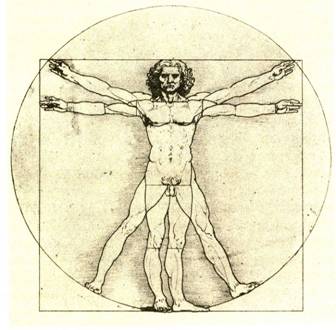
81. ЛЕОНАРДО ДА ВИНЧИ. «Квадрат древних»
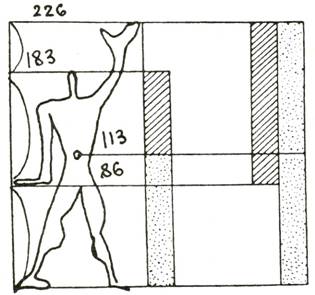
82. ЛЕ КОРБЮЗЬЕ. Модулор
Расстояние от бровей до основания носа определяет величину ушей. В действительности редко встречаются у людей такие идеальные пропорции, но знать их необходимо, чтобы видеть отклонения от нормы и лучше понимать индивидуальные пропорции живой натуры.
Пока общая форма головы не решена, не найдены ее пропорции, нельзя переходить к отделке деталей. Портретное сходство зависит во многом от правильно выдержанных общих пропорций.

Следует помнить, что при определении пропорций лучше сравнивать отношения нескольких деталей на рисунке с соотношениями таких же деталей в натуре.
Переходя к эмоциональной характеристике портретируемого, полезно изучить схемы лица при различных психологических состояниях на ил. 84.

83. Пропорции головы
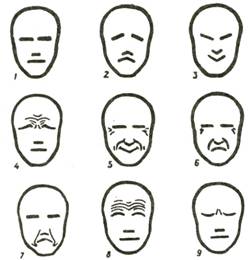
84. Схематическая таблица сокращения мускулов лица при различных психологических состояниях (по М. Дювалю): 1 – спокойствие, 2 – печаль, 3 – радость, 4 – боль, 5 – смех, 6 – плач, 7 – презрение, 8 – внимание, 9 – размышление

Посмотрите, как с помощью самых простых средств, всего лишь опуская или приподнимая уголки губ, брови или веки, можно передать печаль, радость, боль, смех, презрение, внимание и т. д. (ил. 84-85).
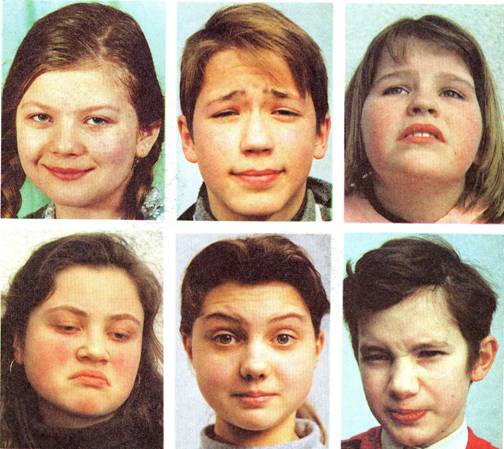
85. Лица в различном эмоциональном состоянии
Основы учебного академического рисунка. Пропорции и их значение в рисовании
December 6, 2020
Соблюдение пропорций и их значение столь велико и значимо, что без них практически невозможно обойтись не только в изобразительном искусстве и архитектуре, но и в науке, технике, медицине и многих других сферах жизнедеятельности человека. Вот почему такое пристальное внимание уделяют изучению столь важного и необходимого предмета, как пропорция.
Изучение и постижение законов гармонии способно направить творческую деятельность архитекторов и художников на созидание новых, созвучных объективным законам восприятия и гармонии природы, произведений. Знание и изучение этих законов формирует мировоззрение и профессиональное отношение к творчеству и жизни. Об этом красноречиво свидетельствует утверждение: “Красота предмета образуется пропорциями, становясь строгой соразмерностью и гармоничностью”. К сожалению, нередко приходится слышать и видеть, как рисовальщики, даже имея за плечами немалый опыт, пренебрежительно относятся к пропорциям, сосредотачиваясь всецело на передаче характера и формы предмета. Между тем, из-за нарушенных пропорциональных величин изображение предмета, особенно живой формы, такой, как голова или фигура человека, приобретает уродливый вид, не говоря уже о недостаточной убедительности. Это относится не только к студентам, но и ко всем, кто недооценивает значение пропорции в учебном академическом рисунке. Пропорция в рисунке при создании реалистического изображения занимает главное положение наряду с такими понятиями, как композиция, объемная форма, конструкция и анатомия.
Хорошие пропорции в рисунке предполагают наличие полного сходства с изображаемым предметом. Иначе говоря, чем точнее определены пропорции предмета на рисунке, тем большего сходства с натурой достигает его изображение.
Следует помнить, что все тела, а также и их части должны сравниваться или соизмеряться друг с другом по признаку пропорциональных отношений.
Чтобы правильно определять соотношения частей предмета, рисующий должен, помимо знаний, обладать чувством пропорции/Чувство пропорции подразумевает наличие хорошего глазомера, а глазомер, как правило, развивается в процессе длительных упражнений в рисовании с натуры. Тренируя глазомер, необходимо развивать аналитическое мышление. Полагаясь только на глазомер, можно вновь повторить свои ошибки. Подобный подход недопустим при рисовании более сложных предметных форм, особенно таких, как голова человека. Немало примеров, когда студенты, полагаясь на глазомер, становятся заложниками натуры, срисовывая подряд все, что видит глаз. Такое рисование следует исключить из своей практики, так как это не грамотное рисование, а всего лишь слепое поверхностное копирование. Великий педагог П.П.Чистяков писал: “… Прежде всего расположи фигуру на бумаге, а затем приступай к ее построению. Построить – это значит взять правильные пропорции и поставить фигуру”.
Для большей убедительности приведем множество примеров, касающихся возможности соблюдения пропорции не только в изобразительном искусстве и архитектуре, но и в области науки: в физике, химии, математике, технике и т.д. К примеру, когда в строительной технологии нарушаются пропорции составов строительных материалов и размеров элементов конструкций, это может привести к разрушению сооружений. Архитектор, нарушая пропорции сооружения, тем самым разрушает принципы пропорциональной соразмерности его элементов. Если живописец нарушает пропорции в технологии грунтовки холста, это может привести к разрушению и холста и красочного слоя. В химии точные весовые пропорции реагентов обусловливают возможность получения необходимого вещества. Когда мы посещаем заповедники человеческой культуры и встречаемся с произведениями зодчества, музыкой или картинами художников, нас охватывает особое чувство необъяснимого волнения и восторга от увиденного и услышанного. И наоборот, когда эстетические качества сооружения или картины оставляют желать лучшего, мы испытываем чувство сожаления или равнодушия.

Сопоставляя выдающиеся памятники искусства и архитектуры, созданные в определенные исторические периоды культурами различных народов, и изучая их композиционную структуру, мы приходим к убеждению, что принципы пропорциональной соразмерности элементов являются непременным условием формирования облика объекта.
Пренебрежение пропорцией приводит к безграмотному, несостоятельному рисунку. Нетрудно представить, что если изображенный предмет непропорционален в своих отношениях, то он становится менее убедительным. Это очевидно в изображении головы человека, где лицевая часть доминирует в своих объемных размерах по отношению к черепной (мозговой) части, или когда голова человека по отношению к остальной фигуре слишком мала или велика и т.п. При изображении предметов нередко пренебрегают различиями в их размерах, пытаясь акцентировать внимание лишь на их конфигурации и форме, искажая тем самым пропорции и гармонию целого.
По мнению древних греков, гармония есть связь различных частей в единое целое. Для того чтобы получить это единое целое, необходимо связать части между собой таким образом, чтобы они представляли собой законченное единство.
Выдающиеся памятники древнего искусства и архитектуры обязаны своими соразмерностями и пропорциями человеку. Об этом свидетельствует фундаментальный тезис античной философии: “Человек – мера вещей”.
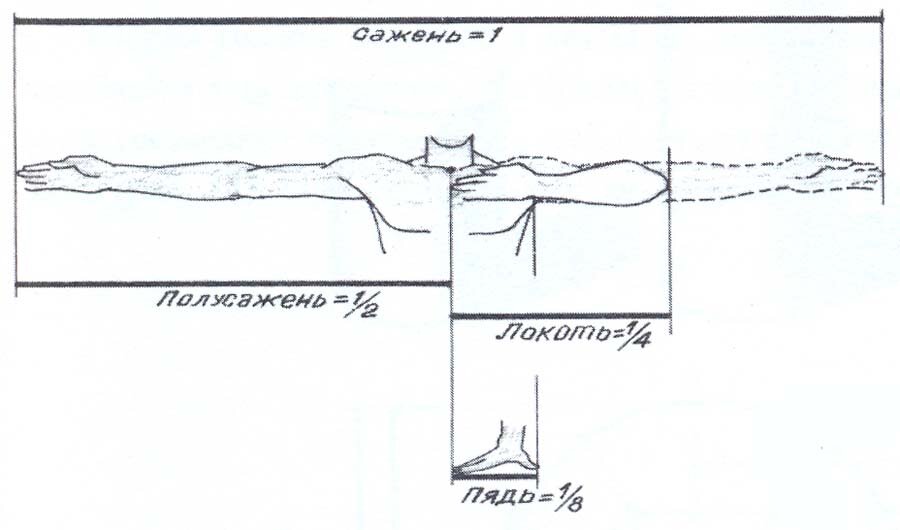
Именно человек является эталоном или модулем пропорционального строя архитектурных объектов древнего мира.
Пропорция человеческого тела имеет решающее значение при определении создаваемых вещей, оказывает влияние на формируемое им предметное окружение. Сообразно пропорциям человеческого тела зодчие устанавливали соразмерность и пропорцию храмов, сооружений и построек.
Пропорция есть соответствие между членами всего произведения и его целым по отношению к части, принятой за исходную, на чем и основана всякая соразмерность. Без соразмерности и пропорции не может быть правильной композиции, если в ней не будет членения, сопоставимого с телом хорошо сложенного человека.

Так, например, основной мерой в Древней Руси являлась давно известная, так называемая тьмутараканская сажень – 142 см (рис. 20). Она соответствовала двойному шагу человека. При пропорциональном сложении тела эта мера соотносится как 1 и . Новгородская мерная трость, в которой сопряжены парные меры Древней Руси, заключает в себе пропорцию храмов конца XII века, промеренных ею. Новгородская мерная трость, как и меры античного Рима и классической Греции, принадлежит двойному квадрату – канону строителей египетских пирамид. Этими мерами соизмеряли архитектурные сооружения в Древней Руси, привнося в архитектуру свойство взаимопроникновения, т.е. гармонию. Вот почему человек является камертоном гармонического строя архитектуры и искусства, что нам и следует рассмотреть более детально. Но прежде рассмотрим пропорции простых и сложных предметов.

Понятие о пропорциях предметов
Любое правдивое изображение какого-либо предмета передает в рисунке или картине его основные, характерные признаки, понятные зрителю.
Если задать себе вопрос, по каким внешним особенностям зритель узнает изображение, долго искать ответ на него не придется. Каждому из нас понятно, что «узнавание» изображения происходит благодаря переданным художником в произведении именно основным, характерным признакам предметов или явлений. Безусловно, такой передаче признаков способствуют многие факторы реалистического изображения: перспективные построения, светотеневые отношения, фактура поверхности и т.д.
Что же такое признаки предмета? Это свойства предмета, его приметы. На языке изобразительного искусства отличительные черты объектов рисования называются пропорциями и конструкцией.
Пропорции (лат. proportio — соразмерность) — соразмерность всех частей художественного произведения или архитектурного сооружения, их соответствие друг другу и определенное соотношение с целым.
Конструкция (лат. constructio — оставление, построение) — строение, взаимное расположение частей предмета, структура его формы.
Красота предмета образуется пропорциями, становясь строгой соразмерностью, гармонией всех частей, такой, что ни прибавить, ни убавить ничего нельзя, и все детали, части должны взаимно соответствовать друг другу.
Итак, в окружающем нас мире все предметы характеризуются не только конструктивным строением, но и размерами. Возьмем, например, садовую лейку — предмет сложной комбинированной формы с неполной симметрией частей (рис. 13). При рисовании лейки с натуры важно увидеть, что две ее части — трубка и ручка — расположены в одной вертикальной плоскости, проходящей через ось симметрии цилиндрического корпуса, и тогда в зависимости от поворота модели не будет допущена ошибка при построении изображения. Одновременно рисовальщик обязан следить за соотношением основных величин предмета — его высотой и шириной, определяя их на глаз.
Натурные постановки из двух и более предметов заставляют рисовальщика учитывать пропорциональные отношения между ними. Например, при рисовании с натуры цветущих комнатных растений (возьмем кактус опунция и бегонию крупнолистную) из-за различных размеров внимание рисующего непременно сосредоточивается на их соотношениях, а при построении рисунка — на своеобразной композиционно-пластической и конструктивной выразительности. На этой основе образуются представления о натуре, организовываются в изображении ее объемно-пространственные свойства, пропорциональность, пластичность.

Рис. 13
Грамотный рисунок — это прежде всего изображение пропорций предмета. Но это не значит, что предмет надо непременно рисовать в натуральную величину. Это невозможно, если принять во внимание наше зрительное восприятие, и не нужно, если учитывать расстояние от вашего места до натуры. Иное дело, что размеры предмета выдержаны в пропорциях, а также по отношению к окружающей среде и в любом уменьшенном виде выглядят правдиво. Следовательно, здесь все зависит от выбранного вами масштаба изображения. Это касается также и установления размеров отдельных частей предмета по отношению к общим массам.
Таким образом, выдержать пропорции в рисунке — значит добиться соотношения величин всех частей предмета к целому в пределах формата и выбранного масштаба изображения.
Но пропорции есть не только в соотношении величин предмета. В каждом светотеневом рисунке нужно передать еще и пропорциональные натуре отношения в тоне. Известно, что правдивого изображения натурной постановки рисовальщик достигает на основе передачи как раз взаимных отношений по светлоте. Вы уже знаете, что самая светлая на предмете в натуре часть или точка во много раз светлее самой белой бумаги, не говоря уже о карандаше, не способном проложить темного пятна, адекватного пятну в натуре. Что же должен делать в этом случае рисовальщик? Правдивости в тоне добиваются выдержанностью в рисунке тонального масштаба.
Пропорциональных натуре отношений достигают благодаря учету белизны бумаги и кроющей силе карандаша. А за основу таких отношений берут, например, блик и самое темное пятно в тени, сравнивая в рисунке с ними все остальные градации светотени. Умелое владение тоном завершает правдивую передачу натурной постановки.
При изложении понятия о пропорциях предметов нужно подробнее остановиться на так называемом «золотом сечении». Сведения о нем восходят ко времени расцвета античной культуры и упоминаются в трудах великих древнегреческих мыслителей Пифагора, Платона, Евклида. До сих пор считается, что понятие о золотом делении ввел в научный обиход в VI в. до н.э. философ и математик Пифагор, позаимствовавший, вероятно, знание его у египтян и вавилонян, широко применявших это красивое пропорциональное соотношение величин при создании пирамид, храмов, рельефов, пальметок. Волею судьбы Пифагор посетил землю фараонов, где увидел нечто его глубоко поразившее, затем был пленен персами, от которых попал в Вавилон. Тамошние жрецы помогли любознательному греку изучить теорию чисел, музыку, философию. Вернувшись в зрелом возрасте на родину, Пифагор основал в городе Кротоне общество математиков и философов, занимавшихся не только геометрией и наукой мудрости, но и теорией музыки. Пифагор открыл знаменитое математическое соотношение: квадрат гипотенузы равен сумме квадратов катетов.
Если Пифагор позаимствовал золотую пропорцию у египтян, то последние, вероятно, переняли ее у более древних предшественников, о которых мы уже, к сожалению, никогда не узнаем. Древний мир загадочен, и вот новые доказательства этого: при археологических раскопках палеолитической стоянки на реке Ангаре в Сибири была найдена пластинка из бивня мамонта с рисунком-календарем на ее поверхности. Удивляют размеры пластинки (13,6*8,2 см), с точностью до 1 мм отвечающие золотой пропорции. Возможно это случайность, но впечатляющая. Как тут не подумать о том, что законы красоты — в соизмеримости формы: эта пластинка для человека эпохи позднего каменного века только в таком соотношении сторон была приемлемой. Наш далекий предок, конечно, не мог знать о закономерностях зрительного восприятия и эмоционального воздействия вещи. Интуитивное познание мира привело человека, жившего 15 тысяч лет назад, к неожиданному для современной науки результату. Почему же тогда подобные пропорции выдерживались в разных других предметах и изображениях, найденных археологами?
Например, пропорции «золотого сечения» обнаружены в некоторых первобытных фресках пещер Франции, Испании и Швейцарии, в наскальных рисунках близ села Шишкино на реке Лене. Все это было бы странным, если бы не оказалось закономерным: наблюдательность человека подсказала ему эту пропорцию на основе природных проявлений данного соотношения. Поистине «божественная» назвал эту пропорцию современник великого Леонардо да Винчи монах-математик Лука Пачоли. И вообще, вся история учения о пропорциях связана с поисками теории гармонии и красоты. Античная эстетика и эстетика Ренессанса искали законы красоты в соотношениях отдельных частей и целого. Эти соотношения в формах предметов дают симметрия и золотая пропорция. Пропорции золотого сечения» и симметрия позволяют бесконечно разнообразить композиционные построения в произведениях искусства всех родов и видов.
Математики разных веков объяснили, изучили и глубоко проанализировали золотую пропорцию. Из пропорции вытекает, что если высоту или длину формата бумаги, картины разделить на 100 частей, то больший отрезок «золотого сечения» равен 62 частям, а меньший — 38. Эти три величины — целое, больший отрезок, меньший отрезок — позволяют построить нисходящий ряд отрезков: 100 – 62 = 38; 62 – 38 = 24; 38 – 24 = 14; 24 – 14 = 10. Значит, для художника числа 100, 62, 38, 24, 14, 10 являются рядом величин «золотого сечения», выраженных арифметически. Достаточно убедиться в этом при анализе, например, любого произведения Рафаэля: здесь все подчинено бесконечному разнообразию чисел золотого деления. Рафаэль, возможно, в процессе создания своих композиций использовал циркуль-измеритель, изготовленный из двух деревянных планок и скрепленный одной осью, находящейся на линии «золотого сечения» (62, 38). При работе этого циркуля длинные и короткие концы все время дают требуемое соотношение пропорциональных отрезков.
Благодаря повторению равных, чередованию равных и неравных величин в пропорциях «золотого сечения» в рисунке или картине создастся определенный ритмический строй, втягивающий зрителя в рассматривание изображения. О картинах Рафаэля убедительно сказал выдающийся художник Кузьма Сергеевич Петров-Водкин: «К Рафаэлю… приходишь как на отдых. Эта нежная ясность, детская гениальная шаловливость с цветом и формой, то беззаботно жизнерадостная, то задумчивая и грустная…— она обезоруживает вас, распускает напряженные мускулы. Как совершенный в своих силах, Рафаэль не боится… композиционных канонов».
Но если даже. Рафаэль повторял и чередовал все величины в золотой пропорции лишь благодаря гениальному композиционному чутью и интуиции, то остается констатировать, что так устроила единство мозга и глаза человека сама природа, которая к тому же как бы приложила «божественную» пропорцию к себе самой.
Итальянский математик Леонардо из города Пизы, более известный под прозвищем Фибоначчи (сын Боначчи), в 1202 г. написал математический труд под названием «Книга об абаке» (абакой называли счетную доску), в котором собрал все известные тогдашним любителям счета задачи. Там, например, одна задача была связана с вопросом «Сколько пар кроликов в один год от одной пары рождается?» Поразмыслив на тему кроликов, Фибоначчи выстроил знаменитый ряд цифр: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 277, 610 и т.д. Особенность этого ряда такова, что каждый его член, начиная с третьего, равен сумме двух предыдущих: 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13; 8 + 13 = 21; 13 + 21 = 34; 21 + 34 = 55; 34 + 55 = 89 и т.д. (Это отношение же чисел ряда Фибоначчи все больше и больше приближается к отношению «золотого сечения» (21 : 34 = 0,617; 34 : 55 = 0,618). Таким образом, суммы, полученные Леонардо Фибоначчи, примечательны тем, что отношение рядом расположенных чисел в пределе стремится к золотой пропорции. Что касается ряда Фибоначчи в качестве задачи, то она оказала косвенное влияние на исследователей растительного и животного мира, приходивших в конце концов к этому ряду как арифметическому выражению закона золотого деления.
Альбрехт Дюрер разработал способ геометрического деления отрезка прямой по «золотому сечению»: ВС = ½ АВ; CD=BC (рис. 14)

Рис. 14
Советский художник А. Н. Лаптев в 1954 г. написал в сборнике «Вопросы изобразительного искусства» статью «Некоторые вопросы композиции» и в ней, в частности, говорилось: «…Хочу упомянуть о давно известном, особенно в классическом искусстве, законе пропорций «золотого сечения». В силу некоторого свойства нашего зрительного восприятия эти пропорции (примерно 6 к 4) являются наиболее гармоническими и наиболее отвечающими общему понятию красоты и наиболее часто употребляемыми» (М., 1954. С. 66 — 67).
При изложении о пропорциях в рисовании с натуры какого-либо предмета нужно подчеркнуть, что точность определения соразмерных величин зависит от того, как развит глазомер рисующего. Глазомер развивается у каждого при условии систематических занятий изобразительной деятельностью.
Существуют
определенные
пропорциональные отношения
в построении фигуры
человека, его окружения,
при этом эмоциональное
начало художественного
творчества проверяется точной
наукой. Выдающиеся мастера
былых эпох всегда стремились
проверить алгеброй
гармонию.
Когда
мы знакомимся с историей изобразительного
искусства,
любуемся совер-
шенными
произведениями, например античной
статуей или храмом, картинами
Леонардо да Винчи, Рафаэля, Энгра, то
нас поражает их удивительная гармония.
Во многом она определяется таким
эстетическим качеством, как
пропорциональность
целого и деталей. Слово пропорция
в
переводе с латыни обозначает
«соотношение, соразмерность».
Сравнивая
предметы, окружающие нас, по величине,
высоте, ширине, объему,
мы можем сказать, что одни длинные, а
другие короткие, высокие и
низкие, широкие и узкие, большие и
маленькие и т. д. Как известно, устанавливая
соотношение между предметами и между
частями формы отдельного
предмета, мы выясняем их пропорциональные
характеристики.
Пропорциями
называются размерные соотношения
элементов или частей формы
между собой, а также между различными
объектами.
Пропорция
— это гармонизация формы художественного
произведения, пропорциональность
— ее эстетическое качество.
Соразмерность
частей создает красоту формы. В основе
определения пропорций
лежит метод сравнения. Он очень важен
для грамотного рисунка. В
художественной практике существует
известный метод определения пропорций,
называемый визированием, — с помощью
карандаша в вытянутой руке.
Ппыяк-п нмк-якие
механические способы определения
пропорций не могут
30
заменить
развитого глазомера. Именно
эту способность необходимо
развивать тренировкой на занятиях
изобразительным искусством. Рисуя,
нужно помнить, что обычно
предметы изображают несколько
меньше их натуральной величины. Поэтому
необходимо придерживаться
единого масштаба при
определении пропорций всех объектов,
составляющих композицию.
Таким образом, выдержать пропорции
в рисунке — значит найти
соотношение величин всех частей
предмета к целому в пределах выбранного
формата листа. Поиск пропорций в
изображении фигуры

человека
является сложной задачей. Обратимся
к истории и посмотрим, как
решали эту задачу художники разных
эпох и разных культур.
В
Древнем Египте для изображения
человеческой фигуры был разработан
специальный канон, то есть такая система
пропорций человеческой
фигуры, которая делила изображение
на части и позволяла по части
определить величину целого или
другой части тела. Известно, что египтяне
положили в основу деления
фигуры 21 часть. Из них 19 равных
частей приходились на саму фигуру,
а 2 части — на изображение традиционного
головного убора.
Египтяне
пользовались и специальными
сетками-таблицами, которые
наносили на поверхность каменной
плиты или стены для создания рельефа
или росписи.
На
сохранившихся и дошедших до нас
памятниках можно видеть, как
горизонтальные и вертикальные линии
делят рисунок в определенных местах,
что соответствует деленению фигур на
части.
Были установлены также определенные
размеры для изображения сидяших
фигур и разных богов
в соответствии с их иерархическим
положением
(одни должны быть выше, другие немного
ниже). Детей изображали в соответствии
с пропорциями
взрослых, но значительно меньшими по
размеру. Художнику необходимо было
знать установленные
каноном нормы, соблюдать их, пользуясь
сеткой-таблицей. Единая система обучения
и строгое следование выработанным
нормам
позволяли выполнять части одного
произведения разным мастерам. При
соединении частей в единую
композицию они точно сходились, нарушения
пропорций не было.
Вся
история рисунка связана с поисками
законов
гармонии и красоты. В Древней Греции
систему
идеальных пропорций человеческой
фигуры
создал скульптор Поликлет в V
в. до н. э. Его теоретическое
сочинение на эту тему называлось «Канон»,
а выражением этой системы на практике
явилась его статуя «Дорифор», что
означает копьеносец. Мастер изобразил
атлета-юношу, победителя
в соревнованиях по метанию копья, в
момент,
когда после одержанной победы он
совершает
круг почета по стадиону и его приветствуют
восторженные зрители.
31
Открытие
пропорций, как
полагают,
заслуга древнево
сточной
математики, антич
ная
же традиция связывает
его
с именем выдающегося
философа
и математика Пи
фагора,
жившего в VI
в. до н.
э.
Универсальный принцип
гармонии
и красоты в про порциях
назвали
золотое
сечение, которое
оли
цетворяло
равновесие зна
ния,
чувств и силы. Золотое
сечение
получается при де
лении
отрезка на две нерав
ные
части таким образом,
при
котором весь отрезок от
носится
к большей его час
ти,
как большая к меньшей
(0,618).
Знакомство
с золотым сечением сыграло немалую роль
в работе античных архитекторов,
скульпторов и живописцев. Древние греки
приняли во внимание
гармонию, которую они видели в природе,
для создания своих произведений. Они
отмечали гармонию как симметричных,
так и асимметричных объектов природы.
На основе теории золотого сечения была
разработана система, позволяющая
создавать пропорции, которые на рисунке
выглядят естественно. Например,
если построить квадрат, найти середину
одной из сторон и провести
из этой точки диагональ, а затем увеличить
квадрат с помощью этой диагонали, то
получится формат, стороны которого
соответствуют пропорции золотого
сечения. Длинные и короткие стороны
этого формата гармонично относятся
друг к другу.
Формат с подобным
отношением сторон прекрасно подойдет
для изображения многофигурной
композиции, широкого пейзажного мотива,
движения объектов вдоль картинной
плоскости.
Вам
будет интересно узнать правило, наглядно
прослеживающееся в древнегреческих
статуях: при делении туловища человека
в соответствии с золо-
32

тым
сечением легко найти уровень пупка и
локтя, при
повторном делении двух отрезков в
противоположных
направлениях определяется высота
колена
и нижний уровень шеи.
В
поисках гармонии художники интуитивно
следовали
этому принципу и в той или иной мере
приближались
к идеальным соотношениям, но теоретически
принцип золотого сечения был сформулирован
в эпоху Возрождения. Леонардо да Винчи
на основе опыта древних разработал
правила изображения
человеческой фигуры. Он восстановил
так называемый «квадрат древних». Его
рисунок показывает пропорциональную
закономерность в
соотношении частей тела человека.
Пропорции
имели для Леонардо основополагающее
значение «не только… в исчислениях и
измерениях,
но и в звуках, весах, положениях — в
любом
месте, где они могут быть».
Каноны
пропорциональных соотношений разрабатывали
такие знаменитые
мастера эпохи Возрождения, как С.Боттичелли
и Микеланджело. Проблема
поиска системы идеальных пропорций
остается актуальной для художников
и архитекторов XX
в. Французский зодчий Ле Корбюзье в 1947
г. разработал «Модулор»
— систему деления человеческой фигуры
в соответствии с принципом
золотого сечения на отрезки от ступни
до талии, от талии до затылка и
от затылка до верха пальцев поднятой
руки. На этой основе была создана школа
модулей для архитектурного проектирования
и дизайна.
Примерами
использования золотого сечения могут
быть античные статуи, живописные
полотна художников эпохи Возрождения,
некоторые современные
архитектурные сооружения и многие
другие произведения.
Античное
искусство установило идеальные пропорции
и для головы человека,
согласно которым она по вертикали от
темени до конца подбородка делится
на две равные части линией глазных
впадин. Каждую из этих половин можно,
в свою очередь, разделить на две равные
части: верхнюю — линией волос,
а нижнюю — основанием носа. Получается
четыре равные части. Расстояние
между глазами принимается равным ширине
крыльев носа.

Расстояние
от бровей до основания
носа определяет величину ушей.
В действительности у людей редко
встречаются такие идеальные
пропорции, но знать их необходимо,
чтобы видеть отклонения
от нормы и лучше понимать индивидуальные
пропорции живой
натуры.
Пропорции
всякого живого организма
изменяются в процессе его
развития. Пропорции маленького
ребенка сильно отличаются от пропорций
взрослого человека. ■ Размер
головы взрослого, занимает примерно
4i
или
‘А часть от его роста, а у ребенка
четырех-пяти лет — ‘А
33
или
‘Л часть. Величина головы подростков
примерно шесть раз укладывается в
длине тела.
Есть
определенные соотношения и у других
частей тела. Линия, делящая фигуру
пополам, проходит через начало бедер,
то есть длина ног человека равняется
половине его роста. Концы пальцев
опущенной руки взрослого человека
в положении стоя приходятся обычно чуть
ниже середины бедра. Предплечье
и плечевая часть руки, голень и бедро
ноги примерно равны между собой.
У каждого человека свои характерные
пропорции.
Ответьте на
вопросы и выполните задания
-
Как можно выдержать
пропорции в рисунке? -
Какие пропорции
установило античное искусство для
головы человека?
-
Рассмотрите
этот египетский рельеф, скажите, что
означает разница впропорциональных
отношениях фигур.
-
Приведите
примеры произведений живописи,
скульптуры, архитектуры,
построенных на основе пропорции золотого
сечения. -
Расскажите,
как определить пропорции фигуры человека
на основе золотого
сечения. -
Как
различаются пропорциональные отношения
ребенка, подростка ивзрослого
человека?
-
Какие пропорциональные
соотношения частей тела человека вы
знаете?
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
