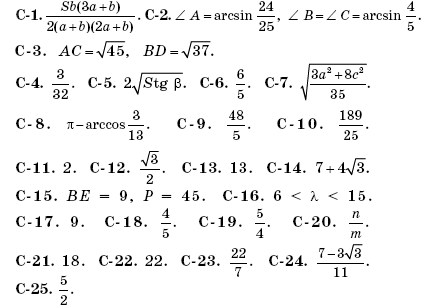Отношением двух отрезков называется отношение их длин.
Рассмотрим два отрезка (AB) и (VN), где отрезок (AB) в (2) раза больше второго отрезка.

Отношение отрезков (AB) и (VN) равно (2 : 1):
Можно также сказать, что отношение отрезков (VN) и (AB) равно (1 : 2):
В этом примере отрезок (AR) равен трём единицам, а (VZ) равен двум единицам.

Отношение отрезков (AR) и (VZ) равно (3 : 2):
ARVZ=32
или
Если отношение отрезков (a) и (b) равно отношению отрезков (c) и (d), т. е.
ab=cd
,
то эти отрезки называются пропорциональными.
Сравниваем данные ранее отрезки, они не пропорциональны, т. к.
ABVN≠ARVZ
.
Рассмотрим данные рисунки:


Сравним отношения отрезков
ABVNиAHVT
.
ABVN=21иAHVT=4221=21
.
Значит,
ABVN=AHVT
— эти пары отрезков пропорциональны.
Чтобы записать отношение отрезков, необходимы два отрезка. Чтобы найти пропорциональные отрезки, необходимы две пары отрезков.
Пропорциональные отрезки


4.5
Средняя оценка: 4.5
Всего получено оценок: 498.
4.5
Средняя оценка: 4.5
Всего получено оценок: 498.
Пропорциональные отрезки очень важны для определения подобия фигур. К тому же, правильно нареченные пропорционально рисунки помогают в правильном решении математических задач. Именно поэтому так важно разбираться в данной тематике.

Опыт работы учителем математики – более 33 лет.
Определение
Пропорциональными отрезками называются отрезки, у которых имеется постоянный коэффициент пропорциональности. Под коэффициентом пропорциональности понимается отношение длин отрезков.

Согласно определению пропорциональных отрезков, два отрезка всегда пропорциональны между собой, поскольку их длины не меняются со временем. Значит, не меняется и коэффициент пропорциональности.
Несмотря на это, чаще всего под пропорциональными отрезками понимают отрезки с коэффициентом кратным 0,5. Например, отрезки с коэффициентом 2,5, 1,5, 2 и тому подобные.
Пропорциональными будут являться и отрезки, составляющие подобные фигуры. Это действует в обе стороны. Если фигуры подобны, то их стороны пропорциональны, если все стороны пропорциональны, то фигуры подобны.
Подобные фигуры
Нужно понимать, что подобными фигурами могут быть не только треугольники, но вообще любые фигуры в геометрии, если все углы этих фигур равны, а длины сторон пропорциональны.

Но при этом признаки подобия существуют только для треугольников. Их всего 3:
- Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Пропорциональными могут быть только отрезки, как объекты имеющие длину. Прямая или луч бесконечны, а потому не могут быть подобными.
Пример
Решим небольшую задачу на пропорциональность отрезков. Имеется 3 пропорциональных отрезка. Каждый из которых больше предыдущего. Первый отрезок равен 5, третий 20. Необходимо найти длину второго отрезка.
Отрезки пропорциональны, значит отношение больших к меньшим будет постоянным. Обозначим неизвестны отрезок за х и решим уравнение.
$${хover{5}}={20over{x}}$$
Перенесем выражение из правой части в левую. Приведем получившееся выражение под один знаменатель и решим дробно-рациональное уравнение.
$${хover{5}}-{20over{x}}=0$$
$${{х^2-100}over{5x}}=0$$
$$х^2-100=0$$
$х^2=100$ – х может являться положительным или отрицательным числом , но отрезок не может иметь отрицательную длину, значит х=10.
Задача решена

Что мы узнали?
Мы узнали, что такое пропорциональные отрезки. Выделили области, где могут быть применены навыки обращения с пропорциональными длинами и привели пример на заданную тему.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Эдуард Ройтбурд
5/5
Оценка статьи
4.5
Средняя оценка: 4.5
Всего получено оценок: 498.
А какая ваша оценка?
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Подобные треугольники
- Пропорциональные отрезки
Отношением отрезков АВ и CD называется отношение их длин, т.е. 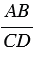 или АВ : СD (читается: “отношение АВ к СD“).
или АВ : СD (читается: “отношение АВ к СD“).
Если 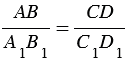 или АВ : А1В1 = СD : С1D1, то отрезки АВ и СD пропорциональны отрезкам А1В1 и С1D1.
или АВ : А1В1 = СD : С1D1, то отрезки АВ и СD пропорциональны отрезкам А1В1 и С1D1.
Пример:
Отрезки АВ = 2 см и СD = 1 см, пропорциональны отрезкам А1В1 = 3 см и С1D1 = 1,5 см. Составим отношение отрезков АВ и А1В, СD и С1D1, получим: 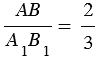 и
и 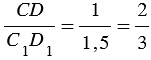 , значит,
, значит, 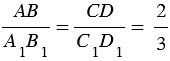 .
.
Понятие пропорциональности вводится и для большего числа отрезков. Так, три отрезка АВ, СD и ЕF пропорциональны трем отрезкам А1В1, С1D1, Е1F1, если справедливо равенство 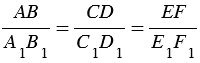 или АВ : А1В1 = СD : С1D1 = ЕF : E1F1.
или АВ : А1В1 = СD : С1D1 = ЕF : E1F1.
Советуем посмотреть:
Определение подобных треугольников
Отношение площадей подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Средняя линия треугольника
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
О подобии произвольных фигур
Синус, косинус и тангенс острого угла прямоугольного треугольника
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Подобные треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 533,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 535,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 536,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 537,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 559,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 2,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 9,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 847,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 852,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 855,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
При сравнении двух значений какой-то величины часто
возникает вопрос:
во сколько раз одно значение больше другого? или
какую часть по отношению к другому оно составляет?
Например, во сколько раз заяц пробежит быстрее
некоторое расстояние, чем это же расстояние проползёт улитка? Или какую часть
всех деревьев леса составляют берёзы?
Вы знаете, что ответ в таких случаях дается в виде
частного двух чисел, которое называют отношением. Отношение показывает,
во сколько раз первое число больше второго, или какую часть первое число
составляет от второго.
Отношением отрезков и
называется
отношение их длин, т. е. (или
).
Отрезки и
пропорциональны
отрезкам и
,
если .
Например, отрезки AB
и
A1B1
равны соответственно 3 сантиметра и 5 сантиметров; а отрезки CD
и C1D1
– соответственно сантиметра
и 7,5 сантиметра.
;
.
Отрезки и
пропорциональны
отрезкам и
.
Следует отметить, что понятие пропорциональности
справедливо и для большего количества отрезков. Например, отрезки AB,
CD и EF
пропорциональны отрезкам A1B1;
C1D1
и E1F1,
если справедливо равенство: .
А теперь давайте посмотрим на рисунок.
Так, матрёшки имеют одинаковую форму, но разные
размеры. То же самое можем сказать про футбольный и теннисный мячи, про
одинаковые фотографии разных размеров.
В геометрии фигуры одинаковой формы называют
подобными. Любые два квадрата и любые два круга являются подобными.
А какие два треугольника называют подобными? Возьмём
два треугольника ABC
и A1B1C1,
у которых угол А равен углу A1,
угол B равен углу B1,
а угол C равен углу C1.
Тогда стороны AB
и A1B1,
BC и B1C1,
AC и A1C1
называются сходственными. И если эти сходственные стороны
пропорциональны ,
то треугольники ABC
и
A1B1C1
являются подобными. Подобие треугольников обозначается следующим образом
Сформулируем определение: подобными называются
треугольники, у которых углы соответственно равны, а сходственные стороны
пропорциональны.
Отношение сходственных сторон называют коэффициентом
подобия. Если стороны треугольника ABC
в два раза больше сторон треугольника A1B1C1,
то отношение сходственных сторон равно 2, то есть коэффициент подобия равен 2.
Подобие треугольников можно установить, проверив
только некоторые из равенств:
,
т. е.
И позднее мы с вами познакомимся с тремя признаками
подобия треугольников.
Решим несколько задач.
Задача. Найдите
отношение отрезков и
,
если их длины соответственно равны см
и см.
Изменится ли это отношение, если длины отрезков выразить в миллиметрах?
Решение.
см
мм,
см
мм.
.
Ответ: ;
не
изменится.
Задача. Пропорциональны
ли отрезки и
,
соответственно равные см
и см,
отрезкам и
,
соответственно равным см
и см?
Решение.
;
;
.
Ответ: пропорциональны.
Задача. В подобных
треугольниках и
стороны
и
,
и
являются
сходственными. Найдите стороны треугольника ,
если см,
см,
см,
а отношение сторон .
Решение.
то есть
(см).
(см).
(см).
Ответ: см,
см,
см.
Итак, на уроке мы узнали, что отношением отрезков и
называется
отношение их длин, т. е. (или
);
что отрезки и
пропорциональны
отрезкам и
,
если .
Также мы выяснили, что подобными называются
треугольники, у которых углы соответственно равны, а сходственные стороны
пропорциональны.
Решаем задачи по геометрии: пропорциональные отрезки
Теорема 1 (теорема Фалеса). Параллельные прямые высекают на пересекающих их прямых пропорциональные отрезки (рис. 1).
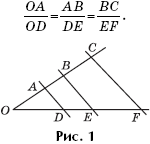
Определение 1. Два треугольника (рис. 2) называются подобными, если соответствующие стороны у них пропорциональны.

Теорема 2 (первый признак подобия). Если угол первого треугольника равен углу второго треугольника, а прилежащие к этим углам стороны треугольников пропорциональны, то такие треугольники подобны (см. рис. 2).
![]()
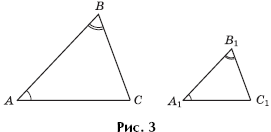
Теорема 3 (второй признак подобия). Если два угла одного треугольника равны соответственно двум углам другого треугольника, то такие треугольники подобны (рис. 3).
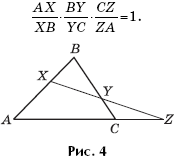
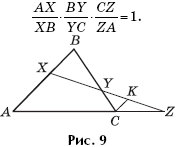
Теорема 4 (теорема Менелая). Если некоторая прямая пересекает стороны AB и BC треугольника ABC в точках X и Y соответственно, а продолжение стороны AC — в точке Z (рис. 4), то
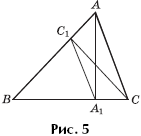
Теорема 5. Пусть в остроугольном треугольнике ABC проведены высоты AA1 и CC1 (рис. 5). Тогда треугольники A1BC1 и ABC подобны, причем коэффициент подобия равен cos ∠B.
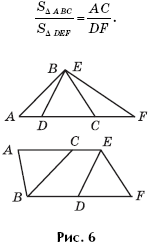
Лемма 1. Если стороны AC и DF треугольников ABC и DEF лежат на одной прямой или на параллельных прямых (рис. 6), то
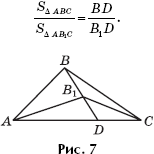
Лемма 2. Если два треугольника имеют общую сторону AC (рис. 7), то
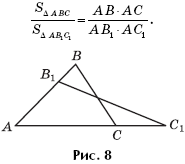
Лемма 3. Если треугольники ABC и AB1C1 имеют общий угол A, то
Лемма 4. Площади подобных треугольников относятся как квадрат коэффициента подобия.
Доказательства некоторых теорем
Доказательство теоремы 4. Проведем через точку C прямую, параллельную прямой AB, до пересечения с прямой XZ в точке K (рис. 9). Надо доказать, что
Рассмотрим две пары подобных треугольников:
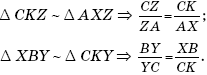
Перемножив почленно эти равенства, получим:
![]()
что и требовалось доказать.
Доказательство теоремы 5. Докажем подобие треугольников A1BC1 и ABC при помощи первого признака подобия. Так как эти два треугольника имеют общий угол B, достаточно доказать, что
![]()
Но это следует из того, что ![]() из прямоугольного треугольника ABA1, а
из прямоугольного треугольника ABA1, а ![]() из прямоугольного треугольника CBC1. Попутно доказана и вторая часть теоремы.
из прямоугольного треугольника CBC1. Попутно доказана и вторая часть теоремы.
Решения задач
Задача 1. Дана трапеция ABCD, причем известно, что BC = a и AD = b. Параллельно ее основаниям BC и AD проведена прямая, пересекающая сторону AB в точке P, диагональ AC в точке L, диагональ BD в точке R и сторону CD в точке Q (рис. 10). Известно, что PL = LR. Найти PQ.
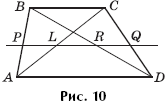
Решение. Докажем сначала, что PL = RQ. Рассмотрим две пары подобных треугольников:
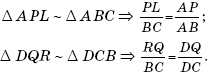
Согласно теореме Фалеса имеем:
![]()
Обозначим теперь PL = LR = RQ = x и рассмотрим снова две пары подобных треугольников:
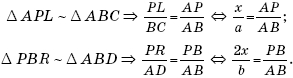
Имеем далее:
![]()
Значит, ![]()
Ответ: ![]()
Задача 2. В треугольнике ABC угол A равен 45°, а угол C — острый. Из середины N стороны BC опущен перпендикуляр NM на сторону AC (рис. 11). Площади треугольников NMC и ABC относятся соответственно как 1 : 8. Найти углы треугольника ABC.
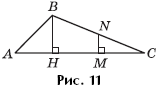
Решение. Пусть BH — высота, опущенная из вершины B на сторону AC.
Так как NM — средняя линия треугольника BHC, то S∆BHC = 4S∆NMC.
Но, согласно условию задачи, S∆ABC = 8S∆NMC.
Следовательно, S∆ABC = 2S∆BHC, поэтому S∆ABH = S∆BHC. Значит, AH = HC,
откуда ∠CAB = ∠ACB = 45°, ∠ABC = 90°.
Ответ: ∠CAB = ∠ACB = 45°, ∠ABC = 90°.
Задача 3. Дан треугольник ABC, в котором угол B равен 30°, AB = 4 и BC = 6. Биссектриса угла B пересекает сторону AC в точке D (рис. 12). Определить площадь треугольника ABD.
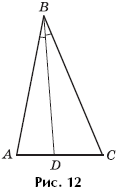
Решение. Применим к треугольнику ABC теорему о биссектрисе внутреннего угла:
![]()
Значит, ![]()
Ответ: ![]()
Статья опубликована при поддержке компании “Мир цветов”. Оптово-розничный склад свадебных и ритуальных товаров, искусственных цветов в Краснодаре. Свадебные аксессуары – свечи, плакаты, бокалы, ленты, приглашения и многое другое. Ритуальные товары – ткани, одежда, фурнитура. Узнать подробнее о компании, посмотреть каталог товаров, цены и контакты Вы сможете на сайте, который располагается по адресу: flowersworld.su.
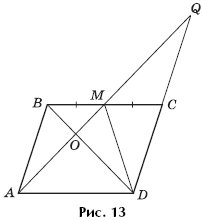
Задача 4. Через середину M стороны BC параллелограмма ABCD, площадь которого равна 1, и вершину A проведена прямая, пересекающая диагональ BD в точке O (рис. 13). Найти площадь четырехугольника OMCD.
Решение. Площадь четырехугольника OMCD будем искать как разность площадей треугольников BCD и BOM. Площадь треугольника BCD равна половине площади параллелограмма ABCD и равна ![]() Найдем площадь треугольника BOM. Имеем:
Найдем площадь треугольника BOM. Имеем:
∆BOM ∼ ∆AOD ⇒ ![]()
Далее:
![]()
Значит, ![]()
Ответ: ![]()
Задача 5. В прямоугольный равнобедренный треугольник ABC с прямым углом при вершине B вписан прямоугольный треугольник MNC так, что угол MNC прямой, точка N лежит на AC, а точка M на стороне AB (рис. 14). В каком отношении точка N должна делить гипотенузу AC, чтобы площадь треугольника MNC составляла 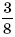 от площади треугольника ABC?
от площади треугольника ABC?
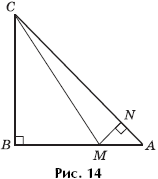
Решение. Можно считать, что AB = 1. Обозначим AM = x, 0 < x < 1, тогда BM = 1 – x,
Задача 6. В трапеции ABCD диагональ AC перпендикулярна боковой стороне CD, а диагональ DB перпендикулярна боковой стороне AB. Продолжения боковых сторон AB и DC пересекаются в точке K, образуя треугольник AKD с углом 45° при вершине K (рис. 15). Площадь трапеции ABCD равна S. Найти площадь треугольника AKD.
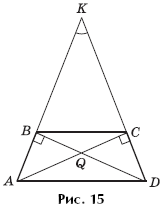
Решение. Согласно теореме 5, треугольник BKC подобен треугольнику AKD с коэффициентом подобия 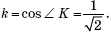 Следовательно, площади этих треугольников относятся как 1 : 2, а это значит, что площадь трапеции ABCD равна площади треугольника BKC. Поэтому площадь треугольника AKD равна 2S.
Следовательно, площади этих треугольников относятся как 1 : 2, а это значит, что площадь трапеции ABCD равна площади треугольника BKC. Поэтому площадь треугольника AKD равна 2S.
Ответ: 2S.
Задача 7. В треугольнике ABC на стороне AB взята точка K так, что AK : KB = 1 : 2, а на стороне BC взята точка L так, что CL : LB = 2 : 1. Пусть Q — точка пересечения прямых AL и CK (рис. 16). Найти площадь треугольника ABC, зная, что площадь треугольника BQC равна 1.
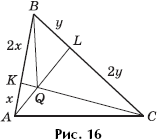
Решение. Пусть AK = x, BL = y. Тогда KB = 2x,
LC = 2y, значит, AB = 3x и BC = 3y. Применим к треугольнику ABL и секущей KQ теорему Менелая:
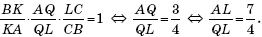
Далее применим к треугольникам ABC и QBC лемму о площадях, получим:
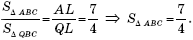
Ответ: 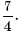
Задача 8. Из точки M, которая расположена внутри остроугольного треугольника ABC, опущены перпендикуляры на стороны (рис. 17). Длины сторон и опущенных на них перпендикуляров соответственно равны a и k, b и m, c и n. Вычислить отношение площади треугольника ABC к площади треугольника, вершинами которого служат основания перпендикуляров.
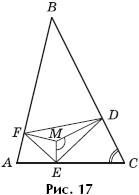
Решение. Введем стандартные обозначения, то есть обозначим длины сторон треугольника ABC: BC = a, CA = b, AB = c; величины углов: ∠BAC = α,
∠ABC = β, ∠ACB = γ. Основания перпендикуляров, опущенных из точки M на стороны BC, CA и AB, обозначим соответственно через D, E и F. Тогда, согласно условию задачи, MD = k, ME = m, MF = n. Очевидно, что угол EMF равен π – α, угол DMF равен π – β, угол DME равен π – γ и точка M расположена внутри треугольника DEF. Площадь треугольника DEF равна:
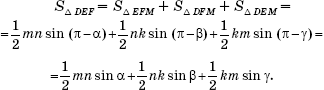
Площадь треугольника ABC равна:
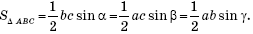
Найдем отношение площадей треугольников DEF и ABC:
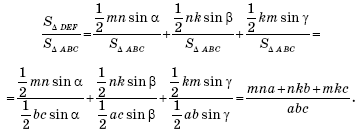
Следовательно, 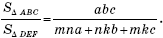
Ответ: 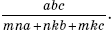
Задача 9. Точки P и Q расположены на стороне BC треугольника ABC так, что BP : PQ : QC = 1 : 2 : 3.
Точка R делит сторону AC этого треугольника таким образом, что AR : RC = 1 : 2 (рис. 18). Чему равно отношение площади четырехугольника PQST к площади треугольника ABC, где S и T — точки пересечения прямой BR с прямыми AQ и AP соответственно?
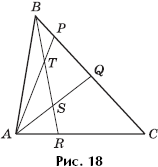
Решение. Обозначим BP = x, AR = y; тогда
PQ = 2x, QC = 3x, RC = 2y. Вычислим, какую часть площадь четырехугольника PQST составляет от площади треугольника APQ, а значит, и от площади треугольника ABC. Для этого нам понадобятся отношения, в которых точки S и T делят прямые AQ и AP соответственно. Применим к треугольнику ACQ и секущей SR теорему Менелая:
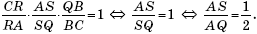
Аналогично, применив теорему Менелая к треугольнику ACP и секущей TR, получим:
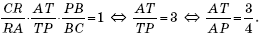
Далее:
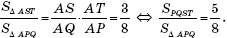
С другой стороны, применив лемму о площадях к треугольникам APQ и ABC, получим, что
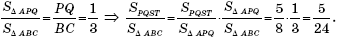
Ответ: 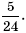
Задача 10. В треугольнике ABC длина высоты BD равна 6, длина медианы CE равна 5, расстояние от точки пересечения BD с CE до стороны AC равно 1 (рис. 19). Найти длину стороны AB.
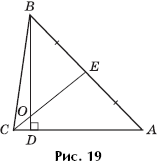
Решение. Пусть точка O — точка пересечения прямых BD и CE. Расстояние от точки O до стороны AC (равное по условию единице) есть длина отрезка OD. Итак, OD = 1 и OB = 5. Применим к треугольнику ABD и секущей OE теорему Менелая:
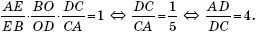
Применив теперь теорему Менелая к треугольнику ACE и секущей OD, получим, что
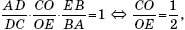
откуда OE = 2CO, и с учетом OE + CO = CE = 5
получаем, что 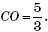 К прямоугольному треугольнику CDO применим теорему Пифагора:
К прямоугольному треугольнику CDO применим теорему Пифагора:
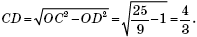
Значит, 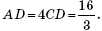 Наконец, рассмотрим прямоугольный треугольник ABD, в нем также воспользуемся теоремой Пифагора:
Наконец, рассмотрим прямоугольный треугольник ABD, в нем также воспользуемся теоремой Пифагора: 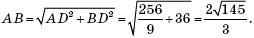
Ответ: 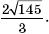
Задача 11. На отрезке AB лежат точки C и D, причем точка C находится между точками A и D. Точка M взята так, что прямые AM и MD перпендикулярны, и прямые CM и MB тоже перпендикулярны (рис. 20). Найти площадь треугольника AMB, если известно, что величина угла CMD равна α, а площади треугольников AMD и CMB равны S1 и S2 соответственно.
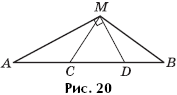
Решение. Обозначим площади треугольников AMB и CMD соответственно через
x и y (x > y). Заметим, что x + y = S1 + S2. Покажем теперь, что xy = S1S2sin2 α. Действительно, 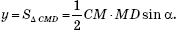
Аналогично, 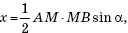
так как ∠AMB = ∠AMC + ∠CMD + ∠DMB =
= 90° – α + α + 90° – α = 180° – α, и sin ∠AMB =
= sin α. Значит:
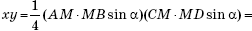
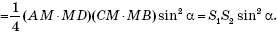
Таким образом, числа x и y являются корнями квадратного уравнения
t2 – (S1 + S2)t + S1S2sin2 α = 0.
Больший корень этого уравнения:
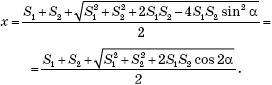
Ответ: 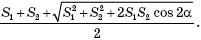
Задачи для самостоятельного решения
С-1. В треугольнике ABC, площадь которого равна S, проведена биссектриса CE и медиана BD, пересекающиеся в точке O. Найдите площадь четырехугольника ADOE, зная, что BC = a, AC = b.
С-2. В равнобедренный треугольник ABC вписан квадрат так, что две его вершины лежат на основании BC, а две другие — на боковых сторонах треугольника. Сторона квадрата относится к радиусу круга, вписанного в треугольник, как
8 : 5. Найдите углы треугольника.
С-3. В параллелограмме ABCD со сторонами AD = 5 и AB = 4 проведен отрезок EF, соединяющий точку E стороны BC с точкой F стороны CD. Точки E и F выбраны так, что
BE : EC = 1 : 2, CF : FE = 1 : 5. Известно, что точка M пересечения диагонали AC с отрезком FE удовлетворяет условию MF : ME = 1 : 4. Найдите диагонали параллелограмма.
С-4. Площадь трапеции ABCD равна 6. Пусть E — точка пересечения продолжений боковых сторон этой трапеции. Через точку E и точку пересечения диагоналей трапеции проведена прямая, которая пересекает меньшее основание BC в точке P, большее основание AD — в точке Q. Точка F лежит на отрезке EC, причем EF : FC = EP : EQ = 1 : 3.
Найдите площадь треугольника EPF.
С-5. В остроугольном треугольнике ABC (где AB > BC) проведены высоты AM и CN, точка O — центр описанной около треугольника ABC окружности. Известно, что величина угла ABC равна β, а площадь четырехугольника NOMB равна S. Найдите длину стороны AC.
С-6. В треугольнике ABC точка K на стороне AB и точка M на стороне AC расположены так, что выполняются соотношения AK : KB = 3 : 2 и AM : MC = 4 : 5. В каком отношении точка пересечения прямых KC и BM делит отрезок BM?
С-7. Внутри прямоугольного треугольника ABC (угол B прямой) взята точка D так, что площади треугольников ABD и BDC соответственно в три и четыре раза меньше площади треугольника ABC. Длины отрезков AD и DC равны соответственно a и c. Найдите длину отрезка BD.
С-8. В выпуклом четырехугольнике ABCD на стороне CD взята точка E так, что отрезок AE делит четырехугольник ABCD на ромб и равнобедренный треугольник, отношение площадей которых равно 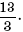 Найдите величину угла BAD.
Найдите величину угла BAD.
С-9. Высота трапеции ABCD равна 7, а длины оснований AD и BC равны соответственно 8 и 6. Через точку E, лежащую на стороне CD, проведена прямая BE, которая делит диагональ AC в точке O в отношении AO : OC = 3 : 2. Найдите площадь треугольника OEC.
С-10. Точки K, L, M делят стороны выпуклого четырехугольника ABCD в отношении AK : BK = CL : BL = CM : DM = 1 : 2. Известно, что радиус описанной около треугольника KLM окружности равен KL = 4, LM = 3 и KM < KL. Найдите площадь четырехугольника ABCD.
С-11. Продолжения сторон AD и BC выпуклого четырехугольника ABCD пересекаются в точке M, а продолжения сторон AB и CD — в точке O. Отрезок MO перпендикулярен биссектрисе угла AOD. Найдите отношение площадей треугольников AOD и BOC, если OA = 6, OD = 4, CD = 1.
С-12. В треугольнике ABC угол при вершине A равен 30°, а высоты BD и CE пересекаются в точке O. Найдите отношение радиусов окружностей, описанных около треугольников DEO и ABC.
С-13. Отрезки, соединяющие основания высот остроугольного треугольника, равны 5, 12 и 13. Найдите радиус описанной около треугольника окружности.
С-14. В остроугольном треугольнике ABC на высоте AD взята точка M, а на высоте BP — точка N так, что углы BMC и ANC — прямые. Расстояние между точками M и N равно 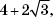 а ∠MCN = 30°.
а ∠MCN = 30°.
Найдите биссектрису CL треугольника CMN.
С-15. На сторонах AB, BC и AC треугольника ABC взяты точки D, E и F соответственно. Отрезки AE и DF проходят через центр вписанной в треугольник ABC окружности, а прямые DF и BC параллельны. Найдите длину отрезка BE и периметр треугольника ABC, если BC = 15, BD = 6, CF = 4.
С-16. В треугольнике ABC биссектриса BB’ пересекает медиану AA’ в точке O.
Найдите отношение площади треугольника BOA’ к площади треугольника AOB’, если AB : AC = 1 : 4.
С-17. В треугольнике ABC точка D лежит на AC, причем AD = 2DC. Точка E лежит на BC. Площадь треугольника ABD равна 3, площадь треугольника AED равна 1. Отрезки AE и BD пересекаются в точке O. Найдите отношение площадей треугольников ABO и OED.
С-18. В параллелограмме ABCD точки E и F лежат соответственно на сторонах AB и BC, M — точка пересечения прямых AF и DE, причем AE = 2BE, а BF = 3CF. Найдите отношение AM : MF.
С-19. В прямоугольнике ABCD на сторонах
AB и AD выбраны соответственно точки E и F так, что AE : EB = 3 : 1, AF : FD = 1 : 2. Найдите EO : OD, где O — точка пересечения отрезков
DE и CF.
С-20. На стороне PQ треугольника PQR взята точка N, а на стороне PR — точка L, причем
NQ = LR. Точка пересечения отрезков QL и NR делит отрезок QL в отношении m : n, считая от точки Q. Найдите отношение PN : PR.
С-21. На сторонах острого угла с вершиной O взяты точки A и B. На луче OB взята точка M на расстоянии 3OA от прямой OA, а на луче OA — точка N на расстоянии 3OB от прямой OB. Радиус окружности, описанной около треугольника AOB, равен 3. Найдите MN.
С-22. В выпуклом пятиугольнике ABCDE диагонали BE и CE являются биссектрисами углов при вершинах B и C соответственно, ∠A = 35°, ∠D = 145°, S∆BCE = 11. Найдите площадь пятиугольника ABCDE.
С-23. На основаниях AD и BC трапеции ABCD построены квадраты ADEF и BCGH, расположенные вне трапеции. Диагонали трапеции пересекаются в точке O. Найдите длину отрезка AD, если BC = 2, GO = 7, а GF = 18.
С-24. В треугольнике ABC известно, что AB = BC, а угол BAC равен 45°. Прямая MN пересекает сторону AC в точке M, а сторону BC — в точке N, причем AM = 2MC, а ∠NMC = 60°. Найдите отношение площади треугольника MNC к площади четырехугольника ABNM.
С-25. В треугольнике ABC взяты точка N на стороне AB, а точка M — на стороне AC. Отрезки CN и BM пересекаются в точке O, AN : NB = 2 : 3,
BO : OM = 5 : 2. Найдите CO : ON.
Ответы: