Как найти пропорциональные отрезки в трапеции

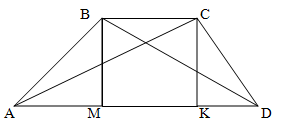
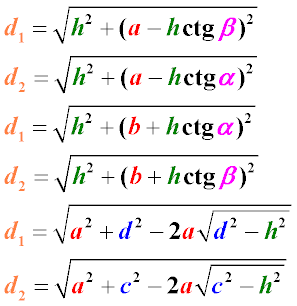Через известную площадь трапеции и пропорциональные отрезки найти площадь треугольника APQ заключённого внутри трапеции

Пропорциональные отрезки – это, наверняка, самая сложная тема в геометрии 8-го класса. И, также наверняка, самая интересная тема. Столько различных задач уже попадалось и вот снова. Только тут ещё замешаны площади, но это всё равно по темам восьмого класса.

Уверен, у Вас получится решить самостоятельно! Но вот несколько подсказок.

Если провести диагонали BD, можно узнать отношение площадей получившихся треугольников, а потом площадь каждого. В треугольнике с большим основанием, PD – медиана. Знаем площадь треугольника APD. Дальше средняя линия в треугольнике ABD параллельно AD и выводы о площадях в получившейся трапеции.

Самый важный вопрос: как применить отношение CD и RD!?

Условие

Площадь трапеции ABCD равна 30. Точка Р — середина боковой стороны АВ. Точка R на стороне CD выбрана так, что 2CD = 3RD. Прямые AR и PD пересекаются в точке Q. Найдите площадь треугольника APQ, если AD = 2ВС.

Решайте

👌 Задача по Геометрии на нахождение площади трапеции

👌 Площадь треугольника через площадь трапеции

👌 Площадь трапеции известны диагонали и снова отрезок соединяющий середины оснований

#огэ по математике #егэ по математике #экзамены #обучение #вуз

В формуле (2) m – это отрезок, параллельный основаниям и разбивающий трапецию на две подобные трапеции, следовательно

Для получения формул (1), (3), и (4) можно воспользоваться следующей задачей:

В формуле (4) m – это отрезок, параллельный основаниям и делящий трапецию на две равновеликие части, т.е. S₁=S₂, тогда получим:

Из подобия треугольников ECN и FND имеем: .

В формуле (3) m – это средняя линия трапеции, следовательно, х=у, и получим .

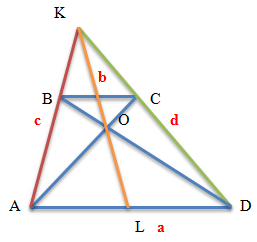
В формуле (1) m – это отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей, следовательно (т.к. диагонали делятся точкой пересечения на отрезки, пропорциональные основаниям трапеции), и получим .

Другой способ доказательства формулы (1):

План урока:

Средняя линия треугольника

Средняя линия трапеции

Теорема о точке пересечения медиан

Подобие в прямоугольном треугольнике

Практические задачи

Задачи на построение

Свойство биссектрисы

Средняя линия треугольника

Отметим в треугольнике середины двух сторон и соединим их. В итоге получится отрезок, который именуют средней линией треугольника.

Здесь точки N и M– это середины АС и ВС соответственно, поэтому NM – это средняя линия. Обратим внимание на ∆АBС и ∆СNM. По рисунку видно, что они подобны, и это действительно так. Ясно, что отношение отрезков АС и СN равно 2, ведь середина N разбивает АС на отрезки, которые вдвое меньше АС:

При этом ∠С является общим для обоих треуг-ков. Это значит, что ∆АBС и ∆NMC подобны (по второму признаку подобия треугольников), причем коэффициент их подобия равен 2. Отсюда сразу следует, что и NM вдвое короче, чем АB.

Из подобия треугольников также следует, что

Но эти два угла являются соответственными для отрезков АB и NM и их секущей AN. Из равенства соответственных углов вытекает, что отрезки АB и NM параллельны. В итоге можно сформулировать два основных свойства средней линии:

Задание. Найдите длину средней линии треугольника FDE, параллельной стороне DE:

Решение. Средняя линия будет вдвое короче DE. Видно, что DE имеет длину 10 клеточек, значит, средняя линия равна 10:2 = 5.

Ответ: 5.

Задание. Стороны треуг-ка имеют длину 8, 5 и 7 см. Середины всех сторон соединили отрезками и получили новый треуг-к. Каков его периметр?

Решение. В данном задаче в треуг-ке построили не одну, а сразу 3 средние линии:

Пусть стороны АB, АС и ВС соответственно составляют 8, 7 и 5 см. Тогда средние линии, параллельные им, будут вдвое меньше:

Задание. Докажите, что три средние линии треуг-ка разбивают его на 4 равные части.

Решение. Пусть стороны треуг-ка равны а, b и с.Отметим середины каждой стороны. Эти середины разобьют стороны на отрезки длиной а/2, b/2 и с/2. Средние же линии, построенные в треуг-ке, будут вдвое меньше сторон значит, их длина также будет составлять а/2, b/2 и c/2:

В итоге у каждого из получившегося треуг-ка стороны равны величинам а/2, b/2 и c/2. Значит, по 3-ему признаку равенства треуг-ков, они все равны друг другу, ч. т. д. 

Задание. В произвольном четырехугольнике отрезками соединили середины смежных сторон. Докажите, что эти отрезки образуют параллелограмм.

Решение. Отметим буквами M, E, Fи H середины сторон четырехуг-ка АBСD. Также построим диагонали АС и BD:

Легко заметить, что МН оказывается средней линией в ∆АBD, ведь она соединяет середины AD и AB. Значит, МН параллельна BD. Но и EF в свою очередь – это средняя линия в ∆BDC, и поэтому она также параллельна BD. Но два отрезка, параллельные третьему, должны быть параллельны и друг другу, то есть МН||EF.

Аналогично и отрезки МЕ и HF – это средние линии в ∆АСD и ∆АBС, поэтому они оба параллельны АС, а значит, и друг другу. В итоге в четырехуг-ке МНFE противоположные стороны оказываются параллельными. Это значит, что он по определению является параллелограммом.

Примечание. Геометрия – наука, развивавшаяся ещё во времена Античности, и большинство теорем и фактов из школьного курса было известно ещё древним грекам. Однако тот приведенный выше факт, что середины любого четырехуг-ка образуют параллелограмм, был доказан только в XVII в. французом Пьером Вариньоном. Соответственно, такой параллелограмм называют вариньоновским.

Вариньоновский параллелограмм обладает множеством свойств. В частности, его площадь вдвое меньше площади исходного четырехуг-ка, а периметр – это сумма длин его диагоналей. Попробуйте самостоятельно доказать это.

Средняя линия трапеции

Напомним, что ранее мы уже изучили другую среднюю линию, которую можно провести в трапеции. Мы доказали, что она параллельна основаниям трапеции. Попробуем найти способ для нахождения ее длины.

Пусть точки M и N – середины боковых сторон АB и CD трапеции АBСD. Построим отрезок BN, а далее продлим прямые BN и AD до их пересечения в некоторой точке K:

Посмотрим на ∆ВNC и ∆KND. У них есть два одинаковых угла:

Отсюда вытекает, что эти треуг-ки подобны (по первому признаку подобия), причем стороны ND и CN – сходственные. Однако эти же отрезки одинаковы, ведь N – середина СD. То есть коэффициент подобия треуг-ков – единица. Это означает, что ∆ВСN и ∆KND равны, и тогда ВС = DK, а. Следовательно, длина АК равна сумме длин оснований трапеции:

Из равенства треуг-ков также вытекает, что BN = NK, то есть N– это середина BK. Но тогда MN по определению – это средняя линия для ∆АBK. Значит, она составляет половину AK, которая в свою очередь является суммой оснований трапеции:

Задание. Найдите длину средней линии трапеции, показанной на рисунке:

Решение. По рисунку видно, что основания имеют длины 10 и 4. Надо лишь сложить эти числа и поделить их надвое:

(10 + a):2 = 14:2 = 7

Ответ: 7.

Задание. Длины боковых сторон трапеции имеют длину 13 и 15 см, ее периметр составляет 48 см. Вычислите длину ее средней линии.

Решение. Задачу можно решить и без рисунка. Обозначим основания трапеции буквами a и b. Периметр – это сумма всех сторон фигуры, поэтому, зная его и длины боковых сторон, можем составить уравнение, из которого найдем величину a + b:

Задание. Докажите, что средняя линия трапеции делит ее диагонали пополам.

Решение. Обозначим середину диагонали BD трапеции АBСD как точку К. Нам надо доказать, эта точка лежит на средней линии MN. Будем доказывать способом «от противного». Пусть точка K не лежит на MN:

Тогда МК будет средней линией в ∆АBD, ведь она соединяет середины АB и BD. Значит, отрезок МК параллелен AD. Аналогично и МN как средняя линия в АBСD также параллельна AD. Однако тогда получается, что через точку М проходят сразу две прямые, параллельные AD, что противоречит аксиоме параллельности. Значит, K не может НЕ лежать на MN, то есть эта точка лежит на средней линии.

Очевидна схожесть формул для вычисления средней линии как в трапеции, так и в треуг-ке. Эта схожесть подсказывает нам, что треуг-к можно рассматривать как особый частный случай трапеции, у которой одно из оснований как бы «стянулось» в точку и стало иметь нулевую длину. Такие частные случаи в математике называются вырожденными.

Теорема о точке пересечения медиан

Подобие позволяет найти отношение, в котором медианы треуг-ка делят друг друга. Построим произвольный ∆АBС и отметим середины сторон АC и ВС точками N и M. По определению NM – это средняя линия, а AМ и BN– медианы. Пусть эти медианы пересекаются в точке O:

Отрезки NM и AB параллельны друг другу, ведь NM – средняя линия. Тогда

ведь они накрест лежащие. Тогда в ∆ОАB и ∆ONM есть два одинаковых угла, следовательно, они подобны. АB и NM –сходственные стороны, поэтому их отношение равно коэффициенту подобия. Но MN как средняя линия вдвое короче, чем АB, то есть

k = AB/MN = 2

Тогда и отношение других сходственных сторон треугольников должно быть таким же:

Таким образом, точка пересечения двух медиан делит их в отношении 2:1, причем больший отрезок начинается от вершины, а меньший – от середины противоположной стороны.

Естественно, что аналогичное утверждение можно доказать и для любой другой пары медиан. Но только одна точка на отрезке может делить ее в каком-нибудь конкретном отношении, в частности, 2:1, поэтому все медианы должны пересечься в одной точке.

Задание. Медианы АМ и BN в ∆АBС пересекаются в точке О. Известны их длины: АМ = 15 и BN = 12. Каковы длины отрезков АО, ОВ, ОN и OM?

Решение:

Медиана АМ делится точкой О в отношении 2:1. Это значит, что АО вдвое длиннее М. Обозначим длину ОМ буквой х, тогда длина АО будут записываться как 2х, в сумме же эти величины дают АМ, то есть 15. Отсюда находим х:

Итак, ОМ = 5, а АО вдвое длиннее, то есть АО = 10. Аналогично, обозначив ОN как у, а ОВ как 2у, найдем и эти отрезки:

Задание. Докажите, что медианы треуг-ка разбивают его на 6 равновеликих треуг-ков.

Решение. Сначала напомним уже известный нам факт, что всякая медиана делит треуг-к на две равновеликие части. Действительно, проведем в произвольном треуг-ке из одной вершины и медиану, и высоту:

Площадь ∆АМС можно по формуле

Теперь рассмотрим случай с тремя медианами, которые мы обозначим как AM, BN и СК. Они разбивают ∆АBС на 6 треуг-ков, площади которых обозначим буквами S₁, S₂, S₃, S₄, S₅ и S₆:

СК делит весь ∆АBС на равновеликие ∆АСК (показан желтым цветом) и ∆СКВ (показан красным цветом), поэтому можно записать равенство:

Но заметим, что отрезки ON, OM и ОК являются также медианами для ∆АОС, ∆ВОС и ∆АОВ, то есть они тоже разделены на равновеликие части:

Мы уже доказали, что есть 4 равновеликих фигуры. Чтобы включить сюда оставшиеся 2 фигуры, нужно записать ещё какое-нибудь равенство. Например, медиана BN делит ∆АBС на две равновеликих части, то есть

Подобие в прямоугольном треугольнике

Прямоугольный треуг-к отличается тем, что его легко можно разбить на два подобных ему треуг-ка. Для этого надо всего лишь опустить высоту на его гипотенузу:

Действительно, пусть на гипотенузу АB опущена высота СН. Пусть в ∆АBС ∠А = α. Вспомним, что сумма острых углов в прямоугольном треугольнике составляет 90°. Тогда, рассматривая ∆АBС, мы можем записать, что

Получается, что в ∆АBС, ∆АСН и ∆ВСН есть по два (и даже по три) одинаковых угла, а потому они подобны друг другу.

Этот факт можно использовать в том числе и для того, чтобы доказать теорему Пифагора. Действительно, из подобия ∆АСН и ∆АBС можно записать, что отношение их гипотенуз равно отношению их катетов, лежащих против угла 90° – α:

Перемножая члены пропорции крест накрест, получаем, что

Аналогично из подобия ∆ВСН и ∆АBС получаем, что отношение их гипотенуз равно отношению тех катетов, что лежат против угла α:

Преимущество этого доказательства заключается в том, что оно никак не опирается на понятие площади фигур.

Всего, если опустить на гипотенузу высоту, получается 6 разных отрезков (на рисунке это АB, АС, ВС, СН, АН, ВН). Зная длину лишь любых двух их них, можно найти и все остальные.

Задание. В прямоугольном ∆АBС опустили высоту АН на гипотенузу ВС. Известно, что СН = 90, НВ = 160. Вычислите все остальные неизвестные отрезки на рисунке.

Решение. Проще всего найти ВС, ведь это просто сумма СН и НВ:

Отрезки же АB и АС найдем, применяя теорему Пифагора. Сначала запишем ее для ∆АBН:

Практические задачи

Подобие треуг-ков может быть использовано и на практике, для измерения некоторых размеров. Например, пусть надо измерить высоту одиноко стоящего дерева. Для этого можно просто поставить рядом, например, человека, чей рост известен. Далее надо измерить длину тени этого человека и самого дерева:

Так как тень должна падать под одним и тем же углом, то в итоге можно получить два подобных треугольника:

Например, пусть высота человека составляет 1,8 м, а тени человека и дерева имеют протяженность 1,2 и 4,8 м. На рисунке ∆АBD и ∆АСЕ подобны, причем стороны AD и АЕ – сходственные. Поделим их чтобы найти коэффициент подобия треугольников:

Также подобие помогает находить расстояние до недоступных точек, например, до горных вершин. Пусть точка В недоступна нам. Выберем две доступные нам точки А и С и измерим расстояние между ними. Также измерим∠А и ∠С в ∆АBС (для этого используется какой-нибудь прибор, например, астролябия). Далее построим на бумаге треуг-к А₁В₁С₁ с такими же углами, но меньшей длиной А₁С₁:

При построении можно выбрать определенный масштаб, например, 1:1000. Так, если реальная длина АB оказалась равной 57 метрам, то на чертеже отрезок А₁В₁ должен быть в тысячу раз короче, то есть равен 57 мм (в 1 метр как раз составляет 1000 мм). Далее на чертеже измеряют длину А₁С₁. Пусть она оказалась равной 519 мм. Тогда длина реального размера АС будет составлять уже 519 метров.

Задачи на построение

Подобие помогает решать некоторые задачи, связанные с построением фигур. Пусть требуется построить треуг-к, если известны только два его угла, а также длина биссектрисы, выходящей из третьего угла. Решение состоит из 5 шагов:

На первом шаге строится произвольный треуг-к, в котором два угла равны заданным в условии. На втором шаге третий угол получившегося треуг-ка разбивается пополам, то есть строится его биссектриса, причем она строится в виде луча, а не конечного отрезка. На третьем шаге на этом луче откладывается отрезок, длина которого совпадает с заданной длиной биссектрисы. В результате на луче можно отметить точку, которая соответствует концу этого отрезка. На шаге 4 через эту точку проводится прямая, параллельная основанию уже построенного треуг-ка. Наконец, на последнем шаге стороны треуг-ка продлеваются до пересечения с новой прямой. В итоге получается новый треуг-к, который будет соответствовать условиям задачи.

Свойство биссектрисы

В заключение рассмотрим одно важное свойство биссектрисы, которое напрямую не связано с подобием, однако использует понятие пропорциональных отрезков. Пусть в ∆АBС, в котором известны стороны АС и ВС, проведена биссектриса СМ. Она разбивает АB на два отрезка, АМ и МВ. Можно ли что-то сказать о длине АМ и МВ?

Оказывается, биссектриса будет делить АB на отрезки, которые окажутся пропорциональными сторонам АС и ВС. Докажем это.

Опустим из точки М высоты на МD и MF на стороны АС и ВС:

Исследуем ∆СМD и ∆СМF. Они прямоугольные, причем у них общая гипотенуза СМ и одинаковые острые углы (∠МСD = ∠МСF, ведь МС – биссектриса). Следовательно, они равны, и тогда высоты МD и МF оказываются одинаковыми:

Теперь запишем эти же площади, проведя другую высоту, СН, которая будет общей для ∆АСМ и ∆СМВ:

В итоге получили вывод:

Задание. AD – биссектриса в ∆АBС. Известно, что

Решение.Отношение отрезка BD к DC равно отношению АB к АС:

Сегодня мы увидели, что пропорциональные отрезки в треугольнике возникают и при выполнении множества построений, а подобие фигур позволяет на практике находить размеры, которые сложно измерить непосредственно. Это подчеркивает практическую значимость изучения геометрии.

В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.

Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.

Трапеция и все-все-все

Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.

Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.

В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.

Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.

Свойства диагоналей трапеции

Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.

1. Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2.
2. Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
   Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k².
3. Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
4. Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении  меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
   Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т.
5. Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ.
6. А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b).

Свойства средней линии трапеции

Среднюю линию проведите в трапеции параллельно ее основаниям.

1. Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2.
2. Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.

Свойство биссектрисы трапеции

Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.

Свойства углов трапеции

1. Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180⁰: α + β = 180⁰  и γ + δ = 180⁰.
2. Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90⁰ , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2.
3. Если через стороны  угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.

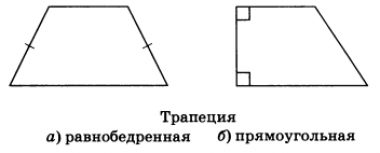
Свойства равнобедренной (равнобокой) трапеции

1. В равнобедренной трапеции равны углы при любом из оснований.
2. Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
3. Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
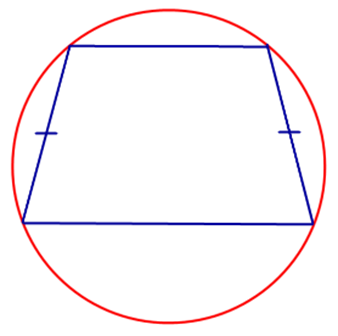
4. Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180⁰ – обязательное условие для этого.
5. Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
6. Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2.
7. Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
8. На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим  на два: (a – b)/2.

Свойства трапеции, вписанной в окружность

Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.

1. Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
2. Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
3. Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
4. Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ.
5. Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ. Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
6. Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S_АМЕ.

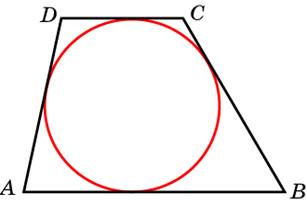
Свойства трапеции, описанной около окружности

Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.

1. Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2.
2. У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ.
3. Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
4. Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab.
5. И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
   Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.

Свойства прямоугольной трапеции

Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.

1. У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
2. Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
3. Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.

Доказательства некоторых свойств трапеции

Равенство углов при основании равнобедренной трапеции:

• Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).

Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.

АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.

Откуда АКМ = 180⁰ – МЕТ = 180⁰ – КАЕ = КМЕ.

Что и требовалось доказать.

Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной:

• Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).

∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.

МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.

У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.

Задача для повторения

Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150⁰ с меньшим основанием. Требуется найти площадь трапеции.

Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.

Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180⁰. Поэтому КАН = 30⁰ (на основании свойства углов трапеции).

Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30⁰. Поэтому КН = ½АВ = 4 см.

Площадь трапеции находим по формуле: S_АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см².

Послесловие

Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.

Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.

Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Диагонали трапеции

Свойства диагоналей трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

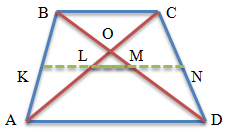
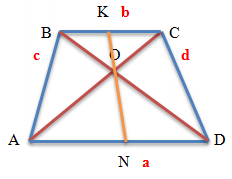
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM. 

Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции.

Данный отрезок параллелен основаниям трапеции.

Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD – BC)/2

или

LM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции

Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции – являются подобными.

Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными – они равны.

Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны. 

Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).

Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.

Что из этого следует?

Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

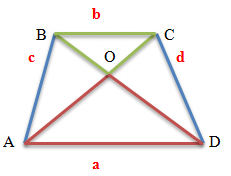
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это – треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.

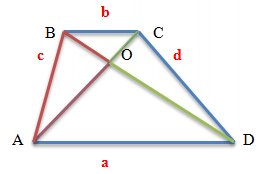
Свойства трапеции, достроенной до треугольника

Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований. 

Таким образом, любая трапеция может быть достроена до треугольника. При этом:

Свойства отрезка, соединяющего основания трапеции

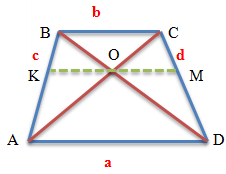
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей ( KO/ON ) будет равно соотношению оснований трапеции ( BC/AD ).

KO / ON = BC / AD

Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:

Формулы для нахождения диагоналей трапеции

Далее приведены формулы, отображающие зависимость между сторонами, углами трапеции и величиной ее диагоналей. Эти формулы пригодятся для решения задач по геометрии на тему “диагонали трапеции”

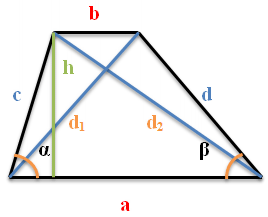
Далее, в формулах используются следующие обозначения:

a, b – основания трапеции

c, d – боковые стороны трапеции

d1 d2 – диагонали трапеции

α β – углы при большем основании трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

 

Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:

1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема

2. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.

3. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ

Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.

Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции,  одна боковая сторона и угол при основании.

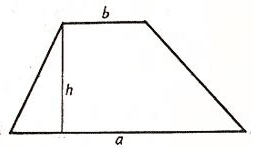
Формулы нахождения диагоналей трапеции через высоту

Примечание. В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа – задайте вопрос на форуме.

Задача.

Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.

Решение.

Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.

Треугольники AOD и BOC являются подобными по трем углам – AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.

Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть

AO / OC = AD / BC

9 / 6 = 24 / BC

BC = 24 * 6 / 9 = 16

Ответ: 16 см

Задача.

В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.

Решение.

Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая – то обозначим длину AM = a, длину  KD = b (не путать с обозначениями в формуле нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK – прямоугольник.

Значит

AD = AM+BC+KD

a + 8 + b = 24

a = 16 – b

Треугольники DBM и ACK – прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора

h² + (24 – a)² = (5√17)²

и

h² + (24 – b)² = 13²

Учтем, что a = 16 – b , тогда в первом уравнении

h² + (24 – 16 + b)² = 425

h²  = 425 – (8 + b)²

Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:

425 – (8 + b)² + (24 – b)²  = 169

-(64 + 16b + b)² + (24 – b)² = -256

-64 – 16b – b² + 576 – 48b + b²  = -256

-64b = -768

b = 12

Таким образом, KD = 12

Откуда

h²  = 425 – (8 + b)² = 425 – (8 + 12)² = 25

h = 5

Найдем площадь трапеции через ее высоту и полусумму оснований

, где a b – основания трапеции, h – высота трапеции

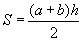
S = (24 + 8) * 5 / 2 = 80 см²

Ответ: площадь трапеции равна 80 см².

0
 

 Трапеция (задачи про основания) |

Описание курса

| Прямоугольная трапеция