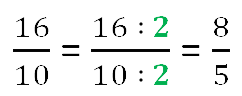Как найти пропорцию двух чисел

Пожалуйста напишите с чем связна такая низкая оценка:

Запомните!

Отношение двух чисел — это их частное.

Запомните!

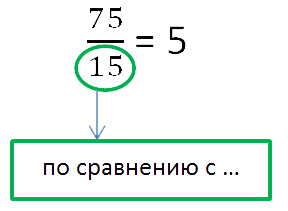
При записи отношения двух чисел в знаменатель дроби (вниз) записывается
то число, с которым сравнивают.
Обычно это число идёт после слов «по сравнению с …» или
предлога «к …».

Запомните!

Если умножить или разделить оба члена отношения на одно и то же число, неравное нулю, то получится отношение, равное данному.

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

0
Спасибо
Ответить

1. 

   1

   Узнайте, для чего служат пропорции. Пропорции используются как в научных исследованиях, так и в повседневной жизни для сравнения различных величин и количеств. В простейшем случае сравниваются два числа, но пропорция может включать в себя любое количество величин. При сравнении двух или большего количества величин всегда можно применить пропорцию. Знание того, как величины соотносятся друг с другом, позволяет, к примеру, записать химические формулы или рецепты различных блюд. Пропорции пригодятся вам для самых разных целей.^[1]
   

2. 

   2

   Ознакомьтесь с тем, что означает пропорция. Как отмечено выше, пропорции позволяют определить соотношение между двумя и более величинами. Например, если для приготовления печенья необходимо 2 стакана муки и 1 стакан сахара, мы говорим, что между количеством муки и сахара существует пропорция (отношение) 2 к 1.

   • С помощью пропорций можно показать, как различные величины относятся друг к другу, даже если они не связаны между собой непосредственно (в отличие от рецепта). Например, если в классе пять девочек и десять мальчиков, отношение количества девочек к числу мальчиков составляет 5 к 10. В этом случае одно число не зависит от другого и не связано с ним непосредственно: пропорция может измениться, если кто-то покинет класс или наоборот, в него придут новые ученики. Пропорция просто позволяет сравнить две величины.

3. 

   3

   Обратите внимание на различные способы выражения пропорций. Пропорции можно записать словами или использовать математические символы.^[2]
   

   • В обыденной жизни пропорции чаще выражают словами (как приведено выше). Пропорции используются в самым разных областях, и если ваша профессия не связана с математикой или другой наукой, чаще всего вам будет попадаться именно такой способ записи пропорций.
   • Пропорции часто записывают посредством двоеточия. При сравнении двух чисел с помощью пропорции их можно записать через двоеточие, например 7:13. Если сравнивается более двух чисел, двоеточие ставится последовательно между каждыми двумя числами, например 10:2:23. В приведенном выше примере для класса мы сравниваем количество девочек и мальчиков, причем 5 девочек : 10 мальчиков. Таким образом, в этом случае пропорцию можно записать в виде 5:10.
   • Иногда при записи пропорций используют знак дроби. В нашем примере с классом отношение 5 девочек к 10 мальчикам запишется как 5/10. В этом случае не следует читать знак “делить” и необходимо помнить, что это не дробь, а соотношение двух разных чисел.

   Реклама

1. 

   1

   Приведите пропорцию к простейшей форме. Пропорции можно упрощать, как и дроби, за счет сокращения входящих в них членов на общий делитель. Чтобы упростить пропорцию, поделите все входящие в нее числа на общие делители. Однако при этом не следует забывать о первоначальных величинах, которые привели к данной пропорции.^[3]
   

   • В приведенном выше примере с классом из 5 девочек и 10 мальчиков (5:10) обе стороны пропорции имеют общий делитель 5. Поделив обе величины на 5 (наибольший общий делитель), получаем отношение 1 девочка на 2 мальчика (то есть 1:2). Однако при использовании упрощенной пропорции следует помнить о первоначальных числах: в классе не 3 ученика, а 15. Сокращенная пропорция лишь показывает отношение между количеством девочек и мальчиков. На каждую девочку приходится два мальчика, но это отнюдь не означает, что в классе 1 девочка и 2 мальчика.
   • Некоторые пропорции не поддаются упрощениям. Например, отношение 3:56 нельзя сократить, так как входящие в пропорцию величины не имеют общего делителя: 3 является простым числом, а 56 не делится на 3.

2. 

   2

   Для “масштабирования” пропорции можно умножать или делить. Пропорциями часто пользуются для того, чтобы увеличить или уменьшить числа в пропорции друг к другу. Умножение или деление всех входящих в пропорцию величин на одно и то же число сохраняет неизменным отношение между ними. Таким образом, пропорции можно умножать или делить на “масштабный” фактор.^[4]
   

   • Предположим, пекарю необходимо утроить количество выпекаемого печенья. Если мука и сахар берутся в пропорции 2 к 1 (2:1), для увеличения количества печенья в три раза данную пропорцию следует умножить на 3. В результате получится 6 стаканов муки на 3 стакана сахара (6:3).
   • Можно поступать и наоборот. Если пекарю необходимо уменьшить количество печенья в два раза, следует обе части пропорции поделить на 2 (или умножить на 1/2). В результате получится 1 стакан муки на полстакана (1/2, или 0,5 стакана) сахара.

3. 

   3

   Научитесь по двум эквивалентным пропорциям находить неизвестную величину. Еще одной распространенной задачей, для решения которой широко используются пропорции, является нахождение неизвестной величины в одной из пропорций, если дана аналогичная ей вторая пропорция. Правило умножения дробей значительно упрощает эту задачу. Запишите каждую пропорцию в виде дроби, затем приравняйте эти дроби друг другу и найдите искомую величину.^[5]
   

   • Предположим, у нас есть небольшая группа учеников из 2 мальчиков и 5 девочек. Если мы хотим сохранить соотношение между мальчиками и девочками, сколько мальчиков должно быть в классе, в который входит 20 девочек? Для начала составим обе пропорции, одна из которых содержит неизвестную величину: 2 мальчика : 5 девочек = x мальчиков : 20 девочек. Если мы запишем пропорции в виде дробей, у нас получится 2/5 и x/20. После умножения обеих частей равенства на знаменатели получаем уравнение 5x=40; делим 40 на 5 и в итоге находим x=8.

   Реклама

1. 

   1

   При операциях с пропорциями избегайте сложения и вычитания. Многие задачи с пропорциями звучат подобно следующей: “Для приготовления блюда требуется 4 картофелины и 5 морковок. Если вы хотите использовать 8 картофелин, сколько морковок вам понадобится?” Многие допускают ошибку и пытаются просто сложить соответствующие величины. Однако для сохранения прежней пропорции следует умножать, а не складывать. Вот ошибочное и правильное решение данной задачи:

   • Неправильный метод: “8 – 4 = 4, то есть в рецепте добавилось 4 картофелины. Значит, необходимо взять прежние 5 морковок и прибавить к ним 4, чтобы… что-то не то! С пропорциями действуют по-другому. Попробуем еще раз“.
   • Правильный метод: “8/4 = 2, то есть количество картофелин выросло в 2 раза. Это значит, что и число морковок следует умножить на 2. 5 x 2 = 10, то есть в новом рецепте необходимо использовать 10 морковок“.

2. 

   2

   Переведите все значения в одинаковые единицы измерения. Иногда проблема возникает из-за того, что величины имеют разные единицы измерения. Прежде чем записывать пропорцию, переведите все величины в одинаковые единицы измерения. Например:

   • У дракона есть 500 граммов золота и 10 килограммов серебра. Каково соотношение золота к серебру в драконьих запасах?
   • Граммы и килограммы являются различными единицами измерения, поэтому их следует унифицировать. 1 килограмм = 1 000 граммов, то есть 10 килограммов = 10 килограммов x 1 000 граммов/1 килограмм = 10 x 1 000 граммов = 10 000 граммов.
   • Итак, дракон имеет 500 граммов золота и 10 000 граммов серебра.
   • Отношение массы золота к массе серебра составляет 500 граммов золота/10 000 граммов серебра = 5/100 = 1/20.

3. 

   3

   Записывайте в решении задачи единицы измерения. В задачах с пропорциями намного легче найти ошибку в том случае, если записывать после каждой величины ее единицы измерения. Помните о том, что если в числителе и знаменателе стоят одинаковые единицы измерения, они сокращаются. После всех возможных сокращений в ответе должны получиться правильные единицы измерения.

   • Например: даны 6 коробок, и в каждых трех коробках находится 9 шариков; сколько всего шариков?
   • Неправильный метод: 6 коробок х 3 коробки/9 шариков = … Хм, ничего не сокращается, и в ответе выходит “коробки x коробки / шарики“. Это не имеет смысла.
   • Правильный метод: 6 коробок х 9 шариков/3 коробки = 6 коробок х 3 шарика/1 коробка = 6 х 3 шарика/1 = 18 шариков.

   Реклама

Download Article

Download Article

You’ve already met fractions like . A proportion is a pair of fractions that are equal to each other, like . There are many different ways to solve proportion problems that ask you to find the missing number , and you don’t need to learn all of them today. If you’re learning pre-algebra and are just starting to use proportions, read from the top until you find a method that makes sense to you. If you’re taking algebra and are working on more advanced proportions problems, you might need to skip down to later methods.

Advertisement

About This Article

Article SummaryX

To solve proportions, start by taking the numerator, or top number, of the fraction you know and multiplying it with the denominator, or bottom number, of the fraction you don’t know. Next, take that number and divide it by the denominator of the fraction you know. Now you can replace x with this final number. For example, to figure out “x” in the problem 3/4 = x/8, multiply 3 x 8 to get 24, then divide 24 / 4 to get 6, or the value of x. To learn how to use proportions to determine percentages, read on!

Thanks to all authors for creating a page that has been read 59,204 times.