Как посчитать пропорцию
- Главная
- /
- Математика
- /
- Арифметика
- /
- Как посчитать пропорцию
Пропорция – это очень удобный математический инструмент, который нашёл широкое применение в различных сферах нашей жизни. Чтобы посчитать пропорцию воспользуйтесь нашим простым онлайн калькулятором:
Онлайн калькулятор
Заполните поля a, c и b, и получите результат X
Теория
a/b = c/X или, другими словами, a относится к b так же как c относится к X – это геометрическая пропорция, которая позволяет выяснить как одно число относится к другому, если известно, как третье относится к четвёртому. Например, с помощью геометрической пропорции можно посчитать процент от числа.
Формула
a/b = c/X
X = (b*c)/a
Пример
Мы положили в банк 4000 рублей под 5% годовых и хотим выяснить сколько в рублях составят эти пять процентов. Мы понимаем, что 4000 – это 100%, а сколько 5% –?
Геометрическая пропорция в данном случаи будет выглядеть так: 100/5=4000/X
X = (4000*5)/100 = 200
Ответ: 5% от 4000 рублей составляет 200 рублей
Proportion in Maths is an equation used to find that the two given ratios are equivalent to each other. Generally, we say that proportion defines that the equality of the two fractions of the ratios. If two sets of given numbers are increasing or decreasing in the same ratio with respect to each other, then the ratios are said to be directly proportional to each other. For example, the time taken by car to cover 200km per hour is equal to the time taken by it to cover the distance of 1200km for 6 hours. Such as 200km/hr = 1200km/6hrs.
Also, See:
- Ratios
- Practice Test on Ratio and Proportion
- Worked out Problems on Ratio and Proportion
Let us take, in proportion, the two ratios are x:y and m:n. The two terms m and n are called means or mean terms and x and y are called extremes or extreme terms.
x : y :: m: n
(frac { x }{ y } ) = (frac { m }{ n } )
Example:
Let us consider the number of persons in a theater. Our first ratio of the number of girls to boys is 5:7 and that of the other is 3:5, then the proportion can be written as:
5 : 7 :: 3 : 5 or 5/7 = 3/5
Here, 5 & 5 are the extremes, while 7 & 3 are the means.
Note: The ratio value does not affect when the same non-zero number is multiplied or divided on each term.
Important Properties of Proportion
The below are the important properties of proportions.
- Addendo – If a : b = c : d, then a + c : b + d
- Subtrahendo – If a : b = c : d, then a – c : b – d
- Componendo – If a : b = c : d, then a + b : b = c+d : d
- Dividendo – If a : b = c : d, then a – b : b = c – d : d
- Invertendo – If a : b = c : d, then b : a = d : c
- Alternendo – If a : b = c : d, then a : c = b: d
- Componendo and dividendo – If a : b = c : d, then a + b : a – b = c + d : c – d
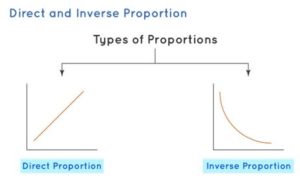
Types of Proportions
The Proportions are classified into two types. They are
- Direct Proportion
- Inverse Proportion
Direct Proportion: The Direct Proportion describes the direct relationship between two quantities. If one of the quantities increases, the other quantity increases and if one of the quantities decreases, the other quantity also decreases.
Example: If the speed of a vehicle increased, then it covers more distance in a fixed amount of time. It is denoted as y ∝ x.
Inverse Proportion: The Inverse Proportion describes the indirect relationship between two quantities. If one quantity increases, the other quantity decreases, and If one quantity decreases the other quantity increases. It is denoted as y ∝ 1/x.
Example: If a vehicle speed increases, then the result in converting a fixed distance in less time.
Important Points on Proportion
Check out the important points that need to remember in the proportion concept.
- Proportion is the comparison between two quantities.
- The proportions are two types. One is direct proportions and inverse proportions.
- Formula of proportion is (frac { x }{ y } ) = (frac { m }{ n } )
- The proportion is an equation.
How to Solve Proportions?
Finding proportion is easy if the ratios are given. Follow the below procedure and find out the process to calculate proportions.
1. Multiply the first term with the last term: x x n
2. Multiply the second term with the third term: y x m
3. If the product of extreme terms is equal to the product of mean terms, then the ratios are proportional: x x n = y x m.
Continued Proportions
If we considered three quantities and the ratio of the first and second quantities is equal to the ratio between the second and the third quantities, then the three quantities are in Continued Proportions.
Example:
Let us take the ratios a:b and c:d
If a: b :: b: c, then we can say that a, b, c quantities are in continued proportion. Also, c is the third proportional of a and b.
b is called the mean proportional between a and C.
If a, b, c are in continued proportion then b² = ac or b = √ac.
Proportion Examples with Answers
Example 1.
Determine if 4, 7, 8, 14 are in proportion?
Solution:
Given numbers are 4, 7, 8, 14.
From the given data, extreme terms are 4 and 13, mean terms are 7 and 6.
Find the Product of extreme terms and mean terms.
Product of extreme terms = 4 × 14 = 56
Product of mean terms = 7 × 8 = 56.
Compare the Product of extreme terms and the Product of mean terms.
The product of means = product of extremes
56 = 56
Therefore, 4, 7, 8, 14 are in proportion.
Example 2.
Check if 3, 6, 12 are in proportion.
Solution:
Given numbers are 3, 6, 12.
From the given data, 3 is the first term, 6 is the middle term, and 12 is the third term.
Find the Product of the first term and third term.
Product of first and third term = 3 × 12 = 36
Square of the middle terms = 6 × 6 = 36 = 3 × 12.
Compare the Product of the first and third term and Square of the middle terms.
The Product of first and third term = Square of the middle terms
56 = 56
Therefore, 3, 6, 12 are in proportion, and 6 is called the mean proportional between 3 and 12.
Example 3.
Find the fourth proportional to 3, 19, 21?
Solution:
Given numbers are 3, 19, 21.
To find the fourth Proportional, let us assume the fourth proportional is x.
Then, 3: 19 :: 21: x
Compare the Product of extreme terms and Product of mean terms.
3x = 19 × 21
3x = 399
x = 399/3
x = 133.
Hence, the fourth proportional to 3, 19, 21 is 133.
Example 4.
Find the third proportional to 4 and 8?
Solution:
Given numbers are 4 and 8.
Let the third proportional to 4 and 8 be x.
Compare the Product of the first and third term and Square of the middle terms.
4x = 8 × 8
4x = 64
x = 64/4
x = 16
Therefore, the third proportional to 4 and 8 is 16.
Example 5.
The ratio of income to expenditure is 3: 4. Find the savings if the expenditure is $24,000.
Solution:
Given that the ratio of income to expenditure is 3: 4.
Therefore, income = $ (3 × 24000)/4 = $18000
Savings = Income – Expenditure = $24,000 – $18000 = $6000
The savings are $6000 if the expenditure is $24,000.
Example 6.
Find the mean proportional between 3 and 27?
Solution:
Given numbers are 3 and 27.
Let the mean proportional between 3 and 27 be x.
Then, x × x = 3 × 27
x² = 81
x = √81
x = 9.
Therefore, the mean proportion between 3 and 27 is 9.
Загрузить PDF
Загрузить PDF
Пропорция — это математическое выражение, в котором два или более числа сравниваются друг с другом. В пропорциях могут сравниваться абсолютные величины и количества или части более крупного целого. Пропорции можно записывать и вычислять несколькими различными способами, однако в основе лежит один и тот же общий принцип.
-
1
Узнайте, для чего служат пропорции. Пропорции используются как в научных исследованиях, так и в повседневной жизни для сравнения различных величин и количеств. В простейшем случае сравниваются два числа, но пропорция может включать в себя любое количество величин. При сравнении двух или большего количества величин всегда можно применить пропорцию. Знание того, как величины соотносятся друг с другом, позволяет, к примеру, записать химические формулы или рецепты различных блюд. Пропорции пригодятся вам для самых разных целей.[1]
-
2
Ознакомьтесь с тем, что означает пропорция. Как отмечено выше, пропорции позволяют определить соотношение между двумя и более величинами. Например, если для приготовления печенья необходимо 2 стакана муки и 1 стакан сахара, мы говорим, что между количеством муки и сахара существует пропорция (отношение) 2 к 1.
- С помощью пропорций можно показать, как различные величины относятся друг к другу, даже если они не связаны между собой непосредственно (в отличие от рецепта). Например, если в классе пять девочек и десять мальчиков, отношение количества девочек к числу мальчиков составляет 5 к 10. В этом случае одно число не зависит от другого и не связано с ним непосредственно: пропорция может измениться, если кто-то покинет класс или наоборот, в него придут новые ученики. Пропорция просто позволяет сравнить две величины.
-
3
Обратите внимание на различные способы выражения пропорций. Пропорции можно записать словами или использовать математические символы.[2]
- В обыденной жизни пропорции чаще выражают словами (как приведено выше). Пропорции используются в самым разных областях, и если ваша профессия не связана с математикой или другой наукой, чаще всего вам будет попадаться именно такой способ записи пропорций.
- Пропорции часто записывают посредством двоеточия. При сравнении двух чисел с помощью пропорции их можно записать через двоеточие, например 7:13. Если сравнивается более двух чисел, двоеточие ставится последовательно между каждыми двумя числами, например 10:2:23. В приведенном выше примере для класса мы сравниваем количество девочек и мальчиков, причем 5 девочек : 10 мальчиков. Таким образом, в этом случае пропорцию можно записать в виде 5:10.
- Иногда при записи пропорций используют знак дроби. В нашем примере с классом отношение 5 девочек к 10 мальчикам запишется как 5/10. В этом случае не следует читать знак “делить” и необходимо помнить, что это не дробь, а соотношение двух разных чисел.
Реклама
-
1
Приведите пропорцию к простейшей форме. Пропорции можно упрощать, как и дроби, за счет сокращения входящих в них членов на общий делитель. Чтобы упростить пропорцию, поделите все входящие в нее числа на общие делители. Однако при этом не следует забывать о первоначальных величинах, которые привели к данной пропорции.[3]
- В приведенном выше примере с классом из 5 девочек и 10 мальчиков (5:10) обе стороны пропорции имеют общий делитель 5. Поделив обе величины на 5 (наибольший общий делитель), получаем отношение 1 девочка на 2 мальчика (то есть 1:2). Однако при использовании упрощенной пропорции следует помнить о первоначальных числах: в классе не 3 ученика, а 15. Сокращенная пропорция лишь показывает отношение между количеством девочек и мальчиков. На каждую девочку приходится два мальчика, но это отнюдь не означает, что в классе 1 девочка и 2 мальчика.
- Некоторые пропорции не поддаются упрощениям. Например, отношение 3:56 нельзя сократить, так как входящие в пропорцию величины не имеют общего делителя: 3 является простым числом, а 56 не делится на 3.
-
2
Для “масштабирования” пропорции можно умножать или делить. Пропорциями часто пользуются для того, чтобы увеличить или уменьшить числа в пропорции друг к другу. Умножение или деление всех входящих в пропорцию величин на одно и то же число сохраняет неизменным отношение между ними. Таким образом, пропорции можно умножать или делить на “масштабный” фактор.[4]
- Предположим, пекарю необходимо утроить количество выпекаемого печенья. Если мука и сахар берутся в пропорции 2 к 1 (2:1), для увеличения количества печенья в три раза данную пропорцию следует умножить на 3. В результате получится 6 стаканов муки на 3 стакана сахара (6:3).
- Можно поступать и наоборот. Если пекарю необходимо уменьшить количество печенья в два раза, следует обе части пропорции поделить на 2 (или умножить на 1/2). В результате получится 1 стакан муки на полстакана (1/2, или 0,5 стакана) сахара.
-
3
Научитесь по двум эквивалентным пропорциям находить неизвестную величину. Еще одной распространенной задачей, для решения которой широко используются пропорции, является нахождение неизвестной величины в одной из пропорций, если дана аналогичная ей вторая пропорция. Правило умножения дробей значительно упрощает эту задачу. Запишите каждую пропорцию в виде дроби, затем приравняйте эти дроби друг другу и найдите искомую величину.[5]
- Предположим, у нас есть небольшая группа учеников из 2 мальчиков и 5 девочек. Если мы хотим сохранить соотношение между мальчиками и девочками, сколько мальчиков должно быть в классе, в который входит 20 девочек? Для начала составим обе пропорции, одна из которых содержит неизвестную величину: 2 мальчика : 5 девочек = x мальчиков : 20 девочек. Если мы запишем пропорции в виде дробей, у нас получится 2/5 и x/20. После умножения обеих частей равенства на знаменатели получаем уравнение 5x=40; делим 40 на 5 и в итоге находим x=8.
Реклама
-
1
При операциях с пропорциями избегайте сложения и вычитания. Многие задачи с пропорциями звучат подобно следующей: “Для приготовления блюда требуется 4 картофелины и 5 морковок. Если вы хотите использовать 8 картофелин, сколько морковок вам понадобится?” Многие допускают ошибку и пытаются просто сложить соответствующие величины. Однако для сохранения прежней пропорции следует умножать, а не складывать. Вот ошибочное и правильное решение данной задачи:
- Неправильный метод: “8 – 4 = 4, то есть в рецепте добавилось 4 картофелины. Значит, необходимо взять прежние 5 морковок и прибавить к ним 4, чтобы… что-то не то! С пропорциями действуют по-другому. Попробуем еще раз“.
- Правильный метод: “8/4 = 2, то есть количество картофелин выросло в 2 раза. Это значит, что и число морковок следует умножить на 2. 5 x 2 = 10, то есть в новом рецепте необходимо использовать 10 морковок“.
-
2
Переведите все значения в одинаковые единицы измерения. Иногда проблема возникает из-за того, что величины имеют разные единицы измерения. Прежде чем записывать пропорцию, переведите все величины в одинаковые единицы измерения. Например:
- У дракона есть 500 граммов золота и 10 килограммов серебра. Каково соотношение золота к серебру в драконьих запасах?
- Граммы и килограммы являются различными единицами измерения, поэтому их следует унифицировать. 1 килограмм = 1 000 граммов, то есть 10 килограммов = 10 килограммов x 1 000 граммов/1 килограмм = 10 x 1 000 граммов = 10 000 граммов.
- Итак, дракон имеет 500 граммов золота и 10 000 граммов серебра.
- Отношение массы золота к массе серебра составляет 500 граммов золота/10 000 граммов серебра = 5/100 = 1/20.
-
3
Записывайте в решении задачи единицы измерения. В задачах с пропорциями намного легче найти ошибку в том случае, если записывать после каждой величины ее единицы измерения. Помните о том, что если в числителе и знаменателе стоят одинаковые единицы измерения, они сокращаются. После всех возможных сокращений в ответе должны получиться правильные единицы измерения.
- Например: даны 6 коробок, и в каждых трех коробках находится 9 шариков; сколько всего шариков?
- Неправильный метод: 6 коробок х 3 коробки/9 шариков = … Хм, ничего не сокращается, и в ответе выходит “коробки x коробки / шарики“. Это не имеет смысла.
- Правильный метод: 6 коробок х 9 шариков/3 коробки = 6 коробок х 3 шарика/1 коробка = 6 х 3 шарика/1 = 18 шариков.
Реклама
Об этой статье
Эту страницу просматривали 57 674 раза.
Была ли эта статья полезной?
Онлайн калькулятор пропорций
Формула пропорций
Пропо́рция — это равенство двух отношений, когда a:b=c:d
| средние | ||||||
| ╭ | члены | ╮ | ||||
| 1 | : | 10 | = | 7 | : | 70 |
| ╰ | крайние члены | ╯ | ||||
| 0,1 | = | 0,1 |
Основные свойства пропорции
Произведение крайних членов равно произведению средних членов (крест-накрест): если a:b=c:d, то a⋅d=b⋅c
1 10 ✕ 7 70 1 ⋅ 70 = 10 ⋅ 7
Обращение пропорции: если a:b=c:d, то b:a=d:c
1 10 7 70 10 1 = 70 7
Перестановка средних членов: если a:b=c:d, то a:c=b:d
1 10 7 70 1 7 = 10 70
Перестановка крайних членов: если a:b=c:d, то d:b=c:a
1 10 7 70 70 10 = 7 1
Решение пропорции с одним неизвестным | Уравнение
1 : 10 = x : 70 1 10 = x 70
Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение
x = 1 ⋅ 70 10 = 7
Как посчитать пропорцию
Задача: нужно пить 1 таблетку активированного угля на 10 килограмм веса. Сколько таблеток нужно выпить, если человек весит 70 кг?
Составим пропорцию: 1 таблетка — 10 кг x таблеток — 70 кг Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение: 1 таблетка x таблеток ✕ 10 кг 70 кг x = 1 ⋅ 70 : 10 = 7 Ответ: 7 таблеток
Задача: за пять часов Вася пишет две статьи. Сколько статей он напишет за 20 часов?
Составим пропорцию: 2 статьи — 5 часов x статей — 20 часов x = 2 ⋅ 20 : 5 = 8 Ответ: 8 статей
Будущим выпускникам школ могу сказать, что умение составлять пропорции мне пригодилось и при расчёте процентов, и для того, чтобы пропорционально уменьшать картинки, и в HTML-вёрстке интернет-страницы, и в бытовых ситуациях.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 апреля 2022 года; проверки требуют 5 правок.
У этого термина существуют и другие значения, см. Пропорция.
Пропо́рция (лат. proportio «соразмерность, выравненность частей; определённое соотношение частей между собой») — равенство отношений двух [и более] пар чисел 
и 
, т. е. равенство вида 
, или, в других обозначениях, равенство 
(часто читается как: «
относится к 
так же, как 
относится к 
»). В этом случае и называют крайними, и — средними членами пропорции. Такую пропорцию ещё называют геометрической, чтобы не путать с арифметической и гармонической пропорциями.
Основные свойства пропорций[править | править код]
- (перестановка средних членов пропорции),
- (перестановка крайних членов пропорции).
- Увеличение и уменьшение пропорции. Если , то
- (увеличение пропорции),
- (уменьшение пропорции).
- Составление пропорции сложением и вычитанием. Если , то
- (составление пропорции сложением),
- (составление пропорции вычитанием).
Доказательство (составление пропорции сложением и вычитанием)
Докажем для сложения. Выразим через остальные члены пропорции: 
. Тогда:
Для вычитания доказательство аналогично. ■
История[править | править код]
Первое известное определение равных пропорций было дано как равенство последовательных вычитаний[1], современным языком это можно выразить как равенство цепных дробей для отношений величин.[2]
Позже Евдокс Книдский упростил определение, равенство пропорций им определялось как одновременное выполнение одной из трёх пар соотношений
для любой пары натуральных чисел 
и 
.
Это определение даётся в «Началах» Евклида.
С появлением вещественных чисел отпала необходимость в специальной теории пропорций, древние математики не рассматривали пропорции длины как числа.
Определение Евдокса, данное в несколько более абстрактном виде, использовалось далее при определении вещественных чисел Дедекиндом через сечения.
Связанные определения[править | править код]
Арифметическая пропорция[править | править код]
Равенство двух разностей 
иногда называют арифметической пропорцией[3].
Гармоническая пропорция[править | править код]
Если у геометрической пропорции средние члены равны, а последний является разницей между первым и средним, такая пропорция называется гармонической: 
. В этом случае, разложение на сумму двух слагаемых и 
называется гармоническим делением или золотым сечением[4].
Задачи на тройное правило[править | править код]
В содержание задачи на простое тройное правило входят две величины, связанные пропорциональной зависимостью, при этом даются два значения одной величины и одно из соответствующих значений другой величины, требуется же найти её второе значение.
Задачами на сложное тройное правило называют задачи, в которых по ряду нескольких (более двух) пропорциональных величин требуется найти значение одной из них, соответствующее другому ряду данных значений величин[5][6].
См. также[править | править код]
- Пропорциональность
Примечания[править | править код]
- ↑ Топика Аристотеля
- ↑ Von Fritz, Kurt. «The discovery of incommensurability by Hippasus of Metapontum». Annals of mathematics. — 1945. — S. 242—264.
- ↑ Пропорции арифметические // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- ↑ Гармоническая пропорция // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- ↑ Справочник по элементарной математике. Дата обращения: 8 января 2018. Архивировано 8 января 2018 года.
- ↑ Решение задач на простое тройное правило. Способы решения. Дата обращения: 8 января 2018. Архивировано 8 января 2018 года.
Литература[править | править код]
- Ван дер Варден, Б. Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. / пер. с голл. И. Н. Веселовского. — М.: ГИФМЛ, 1959.
