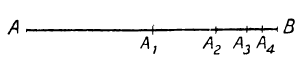
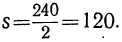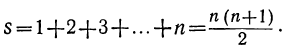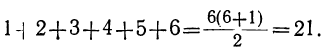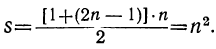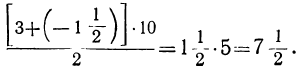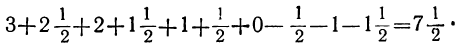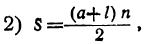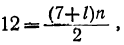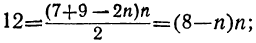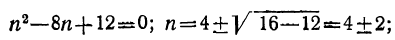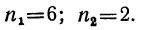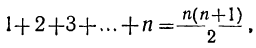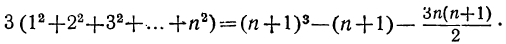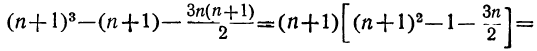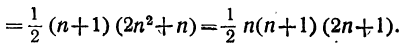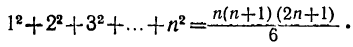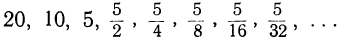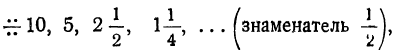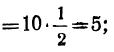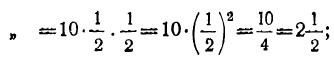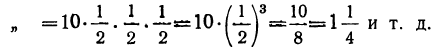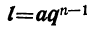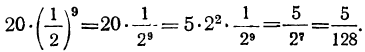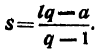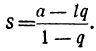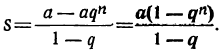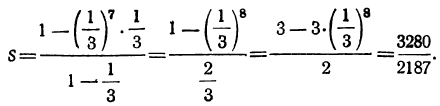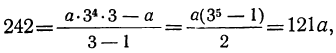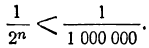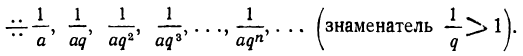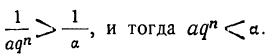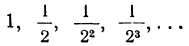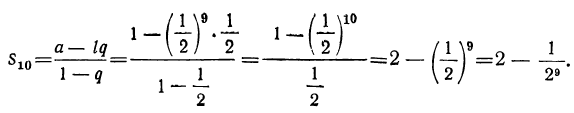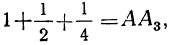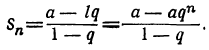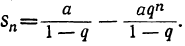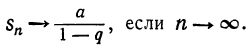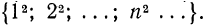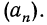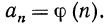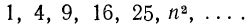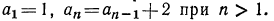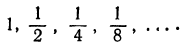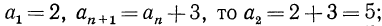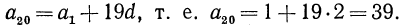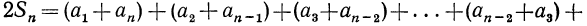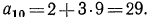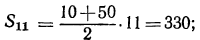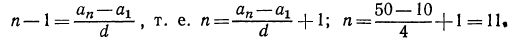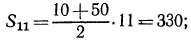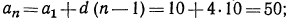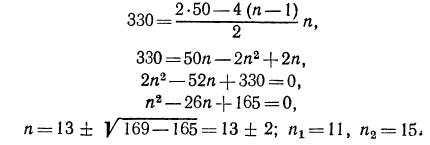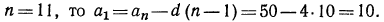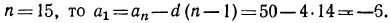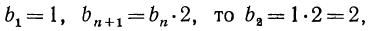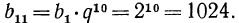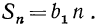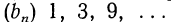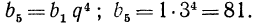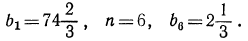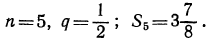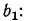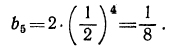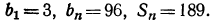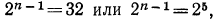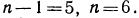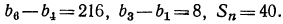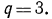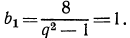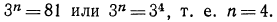Given an array that represents elements of arithmetic progression in order. One element is missing in the progression, find the missing number.
Examples:
Input: arr[] = {2, 4, 8, 10, 12, 14}
Output: 6
Input: arr[] = {1, 6, 11, 16, 21, 31};
Output: 26
A Simple Solution is to linearly traverse the array and find the missing number. Time complexity of this solution is O(n). Below is the implementation
From Mathematical formulae we know that in an AP,
Sum of the n elements = (n/2)(a+l)
n is the number of elements, a is the first element and l is the last element
If we apply this formulae and keep it in a variable s, And take the sum of all elements and keep them in sum. We will get the missing number by s-sum(As sum doesnt includes the missing number)
Implementation:
C++
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int findMissing(int arr[], int n)
{
int a,d,l,s,i,sum=0,missingnumber;
a=arr[0];
l=arr[n-1];
if((a+l)%2==0)
{
s = (a+l)/2;
s = s*(n+1);
}
else
{
s = (n+1)/2;
s = (a+l)*s;
}
for(i=0;i<=n-1;i++)
{
sum = sum + arr[i];
}
missingnumber=s-sum;
return missingnumber;
}
int main()
{
int arr[] = {2, 4, 8, 10, 12, 14};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "The missing element is "
<< findMissing(arr, n);
return 0;
}
Java
class GFG {
static int findMissing(int[] arr, int n)
{
int a, l, s, i, sum = 0, missingnumber;
a = arr[0];
l = arr[n - 1];
if ((a + l) % 2 == 0)
{
s = (a + l) / 2;
s = s * (n + 1);
}
else {
s = (n + 1) / 2;
s = (a + l) * s;
}
for (i = 0; i <= n - 1; i++) {
sum = sum + arr[i];
}
missingnumber = s - sum;
return missingnumber;
}
public static void main(String[] args)
{
int[] arr = { 2, 4, 8, 10, 12, 14 };
int n = arr.length;
System.out.println("The missing element is "
+ findMissing(arr, n));
}
}
Python3
def find_missing(arr, n):
first = arr[0]
last = arr[-1]
if (first + last) % 2:
s = (n + 1) / 2
s *= (first + last)
else:
s = (first + last) / 2
s *= (n + 1)
missing = s - sum(arr)
return missing
if __name__ == "__main__":
arr = [2, 4, 8, 10, 12, 14]
n = len(arr)
missing = find_missing(arr, n)
print(missing)
C#
using System;
class GFG {
static int findMissing(int[] arr, int n)
{
int a, l, s, i, sum = 0, missingnumber;
a = arr[0];
l = arr[n - 1];
if ((a + l) % 2
== 0)
{
s = (a + l) / 2;
s = s * (n + 1);
}
else {
s = (n + 1) / 2;
s = (a + l) * s;
}
for (i = 0; i <= n - 1; i++) {
sum = sum + arr[i];
}
missingnumber = s - sum;
return missingnumber;
}
public static void Main(string[] args)
{
int[] arr = { 2, 4, 8, 10, 12, 14 };
int n = arr.Length;
Console.Write("The missing element is "
+ findMissing(arr, n));
}
}
Javascript
function findMissing(arr, n)
{
let a, d, l, s, i, sum = 0, missingnumber;
a = arr[0];
l = arr[n - 1];
if((a+l)%2==0)
{
s = (a+l)/2;
s = s*(n+1);
}
else
{
s = (n+1)/2;
s = (a+l)*s;
}
for(i = 0; i <= n - 1; i++)
{
sum = sum + arr[i];
}
missingnumber = s - sum;
return missingnumber;
}
let arr = [2, 4, 8, 10, 12, 14];
let n =arr.length;
console.log("The missing element is", findMissing(arr, n));
Output
The missing element is 6
The Time Complexity is O(n) as we are iterating the array once and the Space Complexity is O(1)
We can also solve this problem in O(Logn) time using Binary Search. The idea is to go to the middle element. Check if the difference between middle and next to middle is equal to diff or not, if not then the missing element lies between mid and mid+1. If the middle element is equal to n/2th term in Arithmetic Series (Let n be the number of elements in input array), then missing element lies in right half. Else element lies in left half.
Following is implementation of above idea.
C++
#include<iostream>
using namespace std;
#define INT_MAX 2147483647;
class GFG
{
public:int findMissingUtil(int arr[], int low,
int high, int diff)
{
if (high <= low)
return INT_MAX;
int mid = low + (high - low) / 2;
if (arr[mid + 1] - arr[mid] != diff)
return (arr[mid] + diff);
if (mid > 0 && arr[mid] - arr[mid - 1] != diff)
return (arr[mid - 1] + diff);
if (arr[mid] == arr[0] + mid * diff)
return findMissingUtil(arr, mid + 1,
high, diff);
return findMissingUtil(arr, low, mid - 1, diff);
}
int findMissing(int arr[], int n)
{
int diff = (arr[n - 1] - arr[0]) / n;
return findMissingUtil(arr, 0, n - 1, diff);
}
};
int main()
{
GFG g;
int arr[] = {2, 4, 8, 10, 12, 14};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "The missing element is "
<< g.findMissing(arr, n);
return 0;
}
C
#include <stdio.h>
#include <limits.h>
int findMissingUtil(int arr[], int low, int high, int diff)
{
if (high <= low)
return INT_MAX;
int mid = low + (high - low)/2;
if (arr[mid+1] - arr[mid] != diff)
return (arr[mid] + diff);
if (mid > 0 && arr[mid] - arr[mid-1] != diff)
return (arr[mid-1] + diff);
if (arr[mid] == arr[0] + mid*diff)
return findMissingUtil(arr, mid+1, high, diff);
return findMissingUtil(arr, low, mid-1, diff);
}
int findMissing(int arr[], int n)
{
int diff = (arr[n-1] - arr[0])/n;
return findMissingUtil(arr, 0, n-1, diff);
}
int main()
{
int arr[] = {2, 4, 8, 10, 12, 14};
int n = sizeof(arr)/sizeof(arr[0]);
printf("The missing element is %d", findMissing(arr, n));
return 0;
}
Java
import java.io.*;
class GFG
{
static int findMissingUtil(int arr[], int low,
int high, int diff)
{
if (high <= low)
return Integer.MAX_VALUE;
int mid = low + (high - low) / 2;
if (arr[mid + 1] - arr[mid] != diff)
return (arr[mid] + diff);
if (mid > 0 && arr[mid] -
arr[mid - 1] != diff)
return (arr[mid - 1] + diff);
if (arr[mid] == arr[0] + mid * diff)
return findMissingUtil(arr, mid + 1,
high, diff);
return findMissingUtil(arr, low, mid - 1, diff);
}
static int findMissing(int arr[], int n)
{
int diff = (arr[n - 1] - arr[0]) / n;
return findMissingUtil(arr, 0, n - 1, diff);
}
public static void main (String[] args)
{
int arr[] = {2, 4, 8, 10, 12, 14};
int n = arr.length;
System.out.println("The missing element is "+
findMissing(arr, n));
}
}
Python3
import sys
def findMissingUtil(arr, low, high, diff):
if (high <= low):
return sys.maxsize;
mid = int(low + (high - low) / 2);
if (arr[mid + 1] - arr[mid] != diff):
return (arr[mid] + diff);
if (mid > 0 and arr[mid] -
arr[mid - 1] != diff):
return (arr[mid - 1] + diff);
if (arr[mid] == arr[0] + mid * diff):
return findMissingUtil(arr, mid + 1,
high, diff);
return findMissingUtil(arr, low,
mid - 1, diff);
def findMissing(arr, n):
diff = int((arr[n - 1] - arr[0]) / n);
return findMissingUtil(arr, 0, n - 1, diff);
arr = [2, 4, 8, 10, 12, 14];
n = len(arr);
print("The missing element is",
findMissing(arr, n));
C#
using System;
class GFG
{
static int findMissingUtil(int []arr, int low,
int high, int diff)
{
if (high <= low)
return int.MaxValue;
int mid = low + (high -
low) / 2;
if (arr[mid + 1] -
arr[mid] != diff)
return (arr[mid] + diff);
if (mid > 0 && arr[mid] -
arr[mid - 1] != diff)
return (arr[mid - 1] + diff);
if (arr[mid] == arr[0] +
mid * diff)
return findMissingUtil(arr, mid + 1,
high, diff);
return findMissingUtil(arr, low,
mid - 1, diff);
}
static int findMissing(int []arr, int n)
{
int diff = (arr[n - 1] -
arr[0]) / n;
return findMissingUtil(arr, 0,
n - 1, diff);
}
public static void Main ()
{
int []arr = {2, 4, 8,
10, 12, 14};
int n = arr.Length;
Console.WriteLine("The missing element is "+
findMissing(arr, n));
}
}
PHP
<?php
function findMissingUtil($arr, $low, $high, $diff)
{
if ($high <= $low)
return PHP_INT_MAX;
$mid = $low + ($high - $low) / 2;
if ($arr[$mid + 1] - $arr[$mid] != $diff)
return ($arr[$mid] + $diff);
if ($mid > 0 && $arr[$mid] - $arr[$mid - 1] != $diff)
return ($arr[$mid - 1] + $diff);
if ($arr[$mid] == $arr[0] + $mid * $diff)
return findMissingUtil($arr, $mid + 1,
$high, $diff);
return findMissingUtil($arr, $low, $mid - 1, $diff);
}
function findMissing($arr, $n)
{
$diff = ($arr[$n - 1] - $arr[0]) / $n;
return findMissingUtil($arr, 0, $n - 1, $diff);
}
$arr = array(2, 4, 8, 10, 12, 14);
$n = sizeof($arr);
echo "The missing element is ",
findMissing($arr, $n);
?>
Javascript
<script>
function findMissingUtil(arr, low, high, diff)
{
if (high <= low)
return Number.MAX_VALUE;
let mid = low + parseInt((high - low) / 2, 10);
if (arr[mid + 1] - arr[mid] != diff)
return (arr[mid] + diff);
if (mid > 0 && arr[mid] -
arr[mid - 1] != diff)
return (arr[mid - 1] + diff);
if (arr[mid] == arr[0] + mid * diff)
return findMissingUtil(arr, mid + 1, high, diff);
return findMissingUtil(arr, low, mid - 1, diff);
}
function findMissing(arr, n)
{
let diff = parseInt((arr[n - 1] - arr[0]) / n, 10);
return findMissingUtil(arr, 0, n - 1, diff);
}
let arr = [2, 4, 8, 10, 12, 14];
let n = arr.length;
document.write("The missing element is "+
findMissing(arr, n));
</script>
Output
The missing element is 6
Time Complexity: O(log n)
Auxiliary Space: O(1)
Iterative: The idea is to go to the middle element. Check if the index of middle element is equal to (nth position of middle element in AP) – 1 then the missing element lies at right half if not then the missing element lies at left half (this idea is similar to Find the only repeating element in a sorted array of size n ). After breaking out of binary search loop the missing element will lie between high and low. We can find the missing element by adding a common difference with element at index high or by subtracting a common difference with element at index low.
Following is implementation of above idea.
C++
#include<iostream>
using namespace std;
#define INT_MAX 2147483647;
class GFG
{
public:int findMissingUtil(int arr[], int low,
int high, int diff)
{
int mid;
while (low <= high)
{
mid = (low + high) / 2;
if ((arr[mid] - arr[0]) / diff == mid)
low = mid + 1;
else
high = mid - 1;
}
return arr[high] + diff;
}
int findMissing(int arr[], int n)
{
int diff = (arr[n - 1] - arr[0]) / n;
return findMissingUtil(arr, 0, n - 1, diff);
}
};
int main()
{
GFG g;
int arr[] = {2, 4, 8, 10, 12, 14};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "The missing element is "
<< g.findMissing(arr, n);
return 0;
}
C
#include <stdio.h>
#include <limits.h>
int findMissingUtil(int arr[], int low, int high, int diff)
{
int mid;
while (low <= high)
{
mid = (low + high) / 2;
if ((arr[mid] - arr[0]) / diff == mid)
low = mid + 1;
else
high = mid - 1;
}
return arr[high] + diff;
}
int findMissing(int arr[], int n)
{
int diff = (arr[n-1] - arr[0])/n;
return findMissingUtil(arr, 0, n-1, diff);
}
int main()
{
int arr[] = {2, 4, 8, 10, 12, 14};
int n = sizeof(arr)/sizeof(arr[0]);
printf("The missing element is %d", findMissing(arr, n));
return 0;
}
Java
import java.io.*;
class GFG
{
static int findMissingUtil(int arr[], int low,
int high, int diff)
{
int mid;
while (low <= high)
{
mid = (low + high) / 2;
if ((arr[mid] - arr[0]) / diff == mid)
low = mid + 1;
else
high = mid - 1;
}
return arr[high] + diff;
}
static int findMissing(int arr[], int n)
{
int diff = (arr[n - 1] - arr[0]) / n;
return findMissingUtil(arr, 0, n - 1, diff);
}
public static void main (String[] args)
{
int arr[] = {2, 4, 8, 10, 12, 14};
int n = arr.length;
System.out.println("The missing element is "+
findMissing(arr, n));
}
}
Python3
import sys
def findMissingUtil(arr, low, high, diff):
while low <= high:
mid = (low + high)//2
if (arr[mid] - arr[0])//diff == mid:
low = mid + 1
else:
high = mid - 1
return arr[high] + diff
def findMissing(arr, n):
diff = int((arr[n - 1] - arr[0]) / n);
return findMissingUtil(arr, 0, n - 1, diff);
arr = [2, 4, 8, 10, 12, 14];
n = len(arr);
print("The missing element is",
findMissing(arr, n));
C#
using System;
class GFG
{
static int findMissingUtil(int []arr, int low,
int high, int diff)
{
int mid;
while (low <= high)
{
mid = (low + high) / 2;
if ((arr[mid] - arr[0]) / diff == mid)
low = mid + 1;
else
high = mid - 1;
}
return arr[high] + diff;
}
static int findMissing(int []arr, int n)
{
int diff = (arr[n - 1] -
arr[0]) / n;
return findMissingUtil(arr, 0,
n - 1, diff);
}
public static void Main ()
{
int []arr = {2, 4, 8,
10, 12, 14};
int n = arr.Length;
Console.WriteLine("The missing element is "+
findMissing(arr, n));
}
}
PHP
<?php
function findMissingUtil($arr, $low, $high, $diff)
{
while ($low <= $high)
{
$mid = ($low + $high) / 2;
if (($arr[$mid] - $arr[0]) / $diff == $mid)
$low = $mid + 1;
else
$high = $mid - 1;
}
return $arr[$high] + $diff;
}
function findMissing($arr, $n)
{
$diff = ($arr[$n - 1] - $arr[0]) / $n;
return findMissingUtil($arr, 0, $n - 1, $diff);
}
$arr = array(2, 4, 8, 10, 12, 14);
$n = sizeof($arr);
echo "The missing element is ",
findMissing($arr, $n);
?>
Javascript
<script>
function findMissingUtil(arr, low, high, diff)
{
int mid;
while (low <= high)
{
mid = (low + high) / 2;
if ((arr[mid] - arr[0]) / diff == mid)
low = mid + 1;
else
high = mid - 1;
}
return arr[high] + diff;
}
function findMissing(arr, n)
{
let diff = parseInt((arr[n - 1] - arr[0]) / n, 10);
return findMissingUtil(arr, 0, n - 1, diff);
}
let arr = [2, 4, 8, 10, 12, 14];
let n = arr.length;
document.write("The missing element is "+
findMissing(arr, n));
</script>
Output
The missing element is 6
Time Complexity: O(log n)
Auxiliary Space: O(1)
Thanks to gurudev620gs for suggesting the above solution.
Exercise:
Solve the same problem for Geometrical Series. What is the time complexity of your solution? What about Fibonacci Series?
Last Updated :
15 Jul, 2022
Like Article
Save Article
Реферат на тему » Арифметическая прогрессия»
Реферат на тему:
«Арифметическая
прогрессия».
Автор:
Козлова Кристина ученица 9 класса МКОУ «Борковская основная общеобразовательная школа» Суджанского района Куврской области
Руководитель:
Барсова Мария Ивановна, учитель, математики первой квалификационной категории
МКОУ «Борковская основная общеобразовательная школа» Суджанского района Куврской области
Содержание
Аннотация……………………………………………………………………………………….. 2
Введение …………………………………………………………………………………………3
1.Определения и формулы……………………………………………………………………..3
2. Примеры решения заданий на Тему: «Нахождение разности, суммы и п-го члена
арифметической прогрессии»………………………………………………………………….. 4
З. Решение задач на формулы арифметической прогрессии………………………… …6
Заключение……………………………………………………………………………………. . 7
Аннотация.
Тема актуальна, имеет широкое практическое применение. Арифметические прогрессии и их свойства изучались математиками с древних времен. Автор стремится, раскрыть в полной мере свои познания в этой области умело совершает экскурс в историю, решал задачу немецкого математика Карла Фридриха Гаусса. Хотя задачи на нахождение последовательностей начинают решать в 9 классе, автор выбрал эту тему, потому что математика имеет постоянно дело с бесконечностью. Опровержение известного изречения нельзя объять необъятное, мы не только научимся задавать такие необъятные объекты, как бесконечные последовательности, но сумеем выделить некоторые их группы, такие как арифметическая прогрессия, но и опишем отдельные свойства. Знание свойств арифметической прогрессии позволяет решить немало различных задач. В работе автор уделил достаточное место теме арифметическая прогрессия: определению, свойствам делает вывод формулы суммы n первых членов арифметической прогрессии.
Рассмотрены примеры решения заданий на тему:
«Нахождение разности, суммы и n-го члена арифметической прогрессию». Решены задачи на формулы арифметической прогрессии.
Автор исследует актуальную тему математики, решал сознательно задачи об арифметической прогрессии. Тема дана блоком. Идет отработка вычислительных навыков, даны задания трех уровней сложности, в том числе предлагаемые на ЕГЭ. Затем идет отработка применения знаний при решении задач практического содержания.
В работе подробно освещена теоретическая часть, доказаны теоремы, рассмотрен аналитический способ решения арифметической последовательности.
Особый интерес у автора вызвало решение нестандартных задач. Приведены примеры решения последовательности из сборника Подготовка к «малому ЕГЭ)» М.: Эксмо, 2008. Использована обширная литература. Данная работа заслуживает интерес, и лишь начало в исследовании важной и интересной темы. Эти исследования обеспечат молодому автору развитие математических способностей и знаний.
(Барсова М. И.)
Введение.
Я выбрала эту тему потому, что людям свойственно подмечать закономерности в окружающих явлениях.
С последовательностями люди столкнулись в древнейшие времена, считая тройками, десятками, дюжинами….
Мир чисел — не исключение. Простейших навыков счета достаточно, чтобы подметить систему в последовательности: 1, 7, 13, 19… или 1, 2,4, 8…
Встретив новое понятие, хочется узнать о происхождении названия. Почему прогрессия? Почему арифметическая?
Ответ на первый вопрос почти очевиден. Члены такой последовательности все время прогрессируют на одно и тоже число (1, т.е. либо все ниже опускаются (при dО). Возможно, конечно, когда (d=0, это последовательность из одинаковых чисел.
Ну, а арифметической прогрессия названа потому, что в ней каждый член, кроме первого, равен среднему арифметическому двух соседних с ним — предыдущего и последующего.
Цель работы:
Рассмотреть определение и свойства арифметической прогрессии. Уделить внимание выводу формулы суммы n первых членов арифметической прогрессии. Рассмотреть примеры решения заданий на тему: «Нахождение разности, суммы и n-го члена арифметической прогрессию», раскрыть в полной мере свои познания в этой области; совершить экскурс в историю, решить задачу немецкого математика Карла Фридриха Гаусса. Решить задачи на формулы арифметической прогрессии.
Задача:
Сознательно овладеть системой знаний и умений об арифметической прогрессии.
Рассмотреть свойства и задания на тему: «Нахождение разности, суммы и n-го члена арифметической прогрессии», сознательно решить задачи об арифметической прогрессии.
1.Определения и формулы.
Определение: арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
Любая арифметическая прогрессия может быть задана формулой вида:
an=kn+b, (1)
где k и b — некоторые числа.
Верно и обратное, что последовательность (аn ), заданная формулой вида:
an=kn+b,
где k и b — некоторые числа, является арифметической прогрессией.
Действительно, найдем разность (n-1)-го и n-го членов последовательности (аn ):
аn+1- an =(n +1)+ b —(kn+b)= kn+k+ b — kn — b = k.
Значит, при любом n справедливо равенство аn+1=аn + k, и по определению последовательность (аn) является арифметической прогрессией, причем разность этой прогрессии равна k
Рассмотрим последовательность (аn), каждый член которой, начиная со второго равен предыдущему, сложенному с одним и тем же числом а, называемым разностью прогрессии. Чтобы найти разность арифметической прогрессии нужно из второго члена вычесть первый:
d=а2—а1 (2)
Также для нахождения разности верно неравенство:
d = аn+1 — an (З)
для любого натурального числа n характерна рекуррентная формула:
аn+1 = an + d(4)
где d — некоторое число.
Легко найти явное выражение an через n.
При переходе к очередному элементу его значение возрастет на разность — по сравнению с предыдущим. Чтобы добраться от первого члена прогрессии до n-го, нужно n-1 таких переходов, вследствие чего an , превышает а1 на (n-1) d, 1т.е.
а а1 на — (n -1) d. (5)
Последнее равенство позволяет вычислить сумму n —первых членов арифметической прогрессии: Sn а1+ а2 + .. .+ аn-1 + an
Говорят, немецкий математик Карл Фридрих Гаусс, еще, будучи школьником, сумел за считанные секунды найти сумму всех натуральных чисел от 1 до 100. Он заметил, что суммы равностоящих от концов чисел равны: 1+100 = 2 +99 = 3 +98=.. .=50+51=101.
Всего получается 50 пар чисел, и сумма каждой пары 101, поэтому общая сумма 50*101= 5050.
действительно, последовательность натуральных чисел является арифметической прогрессией. Здесь а1 = d и d =1.
Гаусс рассматривал четное количество слагаемых, поэтому он сумел разбить их на пары. У нас же n любое натуральное число. Неужели придётся рассматривать отдельно случаи чётного и нечётного n? Нет, сделаем по-другому.
Возьмем ещё одну такую же сумму, но слагаемые запишем в обратном порядке:
S n = an+ аn-1+…+ а1+ а2
далее, сложим её почленно с исходной суммой, причём слагаемые сразу попарно
сгруппируем. Получим
2 Sn= (а1 + an) + (а2+ аn-1)+…+( аn-1 +а2)+( an +а1).
В каждых скобках заключена сумма двух равноотстоящих от концов членов прогрессии, которая, как мы знаем, равна 2 а1 + (n -1) d . Всего же таких сумм n, поэтому
2 S n =n (2а1+(n -1) d) = 2na1 + n (n -1) d,
Откуда (6)
Таким образом, сумма n первых членов арифметической прогрессии выражается через первый член и разность. Арифметическая прогрессия возрастает пропорционально n, а сумма первых n её членов — гораздо быстрее, примерно как n 2 /2. И это не случайность, а «далёкий отзвук> интегрального исчисления. Теперь найдём выражение для суммы первых n членов арифметической прогрессии, если известны лишь первый и последний члены, т. е. аi и а Рассмотрим ещё раз равенство
2 Sn= (а1 + an)+(а2+ аn-1)+.
..+( аn-1 +а2)+( an +а1).
Суммы в каждой из скобок равны между собой, значит,
2 Sn= n(а1 + an),
Sn = (7)
Наконец, дадим ещё более простое выражение для Snпригодное, правда, лишь для нечетных n, т.е. для n = 2k — 1. Поскольку при этом 1+n1+(2k-1)= 2k=k+k, то в силу раннее найденною свойства арифметической прогрессии а1 + аn = аk+ аk=2 аk
Поэтому S n = S n = n * аk (8)
2. Примеры решения заданий на тему: «Нахождение разности, суммы и n-го члена арифметической прогрессии».
Пример 1 При хранении бревен строевого леса их укладывают так, как показано на рисунке. Сколько бревен находится в одной кладке, если в ее основание положить 12
бревен?
Дано: а. n: а1=12, а2 =11, an = 1
Найти : Sn- ?
Решение : а а1 + — , где — а1 1
12+( n—1)(-1) =1
12 — n+1=1
2) Найдем S n
Sn =
S n =
Ответ : 78 бревен в одной кадке.
Пример2 Свободно падающее тело проходит в первую секунду 4,9 м, а в каждую следующую секунду на 9,8 м больше, чем в предыдущую.
Найдите глубину шахты, если свободно падающее тело достигло дна шахты через 5 секунд после начала падения”.
Дано: а. n: а1 = 49м, d1 =9,8м n1= 5с.
Найти : S 5 — ?
Решение:
Sn =
S 5 =
Ответ: глубина шахты 122,5 м.
Пример З Сколько отрицательных членов содержит арифметическая прогрессии (аn):
-18; -17,3;…?
Нам требуется найти отрицательные члены прогрессии, т.е. требуется найти n. Запишем формулу n-го члена для данной прогрессии, аn = -18 + (n -1) d.
Найдем разность прогрессии:
d = а2 — а1
d= -17,3— (-18)=0.7.
Подставим значение d в формулу n-го члена: а -18 + 0,7 (n-1). Так как n члены
прогрессии отрицательные, то они будут меньше 0, т.е. аn
Решим неравенство, аn
-18+ 0,7 (n-1)
-18,7 + 0,7 n
7 n
n
Значит, двадцать шестой член прогрессии — последний отрицательный член прогрессии, а двадцать седьмой — положительный. В этом можно убедиться, используя формулу n-го
члена.
a26 = 18+ 0,7 (26-1) = — 18 +0,7*25 = -0,5
а27= 18+0, 7(27-1) = — 18 +0,7*26=0,2
Ответ: 26.
Пример 4 В арифметической прогрессии (аn ) а1 -5, a15 -30.
Найдите сумму пятнадцатых членов прогрессии.
Сумму пятнадцатых членов прогрессии найдем по формуле нахождения суммы n-го члена арифметической прогрессии:
Sn = S 15 =
Ответ: S 15=262,5.
Пример 5 Известно, что в арифметической прогрессии (an ) а1 +а5 = -4, а2*а6= -16. Найдите разность и первый член прогрессии.
По условию известно, что
Чтобы решить систему уравнений, выразим каждый из членов прогрессии через а1 и d.
Используем формулу n-го члена для а2, а5, а6.
а2 = а1 + d
а5 = а1 + 4 d
а6=а1 + 5 d
Подставим в систему:
Решим систему методом подстановки, для этого выразим из первого уравнения а1 и
подставим во второе уравнение:
Решим второе уравнение системы — квадратное уравнение относительно переменной 1.
(-2 — d) * (-2 +3d) = -16
4+ 2 d — 6 d – 3d2=-16
-3d2+4d+20=0
3d2+4d-20=0
Его корни: 2 и -3 .
Система имеет два решения:
Ответ :
З. Решение задач на формулы арифметической прогрессии.
Задача 1
Хозяин нанял работника на неделю (с понедельника по воскресенье включительно), повышая ему каждый день зарплату на одну и ту же величину. Сколько всего получил работник, если за четверг ему заплатили 3 рубля?
В этой задаче угадывается арифметическая прогрессия, но кажется, что не хватает данных. Известно только число членов n = 7 и значение четвертого члена а4 = 3. Зная разность прогрессии или первый член, мы легко определили бы все что требуется. А так не найдем.
И все — таки попробуем ее решить. 1 способ.
Пусть а — первый член прогрессии, а d — разность. Запишем заработок по дням в виде таблицы:
За неделю работник получил 7а +21 d = 7(а +3 d). Но а +3 d —это оплата за четверг, т.е. 3 рубля. Значит, всего он заработал 21 рубль.
2 способ.
Зарплата за неделю — это сумма нечетного числа первых членов арифметической прогрессии.
Заметим, что если нужно найти сумму 7 членов, то 4-Ый член как раз является средним. Поэтому можно применить формулу
S n = n *ak
где n= 2k— 1. Так что общая зарплата за неделю равна 7а4 =7*3= 21 рубль.
Ответ: 21 рубль.
Задача 2
Турист, поднимаясь в гору, достиг в первый час высоты 580м., а каждый следующий час поднимался на высоту на 40м. меньшую, чем предыдущий. Через сколько часов он достигнет высоты 2500м?
Высоты, на которые поднимался турист каждый час, образуют арифметическую прогрессию с первым членом равным 580 и разностью — 40. Пусть n — количество часов, через которое он достигнет высоты 2500м, тогда по формуле суммы первых n членов арифметической прогрессии, получаем
Sn = 2500= 2
В результате получаем квадратное уравнение 20n2 — 600n + 2500 =0. Решаем уравнение и находим корни n=5 и n= 25. Второй корень не удовлетворяет условию задачи.
Ответ: 5часов.
Заключение.
В ходе проведенного исследования была проведена большая работа по изучению и овладению знаниями об арифметической прогрессии.
В опровержение известного изречения «Нельзя объять необъятное», мы не только научились задавать такие необъятные объекты, как бесконечные последовательности, и сумели вычислить некоторые их группы, но и описали отдельные свойства. Знание свойств арифметической прогрессии позволяет решить немало различных задач. Однако настоящая революция в постижении природы бесконечности связана с понятием предела.
Урок №3 Арифметическая и геометрическая прогрессия
Сегодня, мы рассмотрим тему «Прогрессии», которую большинство в школе либо не понимают, либо после забывают, хотя делать этого не нужно!
Числовые последовательности
Если каждому натуральному числу поставлено в соответствие некоторое действительное число , то говорят, что задана числовая последовательность (или просто последовательность):
Кратко последовательность обозначают символом {} или (), число называют членом или элементом этой последовательности, а — номером члена .
Последовательности обычно задаются формулами, при помощи которых можно вычислить каждый ее член по соответствующему номеру. Также последовательности задаются рекуррентными формулами, позволяющей находить члены последовательности по известным предыдущим.
Арифметическая прогрессия
Арифметическая прогрессия — это последовательность {}, которая определяется рекуррентной формулой:
,
где и — заданный числа; число — разность арифметической прогрессии.
Для того чтобы найти n-ый член арифметической прогрессии используют формулу:
Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому его соседних членов, т.е. при справедливо следующее равенство:
Сумму первых n-членов арифметической прогрессии находят по формуле:
Пример №1 Найти седьмой член арифметической прогрессии: 13,4; 14,7;…
Чтобы решить данное задание, в первую очередь, найдем шаг (разницу) прогрессии, т.
е. вычислим :
А теперь, когда все данные известны, согласно формуле найдем седьмой член прогрессии:
Ответ: седьмой член заданной арифметической прогрессии равен — 21,2
Пример №2 Вычислим сумму первых десяти четных чисел.
Можно, конечно, посчитать сумму чисел привычным для нас образом: 2+4+6+8+ и т.д. Но ведь не всегда в задачах такие простые условия, поэтому мы воспользуемся формулой суммы первых n-членов арифметической прогрессии.
Чтобы воспользоваться формулой нам нужно знать шаг и последний член прогрессии, поэтому вычисляем их:
Подставляем полученные данные в формулу:
Ответ: сумма первых десяти четных чисел равна 110.
Ну, думаю, здесь хватит…
Геометрическая прогрессия
Геометрическая прогрессия — это последовательность , которая определяется рекуррентной формулой:
,
где и — заданные числа, не равные нулю; — знаменатель геометрической прогрессии.
Чтобы найти n-ый член геометрической прогрессии используют формулу:
Квадрат каждого члена геометрической прогрессии, начиная со второго, равен произведению его соседних членов, т.е. при справедливо следующее равенство:
,
и сразу очевидно, что, для того чтобы найти нужно вычислить квадратный корень из .
Сумму первых n-членов геометрической прогрессии находят по формуле:
, если q≠1
Пример №3 Вычислить пятый член прогрессии: 1,5; 1,8; 2,16;…
Здесь сразу видно, что прогрессия геометрическая, потому что числа в ряду увеличиваются неровно, как в арифметической прогрессии.
Поэтому для вычисления нужно найти знаменатель :
Ну а теперь, вычислим пятый член прогрессии:
Ответ: пятый член геометрической прогрессии — 3,1104
Пример №4 В геометрической прогрессии b(1)=1,5; q=1,2. Вычислить сумму первых трех членов прогрессии.
Здесь вообще все просто, у нас есть все данные, просто подставим их в формулу:
= = = = =
Ответ: сумма первых трех членов прогрессии — 5,46
Как вы видите, в принципе, особо сложного тут ничего нет, но бывает, что попадаются задачки запутанные, но на это не нужно обращать внимания, а просто «разматывать ниточки» и искать решение.
Задания для самостоятельной работы
Ответы и решения на задания прошлого урока
На прошлом уроке вам было дано одно задание с несколькими пунктами, давайте посмотрим, насколько вы справились с ним
Задача №1 Выяснить, какое из утверждений А и В следует из другого, используя символы ⇒ и ⇔:
1) А ≡ {каждое из чисел а, b делится на 7}, В ≡ {сумма а + b делится на 7};
Ответ: А ⇒ В
2) А ≡ {последняя цифра числа а четная}, В ≡ {число А делится на 4};
Ответ: В ⇒ А
3) А ≡ {треугольник равнобедренный}, В ≡ {две медианы треугольника равны между собой};
Ответ: А ⇔ В
4) А ≡ {из отрезков, длины которых равны а, b, с, можно составить треугольник}, В ≡ {положительные числа а, b, с связаны неравенствами а + b > с, b + с > а, с + а > b}.
Ответ: А ⇔ В
Если вам не понятно, откуда взялись такие ответы, пишите в комментариях.
На следующий урок задам вам пару задач:
Задания на следующий урок
Задание №1 Вычислить номер члена прогрессии 2,1; 3,3; 4,5; … , равный 11,7.
Задание №2 В геометрической прогрессии b(8) = 1,3. Вычислить b(6)*b(10).
Ответы на задания вы найдете в следующем уроке «Суммирование. Бином Ньютона»
Если у вас остаются вопросы по теории или по практической части смело задавайте их в комментариях.
Арифметическая последовательность — математика GCSE
Введение
Что такое арифметические последовательности?
Как продолжить арифметическую последовательность
Рабочий лист арифметических последовательностей
Формула арифметической последовательности
Практикуйте вопросы арифметической последовательности: продолжайте последовательность
Как найти пропущенные числа в арифметической прогрессии
Практикуйте вопросы арифметической последовательности: найдите пропущенные числа
Как сгенерировать арифметическую последовательность
Практикуйте вопросы по арифметическим последовательностям: сгенерируйте последовательность
Вопросы GCSE по арифметической последовательности
Распространенные заблуждения
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Еженедельные онлайн-уроки повторения математики GCSE теперь доступны
Узнать больше
Введение
Что такое арифметические последовательности?
Как продолжить арифметическую последовательность
Рабочий лист арифметических последовательностей
Формула арифметической последовательности
Практикуйте вопросы арифметической последовательности: продолжайте последовательность
Как найти пропущенные числа в арифметической прогрессии
Практикуйте вопросы арифметической последовательности: найдите пропущенные числа
Как сгенерировать арифметическую последовательность
Практикуйте вопросы по арифметическим последовательностям: сгенерируйте последовательность
Вопросы GCSE по арифметической последовательности
Распространенные заблуждения
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем, что такое арифметическая последовательность, как продолжить арифметическую последовательность, как найти пропущенные члены в арифметической последовательности и как создать арифметическую последовательность.
В конце вы найдете рабочие листы арифметической последовательности, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные указания о том, что делать дальше, если вы все еще застряли.
Что такое арифметическая прогрессия?
Арифметическая последовательность представляет собой упорядоченный набор чисел, которые имеют общую разность между каждым последовательным членом.
Например, в арифметической последовательности 3, 9, 15, 21, 27 общая разность равна 6.
Арифметическая последовательность может быть известна как арифметическая прогрессия. Разница между последовательными терминами в арифметической последовательности всегда одинакова.
Если мы прибавим или вычтем из одного и того же числа каждый раз, чтобы составить последовательность, то получится арифметическая последовательность .
Правило от термина к термину говорит нам, как мы переходим от одного термина к другому.
Вот несколько примеров арифметических последовательностей:
2
| Первый термин | Правило с термином к терминам | Первые 5 терминов | ||||||||||||
| 3 | Добавить 6 | 3, | 3 2 | Добавить 6 | 3, | 21, 21, 27, 21, 27, 27, 27, 21, 27, 27, 27, 27, 27, 27, 27, 27, 270104 | . , … | |||||||
| 8 | Вычитание 2 | 8, 6, 4, 2, 0,… | ||||||||||||
| 12 | Добавить 7 | 12, 19, 26, 33, 40104 | ||||||||||||
| . | Вычитание 5 | -4, -9, -14, -19, -24,… | ||||||||||||
| ½ | Добавить ½ | ½, 1, 1 сена. последовательности
Арифметические последовательности также известны как линейные последовательности. Если бы мы представили арифметическую последовательность на графике, она образовала бы прямую линию, каждый раз поднимаясь (или опускаясь) на одну и ту же величину. Линейный значит прямой. Что такое арифметические последовательности?Как продолжить арифметическую последовательностьДля того чтобы продолжить арифметическую последовательность , вы должны быть в состоянии обнаружить или вычислить правило перехода от члена к термину. Это делается путем вычитания двух последовательных членов, чтобы найти общую разницу. Общая разность арифметической последовательности одинакова для каждого последующего члена и может определить, является ли последовательность возрастающей или убывающей.
Объясните, как продолжить арифметическую последовательность в 3 шагаРабочий лист арифметической последовательностиПолучите бесплатный рабочий лист по арифметической последовательности, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы. СКАЧАТЬ БЕСПЛАТНО Икс Рабочий лист арифметической последовательностиПолучите бесплатный рабочий лист арифметической последовательности, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы. СКАЧАТЬ БЕСПЛАТНО Чтобы узнать больше о различных типах последовательностей и о том, как отвечать на вопросы, связанные с последовательностями, вам может быть полезно просмотреть урок «Введение в последовательности» или один из других уроков в этом разделе.
Арифметическая формулаАрифметическая форма. a_{1} — первый термин n — позиция термина d — общая разность Мы получаем формулу арифметической последовательности, глядя на следующий пример: Мы видим, что общая разность (d) равна 6 , так что d = 6 . a_{1} — первый член, равный 3 a_{2} — второй член, равный 9 a_{3} — третий член, равный 15 и т. д. Однако мы можем записать это, используя общая разность 6 , Примеры арифметической последовательности: продолжить последовательностьПример 1: продолжить арифметическую последовательностьВычислить следующие три члена последовательности 4, 7, 10, 13, 16, … Возьмем два последовательные члены последовательности. Здесь мы возьмем числа 10 и 13. Вычтем первый член из следующего, чтобы найти общую разность, d . d = 13 − 10 = 3 Добавьте общую разность к последнему члену последовательности, чтобы найти следующий член. Повторите для каждого нового термина. 16 + 3 = 19 19 + 3 = 22 22 + 3 = 25 Следующие три члена последовательности 19, 22 и 25. отрицательные числа Вычислите следующие три члена последовательности -3, -9, -15, -21, -27, … Возьмите из последовательности два последовательных члена. Здесь мы возьмем числа -15 и -21. Вычтите первый член из следующего, чтобы найти общую разность, d . d = -21 − (-15) = -21 + 15 = -6 Добавьте общую разность к последнему числу в последовательности, чтобы найти следующий член. Повторите для каждого нового термина. -27 + (-6) = -27 — 6 = -33 -33 + (-6) = -33 — 6 = -39 -39 + (-6) = -39 — 6 = -45 Следующие три члена: -33, -39 и — 45. Пример 3: продолжение арифметической последовательности с десятичными знакамиВычислите следующие три члена последовательности 0,1, 0,3, 0,5, 0,7, 0,9, … Возьмите два последовательных члена последовательности. Здесь мы возьмем числа 0,7 и 0,9. Вычтите первый член из следующего, чтобы найти общую разность, д . d = 0,9 − 0,7 = 0,2 Добавьте общую разность к последнему члену последовательности, чтобы найти следующий член. Повторите для каждого нового термина. 0,9 + 0,2 = 1,1 1,1 + 0,2 = 1,3 1,3 + 0,2 = 1,5 Следующие три члена — 1,1, 1,3 и 1,5. Пример 4: продолжение арифметической последовательности, включающей дробиВычислить следующие три члена последовательности [frac{1}{2}, frac{3}{4}, 1, frac{5} {4}, frac{3}{2}, ldots] Возьмите два последовательных члена последовательности. Здесь мы возьмем числа [frac{5}{4} text { и } frac{3}{2}] Вычтем первый член из следующего, чтобы найти общую разность , д . [d=frac{3}{2}-frac{5}{4}=frac{6}{4}-frac{5}{4}=frac{1}{4} ] Добавьте общую разность к последнему члену последовательности, чтобы найти следующий член. Повторите для каждого нового термина. [begin{выровнено} Следующие три термина: [frac{7}{4}, 2, text { и } frac{9}{4}] Практика арифметической последовательности Вопросы: Продолжить последовательность0,42, 0,32, 0,22 0,62, 0,72, 0,82 0,52, 0,62, 0,72 0,63, 0,64, 0,65 Общая разница, D = 0,32-0,22 = 0,1. 0,52+0,1=0,62 0,62+0,1=0,72 0,72+0,1=0,82 -5, -7, -9 -5, -3, -1 5, 7, 9 -1, 1, 3 Общая разность, d = 3-5 = -2 . -3+(-2)=-5 -5+(-2)=-7 -7+(-2)=-9 -7, -1, 5 -7, 1, 7 7, 13, 19 -19, -25, -31 Общая разность, d=-31-(-37) = 6 . -13+6=-7 -7+6=-1 -1+6=5 frac{12}{4}, frac{13}{4}, frac{14}{4} frac{13}{5}, frac{15}{6}, frac {17}{7} frac{13}{4}, frac{15}{4}, frac{17}{4} frac{9}{4}, frac{7} {4}, frac{5}{4} Общая разность, d=frac{5}{4} – frac{3}{4} = frac{2}{4}
начать{массив}{л} Как найти пропущенные числа в арифметической последовательности Чтобы найти пропущенные числа в арифметической последовательности , мы используем общую разность.
Повторяйте шаги 2 и 3, пока не будут вычислены все недостающие значения. Возможно, вам потребуется использовать только шаг 2 или 3 в зависимости от того, какие условия вам были предоставлены. Объясните, как найти пропущенные числа в арифметической прогрессии за 3 шагаПримеры арифметической последовательности: найти пропущенные числаПример 5: найти пропущенные числа в арифметической последовательностиВставьте пропущенные термины в последовательности 5, 8, …, …, 17. Найдите общую разницу между двумя последовательными терминами. d = 8 − 5 = 3 Добавьте общую разность к предыдущему члену перед пропущенным значением. 8 + 3 = 11 Вычесть общую разность из члена после пропущенного значения. 17 − 3 = 14 Пропущены члены 11 и 14. Примечание. Здесь можно повторить шаг 2, используя 11 + 3 = 14. Пример 6: нахождение пропущенных чисел в арифметической последовательности, включая отрицательные числа и десятичные дробиНахождение пропущенных значений в последовательности …, -0,6, …, -1,0, -1,2. Найдите общую разницу между двумя последовательными терминами. d = -1,2 − (-1,0) = -1,2 + 1 = -0,2 Добавьте общую разность к предыдущему члену перед пропущенным значением. -0,6 + (-0,2) = -0,6 − 0,2 = -0,8 Вычесть общую разность из члена после пропущенного значения. -0,6 − (-0,2) = -0,6 + 0,2 = -0,4 Отсутствующие члены равны -0,4 и -0,8. Пример 7: найти пропущенные числа в арифметической последовательности, когда пропущено несколько последовательных членов Найти пропущенные значения в последовательности -6, …, …, 3, …. Найдите расстояние между двумя известными терминами. 3 − (-6) = 3 + 6 = 9 Вычислите обыкновенную разность. Чтобы получить от -6 до 3, мы прыгаем через 3 члена. : Это расстояние имеет значение 9. Нам нужно разделить общее расстояние на количество сделанных прыжков. Здесь 9 ÷ 3 = 3. Это означает, что общая разность равна +3. Добавляйте общую разность к первому известному члену, пока не будут вычислены все члены. -6 + 3 = -3 -3 + 3 = 0 0 + 3 = 3 (Примечание: это один из приведенных терминов) 3 + 3 = 6 Отсутствующие термины — 3, 0 и 6. Пример 8: найти пропущенные числа в арифметической последовательности, включая смешанные числаНайдите пропущенные значения в последовательности [ldots, ldots, frac{15}{16}, 1 frac{1}{2}, ldots] Запишите свои ответы в виде дробей в простейшая их форма. Найдите общую разницу между двумя последовательными терминами. [begin{выровнено} Добавьте общую разницу к термину перед отсутствующим значением. [begin{выровнено} Вычесть общую разницу из члена после пропущенного значения. [begin{выровнено} Повторите этот шаг, чтобы найти первый член в этой последовательности. [begin{выровнено} В последовательности отсутствуют следующие элементы: [frac{-3}{16}, frac{3}{8}, text { и } 2 frac{1 }{16}] Практика арифметических последовательностей: найти недостающие числа20, 34 35, 42 17, 37 21, 35 Общая разность, 4-7 = 7. 14+7=21 28+7=35 1 frac{5}{10}, 1 frac{9}{10} 1 frac{13}{10}, 1 frac{17}{10} 1 frac{3} {10}, 1 frac{7}{10} 1 frac{4}{10}, 1 frac{8}{10} Общая разность, d= frac{9}{ 10} – frac{5}{10} = frac{4}{10}
begin{выровнено} 0,9, 0,4 1,09, 1,04 1, 0,6 1,39, 1,34 Общая разность, d=1,4-1,9 = -0,5 . 1,4+(-0,5)=0,9 0,9+(-0,5)=0,4 12,4, -4 -36, -28, -20 -30, -24, -18 -20, -28, -36 Общая разность, d=-4 – – 12 = 8 . Работа в обратном порядке: 3-й член: -12-8=-20 2-й член: -20-8=-28 1-й член: -28-8=-36 Как сгенерировать арифметическую последовательность Чтобы сгенерировать арифметическую последовательность , нам нужно знать n терм . Мы можем вычислить любое количество членов арифметической последовательности, подставляя значения в n -й триместр. Первый член находится при n = 1, Это известно как правило позиции к термину , так как вы можете вычислить термин, учитывая его позицию в последовательности.
Полезный совет: После того, как вы вычислите первый член последовательности, просто продолжайте добавлять коэффициент n, чтобы сгенерировать последовательность! Объясните, как сгенерировать арифметическую последовательность за 3 шагаПримеры арифметических последовательностей: создание последовательностиПример 9: создание арифметической последовательности с помощью n-й член Сгенерируйте первые 5 членов последовательности 5n − 7. Найдите первый член последовательности, подставив n = 1 в n -й член. Когда n = 1, Найдите второй член, подставив n = 2 в член n th . Когда n = 2, Продолжайте подставлять значения n , пока не будут вычислены все необходимые члены последовательности. При n = 3, При n = 4, При n = 5, Первые 5 членов последовательности 5n − 7 равны -2, 3, 8, 13 и 18. ИЛИ Совет: n-й член = 5n − 7 Когда n = 1, (5 × 1) − 7 = -2 Коэффициент при n равен 5, поэтому мы прибавим 5 к -2, а затем продолжим прибавлять 5 для создания последовательности. Example 10: generate an arithmetic sequence using a tableComplete the table for the first 5 terms of the arithmetic sequence 6 − n
Найдите первый термин в последовательности по обороту n |
Это может быть полезно, когда вас просят найти большие термины в последовательности, и вам дан порядковый номер термина, который вы пытаетесь вычислить. 
.
0643-й триместр.
When n = 1,
6 − 1 = 5.
| n | 1 | 2 | 3 | 4 | 5 |
| 6 − n | 5 |
Найдите второй член, подставив n = 2 в n -й член.
Когда n = 2,
6 − 2 = 4
| n | 1 | 2 | 3 | 4 | 5 |
| 6 − n | 5 | 4 |
Continue to substitute values for n until all the вычисляются искомые члены последовательности.
При n = 3,
6 − 3 = 3
При n = 4,
6 − 4 = 2
При n = 5,
6 − 5 = 1
| n | 1 | 2 | 3 | 4 | 5 |
| 6 − n | 5 | 4 | 3 | 2 | 1 |
OR
Top подсказка: n-й член = 6 – n
Когда n = 1,
6 – 1 = 5
Коэффициент n равен -1, поэтому мы собираемся вычесть -1 из 5, затем продолжаем вычитать -1 для создания последовательности.
Пример 11: создание более крупных членов в арифметической последовательности
Красные и синие фишки помещаются в последовательность, показанную ниже.
Красные фишки имеют n th член 2n.
Синие фишки имеют n -й член 3n − 3.
Укажите количество красных фишек в шаблонах 4 и 10. Укажите количество синих фишек в шаблонах 27.
Вычислите четвертый член в шаблонах последовательность, подставив n = 4 в n -й триместр 2 н .
Когда n = 4,
2 × 4 = 8
В шаблоне 4 8 красных фишек.
Когда n = 10,
2 × 10 = 20
В шаблоне 10 20 красных жетонов.
Когда n = 27,
3n − 3 = (3 × 27) − 3 = 81− 3 = 78
В шаблоне 27 78 синих счетчиков.
Пример 12: создать арифметическую последовательность с алгебраическими членами.
n th член последовательности равен (3a + b)n. Обозначьте первые 5 членов последовательности через a и b.
Найдите первый член последовательности, подставив n = 1 в n -й член.
Когда n = 1,
(3a + b) × 1 = 3a + b
Найдите второй член, подставив n = 2 в член n -й .
Когда n = 2,
(3a + b) × 2 = 6a + 2b
Продолжайте подставлять значения для n , пока не будут вычислены все необходимые члены последовательности.
При n = 3,
(3a + b) × 3 = 9a + 3b
При n = 4,
(3a + b) × 4 = 12a +4 b
При n = 5,
(3a + б) × 5 = 15а + 5б
Первые 5 членов последовательности:
3а + б, 6а + 2б, 9а + 3б, 12а + 4б и 15а + 5б.
Практика арифметических последовательностей: составить последовательность
-4, 3, 10, 17, 24, 31
7, 3, -1, -5, -9, -13
3, 10, 17, 24 , 31, 38
1, 8, 15, 22, 29, 36
begin{align}
7 умножить на 1 — 4 &= 3\
7 умножить на 2 — 4 &= 10 \
7 умножить на 3 — 4 &= 17\
7 умножить на 4 — 4 &= 24\
7 умножить на 5 — 4 &= 31\
7 х 6 – 4 &= 38
end{выровнено}
begin{выровнено}
&quad n quad quad 1 quad quad 2 quad quad 3 quad quad 4 quad quad 5\
&2 — 3n ;; -1 четверка -4 четверка -7 ;; -10 ;; -13
end{выровнено}
begin{выровнено}
&quad n quad quad 1 quad quad 2 quad quad 3 quad quad 4 quad quad 5\
&2 — 3n ;; -1 четверка -3 четверка -5 четверка -7 ;; ; -9
end{выровнено}
begin{выровнено}
&quad n quad quad 1 quad quad 2 quad quad 3 quad quad 4 quad quad 5\
&2 — 3n quad ; 5 quad quad 8 quad quad 11 quad ;; 14четверка;17
end{выровнено}
begin{выровнено}
&quad n quad quad 1 quad quad 2 quad quad 3 quad quad 4 quad quad 5\
&2 − 3n quad ;: 1 quad quad 4 quad quad 7 quad ;; 10 квадрат;; 13
end{выровнено}
begin{выровнено}
2-3 раз 1 &= – 1\
2-3 умножить на 2 &= – 4\
2-3 умножить на 3 &= – 7\
2-3 умножить на 4 &= – 10\
2-3 х 5 &= – 13
end{выровнено}
1-й член: 4 × 1-25=-21
10-й член: (4 × 10)-25=15
100-й член: (4 × 100)-25=37
1000-й член: (4 × 1000)-25=3975
-21+15+375+3975=4344
Так как треугольников 2n и их 12, то
begin{выровнено}
2n&=12\
п&=6
end{выровнено}
В шаблоне номер 6 12 треугольников .
Количество строк 4n+1 .
Когда n=6 ,
(4 х 6) + 1 = 25 .
Арифметическая последовательность Вопросы GCSE
1. N-й член последовательности равен 4n + 5 .
Укажите первые 5 членов последовательности.
(2 балла)
Показать ответ
не менее 3 терминов
(1 )
9, 13, 17, 21, 25
(1)
2. Пропустите пропущенные значения в следующей последовательности:
17, ….., ….., 32, ….
(2 балла)
Показать ответ
begin{align}
d&=frac{32-17}{3}\\
д&=5
end{выровнено}
(1)
22, 27, 37
(1)
3. Вот первые четыре члена арифметической прогрессии
2, 7, 12, 17
Вот первые пять членов другой арифметической прогрессии
-4, -1, 2, 5, 8
Найдите два числа, которые входят в обе числовые последовательности.
(2 балла)
Показать ответ0003
Распространенные заблуждения
- Умножение значения термина для получения другого термина в последовательности
Напр.
Давайте посмотрим на последовательность 4, 10, 16, 22, 28.
Третий член последовательности равен 16 .
Тридцатый член не равен третьему члену, умноженному на 10 или 160 (поскольку 16 × 10 = 160). Тридцатый член равен 178.
- Арифметические последовательности с отрицательными членами не всегда уменьшаются
Напр.
Последовательность -48, -40, -32, -24, -16 имеет общую разность +8.
Это означает, что хотя последовательность показывает отрицательные целые числа, а не положительные целые числа, она увеличивается.
- Добавление константы в член n th вместо общей разности
Напр.
n -й член 3n − 7 даст последовательность чисел, общая разность которых равна 3.
Неправильное представление возникнет, если следующий член будет найден путем вычитания 7, а не прибавления 3.
Неправильное представление возникнет, если следующий член будет найден путем вычитания 7, а не прибавления 3. - Неправильное упрощение термина n th
Напр.
Неправильное упрощение 6n + 2 для получения 8n.
Это неверно для любого значения, кроме n = 1.
Контрольный список обучения
Теперь вы научились: правило термина
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.
Мы используем необходимые и необязательные файлы cookie для улучшения работы нашего веб-сайта. Пожалуйста, ознакомьтесь с нашей Политикой в отношении файлов cookie, чтобы узнать, как мы используем файлы cookie и как управлять вашими настройками файлов cookie или изменять их.
как AP, представляет собой последовательность чисел в определенном или определенном порядке. В нашей повседневной жизни мы часто сталкиваемся с несколькими примерами прогрессии. Например, номера классов в классе, месяцы в году, дни в неделе и так далее.
В математике модель последовательностей и рядов была обобщена и известна как прогрессии. Итак, давайте познакомимся с тем, что такое арифметическая прогрессия, а также с терминами, широко используемыми в рамках этого понятия, включая первый член ряда, общую разность, n-й член и т. д.
Что такое арифметическая прогрессия?
Прогрессия относится к исключительному типу последовательности, для которой мы можем найти и получить формулу для n-го члена. В математике наиболее часто используемой последовательностью является арифметическая прогрессия или AP, и она имеет формулы, которые довольно легко понять. Понятие AP можно понять с помощью трех различных определений, а именно:
-
Определение 1: Арифметическая прогрессия или АР — это математическая последовательность, имеющая постоянную разницу между двумя последовательными элементами.
-
Определение 2: Арифметическая прогрессия или AP — это последовательность чисел, в которой второе число может быть получено путем добавления постоянного или фиксированного числа к первому для каждой пары последовательных членов.
-
Определение 3: Фиксированное или постоянное число, которое прибавляется к любому члену арифметической прогрессии или AP для получения следующего члена, называется «обычной разностью» AP.
Понимание понятий общей разности и первого члена
В арифметической прогрессии или AP для данного ряда или последовательности широко используемые термины включают первый член AP, его общую разность и n-й член.
Предположим, что последовательность [a_{1}, a_{2}, a_{3}, a_{4},…a_{n}] является AP.
Мы можем получить общую разность ‘d’, используя приведенную ниже формулу:
[ d = a_{2} — a_{1} = a_{3} — a_{2} = a_{4} — a_ {3} = a_{n} — a_{n-1} ], где ‘d’ относится к общей разности, которая может быть положительной, отрицательной или нулевой.
С точки зрения общей разности арифметическая прогрессия может быть выражена или записана как:
[a, a + d, a +2d, a +3d……a + (n — 1)d ], где «a» относится к первому члену AP.
Как найти n-ю часть арифметической прогрессии или AP?
Для нахождения n-го члена арифметической прогрессии или AP формула выглядит следующим образом:
an= a + (n — 1)d, где
‘a’ — первый член, d — общая разность, n относится к количеству терминов, а an = n-му термину.
Необходимо отметить тот факт, что последовательность арифметической прогрессии зависит от ее общей разности, то есть d.
Если общая разность или d положительна, то члены АП будут расти в положительную сторону от бесконечности. С другой стороны, если общая разность или d отрицательна, то члены АР будут расти в отрицательную сторону бесконечности.
Как найти сумму первых n членов арифметической прогрессии или АП?
Формула для нахождения суммы первых n членов арифметической прогрессии или AP:
[ S = frac{n}{2}(2a + (n-1) times d)] , где
a — первое слагаемое, d — общая разность, n — количество слагаемых, а S — сумма первых n слагаемых AP.
Формулы арифметической прогрессии
Для решения математических задач, основанных на рядах и последовательностях АП, необходимо знать, понимать и выучить формулы, указанные ниже:
а, а + d, а + 2d, а + 3d …… а + (n — 1)d
ан= а + (n — 1)d
[ S = frac{ n}{2}(2a + (n-1) times d)],
[frac{n}{2}](a + l), где ‘a’ — первый член, и ‘l’ — последний термин.
d = a2-a1 или d=an-an-1, где a1 — первый член, а a2 — второй член. Точно так же an — это последний термин, а an-1 — предпоследний термин.
Решенные примеры на арифметическую прогрессию
Вопрос 1
В арифметической прогрессии или АР a = 10, d = 5 и an = 95. Найдите значение n.
Ответ 1
Дано – первый член арифметической прогрессии или АП равен 10 (а = 10), общая разность равна 5 (d = 5), а ан = 95.
Мы знаем формулу – а n = a + (n – 1)d
Подставим имеющиеся значения и определим значение n (количество слагаемых)
95 = 10 + (n – 1)5
95 = 10 + 5n – 5
95 = 5n + 5
95 – 5 = 5n
90 = 5n
n = 18
Следовательно, количество членов в этой арифметической прогрессии равно 18.
Вопрос 2
Найдите 20-й член указанной ниже арифметической прогрессии:
3, 5, 7, 11, 13, 15……….
Ответ 2
Начнем с нахождения первого члена и общей разности данной арифметической прогрессии.
n = 20 (дано)
a = первый член AP = 3
d = общая разность = разница между двумя последовательными терминами = 5 – 3 = 2
Итак, мы должны найти.
an= a + (n – 1)d
an = 3 + (20 – 1)2
an = 3 + (19)2
an = 3 + 38
an = 41
Следовательно, 20-й член данного AP равен 41.
Важные моменты, которые следует помнить
-
Арифметическая прогрессия – это ряд, в котором сохраняется постоянная разница между любыми двумя последовательными числами
-
В арифметической прогрессии «а» представляется как первый термин, «n» представлен как количество терминов, «d» — общая разность, Sn — сумма терминов AP, а tn — n-й термин AP
-
Арифметическая прогрессия может быть представлена как a, a+d, a+2d, a+3d ….
|
Вопрос, как решать арифметическую прогрессию, ставит поначалу в тупик многих учеников. Быть может, это происходит от того, что кажется сложным само название, а может, оттого, что формулы арифметической прогрессии выглядят устрашающе. На самом деле, арифметическую прогрессию решать совсем несложно, если хорошо понять, что это такое. А суть арифметической прогрессии состоит в том, что каждый последующий член прогрессии равен сумме предыдущего с неким постоянным числом. Математически это можно выразить формулой:
Эта формула позволяет найти любой член арифметической прогрессии. Давайте проверим. Допустим, число d, которое называется разностью арифметической прогрессии, равно 3. А первое число прогрессии равно 1. Тогда 4-й член арифметической прогрессии равен: a4= 1 + 3(4-1)= 10 Давайте проверим, просто суммируя каждый член прогрессии: а2=1+3=4 а3=4+3=7 а4=7+3=10 Все сошлось. Как видите, решать арифметическую прогрессиию несложно, если понять ее смысл. автор вопроса выбрал этот ответ лучшим
Эления 3 года назад Сначала вспомним, что есть арифметическая прогрессия. Это определенная, закономерная последовательность чисел, которая поддается описанию формулой. К каждому из членов прогрессии, кроме самого первого, добавляется определенное число, одинаковое каждый раз, поэтому каждый шаг прогрессии закономерен. Каждый шаг – это добавление числа “d” к предыдущему члену прогрессии, данное число так и называют “шагом” прогрессии или еще говорят “разность” арифметической прогрессии. Всю последовательность членов прогрессии можно обозначить следующим математическим выражением:
в этой формуле каждый последующий член представлен латинской буквой “a”. Кроме первого члена прогрессии, к каждому последующему суммируется шаг с определенным значением “d”. Таким образом, третий член прогрессии – это число “a”, к которому добавили два значения “d” или “2d”, третий шаг – “3d” и т. д. Любое n-нное по счету число “a” можно представить следующей формулой:
Или:
Сумму всех первых членов прогрессии можно представить, как формулу:
Все сказанное можно представить:
Существует возрастающая или убывающая арифметическая прогрессия, смотря выше или ниже нуля значение шага “d”. Посчитаем убывающую арифметическую прогрессию, если известно значение первых двух членов прогрессии. Сначала найдем “шаг” прогрессии, затем все остальные члены прогрессии, схема расчета ниже.
Кареля Топин 9 лет назад Арифметическая прогрессия – это ряд чисел, последующее число которого получается в результате сложения предыдущего числа и коэффициента арифметической прогрессии. Например, 2, 6, 10, 14, и т. д. Коэффициент арифметической прогрессии в данном случае равняется 4.
Галина Скулкина 9 лет назад Чтобы решать задачи по арифметической прогрессии, надо хорошо понять, что же это такое. Последовательность, у которой каждый её член, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом, называется арифметической прогрессией (далее – АП). Чаще всего в задачах подобного рода ставятся такие вопросы: нахождение первого члена АП, n-го члена, разности АП, суммы всех членов АП. Из определения АП можно определить связь соседних членов АП
При известном первом члене и разности АП находится любой её член по формуле
Используя эту же формулу, можно найти первый член АП
Формула разности (при известных первом и n-ом члене АП)
Сумма членов АП
Или, если не известен n-ый член АП, но знаем шаг d и номер n-ого члена АП
Лучше разобраться в этом вопросе поможет видеоурок
Galina7v7 7 лет назад Основные формулы арифметической прогрессии:1)для n-го члена прогрессии:an=a1+d(n-1),где an и a1 -1-й и n-й члены прогрессии,d-разность прогрессии,2)Сумма n членов прогрессии:Sn=(a1+an)*n2.Все остальные формулы -это следствие этих 2-х формул.В каждой задаче по известным параметрам из формул находится какой-то неизвестный параметр.Известна самая знаменитая задача с использованием арифметической прогрессии:Учитель задал задачу ученикам:Просуммировать все числа от 1 до 100.И пока все ученики старательно считали,один из учеников за минуту высчитал сумму:5050!И это был маленький Гаусс!Он догадался-как быстро сосчитать эту непростую сумму:S100=(1+100)*1002=5050! Знаете ответ? |
Это мое решение в Ruby:
number_of_terms = gets.chomp.to_i
Получить количество терминов от STDIN
progression = gets.chomp.split(' ').map(&:to_i)
Получите строку, удалите все начальные и конечные пробелы, разбейте ее на промежутки между числами, а затем преобразуйте каждый элемент в целое число.
expected_sum = (number_of_terms+1)/2.0*(progression.first+progression.last)
Используя формулу для суммирования арифметической прогрессии: n/2 ( a[0] + a[n]).
Здесь деление на 2,0 важно. Нужно соблюдать точность.
actual_sum = progression.inject(:+)
Проверка того, что было суммой данных чисел.
missing_element = (expected_sum - actual_sum).to_i
Разница, конечно, в недостающем элементе. Также преобразование в целое число, чтобы удалить конечный.0
то есть 4.0 => 4
puts "Missing element is: #{missing_element}"
Прогрессия — это последовательность величин, каждая последующая из них находится в некоторой, общей для всей прогрессии, зависимости от предыдущей.
Арифметическая прогрессия
Задача:
Рабочему поручили выкопать колодец и условились платить ему за первый метр глубины 3 руб., за второй 5 руб. ит. д., увеличивая плату за каждый следующий метр на 2 руб. Сколько уплатили рабочему, если колодец был вырыт им в 10 м глубины?
Для решения задачи надо найти сумму таких чисел:
3+5+7+9+11+ 13+15+17+19+21.
Сумму эту мы можем найти проще, чем обыкновенным сложением. Обозначив её буквой s, напишем две такие строки:
s = 3+ 5+ 7+ 9+11 + 13 + 15+17 + 19 + 21,
s=21+19+17+15+13+11+ 9+ 7 + 5+ 3.
Вторую строку мы написали, переставив слагаемые первой строки в обратном порядке, от чего, конечно, сумма не изменилась. Сложим теперь все числа, стоящие друг под другом.
2s=24 + 24 + 24 + 24 + 24 + 24 + 24 + 24 + 24 + 24,
т. е.
2s=24 ∙ 10 = 240,
и, следовательно,
Таким образом, за всю работу уплатили 120 рублей.
В этой задаче нам пришлось иметь дело с рядом чисел, последовательно возрастающих на одно и то же число. Подобные ряды носят название арифметических прогрессий.
Определение:
Арифметической, или разностной, прогрессией называется такой ряд чисел, в котором каждое число, начиная со второго, равняется предыдущему, сложенному с одним и тем же постоянным для этого ряда числом (положительным или отрицательным).
Так, два ряда чисел: 10, 14, 18, 22, 26, 30, 34, 38, 42, 46 и 6, 4, 2, 0, —2, —4, —6 составляют арифметические прогрессии, так как в них каждое число, начиная со второго, равно предыдущему числу, сложенному в первом ряду с положительным числом 4, а во втором—с отрицательным числом —2.
Числа, составляющие прогрессию, называются её членами. Положительное или отрицательное число, которое надо прибавить к предыдущему члену, чтобы получить последующий, называется разностью прогрессии.
Прогрессия называется возрастающей или убывающей, смотря по тому, увеличиваются ли её члены по мере удаления от начала ряда или уменьшаются; разность возрастающей прогрессии есть число положительное, а убывающей — отрицательное.
Для обозначения того, что ряд чисел представляет собой арифметическую прогрессию, иногда ставят в начале ряда знак ÷.
Обыкновенно принято обозначать: первый члена, а последний l, разность d, число всех членов n и сумму их s.
Формула любого члена арифметической прогрессии
Пусть имеем прогрессию: ÷ 10, 14, 18, … (разность 4).
Тогда 2-й член = 10+4 = 14;
3-й „ =10+4+4=10+4∙2=18;
4-й „ =10+4+4+4 = 10+4∙3 = 22 и т. д.
Значит:
10-й член= 10+4∙9=46;
20-й „ =10+4∙19=86 и т. д.
Подобно этому, если имеем прогрессию: ÷ 6, 4, 2,… (разность—2), то
2-й член=6+(—2)=4;
3-й „ =6+(-2)+(-2)=6+(-2)∙2=2 и т. д.
Например:
10-й член=6+(—2) ∙ 9= —12.
Вообще, если прогрессия будет такая: ÷ α, b, с,… (разность d), то
2-й член=а+d;
3-й „ = α+d+d=a+ 2d;
4-й „ =a+2d+d=a+3d и т. д.
Значит, 10-й член окажется a+9d. 15-й член будет a + 14d, вообще m-й член будет a+d(m -1). Таким образом:
Всякий член арифметической прогрессии равен первому её члену, сложенному с произведением разности прогрессии на число членов, предшествующих определяемому.
В частности, последний член равен первому члену, сложенному с произведением разности на число всех членов, уменьшенное на 1, т. е.:
l=a+d(n-1). (1)
Примеры:
1) Найти 10-й член прогрессии: ÷60, 75, 90,…
Так как разность этой прогрессии равна 15, то 10-й член будет
60 + 15 ∙ 9 = 195.
2) Найти 12-й член прогрессии: ÷40, 37, 34,…
Так как разность равна —3, то 12-й член должен быть
40+(-3) ∙ 11=40-33 = 7.
3) Каким будет n-е число в последовательном ряду нечётных чисел: 1, 3, 5, .. .?
Такое число будет
l+2(n-1) = l+2n-2 — 2n-l.
Следствие. Арифметическую прогрессию, у которой первый член есть а, разность d и число членов п, можно изобразить так:
α, α+b, α+2d, a+3d, …, a+d(n-1).
Формула суммы членов арифметической прогрессии
Предварительно убедимся в следующем свойстве:
Сумма двух членов арифметической прогрессии, равноотстоящих от концов, равна сумме крайних членов.
Например, в прогрессии: ÷ 3, 7, 11, 15, 19, 23 находим:
3+23=26; 7+19=26; 11 + 15=26.
Понятно, почему это так: первые слагаемые этих сумм (т. е. 3, 7, 11) идут, возрастая на 4, а вторые слагаемые (23, 19, 15) идут, убывая на 4; поэтому сумма каждой пары остаётся та же.
Возьмём ещё пример убывающей прогрессии: ÷ 8, 6, 4, 2, 0, —2, —4. В ней
8+(-4) = 4, 6 + (-2) = 4, 4+0=4.
Член 2, отстоящий одинаково от начала и от конца, должен быть сложен сам с собой: 2+2=4. И здесь объяснение то же самое: слагаемые 8, 6, 4, 2 идут, уменьшаясь на 2, а слагаемые —4, —2, 0 и 2 идут, увеличиваясь на 2; от этого сумма каждой пары остаётся без изменения.
Теперь выведем формулу для суммы членов любой арифметической прогрессии. Для этого применим тот способ, посредством которого мы нашли сумму членов арифметической прогрессии в задаче, а именно: сложим почленно два таких равенства:
s=a+b+c+.. ∙+i+k+l
s =l+k+i+.. .+c+b+α
2s=(a+l)+(b+k)+(c+i) + … + (i+c) + (k+b)+(l+α).
Но
α+l = b+k=c+i = …=l+a;
следовательно:
2s = (α+l)n, откуда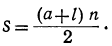 
(2)
Сумма всех членов арифметической прогрессии равна половине произведения суммы крайних членов на число членов.
Таким образом, в задачедля суммы s по этой формуле найдём то число, которое мы нашли ранее другим путём:
s= [(3+21) ∙ 10]: 2=120.
Пример:
Найти сумму натуральных чисел от 1 до n включительно.
Ряд: 1, 2, 3, …, n есть арифметическая прогрессия, у которой первый член 1, разность 1, число членов n и последний член тоже и; поэтому:
Так:
Пример:
Найти сумму первых n нечётных чисел.
Как мы видели, n-е нечётное число равно 2n—1; поэтому
Так:
1 + 3=4=2²; l+3+5=9=3²; 1+3+5+7 = 16=4² и т. д.
Это свойство сумм нечётных чисел наглядно изображается чертежом 25, который составлен так: к квадрату (внизу слева) приставлены 3 таких же квадрата (1 сверху, 1 сбоку и 1 в верхнем углу); к этим квадратам приставлены ещё 5 квадратов (2 сверху, 2 сбоку и 1 в верхнем правом углу). К ним, далее, приложены 7 квадратов, потом 9 квадратов и т. д. Тогда очевидно, что
1 + 3=2² , 1+3+5=3² ,
1 + 3+5 +7 = 4² и т. д.
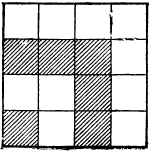
Пример:
Найти сумму 10 членов прогрессии: ÷3,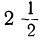 
, 2,…
Здесь α=3,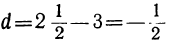 
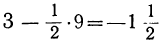
, поэтому 10-й член прогрессии будет
, и потому искомая сумма равна:
Проверка:
77. Замечание. Так как для пяти чисел a, l, d, n и s мы имеем два уравнения: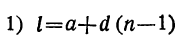
и 
то по данным трём из этих чисел можем находить остальные два. Для примера решим следующую задачу:
Найти число членов прогрессии, у которой первый член 7, разность—2 и сумма всех членов 12.
В этой задаче даны: a=7, d=-2 и s=12; остаются неизвестными l и n. Подставив в формулы (1) и (2) заданные числа, находим:
l =7-2(n-l)=9-2n; 
откуда:
Получаются два ответа: число членов или 6, или 2. И действительно, две прогрессии: 7, 5, 3, 1, —1, —3 и 7, 5 имеют одну и ту же сумму 12.
Формула суммы квадратов чисел натурального ряда
Выведем формулу, определяющую сумму квадратов первых n чисел натурального ряда. Для вывода этой формулы рассмотрим n следующих тождеств:
2³=(1+ 1)³=1³∙1²∙1+3∙1∙1²+1³;
3³=(2+1)³ =2³ +3∙2² ∙ 1+3∙2∙ 1²+1³;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
(n+1)³ =n³ +3n² ∙1+3n∙1²+1³ .
Сложив эти тождества и сократив одинаковые члены в правой и левой частях полученного тождества, будем иметь:
(n+l)³ =1+3(1²+2²+3²+…+n² )+3(1+2+3+…+n)+n.
Но
следовательно:
Упростим правую часть этого равенства:
Итак,
Геометрическая прогрессия
Задача:
По преданию, индийский принц Сирам предложил изобретателю шахматной игры просить у него награду, какую он захочет. Тот попросил, чтобы ему дали за первый квадрат шахматной доски 1 пшеничное зерно, за второй квадрат 2 зерна, за третий 4 и т. д., увеличивая вдвое за каждый из следующих квадратов. Принц согласился. Но когда подсчитали количество зёрен пшеницы, которое следует выдать за все 64 квадрата шахматной доски, то. оказалось, что награда в этом размере не может быть выдана по недостатку пшеницы. Сколько же зёрен пришлось бы выдать изобретателю?
Количество зёрен, которое надлежало бы выдать за все 64 квадрата, равно сумме S следующего ряда чисел:
s = 1+2+2² +2³ +… + 2⁶²+2⁶³.
Мы можем найти эту сумму, не вычисляя отдельно слагаемых, так: умножим обе части написанного равенства на 2:
2s=2+2²+ 2³+2⁴ + …+ 2⁶³+2⁶⁴.
Теперь вычтем из этого равенства предыдущее; тогда в левой части получим s, а в правой 2⁶⁴—1 (числа 2, 2², 2³, …, 2⁶³ все сократятся):
s= 2⁶⁴-1.
Значит, придётся вычислить степень 2⁶⁴, что можно сделать или последовательным умножением на 2 по формуле:
2⁶⁴ =2∙2∙2∙2… (64 множителя),
или по формуле:
2⁶⁴= [(2¹⁶)² ]² =(65 536² )² .
Окончательное число зёрен будет:
s= 2⁶⁴ -l = 118 446 744 073 709 551 615.
Можно вычислить, что если бы такое число зёрен рассыпать равномерно по всей земной суше, то образовался бы слой пшеницы толщиной около 9 мм.
В этой задаче мы имели дело с рядом чисел, из которых каждое начиная со второго равно предыдущему числу, умноженному на одно и то же число. Такие ряды чисел называются геометрическими прогрессиями.
Определение:
Геометрической, или кратной, прогрессией называется такой ряд чисел, в котором каждое число начиная со второго равняется предшествующему, умноженному на одно и то же число, постоянное для этого ряда. Так, три ряда:
2, 4, 8, 16, 32, 64, 128, … ;
8, -16, 32, -64, 128, -256, 512, . . . ;
составляют геометрические прогрессии, потому что в этих рядах каждое число, начиная со второго, получается из предшествующего умножением в первом ряду на 2, во втором на —2 и в третьем на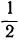 
.
Для обозначения того, что данный ряд есть геометрическая прогрессия, иногда ставят в начале его знак ÷÷.
Как и в арифметической прогрессии, числа, составляющие геометрическую прогрессию, называются её членами; число, на которое надо умножить предыдущий член, чтобы получить последующий, называется знаменателем прогрессии.
Прогрессия называется возрастающей или убывающей, смотря по тому, увеличивается или уменьшается абсолютная величина членов прогрессии по мере удаления от начала ряда; так, из трёх указанных выше прогрессий первая и вторая — возрастающие, а третья — убывающая. В возрастающей прогрессии абсолютная величина знаменателя больше 1, в убывающей она меньше 1.
Обыкновенно знаменатель прогрессии обозначают буквой q, а члены, число их и сумму обозначают также, как это принято для арифметической прогрессии, т. е. a, b, с, … , l (последний член), n (число членов) и s (сумма).
Сравнение геометрической прогрессии с арифметической прогрессией
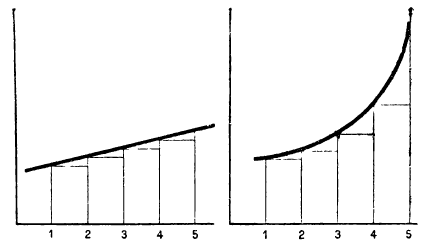
Разность двух рядом стоящих членов арифметической прогрессии остаётся одна и та же, вследствие чего члены её возрастают (или убывают) равномерно (черт. 26, левый). Посмотрим, какова разность двух соседних членов в геометрической прогрессии:
∺ а, b, с, … (знаменатель q).
Из определения прогрессии следует: b=aq, c=bq, d=cq и т. д.; следовательно,
b — a=aq — a=a (q — 1); с — b=bq — b=b(q — 1) и т. д.
Если прогрессия возрастающая и члены её положительные, то тогда a < b < с < … и т. д.; поэтому и
a(q-1)<b (q-1) <c( q-1 )<…,
т. е.
b — a < c — b < d — c < … и т. д.
Значит, в возрастающей геометрической прогрессии с положительными членами разность двух соседних членов увеличивается номере удаления их от начала ряда; вследствие этого члены такой прогрессии по мере их удаления от начала ряда возрастают всё быстрее и быстрее, что наглядно изображено на чертеже 26 (правый). Например:
÷ 2, 4, 6, 8, 10, 12, …
∺ 2, 4, 8, 16, 32, 64, …
Формула любого члена геометрической прогрессии
Пусть мы имеем такую геометрическую прогрессию:
∺ 3, 6, 12, 24, … (знаменатель 2).
Тогда:
2-й член=3∙2=6;
3-й „ =3∙2∙2=3∙2² =12;
4-й „ =3∙2∙2∙2=3∙2³ =24 и т. д.
Например: 10-й член=3-2⁹=3∙512=1536.
Подобно этому, если мы имеем прогрессию:
то
2-й член
3-й 
4-й 
Вообще, если имеем прогрессию в буквенном виде:
∺ а, b, с, … (знаменатель q),
то в ней
2-й член=аq=aq¹;
3-й „ =aq∙q=aq²;
4-й „ = aq² ∙q = aq³ и т. д.
Таким образом, 10-й член=аq⁹, вообще m-й член=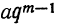
. Значит:
Всякий член геометрической прогрессии, начиная со второго, равен первому члену, умноженному на знаменатель прогрессии в степени, показатель которой равен числу членов, предшествующих определяемому.
В частности, последний член l, которому предшествует n — 1 членов, выразится формулой:
Пример:
Найти 6-й член прогрессии: ∺ 3, 12, …
Знаменатель такой прогрессии есть 12:3=4; поэтому 6-й член= 3∙45 =3072.
Пример:
Найти 10-й член прогрессии: ∺ 20, 10, …
Так как знаменатель этой прогрессии равен 10 : 20=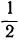 то 10-й член равен:
Следствие. Геометрическую прогрессию, у которой первый член есть а, знаменатель q и число всех членов n, можно изобразить так:
∺ α, aq, aq², aq³ , …, aqⁿ⁻¹.
Формула суммы членов геометрической прогрессии
Применим тот приём, которым мы раньше нашли сумму l+2+2² +… +2⁶³. Умножим обе части равенства
s=α+b+c+…+k+l (1)
на знаменатель q, тогда получим:
sq=aq+bq+cq+…+kq+lq.
Но
aq=b, bq=c, cq = d, … , kq=l,
следовательно,
sq = b+c+d+…+l+lq. (2)
Вычтя почленно из равенства (2) равенство (1), найдём:
sq — s=lq- а, т. е. (q — 1)s=lq — а,
откуда:
Сумма членов геометрической прогрессии равна дроби, у которой числитель есть разность между произведением последнего члена на знаменатель прогрессии и первым членом её, а знаменатель есть разность между знаменателем прогрессии и единицей.
Замечания. 1. Так как для убывающей геометрической прогрессии — 1 < q < 1, то для такой прогрессии лучше придать формуле суммы иной вид, умножив числитель и знаменатель дроби на — 1:
2. Если вместо члена l подставим равное ему выражение aqⁿ⁻¹, то формула для суммы примет такой вид: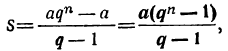
или 
Пример:
Найти сумму восьми членов прогрессии, у которой а=1
и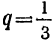 
. Тогда:
Пример на геометрическую прогрессию
Найти первый член а и последний l, если q=3, n=5 и s=242.
Сначала находим l по формуле l=aqⁿ⁻¹=α∙3⁴ и затем эту величину и данные числа подставим в формулу для суммы:
откуда:
α = 242 : 121=2.
Теперь находим:
α =2∙3⁴ =162.
Проверка: 2+6+18+54+162=242.
Бесконечные прогрессии
Некоторые свойства бесконечных прогрессий:
Если ряд чисел, составляющих прогрессию, продолжается неограниченно, то прогрессия называется бесконечной. Рассмотрим некоторые свойства таких прогрессий.
а) Возьмём бесконечно возрастающую арифметическую прогрессию, у которой разность очень мала; например, такую:
∺1; 1,01; 1,02; 1,03; 1,04; …
Несмотря на то, что члены этой прогрессии при удалении от начала ряда растут очень медленно, они, однако, при достаточном удалении превзойдут любое данное число, как бы велико оно ни было; например, они сделаются больше 1 000000. Действительно, для того чтобы (n+ 1)-й член такой прогрессии, равной сумме 1+0,01 n, сделался больше 1 000 000, достаточно для n взять такое большое число, которое удовлетворяло бы неравенству: 1+0,01n> 1 000000.
Из него находим: 
Так как в бесконечной прогрессии число п может быть как угодно большим, то его можно взять большим 99999 900; тогда 14-0,01 n сделается больше 1 000 000.
Рассуждение это можно повторить о всякой арифметической возрастающей бесконечной прогрессии; поэтому мы можем высказать такое общее заключение:
Члены бесконечно возрастающей арифметической прогрессии при достаточном удалении их от начала ряда превосходят любое данное число, как бы оно велико ни было.
Возьмём бесконечно убывающую арифметическую прогрессию, например: ÷ 1900, 998, 996,… (разность—2). Как бы ни был велик начальный член, начиная с некоторого места, члены прогрессии становятся отрицательными, и при достаточном удалении от начала ряда абсолютная величина их превосходит любое данное число, как бы велико оно ни было.
б) Возьмём теперь бесконечно возрастающую геометрическую прогрессию с положительными членами, например такую:
∺1; 1,01; 1,01²=1,0201; 1,01³ = 1,030301; .. . (знаменатель 1,01), и сравним её с бесконечной арифметической прогрессией:
-:-1; 1,01; 1,02; 1,03,… (разность 0,01),
у которой первые два члена одинаковы со взятой нами геометрической прогрессией.
Как мы видели раньше, члены геометрической прогрессии возрастают быстрее, чем члены арифметической прогрессии.
Но члены возрастающей арифметической прогрессии при достаточном удалении их от начала ряда превосходят любое число; значит, члены нашей геометрической прогрессии и подавно могут сделаться больше всякого данного числа. Таким образом:
Члены бесконечно возрастающей геометрической прогрессии (с положительными членами) при достаточном удалении от начала ряда превосходят любое данное число, как бы оно велико ни было.
Свойство это применимо и к такой возрастающей геометрической прогрессии, у которой члены, все или некоторые, — отрицательные числа (например, —5, —10, —20,… или 5, — 10, 20, —40,…); тогда надо только говорить не о самих членах, а об их абсолютной величине.
в) Возьмём теперь какой-нибудь пример бесконечно убывающей геометрической прогрессии с положительными членами, например такой:
Члены такой прогрессии при удалении их от начала ряда, конечно, уменьшаются, но могут ли они при этом сделаться меньше всякого данного положительного числа, например меньше 0,000001, это сразу не видно. Чтобы обнаружить это, возьмём вспомогательную прогрессию, члены которой обратны членам взятой нами прогрессии:
1, 2, 2², 2³,…, 2ⁿ,… (знаменатель 2).
Прогрессия эта возрастающая, и потому, как мы сейчас видели, члены её при достаточном удалении от начала ряда превосходят любое данное число; значит, они превосходят и 1000 000. Если же окажется, что
2ⁿ > 1 000 000,
то тогда, очевидно:
Применим это рассуждение к какой угодно бесконечно убывающей геометрической прогрессии (с положительными членами):
∺ a, b, c,… (знаменатель q < l).
Чтобы показать, что члены этой прогрессии при достаточном удалении от начала ряда делаются меньше любого данного положительного числа а (как бы мало это число ни было), возьмём вспомогательную геометрическую прогрессию:
Прогрессия эта возрастающая, так как её знаменатель больше 1. Но члены возрастающей геометрической прогрессии могут превзойти всякое данное число; следовательно, они превзойдут и число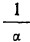 
.
Поэтому при достаточно большом n будет удовлетворено неравенство:
Таким образом:
Члены бесконечно убывающей геометрической прогрессии с положительными членами при достаточном удалении от начала ряда делаются меньше любого данного положительного числа.
Если в бесконечно убывающей геометрической прогрессии все или некоторые члены отрицательны, то указанное свойство применимо и к этой прогрессии, только надо будет говорить не о самих членах, а об их абсолютных величинах.
Понятие о пределе
Положим, что в бесконечно убывающей геометрической прогрессии:
мы взяли 10 членов от начала; тогда последний (10-й) член будет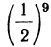 
, а сумма этих 10 членов (которую обозначим s₁₀) будет:
Подобно этому найдём:
Мы видим, что по мере увеличения числа членов сумма их приближается всё более и более к 2. Так, сумма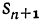 
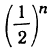
меньше 2 на дробь 
, а эта дробь, как мы видели, при достаточно большом n делается меньше любого данного положительного числа.
Если какая-нибудь переменная величина (в нашем примере — сумма членов прогрессии), изменяясь, приближается всё более и более к некоторому постоянному числу (в нашем примере — к числу 2) так, что абсолютная величина разности между этим числом и переменной делается и остаётся меньше любого данного положительного числа, как бы мало оно ни было, то это постоянное число называется пределом переменной величины.
Заметив это, мы можем сказать, что переменная сумма
при неограниченном возрастании п стремится к пределу 2, что записывают так: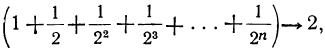
если n→∞
( n→∞ читается: „n стремится к бесконечности»), или пишут так:
Здесь „пред.» есть сокращённое слово „предел», а добавление внизу скобки: n→∞ заменяет собой фразу: „когда n неограниченно увеличивается» (когда n стоемится к ∞).
Можно наглядно показать (черт. 27), что рассматриваемая сумма приближается неограниченно близко к 2. Пусть отрезок AA₁ =1 и АВ=2. Тогда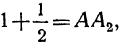 
, 
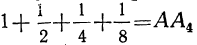
и т.д.; ясно, что при увеличении числа членов прогрессии мы неограниченно приближаемся к точке В, и значит, сумма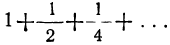 
стремится к отрезку АВ=2.
Формула суммы бесконечно убывающей геометрической прогрессии
Если в бесконечно убывающей геометрической прогрессии:
a, aq, aq², aq³,… (— 1< q < 1)
возьмём п членов от начала, то n-й член будет aq aqⁿ⁻¹ и сумма n членов будет:
Формулу эту можно представить так (подписав знаменатель под каждым членом числителя):
Предположим, что n неограниченно увеличивается. Тогда число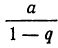 
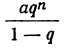
остаётся неизменным, а дробь 
по абсолютной величине уменьшается и притом неограниченно, так как числитель её по абсолютной величине делается меньше любого данного положительного числа, а знаменатель остаётся неизменным. Значит:
Этот предел 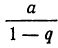и называется суммой бесконечно убывающей геометрической прогрессий, т. е. сумма членов бесконечно убывающей геометрической прогрессии равна частному от деления первого члена прогрессии на разность единицы и знаменателя прогрессии.
Например, сумма членов геометрической прогрессии:
у которой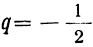 
и α=2, равна
На прилагаемом чертеже изображён ряд ординат, наглядно изображающих сравнительную величину одного, суммы двух, трёх, четырёх и т. д. членов данной прогрессии. Ординаты эти поочерёдно становятся то больше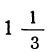 
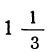
, то меньше , приближаясь всё более к этому числу (черт. 28).
Применение геометрической прогрессии к десятичным периодическим дробям
Возьмём следующие два примера десятичных чистых периодических дробей (т. е. таких, у которых период начинается тотчас после запятой): 1) 0,999… и 2) 0,232323…
Дроби эти представляют собой суммы: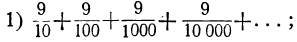
Слагаемые этих сумм — члены бесконечно убывающих геометрических прогрессий, у которых знаменатели прогрессии: у первой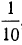 
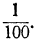
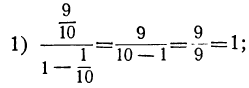
, у второй 
Суммы эти равны:
Из этих примеров видно, что
чистая периодическая дробь равна такой обыкновенной дроби, у которой числитель есть период, а знаменатель — число, изображаемое цифрой 9, повторённой столько раз, сколько цифр в периоде.
Возьмём теперь два примера смешанных периодических дробей (т. е. таких, у которых период начинается не тотчас после запятой):
3) 0,2888… и 4) 0,3545454…
Дроби эти можно представить в виде сумм:
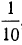
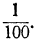
Слагаемые этих сумм, начиная со второго, суть члены бесконечных убывающих геометрических прогрессий; в третьей сумме знаменателем служит дробь , в четвёртой сумме — дробь Поэтому эти суммы равны:
Из этих примеров видно, что:
Смешанная периодическая дробь равна такой обыкновенной дроби, у которой числитель есть число, стоящее до второго периода, без числа, стоящего до первого периода, а знаменатель есть число, изображаемое цифрой 9, повторённой столько раз, сколько цифр в периоде, со столькими нулями на конце, сколько цифр между запятой и первым периодом.
Дополнительный материал по прогрессиям
Смотрите также:
- Решение задач по финансовой математике
Числовые последовательности
Поставим в соответствие каждому натуральному числу квадрат этого числа:
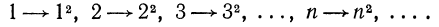
Рассмотренное соответствие является функцией. Обозначим эту функцию буквой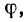 
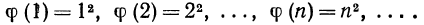
тогда:
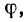
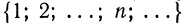
Областью определения этой функции служит множество N натуральных чисел: 
множеством ее значений— множество 
Функция, заданная на множестве натуральных чисел, называется бесконечной последовательностью. Функция, заданная на множестве первых п натуральных чисел, называется конечной последовательностью.
Значения функции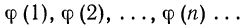 
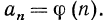
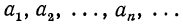
называются членами последовательности. Члены последовательности обозначаются также символами 
где 
Это равенство называют также формулой общего члена. Последовательность 
обозначается так: 
Так как последовательность—это частный вид функции, то способы задания функции применимы и для задания последовательности. Графический и табличный способы могут быть использованы для задания конечных последовательностей. Для бесконечных же последовательностей особенно важны два следующих способа задания, которые мы сейчас рассмотрим.
Последовательность может быть задана аналитически, т. е. с помощью формулы общего (n-го) члена 
Например:
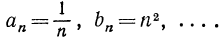
Давая аргументу «значения 1, 2, 3, …, будем получать соответствующие значения последовательности. Так, последовательность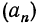 
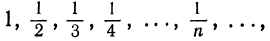
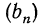
имеет вид 
а последовательность 
имеет вид 
2.Любой член последовательности, начиная с некоторого, часто выражают через предшествующие (один или несколько). Например, последовательность 1; 2; 3; 5; 8; 11; … может быть задана следующим образом:
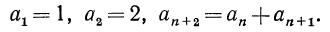
Действительно,
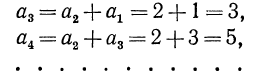
Такой способ задания последовательности называется рекуррентным. При рекуррентном способе задания последовательности обычно указывают: а) первый член последовательности (или несколько первых членов); б) формулу, позволяющую определить любой член последовательности по известным предшествующим членам.
Примеры:
1. Выписать несколько первых членов последовательности, если известно, что 
Решение:
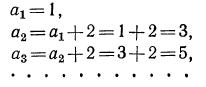
Итак, получаем последовательность 1, 3, 5, 7, 9…..
2.Выписать несколько членов последовательности, если известно, что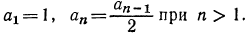 
Решение:
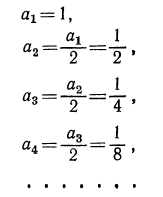
Итак, получаем последовательность 
Последовательность называется возрастающей, если каждый последующий ее член больше предыдущего, т. е.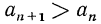 
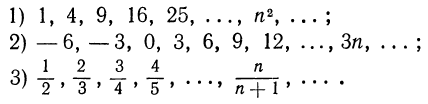
для любого n. Например, возрастающими являются такие последовательности:
Последовательность называется убывающей, если каждый последующий ее член меньше предыдущего, т. е.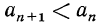 
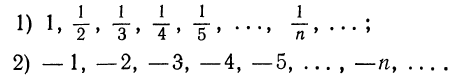
Для любого n. Например, убывающими являются такие последовательности:
Последовательность называется монотонной, если она возрастающая или убывающая.
Арифметическая прогрессия
Основные понятия: Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом d, называется арифметической прогрессией. Число d — называется разностью арифметической прогрессии. Таким образом, арифметическая прогрессия определяется условиями: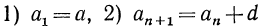 
для любого 
Например, если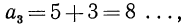 
т. е. получаем последовательность 2, 5, 8, И, 14, 17…..
Очевидно, что при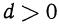 
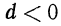
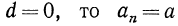
арифметическая прогрессия является возрастающей последовательностью, а если 
— убывающей; если 
—постоянная последовательность.
Например, прогрессии:
возрастающая,
— убывающая,
— постоянная.
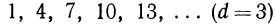
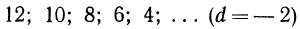
Задание арифметической прогрессии, указанное выше, является по сути дела рекуррентным заданием последовательности. Такое задание во многих случаях неудобно. Действительно, для того чтобы найти какой-нибудь член арифметической прогрессии с достаточно большим номером (например,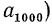 
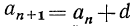
при рекуррентном задании необходимо знать все предшествующие ему члены (в данном случае число их равно 999). Эту вычислительную работу можно сократить, получив из рекуррентного соотношения 
формулу n-го (или общего) члена арифметической прогрессии.
Имеем:
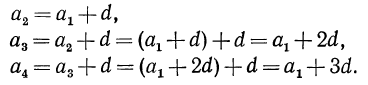
Легко сообразить, что
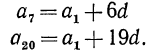
Вообще
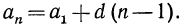
Зная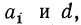 
по формуле общего члена можно непосредственно (без вычисления предыдущих членов) вычислить любой член арифметической прогрессии.
Например, если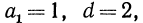 
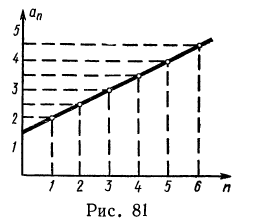
то по формуле общего члена имеем 
Характеристическое свойство
Арифметическая прогрессия обладает следующим характеристическим свойством: любой член ее, начиная со второго, является средним арифметическим предшествующего и последующего членов.
Доказательство. Пусть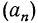 
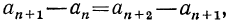
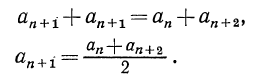
—арифметическая прогрессия. По определению 
откуда
Справедливо и обратное: если некоторая последовательность такова, что любой ее член, начиная со второго, является средним арифметическим предшествующего и последующего членов, то эта последовательность—арифметическая прогрессия.
Действительно, пусть для любых трех соседних членов некоторой последовательности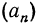 
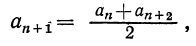
справедливо соотношение6
тогда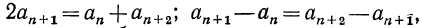 
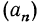
т. е. разность между любым членом последовательности и ему предшествующим равна одному и тому же числу. Значит 
арифметическая прогрессия. Таким образом, рассматриваемое свойство присуще арифметической прогрессии и только ей.
Связь с линейной функцией
На рис. 81 построен график арифметической прогрессии, у которой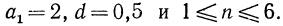 
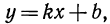
и Рассматривая рисунок, замечаем, что точки графика лежат на одной прямой. Покажем, что это не случайно. Запишем формулу общего члена рассматриваемой арифметической прогрессии 
Мы получили формулу вида 
а такой формулой, как известно, задается линейная функция.
Таким образом, арифметическая прогрессия является линейной функцией, заданной на множестве натуральных чисел.
Справедливо и обратное: линейная функция, областью определения которой служит множество натуральных чисел, является арифметической прогрессией.
Пример:
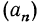
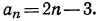
Последовательность задана формулой ее n-го члена 
Доказать, что последовательность есть арифметическая прогрессия и найти ее первый член и разность.
Решение:
Запишем формулу общего члена для члена с номером 
Имеем 
тогда 
Таким образом, разность между последующим и предшествующим членами этой последовательности есть величина постоянная. Следовательно, это арифметическая прогрессия, у которой 
Сама прогрессия имеет такой вид:
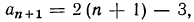
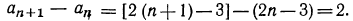
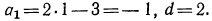
-1; 1; 3; 5; ….
Формула суммы n первых членов
Рассмотрим какую-нибудь конечную арифметическую прогрессию, например
3; 6; 9; 12; 15; 18
и сравним суммы членов, равноудаленных от конца, 3+18; 6+15; 9+12. Легко видеть, что эти суммы равны. Это не случайно, так как можно доказать, что в конечной арифметической прогрессии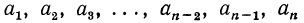 
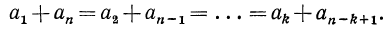
сумма членов, равноудаленных от конца равна сумме первого и последнего членов, т. е.
Например, докажем, что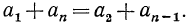 
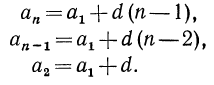
По формуле общего члена арифметической прогрессии имеем
Подставляя в проверяемое равенство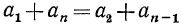 
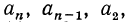
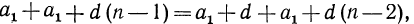
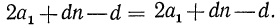
найденные значения для 
получим 
т.е. 
Мы получили верное равенство, что и доказывает сформулированное выше утверждение.
Воспользуемся этим фактом для вывода формулы суммы n первых членов арифметической прогрессии. Обозначим эту сумму через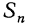 
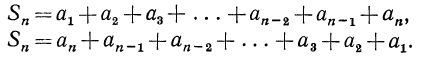
и выпишем эту сумму дважды, поменяв во втором случае порядок слагаемых на обратный:
Сложим почленно эти равенства: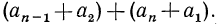
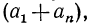
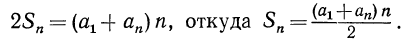
Сумма каждой пары в правой части равенства равна 
а число таких пар равно n, поэтому
Примеры:
1. Найти сумму первых 10 членов арифметической прогрессии 2, 5, 8, 11…..
Решение:
Из условия задачи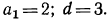 
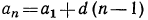
По формуле общего члена 
найдем 
По формуле суммы n членов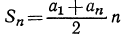 
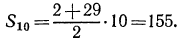
имеем
Замечание. Формулу суммы n членов арифметической прогрессии можно записать в другом виде, если вместо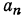 
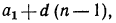
подставить его значение 
тогда
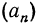
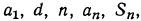
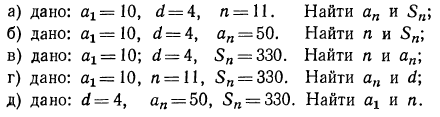
Дана конечная арифметическая прогрессия Зная три пяти: 
найти остальные два:
Решение:
а) По формуле n-го члена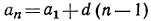 
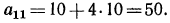
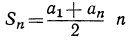
найдем 
Затем по формуле 
найдем 
б) из формулы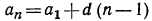 
получим
Далее, имеем 
в) воспользуемся формулой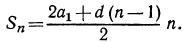 
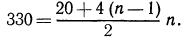
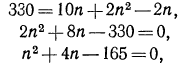
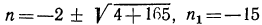
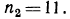
Подставляя данные значения, получаем 
Таким образом, мы получили квадратное уравнение относительно n; решим его:
(не подходит по условию задачи); 
Зная n, найдем 
г) из формулы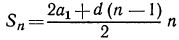 
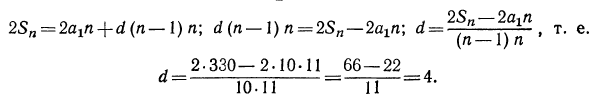
найдем d:
Теперь можно найти 
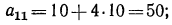
д) из формулы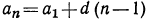 
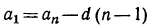
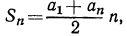
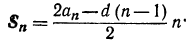
найдем 
и подставим найденное значение 
в формулу 
тогда
Теперь найдем n:
Если 
Если 
Выпишем обе прогрессии:
Легко видеть, что в обоих случаях сумма членов равна 330.
Геометрическая прогрессия
Основные понятия:
Определение:
Числовая последовательность, первый член которой отличен от нуля, а каоюдый член, начиная со второго, равен предшествующему члену, умноженному на одно и то же, не равное нулю число q, называется геометрической прогрессией. Число q называется знаменателем прогрессии.
Таким образом, геометрическая прогрессия определяется условиями:
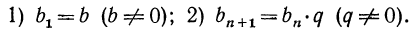
Например, если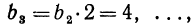 
т. е. получаем последовательность 1, 2, 4, 8, 16…..
Очевидно, что при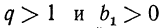 
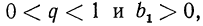
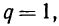
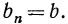
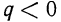
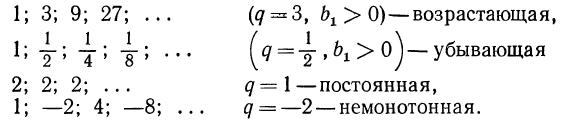
геометрическая прогрессия является возрастающей последовательностью, а если 
то убывающей, если же 
то 
При 
геометрическая прогрессия не является монотонной. Примеры прогрессий:
Задание геометрической прогрессии, указанное выше, является рекуррентным заданием последовательности. Такое задание во многих случаях неудобно. Действительно, для того чтобы найти какой-нибудь член геометрической прогрессии с достаточно большим номером, при рекуррентном задании необходимо знать все предшествующие ему члены. Эту вычислительную работу можно сократить, получив из рекуррентного соотношения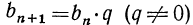 
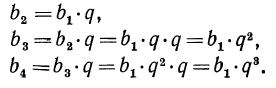
формулу n-то или общего члена геометрической прогрессии. Имеем:
Легко сообразить, что
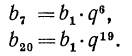
Вообще
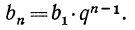
Зная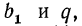 
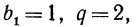
по формуле общего члена можно непосредственно (без вычисления предыдущих членов) вычислить любой член геометрической прогрессии. Так, если 
то по формуле общего члена имеем, например, 
Характеристическое свойство
Геометрическая прогрессия, все члены которой положительные числа, обладает следующим характеристическим свойством.
Любой член геометрической прогрессии, начиная со второго, является средним геометрическим предшествующего и последующего членов.
Доказательство. Пусть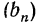 
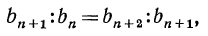
— геометрическая прогрессия. Тогда по определению имеем:
откуда
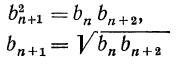
Справедливо и обратное: если некоторая последовательность положительных чисел такова, что любой ее член, начиная со второго, является средним геометрическим предшествующего и последующего членов, то эта последовательность — геометрическая прогрессия.
Действительно, пусть для любых трех соседних членов некоторой последовательности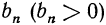 
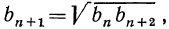
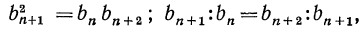
справедливо соотношение 
тогда
а это и означает, что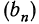 
—геометрическая прогрессия.
Формула суммы n первых членов
В заключение выведем формулу суммы n первых членов геометрической прогрессии. Обозначим эту сумму через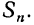 
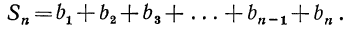
Можно записать, что
Умножим обе части равенства (1) на q
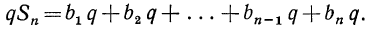
Но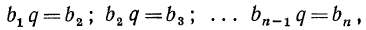 
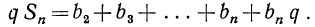
поэтому
Вычтем почленно из равенства (2) равенство (1):
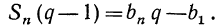
Если положить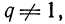 
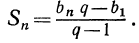
то
Если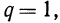 
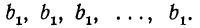
то прогрессия имеет вид 
В этом случае 
Для примера найдем сумму пяти первых членов геометрической прогрессии 
По условию задачи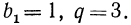 
Найдем пятый член прогрессии по формуле 
Теперь по формуле суммы n первых членов прогрессии найдем 
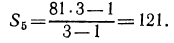
Замечания 1. Формулу суммы n членов геометрической прогрессии можно записать в другом виде, если вместо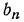 
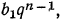
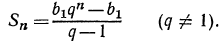
подставить его значение 
тогда
2.В каждой конечной геометрической прогрессии произведение крайних членов прогрессии равно произведению двух членов, одинаково отстоящих от крайних, т. е. в прогрессии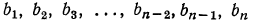 
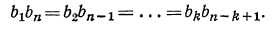
справедливы равенства
Например, докажем, что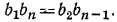 
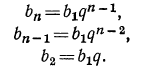
По формуле общего члена геометрической прогрессии имеем:
Подставляя в предполагаемое равенство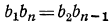 
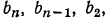
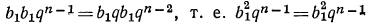
найденные значения для 
получаем:
— вернее равенство, что и доказывает сформулированное выше утверждение.
Сводная таблица, иллюстрирующая свойства арифметической и геометрической прогрессий, приведена на стр. 187.
Примеры:
1. Восьмой член геометрической прогрессии равен 256, знаменатель прогрессии 4. Найти первый член этой прогрессии.
Решение:
По условию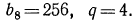 
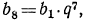
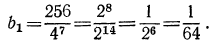
По формуле общего члена имеем 
откуда
Определить знаменатель и сумму n членов геометрической прогрессии, в которой 
Решение:
По формуле общего члена имеем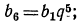 
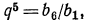
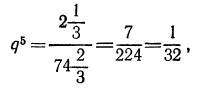
значит, 
или
т. е.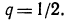 
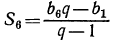
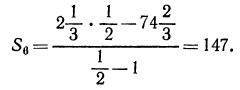
Далее, по формуле 
имеем
3.Определить первый и последний члены геометрической прогрессии, в которой 
Решение:
Воспользуемся формулой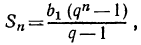 
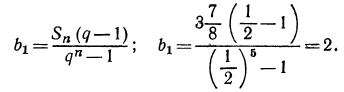
из которой найдем 
Теперь по формуле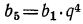 
найдем последний член прогрессии:
4.Определить число членов геометрической прогрессии, в которой 
Решение:
Прежде всего из формулы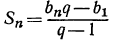 
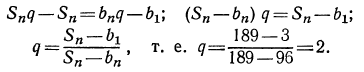
найдем q. Имеем:
Затем воспользуемся формулой n-го члена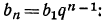 
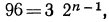
откуда 
т. е. 
Определить первый член, знаменатель и число членов геометрической прогрессии, в которой 
Решение:
Воспользуемся формулой общего члена геометрической прогрессии: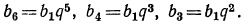 
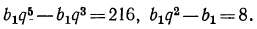
Тогда первые два данных уравнения примут вид:
Разделим почленно одно уравнение на другое:
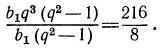
Так как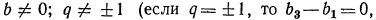 
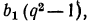
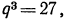
что противоречит условию), то, сократив левую часть уравнения на 
получим 
откуда 
Теперь из уравнения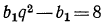 
найдем 
Для определения n воспользуемся формулой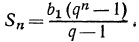 
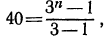
Подставляя в это выражение найденные и данные значения, получим:
откуда 
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
