Учитывая массив n-1 различные целые числа в диапазоне от 1 до n, найти в нем пропущенное число за линейное время.
Например, рассмотрим массив {1, 2, 3, 4, 5, 7, 8, 9, 10} элементы которого различны и находятся в диапазоне от 1 до 10. Недостающее число — 6.
Потренируйтесь в этой проблеме
1. Использование формулы для суммы первых n Натуральные числа
Мы знаем, что сумма первых n натуральные числа можно вычислить по формуле 1 + 2 + … + n = n×(n+1)/2. Мы можем использовать эту формулу, чтобы найти пропущенное число.
Идея состоит в том, чтобы найти сумму целых чисел от 1 до n+1 используя приведенную выше формулу, где n размер массива. Также вычислите фактическую сумму целых чисел в массиве. Теперь недостающее число будет разницей между ними.
Этот подход демонстрируется ниже на C, Java и Python:
C
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
#include <stdio.h> // Находим пропущенное число в заданном массиве int getMissingNumber(int arr[], int n) { // фактический размер `n+1`, так как в массиве отсутствует число int m = n + 1; // получить сумму целых чисел от 1 до `n+1` int total = m*(m + 1)/2; // получаем реальную сумму целых чисел в массиве int sum = 0; for (int i = 0; i < n; i++) { sum += arr[i]; } // недостающее число – это разница между ожидаемой суммой // и фактическая сумма return total – sum; } int main() { int arr[] = { 1, 2, 3, 4, 5, 7, 8, 9, 10 }; int n = sizeof(arr)/sizeof(arr[0]); printf(“The missing number is %d”, getMissingNumber(arr, n)); return 0; } |
Скачать Выполнить код
результат:
The missing number is 6
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
import java.util.Arrays; class Main { // Находим пропущенное число в заданном массиве public static int getMissingNumber(int[] arr) { // получаем длину массива int n = arr.length; // фактический размер `n+1`, так как в массиве отсутствует число int m = n + 1; // получить сумму целых чисел от 1 до `n+1` int total = m * (m + 1) / 2; // получаем реальную сумму целых чисел в массиве int sum = Arrays.stream(arr).sum(); // недостающее число – это разница между ожидаемой суммой // и фактическая сумма return total – sum; } public static void main(String[] args) { int[] arr = { 1, 2, 3, 4, 5, 7, 8, 9, 10 }; System.out.println(“The missing number is “ + getMissingNumber(arr)); } } |
Скачать Выполнить код
результат:
The missing number is 6
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# Найти недостающее число в заданном списке def getMissingNumber(arr): # получить длину массива n = len(arr) # Фактический размер # равен `n+1`, так как в списке отсутствует номер. m = n + 1 # получить сумму целых чисел от 1 до `n+1` total = m * (m + 1) // 2 # пропущенное число – это разница между ожидаемой суммой и # фактическая сумма целых чисел в списке return total – sum(arr) if __name__ == ‘__main__’: arr = [1, 2, 3, 4, 5, 7, 8, 9, 10] print(‘The missing number is’, getMissingNumber(arr)) |
Скачать Выполнить код
результат:
The missing number is 6
2. Использование оператора XOR
Мы знаем, что XOR двух одинаковых чисел отменяет друг друга. Мы можем воспользоваться этим фактом, чтобы найти недостающее число в массиве с ограниченным диапазоном.
Идея состоит в том, чтобы вычислить XOR всех элементов массива и вычислить XOR всех элементов от 1 до n+1, куда n размер массива. Теперь недостающее число будет XOR между ними.
Этот подход демонстрируется ниже на C, Java и Python:
C
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
#include <stdio.h> // Находим пропущенное число в заданном массиве int getMissingNumber(int arr[], int n) { // Вычислить XOR всех элементов массива int xor = 0; for (int i = 0; i < n; i++) { xor = xor ^ arr[i]; } // Вычислить XOR всех элементов от 1 до `n+1` for (int i = 1; i <= n + 1; i++) { xor = xor ^ i; } return xor; } int main() { int arr[] = { 1, 2, 3, 4, 5, 7, 8, 9, 10 }; int n = sizeof(arr) / sizeof(arr[0]); printf(“The missing number is %d”, getMissingNumber(arr, n)); return 0; } |
Скачать Выполнить код
результат:
The missing number is 6
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
class Main { // Находим пропущенное число в заданном массиве public static int getMissingNumber(int[] arr) { // Вычислить XOR всех элементов массива int xor = 0; for (int i: arr) { xor = xor ^ i; } // Вычислить XOR всех элементов от 1 до `n+1` for (int i = 1; i <= arr.length + 1; i++) { xor = xor ^ i; } return xor; } public static void main(String[] args) { int[] arr = { 1, 2, 3, 4, 5, 7, 8, 9, 10 }; System.out.println(“The missing number is “ + getMissingNumber(arr)); } } |
Скачать Выполнить код
результат:
The missing number is 6
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# Найти недостающее число в заданном списке def getMissingNumber(arr): # Вычислить XOR всех элементов в списке xor = 0 for i in arr: xor = xor ^ i # Вычислить XOR всех элементов от 1 до `n+1` for i in range(1, len(arr) + 2): xor = xor ^ i return xor if __name__ == ‘__main__’: arr = [1, 2, 3, 4, 5, 7, 8, 9, 10] print(‘The missing number is’, getMissingNumber(arr)) |
Скачать Выполнить код
результат:
The missing number is 6
Временная сложность обоих рассмотренных выше методов составляет O(n) и не требует дополнительного места, где n это размер ввода.
Далее представлен калькулятор, при помощи которого можно искать пропущенные номера в последовательности целых чисел. Пример такой последовательности (каждое число на новой строке):
1
2
3
4
6
7
12
13
18
Как видно в последовательности есть пропуски и единичных номеров и нескольких подряд следующих номеров. Например, номер 5 пропущен, а также пропущено два куска: между 8 и 11 и между 14 и 17.
В таком простом примере Вы и сами можете найти пропуски, но если речь идет о тысячах номеров, то калькулятор вам сильно пригодится. Просто скопируйте вашу последовательность в текстовое поле и калькулятор найдет все пропуски между числом в первой и последней строках.
Поиск пропущенных номеров
Использовать регулярные выражения для выделения чисел
Использовать пустые строки как разделители групп
Настройки калькулятора пропусков
Для более сложных случаев имеется несколько настроек:
- Установите флажек “В сжатом виде” чтобы калькулятор выдавал диапазоны последовательных пропусков номеров, например 8 – 11, где 8 начало, а 11 конец последовательного пропуска. В противном случае будет выдана вся последовательность пропущенных номеров, например 8, 9, 10, 11.
- Можно установить галочку “Использовать регулярные выражения для выделения номеров”, для выделения чисел из строки при помощи регулярного выражения.
Последняя опция становится актуальной, если в вашем перечне номеров содержатся не только числа, например вот такая последовательность:
1 Бумага побеждает камень
2 Ножницы режут бумагу
3 Камень разрушает ножницы
Вот для таких случаев регулярное выражение выделит числовые данные из этого текста. Регулярное выражение по умолчанию выделяет числа из начала строки, если требуется отредактируйте выражение под вашу задачу.
20 апреля 2020
Отдых
Разгадайте логику построения цепочек и добавьте на место пропусков недостающие числа.
Анастасия Сукманова
Избранное
– 1 –
Показать ответ
Скрыть ответ
– 2 –
Показать ответ
Скрыть ответ
– 3 –
Показать ответ
Скрыть ответ
– 4 –
Показать ответ
Скрыть ответ
– 5 –
Показать ответ
Скрыть ответ
– 6 –
Показать ответ
Скрыть ответ
– 7 –
Показать ответ
Скрыть ответ
– 8 –
Показать ответ
Скрыть ответ
– 9 –
Показать ответ
Скрыть ответ
– 10 –
Показать ответ
Скрыть ответ
Читайте также 🔥
- 10 хитрых головоломок со спичками для тренировки воображения
- Ответьте на вопрос Илона Маска и узнайте, взяли бы вас в SpaceX
- Решите головоломку и узнайте, сможете ли попасть на закрытую вечеринку
Какое число пропущено в следующей последовательности
Перед нами оригинальная и интересная задача на логику с числовым рядом.
Дана определенная последовательность чисел, в которой пропущено одно число, его то и нужно найти.
Итак, дан числовой ряд:
8 10 14 18 ? 34 50 66
Какое число пропущено?
Внимание!
Ниже приведен правильный ответ!
Правильный ответ:
Пропущенное число это 26.
Тут имеются два чередующихся ряда чисел, начинающихся с первых двух чисел. Каждое следующее число образуется умножение предыдущего на два с последующим вычитанием числа 2.
Первы два числа это 8 и 10. 14 получаем умножая 8 на 2 и вычитая из произведения 2, то есть 8*2-2=14. 18 получаем умножая 10 на 2 и вычитая из произведения 2, то есть 10*2-2=18. Таким образом, чтобы найти число под знаком вопроса выполняем следующие действия 2*14=28; 28-2=26.
Задачка: Какое число идёт следующим?
Тесты
Как вы можете увидеть на картинке, цифры идут в следующем порядке: 18, 10, 6, 4, а дальше вам нужно понять логику и найти число.
Задачка кажется простой, но многие Интернет-пользователи решают её неверно или вовсе не могут найти логику.
А вы сможете понять, какое число скрывается за вопросительным знаком?
Правильный ответ вы увидите чуть ниже.

Правильный ответ:
Если ваш ответ 3, тогда вы всё правильно поняли и решили.
18-8=10, 10-(8:2) = 6, 6-(4:2) = 4, и, наконец, 4-(2:2)=3.
Чтобы получить 10, нужно от 18 отнять 8, т.е. (18-10=8). Далее, чтобы получить 6, нужно от 10 отнять половину предыдущего отнимаемого числа, то есть половину от 8. Чтобы получить 4 нужно от 6 отнять половину от 4 (10-4=6), и чтобы получить неизвестное число, мы от 4 отнимаем половину от 2, т.е. 4-1, и получаем 3.
Ещё одно решение:
В данной задаче можно заметить закономерность, связывающую два числа, находящиеся рядом: 2*10 — 2 = 18, 2*6-2=10, 2*4-2=6.
То есть число An = 2*A(n+1) — 2, (Где n и (n+1) являются индексами чисел в последовательности). Это значит, что для выявления следующего числа нужно решить простое уравнение: 4 = 2*x-2.
Узнать ещё
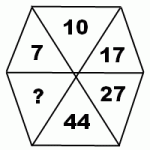
Числа в многоугольнике — один из вариантов оформления заданий из тестов iq. Чтобы найти, какое число следующее в последовательности чисел, заключенных в многоугольник, нужно определить связывающую их закономерность.
Рассмотрим примеры, в которых требуется найти числа в многоугольнике.
Найти пропущенное число
1) Закономерности, связывающие числа в многоугольнике, могут быть самыми разными. Например, это может быть связь последовательно идущих чисел по часовой стрелке или против часовой стрелки, а также чисел, стоящих через одно или два числа, чисел, стоящих напротив друг друга и т.д. Поскольку в данном задании нужно найти всего одно число, можно предположить, что все числа связаны одной закономерностью, а не несколькими. Попробуйте определить, как связаны числа в данном 6-угольнике, и найти, какое число следующее. (Ответ и объяснения скрыты под спойлером).
Каждое следующее число, начиная с 17, получено сложением двух предыдущих.
|
Dimka_Barry 0 / 0 / 0 Регистрация: 12.11.2017 Сообщений: 4 |
||||
|
1 |
||||
Найти в списке пропущенное число12.11.2017, 11:37. Показов 13659. Ответов 4 Метки нет (Все метки)
Здравствуйте, есть задача, суть которой заключается в том, что есть перечень расположенных не по порядку чисел от двух до десяти но пропущено одно число, нужно найти это самое число. Реализация этой задачи выглядит так:
Но как решить эту задачу, если эта перечень чисел (от двух до десяти, но без одного числа) находиться в текстовом файле?
0 |
|
Semen-Semenich 4466 / 3146 / 1112 Регистрация: 21.03.2016 Сообщений: 7,832 |
||||
|
12.11.2017, 16:44 |
2 |
|||
|
находиться в текстовом файле а считать данные из файла что мешает? все зависит как перечень чисел записан в файле. для примера перечень записан в одной строке через пробел 2 5 9 8 3 7 4 10
0 |
|
Dimka_Barry 0 / 0 / 0 Регистрация: 12.11.2017 Сообщений: 4 |
||||
|
16.11.2017, 00:39 [ТС] |
3 |
|||
|
Semen-Semenich, спасибо за помощь))) Добавлено через 1 час 34 минуты
0 |
|
Semen-Semenich 4466 / 3146 / 1112 Регистрация: 21.03.2016 Сообщений: 7,832 |
||||
|
16.11.2017, 18:26 |
4 |
|||
|
enumerate(my_file, 1) а эта строчка для чего? я тоже только основы изучил но я бы сделал так чтобы не путаться с индексами и кучей elif
Добавлено через 5 часов 10 минут
0 |
|
vic5710 856 / 639 / 248 Регистрация: 10.12.2016 Сообщений: 1,557 |
||||||||
|
17.11.2017, 09:29 |
5 |
|||||||
|
х – крестики преобразуйте к виду o -> +1,x -> -1,. -> 0
условие выигрыша – +3/-3 Добавлено через 1 час 11 минут
Входящие данные – текстовый файл, содержащий три строки, по три произвольно расположенных символа (x, o, .).
0 |


.jpg)
.png)