Как найти простое число формула

Как найти простое число формула

Целые числа от нуля до ста. Простые числа отмечены красным.

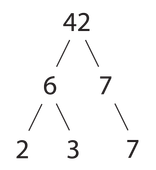
Разложение числа 42 на простые множители: {displaystyle 42=2times 3times 7}

Просто́е число́ — натуральное число, имеющее ровно два различных натуральных делителя. Другими словами, натуральное число p является простым, если оно отлично от 1 и делится без остатка только на 1 и на само p[1].

Пример: число 2 простое (делится на 1 и на 2), а 4 не является простым, так как, помимо 1 и 4, делится на 2 — имеет три натуральных делителя.

Изучением свойств простых чисел занимается теория чисел, а основная теорема арифметики устанавливает в ней их центральную роль: любое целое число, превышающее 1, либо является простым, либо может быть выражено произведением простых чисел, причём такое представление однозначно с точностью до порядка сомножителей[1]. Единицу не относят к простым числам, так как иначе указанное разложение становится неоднозначным[2]: {displaystyle x=1cdot x=1cdot 1cdot x=1cdot 1cdot ...cdot 1cdot x}.

Натуральные числа можно разделить на три класса: единица (имеет один натуральный делитель), простое число (имеет два натуральных делителя), составное число (имеет более двух натуральных делителей)[1]. Как простых, так и составных чисел бесконечно много.

Последовательность простых чисел начинается так:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, …[3]

Существуют различные алгоритмы проверки числа на простоту. Например, известный метод перебора делителей в сравнении с другими примитивный и медленный.Перейти к разделу «#Тест простоты»

Простые числа широко используются в математике и смежных науках. Во многих алгоритмах информационных технологий, например в асимметричных криптосистемах, используются свойства факторизации целых чисел[4].

Многие проблемы, касающиеся простых чисел, остаются открытымиПерейти к разделу «#Открытые вопросы».

Существуют обобщения понятия простого числа для произвольных колец и других алгебраических структурПерейти к разделу «#Вариации и обобщения».

История[править | править код]

Неизвестно, когда было определено понятие простого числа, однако первые свидетельства относят к верхнему палеолиту, что подтверждается костью Ишанго[5].

В сохранившихся записях древнеегипетских математиков есть намёки на то, что у них были некоторые представления о простых числах: например, папирус Райнда, относящийся ко второму тысячелетию до нашей эры, содержит таблицу соотношений числа 2 к n, представленных суммой трёх или четырёх египетских дробей с единицей в числителе и различных знаменателях. Разложения дробей, знаменатели которых имеют общий делитель, похожи, поэтому египтяне по крайней мере знали разницу между простым и составным числами[6].

Фрагмент «Начал» Евклида, обнаруженный в Оксиринхе

Самые ранние дошедшие до нас исследования простых чисел принадлежат математикам Древней Греции. Они изобрели решето Эратосфена — алгоритм последовательного нахождения всех простых чисел от 1 до n. Опубликованные в приблизительно трёхсотом году до нашей эры «Начала» Евклида содержат важные теоремы о простых числах, включая бесконечность их множества, лемму Евклида и основную теорему арифметики[7].

Вплоть до XVII века существенных новых работ в области простых чисел не было[8]. В 1640 году Пьер де Ферма сформулировал малую теорему Ферма, затем доказанную Лейбницем и Эйлером, и теорему о сумме двух квадратов, а также высказал предположение: все числа вида 2^{{2^{n}}}+1 являются простыми, и даже доказал это до n=4. Но уже для следующего числа Ферма {displaystyle 2^{2^{5}}+1} Эйлер доказал делимость на {displaystyle 641}. Новые простые числа в последовательности Ферма не найдены до сих пор. В то же время французский монах Марен Мерсенн обнаружил, что последовательность {displaystyle 2^{p}-1}, где p — простое, даёт также простое число[9] (числа Мерсенна).

Работа Эйлера в теории чисел вместила немало сведений о простых. Он показал, что бесконечный числовой ряд {displaystyle 1/2+1/3+1/5+1/7+1/11+...} — расходящийся. В 1747 году он доказал, что чётные совершенные числа являются значениями последовательности {displaystyle 2^{p-1}(2^{p}-1)}, где сомножитель является числом Мерсенна. В его переписке с Гольдбахом последний изложил свою знаменитую гипотезу о представлении любого чётного числа, начиная с четырёх, суммой двух простых[10]. Доказательство гипотезы пока не найдено.

С начала XIX века внимание многих математиков занимала проблема асимптотического распределения простых чисел[10]. Лежандр и Гаусс независимо друг от друга высказали предположение: плотность простых чисел в среднем близка к величине, обратно пропорциональной натуральному логарифму[11].

Долгое время простые числа считались малоприменимыми за пределами чистой математики. Ситуация изменилась в 1970-е годы, после появления концепций криптографии с открытым ключом, в которых простые числа составили основу первых алгоритмов шифрования, таких как RSA[12].

Разложение натуральных чисел в произведение простых[править | править код]

Представление натурального числа в виде произведения простых называется разложением на простые, или факторизацией числа. На настоящий момент не известны полиномиальные алгоритмы факторизации чисел, хотя и не доказано, что таких алгоритмов не существует. На предполагаемой большой вычислительной сложности задачи факторизации базируется криптосистема RSA и некоторые другие. Факторизация с полиномиальной сложностью теоретически возможна на квантовом компьютере с помощью алгоритма Шора[13].

Основная теорема арифметики[править | править код]

Основная теорема арифметики утверждает, что каждое натуральное число, большее единицы, представимо в виде произведения простых чисел, причём единственным способом с точностью до порядка следования сомножителей[14]. Таким образом, простые числа являются элементарными «строительными блоками» натуральных чисел. Например:

Как было показано в этом примере, один и тот же простой делитель может появляться несколько раз. Разложение:

n = p1 · p2 · … · pt

числа n на (конечное число) простых множителей p1, p2, … ,pt называется разложением на простые множители числа n. Основная теорема арифметики может быть перефразирована таким образом: любое разложение на простые числа будет тождественным с точностью до порядка делителей. На практике для большинства чисел есть много простых алгоритмов разложения на множители, все они дают один и тот же результат[13].

Простота единицы[править | править код]

Большинство древних греков даже не считало 1 числом, поэтому они не могли считать его простым[15]. К Средним векам и эпохе Возрождения многие математики включали 1 в качестве первого простого числа[16]. В середине XVIII века Христиан Гольдбах внёс в список 1 в качестве первого простого числа в своей знаменитой переписке с Леонардом Эйлером; однако сам Эйлер не считал 1 простым числом[17]. В XIX веке многие математики по-прежнему считали число 1 простым числом. Например, список простых чисел Деррика Нормана Лемера до {displaystyle 10006721} числа, переизданный в 1956 году, начинался с 1 в качестве первого простого числа. Говорят, что Анри Лебег является последним математиком, который назвал 1 простым[18]. К началу XX века математики стали приходить к консенсусу о том, что 1 не является простым числом, а скорее формирует свою специальную категорию — «единицу»[16].

Если считать 1 простым числом, то основная теорема Евклида об арифметике (упомянутая выше) не будет выполняться, как было указано в начале статьи. Например, число 15 может быть разложено как 3 · 5 и 1 · 3 · 5. Если бы 1 являлась простым числом, эти два варианта считались бы разными факторизациями 15; следовательно, утверждение этой теоремы пришлось бы изменить[16]. Точно так же решето Эратосфена работало бы неправильно, если бы 1 считалась простым: модифицированная версия решета, которая предполагает, что 1 является простым числом, исключает все множители, кратные 1 (то есть все остальные числа), и даёт на выходе только одно число — 1. Кроме того, простые числа имеют несколько свойств, которых нет у числа 1, такие как отношение числа к его соответствующему значению функции тождества Эйлера или суммы функции делителей[2].

Алгоритмы поиска и распознавания простых чисел[править | править код]

Простые способы нахождения начального списка простых чисел вплоть до некоторого значения дают решето Эратосфена, решето Сундарама и решето Аткина[19].

Однако, на практике вместо получения списка простых чисел зачастую требуется проверить, является ли данное число простым. Алгоритмы, решающие эту задачу, называются тестами простоты. Существует множество полиномиальных тестов простоты, но большинство их являются вероятностными (например, тест Миллера — Рабина) и используются для нужд криптографии[20]. В 2002 году было доказано, что задача проверки на простоту в общем виде полиномиально разрешима, но предложенный детерминированный тест Агравала — Каяла — Саксены имеет довольно большую вычислительную сложность, что затрудняет его практическое применение[21].

Для некоторых классов чисел существуют специализированные эффективные тесты простоты (см. ниже).

Тест простоты[править | править код]

Тестом простоты (или проверкой простоты) называется алгоритм, который, приняв на входе число, позволяет либо не подтвердить предположение о составности числа, либо точно утверждать его простоту. Во втором случае он называется истинным тестом простоты. Задача теста простоты относится к классу сложности P, то есть время работы алгоритмов её решения зависит от размера входных данных полиномиально, что было доказано в 2002 году[22]. Появление полиномиального алгоритма предсказывалось существованием полиномиальных сертификатов простоты и, как следствие, тем, что задача проверки числа на простоту принадлежала классам NP и co-NP одновременно.

Существующие алгоритмы проверки числа на простоту могут быть разделены на две категории: истинные тесты простоты и вероятностные тесты простоты. Результатом вычислений истинных тестов всегда является факт простоты либо составности числа. Вероятностный тест показывает, является ли число простым с некоторой вероятностью. Числа, удовлетворяющие вероятностному тесту простоты, но являющиеся составными, называются псевдопростыми[23]. Одним из примеров таких чисел являются числа Кармайкла[24].

Одним из примеров истинных тестов простоты является тест Люка-Лемера для чисел Мерсенна. Очевидный недостаток этого теста заключается в его применимости только к числам определённого вида. Среди других примеров можно привести основанные на малой теореме Ферма[25]

  • Тест Пепина для чисел Ферма
  • Теорема Прота для чисел Прота
  • Тест Агравала — Каяла — Саксены, первый универсальный, полиномиальный, детерминированный и безусловный тест простоты.
  • Тест Люка — Лемера — Ризеля

А также:

  • метод перебора делителей
  • Теорема Вильсона
  • Критерий Поклингтона
  • Тест Миллера
  • Тест Адлемана — Померанса — Румели, усовершенствованный[26] Коэном и Ленстрой
  • Тест простоты с использованием эллиптических кривых.

К вероятностным тестам простоты относят:

  • Тест Ферма
  • Тест Миллера — Рабина
  • Тест Соловея — Штрассена
  • Тест Бейли — Померанца — Селфриджа — Уогстаффа

Большие простые числа[править | править код]

Уже в течение многих столетий поиск «больших» простых чисел вызывает интерес математиков. В последние десятилетия эти исследования приобрели прикладное значение из-за применения таких чисел в ряде алгоритмов шифрования, таких как RSA[12].

В семнадцатом столетии Марен Мерсенн предположил, что числа вида 2^{n}-1 простые (при n ≤ 257) только для n равных 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 и 257[11]. Проверка верности предположения была намного выше возможностей того времени. Только в XX веке было обнаружено, что гипотеза была ложной и, вероятно, сделана «слепо», поскольку Мерсенн не учел три случая (для n = 61, 89 и 107); кроме того, оказалось, что числа, соответствующие n = 67 и n = 257 — составные[11].

В 1876 году Эдуард Люка доказал, что число M 127 (39-значное число) — простое, оно оставалось самым большим известным простым числом до 1951 года, когда были найдены {displaystyle {frac {2^{148}+1}{17}}} (44 цифры) и, немного позднее, {displaystyle 180*(2^{127}-1)^{2}+1} (из 79 цифр) — последнее простое число, которое было найдено с помощью электронного калькулятора. С тех пор все последующие большие простые числа были обнаружены с помощью компьютера: с 1952 года (когда SWAC показал, что M 521 является простым), по 1996 год они были найдены суперкомпьютером, и все были простыми Мерсенна (найденные с использованием теста Люка-Лемера, специфического алгоритма для таких чисел), за исключением числа {displaystyle 391581*2^{216193}-1}, которое было рекордом между 1989 и 1992 годами[27].

Алгоритмы получения простых чисел[править | править код]

Некоторые задачи математики с использованием факторизации требуют ряд очень больших простых чисел, выбранных случайным образом. Алгоритм их получения, основанный на постулате Бертрана (Для любого натурального n ≥ 2 найдётся простое число p в интервале n < p < 2n.)[28]:

Алгоритм:

  1. Ввод: натуральное число N
  2. Решение (поиск случайного простого числа P)
    1. Pgets Функция генерации произвольного натурального числа на отрезке [N,2N]
    2. Если P составное, то
      1. Pleftarrow ,P+1
      2. Если P=2N то
        1. Pleftarrow ,N
    3. Возврат «P — случайное простое»

Время решения задачи этим алгоритмом не определено, но есть большая вероятность, что оно всегда является полиномиальным, пока имеется достаточно простых чисел, и они распределены более-менее равномерно. Для простых случайных чисел эти условия выполняются[21].

Наиболее эффективным средством построения простых чисел является несколько модифицированная малая теорема Ферма[26].

Пусть N, S — нечётные натуральные числа, N-1 = S*R, причем для каждого простого делителя q числа S существует целое число a такое, что

{displaystyle a^{N-1}=1{pmod {N}}}, {displaystyle gcd(a^{{frac {N-1}{q}}-1},n)=1}

Тогда каждый простой делитель p числа N удовлетворяет сравнению

{displaystyle p=1{pmod {2S}}}

Следствие. Если выполнены условия теоремы Ферма и {displaystyle Rleqslant 4S+2}, то N — простое число[26].

Покажем теперь, как с помощью последнего утверждения, имея большое простое число S, можно построить существенно большее простое число N. Выберем для этого случайным образом чётное число R на промежутке {displaystyle Rleqslant 4S+2} и положим {displaystyle N=SR+1}. Затем проверим число N на отсутствие малых простых делителей, разделив его на малые простые числа; испытаем N некоторое количество раз с помощью алгоритма Рабина. Если при этом выяснится, что N — составное число, следует выбрать новое значение R и опять повторить вычисления. Так следует делать до тех пор, пока не будет найдено число N, выдержавшее испытание алгоритмом Рабина достаточно много раз. В этом случае появляется надежда на то, что N — простое число, и следует попытаться доказать простоту с помощью тестов простоты[26].

Бесконечность множества простых чисел[править | править код]

Простых чисел бесконечно много. Это утверждение упоминается как теорема Евклида в честь древнегреческого математика Евклида, поскольку первое известное доказательство этого утверждения приписывается ему. Известно ещё много доказательств бесконечности простых чисел, в том числе аналитическое доказательство Эйлера, доказательство Гольдбаха на основе чисел Ферма[29], доказательство Фурстенберга с использованием общей топологии и элегантное доказательство Куммера.

Наибольшее известное простое[править | править код]

Издавна ведутся записи, отмечающие наибольшие известные на то время простые числа[30]. Один из рекордов поставил в своё время Эйлер, найдя простое число 231 − 1 = 2 147 483 647.

Наибольшим известным простым числом по состоянию на январь 2019 года является число Мерсенна M82 589 933 = 282 589 933 − 1. Оно содержит 24 862 048 десятичных цифр; в книге с записью этого числа было бы около девяти тысяч страниц. Его нашли 7 декабря 2018 года в рамках проекта по распределённому поиску простых чисел Мерсенна GIMPS. Предыдущее самое большое известное простое число, открытое в декабре 2017 года, было на 1 612 623 знака меньше[31].

Числа Мерсенна выгодно отличаются от остальных наличием эффективного теста простоты: теста Люка — Лемера. Благодаря ему простые числа Мерсенна давно удерживают рекорд как самые большие известные простые.

За нахождение простых чисел из более чем 100 000 000 и 1 000 000 000 десятичных цифр EFF назначила[32] денежные призы соответственно в 150 000 и 250 000 долларов США[33]. Ранее EFF уже присуждала призы за нахождение простых чисел из 1 000 000 и 10 000 000 десятичных цифр.

Простые числа специального вида[править | править код]

Существует ряд чисел, простота которых может быть установлена эффективно с использованием специализированных алгоритмов.

  • Числа Мерсенна — числа вида {displaystyle M_{n}=2^{n}-1}, где n — натуральное число[34]. При этом число Мерсенна может быть простым, только если n — простое число. Как уже было отмечено выше, эффективным тестом простоты является тест Люка — Лемера[35].
  • Числа Ферма — числа вида F_{n}=2^{2^{n}}+1, где n — неотрицательное целое число[36]. Эффективным тестом простоты является тест Пепина. По состоянию на февраль 2015 года известно только 5 простых чисел Ферма (для n = 0, 1, 2, 3, 4), двадцать восемь следующих чисел Ферма (до {displaystyle F_{32}} включительно) оказались составными[37], однако не доказано, что других простых чисел Ферма нет[38].
  • Числа Вудала — числа вида W_{n}=ncdot 2^{n}-1[39]. Эффективным тестом простоты является тест Люка — Лемера — Ризеля[40].
  • Числа Каллена — числа вида C_{n}=ncdot 2^{n}+1[41][42].
  • Числа Прота — числа вида P=kcdot 2^{n}+1, причём k нечётно и 2^{n}>k[43]. Эффективным тестом простоты для чисел Прота является тест Бриллхарта — Лемера — Селфриджа (англ. Brillhart–Lehmer–Selfridge test)[44]. Числа Каллена и числа Ферма являются частным случаем чисел Прота (соответственно при k = n и при k = 1, n=2^{m})[45].
  • Числа Миллса — числа вида P_{n}=[A^{3^{n}}], где A — константа Миллса[46].

Для поиска простых чисел обозначенных типов в настоящее время используются проекты распределённых вычислений GIMPS, PrimeGrid, Ramsey@Home, Seventeen or Bust, Riesel Sieve, Wieferich@Home.

Некоторые свойства[править | править код]

  • Если p — простое, и p делит ab, то p делит a или b. Доказательство этого факта было дано Евклидом и известно как лемма Евклида[7][47]. Она используется в доказательстве основной теоремы арифметики.
  • Кольцо вычетов mathbb {Z} _{n} является полем тогда и только тогда, когда n — простое[48].
  • Характеристика каждого поля — это ноль или простое число[48].
  • Если p — простое, а a — натуральное, то a^{p}-a делится на p (малая теорема Ферма)[49].
  • Если G — конечная группа, порядок которой |G| делится на p, то G содержит элемент порядка p (теорема Коши)[50].
  • Если G — конечная группа, и p^{n} — максимальная степень p, которая делит |G|, то G имеет подгруппу порядка p^{n}, называемую силовской подгруппой, более того, количество силовских подгрупп равно pk+1 для некоторого целого k (теоремы Силова)[51].
  • Натуральное p>1 является простым тогда и только тогда, когда (p-1)!+1 делится на p (теорема Вильсона)[52].
  • Если n>1 — натуральное, то существует простое p, такое, что n<p<2n (постулат Бертрана)[53].
  • Ряд чисел, обратных к простым, расходится[10]. Более того, при xto infty
    sum _{p<x}{frac {1}{p}} sim ln ln x.
  • Любая арифметическая прогрессия вида a,a+q,a+2q,a+3q,..., где a,q>1 — целые взаимно простые числа, содержит бесконечно много простых чисел (теорема Дирихле о простых числах в арифметической прогрессии)[54].
  • Всякое простое число, большее 3, представимо в виде 6k+1 или 6k-1, где k — некоторое натуральное число. Отсюда, если разность между несколькими последовательными простыми числами (при k>1) одинакова, то она обязательно кратна 6 — например: 251-257-263-269; 199-211-223; 20183-20201-20219.
  • Если p>3 — простое, то p^{2}-1 кратно 24 (справедливо также для всех нечётных чисел, не делящихся на 3)[55].
  • Теорема Грина-Тао. Существуют сколь угодно длинные конечные арифметические прогрессии, состоящие из простых чисел[56].
  • Никакое простое число не может иметь вид n^{k}-1, где n>2, k>1. Иначе говоря, число, следующее за простым, не может быть квадратом или более высокой степенью с основанием, бо́льшим 2. Из этого следует также, что если простое число имеет вид 2^{k}-1, то k — простое (см. числа Мерсенна)[34].
  • Никакое простое число не может иметь вид n^{{2k+1}}+1, где n>1, k>0. Иначе говоря, число, предшествующее простому, не может быть кубом или более высокой нечётной степенью с основанием, бо́льшим 1[57].
  • Каждое простое число (кроме чисел вида {displaystyle 8n-1}) можно представить в виде суммы трех квадратов[58].

Применения[править | править код]

Простые числа являются фундаментальными компонентами во многих областях математики.

Арифметические функции[править | править код]

Арифметические функции, а именно функции, определённые на множестве натуральных чисел и принимающих значения во множестве комплексных чисел, играют решающую роль в теории чисел. В частности, среди них наиболее важными являются мультипликативные функции, то есть функции f, обладающие следующим свойством: если пара (a,b) состоит из взаимно простых чисел, то имеет место равенство[59]

{displaystyle f(ab)=f(a)f(b)}

Примерами мультипликативных функций являются функция Эйлера phi , которая ставит в соответствие числу n количество натуральных чисел, меньших n и взаимно простых с ним и количество делителей числа n[60]. Значение этих функций от степени простого числа:

  • Функция phi Эйлера:

{displaystyle phi (p^{m})=p^{m}-p^{m-1}}

  • Функция делителя:

{displaystyle sigma (p^{m})=m+1}

Арифметические функции можно легко вычислить, зная значения, которые они принимают для степеней простых чисел[59]. На самом деле из разложения натурального числа n на множители

{displaystyle n=p_{1}^{q_{1}}cdot ...cdot p_{a}^{q_{a}}}

мы имеем, что

{displaystyle f(n)=f(p_{1}^{q_{1}})cdot ...cdot f(p_{a}^{q_{a}})}

и следовательно, возвращаясь к задаче вычисления f(n) получается что вычислить f от каждой степени простого делителя обычно проще, чем вычислить f по общей формуле[61].

Например, чтобы узнать значение функции Эйлера phi от n = 450 = 2 × 3 2 × 5 2, достаточно вычислить

{displaystyle phi (450)=phi (2)cdot phi (3^{2})cdot phi (5^{2})=(2-1)cdot (9-3)cdot (25-5)=120}

Модульная арифметика[править | править код]

В модульной арифметике простые числа играют очень важную роль: кольцо вычетов mathbb {Z} /nmathbb {Z} является полем тогда и только тогда, когда n является простым[48]. Также существование первообразного корня кольца mathbb {Z} /nmathbb {Z} привязано к простым числам: оно существует, только если n — простое число, 1, 2, 4 или число в форме {displaystyle p^{n}circ 2p^{n}}, где p нечётно.

Одной из важнейших теорем модульной арифметики является малая теорема Ферма[52]. Эта теорема утверждает, что для любого простого числа р и любого натурального числа a имеем:

{displaystyle a^{p}equiv a{pmod {p}}}

или для любого простого р и любого натурального а не делящегося на р, справедливо:

{displaystyle a^{p-1}equiv 1{pmod {p}}}

Это свойство можно использовать для проверки того, что число не является простым. На самом деле, если n таково, что:

{displaystyle a^{n}not equiv a{pmod {n}}}

для некоторого натурального а, то n не может быть простым[52]. Однако это свойство не может быть использовано для проверки числа на простоту: есть некоторые числа, называемые числами Кармайкла (наименьшее — 561) для которых это будет неверно. Числом Кармайкла называется составное число, которое является псевдопростым числом по каждому основанию b, взаимно простому с n. В 1994 году Уильям Роберт Альфорд, Эндрю Гранвиль и Карл Померанс показали, что таких чисел бесконечно много[62].

Теория групп[править | править код]

Простые числа также играют основополагающую роль в алгебре. В теории групп группа, в которой каждый элемент является степенью простого числа р, называется р-группой[63]. P-группа является конечной тогда и только тогда, когда порядок группы (число её элементов) является степенью р. Примером бесконечной р-группы является p-группа Прюфера[64]. Известно, что p-группы имеют нетривиальный центр и, следовательно, не могут быть простыми (кроме группы с p элементами); если группа конечна, более того, все нормальные подгруппы пересекают центр нетривиальным образом.

Примером таких групп является циклическая группа умножения по модулю простого числа[65].

Все группы порядка p являются циклическими и поэтому абелевыми; также абелева каждая группа порядка p 2. Кроме того, любая конечная абелева группа изоморфна прямому произведению конечного числа циклических р-групп.

В теореме Коши утверждается, что если порядок конечной группы G делится на простое число p, то G содержит элементы порядка p. Эта теорема обобщается теоремами Силова[50].

Криптосистема с открытым ключом[править | править код]

Некоторые алгоритмы криптографии с открытым ключом, такие как RSA и обмен ключами Диффи-Хеллмана, основаны на больших простых числах (обычно 1024—2048 бит). RSA полагается на предположение, что намного проще (то есть более эффективно) выполнять умножение двух (больших) чисел x и y, чем вычислять взаимно простые x и y, если известно только их произведение xcdot y . Обмен ключами Диффи-Хеллмана основан на том, что существуют эффективные алгоритмы возведения в степень по модулю, а обратная операция — дискретного логарифмирования считается сложной[66][67].

RSA[править | править код]

Трудность факторизации больших чисел привела к разработке первого эффективного метода криптографии с открытым ключом — RSA[68]. В этой криптографической системе, человек, который должен получить зашифрованное сообщение, генерирует ключ: выбираются два различных случайных простых числа p и q заданного размера (обычно используются, 1024- или 2048-битные числа). Далее вычисляется их произведение {displaystyle n=p*q}, называемое модулем. Вычисляется значение функции Эйлера от числа n: {displaystyle phi (n)=(p-1)(q-1)}. Выбирается целое число e ({displaystyle 1<e<phi (n)}), взаимно простое со значением функции phi(n). Обычно в качестве e берут небольшие простые числа (например, простые числа Ферма). Число e называется открытой экспонентой (англ. public exponent). Вычисляется число d, называемое секретной экспонентой, мультипликативно обратное к числу e по модулю phi(n). Пара {displaystyle {e,n}} публикуется в качестве открытого ключа RSA (англ. RSA public key). Пара {displaystyle {d,phi (n)}} играет роль закрытого ключа RSA (англ. RSA private key) и держится в секрете[12].

Теоретически можно получить закрытый ключ из общедоступной информации: в настоящее время для этого требуется факторизация числа n, что делает передачу защищенного сообщения безопасной, если простые числа удовлетворяют определённым условиям и являются «достаточно большими». Пока не известно, существуют ли эффективные методы для расшифровки сообщения, не связанные с прямой атакой на факторизацию n, но было показано, что плохой выбор открытого ключа может сделать систему более уязвимой для таких атак[69].

В 1991 году RSA Security опубликовала список полупростых чисел, предлагая денежные призы за разложение некоторых из них на множители, с целью подтверждения безопасности метода и поощрения исследования в этой области: инициатива называлась Challenge RSA Factoring[70]. На протяжении многих лет некоторые из этих чисел были разложены, а для других проблема факторизации все ещё остается открытой; однако конкурс был завершен в 2007 году[70].

Формулы для нахождения простых чисел[править | править код]

В разное время предпринимались попытки указать выражение, значениями которого при разных значениях входящих в него переменных были бы простые числа[54].
Л. Эйлер указал многочлен textstyle n^{2}-n+41, принимающий простые значения при n = 0, 1, 2, …, 40. Однако при n = 41 значение многочлена является составным числом. Можно доказать, что не существует многочлена от одной переменной n, который принимает простые значения при всех целых n[54].
П. Ферма предположил, что все числа вида 22k + 1 простые; однако Эйлер опроверг эту гипотезу, доказав, что число 225 + 1 = 4 294 967 297 — составное[54].

Тем не менее, существуют многочлены, множество положительных значений которых при неотрицательных значениях переменных совпадает с множеством простых чисел. Одним из примеров является многочлен

{displaystyle {begin{aligned}{bigl (}k+2{bigr )}{bigl {}1&-{bigl [}wz+h+j-q{bigr ]}^{2}-{bigl [}(gk+2g+k+1)(h+j)+h-z{bigr ]}^{2}-{bigl [}2n+p+q+z-e{bigr ]}^{2}\&-{bigl [}16(k+1)^{3}(k+2)(n+1)^{2}+1-f^{2}{bigr ]}^{2}-{bigl [}e^{3}(e+2)(a+1)^{2}+1-o^{2}{bigr ]}^{2}-{bigl [}(a^{2}-1)y^{2}+1-x^{2}{bigr ]}^{2}\&-{bigl [}16r^{2}y^{4}(a^{2}-1)+1-u^{2}{bigr ]}^{2}-{bigl [}((a+u^{2}(u^{2}-a))^{2}-1)(n+4dy)^{2}+1-(x+cu)^{2}{bigr ]}^{2}-{bigl [}n+l+v-y{bigr ]}^{2}\&-{bigl [}(a^{2}-1)l^{2}+1-m^{2}{bigr ]}^{2}-{bigl [}ai+k+1-l-i{bigr ]}^{2}-{bigl [}p+l(a-n-1)+b(2an+2a-n^{2}-2n-2)-m{bigr ]}^{2}\&-{bigl [}q+y(a-p-1)+s(2ap+2a-p^{2}-2p-2)-x{bigr ]}^{2}-{bigl [}z+pl(a-p)+t(2ap-p^{2}-1)-pm{bigr ]}^{2}{bigr }}end{aligned}}}

содержащий 26 переменных и имеющий степень 25. Наименьшая степень для известных многочленов такого типа — 5 при 42 переменных; наименьшее число переменных — 10 при степени около 1,6·1045[71][72]. Этот результат является частным случаем доказанной Юрием Матиясевичем диофантовости любого перечислимого множества.

Интересно, что приведённый выше многочлен, который порождает простые числа, сам разлагается на множители. Заметим, что второй множитель этого многочлена (в фигурных скобках) имеет форму: единица минус сумма квадратов. Таким образом, многочлен может принимать положительные значения (при положительных k) только если, каждый из этих квадратов (то есть каждый многочлен в квадратных скобках) равен нулю. В этом случае выражение в фигурных скобках будет равно 1[73].

Открытые вопросы[править | править код]

Распределение простых чисел pn = f (Δsn); Δsn = pn+1² — pn². Δpn = pn+1 — pn; Δpn = 2, 4, 6, … .

До сих пор существует много открытых вопросов относительно простых чисел, наиболее известные из которых были перечислены Эдмундом Ландау в 1912 году на Пятом Международном математическом конгрессе[74]:

  1. Проблема Гольдбаха (первая проблема Ландау): верно ли, что каждое чётное число, большее двух, может быть представлено в виде суммы двух простых чисел?
  2. Вторая проблема Ландау: бесконечно ли множество «простых близнецов» — пар простых чисел, разность между которыми равна 2[54]? В 2013 году математик Чжан Итан из университета Нью-Гэмпшира[75][76] доказал, что существует бесконечно большое количество пар простых чисел, расстояние между которыми не превышает 70 миллионов. Позже Джеймс Мэйнард улучшил результат до 600. В 2014 году проект Polymath[en] под руководством Теренса Тао несколько улучшили последний метод, заменив оценку расстояния на 246.
  3. Гипотеза Лежандра (третья проблема Ландау): верно ли, что для всякого натурального числа n между n^{2} и (n+1)^2 всегда найдётся простое число[77]?
  4. Четвёртая проблема Ландау: бесконечно ли множество простых чисел вида n^{2}+1, где n — натуральное число[54]?

Открытой проблемой является также существование бесконечного количества простых чисел во многих целочисленных последовательностях, включая числа Мерсенна[54], числа Фибоначчи, числа Ферма и др.

Вариации и обобщения[править | править код]

Неприводимые и простые элементы[править | править код]

В начале статьи было дано определение простого числа: натуральное число называется простым, если у него ровно два делителя — единица и само число. Аналогичное понятие можно ввести и в других алгебраических структурах; чаще всего рассматривается коммутативные кольца без делителей нуля (области целостности)[78][79]. У таких колец, однако, могут быть делители единицы, образующие мультипликативную группу. Например, в кольце целых чисел существуют два делителя единицы: +1 и -1. Поэтому все целые числа, кроме делителей единицы, имеют не два, а по меньшей мере четыре делителя; например, у числа 7 делителями являются {displaystyle 1;7;-1;-7.} Это означает, что обобщение понятия простого числа должно опираться на иные его свойства.

Аналогом простого числа для области целостности является неприводимый элемент, который определяется следующим образом[80].

Для целых чисел это определение означает, что неприводимыми элементами являются простые натуральные числа, а также противоположные им.

Из определения следует, что множество делителей неприводимого элемента p состоит из двух частей: все делители единицы и произведения p на все делители единицы (эти произведения называются элементами, ассоциированными с p). То есть количество делителей неприводимого p, если оно конечно, вдвое больше количества делителей единицы в кольце.

Важное значение имеет аналог основной теоремы арифметики, который в обобщённом виде формулируется следующим образом[81]:

Кольцо называется факториальным, если в нём каждый ненулевой элемент, не являющийся делителем единицы, может быть представлен в виде произведения неприводимых элементов, причём это представление единственно с точностью до перестановки сомножителей и их ассоциированности (умножения на делители единицы).

Не всякая область целостности факториальна, см. контрпример. Евклидово кольцо всегда факториально[82].

Существует другое, более узкое обобщение понятия простого числа, называемое простым элементом[80].

Простой элемент всегда неприводим. В самом деле, если элемент p простой и {displaystyle p=ab,} то по определению простого элемента один из сомножителей, пусть это будет a, делится на p, то есть {displaystyle a=pq.} Тогда {displaystyle p=ab=pqb} или, сокращая на p (в области целостности сокращение ненулевого множителя всегда возможно): {displaystyle 1=qb,} то есть b является делителем единицы. ■

Обратное, вообще говоря, неверно, неприводимый элемент может не быть простым, если кольцо не является факториальным. Пример[83]: рассмотрим кольцо чисел вида {displaystyle a+b{sqrt {5}}i,} где a,b — целые числа. Число 3 в нём неприводимо, так как у него только 4 делителя: {displaystyle 3,1,-3,-1}. Однако оно не является простым элементом, в чём убеждает равенство:

{displaystyle left(2+{sqrt {5}}iright)left(2-{sqrt {5}}iright)=9}

Число 3 делит правую часть равенства, но не делит ни одного из сомножителей. Можно из этого факта сделать вывод, что рассмотренное кольцо не факториально; и в самом деле, равенство {displaystyle 6=2cdot 3=(1-i{sqrt {5}})(1+i{sqrt {5}})} показывает, что разложение на неприводимые множители в этом кольце не однозначно.

Примеры[править | править код]

Кольцо целых чисел факториально. В нём, как уже упоминалось выше, два делителя единицы.

Гауссовы целые числа[править | править код]

Кольцо гауссовых чисел состоит из комплексных чисел вида {displaystyle a+bi,} где a,b — целые числа. Делителей единицы четыре: {displaystyle 1;-1;i;-i.} Это кольцо факториально, неприводимыми элементами являются часть обычных простых чисел и «простые гауссовы» (например, 1+i). См. критерий простоты гауссова числа.

Пример разложения для числа 2, которое в кольце гауссовых чисел не является простым: {displaystyle 2=(1+i)(1-i)=i(1-i)(1-i)} — неединственность разложения здесь кажущаяся, поскольку 1-i ассоциирована с 1+i, согласно равенству: {displaystyle 1-i=(-i)(1+i).}

Целые числа Эйзенштейна[править | править код]

Кольцо целых чисел Эйзенштейна {displaystyle mathbb {Z} [omega ]} состоит из комплексных чисел следующего вида[84]:

{displaystyle z=a+bomega ,} где a,b — целые числа, {displaystyle omega ={frac {1}{2}}(-1+i{sqrt {3}})=e^{2pi i/3}} (кубический корень из единицы),

В этом кольце шесть делителей единицы: (±1, ±ω, ±ω2), оно евклидово и поэтому факториально. Неприводимые элементы (они же простые элементы) кольца называются простыми числами Эйзенштейна.

Критерий простоты: целое число Эйзенштейна {displaystyle z=a+bomega } является простым числом Эйзенштейна тогда и только тогда, когда выполняется одно из следующих взаимоисключающих условий:

  1. z ассоциировано с натуральным простым числом вида {displaystyle 3n-1.}
  2. {displaystyle |z|^{2}=a^{2}-ab+b^{2}} (норма z) является натуральным простым вида 3n или 3n+1.

Отсюда следует, что норма любого целого числа Эйзенштейна является либо простым натуральным числом, либо квадратом простого натурального числа[84].

Числа, ассоциированные или комплексно-сопряжённые с простыми числами Эйзенштейна, также являются простыми числами Эйзенштейна.

Кольцо многочленов[править | править код]

Большое значение в алгебре имеет кольцо многочленов K[x], образованное многочленами с коэффициентами из некоторого поля K. Делителями единицы являются здесь ненулевые константы (как многочлены нулевой степени). Кольцо многочленов евклидово и поэтому факториально. Если в качестве K взять поле вещественных чисел, то неприводимыми будут все многочлены 1-й степени и те многочлены 2-й степени, у которых нет вещественных корней (то есть их дискриминант отрицателен)[85].

См. также[править | править код]

  • Незаконное простое число
  • Суперпростое число
  • Полупростое число
  • Примориал
  • Простые числа, отличающиеся на шесть
  • Случайное простое число
  • Составное число
  • Список простых чисел
  • Уникальное простое

Примечания[править | править код]

  1. ↑ 1 2 3 Простое число // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 4.
  2. ↑ 1 2 “«Arguments for and against the primality of 1 Архивная копия от 24 февраля 2021 на Wayback Machine». (англ.)
  3. ↑ Последовательность A000040 в OEIS. См. также список простых чисел
  4. ↑ Гарднер, Мартин. От мозаик Пенроуза к надёжным шифрам = Penrose Tiles to Trapdoor Ciphers / пер. с англ. Ю. А. Данилова. — М.: Мир, 1993. — 416 с. — 10 000 экз. — ISBN 5-03-001991-X.
  5. ↑  (фр.) Préhistoire de la géométrie : le problème des sources (PDF) (недоступная ссылка). Site de l’IREM de La Réunion. Voir aussi « Les fables d’Ishango, ou l’irrésistible tentation de la mathématique-fiction» Архивная копия от 22 декабря 2017 на Wayback Machine, analyse par O. Keller sur Bibnum
  6. ↑ Egyptian Unit Fractions // Mathpages. Архивировано 1 апреля 2016 года.
  7. ↑ 1 2 Рыбников К. Русские издания «Начал» Евклида // Успехи математических наук. — Российская академия наук, 1941. — № 9. — С. 318—321.
  8. ↑ John J. O’Connor, Edmund F. Robertson. Prime numbers (англ.). MacTutor.
  9. ↑ List of Known Mersenne Prime Numbers. Great Internet Mersenne Prime Search. Архивировано 15 марта 2016 года.
  10. ↑ 1 2 3 Apostol, Tom M. Introduction to analytic number theory. — New York: Springer-Verlag, 1976. — xii, 338 pages с. — ISBN 0387901639. Архивная копия от 28 апреля 2020 на Wayback Machine
  11. ↑ 1 2 3 Du Sautoy, Marcus. L’enigma dei numeri primi. — Milano: Rizzoli, 2005. — 606 p. с. — ISBN 8817008435.
  12. ↑ 1 2 3 Menezes, A. J. (Alfred J.), 1965-. Handbook of applied cryptography. — Boca Raton: CRC Press, 1997. — xxviii, 780 pages с. — ISBN 9780849385230.
  13. ↑ 1 2 Ишмухаметов Ш. Т. Методы факторизации натуральных чисел: учебное пособие // Казань: Казанский университет. — 2011. — С. 190.
  14. ↑ Dudley, Underwood (1978), Elementary number theory (2nd ed.), W. H. Freeman and Co., ISBN 978-0-7167-0076-0, Section 2, Theorem 2 (англ.)
  15. ↑ См, например, David E. Joyce’s комментарий на Начала (Евклид), Книга VII, определения 1 и 2 Архивная копия от 5 августа 2011 на Wayback Machine.
  16. ↑ 1 2 3 Why is the number one not prime? (from the Prime Pages’ list of frequently asked questions) by Chris K. Caldwell. Архивная копия от 19 апреля 2015 на Wayback Machine (англ.)
  17. ↑ See for instance: L. Euler. Commentarii academiae scientiarum Petropolitanae 9 (1737), 160—188. Variae observationes circa series infinitas, Theorema 19, p.187. Архивная копия от 5 октября 2013 на Wayback Machine (англ.)
  18. ↑
    Derbyshire, John (2003), The Prime Number Theorem, Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics, Washington, D.C.: Joseph Henry Press, с. 33, ISBN 978-0-309-08549-6, OCLC 249210614 (англ.)
  19. ↑ David Gries, Jayadev Misra. A Linear Sieve Algorithm for Finding Prime Numbers. — 1978.
  20. ↑ Knuth, Donald Ervin, 1938-. The art of computer programming. — Reading, Mass.: Addison-Wesley Pub. Co, ©1973-©1981. — 4 volumes с. — ISBN 0201896842. Архивная копия от 15 июня 2020 на Wayback Machine
  21. ↑ 1 2 Vasilenko, O. N. (Oleg Nikolaevich). Teoretiko-chislovye algoritmy v kriptografii. — Moskva: MT︠S︡NMO. Moskovskiĭ t︠s︡entr nepreryvnogo matematicheskogo obrazovanii︠a︡, 2006. — 333 pages с. — ISBN 5940571034.
  22. ↑ Б. Шнайер. Прикладная криптография. — С. 296—300.
  23. ↑ Кормен Т., Лейзер Ч. Алгоритмы. Построение и анализ. — М.: МЦНМО, 2002. — С. 765—772.
  24. ↑ Crandall R., Pomerance C. Prime Numbers: A Computational Perspective. — Springer, 2005.
  25. ↑ Introduction to algorithms. — 2nd ed. — Cambridge, Mass.: MIT Press, 2001. — xxi, 1180 pages с. — ISBN 0262032937. Архивная копия от 29 января 2010 на Wayback Machine
  26. ↑ 1 2 3 4 Нестеренко Ю. В. Введение в криптографию. — Питер, 2001. — 288 с.
  27. ↑ Chris Caldwell. The Largest Known Prime by Year: A Brief History (англ.). The Prime Pages. Дата обращения: 8 марта 2010. Архивировано 19 августа 2013 года.
  28. ↑ Jitsuro Nagura. On the interval containing at least one prime number (EN) // Proceedings of the Japan Academy. — 1952. — Т. 28, вып. 4. — С. 177—181. — ISSN 0021-4280. — doi:10.3792/pja/1195570997. Архивировано 17 ноября 2017 года.
  29. ↑ Letter Архивная копия от 11 июня 2015 на Wayback Machine in Латынь from Goldbach to Euler, July 1730.
  30. ↑ Рекорды простых чисел по годам. Дата обращения: 8 марта 2010. Архивировано 19 августа 2013 года.
  31. ↑ Starr, Michelle. The Largest Prime Number to Date Has Been Discovered And It’s Hurting Our Brains (англ.), ScienceAlert. Архивировано 6 января 2018 года. Дата обращения: 6 января 2018.
  32. ↑ EFF Cooperative Computing Awards Архивная копия от 9 ноября 2008 на Wayback Machine (англ.)
  33. ↑ Юлия Рудый. Профессор из США определил самое большое простое число. Вести.Ru (7 февраля 2013). Дата обращения: 25 февраля 2018. Архивировано 26 февраля 2018 года.
  34. ↑ 1 2 Последовательность A001348 в OEIS
  35. ↑ Последовательность A000668 в OEIS: простые числа Мерсенна
  36. ↑ Последовательность A000215 в OEIS
  37. ↑ Keller, Wilfrid (February 15, 2015), Prime Factors of Fermat Numbers, <http://www.prothsearch.net/fermat.html#Summary>. Проверено 1 марта 2016. Архивная копия от 10 февраля 2016 на Wayback Machine
  38. ↑ Виолант-и-Хольц, Альберт. Загадка Ферма. Трёхвековой вызов математике. — М.: Де Агостини, 2014. — С. 78. — 151 с. — (Мир математики: в 45 томах, том 9). — ISBN 978-5-9774-0625-3.
  39. ↑ Последовательность A003261 в OEIS
  40. ↑ Последовательность A050918 в OEIS: простые числа Вудала
  41. ↑ Последовательность A002064 в OEIS
  42. ↑ Последовательность A050920 в OEIS: простые числа Каллена
  43. ↑ Последовательность A080075 в OEIS
  44. ↑ John Brillhart; Derrick Henry Lehmer; John Selfridge. New Primality Criteria and Factorizations of 2^m ± 1 (англ.) // Mathematics of Computation  (англ.) (рус. : journal. — 1975. — April (vol. 29). — P. 620—647. — doi:10.1090/S0025-5718-1975-0384673-1.
  45. ↑ Последовательность A080076 в OEIS: простые числа Прота
  46. ↑ Caldwell, Chris K. & Cheng, Yuanyou (2005), Determining Mills’ Constant and a Note on Honaker’s Problem, Journal of Integer Sequences Т. 8 (5.4.1), <http://www.cs.uwaterloo.ca/journals/JIS/VOL8/Caldwell/caldwell78.html> Архивная копия от 5 июня 2011 на Wayback Machine
  47. ↑ Dudley, Underwood (1978), Elementary number theory (2nd ed.), W. H. Freeman and Co., ISBN 978-0-7167-0076-0, Section 2, Lemma 5 (англ.)
  48. ↑ 1 2 3 Степанов С. А. Сравнения. — М.: «Знание», 1975. — 64 с.
  49. ↑ Винберг, 2008, с. 43.
  50. ↑ 1 2 Курош А. Г. Теория групп. 3-е изд., М.: Наука, 1967.
  51. ↑ А. И. Кострикин. Введение в алгебру, III часть. М.: Физматлит, 2001.
  52. ↑ 1 2 3 Виноградов И. М. Основы теории чисел. — 5 изд.. — М.—Л.: Гостехиздат, 1952.
  53. ↑ Chris Caldwell, Bertrand’s postulate Архивная копия от 22 декабря 2017 на Wayback Machine at Prime Pages glossary.
  54. ↑ 1 2 3 4 5 6 7 Энциклопедический словарь юного математика, 1985.
  55. ↑ Доказательство. Нечётное число p, не кратное 3, равно 1 или 2 по модулю 3 и равно 1, 3, 5 или 7 по модулю 8. При возведении в квадрат это даёт 1 по модулю 3 и 1 по модулю 8. Вычитая 1, получаем 0 по модулю 3 и 0 по модулю 8. Следовательно, p^{2}-1 кратно 3 и кратно 8; следовательно, оно кратно 24
  56. ↑ Weisstein, Eric W. Green-Tao Theorem (англ.) на сайте Wolfram MathWorld.
  57. ↑ Эти 2 свойства непосредственно следуют из формул разложения суммы и разности степеней
  58. ↑ Энциклопедический словарь юного математика, 1985, с. 332.
  59. ↑ 1 2 Graham, Ronald L. (1935- ). Konkretnaâ matematika : osnovanie informatiki. — Moskva: Izdatelʹstvo “Mir”, 1998. — 703, [1] s. с. — ISBN 5030017933.
  60. ↑ Sandifer, Charles Edward, 1951-. The early mathematics of Leonhard Euler. — Washington, D.C.: Mathematical Association of America, 2007. — xix, 391 pages с. — ISBN 0883855593.
  61. ↑ Bach, Eric. Algorithmic number theory. — Cambridge, Mass.: MIT Press, ©1996-. — volumes <1> с. — ISBN 0262024055.
  62. ↑ W. R. Alford, Andrew Granville, Carl Pomerance. There are Infinitely Many Carmichael Numbers // Annals of Mathematics. — 1994. — Т. 139, вып. 3. — С. 703—722. — doi:10.2307/2118576. Архивировано 26 февраля 2019 года.
  63. ↑ Charles C. Sims. Enumerating p-Groups (англ.) // Proceedings of the London Mathematical Society. — 1965-01-01. — Vol. s3—15, iss. 1. — P. 151—166. — ISSN 1460-244X. — doi:10.1112/plms/s3-15.1.151. Архивировано 23 декабря 2017 года.
  64. ↑ Jacobson, Nathan, 1910-1999. Basic algebra. — 2nd ed., Dover ed. — Mineola, N.Y.: Dover Publications, 2009. — 2 volumes с. — ISBN 9780486471877.
  65. ↑ Сагалович Ю.Л. Введение в алгебраические коды. — 2011. — 302 с. Архивная копия от 25 декабря 2017 на Wayback Machine
  66. ↑ Ferguson, Niels. Practical cryptography. — New York: Wiley, 2003. — xx, 410 pages с. — ISBN 0471223573. Архивная копия от 10 июня 2009 на Wayback Machine
  67. ↑ W. Diffie, M. Hellman. New directions in cryptography // IEEE Transactions on Information Theory. — November 1976. — Т. 22, вып. 6. — С. 644—654. — ISSN 0018-9448. — doi:10.1109/tit.1976.1055638. Архивировано 28 декабря 2017 года.
  68. ↑ Bakhtiari, Maarof, 2012, p. 175.
  69. ↑ Boneh D. Twenty Years of attacks on the RSA Cryptosystem (англ.) // Notices of the American Mathematical Society / F. Morgan — AMS, 1999. — Vol. 46, Iss. 2. — P. 203–213. — ISSN 0002-9920; 1088-9477
  70. ↑ 1 2 RSA Laboratories, The RSA Factoring Challenge Архивировано {{{2}}}.. Опубликовано 18 мая 2007.
  71. ↑ Jones J. P.,
    Sato D., Wada H., Wiens D.     Diophantine representation of the set of prime numbers (англ.) // Amer. Math. Mon. : journal. — 1976. — Vol. 83, no. 6. — P. 449—464. Архивировано 31 марта 2010 года.
  72. ↑ Yuri Matiyasevich, Diophantine Equations in the XX Century (недоступная ссылка)
  73. ↑ Matijasevic’s polynomial Архивная копия от 6 августа 2010 на Wayback Machine. The Prime Glossary.
  74. ↑ Weisstein, Eric W. Landau’s Problems (англ.) на сайте Wolfram MathWorld.
  75. ↑ Неизвестный математик совершил прорыв в теории простых чисел-близнецов. Дата обращения: 20 мая 2013. Архивировано 7 июня 2013 года.
  76. ↑ Bounded Gaps Between Primes. Дата обращения: 21 мая 2013. Архивировано 18 мая 2013 года.
  77. ↑ Weisstein, Eric W. Гитотеза Лежандра (англ.) на сайте Wolfram MathWorld.
  78. ↑ Обобщение на произвольные полугруппы см. в книге Куроша.
  79. ↑ Ван дер Варден, 2004, с. 75.
  80. ↑ 1 2 Курош, 1973, с. 82—83.
  81. ↑ Ленг, 1967, с. 89.
  82. ↑ Ван дер Варден, 2004, с. 77—78.
  83. ↑ William W. Adams, Larry Joel Goldstein (1976), Introduction to Number Theory, p. 250, Prentice-Hall, Inc., ISBN 0-13-491282-9
  84. ↑ 1 2 Eisenstein Integer–from MathWorld. Дата обращения: 23 декабря 2017. Архивировано 15 декабря 2020 года.
  85. ↑ Винберг Э. Б. Алгебра многочленов. — М.: Просвещение, 1980. — С. 122—124. — 176 с.

Литература[править | править код]

  • Ван дер Варден. Алгебра. Определения, теоремы, формулы. — СПб.: Лань, 2004. — 624 с. — ISBN 5-8114-0552-9.
  • Василенко О. Н. Теоретико-числовые алгоритмы в криптографии. — М.: МЦНМО, 2003. — 328 с. — ISBN 5-94057-103-4. Архивная копия от 27 января 2007 на Wayback Machine
  • Винберг Э. Б. Малая теорема Ферма и ее обобщения // Математическое просвещение — М.: Изд-во МЦНМО, 2008. — Т. 12. — С. 43—53.
  • Гальперин Г. Просто о простых числах // Квант. — № 4. — С. 9—14,38.
  • Генри С. Уоррен, мл. Глава 16. Формулы для простых чисел // Алгоритмические трюки для программистов = Hacker’s Delight. — М.: «Вильямс», 2007. — 288 с. — ISBN 0-201-91465-4.
  • Карпушина Н. Палиндромы и «перевёртыши» среди простых чисел // Наука и жизнь. — 2010. — № 5.
  • Кордемский Б. А. Математическая смекалка. — М.: ГИФМЛ, 1958. — 576 с.
  • Кормен Т., Лейзер Ч. Глава 33.8. Проверка чисел на простоту // Алгоритмы. Построение и анализ. — М.: МЦНМО, 2002. — С. 765—772. — ISBN 5-900916-37-5.
  • Крэндалл Р., Померанс К. Простые числа. Криптографические и вычислительные аспекты = Prime Numbers: A Computational Perspective. — М.: УРСС, Либроком, 2011. — 664 с. — ISBN 978-5-397-02060-2.
  • Курош А. Г. Лекции по общей алгебре. — 2-е изд.. — Наука, 1973.
  • Ленг С. Алгебра. — М.: Мир, 1967.
  • Матиясевич Ю.. Формулы для простых чисел // Квант. — 1975. — № 5. — С. 5—13.
  • Нестеренко Ю. В. Алгоритмические проблемы теории чисел // Введение в криптографию / Под редакцией В. В. Ященко. — Питер, 2001. — 288 с. — ISBN 5-318-00443-1.
  • Цагер Д. Первые 50 миллионов простых чисел // Успехи математических наук. — Российская академия наук, 1984. — Т. 39, № 6(240). — С. 175—190.
  • Черёмушкин А. В. Лекции по арифметическим алгоритмам в криптографии. — М.: МЦНМО, 2002. — 104 с. — 2000 экз. — ISBN 5-94057-060-7. Архивировано 31 мая 2013 года..
  • Простое число // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — С. 262—263. — 352 с.
  • Энрике Грасиан . Простые числа. Долгая дорога к бесконечности. — Де Агостини, 2014. — Т. 3. — 148 с. — (Мир математики). — ISBN 978-5-9774-0682-6. — ISBN 978-5-9774-0637-6.
  • Bakhtiari M., Maarof M. A. Serious Security Weakness in RSA Cryptosystem (англ.) // International Journal of Computer Science Issues — 2012. — Vol. 9, Iss. 1, No 3. — P. 175—178. — ISSN 1694-0814; 1694-0784
  • Crandall R., Pomerance C. Глава 3. «Recognizing Primes and Composites». Глава 4. «Primality Proving» // Prime Numbers: A Computational Perspective. — Springer, 2005. — С. 117—224. — ISBN 0-387-25282-7.

Ссылки[править | править код]

  • Кноп К. В погоне за простотой.
  • The Prime Pages (англ.) — база данных наибольших известных простых чисел (англ.).
  • Геометрия простых и совершенных чисел (исп.).
  • Скрипт визуализации
  • Форум искателей простых чисел (англ.).
Источник

Алгоритмы поиска простых чисел

Время на прочтение
6 мин

Количество просмотров 133K

«Самое большое простое число 232582657-1. И я с гордостью утверждаю, что запомнил все его цифры… в двоичной форме».
Карл Померанс

Натуральное число называется простым, если оно имеет только два различных делителя: единицу и само себя. Задача поиска простых чисел не дает покоя математикам уже очень давно. Долгое время прямого практического применения эта проблема не имела, но все изменилось с появлением криптографии с открытым ключом. В этой заметке рассматривается несколько способов поиска простых чисел, как представляющих исключительно академический интерес, так и применяемых сегодня в криптографии.

Решето Эратосфена

Решето Эратосфена — алгоритм, предложенный древнегреческим математиком Эратосфеном. Этот метод позволяет найти все простые числа меньше заданного числа n. Суть метода заключается в следующем. Возьмем набор чисел от 2 до n. Вычеркнем из набора (отсеим) все числа делящиеся на 2, кроме 2. Перейдем к следующему «не отсеянному» числу — 3, снова вычеркиваем все что делится на 3. Переходим к следующему оставшемуся числу — 5 и так далее до тех пор пока мы не дойдем до n. После выполнения вышеописанных действий, в изначальном списке останутся только простые числа.

Алгоритм можно несколько оптимизировать. Так как один из делителей составного числа n обязательно

$leqslant sqrt{n}$, алгоритм можно останавливать, после вычеркивания чисел делящихся на

$sqrt{n}$.

Иллюстрация работы алгоритма из Википедии:

image

Сложность алгоритма составляет

$O(n loglog n)$, при этом, для хранения информации о том, какие числа были вычеркнуты требуется

$O(n)$ памяти.

Существует ряд оптимизаций, позволяющих снизить эти показатели. Прием под названием wheel factorization состоит в том, чтобы включать в изначальный список только числа взаимно простые с несколькими первыми простыми числами (например меньше 30). В теории предлагается брать первые простые примерно до

$sqrt{log n}$. Это позволяет снизить сложность алгоритма в

$loglog n$ раз. Помимо этого для уменьшения потребляемой памяти используется так называемое сегментирование. Изначальный набор чисел делится на сегменты размером

$leqslant sqrt{n}$ и для каждого сегмента решето Эратосфена применяется по отдельности. Потребление памяти снижается до

$O(sqrt{n})$.

Решето Аткина

Более совершенный алгоритм отсеивания составных чисел был предложен Аткином и Берштайном и получил название Решето Аткина. Этот способ основан на следующих трех свойствах простых чисел.

Свойство 1

Если n — положительное число, не кратное квадрату простого числа и такое, что

$n equiv 1(mod 4)$. То n — простое, тогда и только тогда, когда число корней уравнения

$4x^2+y^2=n$ нечетно.

Свойство 2

Если n — положительное число, не кратное квадрату простого числа и такое, что

$n equiv 1(mod 6)$. То n — простое, тогда и только тогда, когда число корней уравнения

$3x^2+y^2=n$ нечетно.

Свойство 3

Если n — положительное число, не кратное квадрату простого числа и такое, что

$n equiv 11(mod 12)$. То n — простое, тогда и только тогда, когда число корней уравнения

$3x^2-y^2=n$ нечетно.

Доказательства этих свойств приводятся в этой статье.

На начальном этапе алгоритма решето Аткина представляет собой массив A размером n, заполненный нулями. Для определения простых чисел перебираются все

$x, y < sqrt n$. Для каждой такой пары вычисляется

$4x^2+y^2$,

$3x^2+y^2$,

$3x^2-y^2$ и значение элементов массива

$A[4x^2+y^2]$,

$A[3x^2+y^2]$,

$A[3x^2-y^2]$ увеличивается на единицу. В конце работы алгоритма индексы всех элементов массива, которые имеют нечетные значения либо простые числа, либо квадраты простого числа. На последнем шаге алгоритма производится вычеркивание квадратов оставшихся в наборе чисел.

Из описания алгоритма следует, что вычислительная сложность решета Аткина и потребление памяти составляют

$O(n)$. При использовании wheel factorization и сегментирования оценка сложности алгоритма снижается до

$O(n / loglog n)$, а потребление памяти до

$O(sqrt{n})$.

Числа Мерсенна и тест Люка-Лемера

Конечно при таких показателях сложности, даже оптимизированное решето Аткина невозможно использовать для поиска по-настоящему больших простых чисел. К счастью, существуют быстрые тесты, позволяющие проверить является ли заданное число простым. В отличие от алгоритмов решета, такие тесты не предназначены для поиска всех простых чисел, они лишь способны сказать с некоторой вероятностью, является ли определенное число простым.

Один из таких методов проверки — тест Люка-Лемера. Это детерминированный и безусловный тест простоты. Это означает, что прохождение теста гарантирует простоту числа. К сожалению, тест предназначен только для чисел особого вида

$2^p-1$, где p — натуральное число. Такие числа называются числами Мерсенна.

Тест Люка-Лемера утверждает, что число Мерсенна

$M_p=2^p-1$ простое тогда и только тогда, когда p — простое и

$M_p$ делит нацело

$(p-1)$-й член последовательности

$S_k$ задаваемой рекуррентно:

$S_1=4, S_k=S_{k-1}^2-2$ для

$k > 1$.

Для числа

$M_p$ длиной p бит вычислительная сложность алгоритма составляет

${displaystyle O(p^{3})}$.

Благодаря простоте и детерминированности теста, самые большие известные простые числа — числа Мерсенна. Самое большое известное простое число на сегодня —

$2^{82,589,933}-1$, его десятичная запись состоит из 24,862,048 цифр. Полюбоваться на эту красоту можно здесь.

Теорема Ферма и тест Миллера-Рабина

Простых чисел Мерсенна известно не очень много, поэтому для криптографии с открытым ключом необходим другой способ поиска простых чисел. Одним из таким способов является тест простоты Ферма. Он основан на малой теореме Ферма, которая гласит, что если n — простое число, то для любого a, которое не делится на n, выполняется равенство

$a^{n-1}equiv 1{pmod {n}}$. Доказательство теоремы можно найти на Википедии.

Тест простоты Ферма — вероятностный тест, который заключается в переборе нескольких значений a, если хотя бы для одного из них выполняется неравенство

$a^{n-1} notequiv 1 pmod n$, то число n — составное. В противном случае, n — вероятно простое. Чем больше значений a использовано в тесте, тем выше вероятность того, что n — простое.

К сожалению, существуют такие составные числа n, для которых сравнение

$a^{n-1}equiv 1{pmod {n}}$ выполняется для всех a взаимно простых с n. Такие числа называются числам Кармайкла. Составные числа, которые успешно проходят тест Ферма, называются псевдопростыми Ферма. Количество псевдопростых Ферма бесконечно, поэтому тест Ферма — не самый надежный способ определения простых чисел.

Тест Миллера-Рабина

Более надежных результатов можно добиться комбинируя малую теорему Ферма и тот факт, что для простого числа p не существует других корней уравнения

$x^2 equiv 1 pmod p$, кроме 1 и -1. Тест Миллера-Рабина перебирает несколько значений a и проверяет выполнение следующих условий.

Пусть p — простое число и

$p-1=2^sd$, тогда для любого a справедливо хотя бы одно из условий:

  1. $a^{d}equiv pm1{pmod {p}}$
  2. Существует целое число r < s такое, что $a^{2^{r}d}equiv -1{pmod {p}}$

По теореме Ферма

$a^{p-1}equiv1pmod p$, а так как

$p-1=2^sd$ из свойства о корнях уравнения

$x^2 equiv 1 pmod p$ следует что если мы найдем такое a, для которого одно из условий не выполняется, значит p — составное число. Если одно из условий выполняется, число a называют свидетелем простоты числа n по Миллеру, а само число n — вероятно простым.

Чем больше свидетелей простоты найдено, тем выше вероятность того, что n — простое. Согласно теореме Рабина вероятность того, что случайно выбранное число a окажется свидетелем простоты составного числа составляет приблизительно

$1/4$.

Следовательно, если проверить k случайных чисел a, то вероятность принять составное число за простое

$approx(1/4)^k$.

Сложность работы алгоритма

$O(klog^3p)$, где k — количество проверок.

Благодаря быстроте и высокой точности тест Миллера-Рабина широко используется при поиске простых чисел. Многие современные криптографические библиотеки при проверке больших чисел на простоту используют только этот тест и, как показал Мартин Альбрехт в своей работе , этого не всегда оказывается достаточно.

Он смог сгенерировать такие составные числа, которые успершно прошли тест на простоту в библиотеках OpenSSL, CryptLib, JavaScript Big Number и многих других.

Тест Люка и Тест Baillie–PSW

Чтобы избежать уязвимости, связанные с ситуациями, когда сгенерированное злоумышленником составное число, выдается за простое, Мартин Альбрехт предлагает использовать тест Baillie–PSW. Несмотря на то, что тест Baillie–PSW является вероятностным, на сегодняшний день не найдено ни одно составное число, которое успешно проходит этот тест. За нахождение подобного числа в 1980 году авторы алгоритма пообещали вознаграждение в размере $30. Приз пока так и не был востребован.

Ряд исследователей проверили все числа до

$2^{64}$ и не обнаружили ни одного составного числа, прошедшего тест Baillie–PSW. Поэтому, для чисел меньше

$2^{64}$ тест считается детерминированным.

Суть теста сводится к последовательной проверке числа на простоу двумя различными методами. Один из этих методов уже описанный выше тест Миллера-Рабина. Второй — тест Люка на сильную псевдопростоту.

Тест Люка на сильную псевдопростоту

Последовательности Люка — пары рекуррентных последовательностей

${U_{n}(P,Q)}, {V_{n}(P,Q)}$, описываемые выражениями:

${displaystyle U_{0}(P,Q)=0,quad U_{1}(P,Q)=1,quad U_{n+2}(P,Q)=Pcdot U_{n+1}(P,Q)-Qcdot U_{n}(P,Q),,ngeq 0}$

${displaystyle V_{0}(P,Q)=2,quad V_{1}(P,Q)=P,quad V_{n+2}(P,Q)=Pcdot V_{n+1}(P,Q)-Qcdot V_{n}(P,Q),,ngeq 0}$

Пусть

$U_n(P,Q)$ и

$V_n(P,Q)$ — последовательности Люка, где целые числа P и Q удовлетворяют условию

${displaystyle D=P^{2}-4Qneq 0}$

Вычислим символ Якоби:

$left({frac {D}{p}}right)=varepsilon$.

Найдем такие r, s для которых выполняется равенство

$n-ε=2^rs$

Для простого числа n выполняется одно из следующих условий:

  1. n делит $U_s$
  2. n делит $V_{2^js}$ для некоторого j < r

В противном случае n — составное.

Вероятность того, что составное число n успешно пройдет тест Люка для заданной пары параметров P, Q не превышает 4/15. Следовательно, после применения теста k раз, эта вероятность составляет

$(4/15)^k$.

Тесты Миллера-Рабина и Люка производят не пересекающиеся множества псевдопростых чисел, соответственно если число p прошло оба теста, оно простое. Именно на этом свойстве основывается тест Baillie–PSW.

Заключение

В зависимости от поставленной задачи, могут использоваться различные методы поиска простых чисел. К примеру, при поиске больших простых чисел Мерсенна, сперва, при помощи решета Эратосфена или Аткина определяется список простых чисел до некоторой границы, предположим, до

$10^8$. Затем для каждого числа p из списка, с помощью теста Люка-Лемера, на простоту проверяется

$M_p=2^p-1$.

Чтобы сгенерировать большое простое число в криптографических целях, выбирается случайное число a и проверяется тестом Миллера-Рабина или более надежным Baillie–PSW. Согласно теореме о распределении простых чисел, у случайно выбранного числа от 1 до n шанс оказаться простым примерно равен

${frac {1}{ln n}}$. Следовательно, чтобы найти простое число размером 1024 бита, достаточно перебрать около тысячи вариантов.

P.S. Исходники

Реализацию всех описанных алгоритмов на Go можно посмотреть на GitHub.

Источник

Красивые аномалии встречаются в каждом предмете, но если есть одна область красоты, с которой согласится большинство математиков, то это простое число.

Эти числа занимают уникальный пьедестал в математике, особенно в области теории чисел. Великие умы потратили бесчисленные часы для расследования этой проблемы, в том числе такие великие умы, как Пол Эрдос, Г.Х. Харди и Сриниваса Рамануджан, и это лишь некоторые из них. Теперь, прежде чем мы углубимся в различные алгоритмы, чтобы найти простые числа, давайте сначала установим предварительное понимание простых чисел.

Что такое простые числа?

Самое техническое определение простых чисел состоит в том, что это натуральное число больше 1 и может быть получено только путем умножения 1 и самого себя. Если бы понимание натуральных чисел было более интуитивным, то можно было бы сказать, что это числа, которые мы используем для подсчета.

Чтобы понять это более точно, давайте выберем два числа – 5 и 6. Теперь 5 – это число, которое можно получить только умножением на 1 и 5 (само число). Однако, когда мы берем число 6, то замечаем, что его можно получить другим способом, кроме умножения 1 и 6 (само число). Его также можно получить умножением чисел 2 и 3, что означает, что это не простое число. Число, которое не является простым, известно как составное число.

Метод Марена Мерсенна

Метод простого числа Мерсенна – это специальный метод нахождения определенного вида простого числа, известный как простые числа Мерсенна. Название для этого метода происходит от французского монаха Марин Мерсенн, который первым определил его. Простые числа Мерсенна – это те, которые сводимы к виду 2n-1, где n-простое число. Первые несколько чисел в этом методе являются 2, 3, 5, 7, 13, 17, 19, 31, 61, и 89. Долгое время метод простых чисел Мерсенна представлял собой тяжёлую работу, так как при переходе к более высоким простым числам он был очень трудоемким.

Марен Мерсенн Французский математик

Однако, с появлением компьютеров, они теперь могли выполнять эти вычислительные вычисления, которые раньше делались людьми самым кропотливым и трудоемким образом. Мы определенно достигли более высоких простых чисел Мерсенна и простых чисел на общем уровне. Поиск простых чисел так же активен, как и другие численные поиски, выполняемые компьютерами. Другой числовой поиск, аналогичный движению простых чисел, заключается в добавлении десятичных разрядов к некоторым иррациональным числам, таким как пи (отношение длины окружности к диаметру). Однако непрерывный поиск следующего по величине простого числа существенно сложнее, чем поиск следующей цифры числа Пи.

Даже самые большие компьютеры (суперкомпьютеры) тратят значительное количество времени, чтобы проверить, является ли новое число (которое обычно ошеломляюще огромным) само по себе простым числом, и требуется еще больше времени, чтобы проверить, является ли число основным числом Мерсенна. По этой причине числа Мерсенна представляют большой интерес в области кибербезопасности и криптографии, особенно в отношении шифрования.

В августе 2008 года системный администратор UCLA Эдсон Смит нашел наиболее значимое простое число, известное на тот момент. Смит установил программное обеспечение для Great Internet Mersenne Prime Search (Gimps), проекта распределенных вычислений на добровольной основе. Это число было простым числом Мерсенна длиной 12 978 189 цифр. Чтобы дать представление о том, насколько он велик, на его написание уйдет почти два с половиной месяца, а в случае печати он растянется на 50 км!

Метод простых чисел Ферма

Число Ферма, как и число Мерсенна, представляет собой особый вид простого числа. Название происходит от математика 17-го века и юриста Пьера де Ферма. Число Ферма похоже на число Мерсенна… с одной маленькой поправкой. Давайте возьмем число Ферма Fm, где мы можем определить Fm как 2m +1. Здесь m снова равно 2, возведенному в степень n или 2n.

Пьер де Ферма (фр. Pierre de Fermat, 17 августа 1601 — 12 января 1665) — французский математик-самоучка, один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел.

Фермат был твердо убежден в том, что все числа вышеуказанной формы – это простые числа. В дальнейшем он сказал, что он будет производить простые числа для всех целочисленных значений m. Что делает эти числа уникальными и красивыми, но очень хитрыми, так это то, что простые числа становятся чрезвычайно большими очень быстро, даже в пределах первых четырех итераций. Чтобы доказать это, возьмем n в качестве следующих значений, n=0, 1, 2, 3 и 4.

Когда n = 0, m = 20 = 1; поэтому F0 = 2 1 + 1 = 2 + 1 = 3, что является простым. Когда n = 1, m = 21 = 2; поэтому F1 = 22 + 1 = 4 + 1 = 5, что является простым. Когда n = 2, m = 22 = 4; следовательно, F2 = 24 + 1 = 16 + 1 = 17, что является простым. Когда n = 3, m = 23 = 8; следовательно, F3 = 28 + 1 = 256 + 1 = 257, что является простым. Когда n = 4, m = 24 = 16; следовательно, F4 = 216 + 1 = 65536 + 1 = 65537, что является простым числом. Теперь, как вы можете заметить, к тому времени, когда мы достигнем F5, значение достигает 4 294 967 297.

На сегодняшний день мы достигли только F11, даже со всеми лучшими компьютерами и параллельными вычислениями и большой точностью. В конце концов, однако, мы можем сказать, что поиск простых чисел всегда будет идти до бесконечности и дальше!

Источник

Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.

Теория чисел

  • Простые числа
  • Разложение на простые множители
  • Решето Эратосфена
  • Линейное решето Эратосфена*
  • НОД и НОК
  • Алгоритм Евклида
  • Расширенный алгоритм Евклида*
  • Операции по модулю
  • Быстрое возведение в степень
  • Деление по простому модулю*

Простые числа

Простым называется натуральное число, которое делится только на единицу и на себя. Единица при этом простым числом не считается. Составным числом называют непростое число, которое еще и не единица.

Примеры простых чисел: (2), (3), (5), (179), (10^9+7), (10^9+9).

Примеры составных чисел: (4), (15), (2^{30}).

Еще одно определение простого числа: (N) — простое, если у (N) ровно два делителя. Эти делители при этом равны (1) и (N).

Проверка на простоту за линию

С точки зрения программирования интересно научиться проверять, является ли число (N) простым. Это очень легко сделать за (O(N)) – нужно просто проверить, делится ли оно хотя бы на одно из чисел (2, 3, 4, ldots, N-1) . (N > 1) является простым только в случае, если оно не делится на на одно из этих чисел.

def is_prime(n):
    if n == 1:
        return False
    for i in range(2, n): # начинаем с 2, так как на 1 все делится; n не включается
        if n % i == 0:
            return False
    return True

for i in range(1, 10):
    print(i, is_prime(i))
(1, False)
(2, True)
(3, True)
(4, False)
(5, True)
(6, False)
(7, True)
(8, False)
(9, False)

Проверка на простоту за корень

Алгоритм можно ускорить с (O(N)) до (O(sqrt{N})).

Пусть (N = a times b), причем (a leq b). Тогда заметим, что (a leq sqrt N leq b).

Почему? Потому что если (a leq b < sqrt{N}), то (ab leq b^2 < N), но (ab = N). А если (sqrt{N} < a leq b), то (N < a^2 leq ab), но (ab = N).

Иными словами, если число (N) равно произведению двух других, то одно из них не больше корня из (N), а другое не меньше корня из (N).

Из этого следует, что если число (N) не делится ни на одно из чисел (2, 3, 4, ldots, lfloorsqrt{N}rfloor), то оно не делится и ни на одно из чисел (lceilsqrt{N}rceil + 1, ldots, N-2, N-1), так как если есть делитель больше корня (не равный (N)), то есть делитель и меньше корня (не равный 1). Поэтому в цикле for достаточно проверять числа не до (N), а до корня.

def is_prime(n):
    if n == 1:
        return False
    # Удобно вместо for i in range(2, n ** 0.5) писать так:
    i = 2
    while i * i <= n:
        if n % i == 0:
            return False
        i += 1
    return True

for i in [1, 2, 3, 10, 11, 12, 10**9+6, 10**9+7]:
    print(i, is_prime(i))
(1, False)
(2, True)
(3, True)
(10, False)
(11, True)
(12, False)
(1000000006, False)
(1000000007, True)

Разложение на простые множители

Любое натуральное число можно разложить на произведение простых, и с такой записью очень легко работать при решении задач. Разложение на простые множители еще называют факторизацией.

[11 = 11 = 11^1] [100 = 2 times 2 times 5 times 5 = 2^2 times 5^2] [126 = 2 times 3 times 3 times 7 = 2^1 times 3^2 times 7^1]

Рассмотрим, например, такую задачу:

Условие: Нужно разбить (N) людей на группы равного размера. Нам интересно, какие размеры это могут быть.

Решение: По сути нас просят найти число делителей (N). Нужно посмотреть на разложение числа (N) на простые множители, в общем виде оно выглядит так:

[N= p_1^{a_1} times p_2^{a_2} times ldots times p_k^{a_k}]

Теперь подумаем над этим выражением с точки зрения комбинаторики. Чтобы «сгенерировать» какой-нибудь делитель, нужно подставить в степень (i)-го простого число от 0 до (a_i) (то есть (a_i+1) различное значение), и так для каждого. То есть делитель (N) выглядит ровно так: [M= p_1^{b_1} times p_2^{b_2} times ldots times p_k^{b_k}, 0 leq b_i leq a_i] Значит, ответом будет произведение ((a_1+1) times (a_2+1) times ldots times (a_k + 1)).

Алгоритм разложения на простые множители

Применяя алгоритм проверки числа на простоту, мы умеем легко находить минимальный простой делитель числа N. Ясно, что как только мы нашли простой делитель числа (N), мы можем число (N) на него поделить и продолжить искать новый минимальный простой делитель.

Будем перебирать простой делитель от (2) до корня из (N) (как и раньше), но в случае, если (N) делится на этот делитель, будем просто на него делить. Причем, возможно, нам понадобится делить несколько раз ((N) может делиться на большую степень этого простого делителя). Так мы будем набирать простые делители и остановимся в тот момент, когда (N) стало либо (1), либо простым (и мы остановились, так как дошли до корня из него). Во втором случае надо еще само (N) добавить в ответ.

Напишем алгоритм факторизации:

def factorize(n):
    factors = []
    i = 2
    while i * i <= n: # перебираем простой делитель
        while n % i == 0: # пока N на него делится
            n //= i # делим N на этот делитель
            factors.append(i)
        i += 1
    # возможно, в конце N стало большим простым числом,
    # у которого мы дошли до корня и поняли, что оно простое
    # его тоже нужно добавить в разложение
    if n > 1:
        factors.append(n)
    return factors

for i in [1, 2, 3, 10, 11, 12, 10**9+6, 10**9+7]:
    print(i, '=', ' x '.join(str(x) for x in factorize(i)))
1 = 
2 = 2
3 = 3
10 = 2 x 5
11 = 11
12 = 2 x 2 x 3
1000000006 = 2 x 500000003
1000000007 = 1000000007

Задание

За сколько работает этот алгоритм?

.

.

.

.

Решение

За те же самые (O(sqrt{N})). Итераций цикла while с перебором делителя будет не больше, чем (sqrt{N}). Причем ровно (sqrt{N}) операций будет только в том случае, если (N) – простое.

А итераций деления (N) на делители будет столько, сколько всего простых чисел в факторизации числа (N). Понятно, что это не больше, чем (O(log{N})).

Задание

Докажите, что число (N) имеет не больше, чем (O(log{N})) простых множителей в факторизации.

Разные свойства простых чисел*

Вообще, про простые числа известно много свойств, но почти все из них очень трудно доказать. Вот еще некоторые из них:

  • Простых чисел, меньших (N), примерно (frac{N}{ln N}).
  • N-ое простое число равно примерно (Nln N).
  • Простые числа распределены более-менее равномерно. Например, если вам нужно найти какое-то простое число в промежутке, то можно их просто перебрать и проверить — через несколько сотен какое-нибудь найдется.
  • Для любого (N ge 2) на интервале ((N, 2N)) всегда найдется простое число (Постулат Бертрана)
  • Впрочем, существуют сколь угодно длинные отрезки, на которых простых чисел нет. Самый простой способ такой построить – это начать с (N! + 2).
  • Есть алгоритмы, проверяющие число на простоту намного быстрее, чем за корень.
  • Максимальное число делителей равно примерно (O(sqrt[3]{n})). Это не математический результат, а чисто эмпирический — не пишите его в асимптотиках.
  • Максимальное число делителей у числа на отрезке ([1, 10^5]) — 128
  • Максимальное число делителей у числа на отрекзке ([1, 10^9]) — 1344
  • Максимальное число делителей у числа на отрезке ([1, 10^{18}]) — 103680
  • Наука умеет факторизовать числа за (O(sqrt[4]{n})), но об этом как-нибудь в другой раз.
  • Любое число больше трёх можно представить в виде суммы двух простых (гипотеза Гольдбаха), но это не доказано.

Решето Эратосфена

Часто нужно не проверять на простоту одно число, а найти все простые числа до (N). В этом случае наивный алгоритм будет работать за (O(Nsqrt N)), так как нужно проверить на простоту каждое число от 1 до (N).

Но древний грек Эратосфен предложил делать так:

Запишем ряд чисел от 1 до (N) и будем вычеркивать числа: * делящиеся на 2, кроме самого числа 2 * затем деляющиеся на 3, кроме самого числа 3 * затем на 5, затем на 7, и так далее и все остальные простые до n. Таким образом, все незачеркнутые числа будут простыми — «решето» оставит только их.

Красивая визуализация

Задание

Найдите этим способом на бумажке все простые числа до 50, потом проверьте с программой:

N = 50
prime = [1] * (N + 1)
prime[0], prime[1] = 0, 0
for i in range(2, N + 1): # можно и до sqrt(N)
    if prime[i]:
        for j in range(2 * i, N + 1, i): # идем с шагом i, можно начиная с i * i
            prime[j] = 0
for i in range(1, N + 1):
    if prime[i]:
        print(i)
2
3
5
7
11
13
17
19
23
29
31
37
41
43
47

У этого алгоритма можно сразу заметить несколько ускорений.

Во-первых, число (i) имеет смысл перебирать только до корня из (N), потому что при зачеркивании составных чисел, делящихся на простое (i > sqrt N), мы ничего не зачеркнем. Почему? Пусть существует составное (M leq N), которое делится на %i%, и мы его не зачеркнули. Но тогда (i > sqrt N geq sqrt M), а значит по ранее нами доказанному утверждению (M) должно делиться и на простое число, которое меньше корня. Но это значит, что мы его уже вычеркнули.

Во-вторых, по этой же самое причине (j) имеет смысл перебирать только начиная с (i^2). Зачем вычеркивать (2i), (3i), (4i), …, ((i-1)i), если они все уже вычеркнуты, так как мы уже вычеркивали всё, что делится на (2), (3), (4), …, ((i-1)).

Асимптотика

Такой код будет работать за (O(N log log N)) по причинам, которые мы пока не хотим объяснять формально.

Гармонический ряд

Научимся оценивать асимптотику величины (1 + frac{1}{2} + ldots + frac{1}{N}), которая нередко встречается в задачах, где фигурирует делимость.

Возьмем (N) равное (2^i – 1) и запишем нашу сумму следующим образом: [left(frac{1}{1}right) + left(frac{1}{2} + frac{1}{3}right) + left(frac{1}{4} + ldots + frac{1}{7}right) + ldots + left(frac{1}{2^{i – 1}} + ldots + frac{1}{2^i – 1}right)]

Каждое из этих слагаемых имеет вид [frac{1}{2^j} + ldots + frac{1}{2^{j + 1} – 1} le frac{1}{2^j} + ldots + frac{1}{2^j} = 2^j frac{1}{2^j} = 1]

Таким образом, наша сумма не превосходит (1 + 1 + ldots + 1 = i le 2log_2(2^i – 1)). Тем самым, взяв любое (N) и дополнив до степени двойки, мы получили асимптотику (O(log N)).

Оценку снизу можно получить аналогичным образом, оценив каждое такое слагаемое снизу значением (frac{1}{2}).

Попытка объяснения асимптотики** (для старших классов)

Мы знаем, что гармонический ряд (1 + frac{1}{2} + frac{1}{3} + ldots + frac{1}{N}) это примерно (log N), а значит [N + frac{N}{2} + frac{N}{3} + ldots + frac{N}{N} sim N log N]

А что такое асимптотика решета Эратосфена? Мы как раз ровно (frac{N}{p}) раз зачеркиваем числа делящиеся на простое число (p). Если бы все числа были простыми, то мы бы как раз получили (N log N) из формули выше. Но у нас будут не все слагаемые оттуда, только с простым (p), поэтому посмотрим чуть более точно.

Известно, что простых чисел до (N) примерно (frac{N}{log N}), а значит допустим, что k-ое простое число примерно равно (k ln k). Тогда

[sum_{substack{2 leq p leq N \ text{p is prime}}} frac{N}{p} sim frac{1}{2} + sum_{k = 2}^{frac{N}{ln N}} frac{N}{k ln k} sim int_{2}^{frac{N}{ln N}} frac{N}{k ln k} dk =N(lnlnfrac{N}{ln N} – lnln 2) sim N(lnln N – lnlnln N) sim N lnln N]

Но вообще-то решето можно сделать и линейным.

Задание

Решите 5 первых задач из этого контеста:

https://informatics.msk.ru/mod/statements/view.php?id=34271

Линейное решето Эратосфена*

Наша цель — для каждого числа до (N) посчитать его минимальный простой делитель. Будем хранить его в массиве min_d. Параллельно будем хранить и список всех найденных простых чисел primes – это ровно те числа (x), у которых (min_d[x] = x).

Основное утверждение такое:

Пусть у числа (M) минимальный делитель равен (a). Тогда, если (M) составное, мы хотим вычеркнуть его ровно один раз при обработке числа (frac{M}{a}).

Мы также перебираем число (i) от (2) до (N). Если (min_d[i]) равно 0 (то есть мы не нашли ни один делитель у этого числа еще), значит оно простое – добавим в primes и сделаем (min_d[i] = i).

Далее мы хотим вычеркнуть все числа (i times k) такие, что (k) – это минимальный простой делитель этого числа. Из этого следует, что необходимо и достаточно перебрать (k) в массиве primes, и только до тех пор, пока (k < min_d[i]). Ну и перестать перебирать, если (i times k > N).

Алгоритм пометит все числа по одному разу, поэтому он корректен и работает за (O(N)).

N = 30
primes = []
min_d = [0] * (N + 1)

for i in range(2, N + 1):
    if min_d[i] == 0:
        min_d[i] = i
        primes.append(i)
    for p in primes:
        if p > min_d[i] or i * p > N:
            break
        min_d[i * p] = p
    print(i, min_d)
print(min_d)
print(primes)
2 [0, 0, 2, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
3 [0, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
4 [0, 0, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
5 [0, 0, 2, 3, 2, 5, 2, 0, 2, 3, 2, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0]
6 [0, 0, 2, 3, 2, 5, 2, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0]
7 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 0, 0, 3, 0, 0, 0, 5, 0, 0, 0, 0, 0]
8 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 0, 0, 0, 3, 0, 0, 0, 5, 0, 0, 0, 0, 0]
9 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 5, 0, 3, 0, 0, 0]
10 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 5, 0, 3, 0, 0, 0]
11 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 0, 5, 0, 3, 0, 0, 0]
12 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 0, 3, 0, 0, 0]
13 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 0, 0, 0]
14 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 0]
15 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
16 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
17 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
18 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
19 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
20 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
21 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
22 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
23 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
24 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
25 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
26 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
27 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
28 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
29 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
30 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
[0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]

Этот алгоритм работает асимптотически быстрее, чем обычное решето. Но на практике, если писать обычное решето Эратсфена с оптимизациями, то оно оказывается быстрее линейнего. Также линейное решето занимает гораздо больше памяти – ведь в обычном решете можно хранить просто (N) бит, а здесь нам нужно (N) чисел и еще массив primes.

Зато один из «побочных эффектов» алгоритма — он неявно вычисляет факторизацию всех чисел от (1) до (N). Ведь зная минимальный простой делитель любого числа от (1) до (N) можно легко поделить на это число, посмотреть на новый минимальный простой делитель и так далее.

НОД и НОК

Введем два определения.

Наибольший общий делитель (НОД) чисел (a_1, a_2, ldots, a_n) — это максимальное такое число (x), что все (a_i) делятся на (x).

Наименьшее общее кратное (НОК) чисел (a_1, a_2, ldots, a_n) — это минимальное такое число (x), что (x) делится на все (a_i).

Например, * НОД(18, 30) = 6 * НОД(60, 180, 315) = 15 * НОД(1, N) = 1 * НОК(12, 30) = 6 * НОК(1, 2, 3, 4) = 12 * НОК(1, (N)) = (N)

Зачем они нужны? Например, они часто возникают в задачах.

Условие: Есть (N) шестеренок, каждая (i)-ая зацеплена с ((i-1))-ой. (i)-ая шестеренка имеет (a_i) зубчиков. Сколько раз нужно повернуть полносьтю первую шестеренку, чтобы все остальные шестеренки тоже вернулись на изначальное место?

Решение: Когда одна шестеренка крутится на 1 зубчик, все остальные тоже крутятся на один зубчик. Нужно найти минимальное такое число зубчиков (x), что при повороте на него все шестеренки вернутся в изначальное положение, то есть (x) делится на все (a_i), то есть это НОК((a_1, a_2, ldots, a_N)). Ответом будет (frac{x}{a_1}).

Еще пример задачи на применение НОД и НОК:

Условие: Город — это прямоугольник (n) на (m), разделенный на квадраты единичного размера. Вертолет летит из нижнего левого угла в верхний правый по прямой. Вертолет будит людей в квартале, когда он пролетает строго над его внутренностью (границы не считаются). Сколько кварталов разбудит вертолёт?

Решение: Вертолет пересечет по вертикали ((m-1)) границу. С этим ничего не поделать — каждое считается как новое посещение какого-то квартала. По горизонтали то же самое — ((n-1)) переход в новую ячейку будет сделан.

Однако еще есть случай, когда он пересекает одновременно обе границы (то есть пролетает над каким-нибудь углом) — ровно тот случай, когда нового посещения квартала не происходит. Сколько таких будет? Ровно столько, сколько есть целых решений уравнения (frac{n}{m} = frac{x}{y}). Мы как бы составили уравнение движения вертолёта и ищем, в скольки целых точках оно выполняется.

Пусть (t = НОД(n, m)), тогда (n = at, m = bt).

Тогда (frac{n}{m} = frac{a}{b} = frac{x}{y}). Любая дробь с натуральными числителем и знаменателем имеет ровно одно представление в виде несократимой дроби, так что (x) должно делиться на (a), а (y) должно делиться на (b). А значит, как ответ подходят ((a, b), (2a, 2b), (3a, 3b), cdots, ((t-1)a, (t-1)b)). Таких ответов ровно (t = НОД(n, m))

Значит, итоговый ответ: ((n-1) + (m-1) – (t-1)).

Кстати, когда (НОД(a, b) = 1), говорят, что (a) и (b) взаимно просты.

Алгоритм Евклида

Осталось придумать, как искать НОД и НОК. Понятно, что их можно искать перебором, но мы хотим хороший быстрый способ.

Давайте для начала научимся искать (НОД(a, b)).

Мы можем воспользоваться следующим равенством: [НОД(a, b) = НОД(a, b – a), b > a]

Оно доказывается очень просто: надо заметить, что множества общих делителей у пар ((a, b)) и ((a, b – a)) совпадают. Почему? Потому что если (a) и (b) делятся на (x), то и (b-a) делится на (x). И наоборот, если (a) и (b-a) делятся на (x), то и (b) делится на (x). Раз множства общих делитей совпадают, то и максимальный делитель совпадает.

Из этого равенства сразу следует следующее равенство: [НОД(a, b) = НОД(a, b operatorname{%} a), b > a]

(так как (НОД(a, b) = НОД(a, b – a) = НОД(a, b – 2a) = НОД(a, b – 3a) = ldots = НОД(a, b operatorname{%} a)))

Это равенство дает идею следующего рекурсивного алгоритма:

[НОД(a, b) = НОД(b operatorname{%} a, a) = НОД(a operatorname{%} , (b operatorname{%} a), b operatorname{%} a) = ldots]

Например: [НОД(93, 36) = ] [= НОД(36, 93spaceoperatorname{%}36) = НОД(36, 21) = ] [= НОД(21, 15) = ] [= НОД(15, 6) = ] [= НОД(6, 3) = ] [= НОД(3, 0) = 3]

Задание:

Примените алгоритм Евклида и найдите НОД чисел: * 1 и 500000 * 10, 20 * 18, 60 * 55, 34 * 100, 250

По-английски наибольший общий делитель — greatest common divisor. Поэтому вместо НОД будем в коде писать gcd.

def gcd(a, b):
    if b == 0:
        return a
    return gcd(b, a % b)

print(gcd(1, 500000))
print(gcd(10, 20))
print(gcd(18, 60))
print(gcd(55, 34))
print(gcd(100, 250))
print(gcd(2465473782, 12542367456))
1
10
6
1
50
6

Вообще, в C++ такая функция уже есть в компиляторе g++ — называется __gcd. Если у вас не Visual Studio, то, скорее всего, у вас g++. Вообще, там много всего интересного.

А за сколько оно вообще работает?

Задание

Докажите, что алгоритм Евклида для чисел (N), (M) работает за (O(log(N+M))).

Кстати, интересный факт: самыми плохими входными данными для алгоритма Евклида являются числа Фибоначчи. Именно там и достигается логарифм.

Как выразить НОК через НОД

(НОК(a, b) = frac{ab}{НОД(a, b)})

По этой формуле можно легко найти НОК двух чисел через их произведение и НОД. Почему она верна?

Посмотрим на разложения на простые множители чисел a, b, НОК(a, b), НОД(a, b).

[ a = p_1^{a_1}times p_2^{a_2}timesldotstimes p_n^{a_n} ] [ b = p_1^{b_1}times p_2^{b_2}timesldotstimes p_n^{b_n} ] [ ab = p_1^{a_1+b_1}times p_2^{a_2+b_2}timesldotstimes p_n^{a_n+b_n} ]

Из определений НОД и НОК следует, что их факторизации выглядят так: [ НОД(a, b) = p_1^{min(a_1, b_1)}times p_2^{min(a_2, b_2)}timesldotstimes p_n^{min(a_n, b_n)} ] [ НОК(a, b) = p_1^{max(a_1, b_1)}times p_2^{max(a_2, b_2)}timesldotstimes p_n^{max(a_n, b_n)} ]

Тогда посчитаем (НОД(a, b) times НОК(a, b)): [ НОД(a, b)НОК(a, b) = p_1^{min(a_1, b_1)+max(a_1, b_1)}times p_2^{min(a_2, b_2)+max(a_2, b_2)}timesldotstimes p_n^{min(a_n, b_n)+max(a_n, b_n)} =] [ = p_1^{a_1+b_1}times p_2^{a_2+b_2}timesldotstimes p_n^{a_n+b_n} = ab]

Формула доказана.

Как посчитать НОД/НОК от более чем 2 чисел

Для того, чтобы искать НОД или НОК у более чем двух чисел, достаточно считать их по цепочке:

(НОД(a, b, c, d, ldots) = НОД(НОД(a, b), c, d, ldots))

(НОК(a, b, c, d, ldots) = НОК(НОК(a, b), c, d, ldots))

Почему это верно?

Ну просто множество общих делителей (a) и (b) совпадает с множеством делителей (НОД(a, b)). Из этого следует, что и множество общих делителей (a), (b) и еще каких-то чисел совпадает с множеством общих делителей (НОД(a, b)) и этих же чисел. И раз совпадают множества общих делителей, то и наибольший из них совпадает.

С НОК то же самое, только фразу “множество общих делителей” надо заменить на “множество общих кратных”.

Задание

Решите задачи F, G, H, I из этого контеста:

https://informatics.msk.ru/mod/statements/view.php?id=34271

Расширенный алгоритм Евклида*

Очень важным для математики свойством наибольшего общего делителя является следующий факт:

Для любых целых (a, b) найдутся такие целые (x, y), что (ax + by = d), где (d = gcd(a, b)).

Из этого следует, что существует решение в целых числах, например, у таких уравнений: * (8x + 6y = 2) * (4x – 5y = 1) * (116x + 44y = 4) * (3x + 11y = -1)

Мы сейчас не только докажем, что решения у таких уравнений существуют, но и приведем быстрый алгоритм нахождения этих решений. Здесь нам вновь пригодится алгоритм Евклида.

Рассмотрим один шаг алгоритма Евклида, преобразующий пару ((a, b)) в пару ((b, a operatorname{%} b)). Обозначим (r = a operatorname{%} b), то есть запишем деление с остатком в виде (a = bq + r).

Предположим, что у нас есть решение данного уравнения для чисел (b) и (r) (их наибольший общий делитель, как известно, тоже равен (d)): [bx_0 + ry_0 = d]

Теперь сделаем в этом выражении замену (r = a – bq):

[bx_0 + ry_0 = bx_0 + (a – bq)y_0 = ay_0 + b(x_0 – qy_0)]

Tаким образом, можно взять (x = y_0), а (y = (x_0 – qy_0) = (x_0 – (a operatorname{/} b)y_0)) (здесь (/) обозначает целочисленное деление).

В конце алгоритма Евклида мы всегда получаем пару ((d, 0)). Для нее решение требуемого уравнения легко подбирается — (d * 1 + 0 * 0 = d). Теперь, используя вышесказанное, мы можем идти обратно, при вычислении заменяя пару ((x, y)) (решение для чисел (b) и (a operatorname{%} b)) на пару ((y, x – (a / b)y)) (решение для чисел (a) и (b)).

Это удобно реализовывать рекурсивно:

def extended_gcd(a, b):
    if b == 0:
        return a, 1, 0
    d, x, y = extended_gcd(b, a % b)
    return d, y, x - (a // b) * y

a, b = 3, 5
res = extended_gcd(a, b)
print("{3} * {1} + {4} * {2} = {0}".format(res[0], res[1], res[2], a, b))
3 * 2 + 5 * -1 = 1

Но также полезно и посмотреть, как будет работать расширенный алгоритм Евклида и на каком-нибудь конкретном примере. Пусть мы, например, хотим найти целочисленное решение такого уравнения: [116x + 44y = 4] [(2times44+28)x + 44y = 4] [44(2x+y) + 28x = 4] [44x_0 + 28y_0 = 4] Следовательно, [x = y_0, y = x_0 – 2y_0] Будем повторять такой шаг несколько раз, получим такие уравнения: [116x + 44y = 4] [44x_0 + 28y_0 = 4, x = y_0, y = x_0 – 2y_0] [28x_1 + 16y_1 = 4, x_0 = y_1, y_0 = x_1 – y_1] [16x_2 + 12y_2 = 4, x_1 = y_2, y_1 = x_2 – y_2] [12x_3 + 4y_3 = 4, x_2 = y_3, y_2 = x_3 – y_3] [4x_4 + 0y_4 = 4, x_3 = y_4, y_3 = x_4 – 3 y_4] А теперь свернем обратно: [x_4 = 1, y_4 = 0] [x_3 = 0, y_3 =1] [x_2 = 1, y_2 =-1] [x_1 = -1, y_1 =2] [x_0 = 2, y_0 =-3] [x = -3, y =8]

Действительно, (116times(-3) + 44times8 = 4)

Задание

Решите задачу J из этого контеста:

https://informatics.msk.ru/mod/statements/view.php?id=34273

Операции по модулю

Выражение (a equiv b pmod m) означает, что остатки от деления (a) на (m) и (b) на (m) равны. Это выражение читается как «(a) сравнимо (b) по модулю (m)».

Еще это можно опрделить так: (a) сравнимо c (b) по модулю (m), если ((a – b)) делится на (m).

Все целые числа можно разделить на классы эквивалентности — два числа лежат в одном классе, если они сравнимы по модулю (m). Говорят, что мы работаем в «кольце остатков по модулю (m)», и в нем ровно (m) элементов: (0, 1, 2, cdots, m-1).

Сложение, вычитение и умножение по модулю определяются довольно интуитивно — нужно выполнить соответствующую операцию и взять остаток от деления.

С делением намного сложнее — поделить и взять по модулю не работает. Об этом подробнее поговорим чуть дальше.

a = 30
b = 50
mod = 71

print('{} + {} = {} (mod {})'.format(a, b, (a + b) % mod, mod))
print('{} - {} = {} (mod {})'.format(a, b, (a - b) % mod, mod)) # на C++ это может не работать, так как модуль от отрицательного числа берется странно
print('{} - {} = {} (mod {})'.format(a, b, (a - b + mod) % mod, mod)) # на C++ надо писать так, чтобы брать модулю от гарантированно неотрицательного числа
print('{} * {} = {} (mod {})'.format(a, b, (a * b) % mod, mod))
# print((a / b) % mod) # а как писать это, пока неясно
30 + 50 = 9 (mod 71)
30 - 50 = 51 (mod 71)
30 - 50 = 51 (mod 71)
30 * 50 = 9 (mod 71)

Задание

Посчитайте: * (2 + 3 pmod 5) * (2 * 3 pmod 5) * (2 ^ 3 pmod 5) * (2 – 4 pmod 5) * (5 + 5 pmod 6) * (2 * 3 pmod 6) * (3 * 3 pmod 6)

Для умножения (в C++) нужно ещё учитывать следующий факт: при переполнении типа всё ломается (разве что если вы используете в качестве модуля степень двойки).

  • int вмещает до (2^{31} – 1 approx 2 cdot 10^9).
  • long long вмещает до (2^{63} – 1 approx 8 cdot 10^{18}).
  • long long long в плюсах нет, при попытке заиспользовать выдает ошибку long long long is too long.
  • Под некоторыми компиляторами и архитектурами доступен int128, но не везде и не все функции его поддерживают (например, его нельзя вывести обычными методами).

Зачем нужно считать ответ по модулю

Очень часто в задаче нужно научиться считать число, которое в худшем случае гораздо больше, чем (10^{18}). Тогда, чтобы не заставлять вас писать длинную арифметику, автор задачи часто просит найти ответ по модулю большого числа, обычно (10^9 + 7)

Кстати, вместо того, чтобы писать (1000000007) удобно просто написать (1e9 + 7). (1e9) означает (1 times 10^9)

int mod = 1e9 + 7; # В C++
cout << mod;
1000000007
N = 1e9 + 7 # В питоне такое число становится float
print(N)
print(int(N))
1000000007.0
1000000007

Быстрое возведение в степень

Задача: > Даны натуральные числа (a, b, c < 10^9). Найдите (a^b) (mod (c)).

Мы хотим научиться возводить число в большую степень быстро, не просто умножая (a) на себя (b) раз. Требование на модуль здесь дано только для того, чтобы иметь возможность проверить правильность алгоритма для чисел, которые не влезают в int и long long.

Сам алгоритм довольно простой и рекурсивный, постарайтесь его придумать, решая вот такие примеры (прямо решать необязательно, но можно придумать, как посчитать значение этих чисел очень быстро):

  • (3^2)
  • (3^4)
  • (3^8)
  • (3^{16})
  • (3^{32})
  • (3^{33})
  • (3^{66})
  • (3^{132})
  • (3^{133})
  • (3^{266})
  • (3^{532})
  • (3^{533})
  • (3^{1066})

Да, здесь специально приведена такая последовательность, в которой каждое следующее число легко считается через предыдущее: его либо нужно умножить на (a=3), либо возвести в квадрат. Так и получается рекурсивный алгоритм:

  • (a^0 = 1)
  • (a^{2k}=(a^{k})^2)
  • (a^{2k+1}=a^{2k}times a)

Нужно только после каждой операции делать mod: * (a^0 pmod c = 1) * (a^{2k} pmod c = (a^{k} pmod c)^2 pmod c) * (a^{2k+1} pmod c = ((a^{2k}pmod c) times a) pmod c)

Этот алгоритм называется быстрое возведение в степень. Он имеет много применений: * в криптографии очень часто надо возводить число в большую степень по модулю * используется для деления по простому модулю (см. далее) * можно быстро перемножать не только числа, но еще и матрицы (используется для динамики, например)

Асимптотика этого алгоритма, очевидно, (O(log c)) – за каждые две итерации число уменьшается хотя бы в 2 раза.

Задание

Решите задачу K из этого контеста:

https://informatics.msk.ru/mod/statements/view.php?id=34271

Задание

Решите как можно больше задач из практического контеста:

https://informatics.msk.ru/mod/statements/view.php?id=34273

Деление по модулю*

Давайте все-таки научимся не только умножать, но и делить по простому модулю. Вот только что это значит?

(a / b) = (a times b^{-1}), где (b^{-1}) – это обратный элемент к (b).

Определение: (b^{-1}) – это такое число, что (bb^{-1} = 1)

Утверждение: в кольце остатков по простому модулю (p) у каждого остатка (кроме 0) существует ровно один обратный элемент.

Например, обратный к (2) по модулю (5) это (3) ((2 times 3 = 1 pmod 5)))

Задание

Найдите обратный элемент к: * числу (3) по модулю (5) * числу (3) по модулю (7) * числу (1) по модулю (7) * числу (2) по модулю (3) * числу (9) по модулю (31)

Давайте докажем это утверждение: надо заметить, что если каждый ненулевой остаток (1, 2, ldots, (p-1)) умножить на ненулевой остаток (a), то получатся числа (a, 2a, ldots, (p-1)a) – и они все разные! Они разные, потому что если (xa = ya), то ((x-y)a = 0), а значит ((x – y) a) делится на (p), (a) – ненулевой остаток, а значит (x = y), и это не разные числа. И из того, что все числа получились разными, это все ненулевые, и их столько же, следует, что это ровно тот же набор чисел, просто в другом порядке!

Из этого следует, что среди этих чисел есть (1), причем ровно один раз. А значит существует ровно один обратный элемент (a^{-1}). Доказательство закончено.

Это здорово, но этот обратный элемент еще хочется быстро находить. Быстрее, чем за (O(p)).

Есть несколько способов это сделать.

Через малую теорему Ферма

Малая теорема Ферма: > (a^{p-1} = 1 pmod p), если (p) – простое, (a neq 0 pmod p)).

Доказательство: В предыдущем пункте мы выяснили, что множества чисел (1, 2, ldots, (p-1)) и (a, 2a, ldots, (p-1)a) совпадают. Из этого следует, что их произведения тоже совпадают по модулю: ((p-1)! = a^{p-1} (p-1)! pmod p).

((p-1)!neq 0 pmod p) а значит на него можно поделить (это мы кстати только в предыдущем пункте доказали, поделить на число – значит умножить на обратный к нему, который существует).

А значит, (a^{p – 1} = 1 pmod p).

Как это применить Осталось заметить, что из малой теоремы Ферма сразу следует, что (a^{p-2}) – это обратный элемент к (a), а значит мы свели задачу к возведению (a) в степень (p-2), что благодаря быстрому возведению в степень мы умеем делать за (O(log p)).

Обобщение У малой теоремы Ферма есть обобщение для составных (p):

Теорема Эйлера: > (a^{varphi(p)} = 1 pmod p), (a) – взаимно просто с (p), а (varphi(p)) – это функция Эйлера (количество чисел, меньших (p) и взаимно простых с (p)).

Доказывается теорема очень похоже, только вместо ненулевых остатков (1, 2, ldots, p-1) нужно брать остатки, взаимно простые с (p). Их как раз не (p-1), а (varphi(p)).

Для нахождения обратного по этой теореме достаточно посчитать функцию Эйлера (varphi(p)) и найти (a^{-1} = a^{varphi(p) – 1}).

Но с этим возникают большие проблемы: посчитать функцию Эйлера сложно. Более того, на предполагаемой невозможности быстро ее посчитать построены некоторые криптографические алгоритм типа RSA. Поэтому быстро делить по составному модулю этим способом не получится.

Через расширенный алгоритм Евклида

Этим способом легко получится делить по любому модулю! Рекомендую.

Пусть мы хотим найти (a^{-1} pmod p), (a) и (p) взаимно простые (а иначе обратного и не будет существовать).

Давайте найдем корни уравнения

[ax + py = 1]

Они есть и находятся расширенным алгоритмом Евклида за (O(log p)), так как (НОД(a, p) = 1), ведь они взаимно простые.

Тогда если взять остаток по модулю (p):

[ax = 1 pmod p]

А значит, найденный (x) и будет обратным элементом к (a).

То есть надо просто найти (x) из решения того уравнения по модулю (p). Можно брать по модулю прямо походу решения уравнения, чтобы случайно не переполниться.

Источник

  • 1-е простое число: p(1)=2
  • 2-е простое число: p(2)=3
  • 3-е простое число: p(3)=5
  • 4-е простое число: p(4)=7
  • 5-е простое число: p(5)=11
  • …
  • n-е простое число: p(n)=? — Какая общая формула n-го члена последовательности простых чисел?

Универсальной формулы, которая давала бы а) все простые числа, и б) только простые числа, не существует. Ну то есть даже если такая и может существовать, то по сей день её не найдено.

Есть несколько формул, которые дают какой-то ограниченный набор простых чисел. Есть формулы, которые дают неограниченный набор простых чисел, но среди значений, которые вычисляются по этим формулам, попадаются и составные числа, то есть требуется дополнительная проверка получаемых результатов.

Подробный разбор различных формул, связанных с порождением простых чисел, можно найти в журнале “Квант”, №5 за 1975 год. По счастью, он доступен по Сети. В частности, там упоминаются полиномиальные многочлены и формула Джулии Робинсон, которая на данный момент удовлетворяет задачи порождения простых чисел наилучшим образом.

автор вопроса выбрал этот ответ лучшим

ОлегТ
[31.7K]

7 месяцев назад 

Вроде длинный ответ надо давать. А как его тут дашь, если ответ простой и тут не разгуляешься.

Давайте поймем, что же это за простые числа. Это Натуральные числа больше 1, такие что имеют только 2 делителя: единицу и само число. А числа, которые имеют более 2 делителей – будут составными. Составные числа можно разложить на простые множители.

Теперь попробуем решить несколько иную задачу: Пусть есть некое число N. Как понять простое оно или составное?

Надо просто проверить делится ли оно на что то еще кроме “1 и N”. Понятно, что если делиться, то делитель будет больше 1 и меньше N.

Немножко поразмыслив, можно понять, что делимость можно проверять только на простые числа из этого диапазона. А еще подумав, можно понять, что можно проверять не все числа, а до некого p(n), такого что p(n)² ≤ N, а p(n+1)² > N. И даже если после проверки окажется, что все p(n) – не являются делителями N, то есть N – будет простым. Все равно неизвестен его номер. Оно может идти по счету “k”-тым после “n”. N = p(n+k). И сколько этих “k” может быть неизвестно.

Вообщем на сегодняшний день нет общей формулы по нахождению простых чисел по его порядковому номеру.

А числа находят путем проверки делимости. Занимаются этим конечно компьютеры.

simpl
[130K]

7 месяцев назад 

Нет никакой формулы нахождения простых чисел, есть большие доводы, что их распределение имеет случайный характер..

И не нужно придумывать ерунду и отсебятину..

Но есть алгоритмы нахождения ряда простых чисел, самый известный и древний – это т.н. “Решето Эратосфена”..

Для нахождения всех простых чисел вплоть до заданного, согласно Решету Эратосфена нужно:

  1. Выписать целые числа от двух до заданного числа, ограничивающего ряд

2.Вычеркнуть из списка числа кратные 2 до заданного числа

3.Первое не зачёркнутое число, большее чем 2, является простым

4.Вычеркнуть из ряда все числа, кратные найденному числу – это 3

Нужно начинать вычёркивание с заранее известного числа, например 2, потом все числа, кратные 2 и так до конца ряда, найти первое попавшееся не зачёркнутое число и вычеркнуть все последующие кратные ему..

Вычёркиваем все кратные числа первому не зачеркнутому..

В итоге – все не вычеркнутые числа в списке — простые числа.

Alex-soldi­er
[138]

более месяца назад 

В англоязычном пространстве можно найти подборки подобных формул, опирающихся на ту или иную теорему или свойство чисел (формулы страшные, здесь их так просто не воспроизвести, поэтому см. ссылки ниже).

Но по факту это синтетически скомпонованные и крайне замороченные выражения, которые сколько-нибудь пригодны для практического использования только для небольших интервалов n (обычно из-за того, что с ростом n происходит колоссальный рост вычислительной сложности выражения, и, в определенный момент, становится проще найти очередное по счету Простое число банальным Решетом).

Кстати о Решетах. Наиболее популярны три: Решето Эратосфена, Решето Аткина, Решето Сундарама. Аткин и Сундарам работают быстрее Эратосфена, но в них необходимо хранить большие массивы данных, поэтому их применение оправдано лишь на небольших начальных интервалах [2;N]. А вот Эратосфен при реализации оказывается более экономичным, поэтому обычно именно его используют для глубокого просеивания в программах поиска больших Простых чисел.

См. https://en.wikipedia­.org/wiki/Formula_fo­r_primes

См. https://mathworld.wo­lfram.com/PrimeFormu­las.html

См. https://ru.wikipedia­.org/wiki/Решето_Атк­ина

См. https://ru.wikipedia­.org/wiki/Решето_Сун­дарама

Знаете ответ?

Источник

Добавить комментарий