Еще раз о поиске простых чисел
Время на прочтение
7 мин
Количество просмотров 220K

На снимке — скульптура абстрактного экспрессиониста Марка Ди Суверо «Решето Эратосфена», установленная в кампусе Стэнфорского университета
Введение
Напомним, что число называется простым, если оно имеет ровно два различных делителя: единицу и самого себя. Числа, имеющие большее число делителей, называются составными. Таким образом, если мы умеем раскладывать числа на множители, то мы умеем и проверять числа на простоту. Например, как-то так:
function isprime(n){
if(n==1) // 1 - не простое число
return false;
// перебираем возможные делители от 2 до sqrt(n)
for(d=2; d*d<=n; d++){
// если разделилось нацело, то составное
if(n%d==0)
return false;
}
// если нет нетривиальных делителей, то простое
return true;
}
(Здесь и далее, если не оговорено иное, приводится JavaScript-подобный псевдокод)
Время работы такого теста, очевидно, есть O(n½), т. е. растет экспоненциально относительно битовой длины n. Этот тест называется проверкой перебором делителей.
Довольно неожиданно, что существует ряд способов проверить простоту числа, не находя его делителей. Если полиномиальный алгоритм разложения на множители пока остается недостижимой мечтой (на чем и основана стойкость шифрования RSA), то разработанный в 2004 году тест на простоту
AKS
[1] отрабатывает за полиномиальное время. С различными эффективными тестами на простоту можно ознакомиться по [2].
Если теперь нам нужно найти все простые на достаточно широком интервале, то первым побуждением, наверное, будет протестировать каждое число из интервала индивидуально. К счастью, если у нас достаточно памяти, можно использовать более быстрые (и простые) алгоритмы решета. В этой статье мы обсудим два из них: классическое решето Эратосфена, известное еще древним грекам, и решето Аткина, наиболее совершенный современный алгоритм этого семейства.
Решето Эратосфена
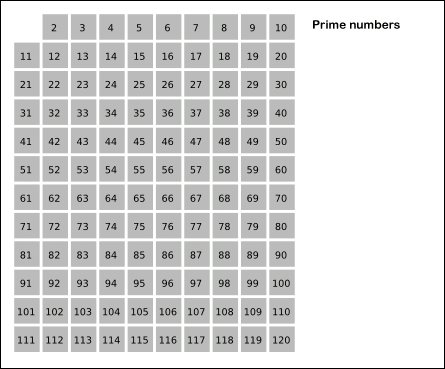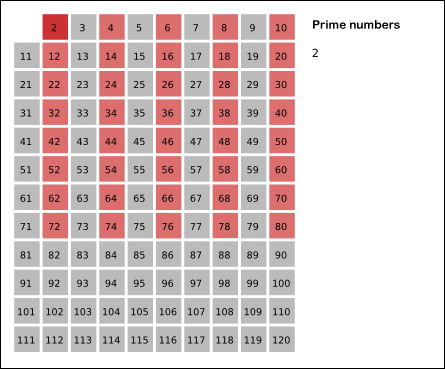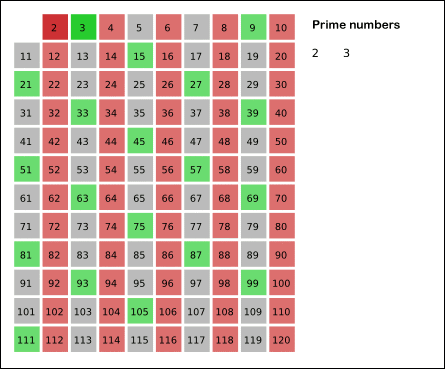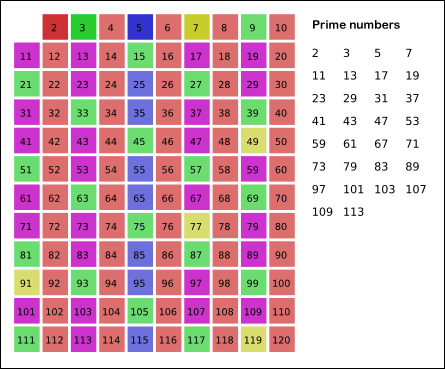
Древнегреческий математик Эратосфен предложил следующий алгоритм для нахождения всех простых, не превосходящих данного числа n. Возьмем массив S длины n и заполним его единицами (пометим как невычеркнутые). Теперь будем последовательно просматривать элементы S[k], начиная с k = 2. Если S[k] = 1, то заполним нулями (вычеркнем или высеем) все последующие ячейки, номера которых кратны k. В результате получим массив, в котором ячейки содержат 1 тогда и только тогда, когда номер ячейки — простое число.
Много времени можно сэкономить, если заметить, что, поскольку у составного числа, меньшего n, по крайней мере один из делителей не превосходит , процесс высевания достаточно закончить на
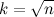
Еще немного операций можно сэкономить, если — по той же причине — начинать вычеркивать кратные k, начиная не с 2k, а с номера k2.
Реализация примет следующий вид:
function sieve(n){
S = [];
S[1] = 0; // 1 - не простое число
// заполняем решето единицами
for(k=2; k<=n; k++)
S[k]=1;
for(k=2; k*k<=n; k++){
// если k - простое (не вычеркнуто)
if(S[k]==1){
// то вычеркнем кратные k
for(l=k*k; l<=n; l+=k){
S[l]=0;
}
}
}
return S;
}
Эффективность решета Эратосфена вызвана крайней простотой внутреннего цикла: он не содержит условных переходов, а также «тяжелых» операций вроде деления и умножения.
Оценим сложность алгоритма. Первое вычеркивание требует n/2 действий, второе — n/3, третье — n/5 и т. д. По формуле Мертенса
так что для решета Эратосфена потребуется O(n log log n) операций. Потребление памяти же составит O(n).
Оптимизация и параллелизация
Первую оптимизацию решета предложил сам Эратосфен: раз из всех четных чисел простым является только 2, то давайте сэкономим половину памяти и времени и будем выписывать и высеивать только нечетные числа. Реализация такой модификации алгоритма потребует лишь косметических изменений (код).
Более развитая оптимизация (т. н. wheel factorization) опирается на то, что все простые, кроме 2, 3 и 5, лежат в одной из восьми следующих арифметических прогрессий: 30k+1, 30k+7, 30k+11, 30k+13, 30k+17, 30k+19, 30k+23 и 30k+29. Чтобы найти все простые числа до n, вычислим предварительно (опять же при помощи решета) все простые до . Теперь составим восемь решет, в каждое из которых будут входить элементы соответствующей арифметической прогрессии, меньшие n, и высеем каждое из них в отдельном потоке. Все, можно пожинать плоды: мы не только понизили потребление памяти и нагрузку на процессор (в четыре раза по сравнению с базовым алгоритмом), но и распараллелили работу алгоритма.
Наращивая шаг прогрессии и количество решет (например, при шаге прогрессии 210 нам понадобится 48 решет, что сэкономит еще 4% ресурсов) параллельно росту n, удается увеличить скорость алгоритма в log log n раз.
Сегментация
Что же делать, если, несмотря на все наши ухищрения, оперативной памяти не хватает и алгоритм безбожно «свопится»? Можно заменить одно большое решето на последовательность маленьких ситечек и высевать каждое в отдельности. Как и выше, нам придется предварительно подготовить список простых до , что займет O(n½-ε) дополнительной памяти. Простые же, найденные в процессе высевание ситечек, нам хранить не нужно — будем сразу отдавать их в выходной поток.
Не надо делать ситечки слишком маленькими, меньше тех же O(n½-ε) элементов. Так вы ничего не выиграете в асимптотике потребления памяти, но из-за накладных расходов начнете все сильнее терять в производительности.
Решето Эратосфена и однострочники
На Хабрахабре ранее публиковалась большая подборка алгоритмов Эратосфена в одну строчку на разных языках программирования (однострочники №10). Интересно, что все они на самом деле решетом Эратосфена не являются и реализуют намного более медленные алгоритмы.
Дело в том, что фильтрация множества по условию (например,
primes = primes.select { |x| x == prime || x % prime != 0 } на Ruby) или использование генераторных списков aka list comprehensions (например,
let pgen (p:xs) = p : pgen [x|x <- xs, x `mod` p > 0] на Haskell) вызывают как раз то, избежать чего призван алгоритм решета, а именно поэлементную проверку делимости. В результате сложность алгоритма возрастает по крайней мере до 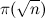
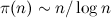
Однострочник
(n: Int) => (2 to n) |> (r => r.foldLeft(r.toSet)((ps, x) => if (ps(x)) ps -- (x * x to n by x) else ps))на Scala ближе к алгоритму Эратосфена тем, что избегает проверки на делимость. Однако сложность построения разности множеств пропорциональна размеру большего из них, так что в результате получаются те же O(n3/2-ε) операций.
Вообще решето Эратосфена тяжело эффективно реализовать в рамках функциональной парадигмы неизменяемых переменных. В случае, если функциональный язык (например, OСaml) позволяет, стоит нарушить нормы и завести изменяемый массив. В [3] обсуждается, как грамотно реализовать решето Эратосфена на Haskell при помощи техники ленивых вычеркиваний.
Решето Эратосфена и PHP
Запишем алгоритм Эратосфена на PHP. Получится примерно следующее:
define("LIMIT",1000000);
define("SQRT_LIMIT",floor(sqrt(LIMIT)));
$S = array_fill(2,LIMIT-1,true);
for($i=2;$i<=SQRT_LIMIT;$i++){
if($S[$i]===true){
for($j=$i*$i; $j<=LIMIT; $j+=$i){
$S[$j]=false;
}
}
}
Здесь есть две проблемы. Первая из них связана с системой типов данных и является характерной для многих современных языков. Дело в том, что наиболее эффективно решето Эратосфена реализуется в тех
ЯП
, где можно объявить гомогенный массив, последовательно расположенный в памяти. Тогда вычисление адреса ячейки S[i] займет всего пару команд процессора. Массив же в PHP — это на самом деле гетерогенный словарь, т. е. он индексируется произвольными строками или числами и может содержать данные различных типов. В таком случае нахождение S[i] становится куда более трудооемкой задачей.
Вторая проблема: массивы в PHP ужасны по накладным расходам памяти. У меня на 64-битной системе каждый элемент $S из кода выше съедает по 128 байт. Как обсуждалось выше, необязательно держать сразу все решето в памяти, можно обрабатывать его порционно, но все равно такие расходы дóлжно признать недопустимыми.
Для решения этих проблем достаточно выбрать более подходящий тип данных — строку!
define("LIMIT",1000000);
define("SQRT_LIMIT",floor(sqrt(LIMIT)));
$S = str_repeat("1", LIMIT+1);
for($i=2;$i<=SQRT_LIMIT;$i++){
if($S[$i]==="1"){
for($j=$i*$i; $j<=LIMIT; $j+=$i){
$S[$j]="";
}
}
}
Теперь каждый элемент занимает ровно 1 байт, а время работы уменьшилось примерно втрое. Скрипт для измерения скорости.
Решето Аткина
В 1999 году Аткин и Бернштейн предложили новый метод высеивания составных чисел, получивший название решета Аткина. Он основан на следующей теореме.
Теорема. Пусть n — натуральное число, которое не делится ни на какой полный квадрат. Тогда
- если n представимо в виде 4k+1, то оно просто тогда и только тогда, когда число натуральных решений уравнения 4x2+y2 = n нечетно.
- если n представимо в виде 6k+1, то оно просто тогда и только тогда, когда число натуральных решений уравнения 3x2+y2 = n нечетно.
- если n представимо в виде 12k-1, то оно просто тогда и только тогда, когда число натуральных решений уравнения 3x2−y2 = n, для которых x > y, нечетно.
C доказательством можно ознакомиться в [4].
Из элементарной теории чисел следует, что все простые, большие 3, имеют вид 12k+1 (случай 1), 12k+5 (снова 1), 12k+7 (случай 2) или 12k+11 (случай 3).
Для инициализации алгоритма заполним решето S нулями. Теперь для каждой пары (x, y), где 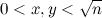
В качестве заключительного этапа пройдемся по предположительно простым номерам последовательно и вычеркнем кратные их квадратам.
Из описания видно, что сложность решета Аткина пропорциональна n, а не n log log n как у алгоритма Эратосфена.
Авторская, оптимизированная реализация на Си представлена в виде primegen, упрощенная версия — в Википедии. На Хабрахабре публиковалось решето Аткина на C#.
Как и в решете Эратосфена, при помощи wheel factorization и сегментации, можно снизить асимптотическую сложность в log log n раз, а потребление памяти — до O(n½+o(1)).
О логарифме логарифма
На самом деле множитель log log n растет крайне. медленно. Например, log log 1010000 ≈ 10. Поэтому с практической точки зрения его можно полагать константой, а сложность алгоритма Эратосфена — линейной. Если только поиск простых не является ключевой функцией в вашем проекте, можно использовать базовый вариант решета Эратосфена (разве что сэкономьте на четных числах) и не комплексовать по этому поводу. Однако при поиске простых на больших интервалах (от 232) игра стоит свеч, оптимизации и решето Аткина могут ощутимо повысить производительность.
P. S. В комментариях напомнили про решето Сундарама. К сожалению, оно является лишь математической диковинкой и всегда уступает либо решетам Эратосфена и Аткина, либо проверке перебором делителей.
Литература
[1] Agrawal M., Kayal N., Saxena N. PRIMES is in P. — Annals of Math. 160 (2), 2004. — P. 781–793.
[2] Василенко О. Н. Теоретико-числовые алгоритмы в криптографии. — М., МЦНМО, 2003. — 328 с.
[3] O’Neill M. E. The Genuine Sieve of Eratosthenes. — 2008.
[4] Atkin A. O. L., Bernstein D. J. Prime sieves using binary quadratic forms. — Math. Comp. 73 (246), 2003. — P. 1023-1030.
Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Теория чисел
- Простые числа
- Разложение на простые множители
- Решето Эратосфена
- Линейное решето Эратосфена*
- НОД и НОК
- Алгоритм Евклида
- Расширенный алгоритм Евклида*
- Операции по модулю
- Быстрое возведение в степень
- Деление по простому модулю*
Простые числа
Простым называется натуральное число, которое делится только на единицу и на себя. Единица при этом простым числом не считается. Составным числом называют непростое число, которое еще и не единица.
Примеры простых чисел: (2), (3), (5), (179), (10^9+7), (10^9+9).
Примеры составных чисел: (4), (15), (2^{30}).
Еще одно определение простого числа: (N) — простое, если у (N) ровно два делителя. Эти делители при этом равны (1) и (N).
Проверка на простоту за линию
С точки зрения программирования интересно научиться проверять, является ли число (N) простым. Это очень легко сделать за (O(N)) – нужно просто проверить, делится ли оно хотя бы на одно из чисел (2, 3, 4, ldots, N-1) . (N > 1) является простым только в случае, если оно не делится на на одно из этих чисел.
def is_prime(n):
if n == 1:
return False
for i in range(2, n): # начинаем с 2, так как на 1 все делится; n не включается
if n % i == 0:
return False
return True
for i in range(1, 10):
print(i, is_prime(i))(1, False)
(2, True)
(3, True)
(4, False)
(5, True)
(6, False)
(7, True)
(8, False)
(9, False)Проверка на простоту за корень
Алгоритм можно ускорить с (O(N)) до (O(sqrt{N})).
Пусть (N = a times b), причем (a leq b). Тогда заметим, что (a leq sqrt N leq b).
Почему? Потому что если (a leq b < sqrt{N}), то (ab leq b^2 < N), но (ab = N). А если (sqrt{N} < a leq b), то (N < a^2 leq ab), но (ab = N).
Иными словами, если число (N) равно произведению двух других, то одно из них не больше корня из (N), а другое не меньше корня из (N).
Из этого следует, что если число (N) не делится ни на одно из чисел (2, 3, 4, ldots, lfloorsqrt{N}rfloor), то оно не делится и ни на одно из чисел (lceilsqrt{N}rceil + 1, ldots, N-2, N-1), так как если есть делитель больше корня (не равный (N)), то есть делитель и меньше корня (не равный 1). Поэтому в цикле for достаточно проверять числа не до (N), а до корня.
def is_prime(n):
if n == 1:
return False
# Удобно вместо for i in range(2, n ** 0.5) писать так:
i = 2
while i * i <= n:
if n % i == 0:
return False
i += 1
return True
for i in [1, 2, 3, 10, 11, 12, 10**9+6, 10**9+7]:
print(i, is_prime(i))(1, False)
(2, True)
(3, True)
(10, False)
(11, True)
(12, False)
(1000000006, False)
(1000000007, True)Разложение на простые множители
Любое натуральное число можно разложить на произведение простых, и с такой записью очень легко работать при решении задач. Разложение на простые множители еще называют факторизацией.
[11 = 11 = 11^1] [100 = 2 times 2 times 5 times 5 = 2^2 times 5^2] [126 = 2 times 3 times 3 times 7 = 2^1 times 3^2 times 7^1]
Рассмотрим, например, такую задачу:
Условие: Нужно разбить (N) людей на группы равного размера. Нам интересно, какие размеры это могут быть.
Решение: По сути нас просят найти число делителей (N). Нужно посмотреть на разложение числа (N) на простые множители, в общем виде оно выглядит так:
[N= p_1^{a_1} times p_2^{a_2} times ldots times p_k^{a_k}]
Теперь подумаем над этим выражением с точки зрения комбинаторики. Чтобы «сгенерировать» какой-нибудь делитель, нужно подставить в степень (i)-го простого число от 0 до (a_i) (то есть (a_i+1) различное значение), и так для каждого. То есть делитель (N) выглядит ровно так: [M= p_1^{b_1} times p_2^{b_2} times ldots times p_k^{b_k}, 0 leq b_i leq a_i] Значит, ответом будет произведение ((a_1+1) times (a_2+1) times ldots times (a_k + 1)).
Алгоритм разложения на простые множители
Применяя алгоритм проверки числа на простоту, мы умеем легко находить минимальный простой делитель числа N. Ясно, что как только мы нашли простой делитель числа (N), мы можем число (N) на него поделить и продолжить искать новый минимальный простой делитель.
Будем перебирать простой делитель от (2) до корня из (N) (как и раньше), но в случае, если (N) делится на этот делитель, будем просто на него делить. Причем, возможно, нам понадобится делить несколько раз ((N) может делиться на большую степень этого простого делителя). Так мы будем набирать простые делители и остановимся в тот момент, когда (N) стало либо (1), либо простым (и мы остановились, так как дошли до корня из него). Во втором случае надо еще само (N) добавить в ответ.
Напишем алгоритм факторизации:
def factorize(n):
factors = []
i = 2
while i * i <= n: # перебираем простой делитель
while n % i == 0: # пока N на него делится
n //= i # делим N на этот делитель
factors.append(i)
i += 1
# возможно, в конце N стало большим простым числом,
# у которого мы дошли до корня и поняли, что оно простое
# его тоже нужно добавить в разложение
if n > 1:
factors.append(n)
return factors
for i in [1, 2, 3, 10, 11, 12, 10**9+6, 10**9+7]:
print(i, '=', ' x '.join(str(x) for x in factorize(i)))1 =
2 = 2
3 = 3
10 = 2 x 5
11 = 11
12 = 2 x 2 x 3
1000000006 = 2 x 500000003
1000000007 = 1000000007Задание
За сколько работает этот алгоритм?
.
.
.
.
Решение
За те же самые (O(sqrt{N})). Итераций цикла while с перебором делителя будет не больше, чем (sqrt{N}). Причем ровно (sqrt{N}) операций будет только в том случае, если (N) – простое.
А итераций деления (N) на делители будет столько, сколько всего простых чисел в факторизации числа (N). Понятно, что это не больше, чем (O(log{N})).
Задание
Докажите, что число (N) имеет не больше, чем (O(log{N})) простых множителей в факторизации.
Разные свойства простых чисел*
Вообще, про простые числа известно много свойств, но почти все из них очень трудно доказать. Вот еще некоторые из них:
- Простых чисел, меньших (N), примерно (frac{N}{ln N}).
- N-ое простое число равно примерно (Nln N).
- Простые числа распределены более-менее равномерно. Например, если вам нужно найти какое-то простое число в промежутке, то можно их просто перебрать и проверить — через несколько сотен какое-нибудь найдется.
- Для любого (N ge 2) на интервале ((N, 2N)) всегда найдется простое число (Постулат Бертрана)
- Впрочем, существуют сколь угодно длинные отрезки, на которых простых чисел нет. Самый простой способ такой построить – это начать с (N! + 2).
- Есть алгоритмы, проверяющие число на простоту намного быстрее, чем за корень.
- Максимальное число делителей равно примерно (O(sqrt[3]{n})). Это не математический результат, а чисто эмпирический — не пишите его в асимптотиках.
- Максимальное число делителей у числа на отрезке ([1, 10^5]) — 128
- Максимальное число делителей у числа на отрекзке ([1, 10^9]) — 1344
- Максимальное число делителей у числа на отрезке ([1, 10^{18}]) — 103680
- Наука умеет факторизовать числа за (O(sqrt[4]{n})), но об этом как-нибудь в другой раз.
- Любое число больше трёх можно представить в виде суммы двух простых (гипотеза Гольдбаха), но это не доказано.
Решето Эратосфена
Часто нужно не проверять на простоту одно число, а найти все простые числа до (N). В этом случае наивный алгоритм будет работать за (O(Nsqrt N)), так как нужно проверить на простоту каждое число от 1 до (N).
Но древний грек Эратосфен предложил делать так:
Запишем ряд чисел от 1 до (N) и будем вычеркивать числа: * делящиеся на 2, кроме самого числа 2 * затем деляющиеся на 3, кроме самого числа 3 * затем на 5, затем на 7, и так далее и все остальные простые до n. Таким образом, все незачеркнутые числа будут простыми — «решето» оставит только их.
Красивая визуализация
Задание
Найдите этим способом на бумажке все простые числа до 50, потом проверьте с программой:
N = 50
prime = [1] * (N + 1)
prime[0], prime[1] = 0, 0
for i in range(2, N + 1): # можно и до sqrt(N)
if prime[i]:
for j in range(2 * i, N + 1, i): # идем с шагом i, можно начиная с i * i
prime[j] = 0
for i in range(1, N + 1):
if prime[i]:
print(i)2
3
5
7
11
13
17
19
23
29
31
37
41
43
47У этого алгоритма можно сразу заметить несколько ускорений.
Во-первых, число (i) имеет смысл перебирать только до корня из (N), потому что при зачеркивании составных чисел, делящихся на простое (i > sqrt N), мы ничего не зачеркнем. Почему? Пусть существует составное (M leq N), которое делится на %i%, и мы его не зачеркнули. Но тогда (i > sqrt N geq sqrt M), а значит по ранее нами доказанному утверждению (M) должно делиться и на простое число, которое меньше корня. Но это значит, что мы его уже вычеркнули.
Во-вторых, по этой же самое причине (j) имеет смысл перебирать только начиная с (i^2). Зачем вычеркивать (2i), (3i), (4i), …, ((i-1)i), если они все уже вычеркнуты, так как мы уже вычеркивали всё, что делится на (2), (3), (4), …, ((i-1)).
Асимптотика
Такой код будет работать за (O(N log log N)) по причинам, которые мы пока не хотим объяснять формально.
Гармонический ряд
Научимся оценивать асимптотику величины (1 + frac{1}{2} + ldots + frac{1}{N}), которая нередко встречается в задачах, где фигурирует делимость.
Возьмем (N) равное (2^i – 1) и запишем нашу сумму следующим образом: [left(frac{1}{1}right) + left(frac{1}{2} + frac{1}{3}right) + left(frac{1}{4} + ldots + frac{1}{7}right) + ldots + left(frac{1}{2^{i – 1}} + ldots + frac{1}{2^i – 1}right)]
Каждое из этих слагаемых имеет вид [frac{1}{2^j} + ldots + frac{1}{2^{j + 1} – 1} le frac{1}{2^j} + ldots + frac{1}{2^j} = 2^j frac{1}{2^j} = 1]
Таким образом, наша сумма не превосходит (1 + 1 + ldots + 1 = i le 2log_2(2^i – 1)). Тем самым, взяв любое (N) и дополнив до степени двойки, мы получили асимптотику (O(log N)).
Оценку снизу можно получить аналогичным образом, оценив каждое такое слагаемое снизу значением (frac{1}{2}).
Попытка объяснения асимптотики** (для старших классов)
Мы знаем, что гармонический ряд (1 + frac{1}{2} + frac{1}{3} + ldots + frac{1}{N}) это примерно (log N), а значит [N + frac{N}{2} + frac{N}{3} + ldots + frac{N}{N} sim N log N]
А что такое асимптотика решета Эратосфена? Мы как раз ровно (frac{N}{p}) раз зачеркиваем числа делящиеся на простое число (p). Если бы все числа были простыми, то мы бы как раз получили (N log N) из формули выше. Но у нас будут не все слагаемые оттуда, только с простым (p), поэтому посмотрим чуть более точно.
Известно, что простых чисел до (N) примерно (frac{N}{log N}), а значит допустим, что k-ое простое число примерно равно (k ln k). Тогда
[sum_{substack{2 leq p leq N \ text{p is prime}}} frac{N}{p} sim frac{1}{2} + sum_{k = 2}^{frac{N}{ln N}} frac{N}{k ln k} sim int_{2}^{frac{N}{ln N}} frac{N}{k ln k} dk =N(lnlnfrac{N}{ln N} – lnln 2) sim N(lnln N – lnlnln N) sim N lnln N]
Но вообще-то решето можно сделать и линейным.
Задание
Решите 5 первых задач из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34271
Линейное решето Эратосфена*
Наша цель — для каждого числа до (N) посчитать его минимальный простой делитель. Будем хранить его в массиве min_d. Параллельно будем хранить и список всех найденных простых чисел primes – это ровно те числа (x), у которых (min_d[x] = x).
Основное утверждение такое:
Пусть у числа (M) минимальный делитель равен (a). Тогда, если (M) составное, мы хотим вычеркнуть его ровно один раз при обработке числа (frac{M}{a}).
Мы также перебираем число (i) от (2) до (N). Если (min_d[i]) равно 0 (то есть мы не нашли ни один делитель у этого числа еще), значит оно простое – добавим в primes и сделаем (min_d[i] = i).
Далее мы хотим вычеркнуть все числа (i times k) такие, что (k) – это минимальный простой делитель этого числа. Из этого следует, что необходимо и достаточно перебрать (k) в массиве primes, и только до тех пор, пока (k < min_d[i]). Ну и перестать перебирать, если (i times k > N).
Алгоритм пометит все числа по одному разу, поэтому он корректен и работает за (O(N)).
N = 30
primes = []
min_d = [0] * (N + 1)
for i in range(2, N + 1):
if min_d[i] == 0:
min_d[i] = i
primes.append(i)
for p in primes:
if p > min_d[i] or i * p > N:
break
min_d[i * p] = p
print(i, min_d)
print(min_d)
print(primes)2 [0, 0, 2, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
3 [0, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
4 [0, 0, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
5 [0, 0, 2, 3, 2, 5, 2, 0, 2, 3, 2, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0]
6 [0, 0, 2, 3, 2, 5, 2, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0]
7 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 0, 0, 3, 0, 0, 0, 5, 0, 0, 0, 0, 0]
8 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 0, 0, 0, 3, 0, 0, 0, 5, 0, 0, 0, 0, 0]
9 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 5, 0, 3, 0, 0, 0]
10 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 5, 0, 3, 0, 0, 0]
11 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 0, 5, 0, 3, 0, 0, 0]
12 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 0, 3, 0, 0, 0]
13 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 0, 0, 0]
14 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 0]
15 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
16 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
17 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
18 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
19 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
20 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
21 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
22 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
23 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
24 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
25 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
26 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
27 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
28 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
29 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
30 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
[0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]Этот алгоритм работает асимптотически быстрее, чем обычное решето. Но на практике, если писать обычное решето Эратсфена с оптимизациями, то оно оказывается быстрее линейнего. Также линейное решето занимает гораздо больше памяти – ведь в обычном решете можно хранить просто (N) бит, а здесь нам нужно (N) чисел и еще массив primes.
Зато один из «побочных эффектов» алгоритма — он неявно вычисляет факторизацию всех чисел от (1) до (N). Ведь зная минимальный простой делитель любого числа от (1) до (N) можно легко поделить на это число, посмотреть на новый минимальный простой делитель и так далее.
НОД и НОК
Введем два определения.
Наибольший общий делитель (НОД) чисел (a_1, a_2, ldots, a_n) — это максимальное такое число (x), что все (a_i) делятся на (x).
Наименьшее общее кратное (НОК) чисел (a_1, a_2, ldots, a_n) — это минимальное такое число (x), что (x) делится на все (a_i).
Например, * НОД(18, 30) = 6 * НОД(60, 180, 315) = 15 * НОД(1, N) = 1 * НОК(12, 30) = 6 * НОК(1, 2, 3, 4) = 12 * НОК(1, (N)) = (N)
Зачем они нужны? Например, они часто возникают в задачах.
Условие: Есть (N) шестеренок, каждая (i)-ая зацеплена с ((i-1))-ой. (i)-ая шестеренка имеет (a_i) зубчиков. Сколько раз нужно повернуть полносьтю первую шестеренку, чтобы все остальные шестеренки тоже вернулись на изначальное место?
Решение: Когда одна шестеренка крутится на 1 зубчик, все остальные тоже крутятся на один зубчик. Нужно найти минимальное такое число зубчиков (x), что при повороте на него все шестеренки вернутся в изначальное положение, то есть (x) делится на все (a_i), то есть это НОК((a_1, a_2, ldots, a_N)). Ответом будет (frac{x}{a_1}).
Еще пример задачи на применение НОД и НОК:
Условие: Город — это прямоугольник (n) на (m), разделенный на квадраты единичного размера. Вертолет летит из нижнего левого угла в верхний правый по прямой. Вертолет будит людей в квартале, когда он пролетает строго над его внутренностью (границы не считаются). Сколько кварталов разбудит вертолёт?
Решение: Вертолет пересечет по вертикали ((m-1)) границу. С этим ничего не поделать — каждое считается как новое посещение какого-то квартала. По горизонтали то же самое — ((n-1)) переход в новую ячейку будет сделан.
Однако еще есть случай, когда он пересекает одновременно обе границы (то есть пролетает над каким-нибудь углом) — ровно тот случай, когда нового посещения квартала не происходит. Сколько таких будет? Ровно столько, сколько есть целых решений уравнения (frac{n}{m} = frac{x}{y}). Мы как бы составили уравнение движения вертолёта и ищем, в скольки целых точках оно выполняется.
Пусть (t = НОД(n, m)), тогда (n = at, m = bt).
Тогда (frac{n}{m} = frac{a}{b} = frac{x}{y}). Любая дробь с натуральными числителем и знаменателем имеет ровно одно представление в виде несократимой дроби, так что (x) должно делиться на (a), а (y) должно делиться на (b). А значит, как ответ подходят ((a, b), (2a, 2b), (3a, 3b), cdots, ((t-1)a, (t-1)b)). Таких ответов ровно (t = НОД(n, m))
Значит, итоговый ответ: ((n-1) + (m-1) – (t-1)).
Кстати, когда (НОД(a, b) = 1), говорят, что (a) и (b) взаимно просты.
Алгоритм Евклида
Осталось придумать, как искать НОД и НОК. Понятно, что их можно искать перебором, но мы хотим хороший быстрый способ.
Давайте для начала научимся искать (НОД(a, b)).
Мы можем воспользоваться следующим равенством: [НОД(a, b) = НОД(a, b – a), b > a]
Оно доказывается очень просто: надо заметить, что множества общих делителей у пар ((a, b)) и ((a, b – a)) совпадают. Почему? Потому что если (a) и (b) делятся на (x), то и (b-a) делится на (x). И наоборот, если (a) и (b-a) делятся на (x), то и (b) делится на (x). Раз множства общих делитей совпадают, то и максимальный делитель совпадает.
Из этого равенства сразу следует следующее равенство: [НОД(a, b) = НОД(a, b operatorname{%} a), b > a]
(так как (НОД(a, b) = НОД(a, b – a) = НОД(a, b – 2a) = НОД(a, b – 3a) = ldots = НОД(a, b operatorname{%} a)))
Это равенство дает идею следующего рекурсивного алгоритма:
[НОД(a, b) = НОД(b operatorname{%} a, a) = НОД(a operatorname{%} , (b operatorname{%} a), b operatorname{%} a) = ldots]
Например: [НОД(93, 36) = ] [= НОД(36, 93spaceoperatorname{%}36) = НОД(36, 21) = ] [= НОД(21, 15) = ] [= НОД(15, 6) = ] [= НОД(6, 3) = ] [= НОД(3, 0) = 3]
Задание:
Примените алгоритм Евклида и найдите НОД чисел: * 1 и 500000 * 10, 20 * 18, 60 * 55, 34 * 100, 250
По-английски наибольший общий делитель — greatest common divisor. Поэтому вместо НОД будем в коде писать gcd.
def gcd(a, b):
if b == 0:
return a
return gcd(b, a % b)
print(gcd(1, 500000))
print(gcd(10, 20))
print(gcd(18, 60))
print(gcd(55, 34))
print(gcd(100, 250))
print(gcd(2465473782, 12542367456))1
10
6
1
50
6Вообще, в C++ такая функция уже есть в компиляторе g++ — называется __gcd. Если у вас не Visual Studio, то, скорее всего, у вас g++. Вообще, там много всего интересного.
А за сколько оно вообще работает?
Задание
Докажите, что алгоритм Евклида для чисел (N), (M) работает за (O(log(N+M))).
Кстати, интересный факт: самыми плохими входными данными для алгоритма Евклида являются числа Фибоначчи. Именно там и достигается логарифм.
Как выразить НОК через НОД
(НОК(a, b) = frac{ab}{НОД(a, b)})
По этой формуле можно легко найти НОК двух чисел через их произведение и НОД. Почему она верна?
Посмотрим на разложения на простые множители чисел a, b, НОК(a, b), НОД(a, b).
[ a = p_1^{a_1}times p_2^{a_2}timesldotstimes p_n^{a_n} ] [ b = p_1^{b_1}times p_2^{b_2}timesldotstimes p_n^{b_n} ] [ ab = p_1^{a_1+b_1}times p_2^{a_2+b_2}timesldotstimes p_n^{a_n+b_n} ]
Из определений НОД и НОК следует, что их факторизации выглядят так: [ НОД(a, b) = p_1^{min(a_1, b_1)}times p_2^{min(a_2, b_2)}timesldotstimes p_n^{min(a_n, b_n)} ] [ НОК(a, b) = p_1^{max(a_1, b_1)}times p_2^{max(a_2, b_2)}timesldotstimes p_n^{max(a_n, b_n)} ]
Тогда посчитаем (НОД(a, b) times НОК(a, b)): [ НОД(a, b)НОК(a, b) = p_1^{min(a_1, b_1)+max(a_1, b_1)}times p_2^{min(a_2, b_2)+max(a_2, b_2)}timesldotstimes p_n^{min(a_n, b_n)+max(a_n, b_n)} =] [ = p_1^{a_1+b_1}times p_2^{a_2+b_2}timesldotstimes p_n^{a_n+b_n} = ab]
Формула доказана.
Как посчитать НОД/НОК от более чем 2 чисел
Для того, чтобы искать НОД или НОК у более чем двух чисел, достаточно считать их по цепочке:
(НОД(a, b, c, d, ldots) = НОД(НОД(a, b), c, d, ldots))
(НОК(a, b, c, d, ldots) = НОК(НОК(a, b), c, d, ldots))
Почему это верно?
Ну просто множество общих делителей (a) и (b) совпадает с множеством делителей (НОД(a, b)). Из этого следует, что и множество общих делителей (a), (b) и еще каких-то чисел совпадает с множеством общих делителей (НОД(a, b)) и этих же чисел. И раз совпадают множества общих делителей, то и наибольший из них совпадает.
С НОК то же самое, только фразу “множество общих делителей” надо заменить на “множество общих кратных”.
Задание
Решите задачи F, G, H, I из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34271
Расширенный алгоритм Евклида*
Очень важным для математики свойством наибольшего общего делителя является следующий факт:
Для любых целых (a, b) найдутся такие целые (x, y), что (ax + by = d), где (d = gcd(a, b)).
Из этого следует, что существует решение в целых числах, например, у таких уравнений: * (8x + 6y = 2) * (4x – 5y = 1) * (116x + 44y = 4) * (3x + 11y = -1)
Мы сейчас не только докажем, что решения у таких уравнений существуют, но и приведем быстрый алгоритм нахождения этих решений. Здесь нам вновь пригодится алгоритм Евклида.
Рассмотрим один шаг алгоритма Евклида, преобразующий пару ((a, b)) в пару ((b, a operatorname{%} b)). Обозначим (r = a operatorname{%} b), то есть запишем деление с остатком в виде (a = bq + r).
Предположим, что у нас есть решение данного уравнения для чисел (b) и (r) (их наибольший общий делитель, как известно, тоже равен (d)): [bx_0 + ry_0 = d]
Теперь сделаем в этом выражении замену (r = a – bq):
[bx_0 + ry_0 = bx_0 + (a – bq)y_0 = ay_0 + b(x_0 – qy_0)]
Tаким образом, можно взять (x = y_0), а (y = (x_0 – qy_0) = (x_0 – (a operatorname{/} b)y_0)) (здесь (/) обозначает целочисленное деление).
В конце алгоритма Евклида мы всегда получаем пару ((d, 0)). Для нее решение требуемого уравнения легко подбирается — (d * 1 + 0 * 0 = d). Теперь, используя вышесказанное, мы можем идти обратно, при вычислении заменяя пару ((x, y)) (решение для чисел (b) и (a operatorname{%} b)) на пару ((y, x – (a / b)y)) (решение для чисел (a) и (b)).
Это удобно реализовывать рекурсивно:
def extended_gcd(a, b):
if b == 0:
return a, 1, 0
d, x, y = extended_gcd(b, a % b)
return d, y, x - (a // b) * y
a, b = 3, 5
res = extended_gcd(a, b)
print("{3} * {1} + {4} * {2} = {0}".format(res[0], res[1], res[2], a, b))3 * 2 + 5 * -1 = 1Но также полезно и посмотреть, как будет работать расширенный алгоритм Евклида и на каком-нибудь конкретном примере. Пусть мы, например, хотим найти целочисленное решение такого уравнения: [116x + 44y = 4] [(2times44+28)x + 44y = 4] [44(2x+y) + 28x = 4] [44x_0 + 28y_0 = 4] Следовательно, [x = y_0, y = x_0 – 2y_0] Будем повторять такой шаг несколько раз, получим такие уравнения: [116x + 44y = 4] [44x_0 + 28y_0 = 4, x = y_0, y = x_0 – 2y_0] [28x_1 + 16y_1 = 4, x_0 = y_1, y_0 = x_1 – y_1] [16x_2 + 12y_2 = 4, x_1 = y_2, y_1 = x_2 – y_2] [12x_3 + 4y_3 = 4, x_2 = y_3, y_2 = x_3 – y_3] [4x_4 + 0y_4 = 4, x_3 = y_4, y_3 = x_4 – 3 y_4] А теперь свернем обратно: [x_4 = 1, y_4 = 0] [x_3 = 0, y_3 =1] [x_2 = 1, y_2 =-1] [x_1 = -1, y_1 =2] [x_0 = 2, y_0 =-3] [x = -3, y =8]
Действительно, (116times(-3) + 44times8 = 4)
Задание
Решите задачу J из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34273
Операции по модулю
Выражение (a equiv b pmod m) означает, что остатки от деления (a) на (m) и (b) на (m) равны. Это выражение читается как «(a) сравнимо (b) по модулю (m)».
Еще это можно опрделить так: (a) сравнимо c (b) по модулю (m), если ((a – b)) делится на (m).
Все целые числа можно разделить на классы эквивалентности — два числа лежат в одном классе, если они сравнимы по модулю (m). Говорят, что мы работаем в «кольце остатков по модулю (m)», и в нем ровно (m) элементов: (0, 1, 2, cdots, m-1).
Сложение, вычитение и умножение по модулю определяются довольно интуитивно — нужно выполнить соответствующую операцию и взять остаток от деления.
С делением намного сложнее — поделить и взять по модулю не работает. Об этом подробнее поговорим чуть дальше.
a = 30
b = 50
mod = 71
print('{} + {} = {} (mod {})'.format(a, b, (a + b) % mod, mod))
print('{} - {} = {} (mod {})'.format(a, b, (a - b) % mod, mod)) # на C++ это может не работать, так как модуль от отрицательного числа берется странно
print('{} - {} = {} (mod {})'.format(a, b, (a - b + mod) % mod, mod)) # на C++ надо писать так, чтобы брать модулю от гарантированно неотрицательного числа
print('{} * {} = {} (mod {})'.format(a, b, (a * b) % mod, mod))
# print((a / b) % mod) # а как писать это, пока неясно30 + 50 = 9 (mod 71)
30 - 50 = 51 (mod 71)
30 - 50 = 51 (mod 71)
30 * 50 = 9 (mod 71)Задание
Посчитайте: * (2 + 3 pmod 5) * (2 * 3 pmod 5) * (2 ^ 3 pmod 5) * (2 – 4 pmod 5) * (5 + 5 pmod 6) * (2 * 3 pmod 6) * (3 * 3 pmod 6)
Для умножения (в C++) нужно ещё учитывать следующий факт: при переполнении типа всё ломается (разве что если вы используете в качестве модуля степень двойки).
intвмещает до (2^{31} – 1 approx 2 cdot 10^9).long longвмещает до (2^{63} – 1 approx 8 cdot 10^{18}).long long longв плюсах нет, при попытке заиспользовать выдает ошибкуlong long long is too long.- Под некоторыми компиляторами и архитектурами доступен
int128, но не везде и не все функции его поддерживают (например, его нельзя вывести обычными методами).
Зачем нужно считать ответ по модулю
Очень часто в задаче нужно научиться считать число, которое в худшем случае гораздо больше, чем (10^{18}). Тогда, чтобы не заставлять вас писать длинную арифметику, автор задачи часто просит найти ответ по модулю большого числа, обычно (10^9 + 7)
Кстати, вместо того, чтобы писать (1000000007) удобно просто написать (1e9 + 7). (1e9) означает (1 times 10^9)
int mod = 1e9 + 7; # В C++
cout << mod;1000000007N = 1e9 + 7 # В питоне такое число становится float
print(N)
print(int(N))1000000007.0
1000000007Быстрое возведение в степень
Задача: > Даны натуральные числа (a, b, c < 10^9). Найдите (a^b) (mod (c)).
Мы хотим научиться возводить число в большую степень быстро, не просто умножая (a) на себя (b) раз. Требование на модуль здесь дано только для того, чтобы иметь возможность проверить правильность алгоритма для чисел, которые не влезают в int и long long.
Сам алгоритм довольно простой и рекурсивный, постарайтесь его придумать, решая вот такие примеры (прямо решать необязательно, но можно придумать, как посчитать значение этих чисел очень быстро):
- (3^2)
- (3^4)
- (3^8)
- (3^{16})
- (3^{32})
- (3^{33})
- (3^{66})
- (3^{132})
- (3^{133})
- (3^{266})
- (3^{532})
- (3^{533})
- (3^{1066})
Да, здесь специально приведена такая последовательность, в которой каждое следующее число легко считается через предыдущее: его либо нужно умножить на (a=3), либо возвести в квадрат. Так и получается рекурсивный алгоритм:
- (a^0 = 1)
- (a^{2k}=(a^{k})^2)
- (a^{2k+1}=a^{2k}times a)
Нужно только после каждой операции делать mod: * (a^0 pmod c = 1) * (a^{2k} pmod c = (a^{k} pmod c)^2 pmod c) * (a^{2k+1} pmod c = ((a^{2k}pmod c) times a) pmod c)
Этот алгоритм называется быстрое возведение в степень. Он имеет много применений: * в криптографии очень часто надо возводить число в большую степень по модулю * используется для деления по простому модулю (см. далее) * можно быстро перемножать не только числа, но еще и матрицы (используется для динамики, например)
Асимптотика этого алгоритма, очевидно, (O(log c)) – за каждые две итерации число уменьшается хотя бы в 2 раза.
Задание
Решите задачу K из этого контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34271
Задание
Решите как можно больше задач из практического контеста:
https://informatics.msk.ru/mod/statements/view.php?id=34273
Деление по модулю*
Давайте все-таки научимся не только умножать, но и делить по простому модулю. Вот только что это значит?
(a / b) = (a times b^{-1}), где (b^{-1}) – это обратный элемент к (b).
Определение: (b^{-1}) – это такое число, что (bb^{-1} = 1)
Утверждение: в кольце остатков по простому модулю (p) у каждого остатка (кроме 0) существует ровно один обратный элемент.
Например, обратный к (2) по модулю (5) это (3) ((2 times 3 = 1 pmod 5)))
Задание
Найдите обратный элемент к: * числу (3) по модулю (5) * числу (3) по модулю (7) * числу (1) по модулю (7) * числу (2) по модулю (3) * числу (9) по модулю (31)
Давайте докажем это утверждение: надо заметить, что если каждый ненулевой остаток (1, 2, ldots, (p-1)) умножить на ненулевой остаток (a), то получатся числа (a, 2a, ldots, (p-1)a) – и они все разные! Они разные, потому что если (xa = ya), то ((x-y)a = 0), а значит ((x – y) a) делится на (p), (a) – ненулевой остаток, а значит (x = y), и это не разные числа. И из того, что все числа получились разными, это все ненулевые, и их столько же, следует, что это ровно тот же набор чисел, просто в другом порядке!
Из этого следует, что среди этих чисел есть (1), причем ровно один раз. А значит существует ровно один обратный элемент (a^{-1}). Доказательство закончено.
Это здорово, но этот обратный элемент еще хочется быстро находить. Быстрее, чем за (O(p)).
Есть несколько способов это сделать.
Через малую теорему Ферма
Малая теорема Ферма: > (a^{p-1} = 1 pmod p), если (p) – простое, (a neq 0 pmod p)).
Доказательство: В предыдущем пункте мы выяснили, что множества чисел (1, 2, ldots, (p-1)) и (a, 2a, ldots, (p-1)a) совпадают. Из этого следует, что их произведения тоже совпадают по модулю: ((p-1)! = a^{p-1} (p-1)! pmod p).
((p-1)!neq 0 pmod p) а значит на него можно поделить (это мы кстати только в предыдущем пункте доказали, поделить на число – значит умножить на обратный к нему, который существует).
А значит, (a^{p – 1} = 1 pmod p).
Как это применить Осталось заметить, что из малой теоремы Ферма сразу следует, что (a^{p-2}) – это обратный элемент к (a), а значит мы свели задачу к возведению (a) в степень (p-2), что благодаря быстрому возведению в степень мы умеем делать за (O(log p)).
Обобщение У малой теоремы Ферма есть обобщение для составных (p):
Теорема Эйлера: > (a^{varphi(p)} = 1 pmod p), (a) – взаимно просто с (p), а (varphi(p)) – это функция Эйлера (количество чисел, меньших (p) и взаимно простых с (p)).
Доказывается теорема очень похоже, только вместо ненулевых остатков (1, 2, ldots, p-1) нужно брать остатки, взаимно простые с (p). Их как раз не (p-1), а (varphi(p)).
Для нахождения обратного по этой теореме достаточно посчитать функцию Эйлера (varphi(p)) и найти (a^{-1} = a^{varphi(p) – 1}).
Но с этим возникают большие проблемы: посчитать функцию Эйлера сложно. Более того, на предполагаемой невозможности быстро ее посчитать построены некоторые криптографические алгоритм типа RSA. Поэтому быстро делить по составному модулю этим способом не получится.
Через расширенный алгоритм Евклида
Этим способом легко получится делить по любому модулю! Рекомендую.
Пусть мы хотим найти (a^{-1} pmod p), (a) и (p) взаимно простые (а иначе обратного и не будет существовать).
Давайте найдем корни уравнения
[ax + py = 1]
Они есть и находятся расширенным алгоритмом Евклида за (O(log p)), так как (НОД(a, p) = 1), ведь они взаимно простые.
Тогда если взять остаток по модулю (p):
[ax = 1 pmod p]
А значит, найденный (x) и будет обратным элементом к (a).
То есть надо просто найти (x) из решения того уравнения по модулю (p). Можно брать по модулю прямо походу решения уравнения, чтобы случайно не переполниться.
Введение
Числа, которые
нельзя разложить в произведение меньших множителей, называются простыми. Любое
натуральное число, большее 1, является или простым, или составным. Само число 1
не относится ни к простым, ни к составным. Среди четных чисел имеется единственное
простое число – 2. Все остальные простые числа
нечетны.
Интерес к простым числам возник в глубокой древности. Одним из первых проблему
выявления простых чисел поставил древнегреческий ученый Эратосфен, позднее
значительных результатов удалось добиться и другим исследователям, среди
которых выдающимися считаются работы П. Ферма, Л. Эйлера, К. Гаусса, А.
Лежандра, П. Чебышева и ряда других учёных. А такие ли они простые «Простые
числа»? Прежде всего, возникает вопрос о том, конечно ли множество простых
чисел? Если простых чисел бесконечное множество, то возникает другой вопрос:
как они расположены в ряду натуральных чисел? Нет ли для них, например,
формулы? Если эффективной формулы для множества простых чисел нет, то его
следует изучать другими методами. Например, насколько редко могут быть
расположены простые числа? Оказывается, последовательные отрезки
числового ряда, не содержащие ни одного простого числа, могут быть сколь угодно
длинными. Соответственно, возникает следующий вопрос: а какое минимальное
расстояние может быть между двумя простыми числами? В нашей исследовательской
работе мы рассмотрели вышеперечисленные вопросы и постарались найти на них
ответы. Все эти и многие другие вопросы, связанные с простыми числами являются
актуальными и по сей день, так как многие из этих вопросов до сих пор не решены
и тревожат умы ученых-математиков.
1.
Простых чисел бесконечно много. Существует
ли формула для записи простых чисел?
Одним
из свойств простых чисел является утверждение, что простых чисел бесконечно
много ( т.е среди простых чисел нет наибольшего). Это свойство простых
чисел было доказано еще Евклидом. Суть доказательства Евклида такая.
Предположим, что множество простых чисел конечно. Тогда существует наибольшее
простое число, обозначим его через k.
Возьмем произведение всех простых чисел от 1 до k,
обозначим его через m. Тогда m+1
– простое число, большее k. Получили противоречие.
Простые
числа играют огромную роль в математике и криптографии. Вот почему издавна люди
пытаются найти универсальную формулу для нахождения простых чисел. В долгое
время формула считалась формулой
простого числа. Эта квадратный трехчлен Л.Эйлера. Можно ли привести пример
такого натурального числа х, при котором р окажется непростым
числом ? Мы выяснили, что первые 40 значений этого трехчлена( при х=0,1,2,…39)
являются простыми числами. Из 2398 первых значений , принимаемых этим
многочленом , ровно половина – простые
числа. Рассмотри другой способ нахождения простых чисел. Предположим, что нам
требуется найти все простые числа, лежащие на отрезке натурального ряда от 1 до
некоторого числа N, например, от 1
до 100. Способ исключения из этого промежутка всех оставшихся чисел был
известен еще древнегреческому математику Эратосфену и носит название Решето
Эратосфена. Приведем его в немного усовершенствованном виде :
1. Выписать
все нечетные числа от 3 до N.
2. Вычеркнуть
и далее каждое третье
число, затем вычеркнуть и далее каждое пятое
число.
3. Продолжать
этот процесс, пока возможно, выбирая всякий раз первое оставшееся невычеркнутым
число, следующее за тем, кратные которому были вычеркнуты последними.
4. Числа,
которые остались невычеркнутыми, составляют множество всех нечетных простых на
отрезке от 1 до N.
Для
ясности, нужные числа не вычеркнуты, а подчеркнуты.
Для
N=100
имеем следующую таблицу :
|
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
|
23 |
25 |
27 |
29 |
31 |
33 |
35 |
37 |
39 |
41 |
|
43 |
45 |
47 |
49 |
51 |
53 |
55 |
57 |
59 |
61 |
|
63 |
65 |
67 |
69 |
71 |
73 |
75 |
77 |
79 |
81 |
|
83 |
85 |
87 |
89 |
91 |
93 |
95 |
97 |
99 |
все заканчивается после трех проходов, так как
первое, оставшееся невычеркнутым число, следующее за 7, есть 11 и = 121 > 100. Числа, оставшиеся неподчеркнутими, и есть
нечетные простые, меньшие или равные сто. Имеется всего 25 простых чисел на
отрезке натурального ряда от 1 до 100.
По
состоянию на 9 апреля 2015 года, наибольшее известное простое число равняется
и содержит 17 425 170
десятичных цифр. На сегодняшний день поиск простых чисел остается
незавершенным.
2.
Существует как угодно большие промежутки,
где нет простых чисел.
Насколько
редко могут быть расположены простые числа? Оказывается, последовательные
отрезки числового ряда, не содержащие ни одного простого числа, могут быть
сколь угодно длинными.
Теорема.
Существуют столь угодно длинные промежутки, не содержащие ни одного
простого числа.
Доказательсто:
Возьмем
произвольное натуральное число n и рассмотрим отрезок натурального ряда вида (n
+ 1)! + 2, (n + 1)! + 3, …, (n + 1)! + n + 1. Каждое из представленных чисел
составное: первое делится на 2, второе — на 3, третье — на 4 и так далее
…..
3.
.(как назвать ?)
Натуральное
число называется составным, если его можно представить в виде
произведения двух множителей, каждый из которых больше 1. Самое маленькое
составное число – это 4+2*2. А как узнать, будет заданное число составным
или нет? Попробуем ответить на этот вопрос.
Правило1.
Натуральное число составное, если оно делится на некоторое число, отличное от
1. Чтобы проверить, пользуясь указанным правилом, будет ли составным число,
например, 1009, нужно проверить, делится ли оно на все числа из ряда
2,3,4,…1007,1008, т.е совершить 1007 делений! А это утомительное занятие! Его
можно значительно сократить, воспользовавшись правилом:
Правило2.
Каждое составное число N имеет
делитель, больший 1 и такой, что квадрат его не превосходит N.
Воспользовавшись правилом 2, получим =961<1009<1024=
следовательно, если число
1009 составное, то у него есть делитель, содержащийся среди чисел 2,3,4,…31.
Таким образом, количество деление при проверке, является число 1009 составным
или нет, может быть сокращено с 1007 до 30. Разделим 1009 на каждое из чисел
2,3,4,…31. 1009 не делится ни на один из этих делителей, значит, число 1009
составным не является.
Задача1.
Будет ли составным число 11111?
Решение:
Задача2.
Будут ли составными числа +1 ?
Решение:
Задание.
Возьмем какое-нибудь двузначное число, например 12,
удвоим его и припишем справа 0. Получим 240. К результату прибавим исходное
число, получим 252. Умножим это число на 481. В записи произведения повторяется
трижды число 12:
252*481=11212.
Возьмем
другое двузначное число, например 23. Проделаем с ним те же операции:
23*2=46; 460+23=483; 483*481=232323.
Опять
получили шестизначное число, в записи которого трижды повторяется исходное
двузначное число 23. Если проделать этот эксперимент еще несколько раз, взяв,
например, числа: 34, 19, 70 и т.д. опять в записи результата будет трижды
повторяться исходное двузначное число.
Попытайтесь
объяснить этот удивительный факт, связанный со свойствами числа 481.
Решение:
4.
Простые числа – близнецы. Проблема
близнецов.
Простые числа, расстояние
между которыми равно двум, называются числами-близнецами. Первые несколько пар
чисел-близнецов легко перечислить — это (3, 5), (5, 7), (11, 13), (17, 19) и
так далее. Самая большая пара чисел-близнецов, из известных на настоящий момент,
была открыта в декабре 2011 года. Она имеет вид (3756801695685 · 2666669 —
1, 3756801695685 · 2666669 + 1). В десятичной записи каждого из
этих чисел по 200700 знаков. Это, конечно, очень большие числа, и само их
существование ставит такой вот вопрос: конечно ли множество чисел-близнецов?
Этот вопрос, точнее предположение о бесконечности этого множества, носит
название «гипотезы о числах-близнецах». предполагают, что простые
числа-близнецы составляют бесконечное множество. Однако эту гипотезу до сих пор
не удалось ни доказать, ни опровергнуть.
Заключение
Простые числа
являются мощным средством, ускоряющим развитие науки. Количество простых чисел
бесконечно. Эту теорему доказал Евклид в III веке до н.э……..
Алгоритм нахождения простых чисел
Дело было давно, в университете, когда мы начали изучать язык программирования Pascal и домашним заданием стало создание алгоритма нахождения простых чисел.
Алгоритм был придуман и тутже реализован на изучаемом языке. Программа запрашивала у пользователя число N и искала все простые числа до N включительно. После первого успешного теста сразу же возникло непреодолимое желание ввести N = «много». Программа работала, но не так быстро как хотелось бы. Естественно, дело было в многочисленных проверках (порядка N*N/2), поэтому пришлось избавиться от лишних. В итоге получилось 5 похожих алгоритмов каждый из которых работал быстре предыдущего. Недавно захотелось их вспомнить и реализовать, но на этот раз на Python.
Итак, поехали. Первый алгоритм, ударивший в студенческую голову, продемонстрирован в Листинге 1.
# Листинг 1 # вводим N n = input(«n python»># Листинг 2 n = input(«n python»># Листинг 3 n = input(«n python»># Листинг 4 from math import sqrt n = input(«n python»># Листинг 5 from math import sqrt n = input(«n python»># Листинг 6 from math import sqrt n = input(«n python»># Листинг 7 n = input(«n python»># Листинг 8 n = input(«n v-portal» style=»display:none;»>
Как найти простые числа?
Красивые аномалии встречаются в каждом предмете, но если есть одна область красоты, с которой согласится большинство математиков, то это простое число.
Эти числа занимают уникальный пьедестал в математике, особенно в области теории чисел. Великие умы потратили бесчисленные часы для расследования этой проблемы, в том числе такие великие умы, как Пол Эрдос, Г.Х. Харди и Сриниваса Рамануджан, и это лишь некоторые из них. Теперь, прежде чем мы углубимся в различные алгоритмы, чтобы найти простые числа, давайте сначала установим предварительное понимание простых чисел.
Что такое простые числа?
Самое техническое определение простых чисел состоит в том, что это натуральное число больше 1 и может быть получено только путем умножения 1 и самого себя. Если бы понимание натуральных чисел было более интуитивным, то можно было бы сказать, что это числа, которые мы используем для подсчета.
Чтобы понять это более точно, давайте выберем два числа — 5 и 6. Теперь 5 — это число, которое можно получить только умножением на 1 и 5 (само число). Однако, когда мы берем число 6, то замечаем, что его можно получить другим способом, кроме умножения 1 и 6 (само число). Его также можно получить умножением чисел 2 и 3, что означает, что это не простое число. Число, которое не является простым, известно как составное число.
Метод Марена Мерсенна
Метод простого числа Мерсенна — это специальный метод нахождения определенного вида простого числа, известный как простые числа Мерсенна. Название для этого метода происходит от французского монаха Марин Мерсенн, который первым определил его. Простые числа Мерсенна — это те, которые сводимы к виду 2 n -1, где n-простое число. Первые несколько чисел в этом методе являются 2, 3, 5, 7, 13, 17, 19, 31, 61, и 89. Долгое время метод простых чисел Мерсенна представлял собой тяжёлую работу, так как при переходе к более высоким простым числам он был очень трудоемким.
Марен Мерсенн Французский математик
Однако, с появлением компьютеров, они теперь могли выполнять эти вычислительные вычисления, которые раньше делались людьми самым кропотливым и трудоемким образом. Мы определенно достигли более высоких простых чисел Мерсенна и простых чисел на общем уровне. Поиск простых чисел так же активен, как и другие численные поиски, выполняемые компьютерами. Другой числовой поиск, аналогичный движению простых чисел, заключается в добавлении десятичных разрядов к некоторым иррациональным числам, таким как пи (отношение длины окружности к диаметру). Однако непрерывный поиск следующего по величине простого числа существенно сложнее, чем поиск следующей цифры числа Пи.
Даже самые большие компьютеры (суперкомпьютеры) тратят значительное количество времени, чтобы проверить, является ли новое число (которое обычно ошеломляюще огромным) само по себе простым числом, и требуется еще больше времени, чтобы проверить, является ли число основным числом Мерсенна. По этой причине числа Мерсенна представляют большой интерес в области кибербезопасности и криптографии, особенно в отношении шифрования.
В августе 2008 года системный администратор UCLA Эдсон Смит нашел наиболее значимое простое число, известное на тот момент. Смит установил программное обеспечение для Great Internet Mersenne Prime Search (Gimps), проекта распределенных вычислений на добровольной основе. Это число было простым числом Мерсенна длиной 12 978 189 цифр. Чтобы дать представление о том, насколько он велик, на его написание уйдет почти два с половиной месяца, а в случае печати он растянется на 50 км!
Метод простых чисел Ферма
Число Ферма, как и число Мерсенна, представляет собой особый вид простого числа. Название происходит от математика 17-го века и юриста Пьера де Ферма. Число Ферма похоже на число Мерсенна. с одной маленькой поправкой. Давайте возьмем число Ферма Fm, где мы можем определить Fm как 2 m +1. Здесь m снова равно 2, возведенному в степень n или 2 n .
Пьер де Ферма (фр. Pierre de Fermat, 17 августа 1601 — 12 января 1665) — французский математик-самоучка, один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел.
Фермат был твердо убежден в том, что все числа вышеуказанной формы — это простые числа. В дальнейшем он сказал, что он будет производить простые числа для всех целочисленных значений m. Что делает эти числа уникальными и красивыми, но очень хитрыми, так это то, что простые числа становятся чрезвычайно большими очень быстро, даже в пределах первых четырех итераций. Чтобы доказать это, возьмем n в качестве следующих значений, n=0, 1, 2, 3 и 4.
Когда n = 0, m = 2 0 = 1; поэтому F0 = 2 1 + 1 = 2 + 1 = 3, что является простым. Когда n = 1, m = 2 1 = 2; поэтому F1 = 2 2 + 1 = 4 + 1 = 5, что является простым. Когда n = 2, m = 2 2 = 4; следовательно, F2 = 2 4 + 1 = 16 + 1 = 17, что является простым. Когда n = 3, m = 2 3 = 8; следовательно, F3 = 2 8 + 1 = 256 + 1 = 257, что является простым. Когда n = 4, m = 2 4 = 16; следовательно, F4 = 2 16 + 1 = 65536 + 1 = 65537, что является простым числом. Теперь, как вы можете заметить, к тому времени, когда мы достигнем F5, значение достигает 4 294 967 297.
На сегодняшний день мы достигли только F11, даже со всеми лучшими компьютерами и параллельными вычислениями и большой точностью. В конце концов, однако, мы можем сказать, что поиск простых чисел всегда будет идти до бесконечности и дальше!
Теория чисел
Простым называется натуральное число, которое делится только на единицу и на себя. Единица при этом простым числом не считается. Составным числом называют непростое число, которое еще и не единица.
Примеры простых чисел: (2) , (3) , (5) , (179) , (10^9+7) , (10^9+9) .
Примеры составных чисел: (4) , (15) , (2^) .
Еще одно определение простого числа: (N) — простое, если у (N) ровно два делителя. Эти делители при этом равны (1) и (N) .
Проверка на простоту за линию
С точки зрения программирования интересно научиться проверять, является ли число (N) простым. Это очень легко сделать за (O(N)) — нужно просто проверить, делится ли оно хотя бы на одно из чисел (2, 3, 4, ldots, N-1) . (N > 1) является простым только в случае, если оно не делится на на одно из этих чисел.
Проверка на простоту за корень
Алгоритм можно ускорить с (O(N)) до (O(sqrt)) .
Пусть (N = a times b) , причем (a leq b) . Тогда заметим, что (a leq sqrt N leq b) .
Почему? Потому что если (a leq b < sqrt) , то (ab leq b^2 < N) , но (ab = N) . А если (sqrt < a leq b) , то (N < a^2 leq ab) , но (ab = N) .
Иными словами, если число (N) равно произведению двух других, то одно из них не больше корня из (N) , а другое не меньше корня из (N) .
Из этого следует, что если число (N) не делится ни на одно из чисел (2, 3, 4, ldots, lfloorsqrtrfloor) , то оно не делится и ни на одно из чисел (lceilsqrtrceil + 1, ldots, N-2, N-1) , так как если есть делитель больше корня (не равный (N) ), то есть делитель и меньше корня (не равный 1). Поэтому в цикле for достаточно проверять числа не до (N) , а до корня.
Разложение на простые множители
Любое натуральное число можно разложить на произведение простых, и с такой записью очень легко работать при решении задач. Разложение на простые множители еще называют факторизацией.
[11 = 11 = 11^1] [100 = 2 times 2 times 5 times 5 = 2^2 times 5^2] [126 = 2 times 3 times 3 times 7 = 2^1 times 3^2 times 7^1]
Рассмотрим, например, такую задачу:
Условие: Нужно разбить (N) людей на группы равного размера. Нам интересно, какие размеры это могут быть.
Решение: По сути нас просят найти число делителей (N) . Нужно посмотреть на разложение числа (N) на простые множители, в общем виде оно выглядит так:
[N= p_1^ times p_2^ times ldots times p_k^]
Теперь подумаем над этим выражением с точки зрения комбинаторики. Чтобы «сгенерировать» какой-нибудь делитель, нужно подставить в степень (i) -го простого число от 0 до (a_i) (то есть (a_i+1) различное значение), и так для каждого. То есть делитель (N) выглядит ровно так: [M= p_1^ times p_2^ times ldots times p_k^, 0 leq b_i leq a_i] Значит, ответом будет произведение ((a_1+1) times (a_2+1) times ldots times (a_k + 1)) .
Алгоритм разложения на простые множители
Применяя алгоритм проверки числа на простоту, мы умеем легко находить минимальный простой делитель числа N. Ясно, что как только мы нашли простой делитель числа (N) , мы можем число (N) на него поделить и продолжить искать новый минимальный простой делитель.
Будем перебирать простой делитель от (2) до корня из (N) (как и раньше), но в случае, если (N) делится на этот делитель, будем просто на него делить. Причем, возможно, нам понадобится делить несколько раз ( (N) может делиться на большую степень этого простого делителя). Так мы будем набирать простые делители и остановимся в тот момент, когда (N) стало либо (1) , либо простым (и мы остановились, так как дошли до корня из него). Во втором случае надо еще само (N) добавить в ответ.
Напишем алгоритм факторизации:
Задание
За сколько работает этот алгоритм?
Решение
За те же самые (O(sqrt)) . Итераций цикла while с перебором делителя будет не больше, чем (sqrt) . Причем ровно (sqrt) операций будет только в том случае, если (N) — простое.
А итераций деления (N) на делители будет столько, сколько всего простых чисел в факторизации числа (N) . Понятно, что это не больше, чем (O(log)) .
Задание
Докажите, что число (N) имеет не больше, чем (O(log)) простых множителей в факторизации.
Разные свойства простых чисел*
Вообще, про простые числа известно много свойств, но почти все из них очень трудно доказать. Вот еще некоторые из них:
- Простых чисел, меньших (N) , примерно (frac) .
- N-ое простое число равно примерно (Nln N) .
- Простые числа распределены более-менее равномерно. Например, если вам нужно найти какое-то простое число в промежутке, то можно их просто перебрать и проверить — через несколько сотен какое-нибудь найдется.
- Для любого (N ge 2) на интервале ((N, 2N)) всегда найдется простое число (Постулат Бертрана)
- Впрочем, существуют сколь угодно длинные отрезки, на которых простых чисел нет. Самый простой способ такой построить — это начать с (N! + 2) .
- Есть алгоритмы, проверяющие число на простоту намного быстрее, чем за корень. равно примерно (O(sqrt[3])) . Это не математический результат, а чисто эмпирический — не пишите его в асимптотиках.
- Максимальное число делителей у числа на отрезке ([1, 10^5]) — 128
- Максимальное число делителей у числа на отрекзке ([1, 10^9]) — 1344
- Максимальное число делителей у числа на отрезке ([1, 10^]) — 103680
- Наука умеет факторизовать числа за (O(sqrt[4])) , но об этом как-нибудь в другой раз.
- Любое число больше трёх можно представить в виде суммы двух простых (гипотеза Гольдбаха), но это не доказано.
Решето Эратосфена
Часто нужно не проверять на простоту одно число, а найти все простые числа до (N) . В этом случае наивный алгоритм будет работать за (O(Nsqrt N)) , так как нужно проверить на простоту каждое число от 1 до (N) .
Но древний грек Эратосфен предложил делать так:
Запишем ряд чисел от 1 до (N) и будем вычеркивать числа: * делящиеся на 2, кроме самого числа 2 * затем деляющиеся на 3, кроме самого числа 3 * затем на 5, затем на 7, и так далее и все остальные простые до n. Таким образом, все незачеркнутые числа будут простыми — «решето» оставит только их.
Задание
Найдите этим способом на бумажке все простые числа до 50, потом проверьте с программой:
У этого алгоритма можно сразу заметить несколько ускорений.
Во-первых, число (i) имеет смысл перебирать только до корня из (N) , потому что при зачеркивании составных чисел, делящихся на простое (i > sqrt N) , мы ничего не зачеркнем. Почему? Пусть существует составное (M leq N) , которое делится на %i%, и мы его не зачеркнули. Но тогда (i > sqrt N geq sqrt M) , а значит по ранее нами доказанному утверждению (M) должно делиться и на простое число, которое меньше корня. Но это значит, что мы его уже вычеркнули.
Во-вторых, по этой же самое причине (j) имеет смысл перебирать только начиная с (i^2) . Зачем вычеркивать (2i) , (3i) , (4i) , …, ((i-1)i) , если они все уже вычеркнуты, так как мы уже вычеркивали всё, что делится на (2) , (3) , (4) , …, ((i-1)) .
Асимптотика
Такой код будет работать за (O(N log log N)) по причинам, которые мы пока не хотим объяснять формально.
Гармонический ряд
Научимся оценивать асимптотику величины (1 + frac + ldots + frac) , которая нередко встречается в задачах, где фигурирует делимость.
Возьмем (N) равное (2^i — 1) и запишем нашу сумму следующим образом: [left(fracright) + left(frac + fracright) + left(frac + ldots + fracright) + ldots + left(frac> + ldots + fracright)]
Каждое из этих слагаемых имеет вид [frac + ldots + frac — 1> le frac + ldots + frac = 2^j frac = 1]
Таким образом, наша сумма не превосходит (1 + 1 + ldots + 1 = i le 2log_2(2^i — 1)) . Тем самым, взяв любое (N) и дополнив до степени двойки, мы получили асимптотику (O(log N)) .
Оценку снизу можно получить аналогичным образом, оценив каждое такое слагаемое снизу значением (frac) .
Попытка объяснения асимптотики** (для старших классов)
Мы знаем, что гармонический ряд (1 + frac + frac + ldots + frac) это примерно (log N) , а значит [N + frac+ frac+ ldots + fracsim N log N]
А что такое асимптотика решета Эратосфена? Мы как раз ровно (frac
) раз зачеркиваем числа делящиеся на простое число (p) . Если бы все числа были простыми, то мы бы как раз получили (N log N) из формули выше. Но у нас будут не все слагаемые оттуда, только с простым (p) , поэтому посмотрим чуть более точно.
Известно, что простых чисел до (N) примерно (frac) , а значит допустим, что k-ое простое число примерно равно (k ln k) . Тогда
Но вообще-то решето можно сделать и линейным.
Задание
Решите 5 первых задач из этого контеста:
Линейное решето Эратосфена*
Наша цель — для каждого числа до (N) посчитать его минимальный простой делитель. Будем хранить его в массиве min_d. Параллельно будем хранить и список всех найденных простых чисел primes — это ровно те числа (x) , у которых (min_d[x] = x) .
Основное утверждение такое:
Пусть у числа (M) минимальный делитель равен (a) . Тогда, если (M) составное, мы хотим вычеркнуть его ровно один раз при обработке числа (frac) .
Мы также перебираем число (i) от (2) до (N) . Если (min_d[i]) равно 0 (то есть мы не нашли ни один делитель у этого числа еще), значит оно простое — добавим в primes и сделаем (min_d[i] = i) .
Далее мы хотим вычеркнуть все числа (i times k) такие, что (k) — это минимальный простой делитель этого числа. Из этого следует, что необходимо и достаточно перебрать (k) в массиве primes, и только до тех пор, пока (k < min_d[i]) . Ну и перестать перебирать, если (i times k > N) .
Алгоритм пометит все числа по одному разу, поэтому он корректен и работает за (O(N)) .
Этот алгоритм работает асимптотически быстрее, чем обычное решето. Но на практике, если писать обычное решето Эратсфена с оптимизациями, то оно оказывается быстрее линейнего. Также линейное решето занимает гораздо больше памяти — ведь в обычном решете можно хранить просто (N) бит, а здесь нам нужно (N) чисел и еще массив primes.
Зато один из «побочных эффектов» алгоритма — он неявно вычисляет факторизацию всех чисел от (1) до (N) . Ведь зная минимальный простой делитель любого числа от (1) до (N) можно легко поделить на это число, посмотреть на новый минимальный простой делитель и так далее.
НОД и НОК
Введем два определения.
Наибольший общий делитель (НОД) чисел (a_1, a_2, ldots, a_n) — это максимальное такое число (x) , что все (a_i) делятся на (x) .
Наименьшее общее кратное (НОК) чисел (a_1, a_2, ldots, a_n) — это минимальное такое число (x) , что (x) делится на все (a_i) .
Например, * НОД(18, 30) = 6 * НОД(60, 180, 315) = 15 * НОД(1, N) = 1 * НОК(12, 30) = 6 * НОК(1, 2, 3, 4) = 12 * НОК(1, (N) ) = (N)
Зачем они нужны? Например, они часто возникают в задачах.
Условие: Есть (N) шестеренок, каждая (i) -ая зацеплена с ((i-1)) -ой. (i) -ая шестеренка имеет (a_i) зубчиков. Сколько раз нужно повернуть полносьтю первую шестеренку, чтобы все остальные шестеренки тоже вернулись на изначальное место?
Решение: Когда одна шестеренка крутится на 1 зубчик, все остальные тоже крутятся на один зубчик. Нужно найти минимальное такое число зубчиков (x) , что при повороте на него все шестеренки вернутся в изначальное положение, то есть (x) делится на все (a_i) , то есть это НОК( (a_1, a_2, ldots, a_N) ). Ответом будет (frac) .
Еще пример задачи на применение НОД и НОК:
Условие: Город — это прямоугольник (n) на (m) , разделенный на квадраты единичного размера. Вертолет летит из нижнего левого угла в верхний правый по прямой. Вертолет будит людей в квартале, когда он пролетает строго над его внутренностью (границы не считаются). Сколько кварталов разбудит вертолёт?
Решение: Вертолет пересечет по вертикали ((m-1)) границу. С этим ничего не поделать — каждое считается как новое посещение какого-то квартала. По горизонтали то же самое — ((n-1)) переход в новую ячейку будет сделан.
Однако еще есть случай, когда он пересекает одновременно обе границы (то есть пролетает над каким-нибудь углом) — ровно тот случай, когда нового посещения квартала не происходит. Сколько таких будет? Ровно столько, сколько есть целых решений уравнения (frac= frac) . Мы как бы составили уравнение движения вертолёта и ищем, в скольки целых точках оно выполняется.
Пусть (t = НОД(n, m)) , тогда (n = at, m = bt) .
Значит, итоговый ответ: ((n-1) + (m-1) — (t-1)) .
Кстати, когда (НОД(a, b) = 1) , говорят, что (a) и (b) взаимно просты.
Алгоритм Евклида
Осталось придумать, как искать НОД и НОК. Понятно, что их можно искать перебором, но мы хотим хороший быстрый способ.
Давайте для начала научимся искать (НОД(a, b)) .
Мы можем воспользоваться следующим равенством: [НОД(a, b) = НОД(a, b — a), b > a]
Оно доказывается очень просто: надо заметить, что множества общих делителей у пар ((a, b)) и ((a, b — a)) совпадают. Почему? Потому что если (a) и (b) делятся на (x) , то и (b-a) делится на (x) . И наоборот, если (a) и (b-a) делятся на (x) , то и (b) делится на (x) . Раз множства общих делитей совпадают, то и максимальный делитель совпадает.
Из этого равенства сразу следует следующее равенство: [НОД(a, b) = НОД(a, b operatorname a), b > a]
(так как (НОД(a, b) = НОД(a, b — a) = НОД(a, b — 2a) = НОД(a, b — 3a) = ldots = НОД(a, b operatorname a)) )
Это равенство дает идею следующего рекурсивного алгоритма:
[НОД(a, b) = НОД(b operatorname a, a) = НОД(a operatorname , (b operatorname a), b operatorname a) = ldots]
Например: [НОД(93, 36) = ] [= НОД(36, 93spaceoperatorname36) = НОД(36, 21) = ] [= НОД(21, 15) = ] [= НОД(15, 6) = ] [= НОД(6, 3) = ] [= НОД(3, 0) = 3]
Задание:
Примените алгоритм Евклида и найдите НОД чисел: * 1 и 500000 * 10, 20 * 18, 60 * 55, 34 * 100, 250
По-английски наибольший общий делитель — greatest common divisor. Поэтому вместо НОД будем в коде писать gcd.
Вообще, в C++ такая функция уже есть в компиляторе g++ — называется __gcd . Если у вас не Visual Studio, то, скорее всего, у вас g++ . Вообще, там много всего интересного.
А за сколько оно вообще работает?
Задание
Докажите, что алгоритм Евклида для чисел (N) , (M) работает за (O(log(N+M))) .
Кстати, интересный факт: самыми плохими входными данными для алгоритма Евклида являются числа Фибоначчи. Именно там и достигается логарифм.
Как выразить НОК через НОД
По этой формуле можно легко найти НОК двух чисел через их произведение и НОД. Почему она верна?
Посмотрим на разложения на простые множители чисел a, b, НОК(a, b), НОД(a, b).
[ a = p_1^times p_2^timesldotstimes p_n^ ] [ b = p_1^times p_2^timesldotstimes p_n^ ] [ ab = p_1^times p_2^timesldotstimes p_n^ ]
Из определений НОД и НОК следует, что их факторизации выглядят так: [ НОД(a, b) = p_1^times p_2^timesldotstimes p_n^ ] [ НОК(a, b) = p_1^times p_2^timesldotstimes p_n^ ]
Как посчитать НОД/НОК от более чем 2 чисел
Для того, чтобы искать НОД или НОК у более чем двух чисел, достаточно считать их по цепочке:
Почему это верно?
Ну просто множество общих делителей (a) и (b) совпадает с множеством делителей (НОД(a, b)) . Из этого следует, что и множество общих делителей (a) , (b) и еще каких-то чисел совпадает с множеством общих делителей (НОД(a, b)) и этих же чисел. И раз совпадают множества общих делителей, то и наибольший из них совпадает.
С НОК то же самое, только фразу “множество общих делителей” надо заменить на “множество общих кратных”.
Задание
Решите задачи F, G, H, I из этого контеста:
Расширенный алгоритм Евклида*
Очень важным для математики свойством наибольшего общего делителя является следующий факт:
Для любых целых (a, b) найдутся такие целые (x, y) , что (ax + by = d) , где (d = gcd(a, b)) .
Из этого следует, что существует решение в целых числах, например, у таких уравнений: * (8x + 6y = 2) * (4x — 5y = 1) * (116x + 44y = 4) * (3x + 11y = -1)
Мы сейчас не только докажем, что решения у таких уравнений существуют, но и приведем быстрый алгоритм нахождения этих решений. Здесь нам вновь пригодится алгоритм Евклида.
Рассмотрим один шаг алгоритма Евклида, преобразующий пару ((a, b)) в пару ((b, a operatorname b)) . Обозначим (r = a operatorname b) , то есть запишем деление с остатком в виде (a = bq + r) .
Предположим, что у нас есть решение данного уравнения для чисел (b) и (r) (их наибольший общий делитель, как известно, тоже равен (d) ): [bx_0 + ry_0 = d]
Теперь сделаем в этом выражении замену (r = a — bq) :
[bx_0 + ry_0 = bx_0 + (a — bq)y_0 = ay_0 + b(x_0 — qy_0)]
Tаким образом, можно взять (x = y_0) , а (y = (x_0 — qy_0) = (x_0 — (a operatorname >b)y_0)) (здесь (/) обозначает целочисленное деление).
В конце алгоритма Евклида мы всегда получаем пару ((d, 0)) . Для нее решение требуемого уравнения легко подбирается — (d * 1 + 0 * 0 = d) . Теперь, используя вышесказанное, мы можем идти обратно, при вычислении заменяя пару ((x, y)) (решение для чисел (b) и (a operatorname b) ) на пару ((y, x — (a / b)y)) (решение для чисел (a) и (b) ).
Это удобно реализовывать рекурсивно:
Но также полезно и посмотреть, как будет работать расширенный алгоритм Евклида и на каком-нибудь конкретном примере. Пусть мы, например, хотим найти целочисленное решение такого уравнения: [116x + 44y = 4] [(2times44+28)x + 44y = 4] [44(2x+y) + 28x = 4] [44x_0 + 28y_0 = 4] Следовательно, [x = y_0, y = x_0 — 2y_0] Будем повторять такой шаг несколько раз, получим такие уравнения: [116x + 44y = 4] [44x_0 + 28y_0 = 4, x = y_0, y = x_0 — 2y_0] [28x_1 + 16y_1 = 4, x_0 = y_1, y_0 = x_1 — y_1] [16x_2 + 12y_2 = 4, x_1 = y_2, y_1 = x_2 — y_2] [12x_3 + 4y_3 = 4, x_2 = y_3, y_2 = x_3 — y_3] [4x_4 + 0y_4 = 4, x_3 = y_4, y_3 = x_4 — 3 y_4] А теперь свернем обратно: [x_4 = 1, y_4 = 0] [x_3 = 0, y_3 =1] [x_2 = 1, y_2 =-1] [x_1 = -1, y_1 =2] [x_0 = 2, y_0 =-3] [x = -3, y =8]
Действительно, (116times(-3) + 44times8 = 4)
Задание
Решите задачу J из этого контеста:
Операции по модулю
Выражение (a equiv b pmod m) означает, что остатки от деления (a) на (m) и (b) на (m) равны. Это выражение читается как « (a) сравнимо (b) по модулю (m) ».
Еще это можно опрделить так: (a) сравнимо c (b) по модулю (m) , если ((a — b)) делится на (m) .
Все целые числа можно разделить на классы эквивалентности — два числа лежат в одном классе, если они сравнимы по модулю (m) . Говорят, что мы работаем в «кольце остатков по модулю (m) », и в нем ровно (m) элементов: (0, 1, 2, cdots, m-1) .
Сложение, вычитение и умножение по модулю определяются довольно интуитивно — нужно выполнить соответствующую операцию и взять остаток от деления.
С делением намного сложнее — поделить и взять по модулю не работает. Об этом подробнее поговорим чуть дальше.
Задание
Посчитайте: * (2 + 3 pmod 5) * (2 * 3 pmod 5) * (2 ^ 3 pmod 5) * (2 — 4 pmod 5) * (5 + 5 pmod 6) * (2 * 3 pmod 6) * (3 * 3 pmod 6)
Для умножения (в C++) нужно ещё учитывать следующий факт: при переполнении типа всё ломается (разве что если вы используете в качестве модуля степень двойки).
- int вмещает до (2^ — 1 approx 2 cdot 10^9) .
- long long вмещает до (2^ — 1 approx 8 cdot 10^) .
- long long long в плюсах нет, при попытке заиспользовать выдает ошибку long long long is too long .
- Под некоторыми компиляторами и архитектурами доступен int128 , но не везде и не все функции его поддерживают (например, его нельзя вывести обычными методами).
Зачем нужно считать ответ по модулю
Очень часто в задаче нужно научиться считать число, которое в худшем случае гораздо больше, чем (10^) . Тогда, чтобы не заставлять вас писать длинную арифметику, автор задачи часто просит найти ответ по модулю большого числа, обычно (10^9 + 7)
Кстати, вместо того, чтобы писать (1000000007) удобно просто написать (1e9 + 7) . (1e9) означает (1 times 10^9)
Быстрое возведение в степень
Задача: > Даны натуральные числа (a, b, c < 10^9) . Найдите (a^b) (mod (c) ).
Мы хотим научиться возводить число в большую степень быстро, не просто умножая (a) на себя (b) раз. Требование на модуль здесь дано только для того, чтобы иметь возможность проверить правильность алгоритма для чисел, которые не влезают в int и long long.
Сам алгоритм довольно простой и рекурсивный, постарайтесь его придумать, решая вот такие примеры (прямо решать необязательно, но можно придумать, как посчитать значение этих чисел очень быстро):
- (3^2)
- (3^4)
- (3^8)
- (3^)
- (3^)
- (3^)
- (3^)
- (3^)
- (3^)
- (3^)
- (3^)
- (3^)
- (3^)
Да, здесь специально приведена такая последовательность, в которой каждое следующее число легко считается через предыдущее: его либо нужно умножить на (a=3) , либо возвести в квадрат. Так и получается рекурсивный алгоритм:
- (a^0 = 1)
- (a^=(a^)^2)
- (a^=a^times a)
Нужно только после каждой операции делать mod: * (a^0 pmod c = 1) * (a^ pmod c = (a^ pmod c)^2 pmod c) * (a^ pmod c = ((a^pmod c) times a) pmod c)
Этот алгоритм называется быстрое возведение в степень. Он имеет много применений: * в криптографии очень часто надо возводить число в большую степень по модулю * используется для деления по простому модулю (см. далее) * можно быстро перемножать не только числа, но еще и матрицы (используется для динамики, например)
Асимптотика этого алгоритма, очевидно, (O(log c)) — за каждые две итерации число уменьшается хотя бы в 2 раза.
Задание
Решите задачу K из этого контеста:
Задание
Решите как можно больше задач из практического контеста:
Деление по модулю*
Давайте все-таки научимся не только умножать, но и делить по простому модулю. Вот только что это значит?
(a / b) = (a times b^) , где (b^) — это обратный элемент к (b) .
Определение: (b^) — это такое число, что (bb^ = 1)
Утверждение: в кольце остатков по простому модулю (p) у каждого остатка (кроме 0) существует ровно один обратный элемент.
Например, обратный к (2) по модулю (5) это (3) ( (2 times 3 = 1 pmod 5) ))
Задание
Найдите обратный элемент к: * числу (3) по модулю (5) * числу (3) по модулю (7) * числу (1) по модулю (7) * числу (2) по модулю (3) * числу (9) по модулю (31)
Давайте докажем это утверждение: надо заметить, что если каждый ненулевой остаток (1, 2, ldots, (p-1)) умножить на ненулевой остаток (a) , то получатся числа (a, 2a, ldots, (p-1)a) — и они все разные! Они разные, потому что если (xa = ya) , то ((x-y)a = 0) , а значит ((x — y) a) делится на (p) , (a) — ненулевой остаток, а значит (x = y) , и это не разные числа. И из того, что все числа получились разными, это все ненулевые, и их столько же, следует, что это ровно тот же набор чисел, просто в другом порядке!
Из этого следует, что среди этих чисел есть (1) , причем ровно один раз. А значит существует ровно один обратный элемент (a^) . Доказательство закончено.
Это здорово, но этот обратный элемент еще хочется быстро находить. Быстрее, чем за (O(p)) .
Есть несколько способов это сделать.
Через малую теорему Ферма
Малая теорема Ферма: > (a^ = 1 pmod p) , если (p) — простое, (a neq 0 pmod p) ).
Доказательство: В предыдущем пункте мы выяснили, что множества чисел (1, 2, ldots, (p-1)) и (a, 2a, ldots, (p-1)a) совпадают. Из этого следует, что их произведения тоже совпадают по модулю: ((p-1)! = a^ (p-1)! pmod p) .
((p-1)!neq 0 pmod p) а значит на него можно поделить (это мы кстати только в предыдущем пункте доказали, поделить на число — значит умножить на обратный к нему, который существует).
А значит, (a^
= 1 pmod p) .
Как это применить Осталось заметить, что из малой теоремы Ферма сразу следует, что (a^) — это обратный элемент к (a) , а значит мы свели задачу к возведению (a) в степень (p-2) , что благодаря быстрому возведению в степень мы умеем делать за (O(log p)) .
Обобщение У малой теоремы Ферма есть обобщение для составных (p) :
Теорема Эйлера: > (a^ = 1 pmod p) , (a) — взаимно просто с (p) , а (varphi(p)) — это функция Эйлера (количество чисел, меньших (p) и взаимно простых с (p) ).
Доказывается теорема очень похоже, только вместо ненулевых остатков (1, 2, ldots, p-1) нужно брать остатки, взаимно простые с (p) . Их как раз не (p-1) , а (varphi(p)) .
Для нахождения обратного по этой теореме достаточно посчитать функцию Эйлера (varphi(p)) и найти (a^ = a^) .
Но с этим возникают большие проблемы: посчитать функцию Эйлера сложно. Более того, на предполагаемой невозможности быстро ее посчитать построены некоторые криптографические алгоритм типа RSA. Поэтому быстро делить по составному модулю этим способом не получится.
Через расширенный алгоритм Евклида
Этим способом легко получится делить по любому модулю! Рекомендую.
Пусть мы хотим найти (a^ pmod p) , (a) и (p) взаимно простые (а иначе обратного и не будет существовать).
Давайте найдем корни уравнения
Они есть и находятся расширенным алгоритмом Евклида за (O(log p)) , так как (НОД(a, p) = 1) , ведь они взаимно простые.
Тогда если взять остаток по модулю (p) :
А значит, найденный (x) и будет обратным элементом к (a) .
То есть надо просто найти (x) из решения того уравнения по модулю (p) . Можно брать по модулю прямо походу решения уравнения, чтобы случайно не переполниться.
Простые числа — это натуральные числа, больше единицы, которые делятся без остатка только на 1 и на само себя. Например: 2, 3, 5, 7, 11, 13, 17, 19, 23… Единица не является ни простым числом, ни составным.
Последовательность простых чисел начинается с 2 и является бесконечной; наименьшее простое число — это 2 (делится на 1 и на самого себя).
Составные числа — это натуральные числа, у которых есть больше двух делителей (1, оно само и например, 2 и/или 3); это противоположность простым числам. Например: 4, 6, 9, 12 (все делятся на 2, на 3, на 1 и на само себя).
Все натуральные числа считаются либо простыми, либо составными (кроме 1).
Натуральные числа — это те числа, которые возникли натуральным образом при счёте предметов; например: 1, 2, 3, 4… (нет ни дробей, ни 0, ни чисел ниже 0).
Зачастую множество простых чисел в математике обозначается буквой P.
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 |
| 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 |
| 113 | 127 | 131 | 137 | 139 | 149 |
151 |
157 |
163 |
167 |
|
173 |
179 |
181 |
191 |
193 |
197 |
199 |
211 |
223 |
227 |
|
229 |
233 |
239 |
241 |
251 |
257 |
263 |
269 |
271 |
277 |
|
281 |
283 |
293 |
307 |
311 |
313 |
317 |
331 |
337 |
347 |
|
349 |
353 |
359 |
367 |
373 |
379 |
383 |
389 |
397 |
401 |
|
409 |
419 |
421 |
431 |
433 |
439 |
443 |
449 |
457 |
461 |
|
463 |
467 |
479 |
487 |
491 |
499 |
503 |
509 |
521 |
523 |
|
541 |
547 |
557 |
563 |
569 |
571 |
577 |
587 |
593 |
599 |
|
601 |
607 |
613 |
617 |
619 |
631 |
641 |
643 |
647 |
653 |
|
659 |
661 |
673 |
677 |
683 |
691 |
701 |
709 |
719 |
727 |
|
733 |
739 |
743 |
751 |
757 |
761 |
769 |
773 |
787 |
797 |
|
809 |
811 |
821 |
823 |
827 |
829 |
839 |
853 |
857 |
859 |
|
863 |
877 |
881 |
883 |
887 |
907 |
911 |
919 |
929 |
937 |
|
941 |
947 |
953 |
967 |
971 |
977 |
983 |
991 | 997 |
Как определить, является ли число простым?
Очень простой способ понять, является ли число простым — нужно его разделить на простые числа и посмотреть, получится ли целое число. Сначала нужно попробовать его разделить на 2 и/или на 3. Если получилось целое число, то оно не является простым.
Если после первого деления не получилось целого числа, значит нужно попробовать разделить его на другие простые числа: 5, 7, 11 и т. д. (на 9 делить не нужно, т. к. это не простое число и оно делится на 3, а на него вы уже делили).
Более структурированный метод — это решето Эратосфена.
Решето Эратосфена
Это алгоритм поиска простых чисел. Для этого нужно:
- Записать все числа от 1 до n (например, записываются все числа от 1 до 100, если нужны все простые числа между ними);
- Вычеркнуть все числа, которые делятся на 2 (кроме 2);
- Вычеркнуть все числа, которые делятся на 3 (кроме 3);
- И так далее по порядку со всеми невычеркнутыми числами до числа n (после 3 это 5, 7, 11, 13, 17 и т. д.).
Те числа, которые не будут вычеркнуты в конце этого процесса, являются простыми.
Взаимно простые числа
Это натуральные числа, у которых 1 — это единственный общий делитель. Например:
- 14 (это 2 х 7) и 15 (это 3 х 5), единственный общий делитель — 1; если числа следуют одно за другим (как 13 и 12 либо 10 и 11), то они всегда будут взаимно простыми;
- 7 (это 7 х 1) и 11 (это 11 х 1) — это два простых числа, а значит единственный общий делитель всегда будет только единица, простые числа всегда являются взаимно простыми;
- или 30 и 48 не являются взаимно простыми, т. к. 6 х 5 = 30 и 6 х 8 = 48 и 6 — это наибольший общий делитель, т. е.: НОД (30; 48) = 6.
Число Мерсенна
Простое число Мерсенна — это простое число вида:
До 1536 г. многие считали, что числа такого вида были все простыми, пока математик Ульрих Ригер не доказал, что 2 (^11) – 1 = 2047 было составным (23 x 89). Затем появились и другие составные числа (p = 23, 29, 31, 37 и др.).
Например, для p = 23 это 2 (^23) – 1 = 8 388 607; И 47 x 178481 = 8 388 607, значит оно составное.
Почему 1 не является простым числом?
Российские математики Боревич и Шафаревич в своей знаменитой работе “Теория чисел” (1964 г.) определяют простое число как p (элемент кольца D), не равен ни 0, ни 1. И p можно называть простым числом, если его невозможно разложить на множители ab (т.е. p = ab), притом ни один из них не является единицей в D. Так как 1 невозможно представить ни в одном, ни в другом виде, 1 не считается ни простым числом, ни составным.
Почему 4 не является простым числом?
Простое число — это натуральное число, больше единицы, которое делится без остатка на 1 и на само себя. Т. к. 4 можно разделить на 1, на 2 и на 4, из-за деления на 2 оно не является простым.
Самое большое простое число
21 декабря 2018 года Great Internet Mersenne Prime Search (проект, целью которого является открытие новых простых чисел Мерсенна) обнаружил новое самое большое известное простое число:
Новое простое число также именуется M82589933 и в нём более чем на полтора миллиона цифр больше, чем в предыдущем (найденном годом ранее).
Узнайте про Рациональные числа и Натуральные числа.