Как найти простое число в пайтоне

Given a positive integer N, The task is to write a Python program to check if the number is Prime or not in Python.

Examples: 

Input:  n = 11
Output: True


Input:  n = 1
Output: False

Explanation: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. The first few prime numbers are {2, 3, 5, 7, 11, ….}. 

Prime Number Program in Python 

The idea to solve this problem is to iterate through all the numbers starting from 2 to (N/2) using a for loop and for every number check if it divides N. If we find any number that divides, we return false. If we did not find any number between 2 and N/2 which divides N then it means that N is prime and we will return True.

11 is a prime number

Time complexity: O(n)
Auxiliary space: O(1)

Fastest Algorithm to Find Prime Numbers

Instead of checking till n, we can check till √n because a larger factor of n must be a multiple of a smaller factor that has been already checked. Now let’s see the code for the first optimization method ( i.e. checking till √n )

Time complexity: O(sqrt(n))
Auxiliary space: O(1)

Check Prime Numbers Using recursion

We can also find the number prime or not using recursion. We can use the exact logic shown in method 2 but in a recursive way.

Time complexity: O(sqrt(n))
Auxiliary space: O(sqrt(n))

Check the Prime Trial Division Method

Time complexity: O(sqrt(n))
Auxiliary space: O(sqrt(n))

RECOMMENDED ARTICLE – Analysis of Different Methods to find Prime Number in Python

Using a while loop to check divisibility:

Approach:

Initialize a variable i to 2.
While i squared is less than or equal to n, check if n is divisible by i.
If n is divisible by i, return False.
Otherwise, increment i by 1.
If the loop finishes without finding a divisor, return True.

Time Complexity: O(sqrt(n))
Auxiliary Space: O(1)

METHOD:USING MATH

APPROACH:

The code implements a basic approach to check if a number is prime or not, by traversing all the numbers from 2 to sqrt(n)+1 and checking if n is divisible by any of those numbers.

ALGORITHM:

1.Check if the given number n is less than or equal to 1, if yes, return False.
2.Traverse all numbers in the range of 2 to sqrt(n)+1.
3.Check if n is divisible by any of the numbers from 2 to sqrt(n)+1, if yes, return False.
4.If n is not divisible by any of the numbers from 2 to sqrt(n)+1, return True.
 

Time complexity: O(sqrt(n))
The time complexity of the code is O(sqrt(n)) because we traverse all numbers in the range of 2 to sqrt(n)+1 to check if n is divisible by any of them.

Auxiliary Space: O(1)
The space complexity of the code is O(1) because we are only using a constant amount of memory to store the input number n and the loop variables.

Method: Using sympy.isprime() method

In the sympy module, we can test whether a given number n is prime or not using sympy.isprime() function. For n < 2⁶⁴ the answer is definitive; larger n values have a small probability of actually being pseudoprimes.

N.B.: Negative numbers (e.g. -13) are not considered prime number.

Syntax: 

sympy.isprime()

Output

False
True
True

Time Complexity: O(sqrt(n)), where n is the input number.
Auxiliary Space: O(1)

Last Updated :
09 May, 2023

Like Article

Save Article

В этом руководстве вы узнаете, как написать программу на Python для проверки, является ли число простым или нет.

Если вы когда-либо проходили тесты по программированию, вы сталкивались с математическим вопросом в тесте на простоту или на проверку того, является ли число простым. И в течение следующих нескольких минут вы научитесь придумывать оптимальное решение этого вопроса.

В этом уроке вы:

• повторить основы простых чисел,
• написать код Python, чтобы проверить, является ли число простым, и
• оптимизируйте его дальше, чтобы получить алгоритм времени выполнения O (√ n).

Для всего этого и многого другого, давайте начнем.

Что такое простое число?

Начнем с рассмотрения основ простых чисел.

В теории чисел натуральное число n называется основной если у него ровно два делителя: 1 и само число (n). Вспомните из школьной математики: говорят, что число i является делителем числа n, если i делит n без остатка. ✅

В следующей таблице перечислены несколько чисел, все их множители и являются ли они простыми.

nFactorsIs Prime?11Нет21, 2Да31, 3Да41, 2, 4Нет71, 7Да151, 3, 5, 15Нет

Из приведенной выше таблицы мы можем записать следующее:

• 2 — наименьшее простое число.
• 1 является множителем каждого числа.
• Каждое число n само по себе является множителем.

Итак, 1 и n — тривиальные множители для любого числа n. И у простого числа не должно быть других делителей, кроме этих двух.

Это означает, что при переходе от 2 к n – 1 вы не сможете найти нетривиальный множитель, который делит n без остатка.

Алгоритм O (n) для проверки того, является ли число простым в Python

В этом разделе давайте формализуем описанный выше подход в виде функции Python.

Вы можете перебрать все числа от 2 до n – 1, используя объект range() в Python.

В Python range(start, stop, step) возвращает объект диапазона. Затем вы можете выполнить итерацию по объекту диапазона, чтобы получить последовательность от начала до конца -1 с шагом шага.

Поскольку нам нужен набор целых чисел от 2 до n-1, мы можем указать диапазон (2, n) и использовать его вместе с циклом for.

Вот что мы хотели бы сделать:

• Если вы найдете число, которое делит n нацело без остатка, вы можете сразу сделать вывод, что это число не простое.

• Если вы перебрали весь диапазон чисел от 2 до n – 1 и не нашли числа, которое делит n без остатка, то это число простое.

Используя вышеизложенное, мы можем пойти дальше и определить функцию is_prime() следующим образом.

def is_prime(n):
  for i in range(2,n):
    if (n%i) == 0:
      return False
  return True

Давайте теперь разберем приведенное выше определение функции.

• Приведенная выше функция is_prime() принимает в качестве аргумента положительное целое число n.
• Если вы найдете множитель в указанном диапазоне (2, n-1), функция вернет False, так как число не является простым.
• И он возвращает True, если вы проходите весь цикл, не найдя множителя.

Далее давайте вызовем функцию с аргументами и проверим правильность вывода.

is_prime(2)
# True

is_prime(8)
# False

is_prime(9)
# False

is_prime(11)
# True

В приведенном выше выводе вы видите, что 2 и 11 — простые числа (функция возвращает True). И 8, и 9 не простые (функция возвращает False).

Как оптимизировать функцию Python is_prime()

Мы можем сделать небольшую оптимизацию здесь. Обратите внимание на список факторов в таблице ниже.

NumberFactors61, 2, 3, 6101, 2, 5, 10181, 2, 3, 6, 9, 18

Итак, мы видим, что единственный множитель n, который больше n/2, — это сам n.

Таким образом, это означает, что вам не нужно зацикливаться до n – 1. Вместо этого вы можете запускать цикл только до n/2.

Если вы не найдете нетривиальный множитель до n/2, вы не сможете найти и множитель выше n/2.

Теперь давайте изменим функцию is_prime() для проверки факторов в диапазоне (2, n/2)

def is_prime(n):
  for i in range(2,int(n/2)):
    if (n%i) == 0:
      return False
  return True

Давайте продолжим и проверим вывод с помощью нескольких вызовов функций.

is_prime(9)
# False

is_prime(11)
# True

Хотя может показаться, что мы оптимизировали, этот алгоритм не эффективнее предыдущего с точки зрения сложности выполнения. На самом деле, они оба имеют сложность выполнения O(n): пропорциональную значению n или линейную по n.

Можем ли мы сделать лучше? Да мы можем!

▶️ Перейдите к следующему разделу, чтобы определить, как улучшить временную сложность тестирования простых чисел.

Алгоритм O(√n) для проверки простого числа в Python

Бывает, что множители числа встречаются парами.

Если a — фактор числа n, то также существует фактор b такой, что axb = n, или просто ab = n.

Давайте проверим это на примере.

В таблице ниже показаны множители числа 18, встречающиеся парами. Вы можете проверить то же самое для еще нескольких номеров, если хотите.

Также обратите внимание, что √18 примерно равно 4,24.

А среди множителей, встречающихся парами (а, b), видно, что если а меньше 4,24, то b больше 4,24 — в этом примере (2, 18) и (3, 6).

Факторы 18 в парах

На рисунке ниже показаны множители 18, нанесенные на числовую прямую.

Если число n является полным квадратом, вы будете иметь a = b = √n в качестве одного из множителей.

▶️ Посмотрите на множители 36 в таблице ниже. Поскольку 36 — полный квадрат, a = b = 6 — один из множителей. Для всех остальных пар факторов (a, b) выполняется a < 6 и b > 6.

Факторы 36 в парах

Подводя итог, имеем следующее:

• Каждое число n можно записать как n = axb
• Если n — полный квадрат, то a = b = √n.
• А если a < b, то a < √n и b > √n.
• В противном случае, если a > b, то a > √n и b < √n.

Таким образом, вместо того, чтобы перебирать все целые числа до n/2, вы можете выбрать до √n. И это намного эффективнее, чем наш предыдущий подход.

Как изменить алгоритм is_prime() на O(√n)

Приступим к оптимизации функции для проверки простых чисел в Python.

import math
def is_prime(n):
  for i in range(2,int(math.sqrt(n))+1):
    if (n%i) == 0:
      return False
  return True

Теперь давайте разберем приведенное выше определение функции:

• Чтобы вычислить квадратный корень числа, давайте импортируем встроенный математический модуль Python и используем функцию math.sqrt().
• Поскольку n не может быть идеальным квадратом, нам придется привести его к целому числу. Используйте int(var) для преобразования var в int.
• Чтобы убедиться, что мы действительно проверяем до √n, мы добавляем плюс один, поскольку функция range() по умолчанию исключает конечную точку диапазона.

Ячейка кода ниже подтверждает, что наша функция is_prime() работает правильно.

is_prime(8)
# False

is_prime(15)
# False

is_prime(23)
# True

В следующем разделе давайте создадим несколько простых графиков, чтобы визуально понять O (n) и O (√ n).

Визуальное сравнение O(n) и O(√n)

▶️ Запустите следующий фрагмент кода в выбранной вами среде ноутбука Jupyter.

import numpy as np
import seaborn as sns
import pandas as pd


n = 20

x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)

В приведенном выше фрагменте показано, как можно построить кривые для n и √n для диапазона значений.

• Мы используем функцию NumPy arange() для создания массива чисел.
• Затем мы собираем значения n и √n до 20, но не включая их, в Панды DataFrame.
• Далее мы строим с помощью линейный график моряка() функция.

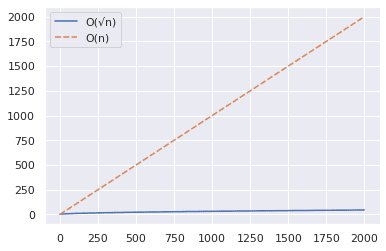
Из графика ниже видно, что √n значительно меньше n.

Давайте теперь увеличим диапазон до 2000 и повторим те же шаги, что и выше.

import numpy as np
import seaborn as sns
import pandas as pd


n = 2000

x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)

Из приведенного выше графика можно сделать вывод, что алгоритм O(√n) работает значительно быстрее, когда вы проверяете, является ли большое число простым.

Вот быстрый пример: 2377 — простое число — проверьте это!😀

В то время как подход O(n) требует порядка 2000 шагов, алгоритм O(√n) может помочь получить ответ всего за 49 шагов.✅

Вывод

⏳ И настало время подвести итоги.

• Чтобы проверить, является ли число простым, наивный подход состоит в том, чтобы перебрать все числа в диапазоне (2, n-1). Если вы не найдете множитель, который делит n, то n — простое число.
• Поскольку единственный множитель n, превышающий n/2, — это само n, вы можете работать только до n/2.
• Оба вышеупомянутых подхода имеют временную сложность O (n).
• Поскольку множители числа встречаются парами, вы можете работать только до √n. Этот алгоритм намного быстрее, чем O (n). И выигрыш заметен при проверке, является ли большое число простым или нет.

Надеюсь, вы понимаете, как проверить, является ли число простым в Python. В качестве следующего шага вы можете ознакомиться с нашим учебным пособием по программам на Python, посвященным операциям со строками, где вы научитесь проверять, являются ли строки палиндромами, анаграммами и т. д.

Увидимся в другом уроке. А пока удачного кодирования!👩🏽‍💻

1. Используйте простой метод итерации для определения простого числа в Python
2. Используйте функцию sympy.isprime(), чтобы проверить, является ли данное число простым числом в Python

Простое число может быть изображено как натуральное число без других положительных делителей, кроме числа 1 и самого себя. Число 1 не учитывается в списке простых чисел.

В этом руководстве будут рассмотрены различные методы, которые вы можете использовать, чтобы проверить, является ли число простым.

Используйте простой метод итерации для определения простого числа в Python

В этом методе мы используем простой метод итерации с использованием цикла for или while. Переберите числа, начиная с 2 и далее до K/2, и проверьте, делит ли какое-либо из этих чисел K.

Если найдено число, соответствующее этому критерию, то возвращается False. С другой стороны, если все числа не соответствуют этому критерию, данное число K является простым числом, и возвращается значение True.

В следующем коде используется метод простой итерации, чтобы проверить, является ли данное число простым числом в Python.

k = 13

# 1 not being a prime number, is ignored
if k > 1:
    for i in range(2, int(k/2)+1):
         if (k % i) == 0:
            print("It is not a prime number")
            break
    else:
        print("It is a prime number")

else:
    print("It is not a prime number")

Выход:

Вы можете оптимизировать приведенный выше код, применив некоторые изменения. Сделайте следующие оптимизации, чтобы сделать код еще быстрее:

• Проверяйте, пока не будет достигнут корень данного числа, вместо проверки точного числа. Этот процесс в основном устраняет избыточность, которая возникает, когда больший множитель числа K кратен меньшему множителю, который уже был повторен.

• Все простые числа существуют в форме 6n ± 1, за исключением 2 и 3. Следовательно, проверка делимости данного числа на 2 и 3, а затем проверка каждого числа, имеющего форму 6n ± 1, является более эффективным решением.

В следующем коде используется оптимизированный метод простой итерации, чтобы проверить, является ли данное число простым числом в Python.

def isitPrime(k):
    if k==2 or k==3: return True
    if k%2==0 or k<2: return False
    for i in range(3, int(k**0.5)+1, 2):
        if k%i==0:
            return False

    return True
print(isitPrime(13))

Выход:

Оптимизированный метод итерации делает его быстрее и эффективнее, чем простой метод итерации, примерно на 30%.

Используйте функцию sympy.isprime(), чтобы проверить, является ли данное число простым числом в Python

SymPy – это библиотека на Python, используемая для реализации символьной математики. Это упрощенная система компьютерной алгебры (CAS), которая содержит все основные функции. Для этого метода необходима установка этого модуля, и его можно загрузить, просто используя команду pip.

sympy.isprime() – это встроенная функция модуля SymPy, которую можно использовать для проверки возможных простых чисел. Это прямая функция, которая возвращает True, если проверяемое число простое, и False, если число не простое.

Следующий код использует функцию sympy.isprime(), чтобы проверить, является ли данное число простым числом в Python.

from sympy import *
  
isprime(8)
isprime(11)

Выход:

Следует отметить, что любое отрицательное число не подпадает под критерии простых чисел. Вывод этих функций может измениться, если ему сопоставить какое-либо отрицательное число.