как найти пространственную диагональ прямоугольного параллелепипеда???
Монах XIV
Мыслитель
(7119),
закрыт
10 лет назад
известна длина, ширина и высота, нужен рисунок, и формула (как выведена)
Лучший ответ
Alexander Alenitsyn
Высший разум
(754527)
10 лет назад
Теорема Пифагора: сначала для диагонали основания,
а затем – квадрат этой диагонали+квадрат высоты дают
как раз квадрат искомой линии.
Остальные ответы
Семен Аркадьевич
Высший разум
(340149)
10 лет назад
Квадрат диагонали равен сумме квадратов его измерений.
Уникум
Мыслитель
(9940)
10 лет назад
Линеечкой, господин мыслитель, линеечкой.
Монах XIVМыслитель (7119)
10 лет назад
это если только ЕГЭ сдавать по геометрии, то проканает, я бы там половину заданий тупо наугад правильно ответил бы
Похожие вопросы
From Wikipedia, the free encyclopedia

AC’ (shown in blue) is a space diagonal, while AC (shown in red) is a face diagonal.
In geometry, a space diagonal (also interior diagonal or body diagonal) of a polyhedron is a line connecting two vertices that are not on the same face. Space diagonals contrast with face diagonals, which connect vertices on the same face (but not on the same edge) as each other.[1]
For example, a pyramid has no space diagonals, while a cube (shown at right) or more generally a parallelepiped has four space diagonals.
Axial diagonal[edit]
An axial diagonal is a space diagonal that passes through the center of a polyhedron.
For example, in a cube with edge length a, all four space diagonals are axial diagonals, of common length 

A regular octahedron has 3 axial diagonals, of length 
A regular icosahedron has 6 axial diagonals of length 


Space diagonals of magic cubes[edit]
A magic square is an arrangement of numbers in a square grid so that the sum of the numbers along every row, column, and diagonal is the same. Similarly, one may define a magic cube to be an arrangement of numbers in a cubical grid so that the sum of the numbers on the four space diagonals must be the same as the sum of the numbers in each row, each column, and each pillar.
See also[edit]
- Distance
- Face diagonal
- Magic cube classes
- Hypotenuse
- Spacetime interval
References[edit]
- ^ William F. Kern, James R Bland,Solid Mensuration with proofs, 1938, p.116
- ^ Sutton, Daud (2002), Platonic & Archimedean Solids, Wooden Books, Bloomsbury Publishing USA, p. 55, ISBN 9780802713865.
- John R. Hendricks, The Pan-3-Agonal Magic Cube, Journal of Recreational Mathematics 5:1:1972, pp 51–54. First published mention of pan-3-agonals
- Hendricks, J. R., Magic Squares to Tesseracts by Computer, 1998, 0-9684700-0-9, page 49
- Heinz & Hendricks, Magic Square Lexicon: Illustrated, 2000, 0-9687985-0-0, pages 99,165
- Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 173, 1994.
External links[edit]
- Weisstein, Eric W. “Space Diagonals”. MathWorld.
- de Winkel Magic Encyclopedia
- Heinz – Basic cube parts
- John Hendricks Hypercubes
Давайте-ка рассмотрим любопытную задачку из многомерной геометрии.
Многомерное пространство это просто множество n-мерных векторов-столбиков. Их можно складывать, умножать на числа, умножать скалярно друг на друга и даже называть точками.
В многомерном пространстве можно определить шары и кубы. Достаточно очевидно: шар — это множество точек, расстояние от которых до данной не больше заданного числа (радиуса). Единичный куб — это множество точек, у которых каждая координата между нулем и единицей (длиной ребра). Далее понятно. Объем единичного куба равен единице, по определению.
У куба есть грани: это множества точек, у которых одна конкретная координата равна нулю или единице. Это тоже кубы в пространстве на единицу меньшей размерности.
И есть диагональ: это отрезок из точки с нулевыми координатами в точку с координатами-единичками. Опять-таки, можно уточнять; но мы не будем.
Куб может быть не единичным, а определяться длиной ребра. А шар определяется радиусом.
Вычислим длину диагонали. Она является гипотенузой в треугольнике, в котором катетами являются ребро и диагональ грани. По индукции имеем
где n — размерность, а — ребро, а D — диагональ. Это уже любопытно, так как в единичный стомерный куб поместится отрезок длиной десять (!) единиц.
Теперь рассмотрим на плоскости такую конструкцию:
Возьмем куб (квадрат) со стороной 4, разделим его на четыре квадрата со стороной 2. В каждый впишем шар (круг) радиусом 1. В промежуток между ними поместим круг так, чтобы касался всех кругов. Каков его радиус?
Надо вычесть из диагонали куба (квадрата) диаметр (2) и поделить на два. Получим
Для трехмерного куба построение аналогично: куб с ребром 4 разделив на 8 кубов… Получим
Аналогичное построение возможно в любом пространстве, и имеем, по индукции, формулу
Построение совершенно строгое, все этапы определены корректно. Но получается забавно. Начиная с пятимерного пространства, радиус маленького шарика больше, чем радиус большого. Ведь у большого вседа 1, а у маленького уже больше 1, если n>4.
А начиная с десятимерного, диаметр шарика больше ребра большого куба (4), так что шарик в куб не поместится и будет торчать по бокам.
Где я видел это прелесть — уже не упомню. Не мое. Если кто подскажет источник или, лучше, оригинал — буду благодарен.
Оглавление рубрики
Путеводитель по каналу
|
Как найти длину диагонали прямоугольного параллелепипеда ? По какой формуле найти диагональ параллелепипеда ?
Диагональ прямоугольного параллелепипеда – это отрезок, соединяющий его противоположные вершины . Итак, у нас есть прямоугольный параллелепипед с диагональю d и со сторонами a, b, c . Одно из свойств параллелепипеда гласит, что квадрат длины диагонали d равен сумме квадратов трёх его измерений a, b, c. Отсюда вывод, что длина диагонали может быть легко рассчитана по следующей формуле :
Также :Как найти высоту параллелепипеда?модератор выбрал этот ответ лучшим
Nonsense 7 лет назад Прямоугольным параллелепипедом (ПП) является ни что иное, как призма, основанием у которой прямоугольник. У ПП все диагонали равны, значит любая его диагональ рассчитывается по формуле:
где
Можно дать и другое определение, рассматривая декартову прямоугольную систему координат: Диагональ ПП это радиус-вектор любой точки пространства, заданной координатами x, y и z в декартовой системе координат. Этот радиус вектор к точке проводится из начала координат. А координатами точки будут проекции радиус-вектора (диагонали ПП) на координатные оси. Проекции совпадают с вершинами данного параллелепипеда.
Zolotynka 8 лет назад Если у прямоугольного параллелепипеда известны длина, высота и ширина (a,b,c) то формула для расчета диагонали будет выглядеть таким образом:
Обычно учителя не предлагают своим ученикам “голую” формулу, а прилагают усилия, чтобы те могли самостоятельно ее вывести, задавая наводящие вопросы:
Обычно после ответа на поставленные вопросы, ученики без труда самостоятельно выводят данную формулу.
Лолочка611 8 лет назад Прямоугольный параллелепипед это один из так званных многогранников, который состоит из 6 граней, каждая из которых является прямоугольником. А диагональ – это отрезок, который соединяет противоположные вершины параллелограмма. Если длину, ширину и высоту прямоугольного параллелепипеда принять за a, b, c соответственно, то формула его диагонали ( D ) будет выглядеть следующим образом: D^2=a^2+b^2+c^2.
дольфаника 8 лет назад Нашлась в интернете неплохая схема-таблица с полным перечислением всего, что есть в параллепипеде. Есть формула, чтобы найти диагональ, которая обозначается d. Есть изображение грани, вершины и других важных для параллепипеде вещей.
Багира999 8 лет назад Прямоугольный параллелепипед – это разновидность многогранника, состоящая из 6 граней, в основании которого — прямоугольник. Диагональ – это отрезок, который соединяет противоположные вершины параллелограмма. Формула нахождения длины диагонали – квадрат диагонали равен сумме квадратов трех измерений параллелограмма.
Koluchiy 8 лет назад Диагонали прямоугольного параллелепипеда равны. Также как и диагонали его противоположных граней. Длину диагонали можно вычислить, зная длину рёбер параллелограмма, исходящих из одной вершины. Эта длина равна корню квадратному из суммы квадратов длин его рёбер.
ДРЕССИРОВЩИК 9 лет назад Квадрат диагонали, квадратного параллилепипеда (смотрите свойства квадратного параллепипеда) равна сумме квадратов трёх его разных сторон (ширине, высоте, толщине), а соответственно диагонали квадратного параллепипеда равна корню из этой суммы.
haleron 8 лет назад Насколько мне известно еще со школьной программы, класс 9 если не ошибаюсь, и если не изменяет память , то диагональ прямоугольного параллелепипеда ровна корню квадратному суммы квадратов его всех трех сторон. [пользователь заблокирован] 8 лет назад квадрат диагонали равен, сумме квадратов ширины , высоты и длинны , исходя с этой формулы получаем ответ , диагональ равно корню квадратному с суммы его трех разных измерений , буквами они позначаюnсz abc
Космос111 7 лет назад Вспоминаю школьную программу по геометрии, можно сказать так: диагональ параллелепипеда равняется корню квадратному полученному из суммы его всех трех сторон (обозначаются они маленькими буквами a, b, c). Николай Л 10 лет назад Длина диагонали прямоугольного параллепипеда равна корню квадратному из суммы квадратов его сторон. Знаете ответ? |
Параллелепипед – это частный случай призмы, в основании которой лежит прямоугольник с длиной a и шириной b. Двигаясь по вертикальной или наклонной оси на определенную высоту c, данный прямоугольник создает объемное тело, именуемое параллелепипедом.
Параллелепипед по определению может быть наклонным или прямым, то есть угол между высотой и прямоугольником в основании варьируется от 0 до 90 градусов. Прямой параллелепипед имеет в качестве граней исключительно прямоугольники, и даже иногда квадрат (в основании), поэтому решение задач с его участием значительно облегчено. В случае с наклонным параллелепипедом в формулах необходимо учитывать, что боковой гранью является параллелограмм, строение которого зависит также от угла его наклона.
Помимо трех вышеуказанных параметров параллелепипеда – длины, ширины высоты, являющихся его ребрами, в данном теле можно также провести еще несколько отрезков, соединяющих его вершины. Как и в геометрических фигурах на плоскости, линии, проходящие внутри основного каркаса через вершины, называются диагоналями. Диагонали боковых граней прямоугольного параллелепипеда идентичны диагоналям прямоугольников, которыми представлены грани – их, соответственно, можно вычислить, используя подходящий онлайн калькулятор для прямоугольников.
Другое дело – диагональ, проходящая не по внешней поверхности прямоугольного параллелепипеда, а сквозь него, соединяя противоположные вершины верхнего и нижнего оснований. При этом, какая именно пара противоположных вершин соединена, не имеет значения для расчетов, так как если рассмотреть сечения, можно увидеть, что обе диагонали параллелепипеда идентичны и найти их можно одним и тем же способом.
Итак, для того чтобы вывести формулу диагонали через длину, ширину и высоту, необходимо заключить диагональ в плоскую геометрическую фигуру, свойства которой можно будет использовать. Для этого в любом основании – верхнем или нижнем, проводится диагональ, которая образует с диагональю параллелепипеда и боковым ребром (высотой) прямоугольный треугольник. Применив одну лишь теорему Пифагора, можно найти диагональ основания через ширину и длину,а затем диагональ прямоугольного параллелепипеда, добавив в расчеты высоту.
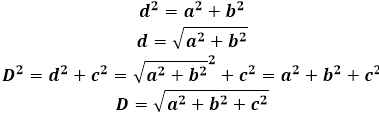
Используя последнюю и предпоследнюю формулу, можно также успешно найти длину, ширину или высоту прямоугольного параллелепипеда, имея в заданных условиях три параметра из четырех, включая диагональ параллелепипеда.
Например: 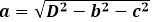
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»











