Упражнение “Найди спрятанную фигуру” – это занятие, в котором ребенок должен найти в сложной фигуре простую фигуру, которая указана в каждом задании.
Цель: развитие наглядно-образного мышления.
Материал: распечатанные бланки методики.
Инструкция для упражнения “Найди фигуру”: В верхнем левом углу каждого задания представлена простая фигура. Она входит в состав четырех сложных фигур. Но в каждом задании дано пять сложных фигур, и в одной из них указанной простой фигуры нет. Вот эту сложную фигуру и должен найти ребенок. Для этого ему следует в каждом задании внимательно рассмотреть все пять фигур. Найдя указанную простую фигуру в одной из сложных фигур, следует переходить к следующей сложной фигуре. Если ребенок не сможет обнаружить простую фигуру в одном из первых рисунков, ему все равно нужно продолжить изучение оставшихся сложных фигур, поскольку он мог просто не заметить простой фигуры, которая хорошо “спрятана” среди линий сложной. Если же ребенок найдет все четыре сложные фигуры, где есть указанная простая фигура, то это будет подтверждением того, что искомой является оставшаяся пятая фигура.
Внимание! Размеры простой фигуры, спрятанной среди четырех сложных фигур, должны быть точно такими же, как на образце.
Примечание_1: можно попросить ребенка закрашивать найденную простую фигуру в сложных фигурах или обводить её по контуру.
Примечание_2: если ребенку не будет даваться решение первых заданий, то вам следует подсказать ему, чтобы он сначала искал не всю простую фигуру, а только какой-то отдельный ее элемент – одну-две линии. Найдя этот элемент среди линий сложной фигуры, надо постараться увидеть следующие составные элементы этой простой фигуры. Таким образом нужно исследовать все 5 сложных фигур.
Ответы:
Бланк №1:
Задание_1 – фигура №5
Задание_2 – фигура №4
Задание_3 – фигура №4
Бланк №2:
Задание_1 – фигура №5
Задание_2 – фигура №3
Задание_3 – фигура №1
Бланк №3:
Задание_1 – фигура №2
Задание_2 – фигура №1
Задание_3 – фигура №4
Бланк №1
Бланк №2
Бланк №3
Скачать бланки упражнения “Найди спрятанную фигуру” в формате Word по ссылке ниже
Привет! В этой статье будем учиться определять перемещения поперечных сечений при изгибе: прогибы и углы поворотов, по методу (способу, правилу) Верещагина. Причем это правило широко используется не только при определении перемещений, но и при раскрытии статической неопределимости систем по методу сил. Я расскажу, о сути этого метода, как перемножаются эпюры различной сложности и когда выгодно пользоваться этим методом.
Что нужно знать для успешного освоения материалов данного урока? Обязательно нужно уметь строить эпюры изгибающих моментов, т.к. в этой статье будем работать с данной эпюрой.
Верещагин и его метод, правило или способ
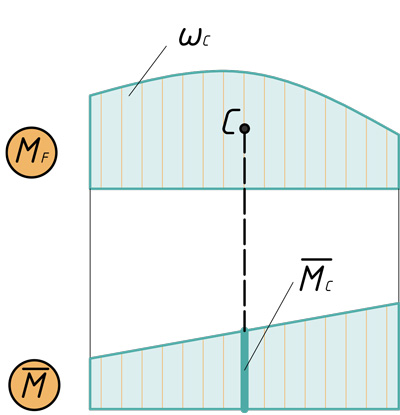
А.К. Верещагин в 1925г. предложил более простой способ решения (формулы) интеграла Мора. Он предложил вместо интегрирования двух функций перемножать эпюры: умножать площадь одной эпюры на ординату второй эпюры под центром тяжести первой. Этим способом можно пользоваться, когда одна из эпюр прямолинейна, вторая может быть как линейной, так и параболической. Кроме того, ордината берется прямолинейной эпюры. Когда эпюры обе прямолинейны, то тут совсем неважно, чью брать площадь, а чью ординату. Таким образом, эпюры по Верещагину перемножаются по следующей формуле:
({ V={ M }_{ F } }cdot overline { M } ={ omega }_{ C }cdot { overline { M } }_{ C } )
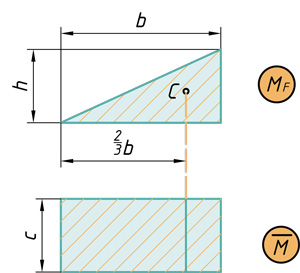
Проиллюстрировано перемножение эпюр по Верещагину: C — центр тяжести первой эпюры, ωс — площадь первой эпюры, Mc — ордината второй эпюры под центром тяжести первой.
Площадь и центр тяжести эпюр
При использовании метода Верещагина берется не сразу вся площадь эпюры, а частями, в пределах участков. Эпюра изгибающих моментов расслаивается на простейшие фигуры.
Любой самый сложный участок эпюры можно расслоить на три простейшие фигуры: прямоугольник, прямоугольный треугольник и параболический сегмент.
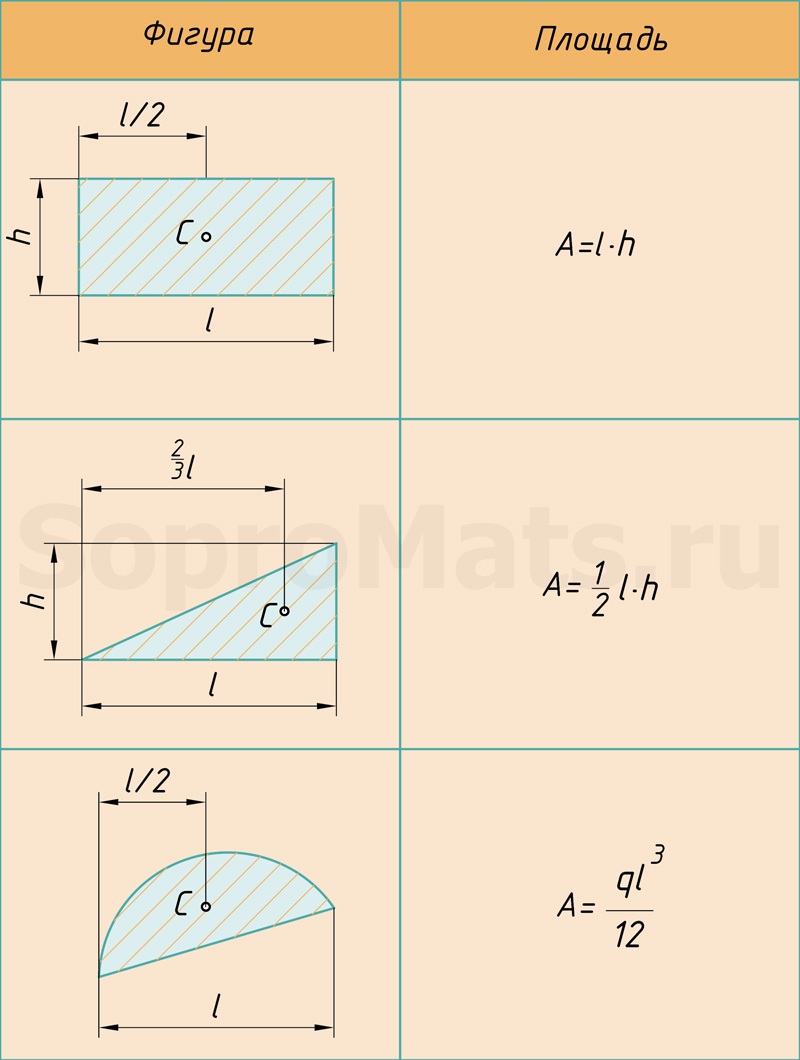
Поэтому именно с этими фигурами будем дальше работать. Напомню, как вычислить их площадь и где у них находится центр тяжести. Все формулы и размеры оформил в виде таблицы:
Перемножение простейших эпюр по Верещагину
В этом блоке статьи покажу простейшие случаи перемножения эпюр по Верещагину.
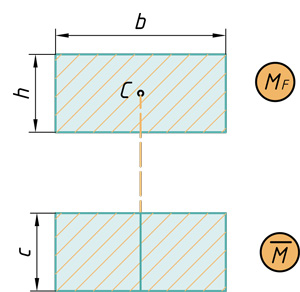
Прямоугольник на прямоугольник
( { V={ M }_{ F } }cdot overline { M } ={ bcdot hcdot c } )
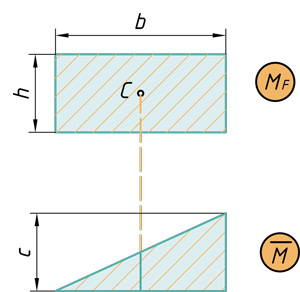
Прямоугольник на треугольник
( { V={ M }_{ F } }cdot overline { M } ={ bcdot hcdot frac { 1 }{ 2 } cdot c } )
Треугольник на прямоугольник
( { V={ M }_{ F } }cdot overline { M } ={ frac { 1 }{ 2 } cdot bcdot hcdot c } )
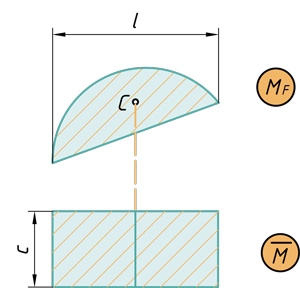
Параболический сегмент на прямоугольник
( { V={ M }_{ F } }cdot overline { M } ={ frac { qcdot { l }^{ 3 } }{ 12 } cdot c } )
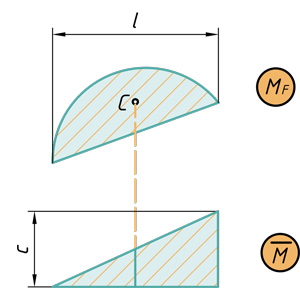
Параболический сегмент на треугольник
( { V={ M }_{ F } }cdot overline { M } ={ frac { qcdot { l }^{ 3 } }{ 12 } cdot frac { 1 }{ 2 } cdot c } )
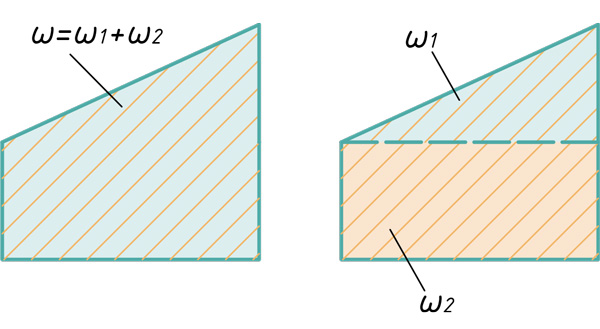
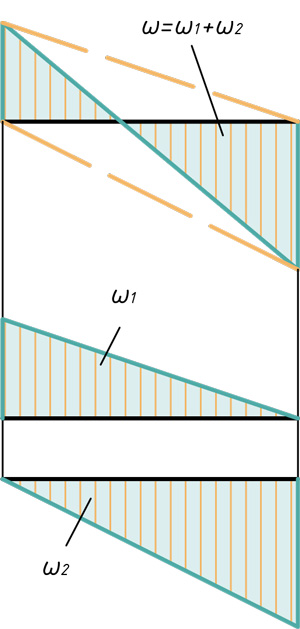
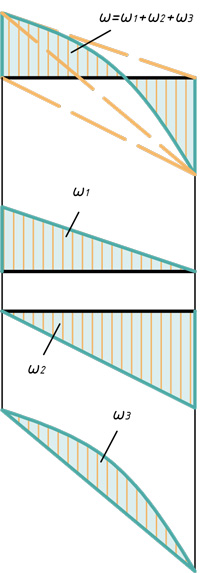
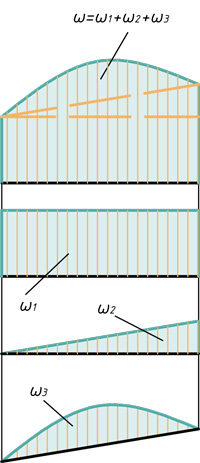
Расслоение эпюр на простые фигуры
В этом блоке статьи покажу способы расслоения эпюр на простые фигуры, для дальнейшего их перемножения по правилу Верещагина.
Прямоугольник и треугольник
Два треугольника
Два треугольника и параболический сегмент
Треугольник, прямоугольник и параболический сегмент
Пример определения перемещений: прогибов и углов поворотов по Верещагину
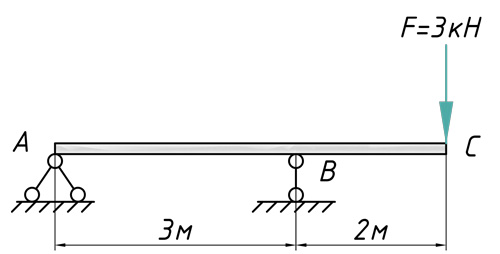
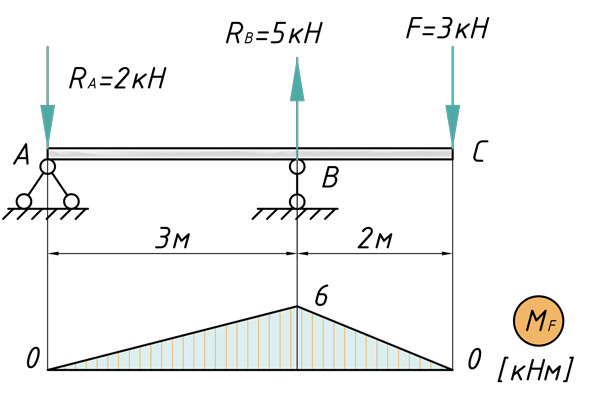
Теперь предлагаю рассмотреть конкретный пример с расчетом перемещений поперечных сечений: их прогибов и углов поворотов. Возьмем стальную балку, которая загружена всевозможными типами нагрузок и определим прогиб сечения C, а также угол поворота сечения A.
Построение эпюры изгибающих моментов
В первую очередь рассчитываем и строим эпюру изгибающих моментов:
Построение единичных эпюр
Теперь для каждого искомого перемещения необходимо приложить единичную нагрузку в ту точку, где это перемещение определяется и построить единичные эпюры:
- для прогибов прикладываются единичные силы.
- для углов поворотов прикладываются единичные моменты.
Все прикладываемые нагрузки являются безразмерными величинами. Причем, направление этих нагрузок неважно! Расчет покажет верное направление перемещений.
Например, после расчета величина прогиба получилась положительной, это значит, что направление перемещения сечения совпадает с направлением ранее прикладываемой единичной силы. То же самое касается и углов поворотов.
Перемножение участков эпюры по Верещагину
После проведения всех подготовительных работ: построения эпюры изгибающих моментов, расслоения ее на элементарные фигуры и построения единичных эпюр от нагрузок, приложенных в местах и направлении искомых перемещений, можно переходить непосредственно к перемножению соответствующих эпюр.
Как уже было написано выше, линейные эпюры можно перемножать в любом порядке, то есть брать площадь любой эпюры: основной или единичной, и умножать на ординату другой. Но обычно, чтобы не путаться в расчетах, площади берут основной эпюры изгибающих моментов, в этом уроке будем придерживаться этого же правила.
Определение прогиба сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем прогиб сечения C по методу Мора — Верещагина:
[ { V }_{ C }=frac { 1 }{ E{ I }_{ x } } (frac { 1 }{ 2 } cdot 6cdot 3cdot frac { 2 }{ 3 } cdot 2+frac { 1 }{ 2 } cdot 6cdot 2cdot frac { 2 }{ 3 } cdot 2)=frac { 20кН{ м }^{ 3 } }{ E{ I }_{ x } } ]
Представим, что рассчитываемая балка имеет поперечное сечение в виде двутавра №24 по ГОСТ 8239-89, тогда прогиб балки будет равен:
[ { V }_{ C }=frac { 20кН{ м }^{ 3 } }{ E{ I }_{ x } } =frac { 20cdot { 10 }^{ 9 }Нcdot { см }^{ 3 } }{ 2cdot { 10 }^{ 7 }frac { Н }{ { см }^{ 2 } } cdot 3460{ см }^{ 4 } } =0.289см ]
Определение угла поворота сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем угол поворота сечения C по правилу Мора — Верещагина:
[ { theta }_{ C }=frac { 1 }{ E{ I }_{ x } } (-frac { 1 }{ 2 } cdot 6cdot 3cdot frac { 1 }{ 3 } cdot 1)=-frac { 3кН{ м }^{ 2 } }{ E{ I }_{ x } } ]
[ { { theta } }_{ C }=-frac { 3кН{ м }^{ 2 } }{ E{ I }_{ x } } =-frac { 3cdot { 10 }^{ 7 }Нcdot { см }^{ 3 } }{ 2cdot { 10 }^{ 7 }frac { Н }{ { см }^{ 2 } } cdot 3460{ см }^{ 4 } } =-0.0004рад ]
Для закрепления пройденного материала рекомендую изучить примеры, где рассмотрены различные случаи расслоения и перемножения эпюр.
МЕТОДИКА «ВКЛЮЧЕННЫЕ ФИГУРЫ»
Существующая в разных модификациях [там
же]. Испытуемый должен найти простую фигуру внутри сложной геометричес-
кой фигуры (при этом он не имеет возможности видеть простую и сложную фи-
гуры вместе). Быстрое и правильное обнаружение простой фигуры в сложной
характеризует ПНЗ стиль, медленное и ошибочное — ПЗ стиль.
Индивидуальный вариант методики «Включенные фигуры», построенный
на основе аналогичного теста Готтшальда (1926), включает 24 сложные фигу-
ры, к каждой из которых предъявляется одна из 8 простых фигур. Показатель:
средняя величина времени обнаружения простой фигуры в сложной.
Групповой вариант методики «Включенные фигуры» состоит из одной
тренировочной (на нее отводится 2 мин) и двух основных серий (на каж-
дую из которых отводится по 5 мин). Испытуемый должен найти в слож-
ной фигуре простую и выделить ее с помощью карандаша. Показатель: ко-
личество правильных ответов в двух основных сериях.
Разновидностью методики «Включенные фигуры» является групповой
вариант методики «АКТ-70» (К.И. Эттрих) (цит. по: [Шкуратова, 1994]).
Уиткин определял ПЗ—ПНЗ как «структурирующую способность в вос-
приятии». Последующие исследования показали, что данная способность со-
относится с рядом показателей интеллектуальной деятельности, таких как:
«гибкость завершения гештальта» по Терстоуну (задания отыскать простую
деталь в ряду сложных геометрических фигур; обнаружить знакомые пред-
меты, которые включены в сложную сцену, например, «спрятаны» среди де-
ревьев); «адаптивная гибкость» по Гилфорду (задачи на сообразительность,
при решении которых испытуемый должен обнаружить противоречие в про-
блемной ситуации, или изменить заданное расположение спичек с целью по-
лучения определенной геометрической фигуры), успешность выполнения
пространственных субтестов шкалы Векслера («Кубики» и «Сложение фи-
гур»), успешность решении задач Дункера (способность преодолевать «фун-
кциональную фиксированность») и Лачинса (способность переходить от ста-
рых способов решения задач к новым при изменении условий деятельнос-
ти). Смысл этих связей, по мнению Уиткина, достаточно ясен: все указан-
ные психологические измерения (включая ПЗ-ПНЗ) в той или иной мере
характеризуют способность преодолевать сложноорганизованиый контекст
[Witkin, Dyk, Faterson, Goodenough, Karp, 1974].
Однако со временем выяснилось, что показатели ПЗ-ПНЗ имеют отно-
шение к более широкому спектру проявлений интеллектуальной активно-
сти. Наибольший интерес представляет связь этого стилевого параметра с
характеристиками обучения. По данным Г. Уиткина и его коллег, незави-
симые от поля люди включаются в процесс обучения скорее как его актив-
ные участники, нежели как зрители. Поэтому, например, в эффективности обучения поленезависимых лиц ведущую роль играет наличие у них
внутренней мотивации.
Обучение же полезависимых лиц оказывается бо-
лее успешным в ситуации внешнего подкрепления. В целом академическая
успеваемость выше у поленезависимых учащихся. У них легче происходит
генерализация и перенос знаний, ярче выражена способность выбирать бо-
лее рациональные стратегии запоминания и воспроизведения материала
[Witkin, Moore, Goodenough, Cox, 1977].
ПЗ-ПНЗ обнаруживает свое влияние и в таких сложных видах интеллек-
туальной деятельности, как работа с текстом. В частности, отмечается пре-
восходство поленезависимых учащихся в условиях, когда текст требует пере-
структурирования и реорганизации. При конспектировании лекций и науч-
ных текстов поленезависимые студенты (их стилевые особенности измерялись
с помощью методик АКТ-70 и «Включенные фигуры» в варианте теста Гот-
тшальда) подвергали текст большей переработке (сокращая количество слов,
перефразируя мысли, используя средства структурирования текста в виде аб-
зацев, подчеркивания, выделения цветом и т.д.) [Шкуратова, 1994].
Наиболее полные данные были получены в процессе изучения связей по-
казателей ПЗ-ПНЗ с особенностями межличностных отношений. Полеза-
висимые лица более чувствительны к социальной информации, доброжела-
тельны и общительны, склонны держать более короткую физическую дис-
танцию в условиях реального общения. Зависимые от поля люди ждут от
окружающих поддержки и помощи. Присутствие других людей интенсифи-
цирует их деятельность. Они легче ладят с людьми, успешнее разрешают
конфликтные ситуации, реже высказывают негативное отношение к окру-
жающим. Эти люди склонны изменять свои взгляды в направлении пози-
ции авторитетов. В свою очередь, поленезависимым лицам присущи прямо
противоположные психологические качества [Witkin, Goodenough, 1977].
Поскольку полезависимые лица обнаруживают такие социальные уста-
новки и социальные качества, которые более полезны в межличностных
отношениях, то, по мнению Уиткина, можно говорить о большей разви-
тости у них социальных способностей. В свою очередь, люди, принадле-
жащие к полюсу ПНЗ, имеют более развитые когнитивно-переструктури-
рующие способности. Это обстоятельство рассматривалось Уиткиным как
доказательство биполярной природы данного когнитивного стиля: полюс
ПНЗ свидетельствует об интеллектуальной компетентности, тогда как по-
люс ПЗ — о социальной компетентности личности.
Впоследствии Уиткин расширил трактовку ПЗ-ПНЗ, сделав акцент на
характере направленности субъекта: либо на внешние факторы (тенденция
быть полезависимым), либо на внутренние факторы (тенденция быть по-
ленезависимым).
Источник
Тест включенных фигур уиткина
Этот тест — определенная вариация методики «Фигуры Готтшальдта» и применяется для диагностики полезависимости/поленезависимости.
Теория
С помощью данной методики определяются различия между полезависимыми и поленезависимыми типами личностями. Выводы делаются на основании степени свободы той или иной личности от внешних референтов. Иными словами, исследуется, насколько человек принимая решения, ориентируется на собственные способности и навыки и насколько он же ориентируется на внешние ориентиры.
Полезависимые и поленезависимые люди в значительной степени отличаются друг от друга. Так, поленезависимые обычно обладают отличным интеллектом, но при этом полезависимые, как правило, лучше социализируются, легко сходятся и общаются с людьми. Что касается профессиональной деятельности, то поленезависимые люди готовы брать на себя ответственность, успешно организуют свой рабочий процесс, уверенно движутся к поставленной цели.
Полезависимые люди, в свою очередь, больше любят работать в коллективе, где задачи четко распределены заранее между членами команды.
Также есть и существенные различия между этими двумя типами людей в области восприятия. Полезависимые люди более склонны к иллюзиям, а поленезависимые воспринимают любую визуальную картинку как более структурированную. Таким образом, полезависимые воспринимают каждый объект отдельно и отдельно же воспринимают все качества этого объекта. Если коротко, то можно сказать, что полезависимые люди склонны к аналитическому восприятию, а поленезевисимые — к синтетическому. Методика позволяет определить тип личности.
Процесс тестирования
Как проводится тестирование? Проведение теста включенных Фигур Готтшальдта: участникам предлагается 30 фигур. В каждой скрыт 1 простой элемент. При этом сложные фигуры даются тестируемым по одной штуке и засекается время, потраченное тестируемыми на прохождение задания. Затем предъявляется инструкция и демонстрируются примеры тестирований, где участники отвечали верно.
Результаты тестирования
Баллы подсчитываются согласно специальной таблице. За один правильный ответ дается один балл.
По данной формуле специалисты рассчитывают индекс полезависимости:
(N – общая сумма баллов а t – количество минут, затраченных на работу.
Подсчет баллов и выводы:
- Если I более 2,5, это указывает на выраженную поленезависимость.
- Если I менее 2,5, это указывает на выраженную полезависимость.
Поленезависмые люди затрачивают на тестирование меньше времени в минутах, чем полезависимые и дают большее количество правильных ответов.
Полезависимые личности испытывают больше доверия к наглядным зрительным образам и впечатлениям. Для них большую сложность представляет преодоление видимого поля, если необходимо детализировать ту или иную ситуацию. В то же время, поленезависимые люди не испытывают таких проблем, уверенно ориентируются на личный опыт, способны без труда детализировать ситуацию.
Узнать больше о типах личности и на основании научных методик научиться предсказывать их поведение, помогут специализированные курсы Викиум — «Профайлинг» и «Менталист». Информация в них представлена в концентрированном виде, что позволит быстро и эффективно овладеть новыми навыками.
Источник
Методика «Фигуры Готтшальдта»
Данный тест является сжатой модификацией «Фигур Готтшальдта» и соответственно направлен на диагностику такого параметра как полезависимость-поленезависимость (ПЗ-ПНЗ).
Теоретические основы
Наиболее общим основанием индивидуальных различий в познавательной деятельности, устанавливаемых с помощью «ПЗ-ПНЗ», является степень свободы от внешних референтов, или, иначе, степень ориентации человека при принятии решений на имеющиеся у него знания и опыт, а не на внешние ориентиры, если они вступают в противоречие с его опытом.
Личностные различия полезависимых и поленезависимых людей появляются многогранно. С одной стороны, поленезависимые люди более успешны в интеллектуальной деятельности. С другой – полезависимые обычно более общительны, расположены к социальным контактам. Поленезависимые, как правило, выбирают сферу деятельности, требующую высокую самостоятельность в средствах достижения постав- ленной цели. Полезависимые обычно выбирают такой род занятий, в котором средства деятельности заранее заданы, оговорены, предпочитают коллективное выполнение задачи.
Наиболее четкие различия между полезависимыми и поленезависимыми проявляются в особенностях восприятия. Полезависимые в большей мере подвержены разного рода иллюзиям восприятия. Для поленезависимых воспринимаемая «картинка» значительно более структурирована, чем для полезависимых. Это проявляется в том, что для первых воспринимаемый объект, качества объекта воспринимаются самостоятельно, отдельно от других объектов, качеств этих объектов, воспринимаемых одновременно с этим объектом. Иначе говоря, восприятие поленезависимых – аналитично, восприятие полезависимых синтетично.
Процедура проведения
Испытуемым предлагается в тридцати замаскированных фигурах найти одну из пяти эталонных фигур и указать ее. Сложные фигуры предъявляются по одной. Фиксируется общее время выполнения задания. После предъявления инструкции следует демонстрация примеров с указанием правильных ответов.
Инструкция
«Вам будут предъявлены сложные фигуры (изображения), в каждой из которых имеется один из простых эталонов, закодированных буквами А, Б, В, Г, Д. Вы должны найти в каждом случае, какой из этих элементов содержится в рисунке и указать его (набрать код элемента)».
Обработка и интерпретация
Подсчет сырых баллов производится в соответствии с ключом, приведенным в таблице:
| 1. А | 6. В | 11. Б | 16. Д | 21. Г | 26. Б |
| 2. Б | 7. А | 12. А | 17. А | 22. Б | 27. А |
| 3. В | 8. В | 13. А | 18. Д | 23. Г | 28. Д |
| 4. Г | 9. Д | 14. В | 19. Б | 24. А | 29. В |
| 5. В | 10. Д | 15. Б | 20. В | 25. Д | 30. Б |
За каждый правильный (совпадающий с ключом) ответ присваивается 1 балл.
Индекс полезависимости рассчитывается по формуле:
где N – общая сумма баллов (т.е. число правильно выполненных заданий), а t – время работы над всем тестом в минутах. Интерпретация
- Если I больше 2,5, то можно делать вывод о выраженной поленезависимости.
- Если I меньше 2,5, то можно делать вывод о выраженной полезависимости.
Таким образом, чем больше правильно выполненных заданий и меньше время работы с тестом тем более выражена поленезависимость.
Представители полезависимого стиля больше доверяют наглядным зрительным впечатлениям и с трудом преодолевают видимое поле при необходимости детализации и структурирования ситуации. Представители поленезависимого стиля, напротив, полагаются на внутренний опыт и легко отвлекаются от влияния поля, быстро и точно выделяя деталь из целостной пространственной ситуации.
Стимульный материал
Инструкция
В каждом сложном рисунке имеется один из следующих элементов:
Назовите в каждом случае, какой из этих элементов содержится в рисунке. Например:
- В каждом рисунке имеется один из элементов той же величины и также расположенный как на образце;
- В каждом рисунке имеется только один из элементов.
Источник
Что ты такое: методика «Фигуры Готтшальдта»
Этот тест — определенная вариация методики «Фигуры Готтшальдта» и применяется для диагностики полезависимости/поленезависимости.
Теория
С помощью данной методики определяются различия между полезависимыми и поленезависимыми типами личностями. Выводы делаются на основании степени свободы той или иной личности от внешних референтов. Иными словами, исследуется, насколько человек принимая решения, ориентируется на собственные способности и навыки и насколько он же ориентируется на внешние ориентиры.
Полезависимые и поленезависимые люди в значительной степени отличаются друг от друга. Так, поленезависимые обычно обладают отличным интеллектом, но при этом полезависимые, как правило, лучше социализируются, легко сходятся и общаются с людьми. Что касается профессиональной деятельности, то поленезависимые люди готовы брать на себя ответственность, успешно организуют свой рабочий процесс, уверенно движутся к поставленной цели.
Полезависимые люди, в свою очередь, больше любят работать в коллективе, где задачи четко распределены заранее между членами команды.
Также есть и существенные различия между этими двумя типами людей в области восприятия. Полезависимые люди более склонны к иллюзиям, а поленезависимые воспринимают любую визуальную картинку как более структурированную. Таким образом, полезависимые воспринимают каждый объект отдельно и отдельно же воспринимают все качества этого объекта. Если коротко, то можно сказать, что полезависимые люди склонны к аналитическому восприятию, а поленезевисимые — к синтетическому. Методика позволяет определить тип личности.
Процесс тестирования
Как проводится тестирование? Проведение теста включенных Фигур Готтшальдта: участникам предлагается 30 фигур. В каждой скрыт 1 простой элемент. При этом сложные фигуры даются тестируемым по одной штуке и засекается время, потраченное тестируемыми на прохождение задания. Затем предъявляется инструкция и демонстрируются примеры тестирований, где участники отвечали верно.
Результаты тестирования
Баллы подсчитываются согласно специальной таблице. За один правильный ответ дается один балл.
По данной формуле специалисты рассчитывают индекс полезависимости:
(N – общая сумма баллов а t – количество минут, затраченных на работу.
Подсчет баллов и выводы:
- Если I более 2,5, это указывает на выраженную поленезависимость.
- Если I менее 2,5, это указывает на выраженную полезависимость.
Поленезависмые люди затрачивают на тестирование меньше времени в минутах, чем полезависимые и дают большее количество правильных ответов.
Полезависимые личности испытывают больше доверия к наглядным зрительным образам и впечатлениям. Для них большую сложность представляет преодоление видимого поля, если необходимо детализировать ту или иную ситуацию. В то же время, поленезависимые люди не испытывают таких проблем, уверенно ориентируются на личный опыт, способны без труда детализировать ситуацию.
Узнать больше о типах личности и на основании научных методик научиться предсказывать их поведение, помогут специализированные курсы Викиум — «Профайлинг» и «Менталист». Информация в них представлена в концентрированном виде, что позволит быстро и эффективно овладеть новыми навыками.
Источник
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Калинова Ю.А.
1
Подходова Н.С.
1
1 Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Российский государственный педагогический университет им. А. И. Герцена», НИИ общего образования
В статье представлены результаты исследования по методике обучения математике, направленного на развитие творческого мышления учащихся. Один из способов управления творчеством – сведение творческого мышления к некоторому его упрощению – дивергентному мышлению. Описана трактовка дивергентного мышления, рассмотрены механизмы его развития, показана возможность его развития в процессе обучения геометрии. В исследовании, описанном в статье, была разработан учебный материал, направленный на развитие дивергентного мышления на основе использования такого механизма его формирования как перецентрирование, была проведена его успешная апробация. Автором построена система задач по планиметрии, описанная в статье, позволяющая решающему неоднократно изменять направления мыслительной деятельности. В основу разработки системы положен анализ этапов решения математической задач, который позволили разделить эти этапы на те, которые преимущественно работают на конвергенцию и дивергенцию. В статье представлено обоснование, что представленная совокупность геометрических задач является системой, раскрыты приемы развития дивергентного мышления – обучение перецентрированию в процессе решения задач.
креативность
дивергентное мышление
перецентрирование
система задач на «перецентрирование»
методика обучения перецентрированию
1. Брудный, А.А. Психологическая герменевтика. М., 1998.
2. Вертгеймер, М. Продуктивное мышление. М.: Прогресс, 1987.
3. Гилфорд, Дж. Три стороны интеллекта // Психология мышления – М.: Прогресс, 1965.
4. Грановская, Р.М. Элементы практической психологии. СПб.: Речь, 2003.
5. Джонс, Дж. К. Методы проектирования. М.: Мир, 1986.
6. Иванов, А. Н. Система специальных заданий как дидактическое средство развития дивергентного мышления младших школьников / Дис. уч. ст. канд. педаг. н., Мурманск 2007.
7. Методика и технология обучения математике. Курс лекций /под ред. Н.Л. Стефановой, Н.С. Подходовой. – М.: Дрофа, 2005.
8. Орлянская, О. Н. Методика формирования у будущих учителей математики умения конструировать системы задач/ Дис. уч. ст. канд. педаг. н., Волгоград, 2004.
9. Поддъяков, А.Н. Мышление дошкольников в процессе экспериментирования со сложными объектами / А.Н. Поддъяков // Вопросы психологии. 1996. – № 4
10. Подходова Н.С., Иванова О.А., Фефилова Е.Ф. Реализация ФГОС ОО: новые решения в обучении математике. Учебно-методическое издание. Архангельск-СПб.:, 2015
11. Флейвелл, Д.Х.: Генетическая психология Жана Пиаже. М.: «Просвещение», 1967.
Одним из важнейших качеств, позволяющих человеку приспособиться к жизни, является креативность. От понимания механизмов функционирования и развития креативности, во многом зависит жизненный успех учащихся. Поэтому от современного образования требуется уже не фрагментарное включение методов развития креативности в образовательную практику, а целенаправленная работа по развитию креативности. Однако проблема обучения творчеству является чрезвычайно сложной. Для творчества нужна большая самостоятельность учащихся, которую они часто не в состоянии проявить. Если же педагог будет оказывать существенную помощь учащимся при решении творческих задач (давать многочисленные подсказки), то творчества в этой деятельности уже не останется. Один из путей управления творчеством – это сведение творческого мышления к некоторому его упрощению – дивергентному мышлению, введенному в научный обиход Дж. Гилфордом [3]. Дивергентное мышление определяется Дж. Гилфордом как «тип мышления, идущий в различных направлениях». Методистами высказывается мысль, что задача развития дивергентного мышления является более прогнозируемой и более поддающейся педагогическому влиянию, чем задача развития творческого мышления. Так А.Н. Иванов считает, что подобная работа, связанная с развитием дивергентного мышления, будет полезна как раз не столько одаренным детям (уровень креативности которых и так высокий), а тем детям, у которых уровень креативности «средне-нормальный» и даже недостаточный [6].
Целью исследования, описанного в статье является разработка приемов и средств дивергентного развития учащихся при обучении геометрии.
Основное содержание статьи
Дивергентное мышление учащихся целесообразно развивать в процессе обучения математики при решения задач. Мы считаем, что организовывать целенаправленную деятельность по развитию дивергентного мышления целесообразно при работе на первом этапе решения задачи – анализе текста задачи. Это можно объяснить следующими соображениями: большинство исследователей мышления считают, что дивергентное мышление особенно активно работает на начальных этапах решения проблемы. А.Н. Поддьяков, например, выделяет две стадии решения исследовательской задачи: дивергенцию и конвергенцию [9]. Дж. К. Джонс выделяет три стадии решения конструкторско-проектировочной задачи: дивергенцию, трансформацию и конвергенцию [5]. Методистами по математике обычно выделяются четыре этапа решения математической задачи [7]: 1) анализ текста задачи; 2) составление плана решения задачи; 3) реализация плана, 4) проверка решения задачи.
Мы считаем, что и при решении математической задачи дивергентное (расходящееся) мышление особенно активно работает на первом этапе решения, т.е. на этапе анализа текста задачи. А на втором этапе – формулировке плана решения задачи – возникает уже первичная конвергенция (схождение к чему-то одному), которая продолжается на последующих этапах решения задачи.
В ходе нашего исследования мы пришли к выводу, что одним из механизмов развития дивергентного мышления является целенаправленное обучение учащихся перецентрированию. В научный обиход термин «перецентрирование» ввел гештальтпсихолог М. Вертгеймер [2]. Гештальтпсихологи считают, что если при репродуктивном мышлении человек ищет в памяти те приемы, которые способствуют решению, то при продуктивном мышлении у него должно возникнуть понимание проблемы. При этом открытие решения задачи возникает в порядке инсайта, как результат перецентрирования, трансформации самой проблемной ситуации. Сходные идеи высказывались и другими авторами. Так Ж. Пиаже ввел термин «децентрация». Ж. Пиаже изучал ошибки, которые совершали дети при решении предлагаемых им интеллектуальных заданий [11]. То, что эти ошибки постепенно изживались благодаря специально организованной деятельности, он объяснял процессом децентрации. Децентрацией он назвал преодоление тенденции к сосредоточению внимания на единичной, бросающейся в глаза особенности предмета, и появление способности принять во внимание другие существенные особенности этого предмета.
А.А. Брудный вводит понятие «перецентровки», как одного из механизмов понимания информации [1]. При перецентровке структура отражаемой в тексте ситуации предстает в изменяющемся виде, т.е. происходит изменение изначальной структуры текста, смещение центра с одного акцента на другой. Она дает возможность взглянуть на тему под другим углом, увидеть новые связи между теми же понятиями, а значит и новые смыслы.
Наше исследование показало, что существует ряд математических задач, при решении которых можно наблюдать четко очерченный момент изменения направления мыслительной деятельности, который мы и назвали перецентрированием. Человеку бывает непросто совершить перецентрирование, для этого требуется преодоление определенного психологического барьера. Перецентрирование легче осуществлять людям, которые получили возможность поупражняться в этом занятии. Мы разработали систему задач на материале планиметрии 7 – 9 классов, выполняя которые учащиеся смогут получить опыт перецентрирования. Это облегчит им в дальнейшем возможность производить перецентрирование в процессе решения различных задач. Вообще говоря, решение практически любой достаточно сложной задачи по планиметрии, как и по любому другому предмету, способствует развитию дивергентного мышления, т.к. в процессе такого решения происходит неоднократное изменение направления мыслительной деятельности. Но при решении многих задач учителю бывает сложно управлять ходом мыслей учеников. Мы же разработали задания, при решении которых в определенные моменты можно организовать процесс перецентрирования ученика. Эти задания мы так и назвали – задачи на «перецентрирование».
Однако в ходе нашего исследования мы выяснили, что при решении задач по планиметрии происходит дивергенция разных видов. Для успешного решения задач нужно овладеть дивергенцией каждого вида. Но для этого необходимы не просто задачи на «перецентрирование», а система таких задач. Это согласуется с современными воззрениями методистов. Различные ученые сходятся к мысли, что ни одна задача, решаемая изолированно, не дает желаемого результата, не позволяет добиться общей цели. Необходимо учитывать не только особенности каждой конкретной задачи, но и ее место среди других задач, выявлять вклад данной задачи в достижение поставленной цели, иными словами, необходимо организовать задачи в систему. Организация задач в систему рассматривалась различными авторами (С.П. Поленкова, Г.В. Дорофеев, Н.Г. Килина, Г. И. Саранцев, Т.М. Калинкина, И.И. Зубова, В.П. Радченко, Ф.М. Юнусов, В.В. Гузеев, И.В. Кононенко, Л.Д. Белова).
Наиболее удачным нам представляется определение О.Н Орлянской, которая под системой задач понимает совокупность упорядоченных и подобранных в соответствии с поставленной целью задач, действующих, как одно целое, взаимосвязь и взаимодействие которых приводит к заранее намеченному результату [8]. В нашем случае результатом является развитие дивергентного мышления учащихся в процессе обучения их анализу текста задачи. При разработке системы задач на «перецентрирование» мы руководствовались основными принципами: полнота системы, иерархичность системы, связность системы, определенная последовательность задач в системе.
Полнота системы в нашем случае проявляется в наличии задач на все виды дивергенции, происходящей при анализе текста задачи. В ходе нашего исследования мы пришли к выводу, что на этапе анализа текста задачи по планиметрии происходит всего четыре различных вида дивергенции.
Первый вид дивергенции возникает при анализе словесной формулировки задачи. При работе с формулировкой мы ищем различные способы переформулировать условие и требование задачи, выявляем различные значения и смыслы понятий, входящих в формулировку, выводим различные следствия из того, что дано и т.д. Чем больше направлений мысли при этом возникнет, тем больше шансов на успех в решении задачи.
Второй вид дивергенции возникает при анализе чертежа (это может быть и данный чертеж, и чертеж, выполненный нами по словесной формулировке). При работе с чертежом мы стремимся вычерпать всю возможную информацию из чертежа. Мы рассматриваем чертеж под разными углами зрения, выявляем различные связи и отношения, в которых находятся изображенные фигуры, пробуем делать различные дополнительные построения и т.д. Поэтому при работе с чертежом тоже нужна активная дивергенция.
Третий вид дивергенции возникает при анализе фигуры, описанной в задаче, на предмет ее существования. В тот момент, когда человек, стремящейся выполнить требование задачи задумывается над вопросом, а существует ли описанная в задаче фигура, происходит дивергенция, поскольку человек мыслит уже в другом направлении.
Четвертый вид дивергенции возникает при анализе фигуры, описанной в задаче, на предмет ее единственности. При переходе от одной ситуации, к которой применимо условие задачи, к другой ситуации, к которой оно также применимо происходит дивергенция, поскольку человек мыслит в разных направлениях.
Иерархичность системы означает, что наша система состоит из нескольких подсистем, каждая из которых в свою очередь является системой, обладающей свойством полноты. В нашей системе четыре подсистемы (каждому виду дивергенции при анализе текста задачи соответствует своя подсистема).
Рассмотрим в качестве примера подсистему, соответствующую второму виду дивергенции – дивергенции при анализе чертежа. Для того чтобы проанализировать сложный чертеж, получив всю возможную информацию из чертежа, человеку требуется способность к перецентрированию, связанному с возможностью изменять точку зрения на чертеж. Используя психологическую терминологию можно сказать, что в процессе анализа чертежа человек выделяет различные объекты из фона [4]. В рамках психологии установлено, что когда человек смотрит на что-либо, воспринимаемая реальность разделяется как бы на два слоя: на объект и на фон. При этом объект воспринимается как конкретное, четко очерченное замкнутое целое, а фон – как нечто более аморфное, неопределенное. Причем, соотношение объекта и фона – это соотношение динамическое. То есть то, что в данный момент в процессе восприятия чертежа относится к фону, может через некоторое время стать объектом, и наоборот, то, что было объектом, может стать фоном.
В ходе нашего исследования мы пришли к выводу, что можно выделить три вида объектов, которые выделяются из фона при работе с чертежом: геометрические фигуры; геометрические фигуры, находящиеся в некотором отношении с данной геометрической фигурой; пары геометрических фигур, находящихся в некотором отношении между собой.
Для того чтобы учащиеся научились анализировать чертеж в процессе решения задач, необходимо чтобы они получили опыт перецентрирования при выделении из фона объектов каждого из трех видов. Поэтому естественно выделить три вида заданий на выделение объектов из фона.
Вид 1. Задания на выделение в качестве объектов различных геометрических фигур заданного типа.
Пример № 1. Найдите на чертеже 3 параллелограмма (рис. 1).
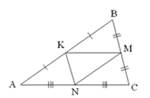
рис. 1.
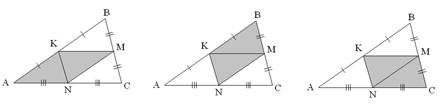
рис. 2.
В данном примере необходимо выделять из фона параллелограммы. Организовать работу с данным заданием можно следующим образом: учащиеся получают карточки с тремя одинаковыми чертежами. Выделенные из фона фигуры они заштриховывают, используя для каждой следующей фигуры новый чертеж, как показано ниже (рис. 2).
Вид 2. Задания на выделение в качестве объектов различных геометрических фигур заданного типа, находящихся в определенном отношении с данной фигурой.
Пример № 1. Найдите на чертеже 4 многоугольника, описанных около окружности (рис. 3.).
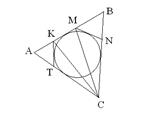
рис. 3.
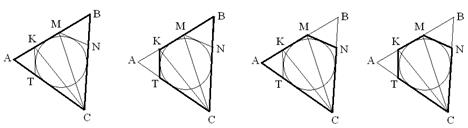
рис. 4.
В данном примере данной фигурой является окружность, а выделять из фона необходимо многоугольники, но не все – а только те, которые находятся в определенном отношении с данной фигурой, а именно: описанные около окружности. При работе с подобными заданиями учащиеся могут не заштриховывать, а обводить контуры выделенных из фона фигур, как показано ниже (рис. 4).
Вид 3. Задания на выделение в качестве объектов различных пар геометрических фигур заданного типа, находящихся в определенном отношении.
Пример. Найдите на чертеже 8 пар равных треугольников (рис. 5).
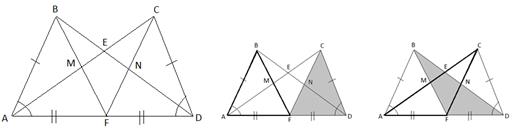
рис. 5. рис. 6.
В данном примере выделять из фона необходимо треугольники, находящиеся в определенном отношении, а именно: в отношении равенства. Фигуры, которые необходимо выделить из фона, могут пересекаться. Поэтому удобно одну из них заштриховать, а у другой выделить контур, как показано ниже (рис.6).
Еще одним принципом, которому должна удовлетворять система задач на «перецентрирование» является связность. Связность системы означает, что вся совокупность задач может быть представлена связным графом, в узлах которого – основные задачи, выше них подготовительные и вспомогательные, ниже – следствия, обобщения и т.д.
Для развития дивергентного мышления используется, прежде всего, основная задача – это достаточно сложная задача, при решении которой наблюдается момент перецентрирования. Однако основной задачи недостаточно, поскольку взятая изолированно она вызывает ряд проблем. Для решения этих проблем используется набор задач, сопутствующих основной задаче. Сопутствующие задачи можно разделить на следующие типы: мотивационная задача, задача на актуализацию знаний, подготовительная задача, вспомогательная задача.
Прежде всего, для решения основной задачи требуется высокий уровень мотивации. Для формирования необходимого уровня мотивации используется мотивационная задача – задача, связанная по содержанию с основной задачей и призванная вызвать интерес к основной задаче. Мотивационная задача может быть привлекательной для учащихся по разным причинам, например, за счет того, что она связана с их субъектным опытом, или же в процессе ее решения привлекается материал по психологии, рассматривается некоторое противоречие, рассматриваются разные мнения по одному и тому же вопросу и т.д. Важно чтобы мотивационная задача казалась учащимся несложной. Мотивационная задача предлагается обычно в начале урока.
Например, в качестве мотивационной задачи для задач на «выделение объектов из фона» можно использовать тест на сложные фигуры, содержащие в своем составе простые фигуры. Можно предложить найти простую фигуру (рис. 7) в составе сложной фигуры (рис. 8) и выделить ее другим цветом. При этом получится изображение, представленное на рис. 9.
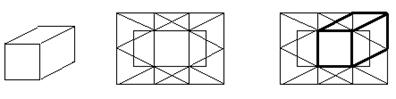
рис. 7. рис. 8. рис. 9.
Для того чтобы учащиеся поупражнялись в перецентрировании, можно предложить им найти все четыре параллелепипеда на чертеже, каждый раз выделяя их другим цветом (для этого понадобятся несколько однотипных изображений сложной фигуры.
Кроме того, возможна ситуация, когда основная задача оказывается непосильной для учащихся. Проблема, как правило, связана с тем, что у учащихся либо не хватает знаний для решения задачи, либо задача перенасыщена деталями (загруженный чертеж, большое количество ситуации, к которым применимо условие задачи и т.д.). В первом случае (если, например, задача содержит термин, недостаточно знакомый учащимся) применяется задача на актуализацию знаний. Важно чтобы в процессе работы с такой задачей происходило выявление и коррекция субъектного опыта учащихся, связанного с недостаточно освоенным материалом [10]. Если же проблема связана с тем, что основная задача перенасыщена деталями, то применяются подготовительные и вспомогательные задачи. Как подготовительная, так и вспомогательная задача является упрощением основной задачи. Причем, одна и та же задача может быть и подготовительной, и вспомогательной. Все зависит от ее местоположения. Подготовительная задача дается до предъявления основной задачи, а вспомогательная – после предъявления основной задачи. Целесообразность данной методики определяется следующим: для того чтобы учащиеся успешно решали задачи на «перецентрирование», необходимо чтобы они, работая с текстом задачи, научились составлять вспомогательные задачи-упрощения основной задачи. Для обучения этому учитель применяет подготовительные и вспомогательные задачи. Подготовительную задачу составляет сам учитель, если он предполагает, что основная задача вызовет затруднения у учащихся. Вспомогательная задача составляется после предъявления основной задачи в процессе совместной работы учителя с детьми с тем, чтобы впоследствии дети научились при необходимости самостоятельно составлять такие задачи. Так, если работа с загруженным чертежом вызывает затруднения у учащихся, необходимо предлагать им подготовительные и вспомогательные задачи, позволяющие работать с менее загруженным чертежом.
Еще одним принципом, которому должна удовлетворять система задач на «перецентрирование» является определенная последовательность задач в системе. В нашем случае это означает, что при работе с определенным понятием сначала изучаются задачи, соответствующие первому и второму виду дивергенции, а только потом задачи, соответствующие третьему и четвертому виду дивергенции. Задачи на первый и второй вид дивергенции даются на этапе введения нового материала. Задачи на третий и четвертый вид дивергенции даются на этапе повторения.
Например, задачи на «выделение объекта из фона» целесообразно предлагать на этапе введения и первичного закрепления понятия. При введении определения новой фигуры (независимо от того, индуктивным или дедуктивным способом это делается) предлагается набор задач на распознавание. В этот набор целесообразно включать задачи на «выделение из фона», используя при этом загруженные чертежи. Работу с задачами на распознавание целесообразно проводить в два этапа. На первом этапе предлагать простые чертежи, содержащие одну фигуру, по поводу которой нужно определить, принадлежит она объему некоторого понятия или нет. На втором этапе можно предлагать загруженные чертежи, их сложность должна постепенно увеличиваться. Такой чертеж должен содержать несколько фигур, принадлежащих объему изучаемого понятия.
Выводы
В ходе опытно-экспериментальной работы были определены пути развития дивергентного мышления через систему задач на перецентрирование, включающую несколько подсистем. С задачами каждой организуется определенная работа, что позволит достичь общей цели – развития дивергентного мышления учащихся и одновременно будет способствовать обучению учащихся решению задач по планиметрии.
Рецензенты:
Снегурова В.И., д.п.н., профессор, зав. кафедры методики обучения математике и информатике РГПУ им. А.И.Герцена, г. Санкт-Петербург;
Татьяна С.Б., д.п.н, профессор, директор научно-образовательного центра «Ломоносовский институт», профессор кафедры педагогики САФУ им. М.В.Ломоносова, г. Санкт-Петербург.
Библиографическая ссылка
Калинова Ю.А., Подходова Н.С. СИСТЕМА ЗАДАЧ НА «ПЕРЕЦЕНТРИРОВАНИЕ» КАК СРЕДСТВО РАЗВИТИЯ ДИВЕРГЕНТНОГО МЫШЛЕНИЯ // Современные проблемы науки и образования. – 2015. – № 6.
;
URL: https://science-education.ru/ru/article/view?id=23362 (дата обращения: 24.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
В этой статье посмотрим, как определяются координаты центра тяжести сложной фигуры — состоящей из простых. В задачах по сопромату часто приходится находить положение центра тяжести составных сечений, для дальнейшего вычисления моментов инерции и т. д.
Также часто, при изучении теоретической механики, студентам предлагается решить подобную задачу, и найти центр тяжести какой-нибудь фигуры.
Условие задачи
Предлагаю рассмотреть следующую фигуру:

В сопромате принято заштриховывать сечения тонкими линиями, вот так:

В своих же уроках я буду использовать заливку. Так, штриховка не будет мешать наносить обозначения.
Разбивка сложной фигуры на простые
Как видишь, сечение состоит из прямоугольника, прямоугольного треугольника, четверти круга, а также имеет круглый вырез:

Отметим центры тяжести (С1, С2, С3, С4) каждой отдельной фигуры, с учётом справочной информации.
Открой эту страничку, и пока не закрывай, она нам ещё понадобится!

Покажем вспомогательные оси (x0, y0) для всего сечения, которые будем использовать для нахождения положения центра тяжести (C):

Как определить положение центра тяжести?
Чтобы определить координату центра тяжести сечения, например, вертикальное расстояние от оси x0 до центра тяжести сечения (yc):

Нужно статический момент сечения относительно этой вспомогательной оси (x0) разделить на площадь всего сечения (A):

Площадь всего сечения (A) найти просто – это алгебраическая сумма площадей всех фигур:

Статический момент сечения, относительно вспомогательной оси будет равен алгебраической сумме статических моментов каждой фигуры (с учётом знака):

где Ai – площадь отдельной фигуры;
yi – расстояние от центра тяжести отдельной фигуры до вспомогательной оси (x0).
Координата центра тяжести (xc), находится аналогично:

Определение площади сечения
Для начала предлагаю сделать самое простое, используя формулы, указанные на этой странице, найти площадь всего сечения (A):


Как видишь, круглый вырез, нужно учесть с «минусом», что очевидно.
Определение расстояний от вспомогательных осей до центров тяжести отдельных фигур
Найдём расстояния от вспомогательных осей (x0, y0) до центров тяжести отдельных фигур, опять же, используя нашу шпаргалку:
Определение статических моментов
Определяем статические моменты сечения относительно вспомогательных осей (x0, y0):


Важно! Статические моменты могут быть и отрицательными.
Определение координат центра тяжести
И, наконец, определяем положение центра тяжести всего сечения (C):

Покажем центр тяжести всего сечения (C):

Если остались какие-то вопросы по данному уроку, можешь смело задавать их в комментариях. Также, другие уроки, на сайте – ssopromat.ru, по определению геометрических характеристик, можешь найти здесь.