Как найти простую скользящую среднюю

Как найти простую скользящую среднюю

График исходной функции (синий) и его скользящая средняя (красная) с шириной окна n = 2

Скользя́щая сре́дняя, скользя́щее сре́днее (англ. moving average, MA) — общее название для семейства функций, значения которых в каждой точке определения равны некоторому среднему значению исходной функции за предыдущий период.

Скользящие средние обычно используются с данными временных рядов для сглаживания краткосрочных колебаний и выделения основных тенденций или циклов[1][2].

Математически скользящее среднее является одним из видов свёртки.

Применение[править | править код]

Скользящие средние используются:

  • В статистике и экономике для сглаживания числовых рядов (в первую очередь временных). Например, для оценки ВВП, показателей занятости или других макроэкономических индикаторов.
  • В технике, при обработке сигналов, анализе систем. См. Скользящая средняя (фильтр).
  • В техническом анализе, в качестве самостоятельного технического индикатора либо в составе других инструментов, см. Скользящая средняя (индикатор).

Этимология[править | править код]

Так как при расчёте скользящего среднего значение функции вычисляется каждый раз заново[2], при этом учитывается конечное значимое[3] множество предыдущих значений, скользящее среднее «перемещается» (движется), как бы «скользя» по временному ряду.

Виды скользящих средних[править | править код]

Общий случай[править | править код]

В общем случае, взвешенные скользящие средние вычисляются по формуле[2]:

{textit {WWMA}}_{t}=sum _{{i=0}}^{{n-1}}w_{{t-i}}cdot p_{{t-i}}, (WWMA 1)
где {textit {WWMA}}_{t} — значение взвешенного скользящего среднего в точке t;
n — количество значений исходной функции для расчёта скользящего среднего;
w_{{t-i}} — нормированный вес (весовой коэффициент) t-i-го значения исходной функции;
p_{{t-i}} — значение исходной функции в момент времени, отдалённый от текущего на i интервалов.

Нормирование весовых коэффициентов означает, что[2]:

sum _{{i=0}}^{{n-1}}w_{{t-i}}=1.

Указанную выше формулу с произвольными значениями весовых коэффициентов можно переписать в виде:

{textit {WWMA}}_{t}={frac {sum _{{i=0}}^{{n-1}}W_{{t-i}}cdot p_{{t-i}}}{sum _{{i=0}}^{{n-1}}W_{{t-i}}}}, (WWMA 2)
где {textit {WWMA}}_{t} — значение взвешенного скользящего среднего в точке t;
n — количество значений исходной функции для расчёта скользящего среднего;
W_{{t-i}} — вес (весовой коэффициент) t-i-го значения исходной функции;
p_{{t-i}} — значение исходной функции в момент времени, отдалённый от текущего на i интервалов.

Весовые коэффициенты в формулах (WWMA 1) и (WWMA 2) соотносятся как:

w_{{t-i}}={frac {W_{{t-i}}}{sum _{{i=0}}^{{n-1}}W_{{t-i}}}}.

Зачастую, в качестве веса используют либо 1 (для простого скользящего среднего — SMA), либо формальные ряды, например, арифметическая прогрессия (WMA) или экспоненциальная функция (EMA). Но в качестве весового коэффициента могут выступать и значения связанного временного ряда. Например, для взвешивания биржевых цен по объёмам сделки (VMA) в качестве p_{{t-i}} следует рассматривать цену сделки по инструменту, а в качестве W_{{t-i}}=V_{{t-i}} — объём в момент времени t-i:

{textit {VMA}}_{t}={frac {sum _{{i=0}}^{{n-1}}V_{{t-i}}cdot p_{{t-i}}}{sum _{{i=0}}^{{n-1}}V_{{t-i}}}}.

Простое скользящее среднее[править | править код]

Исходная функция и её простые скользящие средние по четырём значениям (n = 4).
Зелёная линия — центрирование по середине интервала (истинное положение).
Красная линия — сдвиг графика вправо к последнему значению окна.

Простое скользящее среднее, или арифметическое скользящее среднее (англ. simple moving average, англ. SMA) численно равно среднему арифметическому значений исходной функции за установленный период[1] и вычисляется по формуле[2]:

{displaystyle {textit {SMA}}_{t}={frac {1}{n}}sum _{i=0}^{n-1}p_{t-i}=}

{displaystyle ={frac {p_{t}+p_{t-1}+cdots +p_{t-i}+cdots +p_{t-n+2}+p_{t-n+1}}{n}},}
где {textit {SMA}}_{t} — значение простого скользящего среднего в точке t;
n — количество значений исходной функции для расчёта скользящего среднего (сглаживающий интервал[1]), чем шире сглаживающий интервал, тем более плавным получается график функции[1];
p_{{t-i}} — значение исходной функции в точке t-i.

Полученное значение простой скользящей средней относится к середине выбранного интервала[1], однако, традиционно его относят к последней точке интервала[2].

Из предыдущего своего значения простое скользящее среднее может быть получено по следующей рекуррентной формуле[2]:

{textit {SMA}}_{t}={textit {SMA}}_{{t-1}}-{frac {p_{{t-n}}}{n}}+{frac {p_{{t}}}{n}},
где {textit {SMA}}_{t} — значение простого скользящего среднего в точке t, {textit {SMA}}_{{t-1}} — предыдущее значение простого скользящего среднего;
p_{{t-n}} — значение исходной функции в точке t-n (в случае временного ряда, самое «раннее» значение исходной функции, используемое для вычисления предыдущей скользящей средней);
p_{{t}} — значение исследуемой функции в точке t (в случае временного ряда, текущее — последнее значение).

Данной формулой удобно пользоваться, чтобы избежать регулярного суммирования всех значений.

Например, простое скользящее среднее для временного ряда с количеством периодов равным 10 вычисляется как:

{displaystyle {textit {SMA}}_{t}={frac {p_{t}+p_{t-1}+p_{t-2}+p_{t-3}+p_{t-4}+p_{t-5}+p_{t-6}+p_{t-7}+p_{t-8}+p_{t-9}}{10}}=}

{displaystyle ={textit {SMA}}_{t-1}-{frac {p_{t-10}}{10}}+{frac {p_{t}}{10}},}
где {textit {SMA}}_{t} — значение простого скользящего среднего в точке t;
p_{{t-i}} — значение исходной функции в момент времени, отдалённый от текущего на i интервалов.

Выделяют следующие недостатки простого скользящего среднего[2]:

  1. Равенство весового коэффициента 1.
  2. Двойная реакция на каждое значение (смотрите рекуррентную формулу): в момент входа в окно вычислений и в момент выхода из него.

Взвешенные скользящие средние[править | править код]

Общие положения[править | править код]

Иногда при построении скользящей средней некоторые значения исходной функции целесообразно сделать более значимыми.
Например, если предполагается, что внутри интервала сглаживания имеет место нелинейная тенденция[1], или, в случае временных рядов, последние — более актуальные — данные могут быть весомее предыдущих.

Бывает, что исходная функция многомерна, то есть представлена сразу несколькими связанными рядами. В этом случае может возникнуть необходимость объединить в итоговой функции скользящей средней все полученные данные. Например, временные ряды биржевых цен обычно для каждого момента времени представлены как минимум двумя значениями — ценой сделки и её объёмом. Необходим инструмент для вычисления скользящей средней цены, взвешенной по объёму.

В этих и подобных случаях применяются взвешенные скользящие средние.

Взвешенное скользящее среднее[править | править код]

Веса значений исходной функции при вычислении WMA с n = 15

Взве́шенное скользящее среднее (англ. weighted moving average — англ. WMA), точнее линейно взвешенное скользящее среднее — скользящее среднее, при вычислении которого вес каждого члена исходной функции, начиная с меньшего, равен соответствующему члену арифметической прогрессии. То есть, при вычислении WMA для временного ряда, мы считаем последние значения исходной функции более значимыми чем предыдущие, причём функция значимости линейно убывающая.

Например, для арифметической прогрессии с начальным значением и шагом, равным 1, формула вычисления скользящей средней примет вид[2]:

{displaystyle {textit {WMA}}_{t}={frac {ncdot p_{t}+(n-1)cdot p_{t-1}+cdots +(n-i)cdot p_{t-i}+cdots +2cdot p_{t-n+2}+1cdot p_{t-n+1}}{n+(n-1)+cdots +(n-i)+cdots +2+1}}=}

{displaystyle ={frac {2}{ncdot (n+1)}}sum _{i=0}^{n-1}(n-i)cdot p_{t-i},}
где {textit {WMA}}_{t} — значение взвешенного скользящего среднего в точке t;
n — количество значений исходной функции для расчёта скользящего среднего, : : p_{{t-i}} — значение исходной функции в момент времени, отдалённый от текущего на i интервалов.

При этом знаменатель функции, в этом случае, равен треугольному числу — сумме членов арифметической прогрессии с начальным членом и шагом равными 1:

{frac {ncdot (n+1)}{2}}.

Экспоненциально взвешенное скользящее среднее[править | править код]

Веса значений исходной функции при вычислении EMA с n = 15

Экспоненциально взвешенное скользящее среднее, экспоненциальное скользящее среднее (англ. exponentially weighted moving average — англ. EWMA, англ. exponential moving average — англ. EMA) — разновидность взвешенной скользящей средней, веса которой убывают экспоненциально и никогда не равны нулю[3]. Определяется следующей формулой[1][2][4][5][6]:

{textit {EMA}}_{t}=alpha cdot p_{t}+(1-alpha )cdot {textit {EMA}}_{{t-1}},
где {textit {EMA}}_{t} — значение экспоненциального скользящего среднего в точке t (последнее значение, в случае временного ряда);
{textit {EMA}}_{{t-1}} — значение экспоненциального скользящего среднего в точке t-1 (предыдущее значение в случае временного ряда);
p_{t} — значение исходной функции в момент времени t (последнее значение, в случае временного ряда);
alpha  — (сглаживающая константа от англ. smoothing constant) коэффициент характеризующий скорость уменьшения весов, принимает значение от 0 и до 1, чем меньше его значение тем больше влияние предыдущих значений на текущую величину среднего.

Первое значение экспоненциального скользящего среднего, обычно принимается равным первому значению исходной функции:

{textit {EMA}}_{0}=p_{0}.

Коэффициент alpha , может быть выбран произвольным образом, в пределах от 0 до 1. Например, он может быть выражен через величину окна усреднения:

alpha ={frac {2}{n+1}}.

Экспоненциальное скользящее среднее произвольного порядка[править | править код]

Веса экспоненциально взвешенной скользящей средней третьего порядка — TMA с окном n=10.

В обычном экспоненциальном скользящем среднем сглаживанию подвергаются значения исходной функции, однако, сглаживанию могут подвергаться и значения результирующей функции[2].
Поэтому некоторые авторы определяют понятие экспоненциальные скользящее среднее произвольного порядка[2], которые вычисляются по формуле:

{textit {EMA}}_{t}^{{(n)}}=alpha cdot {textit {EMA}}_{t}^{{(n-1)}}+(1-alpha )cdot {textit {EMA}}_{{t-1}}^{{(n)}},
где {textit {EMA}}_{t}^{{(n)}} — значение экспоненциального скользящего среднего n-го порядка в точке t (последнее значение, в случае временного ряда);
{textit {EMA}}_{{t-1}}^{{(n)}} — значение экспоненциального скользящего среднего n-го порядка в точке t-1 (предыдущее значение в случае временного ряда);
{EMA}_{t}^{{(n-1)}} — значение экспоненциального скользящего среднего (n-1)-го порядка в точке t (последнее значение, в случае временного ряда);
alpha  — сглаживающая константа.

Экспоненциально взвешенные скользящие средние второго и третьего порядка обозначают иногда как, соответственно {textit {DMA}} (от англ. double exponential moving average — двойное (двукратное) экспоненциальное скользящее среднее) и {textit {TMA}} (от англ. triple exponential moving average — тройное (трёхкратное) экспоненциальное скользящее среднее)[2]:

{textit {DMA}}_{t}=alpha cdot {textit {EMA}}_{t}+(1-alpha )cdot {textit {DMA}}_{{t-1}},
{textit {TMA}}_{t}=alpha cdot {textit {DMA}}_{t}+(1-alpha )cdot {textit {TMA}}_{{t-1}}.

Модифицированное скользящее среднее[править | править код]

Модифицированное скользящее среднее (от англ. modified moving average — англ. MMA; иногда называемое англ. running moving average — англ. RMA и англ. smoothed moving average) определятся как:

{text{MMA}}_{t}={frac {p_{t}+(n-1)cdot {text{MMA}}_{{t-1}}}{n}},
где {textit {MMA}}_{t} — значение модифицированного скользящего среднего в точке t (последнее значение, в случае временного ряда);
{textit {MMA}}_{{t-1}} — значение модифицированного скользящего среднего в точке t-1 (предыдущее значение в случае временного ряда);
n — количество значений исходной функции для расчёта скользящего среднего (сглаживающий интервал).

Несложно заметить, что модифицированное скользящее среднее является частным случаем экспоненциального скользящего среднего, для которого сглаживающая константа равна обратному значению величины сглаживающего интервала:

alpha ={frac {1}{n}}.

Смежные функции[править | править код]

Скользящие на основе других усредняющих функций[править | править код]

По аналогии со скользящими средними значениями, построенными на основе арифметического среднего, можно использовать и другие усредняющие функции (среднее степенное: среднее квадратическое, среднее гармоническое и т. д.; среднее геометрическое; медиану и т. п.) и их взвешенные аналоги. Конкретный выбор зависит от природы исследуемой исходной функции.

Простая скользящая медиана[править | править код]

Простая скользящая медиана (англ. simple moving median — англ. SMM) — функция, значение которой в каждой точке определения численно равна медиане значений исходной функции за установленный период:

{textit {SMM}}_{t}={text{Median}}(p_{t},p_{{t-1}},ldots ,p_{{t-n+1}}),
где {textit {SMM}}_{t} — значение простой скользящей медианы в точке t;
n — количество значений исходной функции для расчёта скользящей медианы (сглаживающий интервал);
p_{{t-i}} — значение исходной функции в точке t-i.

Динамические скользящие средние[править | править код]

В 1990-х годах был предложен ряд скользящих средних с динамически изменяемой шириной окна (или сглаживающим коэффициентом), смотрите, например, Адаптивная скользящая средняя Кауфмана.

Кумулятивное скользящее среднее[править | править код]

Кумулятивное скользящее среднее (англ. cumulative moving average) численно равно среднему арифметическому значений исходной функции за весь период наблюдений:

{textit {CA}}_{t}={frac {1}{t}}sum _{{i=1}}^{{t}}p_{i}={frac {p_{t}+p_{{t-1}}+cdots +p_{{2}}+p_{{1}}}{t}},
где {textit {CA}}_{t} — кумулятивное скользящее среднее в момент t;
t — количество доступных для вычисления интервалов;
p_{i} — значение исходной функции в точке i.

В реальных вычислениях, когда предыдущее значение кумулятивного скользящего среднего известны, применяются также следующие формулы:

{textit {CA}}_{t}={frac {p_{t}+(t-1)cdot {textit {CA}}_{{t-1}}}{t}}={textit {CA}}_{{t-1}}+{frac {p_{t}-{textit {CA}}_{{t-1}}}{t}},
где {textit {CA}}_{t} — кумулятивное скользящее среднее в момент t;
{textit {CA}}_{{t-1}} — кумулятивное скользящее среднее в момент t-1 (предыдущее значение, в случае временного ряда);
p_{t} — значение исходной функции в момент времени t (в случае временного ряда — последнее значение);
t — количество доступных, для вычисления интервалов, причём {textit {CA}}_{0}=0.

Кумулятивная сумма[править | править код]

Кумулятивное скользящее среднее не следует путать с кумулятивной суммой, которая вычисляется суммированием всех значений ряда нарастающим итогом:

{textit {Cumulative}}_{t}=p_{t}+{textit {Cumulative}}_{{t-1}}=sum _{{i=1}}^{{t}}p_{i}=p_{t}+p_{{t-1}}+cdots +p_{{2}}+p_{{1}},
где {textit {Cumulative}}_{t},{textit {Cumulative}}_{{t-1}} — текущее и предыдущее значения кумулятивной суммы;
p_{i} — значение исходного ряда в момент i.

См. также[править | править код]

  • Авторегрессионная модель: Модель авторегрессии — скользящего среднего, Модель скользящего среднего
  • Окно (весовая функция)

Примечания[править | править код]

  1. ↑ 1 2 3 4 5 6 7 Грешилов А. А., Стакун В. А., Стакун А. А. Математические методы построения прогнозов. — М.: Радио и связь, 1997. — 112 с. — ISBN 5-256-01352-1.
  2. ↑ 1 2 3 4 5 6 7 8 9 10 11 12 13 Булашев С. В. Статистика для трейдеров. — М.: Компания Спутник+, 2003. — 245 с.
  3. ↑ 1 2 При расчёте экспоненциально взвешенного скользящего среднего теоретически учитываются все значения временного ряда, однако, на практике, начиная с какого-то вклад исходных значений ниже погрешности вычислений. Поэтому ими можно пренебречь и считать множество предыдущих значений конечным.
  4. ↑ В некоторых источниках используется «обратное» представление данной формулы:
    {textit {EMA}}_{t}=(1-alpha )cdot p_{t}+alpha cdot {textit {EMA}}_{{t-1}},

    Математического смысла это не меняет, однако, при использовании и анализе следует внимательно отнестись к контекстному определению.

  5. ↑ Single Exponential Smoothing Архивная копия от 10 марта 2011 на Wayback Machine (англ.) на сайте Национального института стандартов и технологий США.
  6. ↑ EWMA Control Charts Архивная копия от 4 марта 2011 на Wayback Machine (англ.) на сайте Национального института стандартов и технологий США.
Источник

Уровень сложности
Средний

Время на прочтение
8 мин

Количество просмотров 3.1K

Автор статьи: Роман Козлов

Руководитель курса BI-аналитика

Введение

В современном мире данных анализ временных рядов играет ключевую роль во многих отраслях, таких как финансы, розничная торговля, производство и маркетинг. Работа с временными рядами может стать сложным процессом из- за наличия трендов, сезонности и структурных изменений в данных.

Я продолжаю рассказывать о полезных, но менее известных методах работы с данными в Pandas, которые могут значительно повысить вашу эффективность при анализе и обработке данных. По данной ссылке вы можете прочитать первую статью.

В этой статье мы погрузимся в применение скользящих окон для вычислений и смещение данных для анализа временных рядов. Скользящие окна позволяют проводить агрегированные вычисления на подмножествах данных, что может быть полезно для определения трендов, сезонности и аномалий во временных рядах. Мы также изучим использование смещения данных для создания лаговых переменных и их применение в различных задачах прогнозирования. 

Методы работы с временными рядами

Умение работать с временными рядами играет важную роль в прогнозировании различных явлений, оценке трендов текущих событий и анализе влияния сезонных составляющих. Временные ряды представляют собой один из самых распространенных типов данных во многих отраслях, таких как финансы, маркетинг, экономика, здравоохранение, погодные данные и многих других.

Временные ряды – это последовательности данных, измеренных через равные промежутки времени, которые помогают представить динамику изменений значений во времени.

Прогнозирование явлений на основе временных рядов заключается в использовании исторических данных для предсказания будущих значений. Это может включать прогнозирование продаж, акций, погодных условий, экономических показателей и многих других величин.

Оценка тренда текущих событий – это процесс выявления общего направления изменений во времени на основе анализа исторических данных. Тренды могут быть восходящими, нисходящими или горизонтальными. Определение трендов помогает аналитикам лучше понимать долгосрочное направление изменений и предоставлять прогнозы на основе этих наблюдений. Важно отметить, что тренды могут быть долгосрочными, краткосрочными или сезонными, и их выявление может быть основой для адаптации стратегий и принятия более обоснованных решений.

Анализ сезонных составляющих во временных рядах позволяет оценить влияние сезонных факторов на изучаемые явления. Сезонность – это повторяющиеся колебания значений, связанные с определенными временными периодами, такими как месяцы, кварталы или годы. Например, продажи могут увеличиваться перед праздниками или снижаться в определенные сезоны, а температура и осадки также имеют свои сезонные закономерности.

Аналитики, владеющие навыками работы с временными рядами, могут применять разнообразные методы для анализа и прогнозирования данных, включая статистические модели, эконометрические подходы и машинное обучение. Они могут выявлять сезонные и трендовые составляющие, а также адаптировать свои модели, чтобы учесть эти факторы при прогнозировании будущих значений.

Применение скользящих оконных функций, о которых мы сегодня поговорим, относится к статистическим моделям работы с временными рядами. Такие модели используют вычисление скользящего среднего (MA или SMA) для прогнозирования значений временных рядов и обнаружения паттернов.

Скользящие средние в Pandas, метод rolling()

Скользящее среднее (также называемое “простое скользящее среднее” или “конечное скользящее среднее”) представляет собой среднее арифметическое значение наблюдений в определенном окне или периоде, который “скользит” вдоль временного ряда. Скользящее среднее помогает сгладить краткосрочные колебания и шумы, выявлять тренды и улавливать долгосрочные закономерности в данных.

Чтобы вычислить скользящее среднее, нужно определить размер окна (количество наблюдений, включенных в среднее) и, начиная с первого значения в временном ряду, взять среднее арифметическое значение наблюдений в этом окне. Затем окно сдвигается на одно наблюдение вперед, и процесс повторяется до тех пор, пока окно не достигнет конца временного ряда.

В общем виде формула вычисления простого скользящего среднего выглядит так:

SMA_{t}=frac{1}{n}sum_{i=0}^{n-1}p_{t-1}=frac{p_{t}+p_{t-1}+...+p_{t-i}+...+p_{t-n+2}+p_{t-n+1}}{n}

,где n – размер окна для расчёта скользящего среднего, а pt−i – значение исходной функции в точке t − i.

Например, если у нас есть временной ряд данных 4, 5, 6, 7, 8, 9 и размер окна равен 3, то скользящее среднее будет вычислено следующим образом:

SMA3 = (4 + 5 + 6)/3 = 5
SMA4 = (5 + 6 + 7)/3 = 6
SMA5 = (6 + 7 + 8)/3 = 7
SMA6 = (7 + 8 + 9)/3 = 8

Начинаем мы считать с SMA3, так как размер окна равен 3. Именно после третьего элемента временного ряда у нас есть достаточное количество элементов для вычисления среднего значения по окну размером 3.

Поэтому, первое скользящее среднее (для третьего элемента) вычисляется на основе первых трех элементов временного ряда 4, 5, 6. В данном случае индекс указывает на последний элемент окна для каждого расчета скользящего среднего.

Для вычисления скользящего среднего в Pandas реализован метод rolling(),который создает скользящее окно для проведения различных операций на окне данных. Скользящее окно имеет определенный размер и перемещается по временному ряду или другому набору данных с одним шагом за раз. Для каждого положения окна вычисляется статистика, такая как среднее, медиана, сумма и т. д.

При использовании метода rolling(), нужно указать размер окна с помощью параметра window. Затем можете применять различные функции к этому скользящему окну, например mean(), для вычисление скользящего среднего для конкретного элемента.

Таким образом, если взять временной ряд данных выше, то вычислить скользящее среднее для него можно следующим образом:

import pandas as pd

data = [4, 5, 6, 7, 8, 9]
df = pd.DataFrame(data, columns=["Значения"]) 

df["Скользящее_среднее"] = df["Значения"].rolling(window=3).mean()

Результаты вычисления скользящего среднего будут сохранены в одноименный столбик в датафрейме.

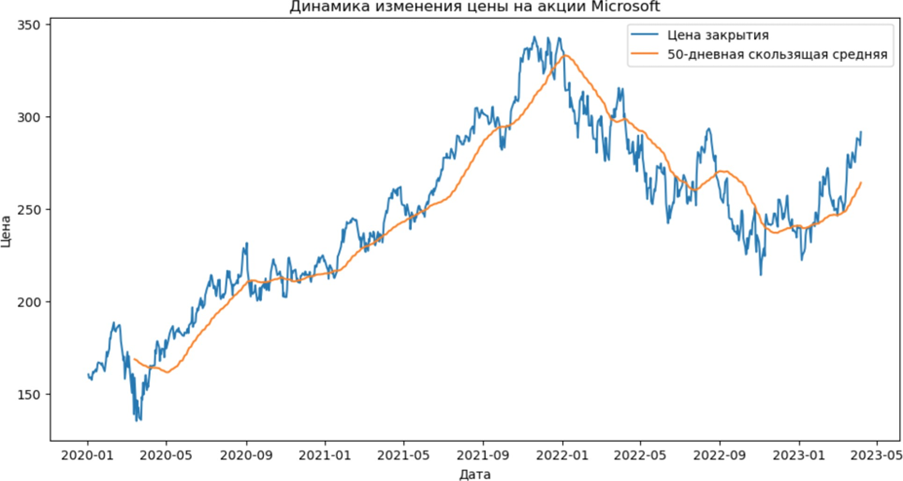
Давайте рассмотрим более интересный и приближенный к реальности пример, где вычисление скользящего среднего могут очень пригодится. Мы проанализируем ежедневное изменение цены на акции компании Microsoft за последние 2 года.

Сначала установим библиотеку yfinance, необходимую для получения цен для акции:

pip install yfinance

 Затем импортируем библиотеки для работы с данными:

import pandas as pd 
import yfinance as yf
import matplotlib.pyplot as plt

Мы используем метод download() библиотеки vfinance и сохраним показатели Open High Low Close Adi Close и Volume, которые характеризуют ежедневное изменение цены на акции Microsoft. 

msft = yf.download("MSFT", start="2020-01-01", end="2023-04-08")

Данные сохранятся в датафрейм, и мы сможем посчитать скользящее среднее для цены закрытия акций с размером окна 50 дней:

msft["SMA_50"] = msft["Close"].rolling(window=50).mean()

А далее мы просто нарисуем обычный линейный график, который отобразит динамику изменения цены закрытия за каждый день и скользящую среднюю за 50-дней.

plt.figure(figsize=(12, 6)) 
plt.plot(msft["Close"], label="Цена закрытия")
plt.plot(msft["SMA_50"], label="50-дневная скользящая средняя") 
plt.title("Динамика изменения цены на акции Microsoft") 
plt.xlabel("Дата")
plt.ylabel("Цена") 
plt.legend() 
plt.show()

Скользящая средняя за 50 дней на графике акций Microsoft помогает увидеть общий тренд и сгладить дневные колебания стоимости акций. Это позволяет аналитикам и инвесторам лучше понять, какие долгосрочные тенденции доминируют на рынке и определить восходящие или нисходящие тренды.

Например, видно, что нисходящий тренд на акции, который продолжался весь 2022 год сменился в начале 2023 года и теперь цены уверенно растут.

Скользящая средняя может давать аналитикам сигналы покупки и продажи акций в моменте пересечения линии цены акции и линии скользящей средней. Если цена акции пересекает скользящую среднюю снизу вверх, это может быть сигналом покупки. Если цена акции пересекает скользящую среднюю сверху вниз, это может быть сигналом продажи.

Однако стоит отметить, что такие сигналы могут быть ложными и необходимо дополнительное подтверждение от других технических индикаторов или анализа.

Смещение данных, метод shift()

Наряду с поиском устойчивых трендов, при помощи скользящей средней, анализ временных рядов также связан с изучением динамики относительных изменений исследуемых показателей. Это может включать в себя вычисление процентного изменения показателей относительно предыдущих значений, что позволяет выявить сезонность, цикличность и другие закономерности в изменениях показателей. Такой анализ может помочь более точно оценить, насколько значимы изменения в показателях, а также сделать более обоснованные выводы на основе данных временных рядов.

В Pandas для создания лаговых переменных можно использовать метод shift(). Он смещает данные на указанное количество строк вверх или вниз. Это полезно, когда нужно сравнить значения на текущей строке с

предыдущими или будущими значениями. Например, мы можем сместить данные на одну строку вниз, чтобы сравнить значения на текущей строке с предыдущей строкой. Мы также можем сместить данные на несколько строк вверх, чтобы сравнить значения на текущей строке с будущими значениями. Например, для создания лаговой переменной для временного ряд данных 4, 5, 6, 7, 8, 9с лагом 1, можно выполнить следующий код:

import pandas as pd

data = pd.Series([4, 5, 6, 7, 8, 9]) 
lag_1 = data.shift(1)

Мы получим новый столбик, который содержит данные из предыдущего временного ряда со смещением вперед на 1 период: [NaN, 4, 5, 6, 7, 8].

Лаговые переменные часто используются для расчета разностей между текущими и предыдущими значениями временного ряда. Это полезно при анализе стационарности и сезонности в данных.

С помощью следующего кода мы сможем теперь посчитать динамику абсолютного изменения показателя временного ряда:

difference = data - lag_1

Мы можем использовать метод shift() и рассчитать показатель ежедневного колебания цены закрытия на акции в процентах.

plt.figure(figsize=(12, 6))
plt.plot((msft.Close/msft.Close.shift(1) - 1)*100, label="Цена закрытия") plt.title("Ежедневные колебания цены закрытия на акции Microsoft") plt.xlabel("Дата")
plt.ylabel("Изменение в %") plt.legend()
plt.show()

На этом графике видно, что в начале 2020 года ежедневное изменение цены закрытия на акции Microsoft достигало 15%. Такая повышенная волатильность возможно связана с мировым локдауном, связанным с пандемией Covid-19.

Также с помощью методаshift()можно вычислять среднемесячные или среднегодовые изменения исследуемых показателей.

Например, чтобы рассчитать среднемесячное изменение цены закрытия акций, можно использовать методshift()с аргументом freq=pd.DateOffset(months=1), чтобы сдвинуть цену закрытия на один месяц назад. Затем можно рассчитать отношение текущей цены закрытия к цене закрытия месяц назад и вычесть из него единицу, чтобы получить процентное изменение цены за месяц.

Аналогично, можно использовать методshift()с аргументом freq=pd.DateOffset(months=1)для расчета среднегодовых изменений показателей.

Таким образом, методshift()представляет собой мощный инструмент для анализа временных рядов и позволяет извлекать ценную информацию из данных.

Заключение

В заключение можно отметить, что помимо методов сглаживания временных рядов и смещения данных в Pandas существует множество других методов работы с временными рядами, которые также могут быть полезны при анализе данных.

Например, одним из таких методов является экспоненциальное сглаживание, которое позволяет вычислять средневзвешенное значение временного ряда с изменяющимся весом, где наибольший вес у более свежих данных. Этот метод может быть особенно полезен в случаях, когда в данных присутствует сезонность или другие циклические изменения.

Еще одним методом является декомпозиция временных рядов на тренд, сезонность и остаток, что позволяет более детально проанализировать изменения в данных.

Кроме того, существует множество методов для прогнозирования временных рядов, включая модели ARIMA, SARIMA, модели на основе экспоненциального сглаживания, нейронные сети и многие другие.

Все эти методы могут быть полезны при работе с временными рядами и выбор конкретного метода зависит от характера данных и задач, которые необходимо решить. Pandas предоставляет широкий спектр инструментов для работы с временными рядами, что делает его мощным инструментом для анализа временных данных.

В следующей статье мы рассмотрим задачи, связанные с преобразованием вложенных структур данных и методы нормализация сложных JSON-структур. Такие задачи очень часто стоят перед аналитиками, особенно после получения данных при работе с различными API.

В заключение приглашаю вас на бесплатный вебинар, который прольет свет на разнообразие вариантов профессиональной специализации внутри обширной сферы аналитики данных. Если вы уже интересовались этой темой хоть немного, то наверняка обратили внимание, какой большой разброс навыков встречается в описаниях вакансий в разделе “Требования”. Возникает тревожный вопрос – неужели ВСЁ это нужно знать и уметь? Неужели дата-аналитик настолько универсальный солдат? А если какая-то сфера мне упорно не дается – что делать?

Мы начнем вебинар со знакомства с предметными областями и специализациями, которые можно выделить в макрообласти “Дата-аналитика”. Затем мы разберем каждое карьерное направление в деталях с точки зрения ключевых навыков и компетенций, а также посмотрим на типичные задачи, которые представителя конкретной специализации могут ждать в условиях реальной бизнес-среды. Завершим урок небольшим разбором реальных вакансий и подсказками, как заранее понять по описанию вакансии, что вас в действительности может ожидать на рабочем месте.

  • Зарегистрироваться на бесплатный вебинар

Источник


Для чего нужен метод скользящей средней и как его используют инвесторы

Один из основных индикаторов технического анализа, который помогает инвесторам определить тенденции на рынке ценных бумаг, — скользящая средняя. Что это такое и как ее правильно использовать — в статье.

Для чего нужен метод скользящей средней и как его используют инвесторы

Специальные индикаторы помогают правильно определить цель инвестирования и увеличить потенциальную прибыль. Сторонники технического анализа используют метод скользящей средней — Moving Average, или MA.

  • Что такое метод скользящей средней
  • Как рассчитать метод скользящей средней
  • Как применять метод скользящей средней
  • Насколько точен метод скользящей средней
  • Кратко

Что такое метод скользящей средней

Метод скользящей средней — усреднение цены акции или другого актива за определенный период времени. Это один из основных и наиболее простых инструментов технического анализа, который показывает тенденции на рынке и помогает инвесторам оценивать текущее состояние актива. Когда рынок растет — скользящая средняя увеличивается. Если он падает — индикатор снижается.

Как рассчитать метод скользящей средней

Существует два основных вида скользящей средней: простая (SMA) и экспоненциальная (EMA). От вида скользящей средней зависит формула расчета показателя.

Рассчитать простую скользящую среднюю. В этом случае данные за определенный период используются, чтобы получить среднее арифметическое. Каждая цена имеет такой же вес, как и все остальные. Этот способ придает всем ценам закрытия одинаковое значение и поэтому не учитывает потенциальную динамику цены актива.

Формула расчета простой скользящей средней:

Сумма цен за период времени / Период времени

Например, цены закрытия торгов для каждого из дней периода такие: 10 рублей, 15 рублей, 20 рублей, 15 рублей. Период времени соответствует количеству дней, то есть равен 4. В этом случае простая скользящая средняя: (10 + 15 + 20 + 15) / 4 = 15.

Рассчитать экспоненциальную скользящую среднюю. В отличии от SMA, этот способ придает больший вес последним ценам периода. Поэтому он чувствительнее к изменениям данных. График EMA более объективно отражает динамику актива.

Формула расчета экспоненциальной скользящей средней:

(Цена закрытия сегодня) * (2 / Период времени ─ 1) + Значение EMA вчера * (1 ─ (2 / Период времени ─ 1))

Простую или экспоненциальную скользящую среднюю не нужно рассчитывать самостоятельно. Готовые данные можно найти на любой аналитической платформе в разделе технического анализа.

На графике динамика акций компании. SMA — кривая фиолетового цвета, EMA — кривая желтого цвета. Видно, как EMA чувствительнее реагирует на спад цены акций в феврале. Она снижается быстрее, чем SMA, и дает более точные результаты. Источник: сервис Yahoo Finance

На графике динамика акций компании. SMA — кривая фиолетового цвета, EMA — кривая желтого цвета. Видно, как EMA чувствительнее реагирует на спад цены акций в феврале. Она снижается быстрее, чем SMA, и дает более точные результаты. Источник: сервис Yahoo Finance

Как применять метод скользящей средней

Скользящие средние могут быть разной длины — это влияет на чувствительность к изменениям цены актива. Обычно длины скользящих средних составляют 10, 20, 50, 100 или 200 дней. Их можно применять на графике к любому периоду времени, который нужен инвестору. MA с короткой длиной будет реагировать на изменение цены актива быстрее, чем MA c более длинным периодом.

Скользящие средние с короткими периодами используют для краткосрочного трейдинга, чтобы видеть все скачки цены актива. Длинные скользящие средние помогают долгосрочным инвесторам следить за общим трендом актива и не отвлекаться на короткие колебания цены.

На графике динамика акций компании за последний год. Кривая зеленого цвета — EMA с длиной 50 дней. Кривая красного цвета — EMA с длиной 100 дней. Зеленая кривая чувствительнее реагирует на снижение цены акции и падает быстрее, чем красная кривая. Источник: сервис Yahoo Finance

На графике динамика акций компании за последний год. Кривая зеленого цвета — EMA с длиной 50 дней. Кривая красного цвета — EMA с длиной 100 дней. Зеленая кривая чувствительнее реагирует на снижение цены акции и падает быстрее, чем красная кривая. Источник: сервис Yahoo Finance

Кроме того, технические аналитики считают, что если цена актива пересекла MA снизу вверх, актив стоит покупать. Если сверху вниз — актив стоит продавать.

На графике динамика акций компании Harrow health. Видно, как пересечение кривой EMA с графиком цены отражает рост или падение стоимости акции. Источник: Yahoo Finance

На графике динамика акций компании Harrow health. Видно, как пересечение кривой EMA с графиком цены отражает рост или падение стоимости акции. Источник: Yahoo Finance

С помощью метода скользящей средней можно найти точку входа для покупки актива. Для этого нужно следить за пересечением графиков: наложите две скользящие средние разной длины, например 20 и 50 дней. Когда краткосрочная MA пересекает долгосрочную снизу вверх — тренд положительный, акцию можно покупать. Такое пересечение в трейдинге называется золотым крестом. Когда краткосрочная скользящая средняя пересекает более долгосрочную сверху вниз — тренд отрицательный, акцию стоит продать. Такое пересечение называется мертвым крестом.

На графике динамика акций Газпрома. Зеленая кривая — MA длиной 20 дней. Красная кривая — MA длиной 50 дней. Пересечения двух скользящих средних отражают падение и рост цены акции компании. Источник: Yahoo Finance

На графике динамика акций Газпрома. Зеленая кривая — MA длиной 20 дней. Красная кривая — MA длиной 50 дней. Пересечения двух скользящих средних отражают падение и рост цены акции компании. Источник: Yahoo Finance

Насколько точен метод скользящей средней

Скользящие средние всегда рассчитываются на основе исторических данных, поэтому они показывают только текущую ситуацию на рынке и ничего не прогнозируют. Обычно в условиях кризиса или других экономических потрясений ситуация на рынке быстро меняется. В таких условиях метод скользящей средней не успевает отражать изменения и может давать необъективные результаты.

Допустим, в прошлом квартале компания по производству полупроводников показала плохие финансовые результаты. Инвесторам это не понравилось, и цена акций упала. Но после этого менеджмент объявил: компания заключила соглашение с Samsung на производство чипов. Такие новости часто становятся сигналом рынку, который корректирует ожидания, и в будущем цена акций может вырасти.

Метод скользящих средних не отразит перспективы роста и не поможет инвестору принять решение. Это слабая сторона технического анализа и метода скользящей средней. Чтобы повысить объективность оценки и снизить потенциальные риски, многие инвесторы применяют фундаментальный анализ. Они изучают отчетность компаний, читают мнения аналитиков и строят собственные прогнозы. Подробнее о том, что такое фундаментальный анализ, — в статье Фундаментальный анализ фондового рынка — минимум, который должен знать каждый инвестор.

Кратко

  • Существует два основных вида скользящей средней: простая (SMA) и экспоненциальная (EMA). В зависимости от вида индикатора меняется формула расчета. EMA учитывает вес последних показателей периода и поэтому дает более точный результат.
  • Чтобы правильно использовать метод скользящей средней, можно определять длину скользящей средней, следить за пересечением скользящей средней с графиком цены актива и наблюдать за пересечением одной MA c другой.
  • Метод скользящей средней учитывает только историческую динамику и поэтому не помогает строить прогнозы. Чтобы избежать рисков, инвесторы применяют фундаментальный анализ.

Данный справочный и аналитический материал подготовлен компанией ООО «Ньютон Инвестиции» исключительно в информационных целях. Оценки, прогнозы в отношении финансовых инструментов, изменении их стоимости являются выражением мнения, сформированного в результате аналитических исследований сотрудников ООО «Ньютон Инвестиции», не являются и не могут толковаться в качестве гарантий или обещаний получения дохода от инвестирования в упомянутые финансовые инструменты. Не является рекламой ценных бумаг. Не является индивидуальной инвестиционной рекомендацией и предложением финансовых инструментов. Несмотря на всю тщательность подготовки информационных материалов, ООО «Ньютон Инвестиции» не гарантирует и не несет ответственности за их точность, полноту и достоверность.

Читайте также

Общество с ограниченной ответственностью «Ньютон Инвестиции» осуществляет деятельность на
основании лицензии профессионального участника рынка ценных бумаг на осуществление
брокерской деятельности №045-14007-100000, выданной Банком России 25.01.2017, а также
лицензии на осуществление дилерской деятельности №045-14084-010000, лицензии на
осуществление деятельности по управлению ценными бумагами №045-14085-001000 и лицензии
на осуществление депозитарной деятельности №045-14086-000100, выданных Банком России
08.04.2020. ООО «Ньютон Инвестиции» не гарантирует доход, на который рассчитывает инвестор,
при условии использования предоставленной информации для принятия инвестиционных
решений. Представленная информация не является индивидуальной инвестиционной
рекомендацией. Во всех случаях решение о выборе финансового инструмента либо совершении
операции принимается инвестором самостоятельно. ООО «Ньютон Инвестиции» не несёт
ответственности за возможные убытки инвестора в случае совершения операций либо
инвестирования в финансовые инструменты, упомянутые в представленной информации.

С целью оптимизации работы нашего веб-сайта и его постоянного обновления ООО «Ньютон
Инвестиции» используют Cookies (куки-файлы), а также сервис Яндекс.Метрика для
статистического анализа данных о посещениях настоящего веб-сайта. Продолжая использовать
наш веб-сайт, вы соглашаетесь на использование куки-файлов, указанного сервиса и на
обработку своих персональных данных в соответствии с «Политикой конфиденциальности» в
отношении обработки персональных данных на сайте, а также с реализуемыми ООО «Ньютон
Инвестиции» требованиями к защите персональных данных обрабатываемых на нашем сайте.
Куки-файлы — это небольшие файлы, которые сохраняются на жестком диске вашего
устройства. Они облегчают навигацию и делают посещение сайта более удобным. Если вы не
хотите использовать куки-файлы, измените настройки браузера.

Условия обслуживания могут быть изменены брокером в одностороннем порядке в любое время в соответствии с условиями
регламента брокерского обслуживания. Клиент обязан самостоятельно обращаться на
сайт брокера
за сведениями об изменениях, произведенных в регламенте
брокерского обслуживания и несет все риски в полном объеме, связанные с неполучением или несвоевременным получением
сведений в результате неисполнения или ненадлежащего исполнения указанной обязанности.

© 2023 Ньютон Инвестиции

Источник

Метод
скользящей средней

метод изучения в рядах динамики основной
тенденции развития явления.

Суть
метода скользящей средней состоит в
том, что вычисляется средний уровень
из определенного числа первых по порядку
уровней ряда, затем 
средний уровень из того же числа уровней,
начиная со второго, далее 
начиная с третьего и т. д. Таким образом,
при расчетах среднего уровня как бы
«скользят» по ряду
динамики
от его начала к концу, каждый раз
отбрасывая один уровень в начале и
добавляя один следующий.

Средняя
из нечетного числа уровней относится
к середине интервала. Если интервал
сглаживания четный, то отнесение средней
к определенному времени невозможно,
она относится к середине между датами.
Для того чтобы правильно отнести среднюю
из четного числа уровней, применяется
центрирование, т. е. нахождение средней
из средней, которую относят уже к
определенной дате.

Покажем применение
скользящей средней на следующем примере.
Пример
3.1.
На
основе данных об урожайности зерновых
культур в хозяйстве за 1989–2003 гг.
проведем сглаживание ряда методом
скользящей средней.

Динамика
урожайности зерновых культур в хозяйстве
за 1989–2003 гг. и расчет скользящих средних

1. Рассчитаем
трехлетние скользящие суммы. Находим
сумму урожайности за 1989–1991 гг.: 19,5 
23,4 
25,0  67,9
и записываем это значение в 1991 г.
Затем из этой суммы вычитаем значение
показателя за 1989 г. и прибавляем
показатель за 1992 г.: 67,9 – 19,5 
22,4 
70,8 и это значение записываем в 1992 г. и
т. д.

2. Определим
трехлетние скользящие средних по формуле
простой средней арифметической:

Полученное
значение записываем в 1990 г. Затем
берем следующую трехлетнюю скользящую
сумму и находим трехлетнюю скользящую
среднюю: 70,8 : 3  23,6,
полученное значение записываем в 1991 г.
и т. д.

Аналогичным
образом рассчитываются четырехлетние
скользящие суммы. Их значения представлены
в графе 4 таблицы данного примера.

Четырехлетние
скользящие средние определяются по
формуле простой средней арифметической:

Это
значение будет отнесено между двумя
годами — 1990 и 1991 гг., т. е. в середине
интервала сглаживания. Для того чтобы
найти четырехлетние скользящие средние
центрированные, необходимо найти среднюю
из двух смежных скользящих средних:

Эта
средняя будет отнесена к 1991 г.
Аналогичным образом рассчитываются
остальные центрированные средние; их
значения записываются в графу 6 таблицы
данного примера.

4. Метод аналитического выравнивания

Уравнение
прямой при аналитическом выравнивании
ряда динамики имеет следующий вид:

где

–
выровненный (средний) уровень динамического
ряда; a0,
a1
– параметры искомой прямой; t–
обозначение времени.

Способ
наименьших квадратов дает систему двух
нормальных уравнений для нахождения
параметров a0
и
a1:

где
у

исходный уровень ряда
динамики;
n

число членов ряда.

Система
уравнений упрощается, если значения t
подобрать так, чтобы их сумма равнялась
нулю, т. е. начало времени перенести в
середину рассматриваемого периода.

Если


то

Исследование
динамики соц.-экон. явлений и установление
основной тенденции развития дают
основание для прогнозирования
(экстраполяции) 
определения будущих размеров уровня
экономического явления. Используют
следующие методы экстраполяции:

■ средний
абсолютный прирост
с/показатель, исчисляемый
для выражения средней скорости роста
(снижения) соц.-эк. процесса. Определяется
по формуле:

■ средний
темп роста;

■ экстраполяцию
на основе выравнивания
по какой-либо аналитической формуле.
Метод
аналитического выравнивания-метод
исследования динамики соц.-экон. явлений,
позволяющий установить основные
тенденции их развития.

Рассмотрим
применение метода аналитического
выравнивания по прямой для выражения
основной тенденции на ПримерЕ 4.1.
Исходные
и расчетные данные определения параметров
уравнения прямой:

Расчет
необходимых значений дан в таблице
примера. По итоговым данным определяем
параметры уравнения:

Уравнение
прямой будет иметь вид:

Подставляя
в уравнение принятые обозначения t,
вычислим выровненные уровни ряда
динамики (см. значения
 в
табл.).

На
основе данных таблицы рассчитаем
показатели колеблемости динамических
рядов, которые характеризуются средним
квадратическим отклонением и коэффициентом
вариации.

Среднее
квадратическое отклонение можно измерить
по формуле:

Рассчитаем
показатель колеблемости урожайности
зерновых культур за анализируемый
период:

Коэффициент
вариации исчисляется по формуле: В
нашем примере:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник
Скользящие средние (МА). Методы анализа.

Помимо анализа динамики изменений цен на рынке с помощью линий поддержки/сопротивления и построения трендов, большинство трейдеров для принятия решения о сделке используют индикаторы движения цены. Очень популярным и весьма полезным среди них являются «Скользящие средние» (Moving Average или коротко МА). Метод расчета простой скользящей средней весьма прост-берутся цены актива за рассматриваемый период (например 10,15,200 часов, дней, недель на выбор), суммируются и делятся на количество выбранных периодов. Проще говоря-это среднеарифметическое значение чисел, знакомое нам еще со школы. Сейчас, правда, используют более сложную методику расчетов, которая позволяет ранжировать цены периодов в зависимости от времени (чем дальше от текущего периода, там меньше «вес» цены в значении скользящей средней). Но суть МА или ЕМА абсолютно тот-же.

Зачем его вычислять? Не секрет, что движением цен на рынке управляют инвесторы. А инвесторы, в свою очередь, подверженные типичным эмоциям, как большинство нормальных людей. А это значит, что рынок подвержен влиянию психологии толпы. Например, когда возникает паника, рациональные решения уступают место эмоциональным. Так было в кризисы 1998 и 2008 годов, так будет и в следующий раз. Как говорил Воланд в бессмертном произведении Михала Булгакова «Мастер и Маргарита»: «Люди, как люди. Любят деньги, но ведь это всегда было… Человечество любит деньги, из чего бы те ни были сделаны, из кожи ли, из бумаги ли, из бронзы или золота. Ну, легкомысленны… ну, что ж… обыкновенные люди… в общем, напоминают прежних…….» И это совершенно верно. Человек по природе своей подвержен эмоциям, так было 1000 лет назад и будет дальше. И в этой ситуации такой индикатор, как скользящие средние, позволяют, так сказать, отфильтровать колебания цен, основанные на эмоциях, оставив только среднестатистическое значение, которое действительно несет в себе рациональное зерно.Отсюда вытекают несколько методов использования скользящих средних для принятия решений.

Рисунок 1.
Рисунок 1.

1. Пересечение графиков цены и скользящей средней. В данном случае обычно берут значение МА большого периода, например 200-значную. Как мы с вами выяснили ранее, она будет отражать среднее значение цены актива за предыдущие 200 периодов (часов, дней, недель) Как видим из рисунка, скользящая средняя движется более плавно, без резких скачков вверх-вниз. Наша задача-искать места пересечения графиков цены и МА. Пересечение графиком цены линии скользящей средней снизу вверх- сигнал к покупке (точка А). Пересечение графиком цена МА сверху вниз-сигнал к продаже (точка В). При этом обратите особое внимание, что индикатор МА очень хорошо работает на восходящем и нисходящем (медвежьем) тренде и очень плохо на боковом (дает много ложных сигналов). Поэтому целесообразно использовать индикатор МА вкупе с трендовыми линиями.

2.Использование двух скользящих средних с разным периодом одновременно.

При таком способе технического анализа мы строим графики двух скользящих средних разного периода- одну с большим, другую с маленьким (например 200 и 50). Принцип принятия решений о совершении сделок аналогичен предыдущему, только мы ищем точки пересечений не графиков цены и МА, а двух МА разных периодов. Использование же вместо графика цены другой скользящей средней с периодом 50 позволяет отсеять ложные сигналы, которые более часто встречаются при использовании графика цены, особенно при боковом движении. (См. Рис.2)

Рисунок 2,
Рисунок 2,

На рисунке 2 мы видим, что график цены на данном отрезке времени дважды дает ложные сигналы к покупке (точка А и В), при этом 50-периодная МА (зеленая линия на Рис.2) помогает нам их отсеять и только в точке С дает сигнал к покупке, который оказывается правильным. Вопрос- зачем же тогда вообще использовать для анализа график цены? Ответ кроется в том, что в каждом методе есть свою плюсы и минусы. Из-за того, что 50-дневная МА движется более плавно, она позволяет отсеять большинство ложных сигналов, однако в то же время часто запаздывает с правильными. Обратите внимание на правую часть рисунка 2. Идет довольно мощная коррекция и график цены уже пересек 200-периодную МА, тогда как 50-дневная средняя только начинает разворачиваться. В случае продолжения развития нисходящей тенденции мы можем получить сигнал к продаже с большим запозданием, что уменьшит нашу прибыль от предыдущей сделки.

Вывод: какой метод анализа скользящих средних использовать, зависит от стратегии торговли, выбранной вами. При среднесрочном инвестировании (сделки 1-2 раза в месяц), более логично использовать метод двух МА. При этом количество периодов каждой средней можно менять. Помните-чем больше период-тем меньше ложных сигналов, но больше запаздывание. Целесообразнее так же использовать данный индикатор в совокупности с трендовыми линиями и линиями поддержки/сопротивления.

В следующей статье мы рассмотри метод анализа рынка с помощью среднеквадратичного отклонения от скользящих средних.

Если вы хотите обучиться интернет-трейдингу, освоить методы технического анализа и ознакомиться с различными стратегиями торговли на фондовом рынке, не забудьте подписаться на канал, чтобы не пропустить очередную статью, а также не стесняйтесь ставить “мне нравится” и поделится прочитанным с друзьями в соц.сетях. Предыдущую статью данного цикла можно прочитать ЗДЕСЬ.

Источник

Добавить комментарий