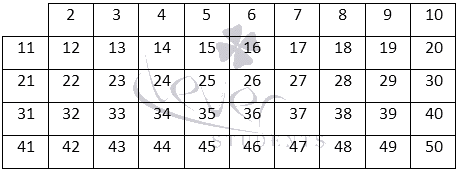Как найти простые числа неравенства

Как найти простые числа неравенства

Алгоритмы поиска простых чисел

Reading time
6 min

Views 134K

«Самое большое простое число 232582657-1. И я с гордостью утверждаю, что запомнил все его цифры… в двоичной форме».
Карл Померанс

Натуральное число называется простым, если оно имеет только два различных делителя: единицу и само себя. Задача поиска простых чисел не дает покоя математикам уже очень давно. Долгое время прямого практического применения эта проблема не имела, но все изменилось с появлением криптографии с открытым ключом. В этой заметке рассматривается несколько способов поиска простых чисел, как представляющих исключительно академический интерес, так и применяемых сегодня в криптографии.

Решето Эратосфена

Решето Эратосфена — алгоритм, предложенный древнегреческим математиком Эратосфеном. Этот метод позволяет найти все простые числа меньше заданного числа n. Суть метода заключается в следующем. Возьмем набор чисел от 2 до n. Вычеркнем из набора (отсеим) все числа делящиеся на 2, кроме 2. Перейдем к следующему «не отсеянному» числу — 3, снова вычеркиваем все что делится на 3. Переходим к следующему оставшемуся числу — 5 и так далее до тех пор пока мы не дойдем до n. После выполнения вышеописанных действий, в изначальном списке останутся только простые числа.

Алгоритм можно несколько оптимизировать. Так как один из делителей составного числа n обязательно

$leqslant sqrt{n}$, алгоритм можно останавливать, после вычеркивания чисел делящихся на

$sqrt{n}$.

Иллюстрация работы алгоритма из Википедии:

image

Сложность алгоритма составляет

$O(n loglog n)$, при этом, для хранения информации о том, какие числа были вычеркнуты требуется

$O(n)$ памяти.

Существует ряд оптимизаций, позволяющих снизить эти показатели. Прием под названием wheel factorization состоит в том, чтобы включать в изначальный список только числа взаимно простые с несколькими первыми простыми числами (например меньше 30). В теории предлагается брать первые простые примерно до

$sqrt{log n}$. Это позволяет снизить сложность алгоритма в

$loglog n$ раз. Помимо этого для уменьшения потребляемой памяти используется так называемое сегментирование. Изначальный набор чисел делится на сегменты размером

$leqslant sqrt{n}$ и для каждого сегмента решето Эратосфена применяется по отдельности. Потребление памяти снижается до

$O(sqrt{n})$.

Решето Аткина

Более совершенный алгоритм отсеивания составных чисел был предложен Аткином и Берштайном и получил название Решето Аткина. Этот способ основан на следующих трех свойствах простых чисел.

Свойство 1

Если n — положительное число, не кратное квадрату простого числа и такое, что

$n equiv 1(mod 4)$. То n — простое, тогда и только тогда, когда число корней уравнения

$4x^2+y^2=n$ нечетно.

Свойство 2

Если n — положительное число, не кратное квадрату простого числа и такое, что

$n equiv 1(mod 6)$. То n — простое, тогда и только тогда, когда число корней уравнения

$3x^2+y^2=n$ нечетно.

Свойство 3

Если n — положительное число, не кратное квадрату простого числа и такое, что

$n equiv 11(mod 12)$. То n — простое, тогда и только тогда, когда число корней уравнения

$3x^2-y^2=n$ нечетно.

Доказательства этих свойств приводятся в этой статье.

На начальном этапе алгоритма решето Аткина представляет собой массив A размером n, заполненный нулями. Для определения простых чисел перебираются все

$x, y < sqrt n$. Для каждой такой пары вычисляется

$4x^2+y^2$,

$3x^2+y^2$,

$3x^2-y^2$ и значение элементов массива

$A[4x^2+y^2]$,

$A[3x^2+y^2]$,

$A[3x^2-y^2]$ увеличивается на единицу. В конце работы алгоритма индексы всех элементов массива, которые имеют нечетные значения либо простые числа, либо квадраты простого числа. На последнем шаге алгоритма производится вычеркивание квадратов оставшихся в наборе чисел.

Из описания алгоритма следует, что вычислительная сложность решета Аткина и потребление памяти составляют

$O(n)$. При использовании wheel factorization и сегментирования оценка сложности алгоритма снижается до

$O(n / loglog n)$, а потребление памяти до

$O(sqrt{n})$.

Числа Мерсенна и тест Люка-Лемера

Конечно при таких показателях сложности, даже оптимизированное решето Аткина невозможно использовать для поиска по-настоящему больших простых чисел. К счастью, существуют быстрые тесты, позволяющие проверить является ли заданное число простым. В отличие от алгоритмов решета, такие тесты не предназначены для поиска всех простых чисел, они лишь способны сказать с некоторой вероятностью, является ли определенное число простым.

Один из таких методов проверки — тест Люка-Лемера. Это детерминированный и безусловный тест простоты. Это означает, что прохождение теста гарантирует простоту числа. К сожалению, тест предназначен только для чисел особого вида

$2^p-1$, где p — натуральное число. Такие числа называются числами Мерсенна.

Тест Люка-Лемера утверждает, что число Мерсенна

$M_p=2^p-1$ простое тогда и только тогда, когда p — простое и

$M_p$ делит нацело

$(p-1)$-й член последовательности

$S_k$ задаваемой рекуррентно:

$S_1=4, S_k=S_{k-1}^2-2$ для

$k > 1$.

Для числа

$M_p$ длиной p бит вычислительная сложность алгоритма составляет

${displaystyle O(p^{3})}$.

Благодаря простоте и детерминированности теста, самые большие известные простые числа — числа Мерсенна. Самое большое известное простое число на сегодня —

$2^{82,589,933}-1$, его десятичная запись состоит из 24,862,048 цифр. Полюбоваться на эту красоту можно здесь.

Теорема Ферма и тест Миллера-Рабина

Простых чисел Мерсенна известно не очень много, поэтому для криптографии с открытым ключом необходим другой способ поиска простых чисел. Одним из таким способов является тест простоты Ферма. Он основан на малой теореме Ферма, которая гласит, что если n — простое число, то для любого a, которое не делится на n, выполняется равенство

$a^{n-1}equiv 1{pmod {n}}$. Доказательство теоремы можно найти на Википедии.

Тест простоты Ферма — вероятностный тест, который заключается в переборе нескольких значений a, если хотя бы для одного из них выполняется неравенство

$a^{n-1} notequiv 1 pmod n$, то число n — составное. В противном случае, n — вероятно простое. Чем больше значений a использовано в тесте, тем выше вероятность того, что n — простое.

К сожалению, существуют такие составные числа n, для которых сравнение

$a^{n-1}equiv 1{pmod {n}}$ выполняется для всех a взаимно простых с n. Такие числа называются числам Кармайкла. Составные числа, которые успешно проходят тест Ферма, называются псевдопростыми Ферма. Количество псевдопростых Ферма бесконечно, поэтому тест Ферма — не самый надежный способ определения простых чисел.

Тест Миллера-Рабина

Более надежных результатов можно добиться комбинируя малую теорему Ферма и тот факт, что для простого числа p не существует других корней уравнения

$x^2 equiv 1 pmod p$, кроме 1 и -1. Тест Миллера-Рабина перебирает несколько значений a и проверяет выполнение следующих условий.

Пусть p — простое число и

$p-1=2^sd$, тогда для любого a справедливо хотя бы одно из условий:

  1. $a^{d}equiv pm1{pmod {p}}$
  2. Существует целое число r < s такое, что $a^{2^{r}d}equiv -1{pmod {p}}$

По теореме Ферма

$a^{p-1}equiv1pmod p$, а так как

$p-1=2^sd$ из свойства о корнях уравнения

$x^2 equiv 1 pmod p$ следует что если мы найдем такое a, для которого одно из условий не выполняется, значит p — составное число. Если одно из условий выполняется, число a называют свидетелем простоты числа n по Миллеру, а само число n — вероятно простым.

Чем больше свидетелей простоты найдено, тем выше вероятность того, что n — простое. Согласно теореме Рабина вероятность того, что случайно выбранное число a окажется свидетелем простоты составного числа составляет приблизительно

$1/4$.

Следовательно, если проверить k случайных чисел a, то вероятность принять составное число за простое

$approx(1/4)^k$.

Сложность работы алгоритма

$O(klog^3p)$, где k — количество проверок.

Благодаря быстроте и высокой точности тест Миллера-Рабина широко используется при поиске простых чисел. Многие современные криптографические библиотеки при проверке больших чисел на простоту используют только этот тест и, как показал Мартин Альбрехт в своей работе , этого не всегда оказывается достаточно.

Он смог сгенерировать такие составные числа, которые успершно прошли тест на простоту в библиотеках OpenSSL, CryptLib, JavaScript Big Number и многих других.

Тест Люка и Тест Baillie–PSW

Чтобы избежать уязвимости, связанные с ситуациями, когда сгенерированное злоумышленником составное число, выдается за простое, Мартин Альбрехт предлагает использовать тест Baillie–PSW. Несмотря на то, что тест Baillie–PSW является вероятностным, на сегодняшний день не найдено ни одно составное число, которое успешно проходит этот тест. За нахождение подобного числа в 1980 году авторы алгоритма пообещали вознаграждение в размере $30. Приз пока так и не был востребован.

Ряд исследователей проверили все числа до

$2^{64}$ и не обнаружили ни одного составного числа, прошедшего тест Baillie–PSW. Поэтому, для чисел меньше

$2^{64}$ тест считается детерминированным.

Суть теста сводится к последовательной проверке числа на простоу двумя различными методами. Один из этих методов уже описанный выше тест Миллера-Рабина. Второй — тест Люка на сильную псевдопростоту.

Тест Люка на сильную псевдопростоту

Последовательности Люка — пары рекуррентных последовательностей

${U_{n}(P,Q)}, {V_{n}(P,Q)}$, описываемые выражениями:

${displaystyle U_{0}(P,Q)=0,quad U_{1}(P,Q)=1,quad U_{n+2}(P,Q)=Pcdot U_{n+1}(P,Q)-Qcdot U_{n}(P,Q),,ngeq 0}$

${displaystyle V_{0}(P,Q)=2,quad V_{1}(P,Q)=P,quad V_{n+2}(P,Q)=Pcdot V_{n+1}(P,Q)-Qcdot V_{n}(P,Q),,ngeq 0}$

Пусть

$U_n(P,Q)$ и

$V_n(P,Q)$ — последовательности Люка, где целые числа P и Q удовлетворяют условию

${displaystyle D=P^{2}-4Qneq 0}$

Вычислим символ Якоби:

$left({frac {D}{p}}right)=varepsilon$.

Найдем такие r, s для которых выполняется равенство

$n-ε=2^rs$

Для простого числа n выполняется одно из следующих условий:

  1. n делит $U_s$
  2. n делит $V_{2^js}$ для некоторого j < r

В противном случае n — составное.

Вероятность того, что составное число n успешно пройдет тест Люка для заданной пары параметров P, Q не превышает 4/15. Следовательно, после применения теста k раз, эта вероятность составляет

$(4/15)^k$.

Тесты Миллера-Рабина и Люка производят не пересекающиеся множества псевдопростых чисел, соответственно если число p прошло оба теста, оно простое. Именно на этом свойстве основывается тест Baillie–PSW.

Заключение

В зависимости от поставленной задачи, могут использоваться различные методы поиска простых чисел. К примеру, при поиске больших простых чисел Мерсенна, сперва, при помощи решета Эратосфена или Аткина определяется список простых чисел до некоторой границы, предположим, до

$10^8$. Затем для каждого числа p из списка, с помощью теста Люка-Лемера, на простоту проверяется

$M_p=2^p-1$.

Чтобы сгенерировать большое простое число в криптографических целях, выбирается случайное число a и проверяется тестом Миллера-Рабина или более надежным Baillie–PSW. Согласно теореме о распределении простых чисел, у случайно выбранного числа от 1 до n шанс оказаться простым примерно равен

${frac {1}{ln n}}$. Следовательно, чтобы найти простое число размером 1024 бита, достаточно перебрать около тысячи вариантов.

P.S. Исходники

Реализацию всех описанных алгоритмов на Go можно посмотреть на GitHub.

Источник

Простые числа – это числа, которые делятся только на себя и на 1; все остальные числа называются составными числами. Существует множество способов определения того, является ли число простым. Некоторые способы являются относительно простыми, но они не подходят для больших чисел. Другие способы, применимые для больших чисел, фактически представляют собой вероятностные алгоритмы, которые иногда ошибочно характеризуют число как простое или составное.

Метод 1 Перебор делителей

Перебор делителей – самый легкий способ определить простоту числа. В случае малых чисел это, пожалуй, также и самый быстрый способ. Он основан на определении простого числа: число является простым, если оно не имеет делителей кроме самого себя и единицы.

  1. 1 Пусть n – проверяемое число. Согласно этому методу вы должны разделить число n на все возможные целые делители. При больших значениях n, например, n = 101, проверка каждого делителя займет много времени. Но существуют способы уменьшить количество делителей, которые нужно проверить.
  2. 2 Определите, является ли число n четным. Любое четное число делится на 2. Если число n — четное, то можно сразу заявить, что оно не является простым (то есть является составным числом). Для быстрого определения четности числа обратите внимание на его последнюю цифру. Если последняя цифра 2, 4, 6, 8,0, то число является четным и не является простым.
    • Единственное исключение из этого правила — число 2. Так как оно делится нацело только на себя и на 1, то число 2 – простое число. Таким образом, число 2 является единственным четным простым числом.
    • 3 Разделите n на каждое число от 2 до n-1. Так как делитель меньше делимого, то проверка всех делителей меньших n и больших 2 должна показать, является ли n простым числом. Вы начинаете с числа большего 2, потому что четные числа (которые кратны 2) не являются простыми числами. Это далеко не самый эффективный способ тестирования чисел на простоту, но здесь существует несколько методов оптимизации проверки.
      • Например, проверим число 11. В этом случае разделим (нацело) 11 на 3, 4, 5, 6, 7, 8, 9, 10. Так как ни одно из этих чисел не делит (нацело) 11, то число 11 – простое число.
      • 4 Чтобы сэкономить время, проверьте делители до округленного значения квадратного корня (n). Проверка всех делителей от 2 до n-1 может занять много времени. Например, если вы хотите проверить число 103, то вам придется протестировать следующие делители: 3, 4, 5, 6, 7. и так далее вплоть до 102! Но этого можно избежать – проверьте только делители от 2 до округленного значения квадратного корня (n).
        • Объяснение этого принципа. Рассмотрим множители 100. 100 = 1 × 100, 2 × 50, 4 × 25, 5 × 20, 10 × 10, 20 × 5, 25 × 4, 50 × 2, 100 × 1. Обратите внимание, что после пары множителей 10 × 10 все пары множителей повторяются (только множители в этих парах переставлены местами). Поэтому вы можете игнорировать делители числа n большие, чем квадратный корень (n).
        • Например, проверим n = 37. Не нужно тестировать все делители от 3 до 36. Вместо этого проверьте делители между 2 и округленным значением квадратного корня (37).
          • Квадратный корень (37) = 6,08. Округлите это число до 7.
          • 37 не делится на 3, 4, 5, 6, 7, поэтому оно — простое.
          • 5 Для дальнейшей экономии времени тестируйте только простые делители. По определению любое составное число может быть выражено как произведение двух или более простых чисел. Поэтому деление числа n на составной делитель – лишняя операция, повторяющая многократное деление числа n на простые делители. Таким образом, вы можете еще больше сузить тестируемый ряд делителей.
            • Это означает, что все четные делители и все делители, кратные простым числам, могут быть опущены.
            • Например, проверим число 103. Квадратный корень из 103 округляется до 11. Простые делители от 2 до 11 это 3, 5, 7, 11. Делители 4, 6, 8, 9, 10 можно опустить (9 кратно 3, а все остальные делители – четные числа). Таким образом, вы уменьшили ряд тестируемых делителей до четырех чисел.
              • Делители 3, 5, 7, 11 не делят (нацело) число 103, поэтому оно — простое.

              Метод 2 Тест Ферма

              В 1640 году французский математик Пьер Ферма впервые сформулировал теорему (малая теорема Ферма), которая используется при определении простоты числа. Фактически, тест Ферма служит для определения составных чисел, а не простых. Этот тест с уверенностью определяет, является ли число составным, или определяет, что число «скорее всего» простое. Тест Ферма полезен в случаях, когда перебор делителей непрактичен и когда доступен список чисел, являющихся исключениями из теоремы.

              1. 1 Пусть n – проверяемое число. Как отмечалось выше, иногда тест ложно идентифицирует составные числа как простые. Поэтому необходимо проверить ответ (способ проверки ответа описан ниже).
              2. 2 Выберите любое целое число «а» от 2 до n-1 (включительно).
                • Например, проверим на простоту число 100. Допустим, а = 3.
                • 3 Вычислите an (mod n). Вычисление этого выражения потребует некоторых знаний из модульной арифметики. В модульной арифметике при достижении определенного значения, называемого модулем, отсчет чисел начинается с нуля. Представьте это как часы: час после полудня — это 1:00, а не 13:00, то есть время после полудня отсчитывается с нуля. Модуль обозначается как mod n. Таким образом, вычислите a n (mod n).
                  • Одним из способов вычисления будет вычислить a n , а затем разделить результат на n, а в качестве ответа записать остаток деления. В этом случае рекомендуется использовать специализированные калькуляторы с функцией модуля , так как они мгновенно вычисляют остаток при делении больших чисел.
                  • В нашем примере, при делении 3 100 /100 получается остаток 1. Таким образом, 3 100 (mod 100) = 1.
                  • 4 Если у вас нет специализированного калькулятора, при вычислении остатка вручную используйте экспоненциальную запись числа.
                    • В нашем примере вручную вычислите 3 100 (mod 100). 3 100 = 515377520732011331036461129765621272702107522001 – огромное число, с которым трудно работать. Вместо того, чтобы работать с 48-значным числом, представьте 3 100 как (((((((3 2 )*3) 2 ) 2 ) 2 )*3) 2 ) 2 . Напомним, что при возведении степени в степень показатели перемножаются: ((x y ) z = x yz ).
                      • Теперь определите остаток. В (((((((3 2 )*3) 2 ) 2 ) 2 )*3) 2 ) 2 начните решение с внутренних скобок и каждый раз результат делите на 100. При получении остатка используйте его в дальнейших расчетах (а не в качестве ответа).
                        • (((((((9)*3) 2 ) 2 ) 2 )*3) 2 ) 2 — 9/100 – остатка нет.
                        • ((((((27) 2 ) 2 ) 2 )*3) 2 ) 2 — 27/100 – остатка нет.
                        • (((((729) 2 ) 2 )*3) 2 ) 2 — 729/100 = 7(ост.29). Остаток 29. Продолжите вычисления с числом 29.
                        • ((((29 2 =841) 2 )*3) 2 ) 2 — 841/100 = 8(ост.41). Остаток 41. Продолжите вычисления с числом 41.
                        • (((41 2 = 1681)*3) 2 ) 2 — 1681/100 = 16(ост.81). Остаток 81. Продолжите вычисления с числом 81.
                        • ((81*3 = 243) 2 ) 2 — 243/100 = 2(ост. 43). Остаток 43. Продолжите вычисления с числом 43.
                        • (43 2 = 1849) 2 — 1849/100 = 18(ост.49). Остаток 49. Продолжите вычисления с числом 49.
                        • 49 2 = 2401 — 2401/100 = 24(ост.1). Конечный остаток 1. Таким образом, 3 100 (mod 100) = 1 (такой же результат был получен при вычислении на калькуляторе).
                        • 5 Проверьте равенство:an (mod n) = a (mod n). Если оно не соблюдено, то n – составное число. Если оно соблюдено, то n, скорее всего, простое число (но не обязательно). Повторите тест с разными значениями «а», чтобы удостовериться в правильности ответа. Но есть составные числа, удовлетворяющие условию Ферма при любых значениях «а». Они называются числами Кармайкла (самое малое из них — число 561).
                          • В нашем примере 3 100 (mod 100) = 1, а 100 (mod 100 ) = 0. Таким образом, 1 ≠ 0 и 100 – составное число.
                          • 6 Используйте числа Кармайкла в качестве гарантии правильности ответа. Числа Кармайкла имеют вид (6k + 1)(12k + 1)(18k + 1) для целых значений k, когда каждый делитель является простым. Вы можете найти полный список чисел Кармайкла в интернете.

                          Метод 3 Тест Миллера-Рабина

                          Тест Миллера-Рабина эффективно определяет, является ли число составным (и лучше обрабатывает исключения, такие как числа Кармайкла).

                          1. 1 Пусть n — нечетное число, которое нужно протестировать на простоту.
                          2. 2 Запишите n-1 в виде 2 s × d, где d – нечетное число. Если n – простое, то оно должно быть нечетным. Поэтому n-1 – четное. Так как n-1 – четное число, то оно может быть представлено в виде произведения числа 2 в некоторой степени на нечетное число. Например, 4 = 2 2 × 1, 80 = 2 4 × 5 и так далее.
                            • Например, определите простоту числа n = 321. 321 — 1 = 320, а 320 = 2 6 × 5. То есть s=6 и d=5.
                              • Например, возьмем более сложное число n = 371. 371 — 1 = 370, а 370 = 2 1 × 185. То есть d=185, что значительно усложнит вычисления.
                              • 3 Возьмите любое число «а» между 2 и n-1.
                                • В нашем примере для n = 321 выберите а = 100.
                                • 4 Вычислите ad (mod n). Если ad = 1 или -1 (mod n), то число n проходит тест Миллера-Рабина и, скорее всего, является простым. Однако этот тест, как и тест Ферма, не может определить простоту числа с абсолютной уверенностью.
                                  • В нашем примере для n = 321: a d (mod n) = 100 5 (mod 321). 100 5 = 10,000,000,000 (mod 321) = 313. Для нахождения остатка 100 5 /321 используйте специализированный калькулятор или расчет вручную (описанный выше).
                                    • Так как результат не равен 1 или -1, вы не можете утверждать, что n – простое число.
                                    • 5 Если результат не равен 1 или -1, вычислите a 2d , a 4d , ... и так далее до a 2 s-1 d . Если один из результатов равен 1 или -1 (mod n), то число n проходит тест Миллера- Рабина и, скорее всего, является простым. Если n проходит тест, проверьте ответ (смотрите следующий шаг). Если n не проходит любой из этих тестов, то n – составное число.
                                      • Напомним, что в нашем примере а=100, s=6, d=5. Продолжите проверку следующим образом:
                                        • 100 2d = 10 = 1 × 10 20 .
                                          • 1 × 10 20 (mod 321) = 64. 64 ≠ 1 или -1. Продолжите вычисления.
                                          • 100 4d = 20 = 1 × 10 40 .
                                            • 1 × 10 40 (mod 321) = 244. 244 ≠ 1 или -1.
                                            • Здесь вы можете закончить вычисления. s — 1 = 6 — 1 = 5. Вы достигли предельного значения 4d = 2 2 . Так как ни один из расчетов не дал 1 или -1, вы можете с уверенностью заявить, что n = 321 – составное число.
                                            • 6 Если n проходит тест Миллера- Рабина, повторите тест с разными значениями «а», чтобы удостовериться в правильности ответа. Если n – простое число, оно пройдет тест с любым значением «а». Если n – составное число, не менее трех четвертей значений «а» не пройдут тест. Поэтому тест Миллера- Рабина является более надежным, чем тест Ферма, в котором составные числа Кармайкла проходят тест при любом значении «а».

                                            Условие задачи 2.30

                                            Задача 2.30
                                            Дан одномерный массив А, состоящий из натуральных чисел. Вывести на экран количество простых чисел в массиве.

                                            Для начала напомню, что такое простые числа.

                                            Простое число — это натуральное число, которое имеет ровно два различных натуральных делителя — единицу и самого себя.

                                            То есть если число делится без остатка только на 1 и на самого себя, то такое число является простым.

                                            Например, простыми числами являются 2, 3, 5 и т.п.

                                            А вот 4 уже не является простым, так как делится без остатка не только на 1 и 4, но ещё и на 2.

                                            Если вы подзабыли, что такое натуральное число, то см. здесь.

                                            А теперь перейдём к задаче. По сути нам нужна программа, определяющая простые числа. А уж перебрать элементы массива в цикле и проверить их значения — это дело техники. Заодно мы можем не только подсчитать, но и вывести на экран простые числа массива.

                                            Как определить простое число в Паскале

                                            Алгоритм решения с подробным разбором приведу на Паскале. Решение на С++ можете посмотреть в примере программы на С++.

                                            ВАЖНО!
                                            На этом многие могут ошибиться. В определении сказано, что простое число имеет ровно два различных делителя. Следовательно, число 1 не является простым (также не является простым, так как ноль можно делить на любые числа).

                                            Проверять, является ли число простым, будем с помощью функции, которую сами и создадим. Эта функция будет возвращать TRUE, если число простое.

                                            В функции сначала будем проверять, не является ли число меньше двух. Если да, то это уже не простое число. Если же число равно 2 или 3, то оно является однозначно простым и делать какие-то дополнительные проверки не требуется.

                                            А вот если число N будет больше трёх, то в этом случае в цикле будем перебирать все возможные делители, начиная от 2 до (N-1). Если на какой-то делитель число N делится без остатка, значит, это тоже не простое число. В этом случае мы прерываем цикл (потому что проверять дальше нет смысла), а функция возвращает FALSE.

                                            Проверять, делится ли число на самоё себя нет смысла (поэтому цикл длится только до N-1).

                                            Саму функцию здесь приводить не буду — посмотрите её в примерах программ.

                                            В статье рассматриваются понятия простых и составных чисел. Даются определения таких чисел с примерами. Приводим доказательство того, что количество простых чисел неограниченно и произведем запись в таблицу простых чисел при помощи метода Эратосфена. Будут приведены доказательства того, является ли число простым или составным.

                                            Простые и составные числа – определения и примеры

                                            Простые и составные числа относят к целым положительным. Они обязательно должны быть больше единицы. Делители также подразделяют на простые и составные. Чтобы понимать понятие составных чисел, необходимо предварительно изучить понятия делителей и кратных.

                                            Простыми числами называют целые числа, которые больше единицы и имеют два положительных делителя, то есть себя и 1 .

                                            Составными числами называют целые числа, которые больше единицы и имеют хотя бы три положительных делителя.

                                            Единица не является ни простым ни составным числом. Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.

                                            Простые числа – это натуральные числа, имеющие только два положительных делителя.

                                            Составное число – это натуральное число, имеющее более двух положительных делителей.

                                            Любое число, которое больше 1 является либо простым, либо составным. Из свойства делимости имеем, что 1 и число а всегда будут делителями для любого числа а , то есть оно будет делиться само на себя и на 1 . Дадим определение целых чисел.

                                            Натуральные числа, которые не являются простыми, называют составными.

                                            Простые числа: 2 , 3 , 11 , 17 , 131 , 523 . Они делятся только сами на себя и на 1 . Составные числа: 6 , 63 , 121 , 6697 . То есть число 6 можно разложить на 2 и 3 , а 63 на 1 , 3 , 7 , 9 , 21 , 63 , а 121 на 11 , 11 , то есть его делители будут 1 , 11 , 121 . Число 6697 разложится на 37 и 181 . Заметим, что понятия простых чисел и взаимно простых чисел – разные понятия.

                                            Таблица простых чисел

                                            Для того, чтобы было проще использовать простые числа, необходимо использовать таблицу:

                                            Таблица для всех существующих натуральных чисел нереальна, так как их существует бесконечное множество. Когда числа достигают размеров 10000 или 1000000000 , тогда следует задуматься об использовании решета Эратосфена.

                                            Рассмотрим теорему, которая объясняет последнее утверждение.

                                            Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.

                                            Возьмем, что а является натуральным числом, которое больше 1 , b является наименьшим отличным от единицы делителем для числа а . Следует доказать, что b является простым числом при помощи метода противного.

                                            Допустим, что b – составное число. Отсюда имеем, что есть делитель для b , который отличен от 1 как и от b . Такой делитель обозначается как b 1 . Необходимо, чтобы условие 1 b 1 b было выполнено.

                                            Из условия видно, что а делится на b , b делится на b 1 , значит, понятие делимости выражается таким образом: a = b · q и b = b 1 · q 1 , откуда a = b 1 · ( q 1 · q ) , где q и q 1 являются целыми числами. По правилу умножения целых чисел имеем, что произведение целых чисел – целое число с равенством вида a = b 1 · ( q 1 · q ) . Видно, что b 1 – это делитель для числа а . Неравенство 1 b 1 b не соответствует, потому как получим, что b является наименьшим положительным и отличным от 1 делителем а .

                                            Простых чисел бесконечно много.

                                            Предположительно возьмем конечное количество натуральных чисел n и обозначим как p 1 , p 2 , … , p n . Рассмотрим вариант нахождения простого числа, отличного от указанных.

                                            Примем на рассмотрение число р, которое равняется p 1 , p 2 , … , p n + 1 . Оно не равняется каждому из чисел, соответствующих простым числам вида p 1 , p 2 , … , p n . Число р является простым. Тогда считается, что теорема доказана. Если оно составное, тогда нужно принять обозначение p n + 1 и показать несовпадение делителя ни с одним из p 1 , p 2 , … , p n .

                                            Если это было бы не так, тогда, исходя из свойства делимости произведения p 1 , p 2 , … , p n , получим, что оно делилось бы на p n + 1 . Заметим, что на выражение p n + 1 делится число р равняется сумме p 1 , p 2 , … , p n + 1 . Получим, что на выражение p n + 1 должно делиться второе слагаемое этой суммы, которое равняется 1 , но это невозможно.

                                            Видно, что может быть найдено любое простое число среди любого количества заданных простых чисел. Отсюда следует, что простых чисел бесконечно много.

                                            Так как простых чисел очень много, то таблицы ограничивают числами 100 , 1000 , 10000 и так далее.

                                            Решето Эратосфена

                                            При составлении таблицы простых чисел следует учитывать то, что для такой задачи необходима последовательная проверка чисел, начиная с 2 до 100 . При отсутствии делителя оно фиксируется в таблицу, если оно составное, то в таблицу не заносится.

                                            Если начать с числа 2 , то оно имеет только 2 делителя: 2 и 1, значит, его можно занести в таблицу. Также и с числом 3 . Число 4 является составным, следует разложить его еще на 2 и 2 . Число 5 является простым, значит, можно зафиксировать в таблице. Так выполнять вплоть до числа 100 .

                                            Данный способ неудобный и долгий. Таблицу составить можно, но придется потратить большое количество времени. Необходимо использовать признаки делимости, которые ускорят процесс нахождения делителей.

                                            Способ при помощи решета Эратосфена считают самым удобным. Рассмотрим на примере таблиц, приведенных ниже. Для начала записываются числа 2 , 3 , 4 , … , 50 .

                                            Теперь необходимо зачеркнуть все числа, которые кратны 2 . Произвести последовательное зачеркивание. Получим таблицу вида:

                                            Далее вычеркиваем все числа, кратные 3 . Получаем таблицу вида:

                                            Переходим к вычеркиванию чисел, кратных 5 . Получим:

                                            Вычеркиваем числа, кратные 7 , 11 . В конечном итоге таблица получает вид

                                            Перейдем к формулировке теоремы.

                                            Наименьший положительный и отличный от 1 делитель основного числа а не превосходит a , где a является арифметическим корнем заданного числа.

                                            Необходимо обозначить b наименьший делитель составного числа а . Существует такое целое число q , где a = b · q , причем имеем, что b ≤ q . Недопустимо неравенство вида b > q , так как происходит нарушение условия. Обе части неравенства b ≤ q следует умножить на любое положительное число b , не равное 1 . Получаем, что b · b ≤ b · q , где b 2 ≤ a и b ≤ a .

                                            Из доказанной теоремы видно, что вычеркивание чисел в таблице приводит к тому, что необходимо начинать с числа , которое равняется b 2 и удовлетворяет неравенству b 2 ≤ a . То есть, если вычеркнуть числа, кратные 2 , то процесс начинается с 4 , а кратных 3 – с 9 и так далее до 100 .

                                            Составление такой таблицы при помощи теоремы Эратосфена говорит о том, что при вычеркивании всех составных чисел, останутся простые, которые не превосходят n . В примере, где n = 50 , у нас имеется, что n = 50 . Отсюда и получаем, что решето Эратосфена отсеивает все составные числа, которые по значению не больше значения корня из 50 . Поиск чисел производится при помощи вычеркивания.

                                            Данное число простое или составное?

                                            Перед решением необходимо выяснять, является ли число простым или составным. Зачастую используются признаки делимости. Рассмотрим это на ниже приведенных примере.

                                            Доказать что число 898989898989898989 является составным.

                                            Сумма цифр заданного числа равняется 9 · 8 + 9 · 9 = 9 · 17 . Значит, число 9 · 17 делится на 9 , исходя из признака делимости на 9 . Отсюда следует, что оно составное.

                                            Такие признаки не способны доказать простоту числа. Если нужна проверка, следует производить другие действия. Самый подходящий способ – это перебор чисел. В течение процесса можно найти простые и составные числа. То есть числа по значению не должны превосходить a . То есть число а необходимо разложить на простые множители. если это будет выполнено, тогда число а можно считать простым.

                                            Определить составное или простое число 11723 .

                                            Теперь необходимо найти все делители для числа 11723 . Необходимо оценить 11723 .

                                            Отсюда видим, что 11723 200 , то 200 2 = 40 000 , а 11 723 40 000 . Получаем, что делители для 11 723 меньше числа 200 .

                                            Для более точной оценки числа 11723 необходимо записать выражение 108 2 = 11 664 , а 109 2 = 11 881 , то 108 2 11 723 109 2 . Отсюда следует, что 11723 109 . Видно, что любое число, которое меньше 109 считается делителем для заданного числа.

                                            При разложении получим, что 2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23 , 29 , 31 , 37 , 41 , 43 , 47 , 53 , 59 , 61 , 67 , 71 , 73 , 79 , 83 , 89 , 97 , 101 , 103 , 107 – это все простые числа. Весь данный процесс можно изобразить как деление столбиком. То есть разделить 11723 на 19 . Число 19 является одним из его множителей, так как получим деление без остатка. Изобразим деление столбиком:

                                            Отсюда следует, что 11723 является составным числом, потому как кроме себя и 1 имеет делитель 19 .

                                            Ответ: 11723 является составным числом.

                                            Источник

                                            Сайт переезжает. Большинство статей уже перенесено на новую версию.
                                            Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.

                                            Теория чисел

                                            • Простые числа
                                            • Разложение на простые множители
                                            • Решето Эратосфена
                                            • Линейное решето Эратосфена*
                                            • НОД и НОК
                                            • Алгоритм Евклида
                                            • Расширенный алгоритм Евклида*
                                            • Операции по модулю
                                            • Быстрое возведение в степень
                                            • Деление по простому модулю*

                                            Простые числа

                                            Простым называется натуральное число, которое делится только на единицу и на себя. Единица при этом простым числом не считается. Составным числом называют непростое число, которое еще и не единица.

                                            Примеры простых чисел: (2), (3), (5), (179), (10^9+7), (10^9+9).

                                            Примеры составных чисел: (4), (15), (2^{30}).

                                            Еще одно определение простого числа: (N) — простое, если у (N) ровно два делителя. Эти делители при этом равны (1) и (N).

                                            Проверка на простоту за линию

                                            С точки зрения программирования интересно научиться проверять, является ли число (N) простым. Это очень легко сделать за (O(N)) – нужно просто проверить, делится ли оно хотя бы на одно из чисел (2, 3, 4, ldots, N-1) . (N > 1) является простым только в случае, если оно не делится на на одно из этих чисел.

                                            def is_prime(n):
    if n == 1:
        return False
    for i in range(2, n): # начинаем с 2, так как на 1 все делится; n не включается
        if n % i == 0:
            return False
    return True

for i in range(1, 10):
    print(i, is_prime(i))
                                            (1, False)
(2, True)
(3, True)
(4, False)
(5, True)
(6, False)
(7, True)
(8, False)
(9, False)

                                            Проверка на простоту за корень

                                            Алгоритм можно ускорить с (O(N)) до (O(sqrt{N})).

                                            Пусть (N = a times b), причем (a leq b). Тогда заметим, что (a leq sqrt N leq b).

                                            Почему? Потому что если (a leq b < sqrt{N}), то (ab leq b^2 < N), но (ab = N). А если (sqrt{N} < a leq b), то (N < a^2 leq ab), но (ab = N).

                                            Иными словами, если число (N) равно произведению двух других, то одно из них не больше корня из (N), а другое не меньше корня из (N).

                                            Из этого следует, что если число (N) не делится ни на одно из чисел (2, 3, 4, ldots, lfloorsqrt{N}rfloor), то оно не делится и ни на одно из чисел (lceilsqrt{N}rceil + 1, ldots, N-2, N-1), так как если есть делитель больше корня (не равный (N)), то есть делитель и меньше корня (не равный 1). Поэтому в цикле for достаточно проверять числа не до (N), а до корня.

                                            def is_prime(n):
    if n == 1:
        return False
    # Удобно вместо for i in range(2, n ** 0.5) писать так:
    i = 2
    while i * i <= n:
        if n % i == 0:
            return False
        i += 1
    return True

for i in [1, 2, 3, 10, 11, 12, 10**9+6, 10**9+7]:
    print(i, is_prime(i))
                                            (1, False)
(2, True)
(3, True)
(10, False)
(11, True)
(12, False)
(1000000006, False)
(1000000007, True)

                                            Разложение на простые множители

                                            Любое натуральное число можно разложить на произведение простых, и с такой записью очень легко работать при решении задач. Разложение на простые множители еще называют факторизацией.

                                            [11 = 11 = 11^1] [100 = 2 times 2 times 5 times 5 = 2^2 times 5^2] [126 = 2 times 3 times 3 times 7 = 2^1 times 3^2 times 7^1]

                                            Рассмотрим, например, такую задачу:

                                            Условие: Нужно разбить (N) людей на группы равного размера. Нам интересно, какие размеры это могут быть.

                                            Решение: По сути нас просят найти число делителей (N). Нужно посмотреть на разложение числа (N) на простые множители, в общем виде оно выглядит так:

                                            [N= p_1^{a_1} times p_2^{a_2} times ldots times p_k^{a_k}]

                                            Теперь подумаем над этим выражением с точки зрения комбинаторики. Чтобы «сгенерировать» какой-нибудь делитель, нужно подставить в степень (i)-го простого число от 0 до (a_i) (то есть (a_i+1) различное значение), и так для каждого. То есть делитель (N) выглядит ровно так: [M= p_1^{b_1} times p_2^{b_2} times ldots times p_k^{b_k}, 0 leq b_i leq a_i] Значит, ответом будет произведение ((a_1+1) times (a_2+1) times ldots times (a_k + 1)).

                                            Алгоритм разложения на простые множители

                                            Применяя алгоритм проверки числа на простоту, мы умеем легко находить минимальный простой делитель числа N. Ясно, что как только мы нашли простой делитель числа (N), мы можем число (N) на него поделить и продолжить искать новый минимальный простой делитель.

                                            Будем перебирать простой делитель от (2) до корня из (N) (как и раньше), но в случае, если (N) делится на этот делитель, будем просто на него делить. Причем, возможно, нам понадобится делить несколько раз ((N) может делиться на большую степень этого простого делителя). Так мы будем набирать простые делители и остановимся в тот момент, когда (N) стало либо (1), либо простым (и мы остановились, так как дошли до корня из него). Во втором случае надо еще само (N) добавить в ответ.

                                            Напишем алгоритм факторизации:

                                            def factorize(n):
    factors = []
    i = 2
    while i * i <= n: # перебираем простой делитель
        while n % i == 0: # пока N на него делится
            n //= i # делим N на этот делитель
            factors.append(i)
        i += 1
    # возможно, в конце N стало большим простым числом,
    # у которого мы дошли до корня и поняли, что оно простое
    # его тоже нужно добавить в разложение
    if n > 1:
        factors.append(n)
    return factors

for i in [1, 2, 3, 10, 11, 12, 10**9+6, 10**9+7]:
    print(i, '=', ' x '.join(str(x) for x in factorize(i)))
                                            1 = 
2 = 2
3 = 3
10 = 2 x 5
11 = 11
12 = 2 x 2 x 3
1000000006 = 2 x 500000003
1000000007 = 1000000007

                                            Задание

                                            За сколько работает этот алгоритм?

                                            .

                                            .

                                            .

                                            .

                                            Решение

                                            За те же самые (O(sqrt{N})). Итераций цикла while с перебором делителя будет не больше, чем (sqrt{N}). Причем ровно (sqrt{N}) операций будет только в том случае, если (N) – простое.

                                            А итераций деления (N) на делители будет столько, сколько всего простых чисел в факторизации числа (N). Понятно, что это не больше, чем (O(log{N})).

                                            Задание

                                            Докажите, что число (N) имеет не больше, чем (O(log{N})) простых множителей в факторизации.

                                            Разные свойства простых чисел*

                                            Вообще, про простые числа известно много свойств, но почти все из них очень трудно доказать. Вот еще некоторые из них:

                                            • Простых чисел, меньших (N), примерно (frac{N}{ln N}).
                                            • N-ое простое число равно примерно (Nln N).
                                            • Простые числа распределены более-менее равномерно. Например, если вам нужно найти какое-то простое число в промежутке, то можно их просто перебрать и проверить — через несколько сотен какое-нибудь найдется.
                                            • Для любого (N ge 2) на интервале ((N, 2N)) всегда найдется простое число (Постулат Бертрана)
                                            • Впрочем, существуют сколь угодно длинные отрезки, на которых простых чисел нет. Самый простой способ такой построить – это начать с (N! + 2).
                                            • Есть алгоритмы, проверяющие число на простоту намного быстрее, чем за корень.
                                            • Максимальное число делителей равно примерно (O(sqrt[3]{n})). Это не математический результат, а чисто эмпирический — не пишите его в асимптотиках.
                                            • Максимальное число делителей у числа на отрезке ([1, 10^5]) — 128
                                            • Максимальное число делителей у числа на отрекзке ([1, 10^9]) — 1344
                                            • Максимальное число делителей у числа на отрезке ([1, 10^{18}]) — 103680
                                            • Наука умеет факторизовать числа за (O(sqrt[4]{n})), но об этом как-нибудь в другой раз.
                                            • Любое число больше трёх можно представить в виде суммы двух простых (гипотеза Гольдбаха), но это не доказано.

                                            Решето Эратосфена

                                            Часто нужно не проверять на простоту одно число, а найти все простые числа до (N). В этом случае наивный алгоритм будет работать за (O(Nsqrt N)), так как нужно проверить на простоту каждое число от 1 до (N).

                                            Но древний грек Эратосфен предложил делать так:

                                            Запишем ряд чисел от 1 до (N) и будем вычеркивать числа: * делящиеся на 2, кроме самого числа 2 * затем деляющиеся на 3, кроме самого числа 3 * затем на 5, затем на 7, и так далее и все остальные простые до n. Таким образом, все незачеркнутые числа будут простыми — «решето» оставит только их.

                                            Красивая визуализация

                                            Задание

                                            Найдите этим способом на бумажке все простые числа до 50, потом проверьте с программой:

                                            N = 50
prime = [1] * (N + 1)
prime[0], prime[1] = 0, 0
for i in range(2, N + 1): # можно и до sqrt(N)
    if prime[i]:
        for j in range(2 * i, N + 1, i): # идем с шагом i, можно начиная с i * i
            prime[j] = 0
for i in range(1, N + 1):
    if prime[i]:
        print(i)
                                            2
3
5
7
11
13
17
19
23
29
31
37
41
43
47

                                            У этого алгоритма можно сразу заметить несколько ускорений.

                                            Во-первых, число (i) имеет смысл перебирать только до корня из (N), потому что при зачеркивании составных чисел, делящихся на простое (i > sqrt N), мы ничего не зачеркнем. Почему? Пусть существует составное (M leq N), которое делится на %i%, и мы его не зачеркнули. Но тогда (i > sqrt N geq sqrt M), а значит по ранее нами доказанному утверждению (M) должно делиться и на простое число, которое меньше корня. Но это значит, что мы его уже вычеркнули.

                                            Во-вторых, по этой же самое причине (j) имеет смысл перебирать только начиная с (i^2). Зачем вычеркивать (2i), (3i), (4i), …, ((i-1)i), если они все уже вычеркнуты, так как мы уже вычеркивали всё, что делится на (2), (3), (4), …, ((i-1)).

                                            Асимптотика

                                            Такой код будет работать за (O(N log log N)) по причинам, которые мы пока не хотим объяснять формально.

                                            Гармонический ряд

                                            Научимся оценивать асимптотику величины (1 + frac{1}{2} + ldots + frac{1}{N}), которая нередко встречается в задачах, где фигурирует делимость.

                                            Возьмем (N) равное (2^i – 1) и запишем нашу сумму следующим образом: [left(frac{1}{1}right) + left(frac{1}{2} + frac{1}{3}right) + left(frac{1}{4} + ldots + frac{1}{7}right) + ldots + left(frac{1}{2^{i – 1}} + ldots + frac{1}{2^i – 1}right)]

                                            Каждое из этих слагаемых имеет вид [frac{1}{2^j} + ldots + frac{1}{2^{j + 1} – 1} le frac{1}{2^j} + ldots + frac{1}{2^j} = 2^j frac{1}{2^j} = 1]

                                            Таким образом, наша сумма не превосходит (1 + 1 + ldots + 1 = i le 2log_2(2^i – 1)). Тем самым, взяв любое (N) и дополнив до степени двойки, мы получили асимптотику (O(log N)).

                                            Оценку снизу можно получить аналогичным образом, оценив каждое такое слагаемое снизу значением (frac{1}{2}).

                                            Попытка объяснения асимптотики** (для старших классов)

                                            Мы знаем, что гармонический ряд (1 + frac{1}{2} + frac{1}{3} + ldots + frac{1}{N}) это примерно (log N), а значит [N + frac{N}{2} + frac{N}{3} + ldots + frac{N}{N} sim N log N]

                                            А что такое асимптотика решета Эратосфена? Мы как раз ровно (frac{N}{p}) раз зачеркиваем числа делящиеся на простое число (p). Если бы все числа были простыми, то мы бы как раз получили (N log N) из формули выше. Но у нас будут не все слагаемые оттуда, только с простым (p), поэтому посмотрим чуть более точно.

                                            Известно, что простых чисел до (N) примерно (frac{N}{log N}), а значит допустим, что k-ое простое число примерно равно (k ln k). Тогда

                                            [sum_{substack{2 leq p leq N \ text{p is prime}}} frac{N}{p} sim frac{1}{2} + sum_{k = 2}^{frac{N}{ln N}} frac{N}{k ln k} sim int_{2}^{frac{N}{ln N}} frac{N}{k ln k} dk =N(lnlnfrac{N}{ln N} – lnln 2) sim N(lnln N – lnlnln N) sim N lnln N]

                                            Но вообще-то решето можно сделать и линейным.

                                            Задание

                                            Решите 5 первых задач из этого контеста:

                                            https://informatics.msk.ru/mod/statements/view.php?id=34271

                                            Линейное решето Эратосфена*

                                            Наша цель — для каждого числа до (N) посчитать его минимальный простой делитель. Будем хранить его в массиве min_d. Параллельно будем хранить и список всех найденных простых чисел primes – это ровно те числа (x), у которых (min_d[x] = x).

                                            Основное утверждение такое:

                                            Пусть у числа (M) минимальный делитель равен (a). Тогда, если (M) составное, мы хотим вычеркнуть его ровно один раз при обработке числа (frac{M}{a}).

                                            Мы также перебираем число (i) от (2) до (N). Если (min_d[i]) равно 0 (то есть мы не нашли ни один делитель у этого числа еще), значит оно простое – добавим в primes и сделаем (min_d[i] = i).

                                            Далее мы хотим вычеркнуть все числа (i times k) такие, что (k) – это минимальный простой делитель этого числа. Из этого следует, что необходимо и достаточно перебрать (k) в массиве primes, и только до тех пор, пока (k < min_d[i]). Ну и перестать перебирать, если (i times k > N).

                                            Алгоритм пометит все числа по одному разу, поэтому он корректен и работает за (O(N)).

                                            N = 30
primes = []
min_d = [0] * (N + 1)

for i in range(2, N + 1):
    if min_d[i] == 0:
        min_d[i] = i
        primes.append(i)
    for p in primes:
        if p > min_d[i] or i * p > N:
            break
        min_d[i * p] = p
    print(i, min_d)
print(min_d)
print(primes)
                                            2 [0, 0, 2, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
3 [0, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
4 [0, 0, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
5 [0, 0, 2, 3, 2, 5, 2, 0, 2, 3, 2, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0]
6 [0, 0, 2, 3, 2, 5, 2, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0]
7 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 0, 0, 3, 0, 0, 0, 5, 0, 0, 0, 0, 0]
8 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 0, 0, 0, 3, 0, 0, 0, 5, 0, 0, 0, 0, 0]
9 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 0, 0, 3, 0, 0, 0, 5, 0, 3, 0, 0, 0]
10 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 0, 0, 0, 5, 0, 3, 0, 0, 0]
11 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 0, 5, 0, 3, 0, 0, 0]
12 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 0, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 0, 3, 0, 0, 0]
13 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 0, 0, 0]
14 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 0]
15 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
16 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 0, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
17 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
18 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 0, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
19 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
20 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
21 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
22 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 0, 2, 5, 2, 3, 2, 0, 2]
23 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
24 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
25 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
26 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
27 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
28 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 0, 2]
29 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
30 [0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
[0, 0, 2, 3, 2, 5, 2, 7, 2, 3, 2, 11, 2, 13, 2, 3, 2, 17, 2, 19, 2, 3, 2, 23, 2, 5, 2, 3, 2, 29, 2]
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]

                                            Этот алгоритм работает асимптотически быстрее, чем обычное решето. Но на практике, если писать обычное решето Эратсфена с оптимизациями, то оно оказывается быстрее линейнего. Также линейное решето занимает гораздо больше памяти – ведь в обычном решете можно хранить просто (N) бит, а здесь нам нужно (N) чисел и еще массив primes.

                                            Зато один из «побочных эффектов» алгоритма — он неявно вычисляет факторизацию всех чисел от (1) до (N). Ведь зная минимальный простой делитель любого числа от (1) до (N) можно легко поделить на это число, посмотреть на новый минимальный простой делитель и так далее.

                                            НОД и НОК

                                            Введем два определения.

                                            Наибольший общий делитель (НОД) чисел (a_1, a_2, ldots, a_n) — это максимальное такое число (x), что все (a_i) делятся на (x).

                                            Наименьшее общее кратное (НОК) чисел (a_1, a_2, ldots, a_n) — это минимальное такое число (x), что (x) делится на все (a_i).

                                            Например, * НОД(18, 30) = 6 * НОД(60, 180, 315) = 15 * НОД(1, N) = 1 * НОК(12, 30) = 6 * НОК(1, 2, 3, 4) = 12 * НОК(1, (N)) = (N)

                                            Зачем они нужны? Например, они часто возникают в задачах.

                                            Условие: Есть (N) шестеренок, каждая (i)-ая зацеплена с ((i-1))-ой. (i)-ая шестеренка имеет (a_i) зубчиков. Сколько раз нужно повернуть полносьтю первую шестеренку, чтобы все остальные шестеренки тоже вернулись на изначальное место?

                                            Решение: Когда одна шестеренка крутится на 1 зубчик, все остальные тоже крутятся на один зубчик. Нужно найти минимальное такое число зубчиков (x), что при повороте на него все шестеренки вернутся в изначальное положение, то есть (x) делится на все (a_i), то есть это НОК((a_1, a_2, ldots, a_N)). Ответом будет (frac{x}{a_1}).

                                            Еще пример задачи на применение НОД и НОК:

                                            Условие: Город — это прямоугольник (n) на (m), разделенный на квадраты единичного размера. Вертолет летит из нижнего левого угла в верхний правый по прямой. Вертолет будит людей в квартале, когда он пролетает строго над его внутренностью (границы не считаются). Сколько кварталов разбудит вертолёт?

                                            Решение: Вертолет пересечет по вертикали ((m-1)) границу. С этим ничего не поделать — каждое считается как новое посещение какого-то квартала. По горизонтали то же самое — ((n-1)) переход в новую ячейку будет сделан.

                                            Однако еще есть случай, когда он пересекает одновременно обе границы (то есть пролетает над каким-нибудь углом) — ровно тот случай, когда нового посещения квартала не происходит. Сколько таких будет? Ровно столько, сколько есть целых решений уравнения (frac{n}{m} = frac{x}{y}). Мы как бы составили уравнение движения вертолёта и ищем, в скольки целых точках оно выполняется.

                                            Пусть (t = НОД(n, m)), тогда (n = at, m = bt).

                                            Тогда (frac{n}{m} = frac{a}{b} = frac{x}{y}). Любая дробь с натуральными числителем и знаменателем имеет ровно одно представление в виде несократимой дроби, так что (x) должно делиться на (a), а (y) должно делиться на (b). А значит, как ответ подходят ((a, b), (2a, 2b), (3a, 3b), cdots, ((t-1)a, (t-1)b)). Таких ответов ровно (t = НОД(n, m))

                                            Значит, итоговый ответ: ((n-1) + (m-1) – (t-1)).

                                            Кстати, когда (НОД(a, b) = 1), говорят, что (a) и (b) взаимно просты.

                                            Алгоритм Евклида

                                            Осталось придумать, как искать НОД и НОК. Понятно, что их можно искать перебором, но мы хотим хороший быстрый способ.

                                            Давайте для начала научимся искать (НОД(a, b)).

                                            Мы можем воспользоваться следующим равенством: [НОД(a, b) = НОД(a, b – a), b > a]

                                            Оно доказывается очень просто: надо заметить, что множества общих делителей у пар ((a, b)) и ((a, b – a)) совпадают. Почему? Потому что если (a) и (b) делятся на (x), то и (b-a) делится на (x). И наоборот, если (a) и (b-a) делятся на (x), то и (b) делится на (x). Раз множства общих делитей совпадают, то и максимальный делитель совпадает.

                                            Из этого равенства сразу следует следующее равенство: [НОД(a, b) = НОД(a, b operatorname{%} a), b > a]

                                            (так как (НОД(a, b) = НОД(a, b – a) = НОД(a, b – 2a) = НОД(a, b – 3a) = ldots = НОД(a, b operatorname{%} a)))

                                            Это равенство дает идею следующего рекурсивного алгоритма:

                                            [НОД(a, b) = НОД(b operatorname{%} a, a) = НОД(a operatorname{%} , (b operatorname{%} a), b operatorname{%} a) = ldots]

                                            Например: [НОД(93, 36) = ] [= НОД(36, 93spaceoperatorname{%}36) = НОД(36, 21) = ] [= НОД(21, 15) = ] [= НОД(15, 6) = ] [= НОД(6, 3) = ] [= НОД(3, 0) = 3]

                                            Задание:

                                            Примените алгоритм Евклида и найдите НОД чисел: * 1 и 500000 * 10, 20 * 18, 60 * 55, 34 * 100, 250

                                            По-английски наибольший общий делитель — greatest common divisor. Поэтому вместо НОД будем в коде писать gcd.

                                            def gcd(a, b):
    if b == 0:
        return a
    return gcd(b, a % b)

print(gcd(1, 500000))
print(gcd(10, 20))
print(gcd(18, 60))
print(gcd(55, 34))
print(gcd(100, 250))
print(gcd(2465473782, 12542367456))
                                            1
10
6
1
50
6

                                            Вообще, в C++ такая функция уже есть в компиляторе g++ — называется __gcd. Если у вас не Visual Studio, то, скорее всего, у вас g++. Вообще, там много всего интересного.

                                            А за сколько оно вообще работает?

                                            Задание

                                            Докажите, что алгоритм Евклида для чисел (N), (M) работает за (O(log(N+M))).

                                            Кстати, интересный факт: самыми плохими входными данными для алгоритма Евклида являются числа Фибоначчи. Именно там и достигается логарифм.

                                            Как выразить НОК через НОД

                                            (НОК(a, b) = frac{ab}{НОД(a, b)})

                                            По этой формуле можно легко найти НОК двух чисел через их произведение и НОД. Почему она верна?

                                            Посмотрим на разложения на простые множители чисел a, b, НОК(a, b), НОД(a, b).

                                            [ a = p_1^{a_1}times p_2^{a_2}timesldotstimes p_n^{a_n} ] [ b = p_1^{b_1}times p_2^{b_2}timesldotstimes p_n^{b_n} ] [ ab = p_1^{a_1+b_1}times p_2^{a_2+b_2}timesldotstimes p_n^{a_n+b_n} ]

                                            Из определений НОД и НОК следует, что их факторизации выглядят так: [ НОД(a, b) = p_1^{min(a_1, b_1)}times p_2^{min(a_2, b_2)}timesldotstimes p_n^{min(a_n, b_n)} ] [ НОК(a, b) = p_1^{max(a_1, b_1)}times p_2^{max(a_2, b_2)}timesldotstimes p_n^{max(a_n, b_n)} ]

                                            Тогда посчитаем (НОД(a, b) times НОК(a, b)): [ НОД(a, b)НОК(a, b) = p_1^{min(a_1, b_1)+max(a_1, b_1)}times p_2^{min(a_2, b_2)+max(a_2, b_2)}timesldotstimes p_n^{min(a_n, b_n)+max(a_n, b_n)} =] [ = p_1^{a_1+b_1}times p_2^{a_2+b_2}timesldotstimes p_n^{a_n+b_n} = ab]

                                            Формула доказана.

                                            Как посчитать НОД/НОК от более чем 2 чисел

                                            Для того, чтобы искать НОД или НОК у более чем двух чисел, достаточно считать их по цепочке:

                                            (НОД(a, b, c, d, ldots) = НОД(НОД(a, b), c, d, ldots))

                                            (НОК(a, b, c, d, ldots) = НОК(НОК(a, b), c, d, ldots))

                                            Почему это верно?

                                            Ну просто множество общих делителей (a) и (b) совпадает с множеством делителей (НОД(a, b)). Из этого следует, что и множество общих делителей (a), (b) и еще каких-то чисел совпадает с множеством общих делителей (НОД(a, b)) и этих же чисел. И раз совпадают множества общих делителей, то и наибольший из них совпадает.

                                            С НОК то же самое, только фразу “множество общих делителей” надо заменить на “множество общих кратных”.

                                            Задание

                                            Решите задачи F, G, H, I из этого контеста:

                                            https://informatics.msk.ru/mod/statements/view.php?id=34271

                                            Расширенный алгоритм Евклида*

                                            Очень важным для математики свойством наибольшего общего делителя является следующий факт:

                                            Для любых целых (a, b) найдутся такие целые (x, y), что (ax + by = d), где (d = gcd(a, b)).

                                            Из этого следует, что существует решение в целых числах, например, у таких уравнений: * (8x + 6y = 2) * (4x – 5y = 1) * (116x + 44y = 4) * (3x + 11y = -1)

                                            Мы сейчас не только докажем, что решения у таких уравнений существуют, но и приведем быстрый алгоритм нахождения этих решений. Здесь нам вновь пригодится алгоритм Евклида.

                                            Рассмотрим один шаг алгоритма Евклида, преобразующий пару ((a, b)) в пару ((b, a operatorname{%} b)). Обозначим (r = a operatorname{%} b), то есть запишем деление с остатком в виде (a = bq + r).

                                            Предположим, что у нас есть решение данного уравнения для чисел (b) и (r) (их наибольший общий делитель, как известно, тоже равен (d)): [bx_0 + ry_0 = d]

                                            Теперь сделаем в этом выражении замену (r = a – bq):

                                            [bx_0 + ry_0 = bx_0 + (a – bq)y_0 = ay_0 + b(x_0 – qy_0)]

                                            Tаким образом, можно взять (x = y_0), а (y = (x_0 – qy_0) = (x_0 – (a operatorname{/} b)y_0)) (здесь (/) обозначает целочисленное деление).

                                            В конце алгоритма Евклида мы всегда получаем пару ((d, 0)). Для нее решение требуемого уравнения легко подбирается — (d * 1 + 0 * 0 = d). Теперь, используя вышесказанное, мы можем идти обратно, при вычислении заменяя пару ((x, y)) (решение для чисел (b) и (a operatorname{%} b)) на пару ((y, x – (a / b)y)) (решение для чисел (a) и (b)).

                                            Это удобно реализовывать рекурсивно:

                                            def extended_gcd(a, b):
    if b == 0:
        return a, 1, 0
    d, x, y = extended_gcd(b, a % b)
    return d, y, x - (a // b) * y

a, b = 3, 5
res = extended_gcd(a, b)
print("{3} * {1} + {4} * {2} = {0}".format(res[0], res[1], res[2], a, b))
                                            3 * 2 + 5 * -1 = 1

                                            Но также полезно и посмотреть, как будет работать расширенный алгоритм Евклида и на каком-нибудь конкретном примере. Пусть мы, например, хотим найти целочисленное решение такого уравнения: [116x + 44y = 4] [(2times44+28)x + 44y = 4] [44(2x+y) + 28x = 4] [44x_0 + 28y_0 = 4] Следовательно, [x = y_0, y = x_0 – 2y_0] Будем повторять такой шаг несколько раз, получим такие уравнения: [116x + 44y = 4] [44x_0 + 28y_0 = 4, x = y_0, y = x_0 – 2y_0] [28x_1 + 16y_1 = 4, x_0 = y_1, y_0 = x_1 – y_1] [16x_2 + 12y_2 = 4, x_1 = y_2, y_1 = x_2 – y_2] [12x_3 + 4y_3 = 4, x_2 = y_3, y_2 = x_3 – y_3] [4x_4 + 0y_4 = 4, x_3 = y_4, y_3 = x_4 – 3 y_4] А теперь свернем обратно: [x_4 = 1, y_4 = 0] [x_3 = 0, y_3 =1] [x_2 = 1, y_2 =-1] [x_1 = -1, y_1 =2] [x_0 = 2, y_0 =-3] [x = -3, y =8]

                                            Действительно, (116times(-3) + 44times8 = 4)

                                            Задание

                                            Решите задачу J из этого контеста:

                                            https://informatics.msk.ru/mod/statements/view.php?id=34273

                                            Операции по модулю

                                            Выражение (a equiv b pmod m) означает, что остатки от деления (a) на (m) и (b) на (m) равны. Это выражение читается как «(a) сравнимо (b) по модулю (m)».

                                            Еще это можно опрделить так: (a) сравнимо c (b) по модулю (m), если ((a – b)) делится на (m).

                                            Все целые числа можно разделить на классы эквивалентности — два числа лежат в одном классе, если они сравнимы по модулю (m). Говорят, что мы работаем в «кольце остатков по модулю (m)», и в нем ровно (m) элементов: (0, 1, 2, cdots, m-1).

                                            Сложение, вычитение и умножение по модулю определяются довольно интуитивно — нужно выполнить соответствующую операцию и взять остаток от деления.

                                            С делением намного сложнее — поделить и взять по модулю не работает. Об этом подробнее поговорим чуть дальше.

                                            a = 30
b = 50
mod = 71

print('{} + {} = {} (mod {})'.format(a, b, (a + b) % mod, mod))
print('{} - {} = {} (mod {})'.format(a, b, (a - b) % mod, mod)) # на C++ это может не работать, так как модуль от отрицательного числа берется странно
print('{} - {} = {} (mod {})'.format(a, b, (a - b + mod) % mod, mod)) # на C++ надо писать так, чтобы брать модулю от гарантированно неотрицательного числа
print('{} * {} = {} (mod {})'.format(a, b, (a * b) % mod, mod))
# print((a / b) % mod) # а как писать это, пока неясно
                                            30 + 50 = 9 (mod 71)
30 - 50 = 51 (mod 71)
30 - 50 = 51 (mod 71)
30 * 50 = 9 (mod 71)

                                            Задание

                                            Посчитайте: * (2 + 3 pmod 5) * (2 * 3 pmod 5) * (2 ^ 3 pmod 5) * (2 – 4 pmod 5) * (5 + 5 pmod 6) * (2 * 3 pmod 6) * (3 * 3 pmod 6)

                                            Для умножения (в C++) нужно ещё учитывать следующий факт: при переполнении типа всё ломается (разве что если вы используете в качестве модуля степень двойки).

                                            • int вмещает до (2^{31} – 1 approx 2 cdot 10^9).
                                            • long long вмещает до (2^{63} – 1 approx 8 cdot 10^{18}).
                                            • long long long в плюсах нет, при попытке заиспользовать выдает ошибку long long long is too long.
                                            • Под некоторыми компиляторами и архитектурами доступен int128, но не везде и не все функции его поддерживают (например, его нельзя вывести обычными методами).

                                            Зачем нужно считать ответ по модулю

                                            Очень часто в задаче нужно научиться считать число, которое в худшем случае гораздо больше, чем (10^{18}). Тогда, чтобы не заставлять вас писать длинную арифметику, автор задачи часто просит найти ответ по модулю большого числа, обычно (10^9 + 7)

                                            Кстати, вместо того, чтобы писать (1000000007) удобно просто написать (1e9 + 7). (1e9) означает (1 times 10^9)

                                            int mod = 1e9 + 7; # В C++
cout << mod;
                                            1000000007
                                            N = 1e9 + 7 # В питоне такое число становится float
print(N)
print(int(N))
                                            1000000007.0
1000000007

                                            Быстрое возведение в степень

                                            Задача: > Даны натуральные числа (a, b, c < 10^9). Найдите (a^b) (mod (c)).

                                            Мы хотим научиться возводить число в большую степень быстро, не просто умножая (a) на себя (b) раз. Требование на модуль здесь дано только для того, чтобы иметь возможность проверить правильность алгоритма для чисел, которые не влезают в int и long long.

                                            Сам алгоритм довольно простой и рекурсивный, постарайтесь его придумать, решая вот такие примеры (прямо решать необязательно, но можно придумать, как посчитать значение этих чисел очень быстро):

                                            • (3^2)
                                            • (3^4)
                                            • (3^8)
                                            • (3^{16})
                                            • (3^{32})
                                            • (3^{33})
                                            • (3^{66})
                                            • (3^{132})
                                            • (3^{133})
                                            • (3^{266})
                                            • (3^{532})
                                            • (3^{533})
                                            • (3^{1066})

                                            Да, здесь специально приведена такая последовательность, в которой каждое следующее число легко считается через предыдущее: его либо нужно умножить на (a=3), либо возвести в квадрат. Так и получается рекурсивный алгоритм:

                                            • (a^0 = 1)
                                            • (a^{2k}=(a^{k})^2)
                                            • (a^{2k+1}=a^{2k}times a)

                                            Нужно только после каждой операции делать mod: * (a^0 pmod c = 1) * (a^{2k} pmod c = (a^{k} pmod c)^2 pmod c) * (a^{2k+1} pmod c = ((a^{2k}pmod c) times a) pmod c)

                                            Этот алгоритм называется быстрое возведение в степень. Он имеет много применений: * в криптографии очень часто надо возводить число в большую степень по модулю * используется для деления по простому модулю (см. далее) * можно быстро перемножать не только числа, но еще и матрицы (используется для динамики, например)

                                            Асимптотика этого алгоритма, очевидно, (O(log c)) – за каждые две итерации число уменьшается хотя бы в 2 раза.

                                            Задание

                                            Решите задачу K из этого контеста:

                                            https://informatics.msk.ru/mod/statements/view.php?id=34271

                                            Задание

                                            Решите как можно больше задач из практического контеста:

                                            https://informatics.msk.ru/mod/statements/view.php?id=34273

                                            Деление по модулю*

                                            Давайте все-таки научимся не только умножать, но и делить по простому модулю. Вот только что это значит?

                                            (a / b) = (a times b^{-1}), где (b^{-1}) – это обратный элемент к (b).

                                            Определение: (b^{-1}) – это такое число, что (bb^{-1} = 1)

                                            Утверждение: в кольце остатков по простому модулю (p) у каждого остатка (кроме 0) существует ровно один обратный элемент.

                                            Например, обратный к (2) по модулю (5) это (3) ((2 times 3 = 1 pmod 5)))

                                            Задание

                                            Найдите обратный элемент к: * числу (3) по модулю (5) * числу (3) по модулю (7) * числу (1) по модулю (7) * числу (2) по модулю (3) * числу (9) по модулю (31)

                                            Давайте докажем это утверждение: надо заметить, что если каждый ненулевой остаток (1, 2, ldots, (p-1)) умножить на ненулевой остаток (a), то получатся числа (a, 2a, ldots, (p-1)a) – и они все разные! Они разные, потому что если (xa = ya), то ((x-y)a = 0), а значит ((x – y) a) делится на (p), (a) – ненулевой остаток, а значит (x = y), и это не разные числа. И из того, что все числа получились разными, это все ненулевые, и их столько же, следует, что это ровно тот же набор чисел, просто в другом порядке!

                                            Из этого следует, что среди этих чисел есть (1), причем ровно один раз. А значит существует ровно один обратный элемент (a^{-1}). Доказательство закончено.

                                            Это здорово, но этот обратный элемент еще хочется быстро находить. Быстрее, чем за (O(p)).

                                            Есть несколько способов это сделать.

                                            Через малую теорему Ферма

                                            Малая теорема Ферма: > (a^{p-1} = 1 pmod p), если (p) – простое, (a neq 0 pmod p)).

                                            Доказательство: В предыдущем пункте мы выяснили, что множества чисел (1, 2, ldots, (p-1)) и (a, 2a, ldots, (p-1)a) совпадают. Из этого следует, что их произведения тоже совпадают по модулю: ((p-1)! = a^{p-1} (p-1)! pmod p).

                                            ((p-1)!neq 0 pmod p) а значит на него можно поделить (это мы кстати только в предыдущем пункте доказали, поделить на число – значит умножить на обратный к нему, который существует).

                                            А значит, (a^{p – 1} = 1 pmod p).

                                            Как это применить Осталось заметить, что из малой теоремы Ферма сразу следует, что (a^{p-2}) – это обратный элемент к (a), а значит мы свели задачу к возведению (a) в степень (p-2), что благодаря быстрому возведению в степень мы умеем делать за (O(log p)).

                                            Обобщение У малой теоремы Ферма есть обобщение для составных (p):

                                            Теорема Эйлера: > (a^{varphi(p)} = 1 pmod p), (a) – взаимно просто с (p), а (varphi(p)) – это функция Эйлера (количество чисел, меньших (p) и взаимно простых с (p)).

                                            Доказывается теорема очень похоже, только вместо ненулевых остатков (1, 2, ldots, p-1) нужно брать остатки, взаимно простые с (p). Их как раз не (p-1), а (varphi(p)).

                                            Для нахождения обратного по этой теореме достаточно посчитать функцию Эйлера (varphi(p)) и найти (a^{-1} = a^{varphi(p) – 1}).

                                            Но с этим возникают большие проблемы: посчитать функцию Эйлера сложно. Более того, на предполагаемой невозможности быстро ее посчитать построены некоторые криптографические алгоритм типа RSA. Поэтому быстро делить по составному модулю этим способом не получится.

                                            Через расширенный алгоритм Евклида

                                            Этим способом легко получится делить по любому модулю! Рекомендую.

                                            Пусть мы хотим найти (a^{-1} pmod p), (a) и (p) взаимно простые (а иначе обратного и не будет существовать).

                                            Давайте найдем корни уравнения

                                            [ax + py = 1]

                                            Они есть и находятся расширенным алгоритмом Евклида за (O(log p)), так как (НОД(a, p) = 1), ведь они взаимно простые.

                                            Тогда если взять остаток по модулю (p):

                                            [ax = 1 pmod p]

                                            А значит, найденный (x) и будет обратным элементом к (a).

                                            То есть надо просто найти (x) из решения того уравнения по модулю (p). Можно брать по модулю прямо походу решения уравнения, чтобы случайно не переполниться.

                                            Источник

                                            Что представляют собой простые и составные числа. Делитель простого и составного числа

                                            Все натуральные числа (исключение составляет лишь единица) относятся к простым или составным. При этом, основным различием между двумя большими группами чисел является количество делителей. Делители, также, подразделяются на составные и простые. Чтобы само определение составных чисел было более понятным, можно предварительно просмотреть понятия делителей и кратных.

                                            Простыми числам являются натуральные числа больше единицы, имеющие два положительных делителя – себя и 1. Например, делителем чисел 7, 11, 19, 131 выступает только единица и само число.

                                            Составными числами являются натуральные числа больше единицы, но в отличие от простого, они имеет больше положительных делителей — оно делится на единицу, на само себя и, как минимум, на одно натуральное число. Например, разложение составных чисел на делители можно представить следующим образом — число 14 делиться на 1, 2, 7, 14, а число 24 делиться на 1,2, 3, 8, 12, 6, 4.

                                            Так, число 2 является единственным первым наименьшим четным простым числом. Все остальные простые числа принадлежат к нечетной группе. А в числовом ряду составных чисел наименьшим первым числом выступает 4. В числовом ряду можно выделить первые составные и простые числа, но определить последние числовые значения невозможно.

                                            Следует обратить внимание на число 1 – оно занимает особое место, поскольку не относится ни  к составным, ни к простым числам. Наличие единственного простого делителя – единицы, является главным отличием от остальных натуральных чисел.

                                            Любое натуральное число  n больше единицы представляет простые или составные числа. Учитывая свойства делимости, можно подытожить, что единица и в всегда будут являться делителями любого числа в. То есть, любое число, кроме 1, будет иметь минимум два делителя — единицу и самого себя.

                                            Учитывая все вышесказанное, можно дать следующие определения. Простыми являются числа, натуральное числовое значение, которое обладает только двумя положительными делителями. Составными являются числа – это натуральное числовое значение, которое обладает минимально тремя положительными делителями.

                                            Так, любое число, которое не будет причислено к составным, можно отнести к простым числам. Исключение составляет лишь единица.

                                            Таблица простых чисел

                                            Часто, при выполнении различных заданий, оптимальным решением станет использование таблицы простых чисел. Так как простых чисел множество, таблицы обычно ограничиваются числовым значением 100, 1000 или 10 000. Так, на Рис.1 представлена Таблица простых чисел до 1000.

                                            Таблица простых чисел
                                            Рис. 1. Таблица простых чисел до 1000

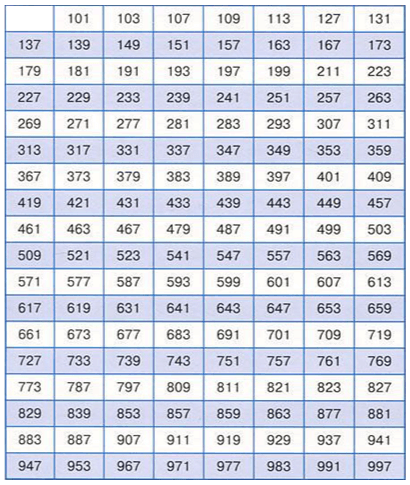
                                            Представить таблицу для всех существующих простых чисел не является возможным. Поэтому, когда числовой ряд достигает 10000 или 1000000000, следует использовать решето Эратосфена.

                                            Самое время будет рассмотреть Теорему 1 и Теорему 2, которые объяснят последнее утверждение.

                                            Теорема 1

                                            Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.

                                            Для данной теоремы можно привести следующее доказательство. Допустим, что в – это отличный от единицы наименьший делитель для числа с. Необходимо привести доказательство, используя методику противного, что является простым числом.

                                            Допустим, что является натуральным составным числом. Отсюда следует, что для натурального числа  в есть простой  делитель составного числа, который отличен как от в, так и от единицы. Данный делитель можно обозначить в1. Далее, требуется, чтобы выполнялось условие 1 < в1 < в.

                                            Из условия следует, что с делится на в, а в делится на в1. Понятие делимости можно выразить следующим образом с = в ⋅ q  и в = в 1 ⋅ q 1  , откуда с = в 1 ⋅ ( q 1 ⋅ q), где q и q1 – это целые числа. Учитывая правило умножения целых чисел следует, что их произведение – это целое число с равенством с = в 1 ⋅ (q 1 ⋅ q). Из равенства видно, что в 1 выступает делителем для числа с. Следовательно, получаем несоответствие неравенства 1 <в 1 < в , поскольку в – это положительный наименьший и отличный от 1 делитель с.

                                            Теорема 2

                                            Простых чисел бесконечно много.

                                            В качестве доказательства можно взять предположительное конечное количество натурального числа m, обозначив, как m1, m2,…….., mn. Далее, необходимо рассмотреть вариант нахождения простого числа, которое будет отлично от указанных.

                                            На рассмотрение можно взять число m, которое равно m1, m2,………, mn + 1. Оно не будет равно любому из чисел, которые соответствуют простым натуральным числам m1, m2,……, mn. Число m – простое. Так, можно считать, что теорема доказана. Если число m будет относиться к натуральным составным числам, тогда обозначение должно принять вид mn+1 и должно быть показано несовпадение делителя с m1, m2,……, mn.

                                            Если бы утверждение не соответствовало этому, то с учетом свойств делимости произведения m1, m2,……, mn, получалось бы, что оно делится на mn+1. Так, второе слагаемое данной суммы, равное 1, требовалось бы делить на выражение mn+1, что является невозможным.

                                            Среди любого заданного количества простых чисел может быть найдено любое простое число. Из данного утверждения следует вывод, что простых чисел представлено бесконечное множество.

                                            Математика Эратосфена. Простые и составные числа

                                            Решето Эратосфена   — это специальный алгоритм, который позволяет определять все простые числа до целого заданного натурального числа N. Само название методики содержит основной принцип ее функционирования. «Решето» представляет собой «фильтр», пропускающий все ненужные числа, кроме простых.

                                            Так, при составлении «решета» – таблицы, необходимо учитывать, что для выполнения задачи важна проверка чисел в последовательном порядке – начиная с двух и до 100, 1000 и т.д. Если у числа невозможно разложить на простые множители и делители отсутствуют – оно фиксируется в таблице, а если оно является натуральным составным числом, значит необходимо его исключить.

                                            Составляя таблицу простых чисел в привычном порядке приходится поэтапно рассматривать каждую цифру. Необходимо начать с 2 – у нее можно выделить два делителя (1 и 2), поэтому оно является простым числом и может быть занесено в таблицу. Число 2, также, заносим в таблицу. Число 4 можно разложить на простые множители 2 и 2, а значит, в таблице его быть не должно, поскольку оно является составным. А 5 имеет всего два делителя, соответственно, оно фиксируется в таблице. Так, поочередно рассматривается каждое число, вплоть до 100, 1000, 10000 и т, д.

                                            Данная методика является понятной, но весьма долгой и неудобной. Именно решето Эратосфена принято считать оптимальным алгоритмом. Далее, на примере приведенных таблиц будет рассмотрен сам алгоритм.

                                            Найдем все простые натуральные числа от 2 до 50. Для начала, в таблицу заносятся все числа, которые располагаются в указанном числовом ряду

                                            2 3 4 5 6 7 8 9 10
                                            11 12 12 14 15 16 17 18 19 20
                                            21 22 23 24 25 26 27 28 29 30
                                            31 32 33 34 35 36 37 38 39 40
                                            41 42 43 44 45 46 47 48 49 50
                                            (Рис.2).

                                            Далее выполняется последовательное зачеркивание всех чисел, кратных 2 (Рис.3).

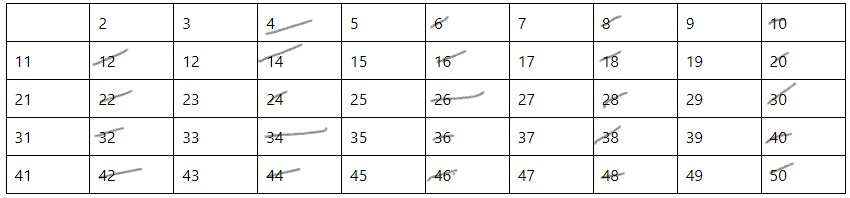
                                            Решето Эратосфена 1
                                            Рис. 3 Зачеркивание чисел, кратных двум

                                            Затем, необходимо поочередно вычеркнуть все числа, кратные 3 (Рис. 4).

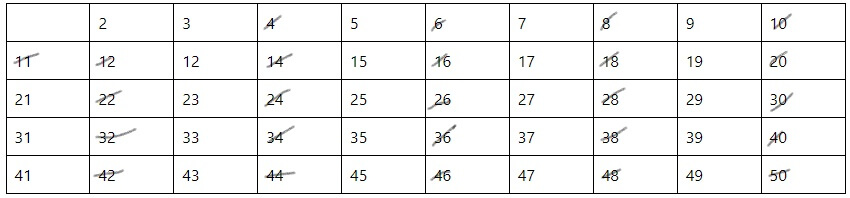
                                            Решето Эратосфена 2
                                            Рис. 4. Зачеркивание чисел, кратных 3

                                            Также, необходимо поступить с числами, которые кратны 5 (Рис. 5).

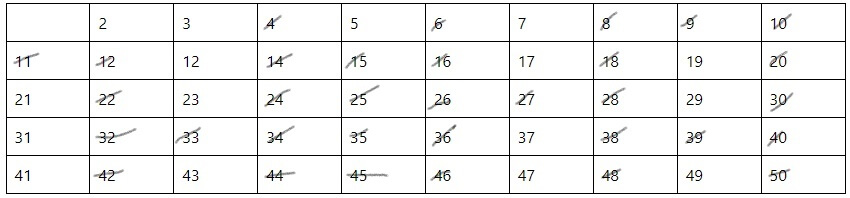
                                            Решето Эратосфена 3
                                            Рис. 5. Зачеркивание чисел, кратных 5

                                            На последнем этапе зачеркиваются числа, кратные 7 и 11 (Рис. 6). В итоге будет получена окончательная таблица натуральных простых чисел от 2 до 50.

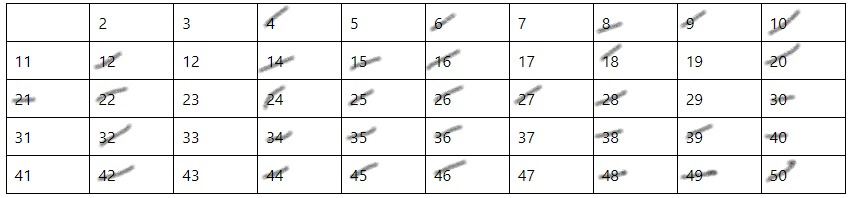
                                            Решето Эратосфена 4
                                            Рис. 6. Зачеркивание чисел, кратных 7 и 11

                                            Далее стоит остановиться на формулировке Теоремы 3 и ее доказательстве.

                                            Теорема 3

                                            Наименьший положительный и отличный от 1 делитель основного числа a
                                            не превосходит √a, где √a арифметическим корнем заданного числа.

                                            Доказательство 3

                                            Необходимо обозначить b наименьший делитель составного числа a. Существует такое целое число q, где a=b·q, причем имеем, что b≤q. Недопустимо неравенство вида b>q, так как происходит нарушение условия. Обе части неравенства b≤q следует умножить на любое положительное число b, не равное 1. Получаем, что b·b≤b·q, где b2≤a и b≤√a

                                            Доказанная теорема  показывает, что при поочередном вычеркивании чисел из таблицы, необходимо начинать с числа, которое будет равно b² и должно соответствовать неравенству b² ≤ a. Если вычеркивание начнется с чисел, кратных 2, то в первую очередь будет вычеркнуто число 4, а если с кратных 3, то – число 9.

                                            Используя методику Эратосфена при составлении простой числовой таблицы, можно обнаружить, что в процессе вычеркивания натуральных составных чисел, останутся лишь те простые числа, которые не будут превосходить значение квадратного корня из n.

                                            Нет времени решать самому?

                                            Наши эксперты помогут!

                                            Какие числа простые, а какие составные: примеры

                                            Чтобы выяснить, какие числа простые, а какие составные, оптимальным решением станет использование признаков делимости. Более подробно можно рассмотреть это на Примере 1:

                                            Пример 1

                                            Необходимо доказать, что число 696969696969696969 является составным.

                                            Решение

                                            Сумма цифр данного числа будет равняться 9 ⋅ 6 + 9 ⋅ 9 = 9 ⋅ 15. Из этого следует, что для числа 9 ⋅ 15, 9 и 15 будут являться простыми делителями составного числа. Соответственно, число является составным и имеет как минимум три делителя.

                                            Но, если необходима будет проверка, то следует использовать другие действия. Оптимальным способом станет числовой перебор. В процессе могут быть найдены составные и простые числа, которые не должны превосходить квадратный корень из а. Число разлаживается на простые множители. Если данное условие будет выполнено, значит, его можно считать простым.

                                            Источник

                                            В статье рассматриваются понятия простых и составных чисел. Даются определения таких чисел с примерами. Приводим доказательство того, что количество простых чисел неограниченно и произведем запись в таблицу простых чисел при помощи метода Эратосфена. Будут приведены доказательства того, является ли число простым или составным.

                                            Простые и составные числа – определения и примеры

                                            Простые и составные числа относят к целым положительным. Они обязательно должны быть больше единицы. Делители также подразделяют на простые и составные. Чтобы понимать понятие составных чисел, необходимо предварительно изучить понятия делителей и кратных.

                                            Определение 1

                                            Простыми числами называют целые числа, которые больше единицы и имеют два положительных делителя, то есть себя и 1.

                                            Определение 2

                                            Составными числами называют целые числа, которые больше единицы и имеют хотя бы три положительных делителя.

                                            Единица не является ни простым ни составным числом. Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.

                                            Определение 3

                                            Простые числа – это натуральные числа, имеющие только два положительных делителя.

                                            Определение 4

                                            Составное число – это натуральное число, имеющее более двух положительных делителей.

                                            Любое число, которое больше 1 является либо простым, либо составным. Из свойства делимости имеем, что 1 и число а всегда будут делителями для любого числа а, то есть оно будет делиться само на себя и на 1. Дадим определение целых чисел.

                                            Определение 5

                                            Натуральные числа, которые не являются простыми, называют составными.

                                            Простые числа: 2, 3, 11, 17, 131, 523. Они делятся только сами на себя  и на 1. Составные числа: 6, 63, 121, 6697. То есть число 6 можно разложить на 2 и 3, а 63 на 1, 3, 7,9, 21, 63, а 121 на 11, 11, то есть его делители будут 1, 11, 121. Число 6697 разложится на 37 и 181. Заметим, что понятия простых чисел и взаимно простых чисел – разные понятия.

                                            Таблица простых чисел

                                            Для того, чтобы было проще использовать простые числа, необходимо использовать таблицу:

                                            Таблица простых чисел

                                            Таблица для всех существующих натуральных чисел нереальна, так как их существует бесконечное множество. Когда числа достигают размеров 10000 или 1000000000, тогда следует задуматься об использовании решета Эратосфена.

                                            Рассмотрим теорему, которая объясняет последнее утверждение.

                                            Теорема 1

                                            Наименьший положительный и  отличный от 1 делитель натурального числа, большего единицы, является простым числом.

                                            Доказательство 1

                                            Возьмем, что а является натуральным числом, которое больше 1, b является наименьшим отличным от единицы делителем для числа а. Следует доказать, что b является простым числом при помощи метода противного.

                                            Допустим, что b – составное число. Отсюда имеем, что есть делитель для b, который отличен от 1 как и от b. Такой делитель обозначается как b1. Необходимо, чтобы условие 1<b1<b было выполнено.

                                            Из условия видно, что а делится на b, b делится на b1, значит, понятие делимости  выражается таким образом: a=b·q и b=b1·q1, откуда a= b1·(q1·q), где q и q1 являются целыми числами. По правилу умножения целых чисел имеем, что произведение целых чисел – целое число с равенством вида a=b1·(q1·q). Видно, что b1 – это делитель для числа а. Неравенство 1<b1<b не соответствует, потому как получим, что b является наименьшим положительным и отличным от 1 делителем а.

                                            Теорема 2

                                            Простых чисел бесконечно много.

                                            Доказательство 2

                                            Предположительно возьмем конечное количество натуральных чисел n и обозначим как p1, p2, …, pn. Рассмотрим вариант нахождения простого числа, отличного от указанных.

                                            Примем на рассмотрение число р, которое равняется p1, p2, …, pn+1. Оно не равняется каждому из чисел, соответствующих простым числам вида p1, p2, …, pn. Число р является простым. Тогда считается, что теорема доказана. Если оно составное, тогда нужно принять обозначение pn+1 и показать несовпадение делителя ни с одним из p1, p2, …, pn.

                                            Если это было бы не так, тогда, исходя из свойства делимости произведения p1, p2, …, pn, получим, что оно делилось бы на pn+1. Заметим, что на выражение pn+1 делится число р равняется сумме p1, p2, …, pn+1. Получим, что  на выражение pn+1 должно делиться второе слагаемое этой суммы, которое равняется 1, но это невозможно.

                                            Видно, что может быть найдено любое простое число среди любого количества заданных простых чисел. Отсюда следует, что простых чисел бесконечно много.

                                            Так как простых чисел очень много, то таблицы ограничивают числами 100, 1000, 10000 и так далее.

                                            Решето Эратосфена

                                            При составлении таблицы простых чисел следует учитывать то, что для такой задачи необходима последовательная проверка чисел, начиная с 2 до 100. При отсутствии делителя оно фиксируется в таблицу, если оно составное, то в таблицу не заносится.

                                            Рассмотрим пошагово.

                                            Если начать с числа 2, то оно имеет только 2 делителя: 2 и 1, значит, его можно занести в таблицу. Также и с числом 3. Число 4 является составным, следует разложить его еще на 2 и 2. Число 5 является простым, значит, можно зафиксировать в таблице. Так выполнять вплоть до числа 100.

                                            Данный способ неудобный и долгий. Таблицу составить можно, но придется потратить большое количество времени. Необходимо использовать признаки делимости, которые ускорят процесс нахождения делителей.

                                            Способ при помощи решета Эратосфена считают самым удобным. Рассмотрим на примере таблиц, приведенных ниже. Для начала записываются числа 2, 3, 4, …, 50.

                                            Решето Эратосфена

                                            Теперь необходимо зачеркнуть все числа, которые кратны 2. Произвести последовательное зачеркивание. Получим таблицу вида:

                                            Решето Эратосфена

                                            Далее вычеркиваем все числа, кратные 3. Получаем таблицу вида:

                                            Решето Эратосфена

                                            Переходим к вычеркиванию чисел, кратных 5. Получим:

                                            Решето Эратосфена

                                            Вычеркиваем числа, кратные 7, 11. В конечном итоге таблица получает вид

                                            Решето Эратосфена

                                            Перейдем к формулировке теоремы.

                                            Теорема 3

                                            Наименьший положительный и отличный от 1 делитель основного числа а не превосходит a, где a является арифметическим корнем заданного числа.

                                            Доказательство 3

                                            Необходимо обозначить b наименьший делитель составного числа а. Существует такое целое число q, где a=b·q, причем имеем, что b≤q. Недопустимо неравенство вида b>q, так как происходит нарушение условия. Обе части неравенства b≤q следует умножить на любое положительное число b, не равное 1. Получаем, что b·b≤b·q, где b2≤a и b≤a.

                                            Из доказанной теоремы видно, что вычеркивание чисел в таблице приводит к тому, что необходимо начинать с числа , которое равняется b2 и удовлетворяет неравенству b2≤a. То есть, если вычеркнуть числа, кратные 2, то процесс начинается с 4, а кратных 3 – с 9 и так далее до 100.

                                            Составление такой таблицы при помощи теоремы Эратосфена говорит о том, что при вычеркивании всех составных чисел, останутся простые, которые не превосходят n. В примере, где n=50,  у нас имеется, что n=50. Отсюда и получаем, что решето Эратосфена отсеивает все составные числа, которые по значению не больше значения корня из 50. Поиск чисел производится при помощи вычеркивания.

                                            Данное число простое или составное?

                                            Перед решением необходимо выяснять, является ли число простым или составным. Зачастую используются признаки делимости. Рассмотрим это на ниже приведенных примере.

                                            Пример 1

                                            Доказать что число 898989898989898989 является составным.

                                            Решение

                                            Сумма цифр заданного числа равняется 9·8+9·9=9·17. Значит, число 9·17 делится на 9, исходя из признака делимости на 9. Отсюда следует, что оно составное.

                                            Такие признаки не способны доказать простоту числа.  Если нужна проверка, следует производить другие действия. Самый подходящий способ – это перебор чисел. В течение процесса можно найти простые и составные числа. То есть числа по значению не должны превосходить a.  То есть число а необходимо разложить на простые множители. если это будет выполнено, тогда число а можно считать простым.

                                            Пример 2

                                            Определить составное или простое число 11723.

                                            Решение

                                            Теперь необходимо найти все делители для числа 11723. Необходимо оценить 11723.

                                            Отсюда видим, что 11723<200, то 2002=40 000, а 11 723<40 000. Получаем, что делители для 11 723 меньше числа 200.

                                            Для более точной оценки числа 11723 необходимо записать выражение 1082=11 664, а 1092=11 881, то 1082<11 723<1092. Отсюда следует, что 11723<109. Видно, что любое число, которое меньше 109 считается делителем для заданного числа.

                                            При разложении получим, что 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107 – это все простые числа.  Весь данный процесс можно изобразить как деление столбиком. То есть разделить 11723 на 19. Число 19 является одним из его множителей, так как получим деление без остатка. Изобразим деление столбиком:

                                            Данное число простое или составное?

                                            Отсюда следует, что 11723 является составным числом, потому как кроме себя и 1 имеет делитель 19.

                                            Ответ: 11723 является составным числом.

                                            Источник

                                            Добавить комментарий