Как найти противоположные углы квадрата

Квадрат, свойства и формулы, площадь и периметр.

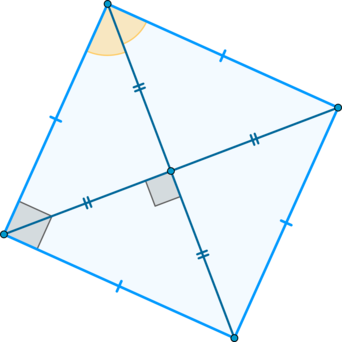
Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Квадрат (понятие, определение), диагональ квадрата

Свойства квадрата

Формулы квадрата. Площадь квадрата. Периметр квадрата

Квадрат (понятие, определение), диагональ квадрата:

Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Квадрат – это четырехугольник, имеющий равные стороны и углы.

Рис. 1. Квадрат

Все углы квадрата прямые. Каждый из них прямой и равен 90°.

Таким образом, все квадраты отличаются друг от друга только длиной стороны.

Рис. 2. Квадрат и диагонали квадрата

Диагональ квадрата – это отрезок, соединяющий две вершины противоположных углов квадрата. AC и BD – это диагонали квадрата.

Квадрат является одновременно частным случаем других фигур: параллелограмма, ромба и прямоугольника. Поэтому квадрату присущи все свойства параллелограмма, ромба и прямоугольника.

Квадрат – это равносторонний прямоугольник.

Квадрат – это ромб с прямыми углами.

Свойства квадрата:

1. Длины всех сторон равны.

Рис. 3. Квадрат

AB = BC = CD = AD

2. Противоположные стороны квадрата параллельны.

Рис. 4. Квадрат

AB||CD,   BC||AD

3. Все углы квадрата прямые. Каждый из них равен 90°.

Рис. 5. Квадрат

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

4. Сумма углов квадрата равна 360 градусам.

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.

5. Диагонали квадрата равны между собой.

Рис. 6. Квадрат

AC = BD

6. Диагонали квадрата взаимно перпендикулярны. 

Рис. 7. Квадрат

AC ┴ BD 

7. Диагонали квадрата точкой пересечения делятся пополам.

Рис. 8. Квадрат

BO = OD = AO = OC 

8. Угол между диагональю и стороной квадрата равен 45 градусам.

Рис. 9. Квадрат

∠BCA = ∠ACD = ∠DAC = ∠CAB = 45° 

9. Диагонали квадрата являются биссектрисами углов и делят углы пополам.

Рис. 10. Квадрат

∠ABD = ∠DBC = ∠BCA = ∠ACD = ∠CDB = ∠BDA = ∠DAC = ∠CAB = 45°

10. Каждая из диагоналей делит квадрат на два равных равнобедренных прямоугольных треугольника.

Обе диагонали делят квадрат на 4 равных равнобедренных прямоугольных треугольника.

 

Рис. 11. Квадрат

△ABD = △CBD = △ABC = △ACD,

△AOB = △BOC = △COD = △AOD 

11. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности.

Рис. 12. Квадрат

Формулы квадрата. Площадь квадрата. Периметр квадрата:

Пусть a – длина стороны квадрата, d – диагональ квадрата, R – радиус описанной окружности квадрата, r – радиус вписанной окружности квадрата, P – периметр квадрата, S – площадь квадрата.

Формула диагонали квадрата:

 , , , , . 

Формула радиуса вписанной окружности квадрата:

Радиус вписанной окружности квадрата равен половине его стороны.

. 

Формула радиуса описанной окружности квадрата:

.

Формула периметра квадрата:

, , .

Формула площади квадрата:

, , , , .

Квадрат

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Шестиугольник

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Коэффициент востребованности
3 726

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Свойства квадрата

• Длины всех сторон квадрата равны.
• Все углы квадрата прямые.
• Диагонали квадрата равны.
• Диагонали пересекаются под прямым углом.
• Диагонали квадрата являются биссектрисами углов.
• Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

или

Из равенства (1) найдем d:

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

или

Из формулы (5) найдем R:

или, умножая числитель и знаменатель на , получим:

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

Так как AD и BC перпендикулярны, то

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

Эти реугольники также равнобедренные. Тогда

Из (13) следует, что

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).

Смотрите также:

• Площадь квадрата онлайн

[{Large{text{Прямоугольник}}}]

Определение

Прямоугольник – это параллелограмм, у которого один угол прямой.

Таким образом, прямоугольник обладает всеми свойствами параллелограмма:

(sim) противоположные стороны попарно равны;

(sim) диагонали точкой пересечения делятся пополам.

Теоремы: свойства прямоугольника

1) Все углы прямоугольника прямые.

2) Диагонали прямоугольника равны.

Доказательство

1) Пусть (angle A=90^circ). Т.к. в параллелограмме сумма соседних углов равна (180^circ), то (angle B=180^circ-angle A=90^circ).

Т.к. в параллелограмме противоположные углы равны, то (angle
C=angle A=90^circ, angle D=angle B=90^circ), чтд.

Прямоугольные треугольники (ACD) и (DBA) равны по двум катетам ((CD = BA), (AD) – общий катет). Отсюда следует, что гипотенузы этих треугольников равны, т.е. (AC = BD).

Следствие

Таким образом, половинки диагоналей в прямоугольнике равны, т.е. (OA=OB=OC=OD).

Теоремы: признаки прямоугольника

1) Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

2) Если в выпуклом четырехугольнике все углы прямые, то он – прямоугольник.

Доказательство

Треугольники (ABD) и (DCA) равны по трем сторонам ((AB = CD), (BD =
AC), (AD) – общая сторона). Отсюда следует, что (angle A = angle
D). Так как в параллелограмме противоположные углы равны, то (angle
A = angle C) и (angle B = angle D). Таким образом, (angle A =
angle B = angle C = angle D). Параллелограмм – выпуклый четырехугольник, поэтому (angle A + angle B + angle C + angle D
= 360^circ). Следовательно, (angle A = angle B = angle C =
angle D = 90^circ).

Т.к. (angle A+angle B=180^circ) – односторонние углы при прямых (AD) и (BC) и секущей (AB), следовательно, (ADparallel BC).

Аналогично доказывается, что (ABparallel CD). Значит, (ABCD) – параллелограмм. Т.к. у него к тому же все углы прямые, то по определению это прямоугольник.
 

[{Large{text{Квадрат}}}]

Определение

Два эквивалентных определения квадрата:

Квадрат – это прямоугольник, у которого все стороны равны.

Квадрат – это ромб, у которого один угол прямой.

Свойства квадрата

Так как квадрат является прямоугольником и ромбом, то он обладает всеми свойствами прямоугольника и ромба:

(sim) Все углы квадрата равны (90^circ);

(sim) Все стороны квадрата равны;

Прямоугольник — четырёхугольник, у которого все углы прямые.

Свойства прямоугольника:

• Противоположные стороны параллельны и равны между собой

• Все углы прямые, равны 90°

• Квадрат диагонали прямоугольника равен сумме квадратов его смежных сторон

• Диагонали прямоугольника равны и точкой пересечения делятся попалам

Формулы вычисления площади прямоугольника:

• S = ab, где a и b – стороны прямоугольника.

• S = ah, где а – его сторона, h – высота, проведённая к этой стороне.

• S = ab sin α, где а и b – стороны, α – градусная мера угола прямоцгольника.

Квадра́т — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Свойства прямоугольника:

• Противоположные стороны параллельны

• Все стороны равны

• Диагонали квадрата являются биссектрисами его углов

• Точка пересечения диагоналей является центром вписанной и описанной окружностей

• Диагонали прямоугольника равны, расположены под прямым углом и точкой пересечения делятся попалам

Формулы вычисления площади квадрата:

• S = a2, где а – сторона квадрата.

• Все формулы для вычисления площади прямоугольника, т.к. квадрат является прямоугольником.