Решение задач на углы параллелограмма опирается на свойства параллелограмма.
Сумма двух углов параллелограмма, прилежащих к одной стороне, равны 180º (так как они являются внутренними односторонними при параллельных прямых (противолежащих сторонах параллелограмма) и секущей (пересекающей их стороне).
Противоположные углы параллелограмма равны.
Поэтому, если в задаче дана сумма углов параллелограмма (не 180º ), то речь идет о его противолежащих углах.
Если сказано, что один из углов параллелограмма больше или меньше другого на некоторое количество градусов (или в несколько раз, или углы относятся в некотором отношении), то речь идет об углах, прилежащих к одной стороне параллелограмма.
Если в задаче требуется найти все углы параллелограмма, в начале изучения темы ищут все четыре угла.
В дальнейшем обычно находят только два из них (прилежащие к одной стороне), поскольку другие два им равны.
Рассмотрим некоторые задачи на нахождение углов параллелограмма.
Задача 1.
Найти углы параллелограмма, если один из его углов на 40º больше другого.
Дано: ABCD — параллелограмм,
∠B на 40º больше ∠A.
Найти: ∠A, ∠B, ∠C,∠D.
Решение:
Пусть ∠A=хº, тогда ∠B=х+40º.
Так как противоположные стороны параллелограмма параллельны, то
∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB).
Имеем уравнение:
х+х+40=180
2х=180-40
2х=140
х=70
Значит, ∠A=70º, тогда ∠B=70+40=110º.
∠C=∠A=70º, ∠D=∠B=110º (как противолежащие углы параллелограмма).
Ответ: 70º, 70º, 110º, 110º.
Задача 2.
Найти углы параллелограмма, если два из них относятся как 2:3.
Дано: ABCD — параллелограмм,
∠A:∠B=2:3.
Найти: ∠A, ∠B, ∠C,∠D.
Решение:
Пусть k — коэффициент пропорциональности. Тогда ∠A=2kº, ∠B=3kº.
∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB).
Составим уравнение и решим его:
2k+3k=180
5k=180
k=36
Значит, ∠A=2∙36=72º, ∠B=3∙36=108º.
∠C=∠A=72º, ∠D=∠B=108º (как противолежащие углы параллелограмма).
Ответ: 72º, 72º, 108º, 108º.
Задача 3.
Найти углы параллелограмма, если сумма двух из них равна 150º.
Дано: ABCD — параллелограмм,
∠A+∠C=150º.
Найти: ∠A, ∠B, ∠C,∠D.
Решение:
∠A=∠C=150:2=75º (как противолежащие углы параллелограмма).
∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB).
Следовательно, ∠B=180º-∠A=180-75=105º.
∠D=∠B=105º (как противолежащие углы параллелограмма).
Ответ: 75º, 75º, 105º, 105º.
24
Июл 2013
Категория: Справочные материалы
Параллелограмм. Свойства и признаки параллелограмма
2013-07-24
2015-09-16
Определение параллелограмма
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Свойства параллелограмма
1. Противоположные стороны параллелограмма попарно равны
2. Противоположные углы параллелограмма попарно равны
3. Сумма смежных (соседних) углов параллелограмма равна 180 градусов
4. Сумма всех углов равна 360°
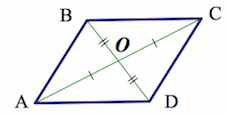5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
6. Точка пересечения диагоналей является центром симметрии параллелограмма
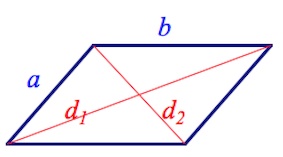
7. Диагонали 
параллелограмма и стороны
связаны следующим соотношением: 
8. Биссектриса отсекает от параллелограмма равнобедренный треугольник
Признаки параллелограмма
Четырехугольник 
является параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Противоположные стороны попарно равны: 
2. Противоположные углы попарно равны: 
3. Диагонали пересекаются и в точке пересечения делятся пополам
4. Противоположные стороны равны и параллельны: 
5. 
Небольшой видеоролик о свойствах параллелограмма (в том числе ромба, прямоугольника, квадрата) и о том, как эти свойства применяются в задачах:
Формулы площади параллелограмма смотрите здесь.
Хорошую подборку задач на нахождение углов и длин в параллелограмме смотрите здесь.
Автор: egeMax |
комментариев 7
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Параллелограмм и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства параллелограмма:
(blacktriangleright) Противоположные стороны попарно равны;
(blacktriangleright) Диагонали точкой пересечения делятся пополам;
(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).
Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
(blacktriangleright) если противоположные стороны попарно равны;
(blacktriangleright) если две стороны равны и параллельны;
(blacktriangleright) если диагонали точкой пересечения делятся пополам;
(blacktriangleright) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.
Задание
1
#1783
Уровень задания: Легче ЕГЭ
Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.
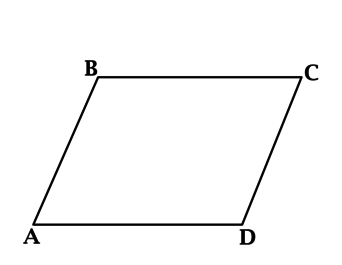
Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 – 32 = 18).
Ответ: 18
Задание
2
#1784
Уровень задания: Равен ЕГЭ
Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).
Ответ: 1,25
Задание
3
#273
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).
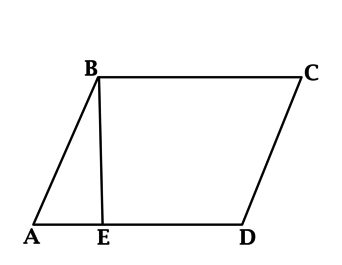
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).
Ответ: 2
Задание
4
#1785
Уровень задания: Равен ЕГЭ
Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.
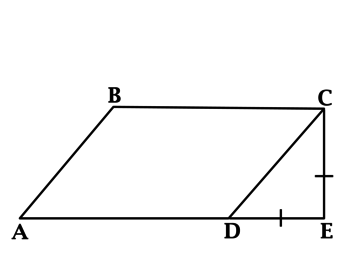
В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} – 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).
Ответ: 135
Задание
5
#1686
Уровень задания: Равен ЕГЭ
Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).
По теореме Пифагора находим: (AB^2=AD^2 – BD^2 = 25 – 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).
Ответ: 12
Задание
6
#1685
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (P_{triangle AOB} = 8), (P_{triangle AOD} = 9), а сумма смежных сторон равна (7). Найдите произведение этих сторон параллелограмма (ABCD).
(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} – P_{triangle AOB} = AD – AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).
Ответ: 12
Задание
7
#3617
Уровень задания: Равен ЕГЭ
Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.
Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]
Ответ: 6
Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.
Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».
Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.
УСТАЛ? Просто отдохни
Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.
Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
При этом параллелограмм обладает всеми свойствами четырехугольника. Поэтому запоминать надо свойства, которые характерны для параллелограмма.
Определения:
Высота параллелограмма (h) — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.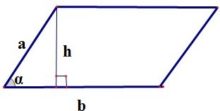
Частными случаями параллелограмма являются ромб, прямоугольник и квадрат.
Свойства углов и сторон параллелограмма
- Сумма углов параллелограмма равна 360°
- Сумма любых двух соседних углов параллелограмма равна 180°.
На рисунке: ∠A+∠B=180∘,∠A+∠D=180∘,∠C+∠B=180∘,∠C+∠D=180∘. - У параллелограмма противоположные углы равны.
На рисунке: ∠A=∠C,∠B=∠D. - У параллелограмма противоположные стороны параллельны и равны.
На рисунке: AB||CD и BC||AD; AB=CD,BC=AD.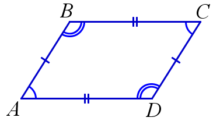
Диагонали параллелограмма
Признаки параллелограмма
- Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм. На рисунке: AB=CD,BC=AD.
- Если в четырёхугольнике противоположные углы попарно равны, то этот четырёхугольник – параллелограмм. На рисунке: ∠A=∠C,∠B=∠D.
- Если в четырёхугольнике две противоположные стороны параллельны и равны, то этот четырёхугольник – параллелограмм. На рисунке: AB=CD,AB||CD.
- Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм. На рисунке: AO=CO,BO=DO.
Параллелограмм и окружность
В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Таким образом, если в параллелограмм можно вписать окружность, то это – ромб.
Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.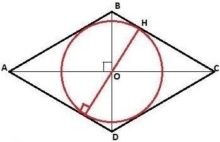
Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°. Таким образом, параллелограмм, вписанный в окружность – это прямоугольник. Центр окружности совпадает с точкой пересечения диагоналей.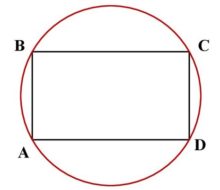
Основные формулы:
Стороны и диагональ связаны соотношением: 
Периметр параллелограмма: 
Площадь параллелограмма можно найти по трём формулам.
1. Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне.
2. Площадь параллелограмма равна произведению двух смежных (соседних) сторон на синус угла между ними.
3. Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.
Комментарий:
- a, b — длины сторон,
- d1, d2 –диагонали,
- P-периметр,
- S-площадь,
h-высота, проведенная к противоположной стороне - α — угол между сторонами параллелограмма,
- γ — угол между диагоналями параллелограмма (острый).
Рис. (1). Параллелограмм
1. Противоположные стороны параллелограмма равны:
(AB = DC), (BC = AD).
Рис. (2). Первое свойство параллелограмма
2. Противоположные углы параллелограмма равны:
(A =)
∠
(C),
∠
(B =)
∠
(D).
Рис. (3). Второе свойство параллелограмма
3. Диагонали параллелограмма точкой пересечения делятся пополам:
(BO = OD), (AO = OC).
Рис. (4). Третье свойство параллелограмма
4. Диагональ делит параллелограмм на два равных треугольника:
треугольники (ABC) и (CDA) равны.
Рис. (5). Четвёртое свойство параллелограмма
5. Сумма углов, прилежащих к одной стороне параллелограмма, равна (180) градусам:
∠
(A) (+)
∠
(D = 180)
°
.
Рис. (6). Пятое свойство параллелограмма
6. Накрест лежащие углы при диагонали равны:
(BAC =)
∠
(ACD),
∠
(BCA =)
∠
(CAD).
Рис. (7). Шестое свойство параллелограмма
