Как найти стороны прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти стороны прямоугольного треугольника
Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a =
Катет b =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c =
Катет (известный) =
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
a = √c² – b²
b = √c² – a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² – 4² = √25 – 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c =
Угол (прилежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c =
Угол (противолежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см
См. также
Лучший ответ
Serg
Высший разум
(170536)
11 лет назад
Из определения тангенса
Противол. катет = прилеж. * tg данного угла.
Остальные ответы
Сергей Попов
Мастер
(1334)
11 лет назад
Острый угол? Скажи величины
1. Берешь таблицы Брадиса
2. Находишь тангенс данного тебе угла.
Это отношение и будет отношением данного катета к противоположному
Air
Просветленный
(26339)
11 лет назад
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Зная гипотенузу и катет мы можем найти второй катет.
дед* АБСЕНТ
Просветленный
(42001)
11 лет назад
теорема косинусов- вбей сначала в поиск, потом в мозг!!!
Michael Kirshyn
Просветленный
(30843)
11 лет назад
Нарисовать и измерить.
Tulupov Elexander
Профи
(787)
11 лет назад
Элементарно.
Рассчитывается через тангенс угла (Тангенс – отношение катетов противолежащего к прилежащему)
Противолежащий катет = тангенс угла умноженный на прилежащий катет.
В следующий раз приводи рисунок и числовые данные.
Расчёт катета по катету и противолежащему углу
Значащих цифр:
Введите противолежащий угол
Прямоугольный треугольник это треугольник у которого один из углов равен 90 градусов.
Прямой угол это угол 90 градусов.
Гипотенуза это противолежащая прямому углу сторона, самая длинная сторона прямоугольного треугольника.
Катеты это стороны прямоугольного треугольника прилежащие к прямому углу.
Сумма внутренних углов треугольника равна 180 градусам.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
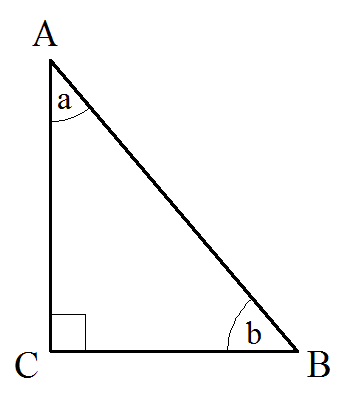
Известен катет BC и противолежащий угол a
Катет будем рассчитывать с помощью тангенса.
tg(a)=BC/AC
AC = BC / tg(a)
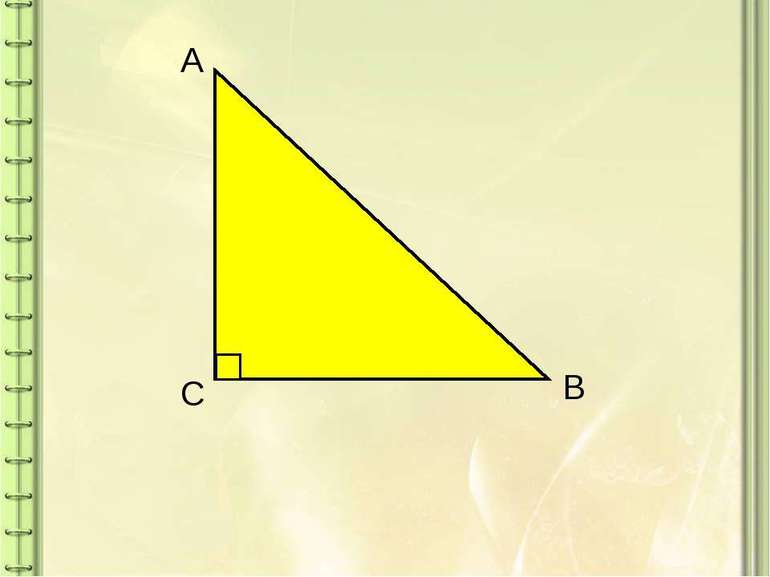
Основные понятия
Прямоугольным треугольником называется геометрическая фигура, состоящая из трех точек и отрезков, которые их соединяют. При этом один из углов обязательно равен 90°.
Чтобы точно знать, как определить противолежащий и прилежащий катеты, стоит запомнить утверждение: противолежащая сторона в прямоугольном треугольнике — это часть фигуры, которая размещена напротив этого угла, другая же будет прилежащей к гипотенузе. Отличить их очень просто: к примеру, в треугольнике ABC катетом, противолежащим ∠А, будет сторона ВС. По отношению к ∠С им станет АВ. Важное свойство: если противолежащий угол равен 30°, то катет будет равняться половине гипотенузы.
Чтобы легко понять размещение, стоит запомнить утверждение: в названии стороны, что находится напротив определенного угла, нет буквы, которая его обозначает. Он всегда будет острым, поскольку напротив 90° находится гипотенуза.
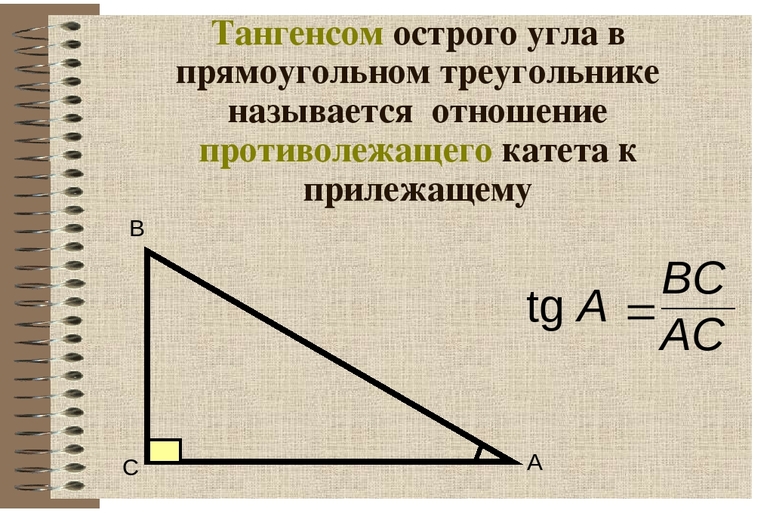
Слово «катет» имеет греческое происхождение. Оно переводится как «перпендикуляр», «опущенный», «отвесной». Это название распространено в архитектуре, здесь оно имеет значение отвеса, который опускают через середину задка ионической капители.
Катет в тригонометрии
Длину сторон можно найти, обратившись к тригонометрии. Синусом острого угла в прямоугольном треугольнике является отношение противоположного катета к гипотенузе. Выражается это утверждение так: sin А = a/с.
Косинус — отношение противоположного угла к гипотенузе. Это выражение описывается формулой cos А = b/с. Тангенс — отношение противолежащего катета к прилежащему, что можно записать следующим образом: tg А = а/b.
Решение задач
Для решения задач часто используются понятия синус, косинус и тангенс. Здесь нужно руководствоваться формулой с = a/sin а = b/sin b, где c — гипотенуза, а и b — катеты, противоположные определенным углам. Если в задаче требуется найти сторону, то формула имеет другой вид:
- a = с* sin b;
- b = с* sin а.
Используя тригонометрическое значение угла (тангенс), для нахождения противолежащей стороны применяют формулы a = b/tg b и b = a/tg a. Часто в заданиях используют углы 30, 45, 60 и 90°, поэтому для практического использования стоит запомнить их тригонометрическое значение. Решение задач происходит по алгоритму, который включает следующие действия:

- Следует проанализировать фигуру, вычислить в ней сторону либо угол.
- Далее нужно подумать, как элементы треугольника связаны с тригонометрическими функциями либо между собой.
В конце приступают к решению, то есть записывают соотношение известных понятий.
Пример задачи: есть треугольник АВС, где ∠С = 90°, sin А = 7/25, АВ = 5 см. Найти сторону АС. При решении нужно использовать формулу sin А = ВС/АВ = 7/25.
Введем длину единичного отрезка, которая равная х см, тогда BC = 7x, АВ = 25x. Используя теорему Пифагора, где c² = a² + b², получаем AC² = (25x)² – (7x)² = 24x.
По условию АВ = 5 см, то есть АВ = 25х = 5, тогда х = 1/5. Если х = 1/5, то АС = 24/5 = 4,8 см.
Таким образом, изучая материал о прямоугольных треугольниках, ученики знакомятся с катетами и их свойствами. Они учатся решать задания, используя различные понятия либо комбинируя приобретенные ранее знания с новой темой.
Как найти стороны прямоугольного треугольника
Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
следовательно: c = √ a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √ 5² – 4² = √ 25 – 16 = √ 9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
Расчёт катетов по гипотенузе и углу
Прямоугольный треугольник это треугольник у которого один из углов равен 90 градусов.
Прямой угол это угол 90 градусов.
Гипотенуза это противолежащая прямому углу сторона, самая длинная сторона прямоугольного треугольника.
Катеты это стороны прямоугольного треугольника прилежащие к прямому углу.
Сумма внутренних углов треугольника равна 180 градусам.
Синусом называется отношение противолежащего катета к гипотенузе.
Косинусом называется отношение прилежащего катета к гипотенузе.
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c – стороны произвольного треугольника
α , β , γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы

a , b – катеты
c – гипотенуза
α , β – острые углы
Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):


Формулы сторон по теореме Пифагора, ( a , b ):



3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b ):


Формулы длины равных сторон , (a):


4. Найти длину высоты треугольника
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
 H – высота треугольника
H – высота треугольника
a – сторона, основание
b, c – стороны
β , γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):
[spoiler title=”источники:”]
http://calc-best.ru/matematicheskie/raschyot-treugolnika/raschyot-katetov-pryamougolnogo-treugolnika-po-gipotenuze-i-uglu
http://www-formula.ru/2011-10-09-11-08-41
[/spoiler]
