Как найти противоположный угол в ромбе

Как найти противоположный угол в ромбе

Найти углы ромба, зная только его сторону, нельзя: существуют ромбы, имеющие разные углы, но одинаковые стороны. На пальцах: сделайте ромб из проволоки, “сплющите” его — он останется ромбом, стороны будут те же, углы изменятся.

Значит, чтобы найти углы ромба нужно знать что-то ещё (или что-то другое). Например, зная сторону и диагональ, найти угол можно по теореме косинусов: если x — сторона, d — диагональ, a — угол напротив диагонали, то условие теоремы косинуов — d^2 = x^2 + x^2 – 2 * x^2 * cos(a), из него следует a = arccos((2x^2 – d^2)/2x^2). (Я говорю “найти угол”, а не “найти углы”, потому что если мы знаем один угол, остальные находятся тривиально: если один угол равен а градусов, то угол напротив него тоже а, остальные два — по 180-а).

Есть и другие варианты: через сторону и площадь (пользуясь тем, что площадь — это квадрат стороны умножить на синус угла), через две диагонали (мы знаем, что диагонали в ромбе пересекаются под прямым углом и делятся точкой пересечения пополам — отсюда следует, что тангенс половины угла ромба равен отношению диагоналей, просто по определнию тангенса; зная сторону и диагональ, кстати, тоже можно искать угол примерно таким способом, вместо теоремы косинусов) и так далее.

Источник

У этого термина существуют и другие значения, см. Ромб (значения).

Rhombus.svg

Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе: «бубен») — это параллелограмм, у которого все стороны равны[1] (см. другие варианты определенияПерейти к разделу «Признаки»).

Термин «ромб» происходит от др.-греч. ῥόμβος — «бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Поэтому название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.

Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.

Свойства[править | править код]

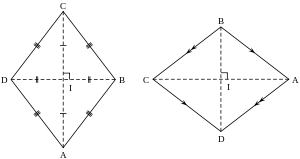
  • Ромб является параллелограммом, поэтому его противолежащие стороны равны и попарно параллельны: АВ || CD, AD || ВС. Противоположные углы ромба равны, а соседние углы дополняют друг друга до 180°.
  • Высоты в ромбе равны между собой.
  • Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам. Тем самым диагонали делят ромб на четыре конгруэнтных прямоугольных треугольника.
  • Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).
  • Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).
  • Середины четырёх сторон ромба являются вершинами прямоугольника.
  • Диагонали ромба являются осями его симметрии.
  • В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.

Признаки[править | править код]

Самое общее определение: ромб — это выпуклый четырёхугольник[2], все стороны которого равны друг другу. Можно показать, что такой четырёхугольник является параллелограммом[3][1].

Параллелограмм ABCD является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий[4]:

  • Две его смежные стороны равны (отсюда следует, что все стороны равны).
  • Его диагонали пересекаются под прямым углом.
  • Одна из диагоналей делит содержащие её углы пополам. Другими словами, диагональ является биссектрисой противоположных углов.
  • Диагонали параллелограмма делят его на четыре равных между собой треугольника.
  • Диагонали параллелограмма являются осями симметрии[5].

Помимо всего, ромб можно рассматривать как частный случай дельтоида, у которого любые две смежные стороны равны между собой.

Квадрат как частный случай ромба[править | править код]

Из определения квадрата, как четырёхугольника, у которого все стороны и углы равны, следует, что квадрат — частный случай ромба. Иногда квадрат определяют, как ромб, у которого все углы равны.

Однако иногда под ромбом может пониматься только четырёхугольник с непрямыми углами, то есть с парой острых и парой тупых углов[6][7].

Уравнение ромба[править | править код]

К уравнению ромба (центр в начале координат)

Уравнение ромба с центром в точке {displaystyle {x_{0},y_{0}}} и диагоналями, параллельными осям координат, может быть записано в виде[8]:

{displaystyle {frac {|x-x_{0}|}{a}}+{frac {|y-y_{0}|}{b}}=1,}

где a,b — половины длин диагоналей ромба по осям X,Y соответственно.

Длина стороны ромба равна {displaystyle {sqrt {a^{2}+b^{2}}}.} Площадь ромба равна {displaystyle 2ab.} Левый угол ромба рассчитывается по формуле:

{displaystyle 2operatorname {arctg} {frac {b}{a}}}

Второй угол дополняет его до 180°.

В случае a = b уравнение отображает повёрнутый на 45° квадрат:

{displaystyle |x-x_{0}|+|y-y_{0}|=a,}

где сторона квадрата равна {displaystyle a{sqrt {2}},} а его диагональ равна {displaystyle 2a.} Соответственно площадь квадрата равна {displaystyle 2a^{2}.}

Из уравнения видно, что ромб можно рассматривать[8] как суперэллипс степени 1.

Площадь ромба[править | править код]

Rhombus1.svg

  • Площадь ромба равна половине произведения его диагоналей.
{displaystyle S={dfrac {ACcdot BD}{2}}}
  • Поскольку ромб является параллелограммом, его площадь также равна произведению его стороны на высоту.
{displaystyle S=acdot h}
  • Кроме того, площадь ромба может быть вычислена по формуле:
{displaystyle S=a^{2}cdot sin alpha },

где alpha  — угол между двумя смежными сторонами ромба.

  • Также площадь ромба можно рассчитать по формуле, где присутствует радиус вписанной окружности и угол alpha :
{displaystyle S={dfrac {4r^{2}}{sin alpha }};}
  • Площадь ромба равна удвоенному произведению стороны и радиуса вписанной окружности:
{displaystyle S=2ar.}

Радиус вписанной окружности[править | править код]

Радиус вписанной окружности r может быть выражен через диагонали p и q в виде[9]:

{displaystyle r={frac {pcdot q}{2{sqrt {p^{2}+q^{2}}}}}.}

В геральдике[править | править код]

Ромб является простой геральдической фигурой.

  • Червлёный ромб в серебряном поле

    Червлёный ромб в серебряном поле

  • В червлёном поле 3 сквозных ромба: 2 и 1

    В червлёном поле 3 сквозных ромба: 2 и 1

  • Просверленный червлёный ромб в серебряном поле

    Просверленный червлёный ромб в серебряном поле

  • В лазури левая перевязь, составленная из пяти вертикальных золотых ромбов

    В лазури левая перевязь, составленная из пяти вертикальных золотых ромбов

Симметрия[править | править код]

Ромб симметричен относительно любой из своих диагоналей, поэтому часто используется в орнаментах и паркетах.

  • Ромбический орнамент

    Ромбический орнамент

  • Ромбические звёзды

    Ромбические звёзды

  • Более сложный орнамент

    Более сложный орнамент

  • Мозаика Пенроуза

См. другие примеры на Викискладе.

См. также[править | править код]

  • Дельтоид
  • Звезда (геометрия)
  • Ромбододекаэдр
  • Ромбоид

Примечания[править | править код]

  1. ↑ 1 2 Элементарная математика, 1976, с. 435..
  2. ↑ Требование выпуклости нужно, чтобы исключить случаи вырожденного четырёхугольника, у которого часть вершин совпадают (например, фигура, имеющая вид буквы V и ромбом не являющаяся).
  3. ↑ Погорелоа А. В. Домашняя работа по геометрии за 8 класс. М.: Просвещение, 2001, С. 18.
  4. ↑ Элементарная математика, 1976, с. 435—436..
  5. ↑ Шахмейстер А. Х. Треугольники и параллелограммы // Геометрические задачи на экзаменах. Часть 1. Планиметрия : книга / А. Х. Шахмейстер. — СПб. : «Петроглиф» : «Виктория плюс» ; М. : Издательство МЦНМО, 2015. — С. 26. — 392 с. : илл. — (Математика. Элективные курсы). — 1500 экз. — ББК 22.141я71.6. — УДК 373.167.1:512(G). — ISBN 978-5-98712-083-5. — ISBN 978-5-91673-155-2. — ISBN 978-5-4439-0347-7.
  6. ↑ Ромб // Малый академический словарь. — М.: Институт русского языка Академии наук СССР. Евгеньева А. П.. 1957—1984.
  7. ↑ Чудинов А. Н. Ромб // Словарь иностранных слов, вошедших в состав русского языка. 1910.
  8. ↑ 1 2 Weisstein, Eric W. Superellipse (англ.) на сайте Wolfram MathWorld. Здесь ромб назван diamond.
  9. ↑ Weisstein, Eric W. Rhombus (англ.) на сайте Wolfram MathWorld.

Литература[править | править код]

  • Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
  • Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
Источник

1. Противоположные стороны ромба равны: (AB = BC = CD = AD) (т. к. все стороны равны).

1 Ромб 0.png

2. Противоположные углы ромба равны:

∠

 (A =)

∠

 (C);  

∠

 (B =)

∠

 (D).

1 Ромб 1.png

3. Диагонали ромба точкой пересечения делятся пополам: (BO = OD);   (AO = OC).

1 Ромб 2.png

4. Сумма углов, прилежащих к одной стороне ромба, равна

180°

: 

∠

 (A) (+)

∠

 (D = 180)

°

.

1 Ромб 3.png

Свойства ромба, присущие только ему

5. Диагонали ромба взаимно перпендикулярны: (AC)

⊥

 (BD).

1 Ромб 4.png

6. Диагонали ромба являются также биссектрисами его углов (делят углы ромба пополам).

1 Ромб 55.png

7. Диагонали делят ромб на четыре равных прямоугольных треугольника.

Треугольники (ABO), (СBO), (CDO), (ADO) — равные прямоугольные треугольники.

1 Ромб 66.png

Источник

В данной публикации мы рассмотрим определение, свойства и признаки (с рисунками) одной из основных геометрических фигур – ромба.

  • Определение ромба

  • Свойства ромба

    • Свойство 1

    • Свойство 2

    • Свойство 3

    • Свойство 4

    • Свойство 5

  • Признаки ромба

Определение ромба

Ромб – это фигура на плоскости; разновидность параллелограмма, у которого все четыре стороны равны и попарно параллельны. Обычно ромб обозначается названиями его вершин (например, ABCD), а длина его стороны – строчной латинской буквой (например, a).

Ромб ABCD со стороной a

  • AB = BC = CD = AD = a
  • AB параллельна CD, BC параллельна AD.

Примечание: квадрат является частным случаем ромба.

Свойства ромба

Свойство 1

Противоположные углы ромба равны между собой, а сумма соседних углов составляет 180°.

Равенство противоположных углов ромба

  • ∠ABC = ∠ADC, ∠BAD = ∠BCD
  • α + β = 180°

Свойство 2

Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.

Диагонали ромба

  • диагональ BD (d1) перпендикулярна диагонали AC (d2)
  • AE = EC
  • BE = ED

В результате пересечения диагоналей ромб делится на 4 прямоугольных треугольника: ΔAEB, ΔBEC, ΔAED и ΔDEC.

Свойство 3

Диагонали ромба являются биссектрисами его углов.

Диагонали ромба

Свойство 4

Сторону ромба a можно найти через его диагонали d1 и d2 (согласно теореме Пифагора).

Формула нахождения стороны ромба через его диагонали

Диагонали ромба

  • a – гипотенуза любого из 4 прямоугольных треугольников (например, ΔBEC);
  • половины диагоналей d1 и d2 – катеты треугольников.

Свойство 5

В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.

Вписанная в ромб окружность

Радиус вписанной в ромб окружности r вычисляется по формуле:

Формула нахождения радиуса вписанной в ромб окружности

Признаки ромба

Параллелограмм является ромбом только в том случае, если для него верно одно из следующих утверждений:

  1. Его диагонали пересекаются под прямым углом.
  2. Если его диагонали являются биссектрисами его углов.
  3. Две смежные стороны равны (следовательно, все стороны равны).

Примечание: Любой четырехугольник, стороны которого равны, является ромбом.

Источник

Определение

Ромб – это параллелограмм, у которого все стороны равны.

Таким образом, ромб обладает всеми свойствами параллелограмма:

(sim) противоположные углы ромба попарно равны;

(sim) соседние углы ромба в сумме дают (180^circ);

(sim) диагонали точкой пересечения делятся пополам.

Теорема: свойство ромба

Диагонали ромба перпендикулярны и делят его углы пополам.

Доказательство

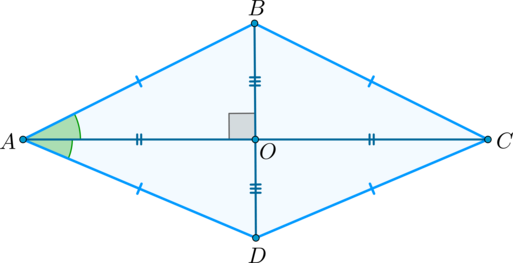
Рассмотрим ромб (ABCD).

По определению ромба (AB = AD), поэтому треугольник (BAD) равнобедренный. Так как ромб – параллелограмм, то его диагонали точкой (O) пересечения делятся пополам. Следовательно, (AO) – медиана равнобедренного треугольника (BAD), а значит, высота и биссектриса этого треугольника. Поэтому (ACperp BD) и (angle BAC =
angle DAC).

Теорема: признаки ромба

1. Если в параллелограмме диагонали перпендикулярны, то это – ромб.

2. Если в параллелограмме диагонали делят его углы пополам, то это – ромб.

3. Если в выпуклом четырехугольнике все стороны равны, то он – ромб.

Доказательство

1) Рассмотрим параллелограмм (ABCD). Пусть (ACperp BD).

Т.к. в параллелограмме диагонали точкой пересечения делятся пополам, то в треугольнике (ABD) отрезок (AO) – медиана. Т.к. к тому же (AO) – высота (следует из условия), то (triangle ABD) – равнобедренный, т.е. (AB=AD). Т.к. у параллелограмма противоположные стороны равны, то отсюда следует, что все его стороны будут равны.

2) Пусть (AC) – биссектриса угла (angle A).

Т.к. в параллелограмме диагонали точкой пересечения делятся пополам, то в треугольнике (ABD) отрезок (AO) – медиана. Т.к. к тому же (AO) – биссектриса (следует из условия), то (triangle ABD) – равнобедренный, т.е. (AB=AD). Т.к. у параллелограмма противоположные стороны равны, то отсюда следует, что все его стороны будут равны.

3) Пусть (ABCD) – произвольный четырехугольник и (AB=BC=CD=AD).

Т.к. противоположные стороны четырехугольника попарно равны, то он – параллелограмм. Т.к. у него все стороны равны, то по определению это ромб.

Источник

Добавить комментарий