Как вычислить расстояние между городами
Чтобы вычислить расстояние между городами, можно воспользоваться картой и специальным приспособлением – дальнометром. Также можно прибегнуть к современным калькуляторам расстояний, они доступны всем пользователям интернета.

Инструкция
Воспользуйтесь атласом или картой. Найдите на ней города, расстояние между которыми вам необходимо определить. Если вам интересно знать расстояние по прямой, просто измерьте отрезок от одного города до другого. Обратите внимание на масштаб, он указан в нижней части карты. Обычно он пишется в формате «1:5 000 000», это значит, 1 см карты соответствует 50 км местности. Таким образом, если расстояние между городами в таком масштабе составляет 5 см, значит, между ними примерно 250 км. Если же вас интересует протяженность дороги, разбейте трассу на участки, измерьте ее расстояние и переведите в километры.
Используйте специальное устройство для измерения расстояний на сантиметры в километры, используйте параметры масштаба, указанные на карте.
Воспользуйтесь современным способом расчета протяженности пути между городами. Программа “Калькулятор расстояний” дает наиболее точные результаты. Найти ее можно с помощью поисковой системы или на сайтах грузоперевозчиков. В специальные поля калькулятора введите названия двух городов, нажмите кнопку «Рассчитать». Если вам необходимо узнать расстояние между небольшими населенными пунктами, возможно, программа не распознает название этого города, поэтому предварительно узнайте районный или областной центр.
Если у вас нет возможности воспользоваться интернетом, обратитесь к печатным материалам. Например, в офисе наверняка найдется ежедневник, на первых страницах в разделе полезной информации вы сможете найти таблицы расстояний, но включены в них лишь крупные города. Чтобы выяснить расстояние между, например, Москвой и Санкт-Петербургом, найдите один из городов в столбце, а второй в верхней строчке. Города перечислены в алфавитном порядке. В точке пересечения соответствующих столбца и строчки вы увидите расстояние между городами. Оно выражено в километрах.
Источники:
- Калькулятор расстояний «Русагросервис» в 2018
- найти город по расстоянию в 2018
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
|
Градусная сетка |
|
|
с Cевера на Юг |
|
|
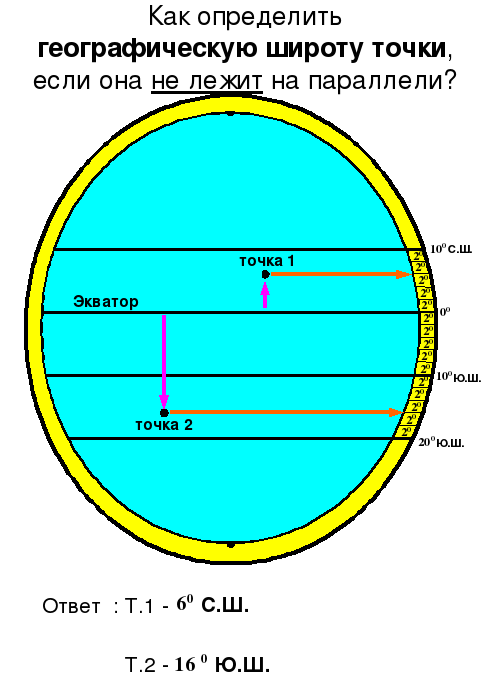
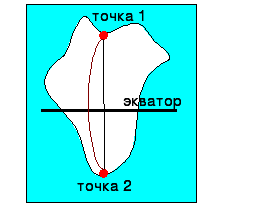
А) Если объект расположен по обе стороны от экватора |
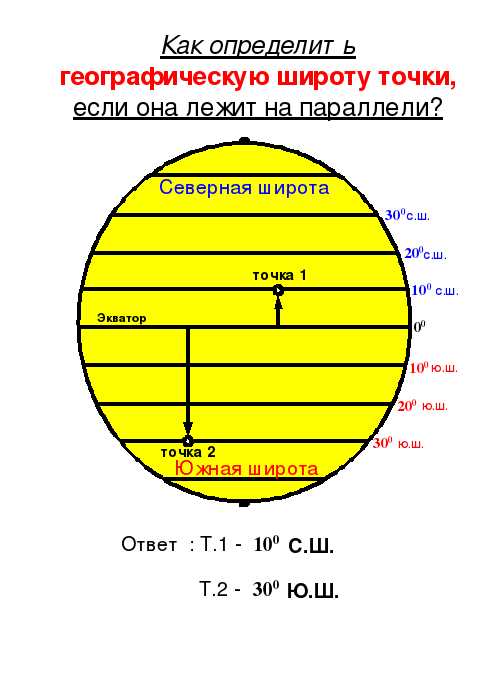
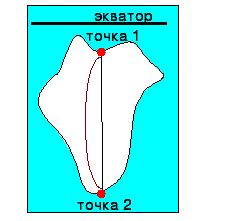
Б) Если объект расположен по одну сторону от экватора |
|
|
|
|
1. Определить географическую широту точек: т.1 – 350 с.ш. т.2 – 250 ю.ш. 2. Сложить полученные данные: 35 + 25 = 60 (получим расстояние в градусах) 3. Умножить расстояние на 111 ( так как в 10 по меридиану 111 км ) 60 х 111 = 6660 4. Ответ: протяжённость объекта 6660 км |
1. Определить географическую широту точек: т.1 – 100 с.ш. т.2 – 440 ю.ш. 2. Вычесть из широты т.2 широту т.1: 44 – 10 = 34 (получим расстояние в градусах) 3. Умножить расстояние на 111 ( так как в 10 по меридиану 111 км ) 34 х 111 = 3774 4. Ответ: протяжённость объекта 3774 км |
|
с Запада на Восток |
|
|
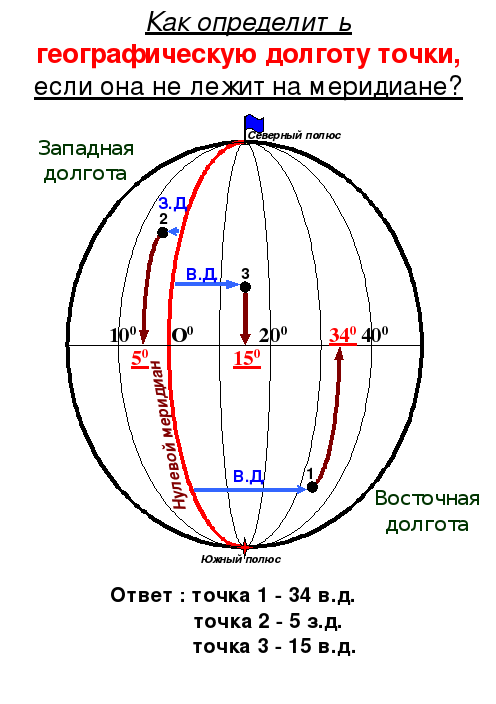
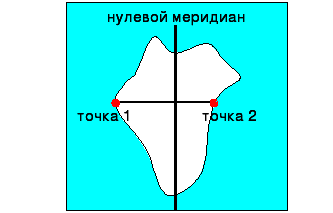
А) Если объект расположен по обе стороны от нулевого меридиана |
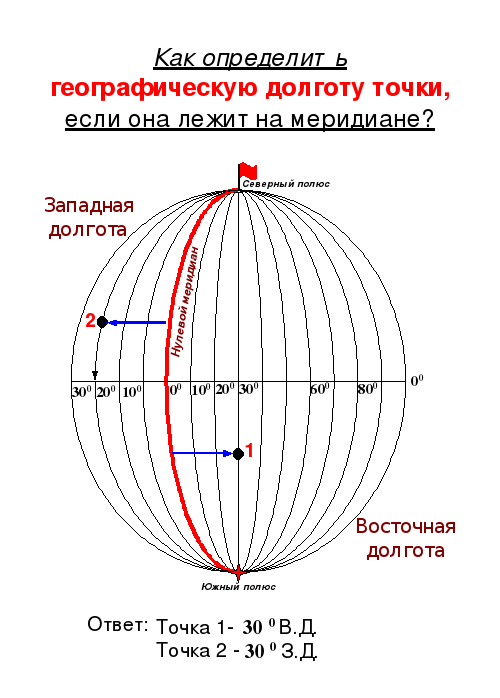
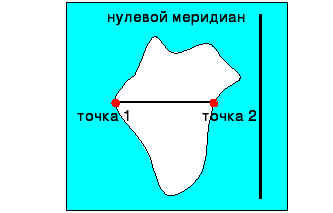
Б) Если объект расположен по одну сторону от нулевого меридиана |
|
00 – 111,3 км 100 – 109,6 км (пример) 200 – 104,6 км 300 – 96,5 км 400 – 85,4 км 500 – 71,7 км 600 – 55,8 км 700 – 38,2 км 800 – 19,4 км |
|
|
1. Определить географическую долготу точек: т.1 – 17 0 з.д. т.2 – 9 0 в.д. 2. Сложить полученные данные 17 + 9 = 26 (получим расстояние в градусах) 3. Умножить полученное число на длину 10 (это зависит от того, по какой параллели мы определяем расстояние, у нас параллель 100) 26 х 109,6 = 2850 4. Ответ: протяжённость объекта 28500 км |
1. Определить географическую долготу точек: т.1 – 80 0 з.д. т.2 – 20 0 з.д. 2. Вычесть из долготы точки1 долготу точки 2 80 – 20 = 60 (получим расстояние в градусах) 3. Умножить полученное число на длину 10 (это зависит от того, по какой параллели мы определяем расстояние, у нас параллель 100) 60 х 109,6 = 6576 4. Ответ: протяжённость объекта 6576 км |
Такая формула, вероятно, уже давненько выведена в математике (или в географии). Это раздел сферической геометрии. Не имею ничего против очень хорошего ответа Сергея Ракитина, он совершенно справедливо заслужил ЛО! И тем не менее попробую добавить ещё свой вариант формулы. Конечно, это не я её придумал.
Даны две точки земной поверхности: пункты 1 и 2. Оказывается, кратчайшее расстояние между ними вдоль поверхности Земли рассчитывается по следующей формуле:
L = R * arccos(sinφ₁ * sinφ₂ + cosφ₁ * cosφ₂ * cos|λ₁ – λ₂|)
где:
L — искомое расстояние между пунктами 1 и 2;
R — усреднённый радиус Земли, это константа: R = 6371 км;
φ₁, φ₂ — географические широ́ты пунктов 1 и 2 — две равноправные величины, можно поменять их в формуле местами;
λ₁, λ₂ — географические долго́ты пунктов 1 и 2; аналогично широтам, можно в формуле поменять их местами.
Кроме того: 1) северная широта — положительное число, берётся для формулы со знаком плюс; 2) южная широта — отрицательное число, берётся для формулы со знаком минус; 3) восточная долгота — плюс; 4) западная долгота — минус; 5) широ́ты и долго́ты, понятно, рационально измерять в угловых градусах — главное, верно взять синусы и косинусы по правилам математики; 6) арккосинус — это функция y = arccos(x), значит, значение, т. е. результат этой функции нужно брать никак не в градусах, а в радианах.
Давайте проверим, работает ли формула.
Я решил взять Киев и Москву (вернее сказать — вероятно, какие-то ключевые точки Киева и Москвы, что-то типа отметок нулевого километра). С угловыми минутами возиться тяжело. Решил взять координаты, выраженные в градусах и десятичных долях градуса. Вычисления делал с помощью гугловского калькулятора.
Имеем: φ₁ = 50,4547° с. ш., φ₂ = 55,7522° с. ш.; λ₁ = 30,5238° в. д., λ₂ = 37,61556° в. д.
Поскольку обе широты северные, а обе долготы восточные, то согласно пп. 1 и 3 доппояснений к формуле берём их как положительные числа.
Имеем:
L = R * arccos(sinφ₁ * sinφ₂ + cosφ₁ * cosφ₂ * cos|λ₁ – λ₂|) = 6371 км * arccos(sin50,4547° * sin55,7522° + cos50,4547° * cos55,7522° * cos|30,5238° – 37,61556°|) = 6371 км * arccos(0,77112 * 0,82661 + 0,63669 * 0,56277 * 0,99235) = 6371 км * arccos0,99298 = 6371 км * 0,11856 = 755,34576 км.
Источники (Гугл) утверждают, что истинное расстояние между Киевом и Москвой по кратчайшему пути вдоль поверхности Земли равно 755,77 км.
Таким образом, абсолютная погрешность у меня получилась равной 755,34576 км – 755,77 км = ок. –0,424 км, или, по модулю, 424 метра. 424 метра, на мой взгляд, ошибка вполне допустимая; конечно, накапливаются ошибочки за счёт погрешностей самих вычислений и количества значащих цифр, но думаю, за это Вы меня как-нибудь простите.
Итак, самый главный вывод: формула верна, она работает для любых двух точек нашей планеты.
Задача простая. Нужно вычислить расстояние между двумя точками на карте, при этом известны только их географические координаты, то есть широта и долгота. Для примера вычислим расстояние между Москвой и Питером, но данная методика, конечно же, будет применима и к другим двум точкам местности. В наше время у многих людей есть такие компасы, например при смартфонах, которые показывают не только направление, но и географические координаты.
Итак, задача: вычислить расстояние между двумя городами. Известно только одно – географические координаты, то есть широта и долгота. Посмотрим эти данные в справочнике, ну или в Википедии.
Итак, что нам известно: координаты Москвы:
55,7522 град. с.ш., 37.6156 град. в.д.
Координаты Петербурга:
59,89444 град. с.ш., 30,26417 град. в.д.
Построим с помощью Excel трапецию:
Итак, у нас есть трапеция ABCD. На ней точка D – это Москва, точка B – это Петербург. Отрезок AB проходит по меридиану Петербурга, BC – по параллели Петербурга, CD – по меридиану Москвы и AD – по параллели Москвы.
Что нам известно? Во-первых известны все географические координаты каждой из точек:
A: 55,7522, 30,26417;
B: 59,89444, 30,26417;
C: 59,89444, 37,6156;
D: 55,7522, 37,6156.
Вычислить AB и CD достаточно просто. На меридианах в градусе примерно одинаковое число километров. Это расстояние можно взять из справочных данных, и оно составляет примерно 111,1 км в каждом градусе.
Нужная нам разница в градусах – это 59,89444-55,7522, или 4,14224. А это значит, что разница в километрах – это 4,14224*111,1=460,2029 км.
Что же касается оснований трапеции, там тоже все достаточно просто. Экватор – это ноль градусов северной широты, и длина каждого градуса на экваторе около 111,3 км. Поскольку косинус ноля – это единица, то для любой параллели верна следующая формула: длина каждого градуса равна произведению 111,3 на косинус того угла, который числится в градусах северной широты (ну или южной, если это происходит южнее экватора).
Итак, с помощью Excel вычислим нужные нам косинусы:
- cos(55.7522) = 0,562773
- cos(59.89444) = 0,501595
Это значит, что 1 градус в верхнем основании нашей трапеции =111,3*0,501595=55,82749 км, а один градус в нижнем основании трапеции =111,3*0,562773=62,6366 км. Поскольку число градусов одинаково как в верхнем, так и в нижнем основаниях трапеции и составляет 37,6156-30,26417, то есть 7,35143 градуса. Но число километров в верхнем и нижнем основаниях трапеции не одинаковое.
Рассчитаем эти расстояния в километрах. BC=7,35143*55,82749=410,4119 км.
AD=7,35143*62,6366=460,469 км.
Теперь проведем высоту BH в нашей трапеции:
В прямоугольном треугольнике ABH нам известно, что гипотенуза равна 460,2029 км, малый катет тоже известен (это половина разницы между длинами оснований трапеции, то есть 0,5*[460,469-410,4119], то есть 0,5*50,05711, или 25,02856 км).
Итак, найдем высоту трапеции ABCD, ее можно вычислить с помощью теоремы Пифагора. Напомню, что мы знаем и длину гипотенузы, и длину наименьшего из катетов.
- Квадрат гипотенузы: 211786,7
- Квадрат известного катета: 626,4
- Разность между этими числами: 211160,2
Корень из этой разности – 459,5218 км. Это и есть наша высота трапеции, то есть BH.
Задача почти решена. Для нахождения расстояния между Москвой и Питером нам нужно вычислить диагональ трапеции, то есть BD. Нарисуем эту линию:
Итак, у нас есть треугольник BHD. BH мы только что вычислили (459,5218 км), HD тоже известно (нужно от большего основания трапеции отнять AH. 460,469-25,02856=435,4404).
Два катета известны, нужно найти гипотенузу. По той же теореме Пифагора, и мы увидим, что гипотенуза будет равна 633,0629 км. Это и есть расстояние от Питера до Москвы.
Проверим наши вычисления, спросив у Яндекса, сколько составляет расстояние от Питера до Москвы.
Мы увидим ответ – 634 км. При вычислениях по нашей методике получилось чуть больше, чем 633 км. Это значит, что погрешность при данном виде вычислений достаточна мала. Но если учесть, что крупные города – это не маленькие точки, а большие расстояния с севера на юг и с запада на восток, то можно сказать, что мы вычислили все правильно.
А на этом пока всё, подписывайтесь на мой канал и до новых встреч!
Расстояние между городами
Примеры расчета расстояний:
-
Расстояние от Москвы до Киева
-
Расстояние от Москвы до Питера
-
Расстояние от Москвы до Нижнего Новгорода
-
Расстояние от Москвы до Ярославля
-
Расстояние от Москвы до Владивостока
-
Расстояние от Москвы до Минска
-
Расстояние от Москвы до Твери
-
Расстояние от Москвы до Тулы
-
Расстояние от Москвы до Казани
-
Маршрут Воронеж – Москва
-
Маршрут Екатеринбург – Москва
-
Маршрут Ростов-на-Дону – Москва
-
Маршрут Рязань – Москва
-
Маршрут Кострома – Москва
-
Маршрут Владимир – Москва
-
Маршрут Смоленск – Москва
-
Маршрут Самара – Москва
-
Маршрут Калуга – Москва
Когда может пригодиться расчет расстояний?
Бесплатный расчет расстояний между городами показывает точное расстояние между городами и считает кратчайший маршрут с расходом топлива.
Он может быть востребован в следующих случаях:
- Сервис расчета расстояний помогает проложить маршрут автопутешественнику, например, для летнего отдыха с семьей
или при планировании деловой поездки на автомобиле.
Зная расход бензина и среднюю цену за литр топлива, нетрудно рассчитать обязательные финансовые затраты в поездке. - Водителю-дальнобойщику расчет расстояния между городами позволяет проложить маршрут на карте при
подготовке к дальнему рейсу. - Калькулятор расстояний пригодится грузоотправителю, чтобы определить километраж и в соответствии
с тарифами транспортной компании оценить стоимость грузоперевозки.
Как пользоваться расчетом расстояний?
Для того чтобы рассчитать маршрут между городами,
начните вводить в поле “Откуда” название начального пункта маршрута.
Из выпадающей контекстной подсказки выберите нужный город.
По аналогии заполните поле “Куда” и нажмите кнопку “рассчитать”.
На открывшейся странице на карте будет проложен маршрут, красными маркерами будут обозначены начальный и конечный
населенные пункты, а красной линией будет показан путь по автодороге.
Над картой будут указаны суммарная длина маршрута, продолжительность пути и расход топлива.
Под этой информацией будет размещена сводная таблица с подробными данными о маршруте и об участках пути: тип дороги,
расчетная длина и продолжительность каждого фрагмента маршрута.
Полученный маршрут можно распечатать или, изменив некоторые параметры, повторить расчет.
В дополнительных настройках можно задать транзитные населенные пункты, а также скорректировать расчетную скорость
движения по дорогам каждого типа.
Ниже дополнительных настроек расположены поля ввода данных топливного калькулятора.
Внесите в них актуальный расход горючего вашей машины и среднюю цену 1 литра топлива.
При повторном расчете эти данные будут использованы для подсчета необходимого количества топлива и его стоимости.
Другие методы прокладки маршрута
Пожалуй, самая простая альтернатива – это открыть атлас автодорог и на глаз проложить маршрут по карте.
Затем, прокатив по маршруту курвиметр, можно получить приблизительный километраж.
Оценить время поездки будет сложнее: для этого придется разбить маршрут на фрагменты с одинаковым классом дорог и
измерить сумму длин фрагментов каждого класса.
Далее, зная среднюю скорость для каждого класса дорог, нетрудно рассчитать время, поделив путь на скорость.
Если курвиметра нет под рукой, то можно воспользоваться линейкой.
Приложите нулевую отметку линейки к начальному пункту маршрута и двигайте линейку, плотно примыкая ее к извилинам
дороги.
Рассчитать расстояние между городами также можно с помощью таблиц, которые опубликованы в атласах и
справочниках.
Это достаточно удобно для маршрутов, начинающихся и заканчивающихся в крупных городах.
Мелких населенных пунктов, как правило, нет в таблицах.
Алгоритм расчета расстояния между городами
Расчет маршрута основан на алгоритме поиска кратчайшего пути во взвешенном графе автодорог (алгоритм Дейкстры).
Расстояния определены по точным спутниковым координатам дорог и населенных пунктов.
Расчет является результатом компьютерного моделирования, а модели не бывают идеальными, поэтому при планировании
маршрута поездки не забудьте заложить резерв.
Смотрите также:
Существует несколько подходов к определению расстояния между городами:
- расстояние по автодорогам включает в себя длину автотрассы и соединяющих ее с городом дорог;
- расстояние по прямой, или как его еще называют “по птичьему полету“, характеризуется меньшей протяженностью, но практически менее ценно, т.к. перемещение обычно происходит по дорогам.
В наших расчетах расстояния между городами берутся по автодорогам.
 Длина 10 параллелей:
Длина 10 параллелей: