Прямая и обратная пропорциональность
- Прямая пропорциональность
- Формула прямой пропорциональности
- Обратная пропорциональность
- Формула обратной пропорциональности
Пропорциональность — это зависимость одной величины от другой, при которой изменение одной величины приводит к изменению другой во столько же раз.
Пропорциональность величин может быть прямой и обратной.
Прямая пропорциональность
Прямая пропорциональность — это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто пропорциональными.
Рассмотрим пример прямой пропорциональности на формуле пути:
s = vt,
где s — это путь, v — скорость, а t — время.
При равномерном движении путь пропорционален времени движения. Если взять скорость v равной 5 км/ч, то пройденный путь s будет зависеть только от времени движения t:
| Скорость v = 5 км/ч | |||||
|---|---|---|---|---|---|
| Время t (ч) | 1 | 2 | 4 | 8 | 16 |
| Путь s (км) | 5 | 10 | 20 | 40 | 80 |
Из примера видно, что во сколько раз увеличивается время движения t, во столько же раз увеличивается пройденное расстояние s. В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.
В данном случае скорость (v = 5 км/ч) является коэффициентом прямой пропорциональности, то есть отношением пути ко времени, которое остаётся неизменным:
следовательно,
| 5 | = | 10 | = | 20 | = | 40 | = | 80 | = 5. |
| 1 | 2 | 4 | 8 | 16 |
Если время движения остаётся неизменным, то при равномерном движении расстояние будет пропорционально скорости:
| Время t = 2 ч | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 5 | 15 | 45 | 90 |
| Расстояние s (км) | 10 | 30 | 90 | 180 |
В этом примере коэффициентом прямой пропорциональности, то есть, отношением пути к скорости, которое остаётся неизменным, является время (t = 2 ч):
следовательно,
| 10 | = | 30 | = | 90 | = | 180 | = 2. |
| 5 | 15 | 45 | 90 |
Из данных примеров следует, что две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз другая увеличивается (или уменьшается) во столько же раз.
Формула прямой пропорциональности
Формула прямой пропорциональности:
y = kx,
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Обратная пропорциональность
Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.
Рассмотрим пример обратной пропорциональности на формуле пути:
s = vt,
где s — это путь, v — скорость, а t — время.
При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь s равным 120 км, то потраченное на преодоление этого пути время t будет зависеть только от скорости движения v:
| Путь s = 120 км | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 10 | 20 | 40 | 80 |
| Время t (ч) | 12 | 6 | 3 | 1,5 |
Из примера видно, что во сколько раз увеличивается скорость движения v, во столько же раз уменьшается время t. В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.
В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:
s = vt,
следовательно,
10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.
Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Формула обратной пропорциональности
Формула обратной пропорциональности:
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
xy = k.
Математика
6 класс
Урок № 7
Прямая и обратная пропорциональность. Решение задач
Перечень рассматриваемых вопросов:
- Понятия прямой и обратной пропорциональной зависимости.
- Краткая запись условия задачи.
- Составление и решение пропорций по условию задачи.
- Решение задач на прямую и обратную пропорциональную зависимость.
Тезаурус
Равенство двух отношений называют пропорцией.
Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Основная литература
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Прямая пропорциональность.
Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Обратная пропорциональность.
Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Для решения задач на пропорциональную зависимость, удобно составить таблицу или сделать краткую запись условия.
Столбцы таблицы соответствуют наименованиям зависимых величин.
Строки таблицы соответствуют значениям величин при первом и втором измерении.
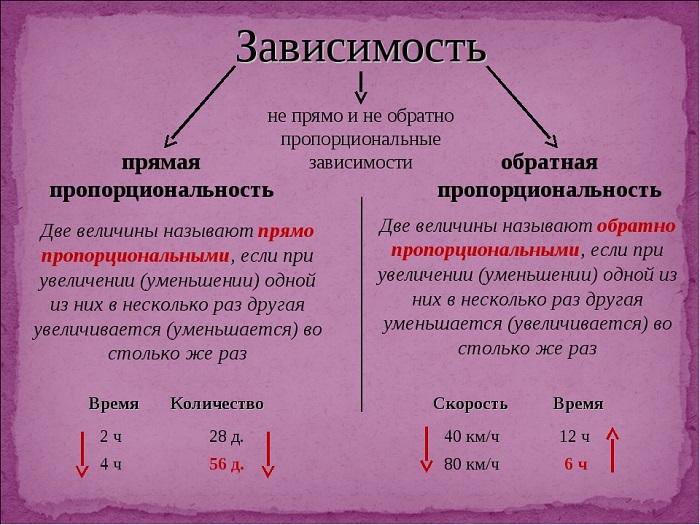
Одинаково направленные стрелки показывают прямо пропорциональную зависимость, противоположно направленные – обратно пропорциональную.
Задача.
Поезд, скорость которого 55 км/ч, был в пути 5 часов. За сколько часов пройдёт этот же участок пути товарный поезд, скорость которого 45 км/ч?
Решение.
При постоянном пути скорость и время движения обратно пропорциональны.
Допустим, товарный поезд пройдёт этот же путь со скоростью 45 км/ч за x ч.
Сделаем краткую запись условия.
Задача.
Двигаясь с постоянной скоростью, велогонщик проезжает 40 метров за 3 с. Какой путь проедет велогонщик за 45 с?
Решение.
При постоянной скорости путь прямо пропорционален времени движения.
Пусть х м проедет велогонщик за 45 с.
Сделаем краткую запись условия.
Задача.
Усилие при восхождении на высоту 600 м равно усилию, требуемому для перехода 25 км по равнине. Турист поднялся в горы на 792 м. Какому расстоянию на равнине соответствует этот подъём?
Решение:
Решение.
Задача.
Четыре программиста могут написать игру за 12 месяцев. За сколько месяцев эту работу могут выполнить три программиста?
Решение.
Количество программистов и скорость написания игры – это обратно пропорциональная зависимость.
Разбор заданий тренировочного модуля
№ 1. Подстановка элементов в пропуски в тексте.
Подставьте нужные элементы в пропуски.
Пешеход шёл 3 часа со скоростью 8 км/ч. За сколько часов он пройдёт то же расстояние со скоростью 6 км/ч?
Решение:
При фиксированном расстоянии время в пути и скорость – ______ пропорциональны.
Пусть _____ часов – пешеход идёт со скоростью 6 км/ч.
Составим пропорцию:
_________
х=_______
х=_______(ч).
Правильный ответ.
Решение:
При фиксированном расстоянии время в пути и скорость – обратно пропорциональны.
Пусть х часов – пешеход идёт со скоростью 6 км/ч.
№ 2. Подстановка элементов в пропуски в таблице.
Заполните таблицу.
Поезд движется со скоростью 45 км/ч. Какое расстояние он пройдёт, если будет в пути 3 ч; 4 ч; 5 ч; 6 ч.
Варианты ответов:
135 км;
180 км;
225 км;
270 км.
Решение.
При постоянной скорости пройденный путь и время прямо пропорциональны. Скорость движения поезда 45 км/ч означает, что за 1 час поезд преодолевает расстояние в 45 км. Обозначим за x км – расстояние, которое поезд пройдёт за 3, 4, 5 и 6 часов.
Таким же способом находим расстояние, которое пройдёт поезд за 4, 5 и 6 часов, и подставляем соответствующие варианты в таблицу.
Ответ:
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Отношения и пропорции
- Прямая и обратная пропорциональные зависимости
Прямая пропорциональная зависимость
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Примеры:
1) 
– периметр квадрата, 
– его сторона.
= 4.
Если = 1 см, то = 4
1 = 4 (см).
Если = 2 см, то = 42 = 8 (см).
Если = 4 см, то = 44 = 16 (см).
Получаем, что каждый раз, увеличивая сторону квадрата в 2 раза, его периметр также будет увеличиваться в 2 раза. Аналогично, если сторону квадрата будем уменьшать в какое-то число раз, то и периметр квадрата будет уменьшаться в это же число раз. Следовательно, величины и прямо пропорциональны. Можно сказать еще и так: “величина прямо пропорциональна величине ” или “зависимость между величинами и является прямой пропорциональностью“.
2) При движении с постоянной скоростью, пройденный путь 
и время движения 
прямо пропорциональны, т.к. пройденный путь равен произведению скорости и времени движения.
Пусть скорость движения пешехода 8 км/ч.
Если = 1 ч, то = 81 = 8 (км).
Если = 3 ч, то = 83 = 24 (км).
Если = 9 ч, то = 89 = 72 (км).
Получаем, что каждый раз, увеличивая время в пути в 3 раза, путь также будет увеличиваться в 3 раза, а это и говорит о том, что зависимость между величинами и является прямой пропорциональностью, при условии движения с постоянной скоростью.
Свойство прямо пропорциональных величин:
Если две величины прямо пропорциональны, то отношение соответствующих значений этих величин равно одному и тому же, постоянному для данных величин, числу.
В рассмотренных выше примерах для величин и это число равно 4, т.к. : = 4 : 1 = 8 : 2 = 16 : 4 = 4, а для величин и это число равно 8, т.к. : = 8 : 1 = 24 : 3 = 72 : 9 = 8.
Обратная пропорциональная зависимость
Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.
Примеры:
1) Если расстояние является постоянной величиной, то скорость 
и время движения обратно пропорциональны, т.к. время движения равно частному от деления расстояния на скорость движения.
Пусть расстояние равно 80 км.
Если = 10 км/ч, то = 80 : 10 = 8 (ч).
Если = 20 км/ч, то = 80 : 20 = 4 (ч).
Если = 40 км/ч, то = 80 : 40 = 2 (ч).
Получаем, что каждый раз, увеличивая скорость движения в 2 раза, время движения будет уменьшаться в 2 раза, а это и говорит о том, что зависимость между величинами и является обратной пропорциональностью, при том условии, что расстояние нужно проехать одинаковое.
2) и 
– стороны прямоугольника, а его площадь 36 см2.
Если = 3 см, то = 36 : 3 = 12 (см).
Если = 6 см, то = 36 : 6 = 6 (см).
Получаем, что величины и обратно пропорциональны, т.к. увеличивая (уменьшая) одну сторону прямоугольника в 2 раза, чтобы его площадь не изменилась, вторую сторону нужно уменьшить (увеличить) в 2 раза.
Свойство обратно пропорциональных величин:
Если две величины обратно пропорциональны, то произведение соответствующих значений этих величин равно одному и тому же для данных величин числу.
В рассмотренных выше примерах для величин и это число равно 80, т.к. = 108 = 204 = 402 = 80, а для величин и это число равно 12, т.к. = 312 = 66 = 36.
Не всякие величины являются прямо пропорциональными или обратно пропорциональными. Например, размер обуви человека увеличивается при увеличении его возраста, но эти величины не являются пропорциональными, т.к. при удвоении возраста размер обуви человека не удваивается.
Пусть нам дана задача:
Украшение состоит из белого и желтого золота массой 192 г. При этом масса белого золота относится к массе желтого золота как 5 : 7. Надо найти массу белого и желтого золота, из которых сделано украшение.
Решение:
Мы можем считать, что все украшение состоит из 5 + 7 = 12 частей одинаковой массы. По условию масса украшения равна 192 г, а значит, масса одной части украшения равна 192 : 12 = 16 г.
Белое золото соответствует 5 частям, то есть имеет массу 5
16 = 80 г, а желтое золото соответствует 7 частям, то есть имеет массу 716 = 112 г.
Итак мы получили, что украшение состоит из 80 г белого золота и 112 г желтого золота.
То есть мы число 192 (масса украшения) представить в виде суммы двух слагаемых – 80 и 112, отношение которых равно 5 : 7.
В этом случае говорят, что число 192 разделили в отношении 5 : 7, или по-другому, число 192 представили в виде суммы двух слагаемых, пропорциональных числам 5 и 7.
Советуем посмотреть:
Отношения
Пропорции
Длина окружности и площадь круга
Отношения и пропорции
Правило встречается в следующих упражнениях:
6 класс
Номер 663,
Мерзляк, Полонский, Якир, Учебник
Номер 667,
Мерзляк, Полонский, Якир, Учебник
Номер 671,
Мерзляк, Полонский, Якир, Учебник
Номер 684,
Мерзляк, Полонский, Якир, Учебник
Номер 686,
Мерзляк, Полонский, Якир, Учебник
Номер 690,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
Задание 784,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 793,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1495,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 846,
Мерзляк, Полонский, Якир, Учебник
Номер 847,
Мерзляк, Полонский, Якир, Учебник
Номер 1000,
Мерзляк, Полонский, Якир, Учебник
Номер 1235,
Мерзляк, Полонский, Якир, Учебник
Одно из основных понятий курса математики в 6 классе – это прямая и обратная пропорциональность. Если некоторая величина (время, масса, цена) изменяется, и одновременно другая величина (расстояние, объем, затраты) тоже меняется, то величины находятся в зависимости между собой, то есть пропорциональны друг другу.
Взаимосвязь между величинами не всегда означает наличие пропорциональности. Так, высота дерева растет с его возрастом, но не во столько же раз. Составление пропорций помогает решить многие задачи как в математике, так и на практике.
Прямая пропорциональность
Если при изменении одного параметра другой изменяется таким же образом, то эти величины прямо пропорциональны друг другу. В этой пропорции увеличение расстояния вдвое означает увеличение времени также двукратно.
Например, при движении автомобиля с постоянной скоростью, время, затраченное на преодоление расстояния, будет прямо пропорционально этому расстоянию. То есть, если 50 км автомобиль проедет за 1 час, то 100 км с той же скоростью он преодолеет за 2 часа.
Функция прямой пропорциональности и ее график
Эта зависимость описывается следующей формулой:
y = k * x.
Здесь k и называется коэффициентом пропорциональности.
Графически функция изображается прямой, которая пройдет через начальную точку координат. Строят график следующим образом: находят одну точку, затем чертят прямую через эту точку и начало координат.
Пример построения
Нужно построить график у = 3х. Подставляем вместо х единицу, вычисляем y = 3, то есть находим координаты (1; 3). Отмечаем эту точку на координатной плоскости, проводим прямую линию через нее и точку (0; 0).
Вот так будет выглядеть график y = k * x при k > 0 (слева) и при k < 0 (справа).
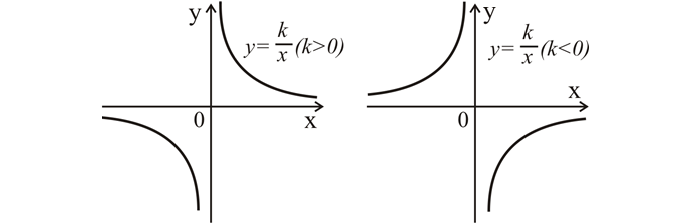
Свойства функции прямой пропорциональности
Основные свойства следующие:
-
область определения, значений составляют все действительные числа;
-
является нечетной;
-
возрастает при всех значениях x, если k > 0;
-
если коэффициент со знаком «-», т. е. если k < 0, то убывает;
-
если k > 0, то прямая располагается в 1 – 3 координатных четвертях и образует острый угол с осью Х, если k < 0, то прямая находится во 2 – 4 четвертях и образует тупой угол с осью Х.
Обратная пропорциональность
Рост одного параметра ведет к уменьшению другого в такое же количество раз, и наоборот, при уменьшении одной величины другая увеличивается во столько же. Это значит, что они обратно пропорциональны друг другу.
Пример: трое рабочих выполнят порученную им работу за 2 часа, а 6 человек такое же задание осилят за 1 час. То есть двукратное увеличение числа работников привело к уменьшению затраченного времени вдвое. Конечно, если прочие факторы неизменны (производительность труда, условия работы).
Функция обратной пропорциональности и ее график
Функция задается формулой:
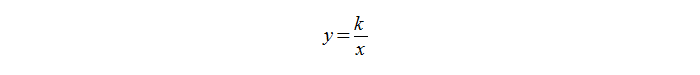
где k – любое действительное число, кроме 0.
График данной зависимости — это гипербола, ее ветви находятся в 1 и 3 четвертях системы координат при k > 0, или во 2 и 4, если коэффициент меньше 0. Ветви гиперболы симметричны относительно точки (0; 0).
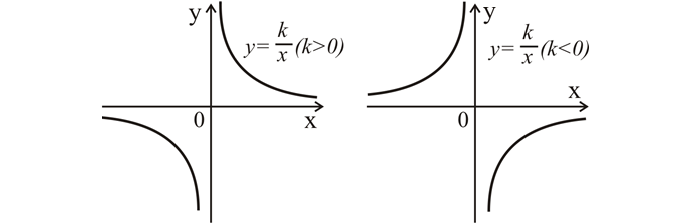
Строят график так: нужно задать значения х, затем вычислить значения у, результаты оформить в виде таблицы. Верхняя строка таблицы заполняется значениями х, нижняя — y.
Пример построения
Нужно построить график функции y = 8/x.
Вот так выглядит таблица для данной функции:
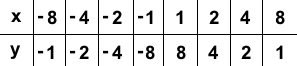
Полученные точки отмечают на координатной плоскости, затем соединяют плавной линией. График будет выглядеть так:
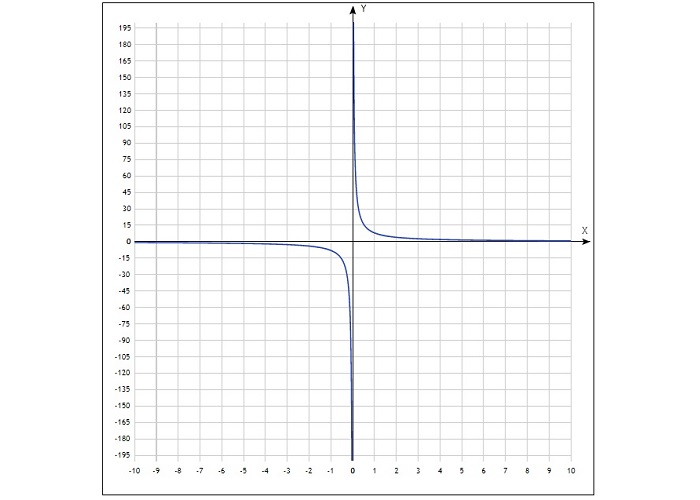
Свойства функции обратной пропорциональности
Основные следующие:
-
области определения, значений функции D(y) – это все действительные числа, кроме 0, т. е. D(y):= x ≠ 0;
-
если коэффициент больше 0, функция является убывающей для всех x; если меньше 0, то y увеличивается для любых значений x;
-
оси координат 0х и 0у – это асимптоты по отношению к ветвям гиперболы, которые приближаются к ним, но не достигают их.
К составлению математических пропорций во многих случаях сводится решение самых разнообразных задач. Например, покупая 1 булочку по определенной цене, подсчитывают затраты на 4 булочки – получается в 4 раза больше.
Ускоряют шаг при ходьбе в 2 раза – достигнут цели вдвое быстрее. Вводят второго кассира в магазине – убывает очередь вдвое. Во всех этих случаях и им подобным применима теория о прямой и обратной пропорциональности.
Прямая и обратная пропорциональность
4.1
Средняя оценка: 4.1
Всего получено оценок: 546.
4.1
Средняя оценка: 4.1
Всего получено оценок: 546.
Прямая и обратная пропорциональность – это одна из основ математики и геометрии 6 класса. Причем, это та основа, знания которой пригодятся не только при решении задач, но и в реальной жизни: пропорциональны друг другу бывают физические величины, заработные платы и конфеты, купленные в магазине.
Опыт работы учителем математики – более 33 лет.
Что такое пропорция?
Пропорция – это взаимосвязь двух величин. То есть, если меняется одна величина, меняется и другая. Если одна величина пропорциональна другой, а друга пропорциональна третьей, то все эти величины связаны между собой. Разделяют прямую и обратную пропорцию. Дадим им определения и приведем наглядные примеры.
Прямая пропорция
Прямая пропорция – это взаимоотношение величин, при котором, увеличивая одну величину, мы автоматически увеличим другую. Самый простой пример это булочки в магазине и цена на них. Булочка в любом случае стоит 30 руб. Покупая одну штуку мы платим 30 руб.
Если увеличим размер покупки, то соразмерно возрастет и цена. Она не может не возрасти, ведь булочник не будет отдавать свой товар просто так. За 2 булочки мы заплатим 60 рублей, за 3 – 90 и так далее.
Если устанавливать зависимость между количеством булочек и ценой на них, то получится следующее отношение:
Цена булочек/количество=30/1=60/2 и так далее. Заметим, что всегда это отношение равно одному и тому же числу. В данном примере это число 30. Оно будет постоянным для любого варианта данной пропорции. Конкретно в данном примере это число является одновременно и ценой одной булочки.
Иными словами, для приведенного примера пропорциональность можно объяснить так: сколько бы булочек мы ни купили, все равно цена одной будет 30 рублей. Вот и все. В рамках математики говорят, что если коэффициент пропорциональности не меняется, то числа пропорциональны.
Для того, чтобы понять, изменяется коэффициент или нет, нужно просто поделить друг на друга числа этой пропорции и сравнить результат. То есть, взять сначала отношение цены одной булочки к ее количеству, а затем цены 30 булочек к их количеству. Коэффициент сохранит свое значение, значит эти числа прямопропорциональны.
Обратная пропорция
Существует также понятие обратной пропорции. Часто бывает так, что одна величина зависит от другой, но не прямопропорционально. Сравним две взаимосвязанные между собой величины. Например, мотоциклист залил в бак бензин. Чем меньше бензина остается в баке мотоциклиста, тем больше проехал водитель. Здесь на лицо обратная зависимость количества бензина и пройденного расстояния.
Как просто запомнить?
Есть 4 простые схемы запоминания темы, по две для каждого вида пропорциональности.
Для прямой пропорции всегда работает схема: «больше-больше» или «меньше-меньше». То есть при увеличении одной величины, увеличится и другая, или при уменьшении одной величины уменьшится другая.
Соответственно, для обратной пропорциональности наоборот: «больше-меньше» или «меньше-больше». То есть, чем больше одна величина, тем меньше другая и наоборот.
Что мы узнали?
Мы привели объяснение прямой и обратной пропорциональности. Вывели простые схемы для запоминания темы и обговорили понятные примеры.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
-
Лариса Раднаева
5/5
-
Валентина Макарова
5/5
Оценка статьи
4.1
Средняя оценка: 4.1
Всего получено оценок: 546.
А какая ваша оценка?
