Как найти прямой дирекционный угол

8,Дирекционные
углы и румбы линий, зависимость между
ними. Прямые и обратные дирекционные
углы.

дирекционным
углом
является угол в горизонтальной плоскости,
отсчитываемый от северного направления
осевого меридиана по ходу часовой
стрелки до данной линии.

Осевым
румбом называется
острый горизонтальный угол, отсчитываемый
от ближайшего направления осевого
меридиана (северного или южного) до
данной линии.

Зависимость
между дирекционными углами и румбами
определяется
для четвертей по следующим формулам:

I
четверть (СВ) r
= α

II
четверть (ЮВ) r
= 180° – α

III
четверть (ЮЗ) r
= α
– 180°

IV
четверть (СЗ) r
= 360° – α

α_BC
является прямым дирекционным углом
линии ВС
в точке М,
а угол α_CB
– обратным дирекционным углом этой же
линии в той же точке.

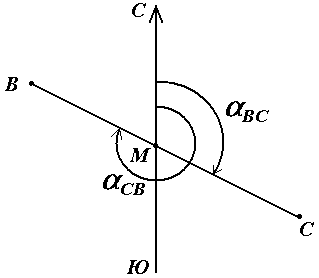
Рис.
17. Прямое и обратное направление линии

Из
рисунка видно, что α_CB
= α_BC
+ 180°, т.е. прямой и обратный дирекционные
углы отличаются друг от друга на 180°.

Министерство образования и науки Республики
Башкортостан

Башкирский колледж архитектуры, строительства
и коммунального хозяйства

    
План – конспект

по дисциплине  «Основы геодезии»

на тему «Ориентирование линий»

Для студентов специальности 08.02.01

Строительство и
эксплуатация зданий и сооружений

Уфа -2020

ЛЕКЦИЯ 5

Тема «Ориентирование
линий»

1.     Дирекционные углы линий.

2.    
Румбы линий.

3.    
Зависимость
дирекционных углов и румбов.

4.    
Методика решения
задач на определение примычных углов.

1.     
Дирекционные углы линий.

Определение положения линий относительно сторон света
называется ориентированием.

Ориентирование заключается в том, что определяется
угол между исходным направлением и данной линией.

За исходное направление для ориентирования принимают
ось абсцисс (ось Х) или меридиан.

Для ориентирования линий служат углы, которые
называются дирекционными углами  и румбами.

Угол, составленный северным концом меридиана и данной
линией, называется дирекционным углом.

Дирекционный угол обозначается  ℒ

ЗАПОМНИТЕ!

Дирекционный угол отсчитывается

от 0 до 360˚ по ходу часовой стрелки.

                   С                                   

                                                            ℒ_1-2  = 50˚                     

                             2                      

З                 
                В

             1                  

                   Ю

             (меридиан)

Задача.

Построить угол, образованный двумя линиями, имеющими
следующие дирекционные углы

ℒ_1-2  = 160˚

ℒ_2-3  = 70˚

и определить величину этого угла.

Решение:

С

       160˚                                                                        <2=70˚+20˚=90˚

  
1

 

20˚   

            20˚      70˚                      3

Ю                      

          2

Дирекционный угол
заданного направления α _пр называется прямым, а
противоположного – обратным α _обр  Прямой
и обратный дирекционные углы, которые отличаются между собой на ±180˚

                                              

   

   С                                                                         ℒ_1-2  = 60˚

             
2                                                         ℒ_2-1 = 240˚

           60˚

1                    180˚ + 60˚ = 240˚

               
                  С                                                     ℒ_1-2   = 300˚

       
2                                                                      ℒ_2-1   = 120˚

                        1  300˚

                                     300^о
– 180^о =  120^о

                         Ю

ЗАПОМНИТЕ!

Прямой дирекционный угол отличается

от обратного на «+»  или « – » 180˚

Иногда для ориентирования линии на
местности пользуются не дирекционными углами, а румбами.

2.     
Румбы линий.

Угол, составленный ближайшим концом меридиана и данной
линией, называется румбом.

  Румб образует острый угол и  откладывается как по
ходу часовой стрелки, так и против, и обозначается    r.                          

ЗАПОМНИТЕ!

Румб имеет значение

от 0 до 90˚ и направление, в
зависимости от четверти, в которой находится данная линия

                      С                                              
r_1-2
=СВ:60˚

                                                                          
r_1-3=ЮВ:60˚

          
СЗ        60˚         2   СВ

    
З             1                В

           ЮЗ                     3  
ЮВ

                      Ю

Задача.

Построить угол, образованный двумя линиями, имеющими
следующие румбы

r _1-2  = ЮВ : 25˚

r _2-3  = СВ : 65˚

и определить величину этого угла.

Решение:

С

                    В                                                             <2=25˚+65˚=90˚

   1

                     С

25˚   

            25˚      65˚                      3

Ю                            В

З         
2

              Ю

Румб заданного направления r _пр. называется прямым, а противоположного – обратным r _обр. Прямой и
обратный румбы равны по величине и отличаются только направлением.

r_1-2
= ЮВ : 40˚

r_2
-1 = СЗ : 40˚

ЗАПОМНИТЕ!

Прямой румб отличается

от обратного  только  направлением

3.     
Зависимость
дирекционных углов и румбов.

На практике часто возникает необходимость определить румбы линий по
дирекционным углам и наоборот.

Таблица зависимости румбов и дирекционных
углов.

Пример перевода дирекционных углов в румбы

1.  
если
дирекционный угол α равен 42°, тогда согласно таблицы румб вычисляется по
формуле r=α=42°, а название румба будет СВ;

                
r = СВ: 42

2. если дирекционный угол α равен 100°, тогда
согласно таблицы румб вычисляется по формуле r=180°-α=180°-100°=80°, а название
румба будет ЮВ;              r = ЮВ: 80

3. если дирекционный угол α равен 210°,
тогда согласно таблицы румб вычисляется по формуле r=α-180°=210°-180°=30°, а
название румба будет ЮЗ;              r = ЮЗ: 30

4. если дирекционный угол α равен 335°, тогда
согласно таблицы румб вычисляется по формуле r=360°-α=360°-335°=25°, а название
румба будет СЗ.

r = СЗ: 25

4.Методика
решения задач  на определение примычных углов.

1.    
Через вершину
примычного угла, который необходимо вычислить, провести меридиан, показать
направление север и юг.

2.    
Определить, какими
линиями составлен примычный угол.

3.    
Показать известные
румбы или дирекционные углы этих линий на чертеже.

4.    
Вычислить примычный
угол.

 

1).     С                                                                 3).

                                                                                  
                      В₁

                    Β₁

 

         Ю

2).      
С

                           
В₁

 

          Ю

 

 

Домашнее задание

1.    
Построить линии по
заданному дирекционному углу

α_1-2 =57^о

α_2-3 =276^о

2.    
Провести линии по заданным
румбам.

r_1-2 = СВ:23^о

r_1-3 = ЮЗ:83^о

3.     По заданному дирекционному углу определить
румб линии

α_1-2 =157^о

α_3-4 =290^о

4. По заданному румбу линии определить дирекционные углы

r_1-2 = СВ:23^о

r_3-4 = ЮВ:43^о

5. Построить угол, образованный двумя линиями,
имеющими следующие румбы r_1-2 = СВ:50˚, r_2-3 = ЮВ:30˚,  и определить величину этого угла.

              
Определить примычные углы β₂ и β₃ , если

                                                                                 
r_2-3 = СВ:70˚

                                                        
3                           r_2-A
= ЮВ:60˚

               20˚                                                             
r_3-B = ЮЗ:20˚

         2        β₂                       β₃       

                                                    20˚

               60˚                           В                   

1                          
А                                                                                             

 

Дирекционный угол

Дирекционный угол это один из углов ориентирования, который применяется в геодезии при ориентировании линий в зональной системе координат (проекция Гаусса-Крюгера).

Дирекционный угол определяют по топографической карте или плану, или вычисляют аналитически, вначале определив азимут линии и угол сближения меридианов. На местности дирекционный угол измерить невозможно.

Дирекционный угол отсчитывается от северного направления осевого меридиана шестиградусной зоны (или параллельного ему направления) по ходу движения часовой стрелки от 0° до 360° и обозначается буквой α.

На рисунке показан дирекционный угол линии BC в одной из шестиградусных зон проекции Гаусса-Крюгера.

Следует ещё раз обратить внимание, что дирекционный угол, в отличие от азимутов, отсчитывается не от географического или магнитного меридианов, а от осевого меридиана зональной системы координат.

На рисунке для линии BC показаны её дирекционный угол α_B-C и азимут A_B-C. Из рисунка видно, что зная истинный азимут и угол сближения меридианов γ, дирекционный угол линии можно вычислить по формуле:

где γ – угол сближения меридианов со своим знаком.

Пример вычисления дирекционного угла линии по азимуту:

вычислить дирекционный угол линии 1-2, если ее истинный азимут равен А_1-2 = 15°25′, а угол сближения меридианов γ = -0°02′.

согласно формулы можем записать

Также, по известному дирекционному углу линии и углу сближения меридианов, можно вычислить истинный азимут линии:

где γ – угол сближения меридианов со своим знаком.

Пример вычисления азимута линии по её дирекционному углу:

вычислить истинный азимут линии 3-4, если ее дирекционный угол равен α_3-4 = 214°11′, а угол сближения меридианов γ = -0°03′.

согласно с формулой запишем

Для определения дирекционного угла по топографической карте или плану, используют координатную сетку (километровую сетку), для чего транспортир прикладывают к координатной линии как показано на рисунке.

Использование дирекционных углов упрощает расчеты – при вычислениях не требуется постоянно учитывать угол сближения меридианов как при ориентировании линий с помощью азимутов.

Дирекционный угол

Дирекционный угол (α) – это угол между проходящими через данную точку направлением на ориентир и линией параллельной оси абсцисс, отчитываемой от северного направления оси абсцисс по ходу часовой стрелки оси 0 до 360°.

Дирекционные углы направлений измеряются преимущественно по карте или определяются по магнитным азимутам.

Дирекционный угол ориентирного направления может определяться геодезическим или гироскопическим способом, из астрономических наблюдений, с помощью магнитной стрелки буссоли и по контурным точкам карты (аэрофотоснимка).

При геодезическом способе ориентирования дирекционный угол ориентирного направления может быть получен непосредственно из каталога (списка) координат, решением обратной геодезической задачи по координатам геодезических пунктов, при выполнении засечек или прокладке полигонометрического хода одновременно с определением координат привязываемых точек, а также путем передачи угловым ходом от направления с известным дирекционным углом.

При гироскопическом способе ориентирования с помощью гирокомпаса определяют истинный (астрономический) азимут ориентирного направления, а затем переходят к дирекционному углу этого направления. Азимут ориентирного направления с помощью гирокомпаса определяется по двум, трем (четырем) точкам реверсии. Увеличение числа точек реверсии до трех (четырех) обеспечивает контроль и повышает точность определения дирекционного угла.

При астрономическом способе ориентирования дирекционный угол ориентирного направления определяют путем перехода от азимута светила к азимуту ориентирного направления, а от последнего — к дирекционному углу. Азимут светила вычисляют по результатам наблюдений, выполненных на местности с данной точки. Азимут ориентирного направления из астрономических наблюдений может быть получен и с помощью азимутальной насадки АНБ-1 к буссоли ПАБ-2А непосредственно на местности без выполнения вычислений.

Способ определения дирекционного угла ориентирного направления из астрономических наблюдений является наиболее точным.

Работы в поле при этом способе заключаются в измерении горизонтального угла Q между направлением на светило и заданным направлением в момент времени наведения прибора на светило. По моменту времени наблюдения светила вычисляют азимут а светила, от него переходят к астрономическому азимуту А направления на ориентир: A’ = a + Q. Зная значение сближения меридианов у в точке наблюдения, определяют дирекционный угол с ориентирного направления: a = A — y.

При определении дирекционного угла ориентирного направления с помощью магнитной стрелки буссоли на местности сначала получают магнитный азимут ориентирного направления, а затем, учитывая поправку буссоли, переходят к дирекционному углу. Дирекционный угол ориентирного направления определяется по формуле: а = Ат + (±dАт).

По карте (аэрофотоснимку) дирекционный угол ориентирного направления получают решением обратной геодезической задачи по координатам двух контурных точек Координаты контурных точек при этом определяются по карте (аэрофотоснимку) с помощью циркуля измерителя и поперечного масштаба. Точность полученного дирекционного угла будет тем выше, чем больше расстояние между начальной и ориентирной точками и чем точнее определены координаты этих точек.

Дирекционный угол по карте также можно определить с помощью хордоугломера. Для этого опознают на карте исходную и ориентирную точки, проводят через них прямую линию и получают на карте ориентирное направление. Измерив с помощью хордоугломера угол между северным направлением вертикальной линии километровой сетки карты и ориентирным направлением, получают дирекционный угол этого направления.

Свойства дирекционных углов: дирекционные углы α₁=α₂=α₃ так как параллельные линии пересекаются одной линией. Следовательно, углы равны.

Рисунок 2. — Дирекционные углы.

Дирекционные углы могут быть прямыми и обратными (они отличаются на 180°):

Рисунок 3. — Прямые и обратные дирекционные углы.

В зависимости от выбора системы поверхностных координат или проекции земного эллипсоида на плоскость дирекционный угол может иметь собственное название. Например, геодезическийдирекционный угол, гауссов дирекционный угол и т.д.

Вычисление дирекционных углов

По известному дирекционному углу a_n и по исправленным горизонтальным углам b_испр вычисляются дирекционные углы остальных сторон теодолитного хода по формулам для правых горизонтальных углов:

– дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180° и минус исправленный горизонтальный угол правый по ходу.

Величина дирекционного угла не может превышать 360° и быть меньше 0°. Если величина дирекционного угла больше 360°, то из результата вычислений необходимо вычесть 360° (см. пример).

Контроль вычисления дирекционных углов. В замкнутом теодолитном ходе в результате вычислений получается дирекционный угол исходной стороны.

Пример вычисления дирекционных углов:

Дирекционный угол исходной стороны a_1-2 равен 45°45¢.

;

;

;

;

При вычислении дирекционного угла получилось значение 405°45¢. Из полученного значения вычитается 360°.

.

Контроль вычисления дирекционных углов получился.

Все результаты вычислений заносятся в таблицу «Ведомость вычисления координат» (табл. 2).

1.3 Вычисление приращений координат

Вычисление приращений координат выполняется по формулам:

,

где d – горизонтальное проложение (длина) линии; a – дирекционный угол этой линии.

Приращения координат вычисляются с точностью два знака после запятой.

Пример вычисления приращений координат:

;

;

;

;

.

;

;

;

;

.

Все результаты вычисления заносятся в табл. 2. Пример вычисления тригонометрических функций на калькуляторе приведен в отдельном файле.

1.4 Уравнивание линейных измерений

Разность между суммой вычисленных приращений координат и теоретической суммой называется линейной невязкой хода и обозначается f_Х и f_Y. Уравнивание линейных измерений выполняется по осям Х и Y.

Линейная невязка вычисляется по формулам:

.

Теоретическая сумма приращений координат зависит от геометрии хода. В замкнутом теодолитном ходе она равна нулю, тогда невязка равна

.

Прежде, чем распределять невязки в приращения координат, необходимо убедиться в их допустимости. Для чего вычисляется абсолютная невязка хода f_абс

,

где Р – периметр хода (сумма длин сторон), м.

Относительная невязка сравнивается с допустимой .

В случае, когда полученная относительная невязка допустима, т.е. , то вычисляются поправки в приращения координат пропорционально длинам сторон. Невязки распределяются с обратным знаком. Если , то проверяются вычисления в п. 3.3 и 3.4.

Поправки в приращения координат d_X и d_Y вычисляются по формулам с округлением до 0,01 м:

,

где d_X и d_Y – поправка в приращение по оси Х и Y, соответственно, м; f_X и f_Y – невязки по осям, м; Р – периметр (сумма сторон), м; d_i – измеренная длина (горизонтальное проложение), м.

Знак у поправки противоположен знаку невязки. Поправки записываются в «Ведомость вычисления координат». В примере (табл. 6) поправки показаны красным цветом.

После вычисления поправок следует сделать проверку, т.е. сложить все поправки. Если их сумма будет равна невязке с обратным знаком, то распределение невязки выполнено правильно. То есть:

.

Вычисляются исправленные приращения.

Полученные поправки алгебраически прибавляются к соответствующим приращениям и получаются исправленные приращения:

.

Контроль: сумма исправленных приращений в замкнутом теодолитном ходе должна равняться нулю, т.е. должно выполняться равенство:

.

Пример вычисления линейной невязки:

;

.

;

.

Пример вычисления поправок в приращения координат:

;

;

;

;

;

Контроль .

;

;

;

;

;

Контроль .

Поправки записываются в «Ведомость вычисления координат» над вычисленными приращениями. В примере поправки показаны красным цветом (Табл. 2).

Пример вычисления исправленных приращений координат:

.

Контроль ; Контроль .

Сумма исправленных приращений равна нулю, т.е. контроль выполняется.

[spoiler title=”источники:”]

http://topogis.ru/adu_2_2.php

http://lektsii.org/14-31376.html

[/spoiler]

 Актуальные цены на услуги геодезистов в Москве и Московской области  в 2022 году.

Решение обратной геодезической задачи онлайн

Обратная геодезическая задача заключается в том, что при известных координатах точек А( X_A, Y_A ) и В( X_B, Y_B ) необходимо найти длину S_AB и направление линии АВ: румб r_AB  и  дирекционный угол α_AB

Ниже представлена форма в которую можно ввести исходные значения и получить искомые данные. Это простое решение, которым может воспользоваться любой кому лень разбираться с формулами.

Если же говорить о сути решения задачи, то обратная геодезическая задача решается следующим образом.

Сначала находим приращения координат:

 ΔX = X_B – X_A ;

 ΔY = Y_B – Y_A .

Величину угла r_AB определяем из отношения

По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим α_AB.

Для контроля расстояние S_AB дважды вычисляют по формулам: