На этой странице вы узнаете
- Как мы сталкиваемся с двугранными углами, когда читаем книгу?
- Где в комнате можно найти перпендикулярные плоскости?
- Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Стереометрия — это не просто раздел математики, который нужно долго и нудно учить. На самом деле стереометрия описывает всю нашу жизнь. Стало интересно? Давайте разбираться.
Углы между плоскостями
Мы точно знаем, что угол между стеной и полом равен 90°. Также, как и угол между стеной и потолком, или полом и любым предметом мебели.
Но чему равен угол между двумя открытыми страницами тетради? Или угол между стеной и полуоткрытой дверью? Угол между перилами и плоскостью пола? Все эти углы достаточно легко найти. И ответы на все эти вопросы нам дает именно стереометрия.
Начнем разбирать в углах между плоскостями с того, что введем понятие двугранного угла.
Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу.
Если мы откроем книгу не полностью и посмотрим на пространство между двумя страницами, это пространство и будет двугранным углом.

На рисунке:
АВ — общая прямая для плоскостей, ее называют ребром двугранного угла;
a, b — плоскости, которые образуют двугранный угол, они называются гранями двугранного угла.
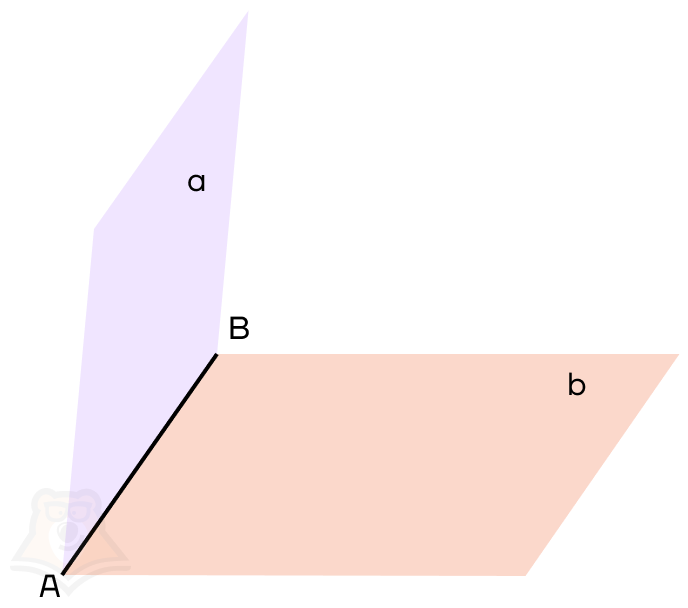
Если раскрыть книгу не полностью, то ее страницы будут образовывать двугранный угол, то есть часть пространства, заключенную между двумя страницами.
Заметим, что при пересечении двух плоскостей обычно образуется четыре двугранных угла. Нас интересует меньший из них.
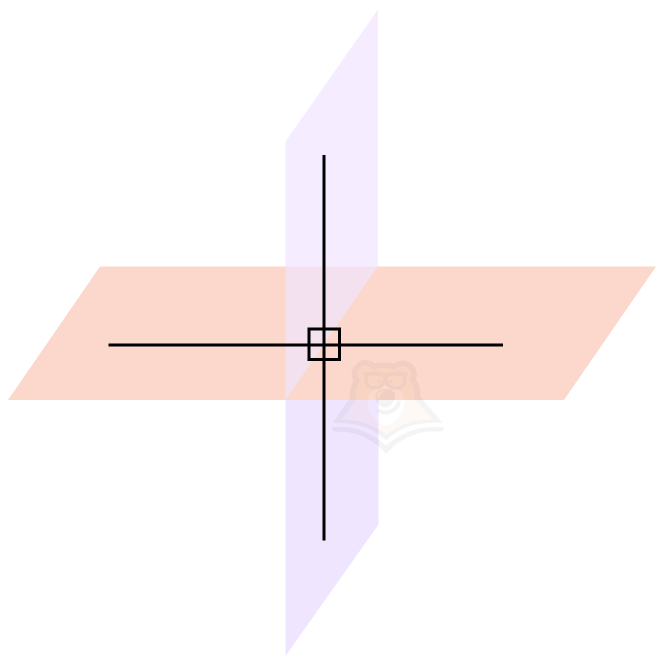
Настало время ввести понятие угла между двумя плоскостями. Но для этого нам нужно провести перпендикуляры к ребру двугранного угла в каждой плоскости. Важно, чтобы перпендикуляры пересекались в одной точке.
Проведенные перпендикуляры образовали четыре угла. Меньший из них и будет называться углом между плоскостями.
Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях.
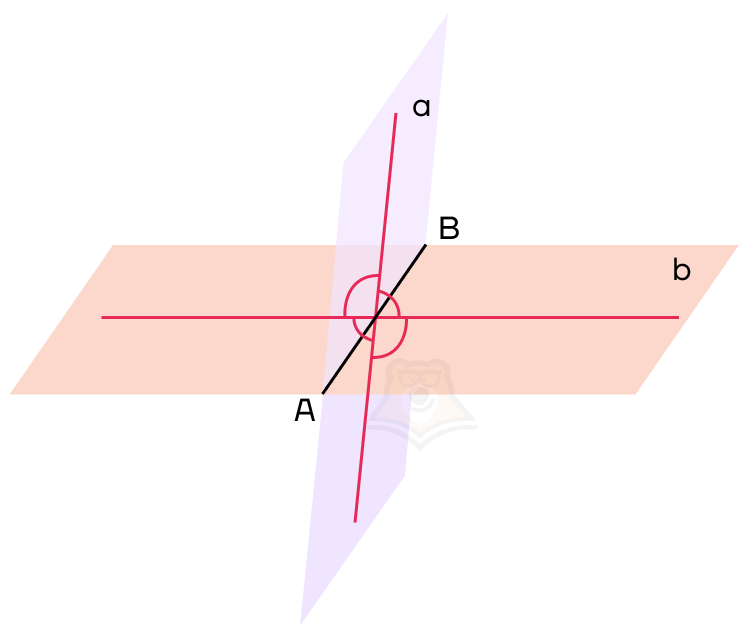
Обозначим нужный нам угол на рисунке как угол COD. Он и будет являться углом между данными плоскостями.
Угол COD также будет называться линейным углом двугранного угла.
Линейный угол двугранного угла показывает градусную меру двугранного угла. Поскольку двугранный угол — это часть пространства, то в этом пространстве можно провести множество линейных углов, которые будут равны между собой.
Как и обычные углы, углы между плоскостями бывают трех видов:
- Острые, то есть меньше 900
- Прямые, равные 900
- Тупые, которые больше 90и меньше 1800
Как уже было сказано выше, за угол между плоскостями всегда принимается острый угол, образованный этими плоскостями.
А что будет, если между плоскостями получится прямой угол?
Такие плоскости называются перпендикулярными.
Достаточно посмотреть на стены и пол, или стены и потолок. А еще на углы потолка — в них будет три перпендикулярные плоскости.
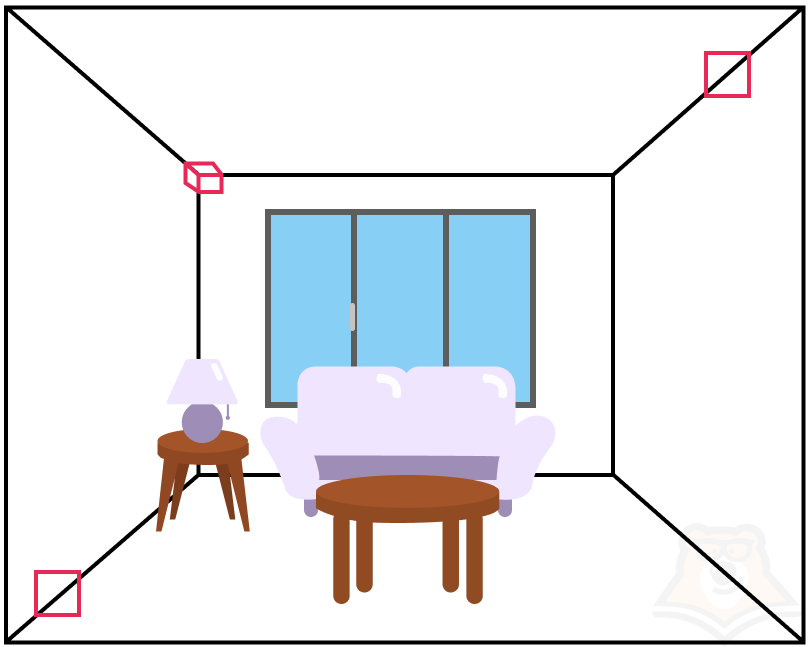
У перпендикулярных плоскостей есть одна очень интересная особенность: все углы, образованные ими, равны между собой и равняются 90° градусам.
Чтобы найти угол между плоскостями, необходимо следовать следующему алгоритму.
1 шаг. Найти линию пересечения плоскостей.
2 шаг. Достроить к этой линии перпендикуляр в каждой плоскости.
3 шаг. Найти острый угол между построенными перпендикулярами.
Углы между прямой и плоскостью
Если нарисовать две прямые на листе бумаги, мы с легкостью можем измерить угол между ними с помощью транспортира. А если провести прямую к плоскости, как точно измерить угол между ними?
И в этом вопросе к нам снова на помощь приходит стереометрия. Но для начала рассмотрим, что такое угол между прямой и плоскостью.
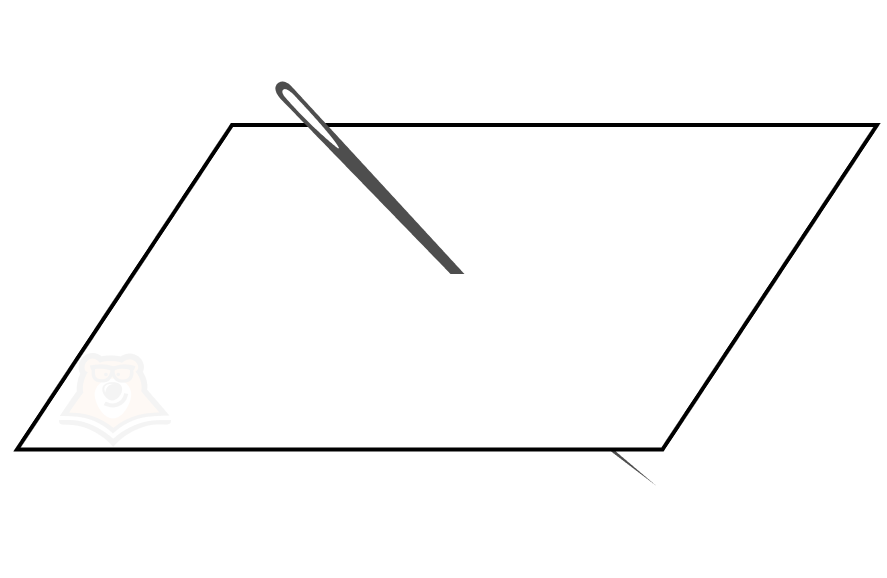
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
Что такое проекция? Предположим, мы проткнем лист бумаги (плоскость) очень длинной иглой.
А теперь сделаем этот рисунок ближе к чертежу. Пусть плоскость а пересекает прямая а в точке О.
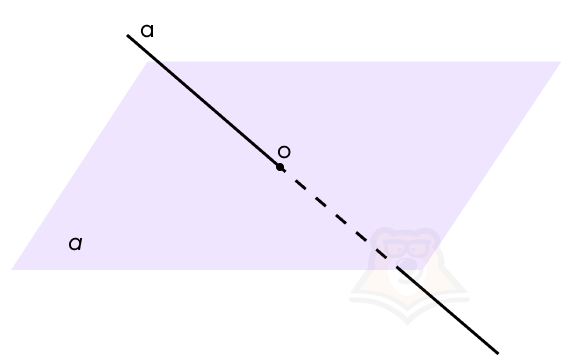
Начнем строить проекцию. Прежде чем разобраться, что такое проекция прямой на плоскость, найдем проекцию точки на плоскость.
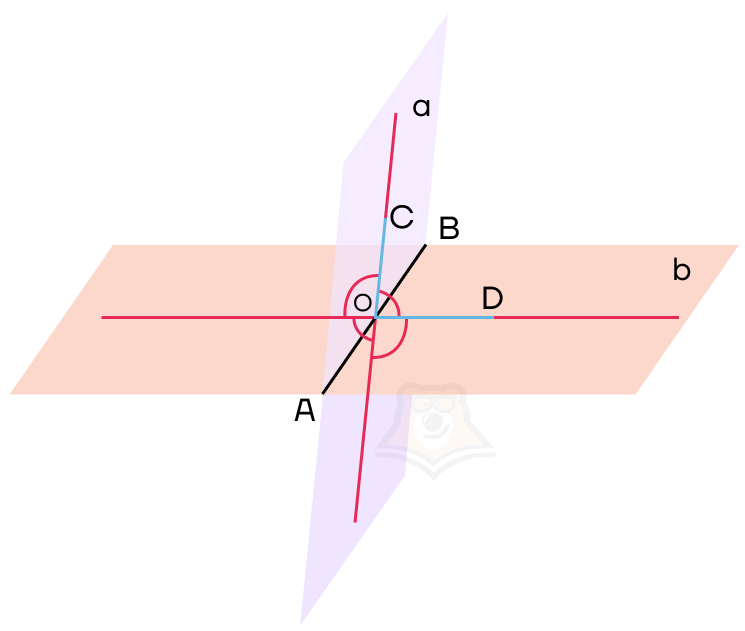
Возьмем на нашей прямой а точку А и опустим из нее перпендикуляр к плоскости а. Точка, в которой перпендикуляр пересечет плоскость, будет называться проекцией точки на плоскость. На рисунке обозначим ее как А1.
Проекция точки на плоскость — это основание перпендикуляра, опущенного из этой точки на плоскость.
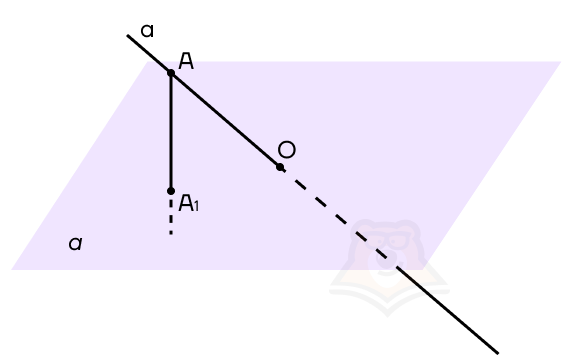
Теперь, если мы будем брать каждую точку на прямой и проектировать ее на плоскость а, то получим проекцию этой прямой на плоскость. Но поскольку на прямой бесконечное множество точек, достаточно соединить точки А1 и О, получаем, что А1О — проекция прямой а на плоскость а.
Заметим, что если мы проведем из любой точки прямой проекцию к плоскости, то попадем на прямую А1О.
Проекция прямой а на плоскость — это прямая а1, образованная проекциями всех точек прямой а на плоскость.
Таким образом можно построить проекции не только прямой, но и любой фигуры.
Мы построили угол из определения. Тогда углом между прямой а и плоскость а будет угол А1ОА.
В этом случае мы также берем острый угол, образованный прямой и плоскостью.
Шаг 1. Построить проекцию прямой на плоскость.
Шаг 2. Найти угол между прямой и построенной проекцией.
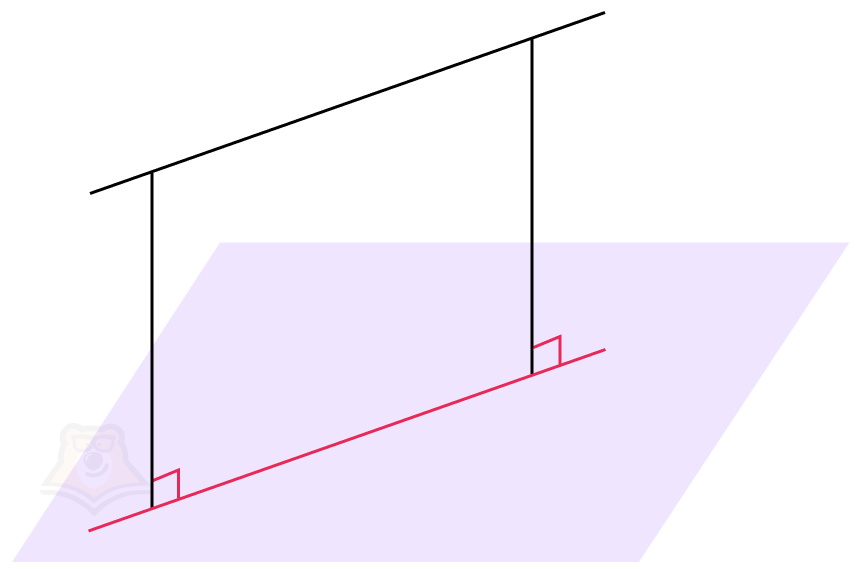
Если прямая параллельна плоскости угол будет равен 0.
Проекция прямой на плоскость будет этой же прямой, просто лежащей в плоскости.
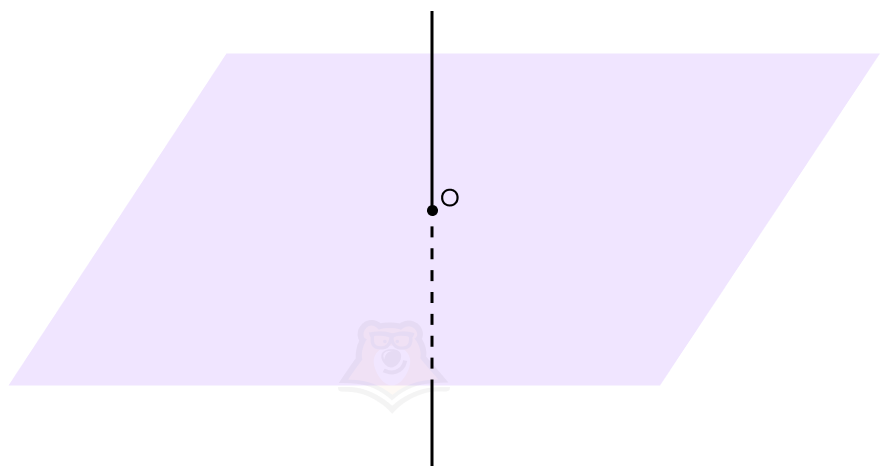
Когда прямая перпендикулярна плоскости, проекцией прямой на плоскость будет точка пересечения прямой и плоскости. Угол между прямой и плоскостью будет равен 90°.
Чуть подробнее остановимся на случае, когда прямая перпендикулярна плоскости.
Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости.
А что делать, если прямая будет перпендикулярна только одной прямой из плоскости? По определению обязательно, чтобы она была перпендикулярна всем прямым из плоскости. Как тогда проверить перпендикулярность?
Для этого существует признак перпендикулярности прямой и плоскости:
- Если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.
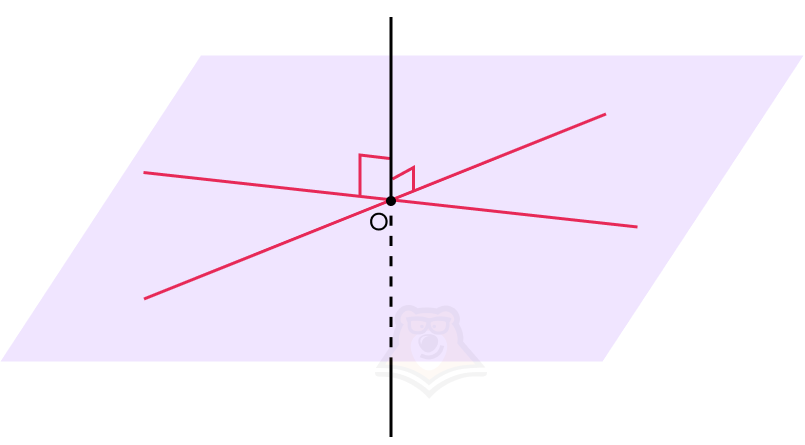
Следовательно, если необходимо в задаче доказать перпендикулярность прямой и плоскости, достаточно доказать, что прямая будет перпендикулярна всего двум пересекающимся прямым в этой плоскости, а не всему множеству прямых, лежащий в данной плоскости.
Рассмотрим несколько интересных свойств, связанных с прямой, перпендикулярной к плоскости.
Свойство 1. Через любую точку пространства можно провести единственную прямую, перпендикулярную плоскости.
Попробуйте подставить уголок к стене из любой точки. Получится ли у вас сделать так, что из одной и той же точки уголок встанет перпендикулярно стене несколько раз? Нет.
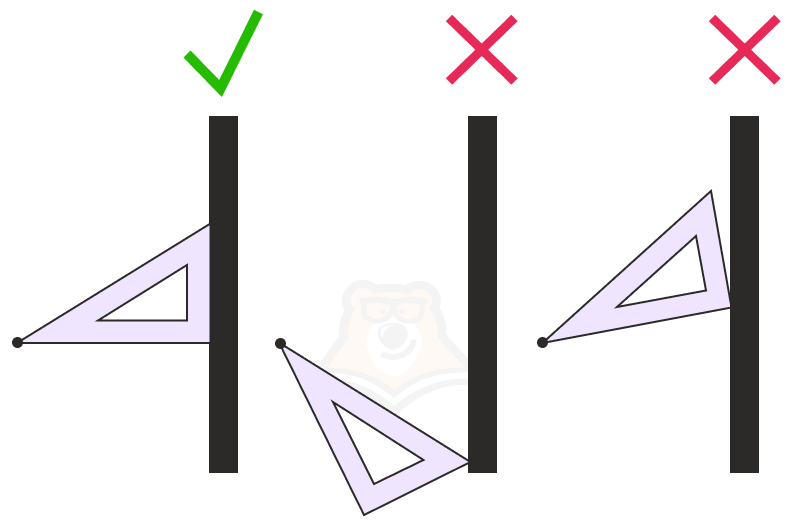
Свойство 2. Если две прямые перпендикулярны одной и той же плоскости, то такие прямые параллельны.
Здесь тоже просто все доказать. Достаточно построить в плоскости прямую, которая пересечет две данные прямые и посмотреть на рисунок “сбоку”. Заметим, что соответственные углы равны, а значит, прямые параллельны.
Подробнее про соответственные углы и параллельные прямые можно прочитать в статье “Основы планиметрии”.

Свойство 3. Если к одной прямой перпендикулярны две плоскости, то такие плоскости параллельны.
Тут такие же рассуждения, как и в предыдущем свойстве: достаточно построить прямые, принадлежащие плоскостям, и посмотреть на них “сбоку”.
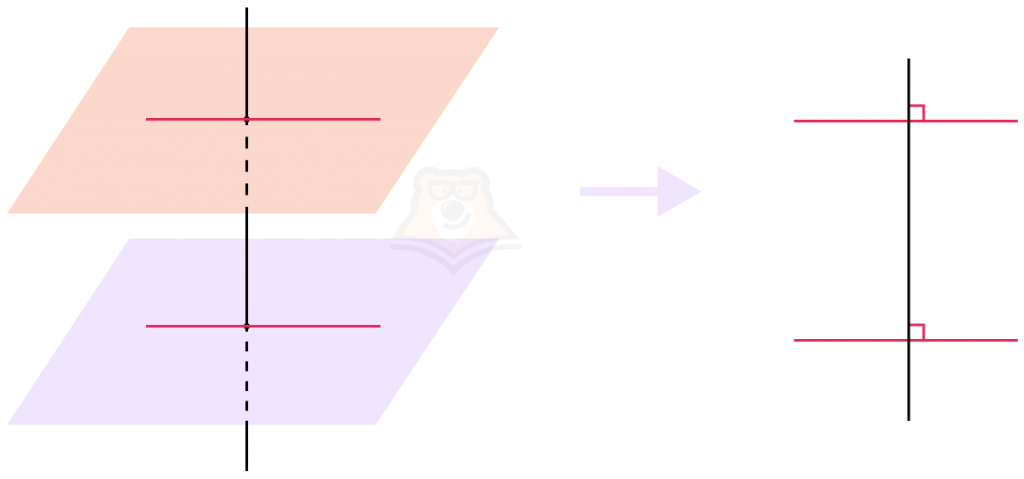
Свойство 4. Если через перпендикулярную к плоскости прямую проходит плоскость, то данные плоскости будут перпендикулярны.
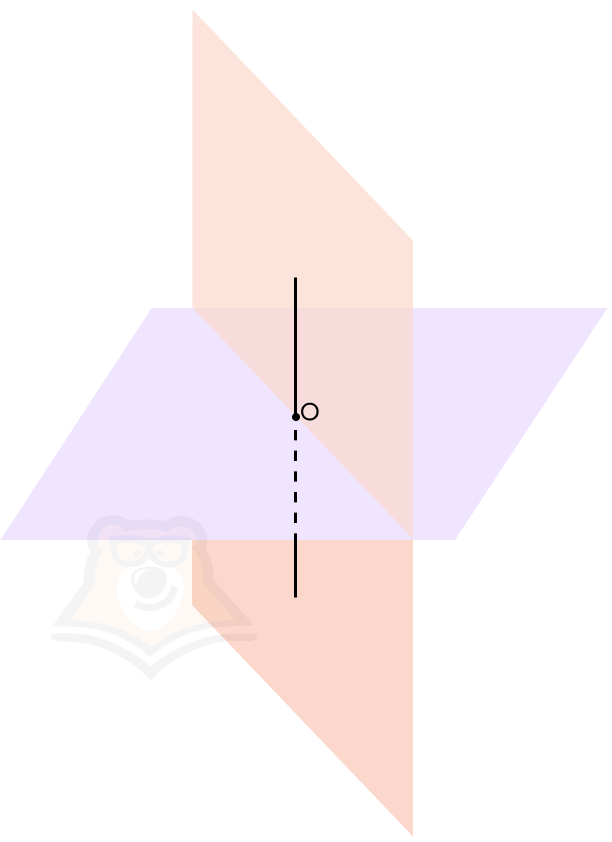
Это легко проверить, если найти любой двугранный угол между построенными плоскостями.
Теорема о трех перпендикулярах
Разберем еще одну очень интересную теорему, связанную с проекциями прямой на плоскость. А именно мы рассмотрим теорему о трех перпендикулярах.
Для начала попробуем понять ее на реальных предметах.
Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Возьмем уголок и зафиксируем его строго вертикально на листе. Для удобства назовем уголок АВС, где С — прямой угол.
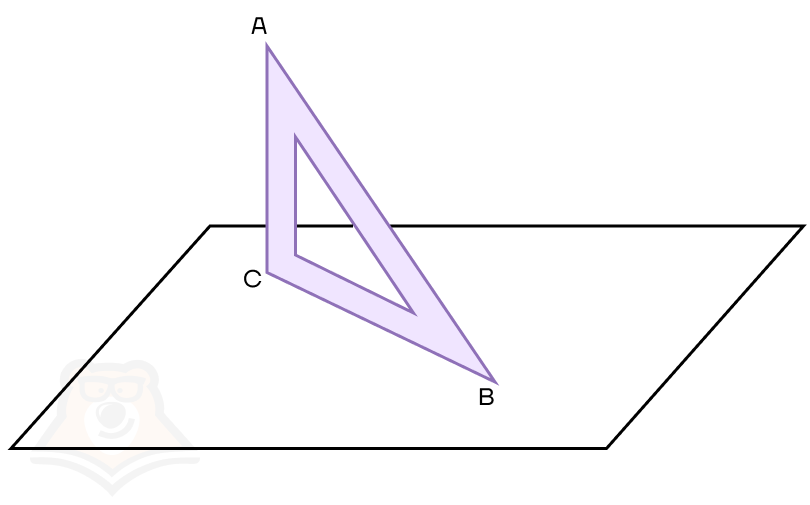
Сразу заметим, что прямая АС будет перпендикулярна плоскости листа (поскольку уголок стоит строго вертикально, а лист лежит строго горизонтально).
Дальше заметим, что прямые АС и ВС также перпендикулярны, поскольку в уголке угол С равен 90°.
Посмотрим чуть-чуть внимательнее и обратим внимание, что прямая ВС при этом будет проекцией на плоскость листа прямой АВ.
Немного достроим наш рисунок и через точку В проведем прямую, перпендикулярную ВС. Назовем эту прямую КМ.
Сразу отмечаем, что прямая КМ перпендикулярна ВС по построению, а также перпендикулярна прямой АС (поскольку АС — перпендикуляр к плоскости листа).
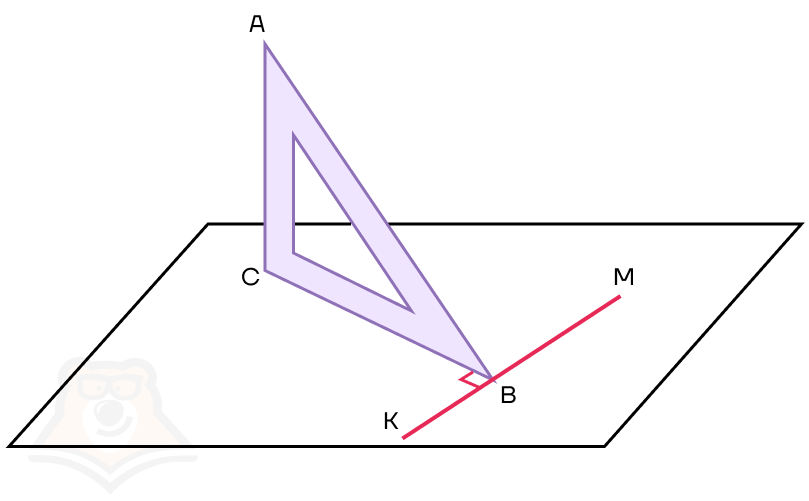
Можем ли мы что-то еще сказать про нашу ситуацию? Оказывается, прямая АВ также будет перпендикулярна прямой КМ.
Возникнет вопрос, почему?
1. Вспомним признак перпендикулярности прямой и плоскости: если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.
Теперь узнаем, как этот признак выполняется в данной ситуации.
2. Посмотрим на ситуацию немного под другим углом и в этот раз возьмем за плоскость не лист, а нашу линейку.
3. Тогда две пересекающиеся прямые в плоскости линейки будут перпендикулярны прямой КМ: BCKM по построению, а ACKM как прямая, перпендикулярная к плоскости листа, а значит, и перпендикулярная всем прямым в этой плоскости.
4. Получается, что прямая КМ перпендикулярна плоскости АВС, следовательно, перпендикулярна и всем прямым в этой плоскости, в том числе прямой АВ.
Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.
Мы рассмотрели теорему о трех перпендикулярах. Осталось ее только сформулировать математическим языком.
Теорема о трех перпендикулярах
Если наклонная прямая АВ к плоскости а перпендикулярна прямой КМ в этой плоскости, то и проекция прямой АВ на плоскость а перпендикулярна к прямой КМ.
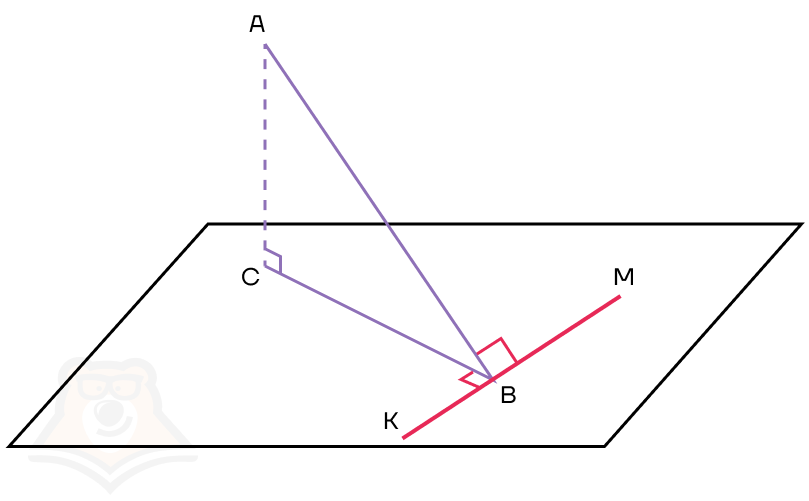
Для построения чертежа заменим линейку на несколько отрезков. Тогда АВ — наклонная, ВС — проекция, КМ — прямая в плоскости.
Для этого нужно взять лист бумаги и треугольную линейку. На листе бумаги построить произвольную прямую, а после поставить линейку строго вертикально так, чтобы основание линейки на листе было перпендикулярно начерченной прямой.
Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.
Вот и все, ничего сложного. А называется теорема так потому, что в построении действительно присутствуют три перпендикуляра, которые отлично видно на рисунке.
Теорему о трех перпендикулярах можно активно использовать для доказательства и решении задач.
Фактчек
- Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу. Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями.
- Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях. За угол между плоскостями принимают острый угол, образованный этими плоскостями. Если угол между плоскостями равен 90°, то такие плоскости перпендикулярны.
- Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость. Чтобы найти угол между прямой и плоскостью, необходимо построить проекцию прямой на плоскость и найти угол между прямой и ее проекцией. Если прямая параллельна плоскости, то угол между ними будет равен 0°. Если прямая перпендикулярна плоскости, то угол между ними будет равен 90°.
- Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости. Чтобы доказать, что прямая перпендикулярна плоскости, достаточно доказать, что эта прямая перпендикулярна двум пересекающимся в плоскости прямым.
- Теорема о трех перпендикулярах гласит, что если наклонная прямая а к плоскости а перпендикулярна прямой b в этой плоскости, то и проекция прямой а на плоскость а перпендикулярна к прямой b.
Проверь себя
Задание 1.
Выберите верное утверждение.
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом все линейные углы двугранного угла равны между собой;
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом линейные углы двугранного угла не равны между собой;
- Грань двугранного угла — это общая прямая плоскостей, которые его образуют;
- Ребра двугранного угла — это плоскости, которые его образуют.
Задание 2.
Угол между плоскостями — это…
- Тупой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Тупой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей.
Задание 3.
Что такое проекция прямой на плоскость?
- Это любая прямая, проведенная из точки пересечения прямой и плоскости;
- Это перпендикуляр, опущенный из любой точки на плоскость;
- Это всегда точка пересечения прямой и плоскости;
- Это прямая, образованная проекциями всех точек прямой на плоскость.
Задание 4.
Какой будет проекция прямой, перпендикулярной к плоскости, на эту плоскость?
- Проекция будет равна этой прямой и параллельна ей;
- Проекция будет меньше прямой и образовывать с ней угол;
- Проекция будет точкой пересечения прямой и плоскости;
- Проекция будет больше прямой и образовывать с ней угол.
Задание 5.
Как доказать, что прямая перпендикулярна плоскости?
- Достаточно доказать, что прямая перпендикулярна одной любой прямой в плоскости;
- Достаточно доказать, что прямая перпендикулярна двум параллельным прямым в плоскости;
- Достаточно доказать, что угол между прямой и любой прямой в плоскости равен 90°;
- Достаточно доказать, что прямая перпендикулярна к двум пересекающимся прямым в этой плоскости.
Ответы: 1. — 1 2. — 2 3. — 4 4. — 3 5. — 4
|
В этом случае для построения прямого угла применяется всем известная формула Пифагора – в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Еще такое построение называют “египетским треугольником”, так как по такому же принципу строились углы пирамид. Натяните строительный шнур по главному фасаду одной из сторон будущего строения. Эта линия свое положение НЕ меняет. На шнуре, в точке где будет угол постройки привяжите еще один шнур и отойдите с ним в сторону, образуя другую, перпендикулярную сторону строения.На первом шнуре от точки, образующей угол отмерьте 4 метра. От этой же точки, но по другому шнуру отмерьте 3 метра. На совершенно отдельном шнуре зафиксируйте длину (расстояние) 5 метров (можно привязать яркие тесемки). Далее работают 2 человека. Один человек крайнюю точку пятиметрового шнура держит на шнуре главного фасада в точке 4 метра. Другой человекпостарается 5-и метровый шнур дотянуть до точки 3 м на другом шнуре.Вторая сторона на момент построения будет подвижной.Подтяните или отодвиньте боковую сторону так, чтобы крайние точки 5-иметрового и 3-х метрового шнура соединились. А угол между шнуром/линией главного фасада и линией бокового фасада у вас будет прямым, то есть 90 градусов. А по теореме это выглядит так – 4² (16) + 3² (9) = 5² (25) 25 = 25
автор вопроса выбрал этот ответ лучшим Rafail 8 лет назад Возьмите три брусочка (рейки, линейки, металлические полоски, какие-нибудь жесткие дюралевые элементы для строительства). Сделайте в них по два отверстия диаметром 4-6 мм. Расстояния между центрами отверстий должны относиться друг к другу как 3:4:5, (например 60 см, 80 см и 100 см, или 15 см, 20 см, 25 см). Скрепите брусочки винтами (болтами) в треугольник. Получится прямоугольный треугольник с прямым углом между короткими сторонами (катетами). Чем длиннее стороны треугольников тем точнее будет прямой угол. Но, слишком длинные брусочки могут оказаться кривыми, или прогнуться в процессе изготовления или эксплуатации. Другой вариант: берете три кусочка мягкой проволоки, с тем же соотношением длин, например 3 4 и 5 м, реально где-то на 10-20 см длиннее. На концах проволоки делаете кольца. Вбиваете в землю два колышка (кусочки труб), допустим, сначала на расстоянии ровно 3 м, накидываете кольца на колышки и сделав петлю где-нибудь в средней части проволоки “скруткой” выбираете излишек длины, чтобы проволока натянулась как можно прямее между колышками. Точно так же натягиваете другую проволоку на колышки с расстоянием между ними 4 м, и третью – с расстоянием 5 м. Теперь, в вершине требующегося прямого угла вбиваете один колышек. На него накидываете концы 3-х и 4-ж метровых проволок. Другие концы этих проволок продеваете в другие колышки, которые держат в руках Ваши помощники. кольца третьей проволоки (5 м) тоже продеваете в эти колышки. Затем помощники расходятся по требуемым направлениям и подбирают положения колышков, которые у них в руках (удерживая их строго вертикально) так, чтобы все три проволоки были натянуты. Когда такое положение достигнуто, угол будет близок к прямому. Можно и другие соотношения, лишь бы между ними соблюдалась теорема Пифагора, например 5, 12 и 13, или 7,24 и 25.
88SkyWalker88 5 лет назад Прямой угол можно построить, применяя теорему Пифагора. Кроме того, существует такое понятие как египетский треугольник. Еще древние египтяне, строя великие пирамиды, пользовались этим методом. Метод такой: натягиваем шнур, от точки, откуда будет начинаться угол, натягиваем другой шнур перпендикулярный этому. Далее на одной стороне нужно отсчитать три метра, а на другой – четыре метра. Затем берем еще один шнур (красного цвета) длиной ровно пять метров. Теперь пытаемся соединить крайние точки с помощью шнура красного цвета. При этом одна сторона нашего угла будет подвижной. Получаем прямой угол.
Ксарфакс 5 лет назад Для того, чтобы построить прямой угол на местности, можно воспользоваться Египетским треугольником, имеющим соотношение длин сторон как 3:4:5. В этом случае потребуется 3 колышка, а также 3 куска веревки – по 3, 4 и 5 метров. Алгоритм такой: 1) Сначала “натягиваем гипотенузу”. Для этого вбиваем в землю 2 колышка так, чтобы расстояние между ними было 5 метров (можно мерить либо по рулетке, либо по имеющейся верёвке). Закрепляем верёвку.
2) Теперь нужно разместить катеты (куски веревки по 3 и 4 метра) – так, чтобы они совпали вершинами между собой и с гипотенузой (понятно, нужна помощь нескольких человек). В этом случае получится искомый прямой угол. После этого вбиваем 3 колышек в то место, где катеты совпали и закрепляем верёвки. Кроме этого, иногда помогает примитивный вариант – обвести по какому-нибудь прямоугольному предмету. Или если есть доски, то нетрудно соотнести их между собой так, чтобы получился угол 90 градусов – если доски образуют прямой угол, то короткая часть первой доски (ширина) будет как бы продолжением длины другой доски.
Galina7v7 7 лет назад Кроме египетского треугольника,размеров которого немало,можно построить неполную окружность (примерно-полукруг),и провести прямую через центр окружности,это и будет диаметр,а 2 точки диаметра-концами лучей прямого угла.Вершина прямого угла может быть в любой удобной точке полуокружности.Доказательства того,что угол будет прямой,думаю,не требуются.А методика,как провести окружность на местности ,описана в литературе:вбивается колышек в землю,натягивается веревка удобного размера,и пошёл двигаться какой-то объект (человек,лошадь) по свободному концу верёвки,прочерчивая эту полуокружность (можно вбивать колышки через 10-15-25 см,как бы очкрчивая эту полуокружность(методов много).А потом на ней,где нужно отметить вершину прямого угла(можно в любом колышке),а лучи,на прямой -диаметре.То есть соединяя вершину с концами диаметр ,получим прямой угол.Если есть сомнения по поводу полуокружности,можно проводить целую окружность,но это затратно по времени.Достаточно немного больше полуокружности. Владмир8 4 года назад Только что родил способ построения прямого угла к условному забору или к прямой линии с помощью длинной неразмеченной (нерастяжимой) веревки.
Или можно растянуть веревку целиком от основания треугольника у забора до вершины и дальше – половина ляжет на сторону треугольника-далее узелок и колышек в земле- далее вторая половина веревки, как продолжение стороны. (Веревка в итоге получится прямой линией)
Основание- либо теорема об угле, вписанном в окружность (а вытянутая веревка- это и есть диаметр ее, а полверевки- радиус окружности- и точка пересечения-на заборе) Либо свойства прямоугольника- его диагонали равны и точкой пересечения делятся пополам.
Чтобы разметить прямой угол на местности не обязательно иметь транспортир или другие приспособления. Достаточно иметь три шнура и помнить теорему Пифагора. Есть очень удобные соседние числа – 3 и 4, квадраты которых в сумме дадут 25, то есть квадрат 5. А это значит, что есть прямоугольный треугольник со сторонами 3, 4 и 5 метров. При этом сторона в 5 метров окажется гипотенузой. Как же построить такой треугольник на местности? Вбиваем колышек в основание прямого угла. Привязываем к нему шнуры длиной 3 и 4 метра. Проводим сторону длиной например 4 метра и вбиваем второй колышек, закрепляем шнур. Привязываем к этому колышку шнур длиной 5 метров и острым колышком чертим небольшую дугу окружности на расстоянии 5 метров от вбитого колышка. Точно также проводим небольшую дугу радиусом 3 метра от первого колышка. Точка пересечения дуг и будет последней вершиной нашего прямоугольного треугольника.
fatalex 8 лет назад Ну, если говоря “на местности”, Вы предполагаете начертить прямой угол прямо на земле, к примеру размечая границы какого-то участка или фундамента будущего дома, то можно воспользоваться тремя колышками и шпагатом или верёвкой, длинна которой кратна 12 метрам. Говорят, этот метод был известен ещё в древнем Египте, а в его основе так называемое правило “золотого сечения”. “Золотое сечение” – это треугольник со сторонами, длинны которых соотносятся, как 3:4:5
Вот так, более подробно, использование этого метода на практике описывается в интернете:
Отсутствие транспортира вполне компенсирует теодолит. Ну и не забываем что диагонали прямоугольника равны между собой.
Проще простого. Сначала строим квадрат, натянув веревки по периметру. Чем больше будет квадрат, тем точнее будет построен прямой угол. Теперь промеряем диагонали нашего, пока еще якобы квадрата. Скорее всего у нас с первого раза получится ромб. Раздвигаем соответствующие углы квадрата, диагональ между которыми меньше. Делаем это пока обе диагонали не выровняться по длине. Как только это произойдет, мы получим правильный квадрат, а значит и четыре прямых угла. Как правило строили когда делают прямые углы меряют диагонали полученного прямоугольника. Если нужно сделать что-то маленькое, то можно этот прямой угол обвести по прямоугольному предмету. Самый простой способ это произвести замер диагоналей. Можно и с помощью веревки, смотрите какой вариант вам больше подходит.
moreljuba 5 лет назад Для этой цели я вам советую воспользоваться Египетским треугольником, а вернее соотношением его сторон, которое выглядит следующим образом 3 к 4 к 5. Берём колышки и натягиваем верёвкой сначала гипотенузу 5, а затем от неё натягиваем катеты. Так и получим прямой угол на местности. Знаете ответ? |
Внимание! Администрация сайта rosuchebnik.ru не несет ответственности за содержание методических разработок, а также за соответствие разработки ФГОС.
Победитель конкурса “Электронный учебник на уроке”.
Цели урока: познакомить учащихся с понятием «угол»; научить выполнять модель прямого угла; учить определять на чертеже прямой и непрямой угол; совершенствовать вычислительные навыки; развивать внимание и глазомер.
Технические средства урока: Интерактивная доска с проектором, компьютер учителя, компьютеры учащихся, подключение к Интернету.
ЭФУ учебника математики В.Н. Рудницкая, Т.В. Юдачева Издательского центра «ВЕНТАНА-ГРАФ».
Учебные задачи, направленные на достижение метапредметных результатов обучения:
- развитие умения работать с информацией;
- развитие умения соединять теоретический материал с практической деятельностью (т.е. формирование интеллектуальной автономности – умения конструировать новое знание на основе имеющегося опыта);
- развитие операций мышления: сравнения, сопоставления, выделение лишнего, анализа, синтеза, обобщения, классификации и др. (познавательные УУД);
- формирование начальных форм познавательной и личностной рефлексии (регулятивные УУД)
- формирование умения грамотно строить речевые высказывания в соответствии с задачами коммуникации и составлять тексты в устной и письменной формах;
- формирование умения слушать и слышать собеседника, вести диалог, излагать свою точку зрения и аргументировать ее;
- формирование умения работать в статичных и мигрирующих группах в режиме интерактивного обучения; (коммуникативные УУД).
Учебные задачи, направленные на достижение предметных результатов обучения:
- развитие речи, мышления, воображения школьников, умения выбирать средства языка в соответствии с целями, задачами и условиями общения;
- освоение первоначальных знаний о прямом угле;
- овладение умениями строить прямой угол при помощи инструментов
- воспитание позитивного эмоционально-ценностного отношения к математике.
Ход урока
I. Организационный момент
– Сегодня на уроке наша задача получить новое знание и научиться его применять в своей жизни. Работать будем в малых группах. Озвучьте алгоритм работы в группе.
Свою работу на уроке будем фиксировать в листе «Самооценки»
|
Лист самооценки |
||||||
|
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
Знаю/научился
|
Запишите в тетрадях число и классная работа.
Лозунг урока
– Попробуйте по представленным графам прочитать народную мудрость (пословицу). (Интерактивное пособие в программе mimioStudio 7, слайд №1, работа в паре)
(Земля освещается Солнцем, а человек знанием)
II. Устный счет
(Работа на компьютере в программе mimioStudio 7 интерактивное пособие в паре). Слайд №2.
Математическое лото
|
3 |
15 |
12 |
|
9 |
разность |
21 |
|
частное |
18 |
6 |
Вопросы:
- Первое число 6, а второе – в 2 раза меньше.
- Одно число 9, а второе – в 2 раза больше.
- Во сколько раз 18 больше 2?
- Разность чисел 45 и 30?
- Как называется выражение со знаком деления?
- Произведение 3 и 4?
- Как называется выражение со знаком вычитания?
- Делимое 54 делитель 9. Чему равно их частное?
- Первый множитель3, второй 7 чисел. Найдите произведение?
– Назовите числа в порядке возрастания (3, 6, 9, 12, 15, 18, 21)
– Какую закономерность заметили? (каждое последующее число увеличиваются на 3)
– Продолжите дальше закономерность (24, 27, 30)
Оцените работу в листе самооценки – 1 задание.
Разминку для ума сделали, за работу.
III. Сообщение темы урока
– Рассмотрите чертеж на доске:
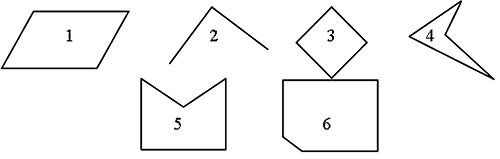
– Какая из данных фигур «лишняя»? (Фигура 2.)
– Как называется эта фигура?
Сегодня мы будем работать с геометрической фигурой – Угол.
Что бы вы хотели узнать об угле сегодня на уроке?
Это и будут наши задачи на урок?
На листе самооценки поставьте себе прогнозируемую оценку по теме «Что я знаю об угле».
– Что такое угол? (Дети выводят правило.)
IV. Изучение нового материала
(Cамостоятельная работа с учебником стр. 105.)
– Что такое угол прочитайте самостоятельно термин в учебнике стр. 105.
Угол это геометрическая фигура. Ее образуют два луча, исходящие из одной точки. (Угол бесконечная фигура)
Демонстрация угла на чертеже (учимся читать угол и называть основные его части).
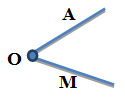
Как можно прочитать название угла?
Точку О называют вершиной угла, лучи ОА, ОМ-сторонами угла.
Работаем с учебником стр. 105 (работа с ЭФУ)
На рисунке представлены три раскрытых веера, каждый из них представляет модель угла
- Что у них общего?
- Чем они различается?
– У каждого из них есть свое название. С ними мы будем знакомиться на следующих уроках. А сегодня будем работать только с одним видом углов, а как он называется, я думаю, вы сможете сами определить.
V. Моделирование прямого угла из модели круга
(У детей лежат модели круга.)
– Возьмите вырезанный из бумаги круг, сложите его пополам, а затем еще пополам. В результате двух сгибаний мы получили модель угла.
– Как вы думаете, как может называться такой угол? (ПРЯМОЙ УГОЛ)
– Где в нашей жизни можно встретиться с прямыми углами? (угольник, на крышке стола, в комнате…)
Задание № 2 (с. 76) – учебник (работа с ЭФУ – демонстрация страниц учебника).
– Рассмотрите рисунки. На каком рисунке дороги пересекаются под прямым углом? (Первый рисунок.)
(Вариант ответа №1)
VI. Изображение прямого угла
(Интерактивное задание из учебника (ЭФУ), работа в тетрадях №5 стр. 107)
Прямой угол можно изображать на бумаге с помощью линейки и угольника.
Сейчас посмотрим интерактивную демонстрацию построения прямого угла, а затем попробуем самостоятельно составить алгоритм построения прямого угла.
Алгоритм
- Отмечаю карандашом точку. Это вершина угла.
- По линейке провожу любой луч с началом в отмеченной точке. Это одна из сторон угла.
- Прикладываю угольник, так, чтобы вершина его прямого угла совпадала с началом луча, а одна из сторон совпала с направлением луча.
- Провожу луч с началом в отмеченной точке по направлению второй стороны прямого угла угольника. Это вторая сторона угольника.
- Обозначаю буквами латинского алфавита вершину и стороны прямого угла.
Построение завершено.
Один ученик работает у доски.
Кто забыл алгоритм построения прямого угла может его еще раз прочитать по карточке помощнице стр. 107 (карточка – помощница).
– Отметьте вершину и стороны угла буквами латинского алфавита.
- Оцените работу в листе самооценки – 2 задание.
VII. Закрепление
А) Работа с учебником №3 стр. 106 (работа с ЭФУ )
Как можно определить прямой угол среди других видов углов.
Посмотрим интерактивную демонстрацию (стр. 105)
Ответ: (В, К)
- Оцените работу в листе самооценки – 3 задание.
 Физкультминутка
Физкультминутка
Лозунг нашего урока «Земля освещается Солнцем, а человек знанием».
Продолжаем получать и закреплять полученные знания.
Б) Дифференцированные задания. Работа в тетрадях на печатной основе стр. 53.
Задания по выбору (учитель нацеливает на задание)
 1 уровень сложности Задание №1 Тетрадь стр.53 №1 (интерактив. доска)
1 уровень сложности Задание №1 Тетрадь стр.53 №1 (интерактив. доска)
 2 уровень сложности Задание №2 Тетрадь стр.53 №2
2 уровень сложности Задание №2 Тетрадь стр.53 №2
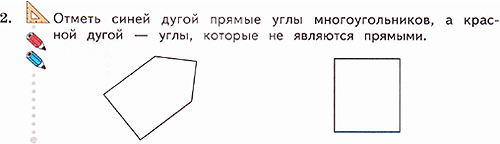
Учитель должен обратить внимание учащихся на то, что в задании углы надо выделять дугой (синей – прямые, а красной – непрямые углы).
 3 уровень сложности Задание №4 Тетрадь стр.54 №3
3 уровень сложности Задание №4 Тетрадь стр.54 №3
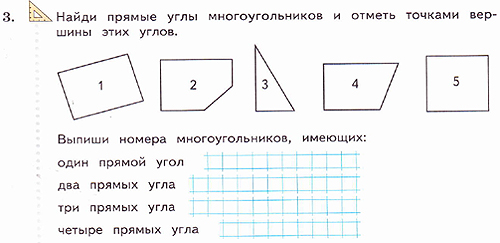
Надо выделять только вершины многоугольников, у которых есть прямые углы.
– Проверка.
- Оцените работу в листе самооценки – 4 задание.
Знание о прямом угле поможет решить геометрическую задачу.
В) решение геометрической задачи (работа в парах)
Задание №4 Тетрадь стр.54 №3
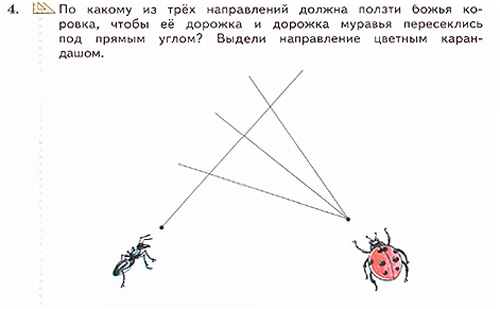
Направление задается лучом, поэтому правильно выполнить задание смогут только те учащиеся, которые выделят, синим цветом именно луч, а не просто линию, соответствующую средней дорожке.
Ответ (направление задается средним лучом).
- Оцените работу в листе самооценки – 5 задание.
VIII. Повторение пройденного материала
(Интерактивное пособие в программе mimioStudio 7 работа в парах на компьютере) слайд №3
В заключении урока проведем тестирование по теме нашего урока.
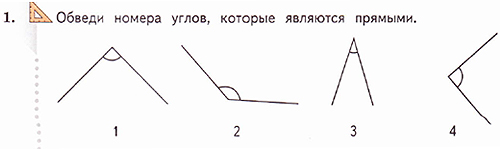
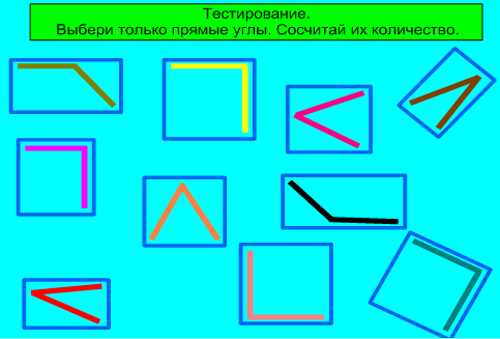
Задание 1. Среди множества углов выберите только прямые углы.
- Оцените работу в листе самооценки – 6 задание.
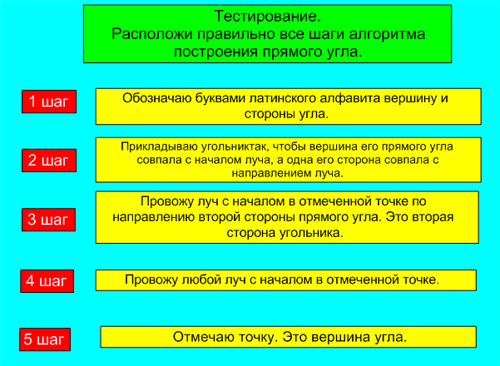
Задание 2. Расположите правильно этапы алгоритма: «Построение прямого угла». Слайд №6
- Оцените работу в листе самооценки – 6 задание.
В итоговой ячейке поставьте общую оценку себе за работу на уроке.
IX. Итог урока
– Какими новыми знаниями об угле мы обогатились на уроке? (возвращение к модели постановки задач на урок)
– Что такое «угол»?
– Как изготовить модель прямого угла?
– Для чего нам нужны знания об угле?
На листе самооценки поставьте итоговую оценку по теме «Угол. Прямой угол» , насколько я узнал эту тему.
У кого оценки совпали?
У кого итоговая оценка получилась выше прогнозируемой?
Мы сегодня еще раз подтвердили народную мудрость «Земля освещается Солнцем, а человек знанием»
X. Домашняя работа
(На листочках, по уровням сложности)
Выбери и выполни задание из предложенных по уровням сложности:
 Задание № 1
Задание № 1
С помощью угольника постройте прямой угол так, чтобы его вершиной была точка А, а одна из сторон проходила через точку В. Закрасьте угол синим цветом.
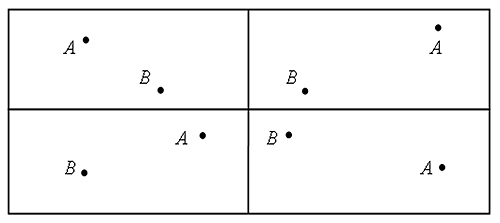
 Задание № 2
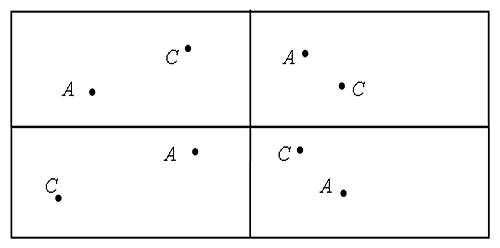
Задание № 2
С помощью угольника постройте прямой угол с вершиной в точке А так, чтобы точка С находилась внутри прямого угла.
Как найти углы прямоугольного треугольника
Онлайн калькулятор

Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для угла α:
- угол β
- длины катетов a и b
- длину гипотенузы (с) и длину одного из катетов
- для угла β:
- угол α
- длины катетов a и b
- длину гипотенузы (с) и длину одного из катетов
Введите их в соответствующие поля и получите результат.
Найти угол α зная угол β и наоборот
Формула
Найти углы прямоугольного треугольника зная катеты
Катет a =
Катет b =
Чему равны острые углы (α и β) прямоугольного треугольника если известны оба катета (a и b)?
Формулы
Пример
Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:
Найти углы прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет =
Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (a или b)?
Углы прямоугольного треугольника
Калькулятор расчёта углов прямоугольного треугольника
Прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние, при этом один из углов прямой (равен 90°).
Тангенс угла tg(α) — это тригонометрическая функция выражающая отношение противолежащего катета a к прилежащему катету b.
Формула тангенса
- tg α – тангенс угла α
- a – противолежащий катет
- b – прилежащий катет
Арктангенс — это обратная тригонометрическая функция. Арктангенсом числа x называется такое значение угла α, выраженное в радианах, для которого tg α = x . Вычислить арктангенс, означает найти угол α, тангенс которого равен числу x.
Углы треугольника
Сумма углов треугольника всегда равна 180 градусов:
Так как у прямоугольного треугольника один из углов равен 90°, то сумма двух других углов равна 90°.
Поэтому, если известен один из острых углов треугольника, второй угол можно посчитать по формуле:
Острый угол — угол, значение которого меньше 90°.
У прямоугольного треугольника один угол прямой, а два других угла – острые.
Точный угол 90 градусов с помощью рулетки
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов – длинна сторон не ограничена. Основной инструмент для измерений – рулетка.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:

Стороны a и b – катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c – гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием “египетский треугольник”. Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 – ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 – все сходится!
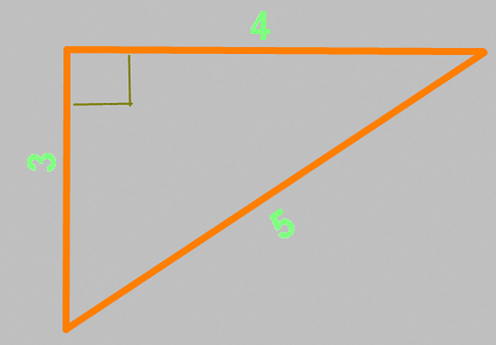
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого – проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены – это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 – это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 – 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали – проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла
Извлечение квадратного корня никогда меня не привлекало – простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. – диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике – это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем – в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе “египетского треугольника”. Однако это только в теории линии просто чертятся на бумаге, “ловить” же все выбранные размеры растянутыми шнурами или линиями на полу – задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!




Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами – дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера – непрофессионально.
[spoiler title=”источники:”]
http://kalk.top/sz/corners-pr-triangle
http://yserogo.ru/remont/pryamoi-ugol.html
[/spoiler]
Как найти прямой угол
Существует несколько геометрических определений прямого угла:
– прямой угол – это смежный угол или угол, который равен смежному углу;
– прямым углом является угол, который равен 90 градусов;
– для вычисления прямого угла необходимы измерения углов- a и b;
– угол равный 90 градусов, составляющий четверть целого угла и половину развернутого называется прямым углом.
Инструкция
Данные понятия и определения указывают на то, что все без исключения прямые углы равны и любые два угла могут быть сравнимы. А само сравнение двух углов с прямым углом вводит понятие – острого и тупого угла.
Для того, чтобы найти прямой угол, необходимо вводить измерение градуса угла с помощью транспортира, если он равен 90 градусов, то, следовательно, этот угол является прямым.
Ряд геометрических фигур имеет один или несколько прямых углов. К таким фигурам относятся прямоугольный треугольник (имеет одни прямой угол), параллелограмм (все углы его прямые), квадрат является ромбом, у которого все углы прямые, а также прямоугольная трапеция с одним прямым углом.
Построить прямой угол самостоятельно без геометрических инструментов можно с использованием отвеса (любая нитка с грузом), уровень для горизонтальной и стеклянная деталь для вертикальной поверхности.
Видео по теме
Источники:
- как вычислить прямой угол
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.