Добрый день, уважаемые гости и подписчики канала “Строю для себя”!
Ниже описаны 3 приема восстановления перпендикуляра или построения прямого угла на местности к любой прямой линии. Данные мероприятия очень важны в строительстве при построении осей на плане и при сооружении обноски для дальнейшего возведения фундаментов или стен.
Имея только отрезок любой веревки, шнурки или троса, пользуясь данными способами – вы сможете совершенно точно построить перпендикуляр.
Итак, способ №1: Равнобедренный треугольник
Определяем точку на прямой линии, к которой будем строить перпендикуляр (для наглядности – я в эту точку воткнул шампур 🙂
Отмечаем по обе стороны от него две равноудаленные точки (с помощью веревки это очень просто сделать). Теперь мы имеем три точки, которые находятся на одной прямой линии и два равных отрезка между ними (на рисунке ниже – 3 шампура).
Затем, нам достаточно определить середину веревки произвольной длины (В своем случае, для удобства, я на противоположных концах сделал петли, накинул их на колышек (шампур) и натянул веревку, тем самым разделил ее на две равные части).
Теперь, концы веревки совмещаем с двумя крайними точками и натягиваем ее за найденную середину.
Перпендикуляр готов (Свойство равнобедренного треугольника, высота которого делит основание на два равных отрезка)
Способ №2: Пересечение двух дуг
Данный способ выручает, когда у вас есть только короткая веревка. Как и в предыдущем способе, нам требуется опять же построить три точки на одной прямой, где две крайние равноудалены от центральной.
Теперь, подобно циркулю, из каждой крайней точки рисуем дуги одинакового радиуса. Точка пересечения двух дуг и будет давать нам перпендикуляр к прямой.
Схематично, это выглядит так (точка О является точкой пересечения дуг):
Способ №3: Теорема Пифагора
Наверное, это самый используемый способ, в котором применяются равные отрезки в соотношении 3:4:5. Данные отрезки могут измеряться в сантиметрах, метрах, километрах или любой произвольной длины, которую мы и будем использовать.
Для наглядности, я сделал на одной веревке 13 узлов с равными расстояниями друг от друга.
Теперь, достаточно просто туго растянуть веревку за вершины, которые отделяются между собой 3, 4 и 5 отрезками. Опять же, использую шампуры :-)))
Прямой угол построен!
На этом всё, спасибо за терпение :-)))
Если Вам было интересно, ставьте палец вверх и подписывайтесь на мой канал! Впереди много интересных тем!
Знания по геометрии на жизненных примерах и чего не хватает детям в школе?
Зная тригонометрию, можно не бегать по крыше с рулеткой
Какие деревья сажают, чтобы не откачивать яму?
Как определить высоту объекта на расстоянии?
Как рассчитать двутавр для перекрытия на прогиб и нагрузку?
Как измерить ширину реки с одного берега?
|
В этом случае для построения прямого угла применяется всем известная формула Пифагора – в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Еще такое построение называют “египетским треугольником”, так как по такому же принципу строились углы пирамид. Натяните строительный шнур по главному фасаду одной из сторон будущего строения. Эта линия свое положение НЕ меняет. На шнуре, в точке где будет угол постройки привяжите еще один шнур и отойдите с ним в сторону, образуя другую, перпендикулярную сторону строения.На первом шнуре от точки, образующей угол отмерьте 4 метра. От этой же точки, но по другому шнуру отмерьте 3 метра. На совершенно отдельном шнуре зафиксируйте длину (расстояние) 5 метров (можно привязать яркие тесемки). Далее работают 2 человека. Один человек крайнюю точку пятиметрового шнура держит на шнуре главного фасада в точке 4 метра. Другой человекпостарается 5-и метровый шнур дотянуть до точки 3 м на другом шнуре.Вторая сторона на момент построения будет подвижной.Подтяните или отодвиньте боковую сторону так, чтобы крайние точки 5-иметрового и 3-х метрового шнура соединились. А угол между шнуром/линией главного фасада и линией бокового фасада у вас будет прямым, то есть 90 градусов. А по теореме это выглядит так – 4² (16) + 3² (9) = 5² (25) 25 = 25
автор вопроса выбрал этот ответ лучшим Rafail 8 лет назад Возьмите три брусочка (рейки, линейки, металлические полоски, какие-нибудь жесткие дюралевые элементы для строительства). Сделайте в них по два отверстия диаметром 4-6 мм. Расстояния между центрами отверстий должны относиться друг к другу как 3:4:5, (например 60 см, 80 см и 100 см, или 15 см, 20 см, 25 см). Скрепите брусочки винтами (болтами) в треугольник. Получится прямоугольный треугольник с прямым углом между короткими сторонами (катетами). Чем длиннее стороны треугольников тем точнее будет прямой угол. Но, слишком длинные брусочки могут оказаться кривыми, или прогнуться в процессе изготовления или эксплуатации. Другой вариант: берете три кусочка мягкой проволоки, с тем же соотношением длин, например 3 4 и 5 м, реально где-то на 10-20 см длиннее. На концах проволоки делаете кольца. Вбиваете в землю два колышка (кусочки труб), допустим, сначала на расстоянии ровно 3 м, накидываете кольца на колышки и сделав петлю где-нибудь в средней части проволоки “скруткой” выбираете излишек длины, чтобы проволока натянулась как можно прямее между колышками. Точно так же натягиваете другую проволоку на колышки с расстоянием между ними 4 м, и третью – с расстоянием 5 м. Теперь, в вершине требующегося прямого угла вбиваете один колышек. На него накидываете концы 3-х и 4-ж метровых проволок. Другие концы этих проволок продеваете в другие колышки, которые держат в руках Ваши помощники. кольца третьей проволоки (5 м) тоже продеваете в эти колышки. Затем помощники расходятся по требуемым направлениям и подбирают положения колышков, которые у них в руках (удерживая их строго вертикально) так, чтобы все три проволоки были натянуты. Когда такое положение достигнуто, угол будет близок к прямому. Можно и другие соотношения, лишь бы между ними соблюдалась теорема Пифагора, например 5, 12 и 13, или 7,24 и 25.
88SkyWalker88 5 лет назад Прямой угол можно построить, применяя теорему Пифагора. Кроме того, существует такое понятие как египетский треугольник. Еще древние египтяне, строя великие пирамиды, пользовались этим методом. Метод такой: натягиваем шнур, от точки, откуда будет начинаться угол, натягиваем другой шнур перпендикулярный этому. Далее на одной стороне нужно отсчитать три метра, а на другой – четыре метра. Затем берем еще один шнур (красного цвета) длиной ровно пять метров. Теперь пытаемся соединить крайние точки с помощью шнура красного цвета. При этом одна сторона нашего угла будет подвижной. Получаем прямой угол.
Ксарфакс 5 лет назад Для того, чтобы построить прямой угол на местности, можно воспользоваться Египетским треугольником, имеющим соотношение длин сторон как 3:4:5. В этом случае потребуется 3 колышка, а также 3 куска веревки – по 3, 4 и 5 метров. Алгоритм такой: 1) Сначала “натягиваем гипотенузу”. Для этого вбиваем в землю 2 колышка так, чтобы расстояние между ними было 5 метров (можно мерить либо по рулетке, либо по имеющейся верёвке). Закрепляем верёвку.
2) Теперь нужно разместить катеты (куски веревки по 3 и 4 метра) – так, чтобы они совпали вершинами между собой и с гипотенузой (понятно, нужна помощь нескольких человек). В этом случае получится искомый прямой угол. После этого вбиваем 3 колышек в то место, где катеты совпали и закрепляем верёвки. Кроме этого, иногда помогает примитивный вариант – обвести по какому-нибудь прямоугольному предмету. Или если есть доски, то нетрудно соотнести их между собой так, чтобы получился угол 90 градусов – если доски образуют прямой угол, то короткая часть первой доски (ширина) будет как бы продолжением длины другой доски.
Galina7v7 7 лет назад Кроме египетского треугольника,размеров которого немало,можно построить неполную окружность (примерно-полукруг),и провести прямую через центр окружности,это и будет диаметр,а 2 точки диаметра-концами лучей прямого угла.Вершина прямого угла может быть в любой удобной точке полуокружности.Доказательства того,что угол будет прямой,думаю,не требуются.А методика,как провести окружность на местности ,описана в литературе:вбивается колышек в землю,натягивается веревка удобного размера,и пошёл двигаться какой-то объект (человек,лошадь) по свободному концу верёвки,прочерчивая эту полуокружность (можно вбивать колышки через 10-15-25 см,как бы очкрчивая эту полуокружность(методов много).А потом на ней,где нужно отметить вершину прямого угла(можно в любом колышке),а лучи,на прямой -диаметре.То есть соединяя вершину с концами диаметр ,получим прямой угол.Если есть сомнения по поводу полуокружности,можно проводить целую окружность,но это затратно по времени.Достаточно немного больше полуокружности. Владмир8 4 года назад Только что родил способ построения прямого угла к условному забору или к прямой линии с помощью длинной неразмеченной (нерастяжимой) веревки.
Или можно растянуть веревку целиком от основания треугольника у забора до вершины и дальше – половина ляжет на сторону треугольника-далее узелок и колышек в земле- далее вторая половина веревки, как продолжение стороны. (Веревка в итоге получится прямой линией)
Основание- либо теорема об угле, вписанном в окружность (а вытянутая веревка- это и есть диаметр ее, а полверевки- радиус окружности- и точка пересечения-на заборе) Либо свойства прямоугольника- его диагонали равны и точкой пересечения делятся пополам.
Чтобы разметить прямой угол на местности не обязательно иметь транспортир или другие приспособления. Достаточно иметь три шнура и помнить теорему Пифагора. Есть очень удобные соседние числа – 3 и 4, квадраты которых в сумме дадут 25, то есть квадрат 5. А это значит, что есть прямоугольный треугольник со сторонами 3, 4 и 5 метров. При этом сторона в 5 метров окажется гипотенузой. Как же построить такой треугольник на местности? Вбиваем колышек в основание прямого угла. Привязываем к нему шнуры длиной 3 и 4 метра. Проводим сторону длиной например 4 метра и вбиваем второй колышек, закрепляем шнур. Привязываем к этому колышку шнур длиной 5 метров и острым колышком чертим небольшую дугу окружности на расстоянии 5 метров от вбитого колышка. Точно также проводим небольшую дугу радиусом 3 метра от первого колышка. Точка пересечения дуг и будет последней вершиной нашего прямоугольного треугольника.
fatalex 8 лет назад Ну, если говоря “на местности”, Вы предполагаете начертить прямой угол прямо на земле, к примеру размечая границы какого-то участка или фундамента будущего дома, то можно воспользоваться тремя колышками и шпагатом или верёвкой, длинна которой кратна 12 метрам. Говорят, этот метод был известен ещё в древнем Египте, а в его основе так называемое правило “золотого сечения”. “Золотое сечение” – это треугольник со сторонами, длинны которых соотносятся, как 3:4:5
Вот так, более подробно, использование этого метода на практике описывается в интернете:
Отсутствие транспортира вполне компенсирует теодолит. Ну и не забываем что диагонали прямоугольника равны между собой.
Проще простого. Сначала строим квадрат, натянув веревки по периметру. Чем больше будет квадрат, тем точнее будет построен прямой угол. Теперь промеряем диагонали нашего, пока еще якобы квадрата. Скорее всего у нас с первого раза получится ромб. Раздвигаем соответствующие углы квадрата, диагональ между которыми меньше. Делаем это пока обе диагонали не выровняться по длине. Как только это произойдет, мы получим правильный квадрат, а значит и четыре прямых угла. Как правило строили когда делают прямые углы меряют диагонали полученного прямоугольника. Если нужно сделать что-то маленькое, то можно этот прямой угол обвести по прямоугольному предмету. Самый простой способ это произвести замер диагоналей. Можно и с помощью веревки, смотрите какой вариант вам больше подходит.
moreljuba 5 лет назад Для этой цели я вам советую воспользоваться Египетским треугольником, а вернее соотношением его сторон, которое выглядит следующим образом 3 к 4 к 5. Берём колышки и натягиваем верёвкой сначала гипотенузу 5, а затем от неё натягиваем катеты. Так и получим прямой угол на местности. Знаете ответ? |
 Каждый из нас учился в школе. Там человек получает огромное количество тех знаний, которые впоследствии могут понадобиться в жизни. Не все, конечно, могут в полной мере оценить значимость полученных знаний в школьной время, но сейчас речь не об этом.
Каждый из нас учился в школе. Там человек получает огромное количество тех знаний, которые впоследствии могут понадобиться в жизни. Не все, конечно, могут в полной мере оценить значимость полученных знаний в школьной время, но сейчас речь не об этом.
Математика. Это страшное для многих слово, которое пугало достаточное количество школьников в своё время. Цифры, формулы и расчёты поддавались только самым пытливым. И с каждым годом этот сложный предмет становился всё сложнее и сложнее.
- Действительно ли прямой угол?
- Что понадобится для определения прямого угла?
- Как можно вычислить прямой угол?
- Вывод
В старших классах появляется геометрия и всё становится ещё сложнее и непонятнее. Возможно, многие хоть раз в жизни, но в сердцах проклинали непонятную им науку и задавались вопросом, зачем это вообще нужно, и понадобится ли это в жизни.
Возможно, в повседневной жизни применить полученные в школе знания не удавалось. Вряд ли требовалось посреди белого дня высчитывать логарифмы и квадратные уравнения или доказывать, что две параллельные никогда не сойдутся. Но, где уж точно могут понадобиться знания геометрии и математике, так это в строительстве и при осуществлении ремонта.
В данной статье речь пойдёт о вычислении прямого угла, что требуется при строительстве зданий. Точность при возведении строений должна быть соблюдена в обязательном порядке, ведь только точные расчёты могут избавить от перекосов и нестабильности организации всего здания. Вычисление прямого угла при строительстве – не такой уж и трудный процесс, при котором потребуется знание и применение некоторых простых правил математики и геометрии. Подробнее об этом будет рассказано ниже.
Действительно ли прямой угол?
 Возможно, некоторые читатели, ознакомившиеся с заголовком данной статьи, возразят, что прямой угол можно получить не всегда, и не всегда при строительстве используются именно ровные и точные прямые углы.
Возможно, некоторые читатели, ознакомившиеся с заголовком данной статьи, возразят, что прямой угол можно получить не всегда, и не всегда при строительстве используются именно ровные и точные прямые углы.
И, в принципе, они правы. Получить его весьма сложно, особенно если наблюдается неровность фундамента, на котором осуществляется строительство здания. Но, даже учитывая это обстоятельство, ни в коем случае нельзя делать вывод, что расчёт прямого угла можно делать просто “на глаз”. В любом случае, если не представляется возможным вычислить идеальный прямой угол, то требуется достичь наиболее приближённого значения к идеальному углу в 90 градусов. И этого можно добиться, используя незатейливые инструменты и не самые сложные математические знания и познания в геометрии.
Что понадобится для определения прямого угла?
 Итак, какие инструменты понадобится использовать для того, чтобы проверить прямой угол. Сразу стоит отметить, что никаких приборов и серьёзных инструментов для этого не потребуется. Нужно будет использовать весьма простые вещи, которые могут найтись практически в каждом хозяйстве. И даже если их не имеется под рукой, их с лёгкостью можно приобрести в магазине. С этим никаких трудностей не возникнет.
Итак, какие инструменты понадобится использовать для того, чтобы проверить прямой угол. Сразу стоит отметить, что никаких приборов и серьёзных инструментов для этого не потребуется. Нужно будет использовать весьма простые вещи, которые могут найтись практически в каждом хозяйстве. И даже если их не имеется под рукой, их с лёгкостью можно приобрести в магазине. С этим никаких трудностей не возникнет.
Для вычисления прямого угла нужно взять:
- Карандаш;
- Строительную рулетку.
И всё. Вот так вот всё просто.
Как можно вычислить прямой угол?
Итак, в этой статье будет описан принцип 3-4-5 при определении угла в 90 градусов. Ничего сложного в этом нет. Потребуется просто лишь чуть пораскинуть мозгами и вникнуть во все расчёты, которые смогут помочь в проверке угла.
Итак, нужно обозначить следующие шаги:
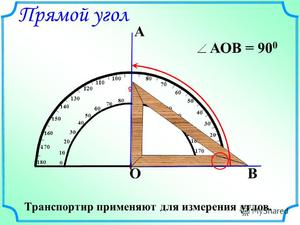 Для начала стоит разобраться в том, почему принцип так обозначен – 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;
Для начала стоит разобраться в том, почему принцип так обозначен – 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;- Итак, потребуется для начала отмерить 3 метра от угла вдоль одной из стен. Тут следует отметить, что 3 метра – предпочтительная длина замера, но в том случае, если комната маленькая, можно отметить всего 30 сантиметров. В месте замера нужно сделать отметку;
- В принципе, можно использовать и другие цифры, но рекомендуется в любом случае использовать пропорционально увеличенные числа, например: 9-12-15 или же 30-40-50;
- После проделанного предварительного замера нужно отмерить 4 метра вдоль другой стены, тоже от угла. Ну или соответственно 40 сантиметров, если комната маленькая. Нужно сделать отметку;
- Теперь остаётся сделать последнее действие, по которому уже можно судить прямой угол или нет. От измеряющего потребуется измерить расстояние между сделанными отметками. По полученным данным можно будет сделать определённые выводы:
- Если расстояние между отметками будет равняться 5 метрам ровно, это будет означать, что угол является прямым;
- В том случае, если измеренное расстояние будет равняться меньше 5 метров, угол будет меньше, чем 90 градусов;
- Ну и, наконец, величина угла будет составлять больше 90 градусов, если полученная величина замера будет равняться больше 5 метров.
Вывод
Вот, как просто можно вычислить прямой угол без использования каких-либо строительных инструментов и приборов. Использовать можно самое простое, но в то же время весьма действенное средство, которое вкупе с использованием имеющихся знаний и бесхитростных расчётов, может помочь произвести измерение.
При использовании предложенных величин, ключевым становится финальный замер между двумя отметками, которые были сделаны ранее. Расстояние, которое будет равняться точно 5 метрам, покажется, что он прямой. Если же величина будет больше или меньше 5 метров, это будет означать, что он прямым не является.
Это – древнейшая геометрическая задача.
Пошаговая инструкция
1й способ. – С помощью «золотого», или «египетского», треугольника. Стороны этого треугольника имеют соотношение сторон 3:4:5, а угол равен строго 90град. Этим качеством широко пользовались древние египтяне и другие пракультуры.

Илл.1. Построение Золотого, или египетского треугольника
- Изготавливаем три мерки (или веревочных циркуля – веревка на двух гвоздях или колышках) с длинами 3; 4; 5 метров. Древние в качестве единиц измерения часто пользовались способом завязывания узелков с равными расстояниями между ними. Единица длины – «узелок».
- Вбиваем в точке О колышек, цепляем на него мерку «R3 – 3 узелка».
- Протягиваем веревку вдоль известной границы – в сторону предполагаемой точки А.
- В момент натяжения на линии границы – точка А, вбиваем колышек.
- Затем – снова от точки О, протягиваем мерку R4 – вдоль второй границы. Колышек пока не вбиваем.
- После этого натягиваем мерку R5 – от А до В.
- В месте пересечения мерок R2 и R3 вбиваем колышек. – Это искомая точка В – третья вершина золотого треугольника, со сторонами 3;4;5 и с прямым углом в точке О.
2й способ. С помощью циркуля.
Циркуль может быть веревочный или в виде шагомера. См: …простейший землемерный инструмент
Наш циркуль-шагомер имеет шаг в 1 метр.

Илл.2. Циркуль-шагомер
Построение – также по Илл.1.
- От точки отсчета – точки О – угла соседа, проводим отрезок произвольной длины – но больше, чем радиус циркуля = 1м – в каждую сторону от центра (отрезок АВ).
- Ставим ногу циркуля в точку О.
- Проводим окружность с радиусом (шагом циркуля) = 1м. Достаточно провести короткие дуги – сантиметров по 10-20, в местах пересечения с отмеченным отрезком (через точки А и В.). Этим действием мы нашли равноудаленные точки от центра – А и В. Величина удаления от центра здесь не имеет значения. Можно эти точки просто отметить рулеткой.
- Далее нужно провести дуги с центрами в точках А и В, но несколько (произвольно) большего радиуса, чем R=1м. Можно перенастроить наш циркуль на больший радиус, если он имеет регулируемый шаг. Но для такой небольшой текущей задачи не хотелось бы его «дергать». Или когда регулировки нет. Можно сделать за полминуты веревочный циркуль.
- Ставим первый гвоздь (или ножку циркуля с радиусом больше, чем 1м) поочередно в точки А и В. И проводим вторым гвоздем – в натянутом состоянии веревки, две дуги – так чтобы они пересеклись друг с дружкой. Можно в двух точках: C и D, но достаточно одной – C. И снова хватит коротких засечек на пересечении в точке С.
- Проводим прямую (отрезок) через точки С и D.
- Все! Полученный отрезок, или прямая, – есть точное направление на север :). Простите, – на прямой угол.
- На рисунке показаны два случая несоответствия границы по участку соседа. На Илл.3а приведен случай, когда забор соседа уходит от нужного направления в ущерб себе. На 3б – он залез на Ваш участок. В ситуации 3а возможно построение двух «направляющих» точек: и C, и D. На 3б же – только С.
- Поставьте на углу О колышек, а в точке C – временный колышек, и протяните от С шнур до задней границы участка. – Так, чтобы шнур едва касался колышка О. Замерив от точки О – в направлении D, длину стороны по генплану, получите достоверный задний правый угол участка.

Илл.3. Построение прямого угла – от угла соседа, с помощью циркуля-шагомера и веревочного циркуля
Если у Вас есть циркуль-шагомер, то можно и вовсе обойтись без веревочного. Веревочный в предыдущем примере мы применили для проведения дуг большего радиуса, чем у шагомера. Большего потому, что эти дуги должны где-нибудь пересечься. Для того чтобы дуги можно было провести шагомером с тем же радиусом – 1м с гарантией их пересечения, надо чтобы точки А и В находились внутри окружности c R =1м.
- Отмерьте тогда эти равноудаленные точки рулеткой – в разные стороны от центра, но обязательно по линии АВ (линии забора соседа). Чем точки А и В будут ближе к центру – тем дальше от него направляющие точки: C и D, и тем точнее измерения. На рисунке это расстояние принято равным около четверти радиуса шагомера = 260мм.

Илл.4. Построение прямого угла с помощью циркуля-шагомера и рулетки
- Не менее актуальна эта схема действий и при построении любого прямоугольника, в частности – контура прямоугольного фундамента. Вы получите его идеальным. Его диагонали, конечно, нужно проверить, но разве не уменьшаются усилия? – По сравнению, когда диагонали, углы и стороны контура фундамента двигают туда-сюда, пока углы не сойдутся..
Собственно, мы решили геометрическую задачу на земле. Для того чтобы Ваши действия были более уверенными на участке, потренируйтесь на бумаге – с помощью обычного циркуля. Что ничем в принципе не отличается.
Download Article
Download Article
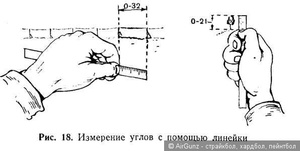
The easiest way to measure an angle is to use a protractor. However, if you don’t have a protractor handy, you can determine the size of an angle using the basic geometric principles of triangles. You’ll need a scientific calculator to solve the equations. Most smartphones are equipped with them, but you can also download a free app or access a free calculator online. The calculations you need to make depend on whether you’re measuring an acute (less than 90 degrees), obtuse (more than 90 degrees but less than 180), or reflex angle (more than 180 degrees but less than 360).[1]
-

1
Draw a vertical line connecting the 2 rays of the angle. To determine the number of degrees in an acute angle, connect the 2 rays to form a triangle. Line up the short end of your ruler with the bottom ray, then draw a vertical line intersecting the other ray using the long side of your ruler.[2]
- The vertical line creates a right triangle. The angle formed by the adjacent side (the bottom ray of the angle) of the triangle and the opposite side (the vertical line) measures 90 degrees.
-

2
Measure the length of the adjacent side to find the run. Place the end of your ruler at the vertex of the angle. Measure the length of the adjacent side from the vertex to the point where it intersects with the opposite side.[3]
- This amount is the run value in your slope equation, where slope = rise/run. If you measured 7, your equation at this point would be “slope = rise/7.”
Advertisement
-

3
Measure the length of the opposite side to find the rise. Set the short end of your ruler flush against the adjacent side of the triangle. Measure the length of the vertical line from the point where it meets the adjacent side to the point where it meets the upper ray of the angle (the hypotenuse of your triangle).[4]
- This amount is the rise value in your slope equation. If you measured 5, you would fill in your equation so that “slope = 5/7.”
-

4
Divide rise by run to find the slope of the angle. The slope is the steepness of the diagonal line, or hypotenuse, of your triangle. Once you know this number, you can calculate the degrees of your acute angle.[5]
- To continue the example, the equation “slope = 5/7” would yield “slope = 0.71428571.”
Tip: Don’t round the number before calculating the degrees in the angle – it could decrease the accuracy of the result.
-

5
Use your calculator to determine the degrees of the angle. Type the value for slope into your scientific calculator, then press the inverse tan button (tan-1). This will give you the degrees of the angle.[6]
- To continue the example, with a slope of 0.71428571, the angle is 35.5 degrees.
Advertisement
-

1
Extend the bottom ray of the angle in a straight line. Mark your vertex with a dot, then use the long side of your ruler to draw a straight line to the left of the vertex. The bottom ray of the angle should be a single long line that extends below the open top ray of the angle.[7]
- Make sure your line is perfectly straight. If it is angled up or down, it will ruin the accuracy of your equation.
Tip: if you’re working on unlined paper, you can line up the short end of your ruler with the side of the paper to make sure your line extension is straight.
-

2
Draw a vertical line connecting the top ray and the line. Line up the short end of your ruler with the bottom ray at a point where the long side crosses the top ray. Follow the long side to draw a line straight up from the bottom ray that connects the two.[8]
- Effectively, you have created a small right angle underneath the obtuse angle you want to measure, turning the top ray of the obtuse angle into the hypotenuse of your right angle.
-

3
Measure the length of the bottom line from the vertex. Place your ruler below the bottom line, with the beginning at the vertical line creating the right angle. Measure the length from that point of intersection to the vertex of the original angle.[9]
- You’re determining the slope for the angle of the acute triangle, which you can use to calculate the degrees in the acute angle. The bottom line is the run value in the equation “slope = rise/run.”
-

4
Measure the length of the vertical line. Line up the short end of your ruler with the bottom line of the small acute triangle. Read up the ruler to the point where the vertical line meets the open ray of your obtuse angle. This is the length of your vertical line.[10]
- The length of your vertical line is the rise value in the equation “slope = rise/run.” Once you know the values for both rise and run, you can calculate the slope of the acute angle.
-

5
Find the slope of the acute angle. Divide the rise value by the run value to determine the slope of the acute angle. You’ll use this value to calculate the degrees of the acute angle.[11]
- For example, the equation “slope = 2/4” would yield “slope = 0.5.”
-

6
Calculate the degrees of the acute angle. Enter your slope value in your scientific calculator, then press the inverse tan button (tan-1). The value displayed is the number of degrees in the acute angle.[12]
- To continue the example, if your slope is 0.5, the acute angle is a 26.565-degree angle.
-

7
Subtract the degrees of the acute angle from 180. A flat line is a straight angle with 180 degrees. Since you drew a straight line, the sum of the acute angle you calculated and the obtuse angle will be 180 degrees. Subtracting the degrees of the acute angle from 180 will give you the degrees of your obtuse angle.[13]
- To continue the example, if you have an acute angle of 26.565 degrees, you have an obtuse angle of 153.435 degrees (180 – 26.565 = 153.435).
Advertisement
-

1
Identify the smaller acute angle associated with the reflex angle. A reflex angle has more than 180 degrees but fewer than 360. This means that if you look at the reflex angle, you’ll also see an acute angle inside the rays of the reflex angle.[14]
- By determining the degrees of the acute angle, you can calculate the degrees in the reflex angle. You can use the basic slope equation and the inverse tangent function on your scientific calculator to find the degrees in the acute angle.
Tip: If you get confused because the angle is upside down, turn your paper and ignore the reflex angle until the last step.
-

2
Draw a vertical line connecting the rays of the acute angle. Line up the short end of your ruler with the ray of the angle that is horizontal rather than diagonal. Then draw a vertical line that meets the horizontal ray of the angle.[15]
- The horizontal line becomes the adjacent side of your triangle, and the vertical line becomes the opposite side of the acute angle you want to measure.
-

3
Measure the rise and the run of the acute angle. In the equation “slope = rise/run,” the rise is the length of the vertical line, or opposite side of your triangle. The run is the length of the horizontal line, or adjacent side of your triangle.[16]
- Measure the horizontal line from the vertex to the point where it meets the vertical line. Measure the vertical line from the point where it meets the horizontal line to the point where it meets the diagonal line.
-

4
Divide rise by run to find the slope of the acute angle. Plug the values you found for the length of the vertical and horizontal lines into your slope equation. When you divide the length of the vertical line by the length of the horizontal line, you’ll get the slope for the angle.[17]
- For example, if your horizontal line measured 8 and your vertical line measured 4, your equation would be “slope = 4/8.” The slope of your angle would be 0.5.
-

5
Use your calculator to find the degrees of the acute angle. Type the value you got for the slope of the angle into your scientific calculator, then press the inverse tangent button (tan-1). The value displayed is the degrees of the smaller acute angle.[18]
- To continue the example, if your slope is 0.5, the acute angle would measure 26.565 degrees.
-

6
Subtract the degrees of the acute angle from 360. A circle has 360 degrees. Since a reflex angle is an angle of more than 180 degrees, you relate it as a portion of a circle. The degrees of the reflex angle and the degrees of the smaller acute angle would add up to 360.[19]
- To continue the example, if the smaller acute angle measures 26.565 degrees, the reflex angle would measure 333.435 degrees.
Advertisement
Add New Question
-
Question
What if the line is curvy?

If there is no straight line, there’s no angle to measure. (An angle is defined as a figure formed by two “rays,” which are straight line segments.)
-
Question
How do I construct a vertical line?

Use a protractor to draw a line perpendicular to the top or bottom edge of the paper, or measuring with a ruler, draw a line parallel to the sides of the paper.
-
Question
How how accurate are the results for each method?

Those methods can usually yield more precise angles than a protractor can.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
Make sure the trig functions of your scientific calculator are set to measure in degrees, not radians.
-
Slope is the relationship between rise and run. The unit of measurement you use to quantify the lengths of the 2 lines is irrelevant – just make sure you’re using the same unit for both lines. In other words, if you measure the length of one line in centimeters, you should also measure the other in centimeters.
Thanks for submitting a tip for review!
Advertisement
Things You’ll Need
- Scientific calculator
- Ruler
References
About This Article
Article SummaryX
To measure an acute angle without a protractor, start by drawing a vertical line connecting the 2 rays of the angle to form a right triangle. Note that the angle formed by the adjacent side of the triangle and the opposite side measures 90 degrees. Next, measure the length of the adjacent side to find the run. Then, measure the length of the opposite side to find the rise. Once you have these measurements, divide rise by run to find the slope, or the steepness, of the diagonal line. When you have this number, you can calculate the degrees of your acute angle by typing the value for slope into a scientific calculator. Finally, press the inverse tan button to get the degrees of the angle. To learn how to measure an obtuse angle without a protractor, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 271,003 times.





