Как найти прямой угол дома

В данной статье описываются три распространенных варианта построения прямых углов при разметке участка для будущего дома, а также описываются методы проверки углов уже возведенных зданий и сооружений без доступа к замеру их диагоналей.

На самом же деле, вариантов существует множество и большинство из них выражаются через тригонометрические функции или с помощью сложных геометрических построений, но здесь это ни к чему, на стройплощадке ни один строитель не возьмется за сложные вещи, упуская время.

Поэтому, рассмотрим три самых простых, но тем не менее надежных метода построения прямых углов:

Теорема Пифагора

Это самый часто используемый и очень надежный способ.

Теорема Пифагора устанавливает соотношение между сторонами прямоугольного треугольника и звучит так: сумма квадратов длин катетов равна квадрату длины гипотенузы.

Для построения прямого угла можно воспользоваться готовым решением (рисунок ниже) или же зная стороны дома, можно без труда вычислить значение диагонали для своего дома и в дальнейшем работать с полученным значением.

Основное соотношение сторон треугольника Пифагора — 3, 4 и 5 единиц. Для удобства, существуют производные треугольники от основного, получаемые при умножении сторон треугольника Пифагора на какой-либо коэффициент. К примеру, стороны 3,4,5 умноженные на К=2 (коэффициент 2), дают треугольник со сторонами 6,8,10, при К=3, стороны 9,12,15 и т.д.

Геометрическое построение

Данный способ ни чуть не хуже Пифагорова треугольника, но редко используемый (в силу забывчивости школьных знаний), хотя очень даже эффективный!

Выглядит сложнее, чем на самом деле.

Зная угол здания (точка О), отмечаем две точки О1 и О2 по оси А, равноудаленные от точки О. Одинаковое расстояние откладывается с помощью рулетки.

Точки О1 и О2 являются центрами окружностей одинакового радиуса. Прямая, проведенная через точку пересечения двух окружностей (точка В) и точку О будет давать прямой угол с прямой А.

По факту, этот способ ни чуть не хуже треугольника Пифагора, имея под рукой два колышка и отрезок веревки, построение осей будущего дома производится всего за 20-40 минут в зависимости от размера и сложности здания.

Две рулетки

Вместо построения окружностей из точек О1 и О2, используются две рулетки (рулетки без погрешности между собой, допустимое отклонение 2-3 мм. на 10 м. по размерной шкале) и прикладываются нулевой отметкой к каждой из точек О1 и О2.

Далее, совмещаем их одинаковыми значениями по мерным шкалам (точка Х) и получаем точку Х, соединив которую с точкой О получим перпендикуляр. В данном случае, построен равнобедренный треугольник, где его высота делит основание ровно пополам и образует с ним прямой угол.

На практике это делается следующим образом: отмечается три контрольные точки по двум рулеткам на пересечении делений (к примеру 1 м., 3м. и 7м.). Далее, через них протягивается разметочный шнур из точки О. Если все точки пересечения шкал лежат на одной прямой (совпадают со шнуром), то построение выполнено верно.

Это настолько быстро делается, что на первый взгляд может показаться неправдоподобным, но поверьте — геометрия работает со 100% гарантией.

Проверка прямого угла построенного здания

Все вышеописанные способы так же применимы и к уже стоящим зданиям. Они используются как проверка за строителями, а так же в случаях, если требуется сооружать фундамент по периметру старого дома и/или ровно облицевать ветхий домик каким-либо материалом.

Все действия аналогичны и главное правило заключается в том, чтобы вынести замеры за пределы строения.

Используя бечевку, протягиваем ее параллельно стенам и закрепляем колышками, а после — снимаем замер.

При геометрическом построении, точка пересечения двух окружностей будет лежать не в основании стены, а по “невидимому” продолжению стены в её же плоскости (на рисунке обозначена точкой Х).

При необходимости, все способы свободно комбинируются или взаимозаменяются.

На этом всё, спасибо Вам за уделенное внимание!

Всего доброго!

Каждый из нас учился в школе. Там человек получает огромное количество тех знаний, которые впоследствии могут понадобиться в жизни. Не все, конечно, могут в полной мере оценить значимость полученных знаний в школьной время, но сейчас речь не об этом.

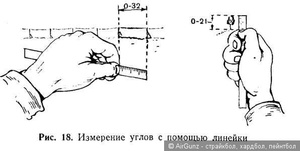
Математика. Это страшное для многих слово, которое пугало достаточное количество школьников в своё время. Цифры, формулы и расчёты поддавались только самым пытливым. И с каждым годом этот сложный предмет становился всё сложнее и сложнее.

В старших классах появляется геометрия и всё становится ещё сложнее и непонятнее. Возможно, многие хоть раз в жизни, но в сердцах проклинали непонятную им науку и задавались вопросом, зачем это вообще нужно, и понадобится ли это в жизни.

Возможно, в повседневной жизни применить полученные в школе знания не удавалось. Вряд ли требовалось посреди белого дня высчитывать логарифмы и квадратные уравнения или доказывать, что две параллельные никогда не сойдутся. Но, где уж точно могут понадобиться знания геометрии и математике, так это в строительстве и при осуществлении ремонта.

В данной статье речь пойдёт о вычислении прямого угла, что требуется при строительстве зданий. Точность при возведении строений должна быть соблюдена в обязательном порядке, ведь только точные расчёты могут избавить от перекосов и нестабильности организации всего здания. Вычисление прямого угла при строительстве – не такой уж и трудный процесс, при котором потребуется знание и применение некоторых простых правил математики и геометрии. Подробнее об этом будет рассказано ниже.

Действительно ли прямой угол?

Возможно, некоторые читатели, ознакомившиеся с заголовком данной статьи, возразят, что прямой угол можно получить не всегда, и не всегда при строительстве используются именно ровные и точные прямые углы.

И, в принципе, они правы. Получить его весьма сложно, особенно если наблюдается неровность фундамента, на котором осуществляется строительство здания. Но, даже учитывая это обстоятельство, ни в коем случае нельзя делать вывод, что расчёт прямого угла можно делать просто “на глаз”. В любом случае, если не представляется возможным вычислить идеальный прямой угол, то требуется достичь наиболее приближённого значения к идеальному углу в 90 градусов. И этого можно добиться, используя незатейливые инструменты и не самые сложные математические знания и познания в геометрии.

Что понадобится для определения прямого угла?

Итак, какие инструменты понадобится использовать для того, чтобы проверить прямой угол. Сразу стоит отметить, что никаких приборов и серьёзных инструментов для этого не потребуется. Нужно будет использовать весьма простые вещи, которые могут найтись практически в каждом хозяйстве. И даже если их не имеется под рукой, их с лёгкостью можно приобрести в магазине. С этим никаких трудностей не возникнет.

Для вычисления прямого угла нужно взять:

• Карандаш;
• Строительную рулетку.

И всё. Вот так вот всё просто.

Как можно вычислить прямой угол?

Итак, в этой статье будет описан принцип 3-4-5 при определении угла в 90 градусов. Ничего сложного в этом нет. Потребуется просто лишь чуть пораскинуть мозгами и вникнуть во все расчёты, которые смогут помочь в проверке угла.

Итак, нужно обозначить следующие шаги:

1. Для начала стоит разобраться в том, почему принцип так обозначен – 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;
2. Итак, потребуется для начала отмерить 3 метра от угла вдоль одной из стен. Тут следует отметить, что 3 метра – предпочтительная длина замера, но в том случае, если комната маленькая, можно отметить всего 30 сантиметров. В месте замера нужно сделать отметку;
3. В принципе, можно использовать и другие цифры, но рекомендуется в любом случае использовать пропорционально увеличенные числа, например: 9-12-15 или же 30-40-50;
4. После проделанного предварительного замера нужно отмерить 4 метра вдоль другой стены, тоже от угла. Ну или соответственно 40 сантиметров, если комната маленькая. Нужно сделать отметку;
5. Теперь остаётся сделать последнее действие, по которому уже можно судить прямой угол или нет. От измеряющего потребуется измерить расстояние между сделанными отметками. По полученным данным можно будет сделать определённые выводы:
   • Если расстояние между отметками будет равняться 5 метрам ровно, это будет означать, что угол является прямым;
   • В том случае, если измеренное расстояние будет равняться меньше 5 метров, угол будет меньше, чем 90 градусов;
   • Ну и, наконец, величина угла будет составлять больше 90 градусов, если полученная величина замера будет равняться больше 5 метров.

Вывод

Вот, как просто можно вычислить прямой угол без использования каких-либо строительных инструментов и приборов. Использовать можно самое простое, но в то же время весьма действенное средство, которое вкупе с использованием имеющихся знаний и бесхитростных расчётов, может помочь произвести измерение.

При использовании предложенных величин, ключевым становится финальный замер между двумя отметками, которые были сделаны ранее. Расстояние, которое будет равняться точно 5 метрам, покажется, что он прямой. Если же величина будет больше или меньше 5 метров, это будет означать, что он прямым не является.

В этой статье хотел бы поделиться, какие вообще распространены варианты построения прямых углов, и как проверить углы уже возведенного дома, не имея доступа к замеру его диагоналей.

Оговорюсь, что вариантов множество, и большинство из них выражается через тригонометрические функции или с помощью сложных геометрических построений))), но нам это ни к чему, так как на стройке никто не будет браться за сложные вещи и сидеть с букварём, теряя время!

В данной статье рассмотрю следующие варианты получения прямого угла:

• теорема Пифагора;
• вариант геометрического построения;
• упрощенный вариант, как производный от геометрического построения.

Теорема Пифагора

Самый часто используемый и очень надежный способ. Теорема устанавливает соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.

Можно воспользоваться готовым решением (рисунок ниже) или же зная стороны дома — самому, согласно формулы, произвести расчет «своей» диагонали, и в дальнейшем работать с этим значением.

Основное соотношение сторон треугольника Пифагора — 3, 4 и 5 единиц. Так же для удобства существуют производные треугольники от основного, получаемые, при умножении его сторон на любой коэффициент. К примеру, стороны 3,4,5 умножены на К=2 (коэффициент 2), получаем треугольник со сторонами 6,8,10, и т.д.

Геометрическое построение

Ни чуть не хуже Пифагорова треугольника, но не часто используемое (наверное, в силу забывчивости), хотя очень даже эффективное!

Выглядит страшно, но на деле — проще простого))).

Зная угол здания (точка О), равноудаляем от него две точки О1 и О2 по оси А. Одинаковое расстояние можем откладывать как хотим, используя: рулетку, циркуль (колышек с веревкой) или обрезок доски, да вообще что угодно, главное иметь равные расстояния от точки О.

Из точек О1 и О2 поочередно одинаковым радиусом (радиус произвольный, но больше чем отложенное расстояние от точки О до О1 или О2) чертим дуги примерно там, где будет пересечение их со второй осью В (со второй стеной). Точка пересечения двух дуг (на рисунке дуги выделены зеленым цветом) и будет давать ровно прямой угол с проведенным отрезком к точке О (к углу будущего здания).

Поверьте, этот способ ни чуть не хуже Пифагора, — имея под рукой два колышка и отрезок веревки, делается построение осей будущего дома за 20-40 минут, в зависимости от размера и сложности здания.

И напоследок упрощенный вариант

Вместо черчения дуг от точек О1 и О2, берутся две рулетки (рулетки без погрешности между собой, допустимое отклонение 2-3 мм. на 10 м. по размерной шкале) и кладутся нулевой отметкой к каждой из точек О1 и О2.

Далее просто совмещаем их одинаковыми значениями по мерной шкале (точка Х) и всё, перпендикуляр готов. В данном случае построен равнобедренный треугольник, где его высота делит основание ровно пополам и образует с ним прямой угол.

На практике делается следующим образом: отмечается несколько контрольных точек по двум рулеткам на пересечении делений (к примеру 1 м., 3м. и 7м.). Далее по ним протягивается шнур от точки О, и если прямая совпадает со всеми точками — вы сделали правильно, если не совпадает — то перемеряем заново!

Это настолько быстро делается, что на первый взгляд может показаться неправдоподобно, но поверьте — всё это работает со 100% гарантией!

Проверка прямого угла построенного здания

Все вышеописанные способы так же применимы и к уже стоящим зданиям. Они используются как проверка за строителями, а так же в случаях, если требуется заливать фундамент по периметру старого дома и/или ровно облицевать ветхий домик каким-либо материалом.

Всё одинаково, главное вынести размеры за пределы строения, так как внутри — работы уже не реальны.

Используя бечевку, протягиваем ее параллельно стенам и закрепляем колышками. После чего снимаем замер.

При геометрическом построении, пересечение дуг будет не по стене, как выше описывалось, а по «невидимому продолжению стены» (на рисунке обозначено точкой Х). То же самое и с двумя рулетками…

При необходимости, все способы свободно комбинируются или взаимозаменяются.

На этом всё, спасибо Вам за уделенное внимание!

Была ли эта статья полезной?