В данной публикации мы рассмотрим, что такое прямой угол, перечислим основные геометрические фигуры, в которых он встречается, а также разберем пример задачи по этой теме.
- Определение прямого угла
- Фигуры с прямыми углами
- Пример задачи
Определение прямого угла
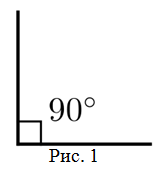
Угол является прямым, если его градусная мера равняется 90 градусам.
На чертежах для обозначения такого угла используется не круглая дуга, а квадратная.
Прямой угол составляет половину развернутого угла (180°) и в радианах равняется π/2.
Фигуры с прямыми углами
1. Квадрат – ромб, все углы которого равны 90°.
2. Прямоугольник – параллелограмм, все углы которого, также, являются прямыми.
3. Прямоугольный треугольник – один из его углов прямой.
4. Прямоугольная трапеция – хотя бы один из углов равняется 90°.
Пример задачи
Известно, что в треугольнике один из углов является прямым, а два остальных равны между собой. Найдем неизвестные значения.
Решение
Как мы знаем из теоремы о сумме углов треугольника, она равняется 180°.
Следовательно, на два неизвестных угла приходится 90° (180° – 90°). Значит каждый из них равняется 45° (90° : 2).
Чему равен прямой угол? Как изобразить прямой угол? Как найти прямые углы на рисунке?
Прямой угол — это угол, градусная мера которого равна 90º.
I. Проще всего изобразить прямой угол по клеточкам.
1) Точку — вершину прямого угла — ставим на пересечении клеточек.
2) Из вершины проводим лучи — стороны угла: один — горизонтально, другой — вертикально.
3) Ставим знак прямого угла — маленький квадрат при вершине: □
∠ABC=90º,
то есть угол ABC — прямой.
II. Другой способ построения прямого угла — при помощи транспортира:
1) Отмечаем точку — вершину угла.
2) От вершины проводим луч — сторону угла.
3) Совмещаем вершину угла с отметкой в центре транспортира (у разных моделей положение отметки может быть различным) так, чтобы отметка 0º располагалась на стороне угла.
4) На отметке 90 градусов ставим точку.
5) От вершины через эту точку проводим второй луч — другую сторону угла:
III. Ещё один способ построения прямого угла — с помощью угольника.
1) Отмечаем точку — вершину угла.
1) От вершины угла проводим луч — первую сторону угла.
2) Прикладываем угольник прямым углом к вершине угла так, чтобы одна сторона угольника проходила через первую сторону угла.
3) Вдоль другой стороны угольника проводим другой луч — вторую сторону угла.
Чтобы по рисунку найти прямой угол, также можно использовать угольник.
Если приложить угольник к вершине угла вдоль одной из сторон, то в остром угле вторую сторону угольник частично закроет (так как градусная мера острого угла меньше 90º), в тупом — вторая сторона окажется за угольником (поскольку тупой угол больше 90º), и только в прямом угле другая сторона угольника пройдёт ровно вдоль второй стороны:
Треугольник, один из углов которого — прямой, называется прямоугольным.
Прямой угол, свойства и фигуры с прямыми углами.
Прямой угол – это угол, градусная мера которого равна 90°.
Прямой угол (определение и понятие)
Геометрические фигуры с прямыми углами
Вертикальные углы, прямой угол, развернутый угол, смежные углы, тупой угол
Прямой угол (определение и понятие):
Прямой угол – это угол, градусная мера которого равна 90°.
Прямой угол – это угол, стороны которого перпендикулярны друг другу. При пересечении перпендикулярных прямых образуются прямые углы.
Прямой угол – это геометрическая фигура, которая состоит из двух перпендикулярных друг другу лучей (сторон), выходящих из одной точки (вершины).
Рис. 1. Прямой угол
Величина прямого угла может быть выражена в разных единицах измерения:
– 90°,
– π / 2 радиан,
– 100 град,
– 1/4 оборота или полного угла,
– 5400 угловых минут,
– 324000 угловых секунд.
Геометрические фигуры с прямыми углами:
У некоторых геометрических фигур имеется один или несколько прямых углов.
Например, прямой угол (или прямые углы ) имеются у прямоугольного треугольника, прямоугольника, квадрата, прямоугольной трапеции.
Прямоугольный треугольник – это треугольник, у которого один угол прямой.
Рис. 2. Прямоугольный треугольник и прямой угол
Прямоугольник – параллелограмм, у которого все углы прямые.
Рис. 3. Прямоугольник и прямые углы
Квадрат – это четырёхугольник, у которого все углы прямые, все углы и стороны равны между собой.
Рис. 4. Квадрат и прямые углы
Прямоугольная трапеция – это трапеция, хотя бы один из углов которой является прямым.
Рис. 5. Прямоугольная трапеция и прямые углы
Квадрат
Полукруг
Прямой угол
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
2 444
Содержание:
- Определение прямого угла
- Величина прямого угла в разных единицах
- Геометрические фигуры с прямыми углами
Определение прямого угла
Определение
Прямой угол – это угол, градусная мера которого равна
$90^{circ}$ (рис. 1).
Прямой угол – это угол, который составляет $frac{pi}{2}$ радиан и он равен половине
развернутого угла.
Прямой угол, в отличие от других углов, обозначается не дугой, а квадратиком (рис. 1).
Величина прямого угла в разных единицах
- $90^{circ}$;
- $frac{pi}{2}$радиан;
- 100 град;
- ¼ оборота или полного угла;
- 5400 угловых минут;
- 324000 угловых секунд.
Геометрические фигуры с прямыми углами
Геометрические фигуры, имеющие один или несколько прямых углов, носят собственные названия:
- Прямоугольный треугольник – это треугольник с одним прямым углом.
- Прямоугольник – параллелограмм, у которого все углы прямые.
- Квадрат – ромб, все углы которого прямые.
- Прямоугольная трапеция – трапеция, хотя бы один из углов которой является прямым.
Пример
Задание. Чему равен смежный угол к прямому углу?
Решение. Как известно, сумма смежных углов равна
$180^{circ}$, а тогда, если прямой угол равен
$90^{circ}$, то смежный с ним угол
$$180^{circ}-90^{circ}=90^{circ}$$
То есть смежный к прямому углу также является прямым углом.
Ответ. $90^{circ}$
Читать дальше: что такое развёрнутый угол.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Виды углов
- Прилежащие углы
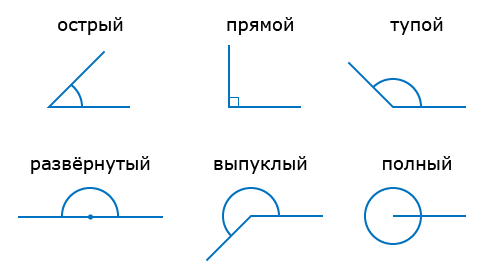
Каждый угол, в зависимости от его величины, имеет своё название:
- Острый угол — это угол, который меньше прямого угла (<90°).
- Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол обозначается буквой d и равен 90°.
Если два смежных угла равны между собой, то каждый из них называется прямым углом. Прямой угол обычно обозначается не дугой, а уголком:
∠AOC и ∠COB — прямые углы. Общая сторона прямых углов OC называется перпендикуляром к прямой AB, а точка O — основанием перпендикуляра.
Сумма двух прямых углов равна развёрнутому углу, значит, прямой угол равен половине развёрнутого угла.
- Тупой угол — это угол, который больше прямого угла, но меньше развёрнутого:
90° < тупой угол < 180°.
- Развёрнутый угол — это угол, образованный двумя дополнительными лучами.
Развёрнутый угол равен сумме двух прямых углов или, короче, двум прямым углам. Следовательно, развёрнутый угол равен 180° или 2d.
Все развёрнутые углы равны между собой.
- Выпуклый угол — это угол, который больше развёрнутого угла, но меньше полного:
180° < выпуклый угол < 360°.
- Полный угол — это угол, обе стороны которого совпадают с одним лучом.
Полный угол равен сумме четырёх прямых углов, то есть 4d (360°).
Прилежащие углы
Прилежащие углы — это пара углов, имеющих общую вершину и общую сторону, другие стороны которых лежат по разные стороны от общей стороны.
∠AOB и ∠BOC — прилежащие углы, O — общая вершина, OB — общая сторона.
Если из вершины любого угла провести луч, разделяющий угол на два угла, то образованные углы будут прилежащими.
Угол, разделённый лучом, будет называться суммой полученных углов, например угол AOB является суммой углов AOC и COB:
∠AOB = ∠AOC + ∠COB.
Каждый из прилежащих углов, ∠AOC и ∠COB, называется разностью углов AOB и другого прилежащего, то есть:
∠AOC = ∠AOB – ∠COB,
∠COB = ∠AOB – ∠AOC.