Как найти прямой вид числа

Двоичное число: прямой, обратный и дополнительный коды

Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Прямой, обратный и дополнительный коды двоичного числа – способы представления двоичных чисел с фиксированной запятой в компьютерной (микроконтроллерной) арифметике, предназначенные для записи отрицательных и неотрицательных чисел

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.

---

Прямой код

Прямой код – способ представления двоичных чисел с фиксированной запятой. Главным образом используется для записи неотрицательных чисел

Прямой код используется в двух вариантах.
В первом (основной) – для записи только неотрицательных чисел:

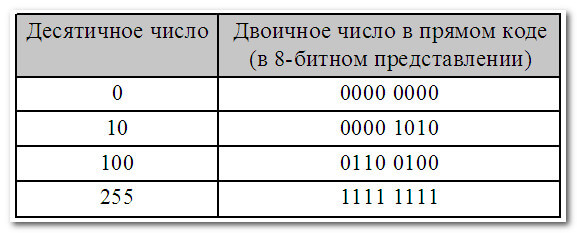В этом варианте (для восьмибитного двоичного числа) мы можем записать максимальное число 255 (всего чисел 256 – от 0 до 255)

Второй вариант – для записи как положительных, так и отрицательных чисел.
В этом случае старший бит (в нашем случае – восьмой) объявляется знаковым разрядом (знаковым битом).
При этом, если:
– знаковый разряд равен 0, то число положительное
– знаковый разряд равен 1, то число отрицательное

В этом случае диапазон десятичных чисел, которые можно записать в прямом коде составляет от – 127 до +127:

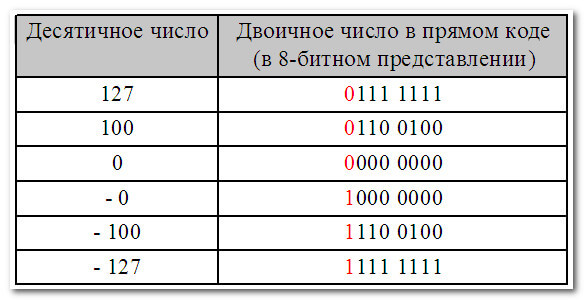Подводя итоги вопроса, не влезая в его дебри, скажу одно:
Прямой код используется главным образом для представления неотрицательных чисел.
 Использование прямого кода для представления отрицательных чисел является неэффективным – очень сложно реализовать арифметические операции и, кроме того, в прямом коде два представления нуля – положительный ноль и отрицательный ноль (чего не бывает):

---

Обратный код

Обратный код – метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения.
Обратный двоичный код положительного числа состоит из одноразрядного кода знака (битового знака) – двоичной цифры 0, за которым следует значение числа.
Обратный двоичный код отрицательного числа состоит из одноразрядного кода знака (битового знака) – двоичной цифры 1, за которым следует инвертированное значение положительного числа.

Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.

При 8-битном двоичном числе – знаковый бит (как и в прямом коде) старший (8-й)

Диапазон десятичных чисел, который можно записать в обратном коде от -127 до + 127

Арифметические операции с отрицательными числами в обратном коде:

(Арифметические операции с двоичными числами)

1-й пример (для положительного результата)
Дано два числа:
100 = 0110 0100
-25 = – 0001 1001
Необходимо их сложить:
100 + (-25) = 100 – 25 = 75

1-й этап
Переводим число -25 в двоичное число в обратном коде:
25 = 0001 1001
-25= 1110 0110
и складываем два числа:
0110 0100 (100) + 1110 0110 (-25) = 1 0100 1010, отбрасываем старшую 1 (у нас получился лишний 9-й разряд – переполнение), = 0100 1010
2-й этап
Отброшенную в результате старшую единицу прибавляем к результату:
0100 1010 + 1 = 0100 1011 (знаковый бит =0, значит число положительное), что равно 75 в десятичной системе

2-й пример (для отрицательного результата)
Дано два числа:
5 = 0000 0101
-10 = – 0000 1010
Необходимо их сложить:
5 + (-10) = 5 – 10 = -5

1-й этап
Переводим число -10 в двоичное число в обратном коде:
10 = 0000 1010
-10= 1111 0101
и складываем два числа:
0000 0101 (5) + 1111 0101 (-10) = 1111 1010 (знаковый бит =1, значит число отрицательное)

2-й этап
Раз результат получился отрицательный, значит число представлено в обратном коде.
Переводим результат в прямой код (путем инвертирования значения, знаковый бит не трогаем):
1111 1010 —-> 1000 0101
Проверяем:
1000 0101 = – 0000 0101 = -5

---

Обратный код решает проблему сложения и вычитания чисел с различными знаками, но и имеет свои недостатки:
– арифметические операции проводятся в два этапа
– как и в прямом коде два представления нуля – положительный и отрицательный

---

Дополнительный код

Дополнительный код – наиболее распространенный способ представления отрицательных чисел. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел.

В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).

Диапазон десятичных чисел которые можно записать в дополнительном коде от -128 до +127. Запись положительных двоичных чисел в дополнительном коде та-же, что и в прямом и обратном кодах.

Дополнительный код отрицательного числа можно получить двумя способами
1-й способ:
– инвертируем значение отрицательного числа, записанного в прямом коде (знаковый бит не трогаем)
– к полученной инверсии прибавляем 1
Пример:
Дано десятичное число -10
Переводим в прямой код:
10 = 0000 1010 —-> -10 = 1000 1010
Инвертируем значение (получаем обратный код):
1000 1010 —-> 1111 0101
К полученной инверсии прибавляем 1:
1111 0101 + 1 = 1111 0110 – десятичное число -10 в дополнительном коде

2-й способ:
Вычитание числа из нуля
Дано десятичное число 10, необходимо получить отрицательное число (-10) в дополнительном двоичном коде
Переводим 10 в двоичное число:
10 = 0000 1010
Вычитаем из нуля:
0 – 0000 1010 = 1111 0110 – десятичное число -10 в дополнительном коде

Арифметические операции с отрицательными числами в дополнительном коде

Дано: необходимо сложить два числа -10 и 5
-10 + 5 = -5
Решение:
5 = 0000 0101
-10 = 1111 0110 (в дополнительном коде)
Складываем:
1111 0110 + 0000 0101 = 1111 1011, что соответствует числу -5 в дополнительном коде

Как мы видим на этом примере – дополнительный код отрицательного двоичного числа наиболее подходит для выполнения арифметических операций сложения и вычитания отрицательных чисел.

---

Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода

---

Предыдущие статьи:
1. Микроконтроллеры – первый шаг
2. Системы счисления: десятичная, двоичная и шестнадцатиричная
3. Логические операции, логические выражения, логические элементы
4. Битовые операции

---

(39 голосов, оценка: 4,69 из 5)

Загрузка…

---

Тема 3: Представление
целых чисел в компьютере.

Представление числовой информации в
компьютере

Любая информация (числа,
текстовая, графическая и т. д.) представляется
в ЭВМ в виде двоичных кодов фиксированной
или переменной длины. Отдельные элементы
двоичного кода, имеющие значение 0 или
1, называют битами.
Двоичный код состоящий из 8 разрядов
носит название байта.

Целые числа могут
представляться в компьютере со знаком
или без знака.

Представление целых чисел без знака
в компьютере

Целые числа без знака обычно  занимают
 в  памяти  компьютера  один,
два или 4 байта.    

В  однобайтовом  формате
 числа принимают  значения  от 
00000000₂  
до   11111111₂.

В двубайтовом формате —
от  00000000 00000000₂  
до   11111111 11111111₂.

В четырехбайтовом –  от
00000000 00000000 00000000 00000000₂
до 11111111 1111111 11111111 11111111₂

Диапазоны значений целых чисел без
знака

Формат числа в байтах	Диапазон
Запись с порядком	Обычная запись
1	0 … 28–1	0 … 255
2	0 … 216–1	0 … 65535
4	0 … 232–1	0…429967295

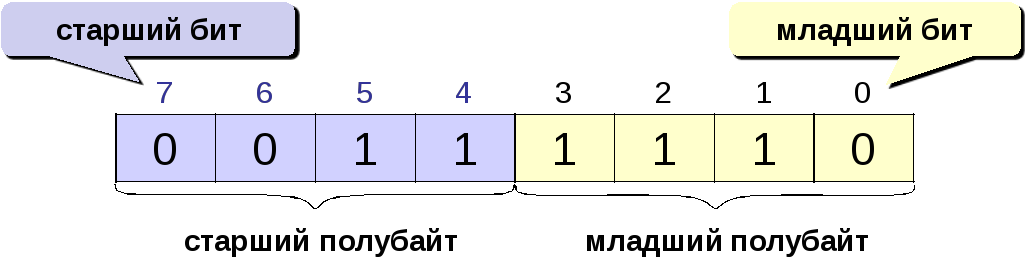
Например,
в однобайтовом формате число 62=111110₂
имеет вид:

В двубайтовом формате число 1402=10101111010₂
имеет вид:

Пример 1. Для хранения целого числа
без знака используется один

байт. Записать представление числа 19 в
компьютере.

1 шаг: Переведем число 19 из десятичной
системы счисления в двоичную.

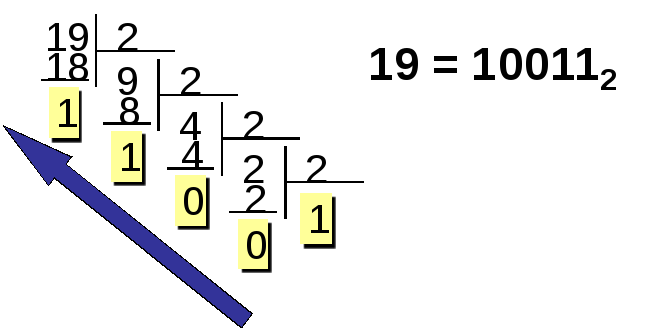
2 шаг:
Так как для представления числа в
компьютере выделен 1 байт, то код числа
должен содержать 8 знаков (8 бит). Поэтому
впереди числа дописываем 3 незначащих
нуля.

0

0

0

1

0

0

1

1

Задания.

1. Запишите числа в беззнаковом коде
(формат 1 байт):

 а) 31;      б)
163;    в) 65;    г) 128. 

2. Найдите десятичные
представления чисел, записанных в
беззнаковом коде:

 а) 0 1011000;     
б) 1 0011011;     в) 0 1101001;     
г) 1 1000000. 

Представление целых чисел со знаком

Так же как беззнаковые целые числа целые
со знаком обычно  занимают  в
 памяти  компьютера  один, два
или 4 байта.

Диапазоны значений целых чисел со
знаком

Формат числа в байтах	Диапазон
Запись с порядком	Обычная запись
1	–27 … 27–1	–128 … 127
2	–215 … 215–1	–32768 … 32767
4	–231 … 231–1	–2147483648 … 2147483647

Самый левый (старший бит)
разряд определяет знак числа. 
 Если
он равен 0, число положительное, если 1,
то отрицательное.

Например,
в однобайтовом формате число 46=101110₂
имеет вид:

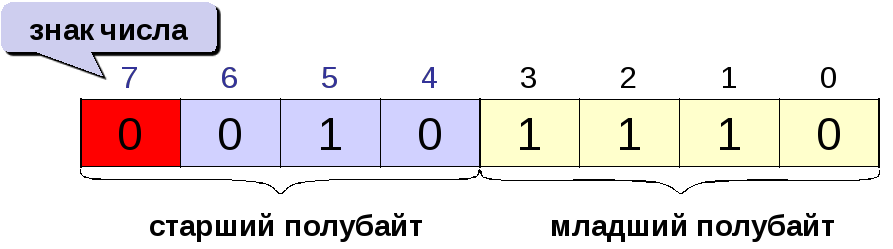
В ЭВМ в целях упрощения
выполнения арифметических операций
применяют специальные коды для
представления чисел. Использование
кодов позволяет свести операцию вычитания
чисел к арифметическому сложению кодов
этих чисел. Применяются прямой,
обратный
и дополнительный
коды чисел. Дополнительный код используется
для хранения чисел в запоминающем
устройстве ЭВМ. Обратный и дополнительный
коды используются для замены операции
вычитания операцией сложения, что
упрощает устройство арифметического
блока ЭВМ.

Прямой код.
Прямой код двоичного числа совпадает
по изображению с записью самого числа.
Значение знакового разряда для
положительных чисел равно 0, а для
отрицательных чисел 1.

Обратный код.
Обратный код для
положительного числа совпадает с прямым
кодом. Для отрицательного числа все
цифры числа заменяются на противоположные
(1 на 0, 0 на 1), а в знаковый разряд заносится
единица.

Дополнительный код.
Дополнительный код
положительного числа совпадает с прямым
кодом. Для отрицательного числа
дополнительный код образуется путем
получения обратного кода и добавлением
к младшему разряду единицы.

Например, в однобайтовом формате числа
27 и -27 имеют вид:

Число	Прямой код	Обратный код	Дополнительный код
27	00011011	00011011	00011011
-27	10011011	11100100	11100101

Пример 1. Найти прямой, обратный и
дополнительный код представления числа
13 в однобайтном формате.

1 шаг: Переведем число 13 из десятичной
системы счисления в двоичную.

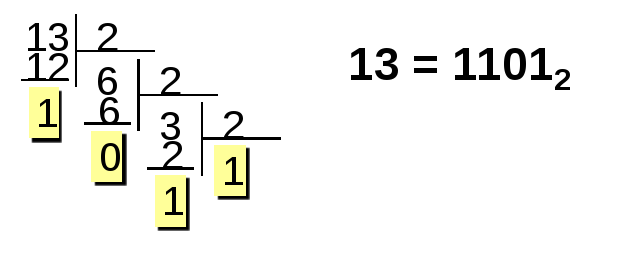
2 шаг: Для представления
числа в компьютере выделен 1 байт. Старший
бит занимает знак числа – 0. Сам код
числа должен занимать 7 бит. Таким образом
прямой код числа 13

0

0

0

0

1

1

0

1

Так как для положительных чисел прямой,
обратный и дополнительный код совпадает,
то ответ 00001101.

Пример 2. Найти прямой, обратный и
дополнительный код представления числа
-23 в однобайтовом формате.

1 шаг: Переведем число -23 из десятичной
системы счисления в двоичную. Получим

-23₁₀=-10111₂

2 шаг: Прямой код числа в однобайтовом
формате, учитывая, что старший бит
занимает знак числа -1, имеет вид

1

0

0

1

0

1

1

1

3 шаг: Найдем обратный код числа -23,
заменив все цифры числа на
противоположные (1 на 0, 0 на 1), а в знаковый
разряд заносится единица. Имеем,

1

1

1

0

1

0

0

0

4 шаг: Найдем дополнительный код
числа -23, добавив 1 к младшему
разряду обратного кода.

1

1

1

0

1

0

0

1

Ответ:
прямой код – 10010111; обратный – 11101000;
дополнительный – 11101001.

Так
вот, прямой
обратный и дополнительный код – это
модели представления целых чисел,
как положительных, так и отрицательных.
Примеры записи некоторых чисел во всех
трех восьмиразрядных кодах показаны в
таблице ниже.

Число	Прямой код	Обратный код	Дополнительный код
0	00000000	00000000	00000000
1	00000001	00000001	00000001
-1	10000001	11111110	11111111
5	00000101	00000101	00000101
-5	10000101	11111010	11111011
8	00001000	00001000	00001000
-8	10001000	11110111	11111000
120	01111000	01111000	01111000
-120	11111000	10000111	10001000
127	01111111	01111111	01111111
-127	11111111	10000000	10000001

Во
всех трех кодах старший разряд указывает
на знак числа и он равен единице, если
число отрицательное и нулю в противном
случае. Остальные разряды содержат
представление модуля числа. Различие
между кодами наблюдается именно в
способах представления модуля. Для
положительного числа модуль во всех
трех кодах представляется одинаково –
это просто естественная запись двоичного
числа.
Для отрицательных чисел, в обратном
коде это просто поразрядная инверсия
прямого кода, а в дополнительном – к
обратному коду, как к числу, просто
прибавляется единица.

Распространёнными
формами представления чисел со знаками
является их представление в прямом,
обратном и дополнительном коде.
Прямой
код числа образуется кодированием знака
числа нулём, если число положительно и
единицей, если число отрицательно (для
двоичной системы)
Для общего случая
(q – 1) – если число отрицательно, и 0 – если
число положительно. q – основание системы
счисления.
Код знака записывается
перед старшей цифрой числа и отделяется
от неё точкой:
-1.01 = 1.101
Прямой, обратный
и дополнительный коды положительных
чисел совпадают между собой.
Обратный
код отрицательного числа образуется
из прямого кода, заменой его цифр на их
дополнения до величины q-1. Код знака
сохраняется без изменения.
Пример
:
+123₁₀ =
0.123_пр =
0.123_об.
-123₁₀ =
9.123_пр =
9.876_об
+3А7С00₁₆ =
0.3А7С00_пр =
0.3А7С00_об.
-3А7С00₁₆ =
F.3А7С00_пр=
F.C583FF_об.
-101₂ =
1.101_пр =
1.010_об.
Замена
цифр их дополнениями для двоичной
системы совпадает с операцией инверсии,
то есть нули заменяются единицами,
единицы – нулями. Знак принимает значение,
равное единице.
Дополнительный код
отрицательного числа образуется из
обратного увеличением на 1 его младшего
разряда. При этом перенос из знакового
разряда игнорируется.
Пример:
+236₁₀ =
0.236_пр.=
0.236_об.=
0.236_доп.
-236₁₀ =
9.236_пр.=
9.763_об.=
9.764_доп.
-101₂=
1.101_пр.=
1.010_об=
1.011_доп.
-3А7С₁₆=
F.3А7С_пр=
F.C583_об.=
F.C584_доп.
Правила
перевода из прямого кода в обратный и
из обратного в прямой, а также из прямого
в дополнительный и из дополнительного
в прямой совпадают между собой.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Летняя онлайн-школа, задание 28 июня для 6 класса. Как определить вид числа по его записи. Нужно знать определения различных чисел.

Натуральные числа — это числа, которые употребляют при счете неделимых предметов.

Целые числа — это натуральные числа, им противоположные и нуль.

Рациональные числа — это числа, которые представляют в виде обыкновенной дроби, где в числителе находится целое число, а в знаменателе — натуральное.

Простые числа — это такие числа, которые имеют только 2 делителя: 1 и само число.

Составные числа имеют больше двух делителей.

Выполни задание, ответы отправь на проверку.

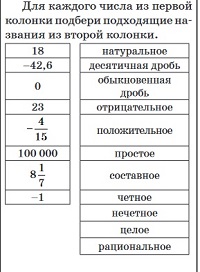
Форма для заполнения ответов на задания

Задания в ОГЭ на виды чисел

Задание 1

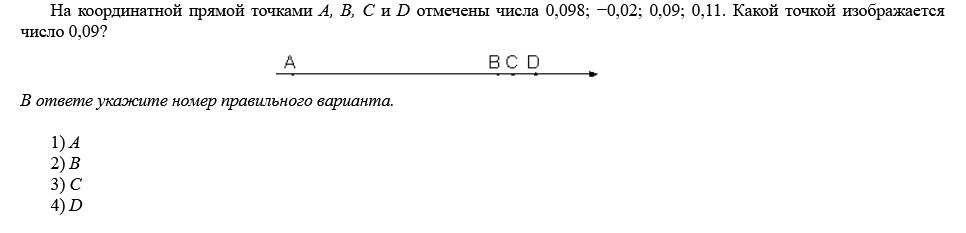
Решение: Сначала нужно определить вид числа в задании. Это десятичные дроби. Нужно расположить их в порядке возрастания, а потом сопоставить с точками на координатной прямой.

Уравняем в числах 0,098; −0,02; 0,09; 0,11 количество знаков после запятой до трех.

0,098; −0,020; 0,090; 0,110.

Расставляем эти числа в порядке возрастания ( от меньшего к большему).

−0,020; 0,090; 0, 098; 0,110.

Вернемся к первоначальному виду чисел.

−0,02; 0,09; 0, 098; 0,11.

Нам нужно определить какой точкой изображается число 0,09. Это число стоит на втором месте в ряде чисел. На координатной прямой на втором месте стоит точка B.

Ответ: 2.

Задание 2

Решение: В данном случае сначала определяем (приблизительно) какому дробному числу соответствует точка а на координатной прямой.

а ≈ 4,5.

Проверяем на истинность утверждения из задания, подставляя значение а.

1) а — 5 = 4,5 — 5 = — 0,5 < 0 ( — )

2) 7 — a = 7 — 4,5 = 2,5 > 0 ( — )

3) a — 3 = 4,5 — 3 = 1,5 > 0 ( +)

4) 2 — a = 2 — 4,5 = — 2,5 < 0 ( — )

Верное утверждение записано под цифрой 2.

Ответ: 2.

Вернуться к выбору заданий 6 класса.

Прямой код

Прямой код – это представление числа в двоичной системе счисления, при котором первый (старший) разряд отводится под знак числа. Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1.

Таким образом, в двоичной системе счисления, используя прямой код, в восьмиразрядной ячейке (байте) можно записать семиразрядное число. Например:

0 0001101 – положительное число
1 0001101 – отрицательное число

Количество значений, которые можно поместить в семиразрядной ячейке со знаком в дополнительном разряде равно 256. Это совпадает с количеством значений, которые можно поместить в восьмиразрядную ячейку без указания знака. Однако диапазон значений уже другой, ему принадлежат значения от -128 до 127 включительно (при переводе в десятичную систему счисления).

При этом в вычислительной технике прямой код используется почти исключительно для представления положительных чисел.

Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами электронными устройствами компьютера.

Дополнительный код

В дополнительном коде, также как и прямом, первый разряд отводится для представления знака числа. Прямой код используется для представления положительных чисел, а дополнительный – для представления отрицательных. Поэтому, если в первом разряде находится 1, то мы имеем дело с дополнительным кодом и с отрицательным числом.

Все остальные разряды числа в дополнительном коде сначала инвертируются, т.е. заменяются противоположными (0 на 1, а 1 на 0). Например, если 1 0001100 – это прямой код числа, то при формировании его дополнительного кода, сначала надо заменить нули на единицы, а единицы на нули, кроме первого разряда. Получаем 1 1110011. Но это еще не окончательный вид дополнительного кода числа.

Далее следует прибавить единицу к получившемуся инверсией числу:

1 1110011 + 1 = 1 1110100

В итоге и получается число, которое принято называть дополнительным кодом числа.

Причина, по которой используется дополнительный код числа для представления отрицательных чисел, связана с тем, что так проще выполнять математические операции. Например, у нас два числа, представленных в прямом коде. Одно число положительное, другое – отрицательное и эти числа нужно сложить. Однако просто сложить их нельзя. Сначала компьютер должен определить, что это за числа. Выяснив, что одно число отрицательное, ему следует заменить операцию сложения операцией вычитания. Потом, машина должна определить, какое число больше по модулю, чтобы выяснить знак результата и определиться с тем, что из чего вычитать. В итоге, получается сложный алгоритм. Куда проще складывать числа, если отрицательные преобразованы в дополнительный код. Это можно увидеть на примерах ниже.

Операция сложения положительного числа и отрицательного числа, представленного в прямом коде

1. Прямой код числа 5: 0 000 0101
   Прямой код числа -7: 1 000 0111
2. Два исходных числа сравниваются. В разряд знака результата записывается знак большего исходного числа.
3. Если числа имеют разные знаки, то вместо операции сложения используется операция вычитания из большего по модулю значения меньшего. При этом первый (знаковый) разряд в операции не участвует.

   _ 000 0111       000 0101     ————-       000 0010

4. После выполнения операции учитывается первый разряд. Результат операции 1 000 0010, или -2₁₀.

Операция сложения положительного числа и отрицательного числа, представленного в дополнительном коде

1. Прямой код числа 5: 0 000 0101
   Прямой код числа -7: 1 000 0111
2. Формирование дополнительного кода числа -7.
   Прямой код : 1 000 0111
   Инверсия : 1 111 1000
   Добавление единицы: 1 111 1001
3. Операция сложения.

   0 000 0101     + 1 111 1001       ————–       1 111 1110

4. Проверка результата путем преобразования к прямому коду.
   Дополнительный код: 1 111 1110
   Вычитание единицы : 1 111 1101
   Инверсия : 1 000 0010 (или -2₁₀)

Примеры из проекта

Источник

Также по теме – порядок чтения байтов.