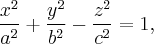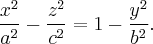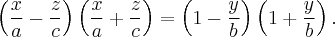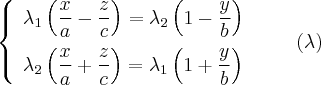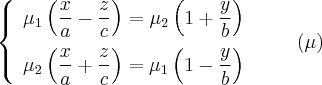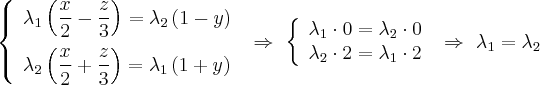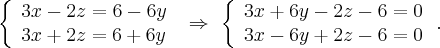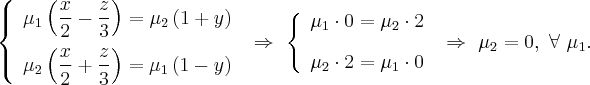Как найти прямолинейные образующие однополостного гиперболоида

255

АГ: Глава 6

При
рассмотрении конических и цилиндрических
поверхностей легко заметить, что эти
поверхности образованы движением
прямой линии.
Движение применялось простейшее:
вращение вокруг неподвижной оси.

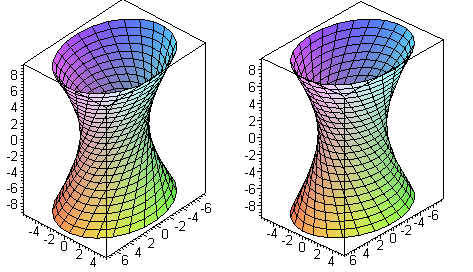
Рисунки
поверхностей однополостного гиперболоида
и гиперболического параболоида не
подсказывают, что эти поверхности могут
быть построены за счёт какого-то, пусть
даже сложного, движения прямолинейных
образующих:
ведь это значило бы, что какие-то прямые
целиком лежат на этих поверхностях!

Не будем
делать выводов, применяя только
впечатления от восприятия формы
геометрических фигур. Применим логически
оправданные действия. Если допустить,
что прямая линия принадлежит какой-то
поверхности, необходимо, выполнить
действия:

▫ взять
произвольную точку
,
принадлежащую исследуемой поверхности;

▫ взять
прямую линию, проходящую через точку

,
и определяемую общими уравнениями;

▫ доказать, что
за счёт выбора значений общих параметров
прямой можно добиться того, что прямая
линия целиком принадлежит поверхности.

Пусть
уравнение прямой задано параметрическими
уравнениями
:

Из этих уравнений следует: точка

принадлежит прямой линии, направление
прямой определяет вектор
=.

У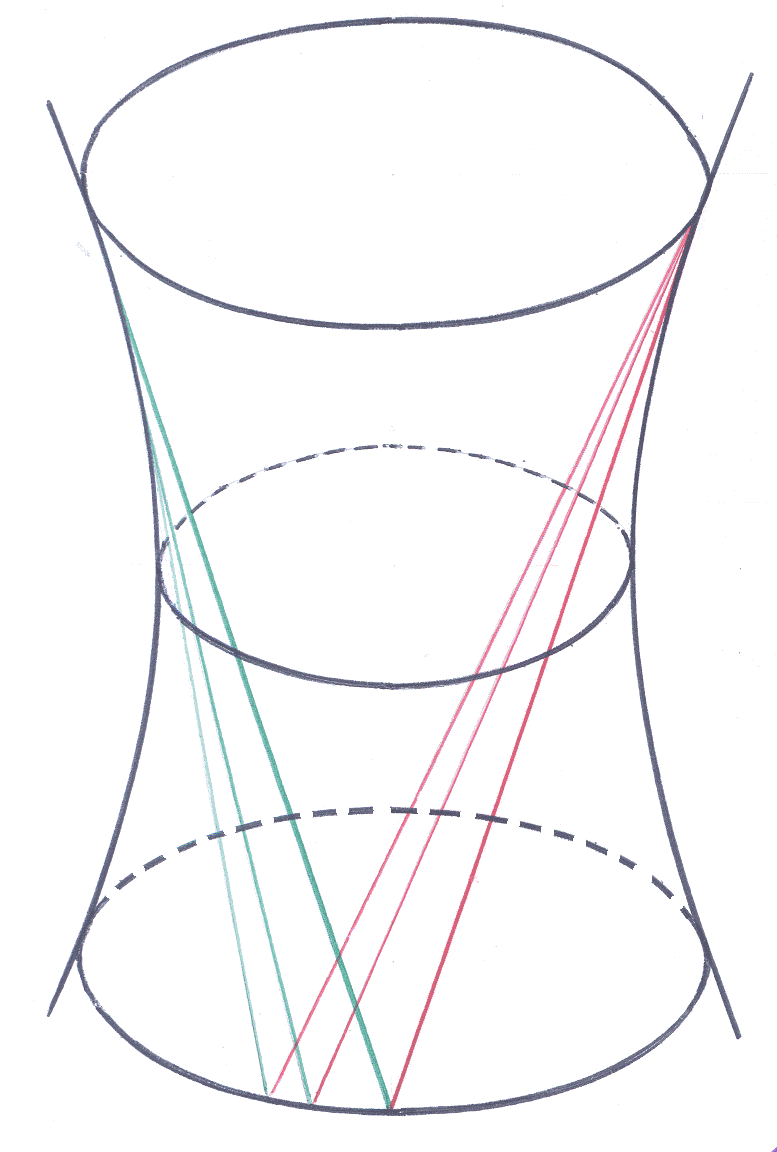читывая,
что любые преобразования прямоугольных
координат не изменяют геометрические
фигуры, расположенные в пространстве,
станем использовать такую систему
координат, в которой рассматриваемая
фигура определяется простейшим
алгебраическим выражением: каноническим
уравнением.

Однополостный
гиперболоид.
Его каноническое уравнение:
.
Для упрощения записи используемых
алгебраических выражений запишем
уравнение поверхности в виде:
.

Пусть
точка

принадлежит поверхности однополостного
гиперболоида. Так как прямая должна
принадлежать его поверхности, то точка

также должна принадлежит рассматриваемой
поверхности. Подставим значения
переменных:

из параметрических уравнений прямой в
каноническое уравнение поверхности.
Получим уравнение 2-го порядка относительно
переменной
:

,
(1)

где
коэффициенты могут быть записаны в виде
выражений:

=;
=; =.

Если
прямая линия

принадлежит рассматриваемой поверхности,
то уравнению (1) удовлетворяют любые
значения
.
Возьмём три различных значения переменной

.
Для этих значений получим систему
уравнений:

определитель
этой системы:
=0.

Так как
система трёх линейных однородных
уравнений относительно неизвестных
,

имеет определитель, не равный нулю, то
её единственным решением является
нулевое решение:
=0,

=0,

=0.

Верно
и обратное. Если коэффициенты уравнения
(1)
=0,

=0,

=0,
то оно удовлетворяется любыми значениями

.
В нашем случае это значит, что прямая
линия

принадлежит поверхности:
.

Применим
полученный результат к однополостному
гиперболоиду. Учтём сразу, что на его
поверхности значения
,,
не могут быть равны нулю одновременно.
Пусть
0.

Из
условия
=0
следует:
.
Тогда можем записать:

==0. (2)

Координаты
вектора
=
не могут быть равны нулю одновременно.
Из условия
=0
мы получили бы одновременно:
=0.
Последнее невозможно, так как
0.

Пусть

0.
Применяя несложные алгебраические
преобразования, равенство (2) можем
записать в виде выражения: =0. (3)

Решая
квадратное уравнение (3) относительно
отношения
,
запишем решение в виде:

=. (4)

Так как

==0,
то

и выражение (4) ещё более упростится: = (5)

Из
выражения (5) следует: для существования
действительных решений уравнения (3)
необходимо и достаточно, чтобы выполнялось
условие:
<
0. Возможны следующие комбинации
знаков в уравнении (1):

	A	B	C
I	–	–	–
II	+	+	–

В случае
I
уравнение (1) определяет мнимый эллипсоид
– прямолинейных образующих не имеет.
В случае II
уравнение (1) определяет однополостный
гиперболоид – прямолинейные образующие
имеет.

Так как
для однополостного гиперболоида
0,
то для каждой точки

имеем две прямолинейные образующие (на
рисунке показаны разным цветом).

Учитывая,
что для однополостного гиперболоида

имеем:
=,

=–,
получаем выражения:
==. (6)

Учитывая
выражение (6), и используя выражение
,
получим полную характеристику необходимого
для точки

вектора
:

=. (7)

Если в
выражении (6) выбирать всё время знак
,
будем получать прямолинейные образующие
поверхности одного семейства. Знаку

будет соответствовать второе семейство
образующих той же поверхности.

Важно
то, что
.
Это значит, что
0,
то есть никакая прямолинейная образующая
не параллельна плоскости координат
.
Из этого следует, что все образующие
однополостного гиперболоида пересекают
горловой
эллипс:

По поводу
прямолинейных образующих однополостного
гиперболоида
полезно знать две теоремы (из рисунка
вполне можно видеть намёк-подтверждение!).

Теорема:

(6.1)

Две
прямолинейные образующие, принадлежащие
различным семействам, всегда лежат в
одной плоскости, и параллельны тогда
и только тогда, когда проходят через
диаметрально противоположные точки
горлового эллипса.

►Пусть
имеем две прямолинейные образующие

и
,
принадлежащие различным семействам.
Пусть

пересекает горловой эллипс в точке
,
а

– в точке
.

Если
точки

и

совпадают, то утверждение очевидно.
Пусть теперь точки

и

различны. Учтём, что для горлового
эллипса
=0
и
.
В этом случае имеем:

=
и
=– или
=. (8)

и
одновременно: =. (9)

Обозначим
векторы
=,

=
и
.
Условием принадлежности образующих

и

одной плоскости является:
=0.

Из
выражений (8) и (9) видно, что векторы

и

только в случае, когда

и

проходят через диаметрально противоположные
точки горлового эллипса:

=,=,==0.

Теорема
доказана! ◄

Замечание:
если
детали доказательства теоремы применить
к тому же рисунку, то нетрудно признаться
себе, что интуиция –
только помощница при доказательстве
теорем, но не само доказательство!

теоремы (из рисунка
вполне можно видеть намёк-подтверждение!).

Теорема:

(6.2)

Любые
две прямолинейные образующие одного
семейства не принадлежат одной
плоскости.

►Пусть
имеем две прямолинейные образующие

и
,
которые принадлежат одному семейству
и пересекают горловой эллипс в точке

и в точке
,
соответственно. Точки

и

различны, иначе образующие совпадали
бы!

В этом случае
имеем:

= и =. (10)

Вычисления
показывают, что на этот раз:
0.
Из этого следует, что

и

– скрещивающиеся прямолинейные
образующие однополостного гиперболоида.

Теорема
доказана! ◄

Используя
результаты теорем, можно попробовать
найти прямолинейные образующие
однополостного гиперболоида, выполняя
формальные алгебраические действия с
исходным выражением
:

→ . (11)

Используя (11),
запишем уравнения прямых линий:

(12)

Нетрудно
заметить, учитывая (11), что при любых
значениях чисел:

и

прямые

и

лежат на поверхности однополосного
гиперболоида: для этого достаточно
перемножить первое и второе уравнения
для системы
,
аналогично для системы
.

Формальное
использование уравнений (12) полезно
тем, что эти уравнения могут быть легко
записаны. Конечно, способ, опирающийся
на выражения (11) и (12), не
отменяет
важность доказанных теорем!

Интересно:
Однополостные гиперболоиды используют
при сооружении прочных, лёгких и простых
в изготовлении башен. Такую конструкцию
предложил русский инженер Шухов В.Г.
(1853-1939). В соответствии с его идеей
построена Останкинская телебашня в
Москве (каждый может ею полюбоваться!).

☺☺

Пример 6–16:
Для однополостного гиперболоида:

найти прямолинейные образующие,
проходящие через точку
(3,2,1).

Решение:

1). Запишем
исходное выражение в виде:
,
откуда уравнения прямолинейных образующих
можно записать в виде:

2).
Подставляя в полученные уравнения
координаты заданной точки
(3,2,1),
получаем: из уравнений системы
:,
причём
–
произвольное число, а для системы
:

–
произвольное число и =0.
Используя полученные значения пар
и ,
запишем уравнения образующих:

и

Ответ: уравнения
образующих:
и

Замечание:
Используя полученные уравнения, без
особого труда можно получить параметрические
уравнения образующих (ведь именно с их
помощью была решена рассмотренная
задача).

☻

Гиперболический
параболоид.
Его каноническое уравнение:
.
Для упрощения записи используемых
алгебраических выражений запишем
уравнение поверхности в виде:
.

,
(1)

где
коэффициенты могут быть записаны в виде
выражений:

=;
=; =.

.
Для этих значений получим систему
уравнений:

определитель
этой системы:
=0. (2)

Так как
система трёх линейных однородных
уравнений относительно неизвестных
,

имеет определитель, не равный нулю, то
её единственным решением является
нулевое решение:
=0,

=0,

=0.

Верно
и обратное. Если коэффициенты уравнения
(1)
=0,

=0,

=0,
то оно удовлетворяется любыми значениями

.
В нашем случае это значит, что прямая
линия

принадлежит поверхности:
.

Используя
условия:
=0,

=0,

=0,
как и в случае однополостного гиперболоида,
получаем: =
и =. (3)

Так как

имеет действительные значения только
в случае, если числа

и

имеют разные знаки, то есть:
,
то это имеет место только в случае
гиперболического параболоида.

Из формул
(3) видно, что через каждую точку поверхности
проходит две прямолинейные образующие,
принадлежащие к различным семействам.
Так как

постоянная величина, то в каждой точке
поверхности одна из прямолинейных
образующих параллельна плоскости
,
а другая плоскости
,
причём
>0,

<
0. Это значит, что образующие одного
семейства параллельны одной плоскости,
а образующие другого параллельны другой
плоскости.

Как и в
случае однополостного гиперболоида,
можно показать, что две прямолинейные
образующие одного семейства не принадлежат
одной плоскости, а две прямолинейные
образующие различных семейств
пересекаются. Нетрудно также получить
прямолинейные образующие, непосредственно
используя уравнение поверхности:

. (4)

Используя (4),
запишем уравнения прямых линий:

(5)

Прямолинейные
образующие

и

принадлежат поверхности гиперболического
параболоида.

☺☺

Пример 6–17:
Убедившись, что точка
(1,3,–1)
лежит на гиперболическом параболоиде:

,
составить уравнения его прямолинейных
образующих, проходящих через точку
.

Решение:

1). Запишем
уравнение гиперболического параболоида
в виде:
.

2). Запишем
уравнения прямолинейных образующих
для заданной поверхности:

3).
Проверка того, что точка

принадлежит поверхности, делается
устно!
Подставляя в полученные уравнения
координаты заданной точки
(1,3,–1),
получаем:

▫ для
образующей

соотношение;

▫ для
образующей

соотношение.

4).
Используя
полученные значения пар
и ,
запишем уравнения образующих:

и
:

5). Найдём
канонические уравнения образующей
:

▫ из
системы выделяем произвольную точку,
принадлежащую
:

(0,–1,1);

▫ используя
нормали:
=(2,
–1,
–1),

=(2,0,
1) плоскостей, вычисляем направляющий
вектор образующей:
=×=(1,4,–2).

▫ записываем
каноническое уравнение образующей:
.

6). Найдём
канонические уравнения образующей
:

▫ из
системы выделяем произвольную точку,
принадлежащую
:

(0,–9,
–3);

▫ используя
нормали:
=(2,
0,–1),

=(6,–1,
3) плоскостей, вычисляем направляющий
вектор образующей:
=×=(1,
12, 2).

▫ записываем
каноническое уравнение образующей:
.

Ответ: уравнения
образующих
:и:.

☻

Исследование
свойств поверхностей 2-го порядка полезно
не только потому, что эти поверхности
всегда привлекали изяществом своих
форм. Эти поверхности великолепны ещё
и своими механическими свойствами: их
прочность изумительна!

Вспомним
давнюю пасхальную шутку на Руси:
предлагают известному своей силой Ване
попытаться раздавить куриное яйцо (чаще
это пасхальное яйцо!). Силач, сцепив
пальцы рук, начинает сжимать его между
ладоней. Доверчивым силачам (и высокого
мнения о своей силе!) кажется, что работа
займёт несколько секунд!..

На самом деле,
редко кому удаётся подтвердить свою
безграничную силу! Обычно успех бывает
только в случае, если яйцо имеет дефекты.
Или силач хитрил: усилия прикладывались
несимметрично!

Вспомним
ещё изящную форму фюзеляжа самолёта,
корпус подводной лодки! У них внутри
спрятаны цилиндрические шпангоуты:
лёгкие, но очень прочные!

Соседние файлы в папке ЛА и АГ пособие

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 9 сентября 2017 года; проверки требуют 2 правки.

Через каждую точку однополостного гиперболоида проходят две различные прямые, целиком расположенные на этой поверхности.

Доказательство[править | править код]

Рассмотрим прямые $L_{1}$ и $L_{2}$ , заданные как линии пересечения плоскостей:

${displaystyle L_{1}:quad alpha left({x over a}-{z over c}right)=beta left(1-{y over b}right);;beta left({x over a}+{z over c}right)=alpha left(1+{y over b}right);;alpha ^{2}+beta ^{2}neq 0}$

${displaystyle L_{2}:quad gamma left({x over a}-{z over c}right)=delta left(1+{y over b}right);;delta left({x over a}+{z over c}right)=gamma left(1-{y over b}right);;gamma ^{2}+delta ^{2}neq 0}$

Прямые $L_{1}$ и $L_{2}$ целиком лежат на поверхности (чтобы убедиться в этом, достаточно почленно перемножить уравнения плоскостей). При этом через каждую точку ${displaystyle M_{0}(X_{0},Y_{0},Z_{0})}$ поверхности проходит единственная прямая из семейства $L_{1}$ и единственная прямая из семейства $L_{2}$ . Эти прямые (то есть пары чисел и ) находятся из однородных систем линейных алгебраических уравнений:

${displaystyle alpha ,beta :quad alpha left({X_{0} over a}-{Z_{0} over c}right)=beta left(1-{Y_{0} over b}right);;beta left({X_{0} over a}+{Z_{0} over c}right)=alpha left(1+{Y_{0} over b}right)}$

${displaystyle gamma ,delta :quad gamma left({X_{0} over a}-{Z_{0} over c}right)=delta left(1+{Y_{0} over b}right);;delta left({X_{0} over a}+{Z_{0} over c}right)=gamma left(1-{Y_{0} over b}right)}$

матрицы которых вырождены (то есть системы имеют нетривиальные решения) и имеют ранг, равный 1 (то есть все решения каждой из систем пропорциональны и определяют единственную прямую). Остается добавить, что прямые не совпадают (достаточно проверить неколлинеарность их направляющих векторов).

См. также[править | править код]

Гиперболоид

Источник

Прямолинейные образующие на поверхности однополостного гиперболоида

Уравнение однополостного гиперболоида имеет вид:

Разложим на множители:

Рассмотрим следующую систему линейных уравнений:

Каждое линейное уравнение задает в пространстве плоскость. Данные плоскости не параллельны, следовательно эта система из двух линейных уравнений задает прямую. Покажем, что эта прямая лежит на Однополостный гиперболоид. Действительно, если точка принадлежит этой прямой, то она удовлетворяет каждое из линейных уравнений системы, следовательно удовлетворяет произведения этих уравнений, то есть уравнению однополостного гиперболоида.

Это утверждение справедливо для любых 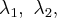которые не равны нулю одновременно. Итак, мы получили уравнение одной семьи прямолинейных образующих на Однополостный гиперболоид.

Уравнение второй семьи :

Теорема. Однополостный гиперболоид несет на себе две семьи прямолинейных образующих, имеющих следующие свойства:

· через любую точку проходит ровно одна прямая с каждой семьи ;

· любые две образующие из разных семей лежат в одной плоскости;

· любые две образующие с одной семьи является скрещивающимися;

· любые три образующие с одной семьи не параллельны одной плоскости.

Доказательство можно посмотреть в методичке.

Пример. Найти прямолинейные образующие поверхности которые проходят через точку

Запишем уравнение первой семьи прямолинейных образующих 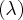и подставим координаты точки

Можем взять любые числа, удовлетворяющие этому равенства, например: 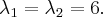Получаем уравнение прямолинейной образующей с первой семьи :

Уравнение второй семьи

Возьмем, 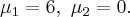получаем уравнение прямолинейной образующей с другойсемье :

121. Однополостные гиперболоиды и его прямолинейные образующие

Определение 1. Поверхность, которая в некоторой прямоугольной системе координат имеет уравнение

, (10)

Называется Однополостным гиперболоидом, A > 0, B > 0, C > 0. Числа A, B, C называются Полуосями однополостным гиперболоидом.

Исследуем поверхность однополостного гиперболоида по уравнению (10). Так как все переменные входят в уравнение (10) в четной степени, то вместе с точкой (X, Y, Z) однополостному гиперболоиду принадлежат все восемь точек (±X, ±Y, ±Z) (с произвольными комбинациями знаков). Таким образом, однополостной гиперболоид симметричен относительно, всех трех координатных плоскостей и начала координат. Он пересекает координатные оси OX, OY соответственно в точках (±A, 0, 0), (0, ±B, 0), которые называются Вершинами Однополостного гиперболоида.

Уравнение прямолинейных образующих однополостного гиперболоида через точку

Глава 46. Поверхности второго порядка

Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

(1).

Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c – сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.

Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (2)

. (3)

Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), – двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.

Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (4)

, (5)

где p и q – положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), – гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).

Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).

Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q . Пусть М – произвольная точка пространства, не лежащая на плоскости , – основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой в новое положение так, чтобы имело место равенство

и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.

Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).

ПРИМЕР. Доказать, что произвольный трехосный эллипсоид

может быть получен из сферы

в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия .

ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть – точка, в которую переходит при этом точка . Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то .

Таким образом, мы получаем искомые выражения:

, , (6)

, , (7)

Предположим, что M(x; y; z ) – произвольная точка сферы

Заменим здесь x, y, z их выражениями (7); получим

Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам

, , ;

тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.

Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.

имеет две системы прямолинейных образующих, которые определяются уравнениями:

, ;

, ,

где и – некоторые числа, не равные одновременно нулю. Гиперболический параболоид

также имеет две системы прямолинейных образующих, которые определяются уравнениями

, ;

, .

Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L – направляющей.

Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).

[spoiler title=”источники:”]

http://matica.org.ua/metodichki-i-knigi-po-matematike/algebra-i-geometriia-tolstikov-a-v/121-odnopolostnye-giperboloidy-i-ego-priamolineinye-obrazuiushchie

http://a-geometry.narod.ru/problems/problems_46.htm

[/spoiler]

Источник

Макеты страниц

Нас интересуют в этом параграфе лишь вещественные прямолинейные образующие только что рассмотренных поверхностей. Мы видели, что эллипсоиды, двуполостные гиперболоиды и эллиптические параболоиды их не имеют вовсе. Докажем, что через каждую точку однополостного гиперболоида и гиперболического параболоида проходят (по крайней мере) две (различные) вещественные прямолинейные образующие

1. Прямолинейные образующие однополостного гиперболоида. Рассмотрим сначала «правильный» однополостный гиперболоид, заданный уравнением

Как мы видели, он описывается гиперболой

при вращении пространства вокруг оси , в соответствии с чем его сечения плоскостями суть окружности

В частности, при получаем так называемую горловую окружность

Докажем, что через каждую точку горловой окружности проходят две прямолинейные образующие гиперболоида.

Повернув систему координат на надлежащий угол вокруг оси z, можно достигнуть того, что ось у пройдет именно через точку причем вид уравнения (1) при этом преобразовании не изменится

Итак, достаточно доказать наше утверждение для точки

Но плоскость

очевидно, пересекает гиперболоид (1) по паре прямых

Они лежат на нашем гиперболоиде (1), проходят через точку и, значит, являются искомыми образующими.

Докажем, что при вращении пространства вокруг оси z каждая из прямых (2), например прямая опишет весь гиперболоид (1).

Рис. 222.

Пусть — какая-нибудь точка прямой она лежит на окружиости, по которой гиперболоид пересекает горизонтальная, т. е. параллельная, плоскость плоскость, проходящая через точку при вращении пространства вокруг осн z точка описывает всю эту окружность, т. е., во-первых, не покидает гиперболоида, а во-вторых, попадает в любую его точку, лежащую на той же высоте (т. е. на той же горизонтальной плоскости), что и точка

Следовательно, при вращении вокруг оси z и вся прямая во-первых, в каждый момент времени всеми своими точками лежит на гиперболоиде (1), а во-вторых, в некоторый момент оказывается проходящей через любую точку М гиперболоида.

То же справедливо и для прямой прямая при вращении пространства вокруг оси z в некоторый момент также пройдет через любую точку М гиперболоида.

Все прямые, в которые при вращении пространства вокруг оси z, переходит каждая из двух прямых составляют два семейства прямолинейных образующих правильного однополостного гиперболоида (1) (рис. 222). Через каждую точку М гиперболоида проходит по одной из образующих каждого семейства.

Можно было бы чисто геометрически доказать, что любые две образующие, принадлежащие различным семействам, лежат в одной плоскости (следовательно, или пересекаются, или параллельны между собою), тогда как любые две образующие, принадлежащие одному и тому же семейству, скрещиваются.

Замечание. Аффинное преобразование пространства

переводит всякую прямую в прямую, а однополостный гиперболоид

в правильный однополостный гиперболоид

поэтому на любом однополостном гиперболоиде имеются два семейства прямолинейных образующих, каждое из которых покрывает его так, что через всякую точку гиперболоида проходит по одной образующей каждого семейства.

Мы сейчас дадим аналитическую трактовку того же вопроса. Пусть однополостный гиперболоид задан своим каноническим уравнением

Перепишем это уравнение в виде

или

Рассмотрим теперь пару вещественных чисел не равных одновременно нулю, и для каждой такой пары напишем систему уравнений

В частности, при получаем

а при

Для каждой пары чисел наши уравнения определяют пару плоскостей, как легко видеть, не параллельных (в широком смысле слова) и, следовательно, пересекающихся по прямой. Прямая эта целиком лежит на гиперболоиде (3). В самом каждая ее точка удовлетворяет обоим уравнениям (5), а следовательно, уравнению, полученному почленным перемножением уравнений (5), и, значит, уравнению (3). Случай, когда один из множителей равен нулю, исключения не представляет, так как точка , удовлетворяющая системе уравнений (6) или (7), удовлетворяет и уравнению (3).

Итак, мы получили семейство прямолинейных образующих гиперболоида (3). Семейство это назовем семейством I; оно, очевидно, зависит от одного параметра

Докажем, что через каждую точку гиперболоида (3) проходит одна – единственная прямая семейства I.

В самом деле, мы ищем прямую (5), проходящую через точку и удовлетворяющую уравнению (3), так что для определения отношения имеем уравнения (5), которые (после замены х, у, z на ) могут быть записаны в виде следующих пропорций:

причем выполнено тождество

получающееся, если подставить в (3) координаты точки . В силу тождества (40) мы можем для определения отношения воспользоваться любым из уравнений (), . Первое из них делается неопределенным, лишь если одновременно но в этом случае мы можем воспользоваться уравнением так как при во всяком случае значит, отношение определится из (52).

Итак, если задана точка то однозначно находится отношение определяющее прямую семейства I, проходящую через точку .

Отсюда следует, что никакие две прямые семейства I не пересекаются (так как если бы они пересекались в некоторой точке то эта точка била бы точкой гиперболоида (3), через которую проходят две прямые семейства I, а такой точки, по только что доказанному, не существует).

Легко проверить, что среди прямых семейства I нет двух параллельных.

Аналогично уравнениям (5) можно было бы для любой пары чисел , не равных одновременно нулю, написать систему уравнений

определяющую прямую, лежащую на гиперболоиде (3): каждая точка , удовлетворяющая двум уравнениям (5), удовлетворяет и уравнению, полученному от почленного перемножения этих уравнений, и, значит, удовлетворяет уравнению (3).

Итак, уравнения (5) также определяют семейство прямолинейных образующих однополостного гиперболоида (3), зависящее от одного параметра это семейство мы назовем семейством II.

Совершенно так же, как выше, мы убеждаемся в том, что через каждую точку гиперболоида (3) проходит одна – единственная образующая семейства II.

Наконец, совместное рассмотрение уравнений (5) и (5) (для данных ) позволяет установить, что каждая образующая семейства I пересекается с каждой образующей семейства II (или параллельна ей в узком смысле слова). Читателю предлагается (в виде задачи) провести относящиеся сюда рассуждения.

2. Прямолинейные образующие гиперболического параболоида. Начинаем с чисто геометрического рассмотрения вопроса. Пусть дан параболоид

Рассмотрим аффинное преобразование

Тогда уравнение параболоида примет вид

Рассматриваем сечения параболоида (9) плоскостями

параллельными плоскостям Подставляя (10) в (9), видим, что пересечение параболоида (9) с плоскостью (10) есть прямая

Аналогично пересечением параболоида (9) с плоскостью (11) есть прямая

Когда с пробегает все значения от до плоскость (10) (так же как и плоскость ) пройдет через все точки параболоида, который, таким образом, оказывается покрытым двумя семействами прямых I и II, определяемыми уравнениями (12) и (13) (рис. 223).

Рис. 223.

Через каждую точку М параболоида (9) проходит единственная плоскость вида (10) и единственная плоскость вида (11), а значит, и единственная прямолинейная образующая каждого из семейств I и II. При этом все образующие семейства I параллельны плоскости а все образующие семейства II параллельны плоскости .

Можно было бы получить тот же результат и для любого параболоида, заданного своим каноническим уравнением

(только вместо плоскостей были бы рассмотрены плоскости ).

Прямолинейные образующие гиперболического параболоида могут быть аналитически найдены способом разложения на множители, аналогичным тому, который мы применили в случае однонолостиого гиперболоида. Именно, перепишем каноническое уравнение

гиперболического параболоида в виде

и рассмотрим для каждой пары чисел , не равных иулю одновременно, уравнения двух плоскостей:

Эти плоскости пересекаются по прямой, целиком лежащей на параболоиде (8). Прямые (13), каждая из которых определена отношением образуют одно семейство прямолинейных образующих параболоида. Второе семейство получим, если рассмотрим (для каждой пары чисел , не ранных нулю одновременно) систему уравнений

Снова доказываем, что через каждую точку гиперболического параболоида (8) проходит по одной образующей каждого семейства, что две образующие, принадлежащие к разным семействам, пересекаются, а принадлежащие к одному и тому же семейству всегда скрещиваются.

Наконец, очевидно, что образующие семейства I, определяемого уравнениями (15), параллельны плоскости

а образующие семейства II, определяемого уравнениями (15), параллельны плоскости

Оглавление

ПРЕДИСЛОВИЕ
ГЛАВА I. КООРДИНАТЫ НА ПРЯМОЙ
§ 1. Отношение отрезков
§ 2. Направленные отрезки (векторы); их отношение
§ 3. Ось. Алгебраическое значение (координата) вектора на оси
§ 4. Сложение векторов на прямой
§ 5. Система координат на прямой
§ 6. Деление отрезка в данном отношении
§ 7. Пропорциональность пар чисел
§ 8. Бесконечно удаленная точка прямой
§ 9. Пропорциональность двух последовательностей, состоящих из и чисел
ГЛАВА II. ВЕКТОРЫ
§ 1. Равенство векторов. Свободный вектор
§ 2. Линейные операции над векторами (сложение и умножение на число)
§ 3. Проекции
§ 4. Коллинеарные и компланарные векторы; координаты вектора относительного данного базиса
§ 5. Линейная зависимость и независимость векторов
§ 6. Геометрический смысл линейной зависимости векторов
§ 7. Векторные многообразия
ГЛАВА III. АФФИННАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
§ 1. Определение аффинной системы координат
§ 2. Перенос начала координат
§ 3. Деление отрезка в данном отношении
ГЛАВА IV. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ. ПОЛЯРНЫЕ КООРДИНАТЫ
§ 1. Прямоугольная система координат на плоскости и в пространстве. Расстояние между двумя точками. Уравнение окружности и сферы
§ 2. Скалярное произведение векторов; угол между двумя векторами
§ 3. Угол от одного вектора до другого на плоскости
§ 4. Полярная система координат на плоскости
§ 5. Полярная система координат в пространстве
ГЛАВА V. ПРЯМАЯ ЛИНИЯ
§ 1. Направляющий вектор и угловой коэффициент прямой (в произвольной аффинной системе координат). Уравнение прямой
§ 2. Расположение двух прямых на плоскости
§ 3. Частные случаи общего уравнения прямой
§ 4. Векторная и параметрическая форма уравнения прямой. Уравнение прямой, проходящей через две заданные точки
§ 5. Задача: когда прямая Ax+By+C=0 на плоскости проходит через точку пересечения двух заданных прямых A1x+B1y+C1=0 и A2x+B2y+C2=0?
§ 6. Две полуплоскости, определяемые данной прямой на плоскости
§ 7. Прямая на плоскости в прямоугольной системе координат. Нормальное уравнение прямой на плоскости
§ 8. Расстояние от точки до прямой (на плоскости)
§ 9. Углы, образуемые двумя прямыми на плоскости
§ 10. Прямая в пространстве, снабженном прямоугольной системой координат
ГЛАВА VI. ПАРАБОЛА. ЭЛЛИПС. ГИПЕРБОЛА
§ 1. Парабола
§ 2. Определение и каноническое уравнение эллипса
§ 3. Параметрическая запись уравнения эллипса; построение эллипса по точкам. Эллипс как результат сжатия окружности к одному из ее диаметров
§ 4. Эллипс как проекция окружности и как сечение круглого цилиндра
§ 5. Определение гиперболы. Каноническое уравнение гиперболы
§ 6. Основной прямоугольник и асимптоты гиперболы
§ 7. Директрисы эллипса и гиперболы
§ 8. Фокальный параметр эллипса и гиперболы. Уравнение при вершине
§ 9. Уравнение эллипса, гиперболы и параболы в полярных координатах
ГЛАВА VII. ДЕТЕРМИНАНТЫ
§ 1. Плошадь ориентированного параллелограмма и треугольника
§ 2. Детерминант второго порядка. Матрицы
§ 4. Разложение детерминанта третьего порядка по элементам какой-либо строки. Приложение к системе трех уравнений с тремя неизвестными (правило Крамера)
§ 5. Системы трех уравнений с тремя неизвестными с детерминантом системы, равным нулю
§ 6. Арифметическое n-мерное векторное многообразие (пространство). Общее определение матрицы. Детерминанты любого порядка
§ 7. Разложение детерминанта n-го порядка по элементам данной строки (данного столбца)
§ 8. Правило Крамера для решений систем и уравнений с n неизвестными
§ 9. Общее определение миноров матрицы. Теорема Лапласа
§ 10. Умножение детерминантов
§ 11. Детерминант n-го порядка как линейная нечетная нормированная функция от n векторов
ГЛАВА VIII. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. МАТРИЦЫ
§ 1. Переход от одной аффинной системы координат к другой
§ 2. Перемножение матриц. Новое определение обратной матрицы
§ 3. Переход от одной прямоугольной системы координат к другой
§ 4. Действия над матрицами в общем случае
ГЛАВА IX. ПРЕОБРАЗОВАНИЕ КООРДИНАТ (ПРОДОЛЖЕНИЕ): ОРИЕНТАЦИЯ ПЛОСКОСТИ И ПРОСТРАНСТВА; УГЛЫ ЭЙЛЕРА; ОБЪЕМ ОРИЕНТИРОВАННОГО ПАРАЛЛЕЛЕПИПЕДА; ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
§ 1. Ориентация пространства (плоскости)
§ 2. Углы Эйлера
§ 3. Объем ориентированного параллелепипеда
§ 4. Векторное произведение двух векторов
ГЛАВА X. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
§ 1. Уравнения плоскости
§ 2. Множество решений системы двух однородных линейных уравнений с тремя неизвестными
§ 3. Взаимное расположение двух плоскостей
§ 4. Прямая как пересечение двух плоскостей
§ 5. Пучок плоскостей
§ 6. Взаимное расположение двух прямых в пространстве
§ 7. О двух полупространствах, определяемых данной плоскостью
§ 8. Плоскость в прямоугольной системе координат; нормальное уравнение плоскости; расстояние от точки до плоскости
§ 9. Угол между прямой и плоскостью; угол между двумя плоскостями
§ 10. Две задачи
ГЛАВА XI. ДВИЖЕНИЯ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
§ 1. Определение движений и аффинных преобразований
§ 2. Преобразование векторов при аффинном преобразовании плоскости и пространства. Основные свойства аффинных преобразований
§ 3. Аналитическое выражение аффинных преобразований
§ 4. Сохранение отношений площадей и объемов при аффинных преобразованиях
§ 5. Получение собственных аффинных преобразований посредством деформации тождественного преобразования. Следствия
§ 6. Движения как изометрические преобразования
§ 7. Преобразования подобия
§ 8. Классификация движений прямой и плоскости
ГЛАВА XII. ВЕКТОРНЫЕ ПРОСТРАНСТВА (МНОГООБРАЗИЯ) ЛЮБОГО КОНЕЧНОГО ЧИСЛА ИЗМЕРЕНИЙ. СИСТЕМЫ ЛИНЕЙНЫХ ОДНОРОДНЫХ УРАВНЕНИЙ
§ 1. Определение векторного пространства
§ 2. Размерность. Базис. Координаты
§ 3. Теорема об изоморфизме между любыми двумя векторными пространствами одной и той же конечной размерности n
§ 4. Подпространства векторного пространства. Дальнейшие теоремы о линейной зависимости векторов и о базисе векторного пространства
§ 5. Алгебраическая (в частности, прямая) сумма подпространств
§ 6. Линейные отображения векторных пространств
§ 7. Теорема о ранге матрицы
§ 8. Системы линейных однородных уравнения
ГЛАВА XIII. ЛИНЕЙНЫЕ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ НА ВЕКТОРНЫХ ПРОСТРАНСТВАХ
§ 1. Линейные функции
§ 2. Билинейные функции и билинейные формы
§ 3. Матрица билинейной и квадратичной формы и ее преобразование при переходе к новому базису (при преобразовании переменных)
§ 4. Ранг билинейной и квадратичной формы (билинейной и квадратичной функции)
§ 5. Существование канонического базиса для всякой квадратичной и всякой билинейной функции («приведение квадратичных форм к каноническому виду»)
ГЛАВА XIV. ТОЧЕЧНО-ВЕКТОРНОЕ АФФИННОЕ n-МЕРНОЕ ПРОСТРАНСТВО
§ 1. Определение n-мерного аффинного пространства
§ 2. Системы координат. Арифметическое пространство. Изоморфизм всех n-мерных пространств между собою
§ 3. r-мерные плоскости n-мерного аффинного пространства; r-мерные параллелепипеды
§ 4. Геометрически независимые системы точек. Барицентрические координаты. Симплексы
§ 5. Системы линейных уравнений
§ 6. Аффинные преобразования n-мерного аффинного пространства
ГЛАВА XV. АЛГЕБРАИЧЕСКИЕ ЛИНИИ И ПОВЕРХНОСТИ. КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
§ 1. Определение алгебраических линий и поверхностей
§ 2. Преобразование многочлена второй степени при преобразовании координат
§ 3. Аффинная эквивалентность линий и поверхностей
§ 4. Комплексная плоскость
§ 5. Прямая линия на комплексной плоскости
§ 6. Замечание о действительных и мнимых линиях
§ 7. Комплексное пространство
§ 8. Распадающиеся линии и поверхности. Цилиндрические и конические поверхности. Поверхности вращения
§ 9. Несколько заключительных замечаний о линиях и поверхностях
ГЛАВА XVI. Различные виды кривых второго порядка
§ 1. О линиях, определяемых уравнениями второй степени с двумя неизвестными
§ 2. Инварианты многочлена второй степени
§ 3. Центральный случай
§ 4. Параболический случай
§ 5. Аффинная классификация кривых второго порядка
§ 6. Несколько заключительных замечаний
ГЛАВА XVII. ОБЩАЯ ТЕОРИЯ КРИВЫХ ВТОРОГО ПОРЯДКА
§ 1. Пересечение алгебраической кривой с прямой. Асимптотические направления и асимптоты алгебраической кривой
§ 2. Теорема единственности для кривых второго порядка. Пучок кривых второго порядка
§ 3. Асимптотические направления кривых второго порядка
§ 4. Пересечение кривой второго порядка с прямой иеасимптотического направления. Касательные
§ 5. Пересечение кривой второго порядка с прямой асимптотического направления. Геометрическая характеристика асимптотических и неасимптотических направлений
§ 6. Центр кривой второго порядка
§ 7. Диаметры кривой второго порядка
§ 8. Взаимно сопряженные векторы (направления). Диаметры и касательные
§ 9. Вид уравнения кривой, если оси координат имеют сопряженные направления
§ 10. Второе доказательство теоремы единственности. О полноте системы ортогональных инвариантов
§ 11. Оси симметрии и главные направления кривой второго порядка
§ 12. Основная теорема об аффинных преобразованиях
ГЛАВА XVIII. КРАТКОЕ ОПИСАНИЕ РАЗЛИЧНЫХ ВИДОВ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
§ 1. Распадающиеся поверхности
§ 2. Цилиндрические поверхности
§ 3. Конусы второго порядка
§ 4. Эллипсоиды и гиперболоиды
§ 5. Параболоиды
§ 6. Прямолинейные образующие
ГЛАВА XIX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. I (ПЕРЕСЕЧЕНИЕ С ПЛОСКОСТЬЮ И С ПРЯМОЙ; АСИМПТОТИЧЕСКИЕ НАПРАВЛЕНИЯ; КАСАТЕЛЬНАЯ ПЛОСКОСТЬ; ЦЕНТР)
§ 1. Ранг и детерминант малой и большой матрицы многочлена второй степени
§ 2. Пересечение поверхности второго порядка с плоскостью
§ 3. Пересечение поверхности второго порядка с прямой. Асимптотические направления. Касательные прямые и касательная плоскость. Особые точки поверхности второго порядка
§ 4. Асимптотические направления, конус асимптотических направлений, прямолинейные образующие поверхностей второго порядка
§ 5. Центр поверхности второго порядка
ГЛАВА XX. ОБЩАЯ ТЕОРИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА. II (ДИАМЕТРАЛЬНЫЕ ПЛОСКОСТИ; ОСОБЫЕ И ГЛАВНЫЕ НАПРАВЛЕНИЯ; АФФИННАЯ КЛАССИФИКАЦИЯ)
§ 1. Диаметральные плоскости. Особые направления
§ 2. Диаметральные плоскости поверхностей различных видов
§ 3. Сопряженные направления
§ 4. Уравнение поверхности второго порядка относительно координатной системы с сопряженными направлениями осей
§ 5. Теорема единственности
§ 6. Главные направления
§ 7. Приведение к каноническому виду уравнения поверхности второго порядка
§ 8. Аффинная классификация поверхностей второго порядка
ГЛАВА XXI. ПРОЕКТИВНАЯ ПЛОСКОСТЬ
§ 1. Перспективное соответствие между плоскостью и связкой
§ 2. Однородные координаты точек на плоскости и лучел в связке
§ 3. Координаты прямой; арифметическая проективная плоскость; общее определение проективной плоскости
§ 4. Принцип двойственности для проективной плоскости
§ 5. Проективная система координат в связке и на проективной плоскости
§ 6. Проективные преобразования и отображения проективной плоскости
§ 7. Проективные координаты на прямой. Проективные отображения прямой
§ 8. Двойное отношение
ГЛАВА XXII. КРИВЫЕ ВТОРОГО ПОРЯДКА НА ПРОЕКТИВНОЙ ПЛОСКОСТИ
§ 1. Определение. Теорема единственности
§ 2. Пересечение кривой второго порядка с прямой. Касательные; асимптоты
§ 3. Пучок кривых второго порядка. Второе доказательство теоремы единственности. Теорема Паскаля. Теорема Штейнера
§ 4. Поляры и полюсы
§ 5. Коррелятивное, в частности полярное, соответствие. Тангенциальное уравнение кривой
§ 6. Диаметры как поляры несобственных точек
§ 7. Автополярный треугольник
§ 8. Проективная классификация кривых второго порядка
ГЛАВА XXIII. НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ ПРОЕКТИВНОГО ПРОСТРАНСТВА
§ 1. Проективное пространство; его плоскости и прямые
§ 2. Проективные координаты. Проективные преобразования.
§ 3. Понятие об n-мерном проективном пространстве
§ 4. Поверхности второго порядка в проективном пространстве. Теорема единственности
§ 5. Пересечение поверхности второго порядка с плоскостью и с прямой. Касательные прямые. Касательная плоскость. Прямолинейные образующие
§ 6. Полюсы и полярные плоскости
§ 7. Проективная классификация поверхностей второго порядка
§ 8. Распределение по проективным классам поверхностей различных аффинных классов. Проективно-аффинная классификация поверхностей второго порядка
ГЛАВА XXIV. ЕВКЛИДОВО n-МЕРНОЕ ПРОСТРАНСТВО
§ 1. Введение. Ортогональные матрицы
§ 2. Положительно определенные симметричные билинейные функции в векторном пространстве
§ 3. Определение евклидовых пространств и простейших относящихся к ним понятий
§ 4. Неравенство Коши—Буняковского и его следствия. Углы
§ 5. Подпространства евклидовых пространств. Ортогональное дополнение к данному подпространству
ГЛАВА XXV. ЛИНЕЙНЫЕ ОПЕРАТОРЫ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФУНКЦИИ В ЕВКЛИДОВЫХ ПРОСТРАНСТВАХ. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
§ 1. Инвариантные подпространства и собственные векторы линейного оператора в любом векторном пространстве
§ 2. Ортогональные преобразования n-мерного евклидова пространства
§ 3. Движения трехмерного евклидова пространства
§ 4. Преобразования подобия. Дальнейшие проблемы
§ 5. Самосопряженные операторы
§ 6. Теорема о структуре произвольного линейного преобразования евклидова пространства
§ 7. Билинейные и квадратичные формы в евклидовых пространствах
§ 8. (n-1)-мерные многообразия (поверхности) второго поряд] в -мерном аффинном и евклидовом пространствах
ПРИБАВЛЕНИЕ. ПЕРЕСТАНОВКИ, МНОЖЕСТВА И ИХ ОТОБРАЖЕНИЯ; ГРУППЫ
§ 1. Перестановки
§ 2. Множества
§ 3. Отображения или функции
§ 4. Разбиение множества на подмножества. Отношение эквивалентности
§ 5. Определение группы
§ 6. Простейшие теоремы о группах
§ 7. Эквивалентность подмножеств данного множества по отношению к дайной группе его преобразований
ЗАДАЧИ
Задачи к главе IV
Задачи к главе V
Задачи к главе VI
Задачи к главе VIII
Задачи к главе IX
Задачи к главе X
Задачи к главе XI
Задачи к главе XII
Задачи к главе XIII
Задачи к главе XIV
Задачи к главе XV
Задачи к главам XVI и XVII
Задачи к главе XVIII
Задачи к главам XIX и XX
Задачи к главе XXI
Задачи к главе XXII

Источник

Определение 1. Поверхность, которая в некоторой прямоугольной системе координат имеет уравнение

, (10)

Исследуем методом сечений поверхность однополостного гиперболоида, проведя его сечения плоскостями, параллельными координатным. Пересекая однополостный гиперболоид плоскостями Z = H (-¥ < H < +¥), параллельными плоскости OXy, получим в сечении эллипсы.

Эллипсы, лежащие в сечениях, наименьшие полуоси имеют при H = 0. Это сечение называется Горловиной однополостного гиперболоида.

Пересекаем однополостный гиперболоид плоскостями X = H (-¥ < H < +¥), параллельными плоскостям OyZ и OXz Получим в сечении гиперболы. стями, параллельными плоскости OXz.

Уравнение однополостного гиперболоида (1) можно записать в виде

. (12)

Составим две системы уравнений первой степени

, (13)

Где M и N произвольные действительные параметры, которые одновременно не равны нулю.

Для любых M и N одновременно не равных нулю каждая из систем (13) определяет прямую и эти прямые пересекаются (проверить это). Если мы перемножим уравнения в каждой из систем (13) почленно и сократим, полученное равенство, на Mn, то получим уравнение (12). Поэтому любая точка (X, Y, Z) , принадлежащая прямым (13), находится на поверхности (12).

Прямые, принадлежащие каждому из двух семейств прямых, определяемых системами (13) называются Прямолинейными образующими однополостного гиперболоида (см рис. 10). При нахождении прямолинейных образующих можно один из двух параметров M или N в системах (13) полагать равным единице.

< Предыдущая		Следующая >

Источник

Доказательство[править | править код]

См. также[править | править код]

Прямолинейные образующие на поверхности однополостного гиперболоида

121. Однополостные гиперболоиды и его прямолинейные образующие

Уравнение прямолинейных образующих однополостного гиперболоида через точку

Глава 46. Поверхности второго порядка

Вам также может понравиться

Как найти питомник в москве

Как найти периметр прямоугольника параллелограмма

Как найти психолога практика

Добавить комментарий Отменить ответ