Как найти прямоугольные координаты вектора - Сайт, где вы сможете решить свои вопросы

Определение 3.4 Проекцией вектора
на осьназывается число, равное длине вектора(рис. 3.9), взятое со знаком «плюс», если
направление векторасовпадает с направлением оси и со знаком
«минус» в противном случае.

Точки
– это точки пересечения осис плоскостями, проходящими через точкии,
перпендикулярно оси.
Обозначение.

Основные свойства проекции:

,
где– угол между вектороми
осью;
;
;
.

Рассмотрим в пространстве прямоугольную
систему координат
.
Построим на координатных осяхиединичные векторы, обозначаемыесоответственно (рис. 3.10).

Единичные векторы
,
имеющие направление положительных
координатных полуосей, называютсяортами координатныхосей.

Произвольный вектор
пространства можно единственным образом
представить в виде линейной комбинации
ортов координатных осей. Для разложения
векторасовместим его начало с началом координат
(рис. 3.10). Из концавекторапроведем плоскости, параллельные
координатным плоскостям. Обозначим,иточки
пересечения этих плоскостей с осямисоответственно. Тогда

,,.

а значит, существуют числа
,
такие что

,,и

,,.

Следовательно, вектор
можно представить в виде:

.
(3.5)

Формула (3.5) называется разложением
вектора
по ортам координатных осей или по базису.
Коэффициентылинейной комбинации (3.5) называют
прямоугольными координатами вектора,
т.е. координаты вектора есть его проекции
на соответствующие координатные оси.

Векторное равенство (3.5) записывают в
виде

(3.6)

Имеет место аналогичное разложение
вектора
по
базисуна плоскости (рис. 3.11).

.
(3.7)

Длина вектора
с координатамиопределяется по формуле

.
(3.8)

Для плоского вектора

.
(3.9)

Направление вектора
в пространстве и на плоскости можно
определить с помощью косинусов углов,
которые образует вектор с осями координат.
Их называютнаправляющими косинусамивектора. Обозначим– углы, которые составляет векторс осямисоответственно, тогда

,,.
(3.10)

Справедливо равенство

.
(3.11)

При выполнении линейных операций над
векторами тем же операциям подвергнутся
и их проекции на координатные оси.

Пусть даны два вектора
и.

При сложении векторов их одноименные
координаты складываются, при вычитании
– вычитаются, при умножении на число –
умножаются на это число:

,
(3.12)

Векторы
иравнытогда и только тогда, когда
равны их соответствующие координаты:

,,.
(3.13)

Векторы
иколлинеарны
тогда и только тогда, когда их
соответствующие координаты пропорциональны,
т.е.

.
(3.14)

Радиус-вектором точки
называется вектор(рис. 3.12), начало которого совпадает с
началом координат, а конец с точкой.

Координаты точки – это координаты её
радиус-вектора
.

Для вектора
,
заданного координатами точкии,
его координаты определяются из векторного
равенства

(3.15)

Здесь
и– радиус-векторы точеки,
т.е. координаты вектора
равны разностям одноименных координат
конечнойи начальнойточек этого вектора.

Соседние файлы в папке Теория ЛА (первый семестр)

#
25.03.2016583.68 Кб5~WRL3348.tmp
#
#
#
#
#

Источник

Прямоуго́льная (Декартова) систе́ма координа́т — прямолинейная система координат с взаимно перпендикулярными координатными осями на плоскости или в пространстве. Часто используемая система координат. Просто обобщается для пространств любой размерности.

Связанные термины: декартовой обычно называют прямоугольную систему координат с одинаковыми масштабами по осям (названной так по имени Рене Декарта), а общей декартовой системой координат называют аффинную систему координат (не обязательно прямоугольную).

История[править | править код]

Впервые прямоугольную систему координат ввёл Рене Декарт в своей работе «Геометрия» в 1637 году. Он применял координаты к исследованию многих геометрических вопросов. Поэтому прямоугольную систему координат называют также — Декартова система координат (хотя современный термин не во всех деталях соответствует тому, что использовал сам Декарт^[1]). Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти^[2]. Декарт и Ферма применяли координатный метод только на плоскости. Французский священнослужитель Николай Орем использовал конструкции, подобные декартовым координатам, задолго до времён Декарта и Ферма^[3].

Развитие системы декартовых координат далее сыграло важную роль в развитии диифференциального и интегрального исчисления Исааком Ньютоном и Лейбницем^[4]. Двухкоординатное описание плоскости позднее было обобщено в понятие векторных пространств^[5].

Координаты в трёхмерном пространстве впервые применил Леонард Эйлер в XVIII веке. Использование единичных векторов впервые применил, по-видимому, Гамильтон и Максвелл.

Прямоугольная система координат на плоскости[править | править код]

Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X'X и Y'Y . Оси координат пересекаются в точке , которая называется началом координат, на каждой оси выбрано положительное направление.

Положение точки на плоскости определяется двумя координатами и . Координата равна длине отрезка , координата — длине отрезка в выбранных единицах измерения. Отрезки и определяются линиями, проведёнными из точки параллельно осям Y'Y и X'X соответственно.

При этом координате приписывается знак минус, если точка лежит на луче OX' (а не на луче , как на рисунке). Координате приписывается знак минус, если точка лежит на луче OY' . Таким образом, OX' и OY' являются отрицательными направлениями осей координат (каждая ось координат рассматривается как числовая ось).

Ось X'X называется осью абсцисс (лат. abscissus — букв. «отрезанный, отделённый»^[6]), а ось Y'Y — осью ординат (лат. ordinatus — букв. «упорядоченный, установленный в определённом порядке»^[6]). Координата называется абсцисса точки , координата — ордината точки .

Символически это записывают так:

или:

или указывают принадлежность координат конкретной точке с помощью индекса:

и т. д.

Прямоугольная система координат в пространстве[править | править код]

Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трёхмерное пространство, о более многомерных пространствах — см. ниже) образуется тремя взаимно перпендикулярными осями координат , и . Оси координат пересекаются в точке , которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно^[7]) одинаковы для всех осей. — ось абсцисс, — ось ординат, — ось аппликат.

Положение точки в пространстве определяется тремя координатами , и . Координата равна длине отрезка , координата — длине отрезка , координата — длине отрезка в выбранных единицах измерения. Отрезки , и определяются плоскостями, проведёнными из точки параллельно плоскостям YOZ , XOZ и XOY соответственно.

Координата

называется абсциссой точки

координата

— ординатой точки

координата

— аппликата (лат. applicata — прилегающая)^[8] точки

Символически это записывают так:

или

или привязывают запись координат к конкретной точке с помощью индекса:

и т. п.

Каждая ось рассматривается как числовая прямая, то есть имеет положительное направление, а точкам, лежащим на отрицательном луче приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка лежала не как на рисунке — на луче , а на его продолжении в обратную сторону от точки (на отрицательной части оси ), то абсцисса точки была бы отрицательной (минус расстоянию ). Аналогично и для двух других осей.

Все прямоугольные системы координат в трехмерном пространстве делятся на два класса — правые (также используются термины положительные, стандартные) и левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении ещё и располагают их, если можно, в одном из нескольких обычных (традиционных) положений. (На рис. 2 изображена правая координатная система). Правую и левую системы координат невозможно поворотами^[9] совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат, можно, используя правило правой руки, правило винта и т. п. (положительное направление осей выбирают так, чтобы при повороте оси против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси , если этот поворот наблюдать со стороны положительного направления оси ).

Любая из восьми областей, на которые пространство делится тремя взаимно перпендикулярными координатными плоскостями, называется октантом.

Прямоугольная система координат в многомерном пространстве[править | править код]

Прямоугольная система координат может быть использована и в пространстве любой конечной размерности аналогично тому, как это делается для трехмерного пространства. Количество координатных осей при этом равно размерности пространства (в этом параграфе будем обозначать её ).

Для обозначения координат обычно^[10] применяют не разные буквы, а одну и ту же букву с числовым индексом. Чаще всего это:

Для обозначения произвольной -й координаты из этого набора используют буквенный индекс:

$x_{i},$

а нередко обозначение $x_{i},$ используют и для обозначения всего набора, подразумевая, что индекс пробегает весь набор значений: .

В любой размерности пространства прямоугольные координатные системы делятся на два класса, правые и левые (или положительные и отрицательные). Для многомерных пространств какую-то одну из координатных систем произвольно (условно) называют правой, а остальные оказываются правыми или левыми в зависимости от того, той же они ориентации или нет^[11].

Обобщение понятий двумерного квадранта и трёхмерного октанта для -мерного евклидова пространства — ортант или гипероктант.

Прямоугольные координаты вектора[править | править код]

Для определения прямоугольных координат вектора (применимых для представления векторов любой размерности) можно исходить из того, что координаты вектора (направленного отрезка), начало которого находится в начале координат, совпадают с координатами его конца^[12].

Для векторов (направленных отрезков), начало которых не совпадает с началом координат, прямоугольные координаты можно определить одним из двух способов:

Вектор можно перенести так, чтобы его начало совпало с началом координат). Тогда его координаты определяются способом, описанным в начале параграфа: координаты вектора, перенесённого так, что его начало совпадает с началом координат, — это координаты его конца.
Вместо этого можно просто вычесть из координат конца вектора (направленного отрезка) координаты его начала.

Для прямоугольных координат понятие координаты вектора совпадает с понятием ортогональной проекции вектора на направление соответствующей координатной оси.

В прямоугольных координатах очень просто записываются все операции над векторами:

Сложение и умножение на скаляр:

mathbf a + mathbf b = (a_1 + b_1, a_2 + b_2, a_3 + b_3, dots, a_n + b_n)

или:

c mathbf a = (c a_1, c a_2, c a_3, dots, c a_n)

или:

а отсюда и вычитание и деление на скаляр:

или:

$frac{mathbf a}{lambda} = Big(frac{a_1}{lambda}, frac{a_2}{lambda}, frac{a_3}{lambda}, dots, frac{a_n}{lambda}Big)$

или:

$Big(frac{mathbf a}{lambda}Big)_i = frac{a_i}{lambda}.$

(Это верно для любой размерности n и даже, наравне с прямоугольными, для косоугольных координат).

Скалярное произведение:

mathbf a cdot mathbf b = a_1 b_1 + a_2 b_2 + a_3 b_3 + dots + a_n b_n

или:

$mathbf a cdot mathbf b = sumlimits_{i=1}^n a_i b_i,$

(Это справедливо только в прямоугольных координатах с единичным масштабом по всем осям).

Через скалярное произведение можно вычислить длину вектора

и угол между векторами:

$angle{(mathbf a, mathbf b)} = mathrm{arccos}frac{mathbf acdotmathbf b}{|mathbf a|cdot|mathbf b|}$

Внешнее произведение:

$(mathbf a and mathbf b)_{ij} = a_i b_j - a_j b_i$

для любой размерности пространства,

Векторное произведение (только для трехмерного же пространства, на котором оно и определено):

(mathbf a times mathbf b)_x = a_y b_z - a_z b_y

(mathbf a times mathbf b)_y = a_z b_x - a_x b_z

(mathbf a times mathbf b)_z = a_x b_y - a_y b_x

Это позволяет свести все операции над векторами к достаточно простым операциям над числами.

Орты[править | править код]

Прямоугольная система координат^[13] (любой размерности) также описывается^[14] набором ортов (единичных векторов), сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу. Такие орты образуют ортонормированныйбазис, притом^[15].

В трёхмерном случае такие орты обычно обозначаются:

или

$mathbf{e}_x$

, $mathbf{e}_y$

и $mathbf{e}_z$

Могут также применяться обозначения со стрелками ( vec{i} , vec{j} и vec{k} или $vec{e}_x$ , $vec{e}_y$ и $vec{e}_z$ ) или другие в соответствии с обычным способом обозначения векторов в той или иной литературе.

При этом в случае правой системы координат действительны следующие формулы с векторными произведениями ортов:

Для размерностей пространства более 3, (или для общего случая, когда размерность может быть любой) обычно для ортов применяют вместо этого обозначения с числовыми индексами, достаточно часто^[16] это:

$mathbf{e}_1, mathbf{e}_2, mathbf{e}_3,dots mathbf{e}_n,$

где n — размерность пространства.

Вектор любой размерности раскладывается по базису (координаты служат коэффициентами разложения):

mathbf a = a_1mathbf e_1 + a_2mathbf e_2 + a_3mathbf e_3 + dots + a_nmathbf e_n

или:

$mathbf a = sumlimits_{i=1}^n a_imathbf e_i,$

а для ортонормированного базиса координаты ещё и очень легко найти через скалярные произведения с ортами:

См. также[править | править код]

Аффинные координаты
Проективные координаты

Примечания[править | править код]

↑ Декарт пользовался не двумя осями, а одной, на которой откладывались абсциссы; ординаты определялись как расстояние от точек плоскости до оси абсцисс; эти расстояния Декарт отсчитывал по любому заранее выбранному направлению, а не обязательно перпендикулярно.
Как абсциссы, так и ординаты у Декарта были всегда величинами положительными независимо от направления соответствующих отрезков. Различие направлений на осях знаками «+» и «‒» было введено лишь его учениками.

Источник: Выгодский М. Я. Раздел VI. Функции, графики (§ 6. Координаты) // Справочник по элементарной математике / сост. М. Я. Выгодский, под ред. Н. А. Шармай. — М.: АСТ; Астрель, 2015. — С. 461. — 509 с. — 1500 экз. — ISBN 978-5-17-084803-4, ББК 22.1я2, УДК 51(03). — ISBN 978-5-271-46916-9.
↑ Bix, Robert A.; D’Souza, Harry J. Analytic geometry. Encyclopædia Britannica. Дата обращения: 6 августа 2017. Архивировано 6 августа 2017 года.
↑ Kent, Alexander J. The Routledge Handbook of Mapping and Cartography : [англ.] / Alexander J. Kent, Peter Vujakovic. — Routledge, 2017-10-04. — ISBN 9781317568216. Архивная копия от 24 ноября 2021 на Wayback Machine
↑ A Tour of the Calculus, David Berlinski
↑ Axler, Sheldon. Linear Algebra Done Right – Springer. — 2015. — P. 1. — ISBN 978-3-319-11079-0. — doi:10.1007/978-3-319-11080-6.
↑ ¹ ² Словарь иностранных слов. — М.: Рус. яз., 1989. — 624 с. ISBN 5-200-00408-8
↑ Иногда это просто принципиально невозможно, если по осям откладываются величины разной физической размерности; впрочем, с геометрической точки зрения это замечание не слишком существенно, так как можно тогда считать масштабы по осям равными условно (например масштабы так, чтобы единицы совпадали при изображая на геометрической плоскости).
↑ Словарь иностранных слов. — М.: «Русский язык», 1989. — 624 с. ISBN 5-200-00408-8
↑ Можно превратить правую координатную систему в левую и наоборот с помощью зеркального отражения.
↑ Но не обязательно: вопрос обозначений в конечном итоге определяется конкретным приложением.
↑ Это можно выяснить, исходя из того, можно ли какими-то вращениями (и переносами, если не совпадают начала координат) совместить данную координатную систему с той, ориентация которой правая по определению. Если да, то данная система считается правой, если нет, то левой. Ещё проще технически это выяснить через знак определителя матрицы преобразования от правого базиса к данному.
↑ Конец направленного отрезка — точка; прямоугольные координаты точки рассмотрены в статье выше.
↑ В этом параграфе будем подразумевать обычную декартову систему координат, то есть прямоугольную систему координат с одинаковым масштабом по всем осям; рассмотрение систем координат с разным масштабом по разным осям внесло бы здесь неоправданные формальные усложнения при довольно малом выигрыше содержательном отношении.
↑ Это описание очевидно полностью эквивалентно обычному заданию осей координат, надо только ещё задать начало координат (последнее нередко очевидно по умолчанию).
↑ При отказе от условия равномасштабности координатных осей — просто ортогональный базис.
↑ Впрочем, вместо буквы e нередко могут быть использованы и другие буквы. Как правило, это явно оговорено.

Ссылки[править | править код]

В. И. Гервидс. Модель декартовой системы координат (flash). НИЯУ МИФИ (10 марта 2011). Дата обращения: 3 мая 2011.

Источник

Марина Николаевна Ковальчук

Эксперт по предмету «Геометрия»

Задать вопрос автору статьи

Прямоугольная система координат

Чтобы определить понятие координат точек, нам необходимо ввести систему координат, в которой мы и будем определять ее координаты. Одна и та же точка в разных системах координат может иметь различные координаты. Здесь мы будем рассматривать прямоугольную систему координат в пространстве.

Возьмем в пространстве точку $O$ и введем для нее координаты $(0,0,0)$. Назовем ее началом системы координат. Проведем через нее три взаимно перпендикулярные оси $Ox$, $Oy$ и $Oz$, как на рисунке 1. Эти оси будут называться осями абсцисс, ординат и аппликат, соответственно. Осталось только ввести масштаб на осях (единичный отрезок) – прямоугольная система координат в пространстве готова (рис. 1)

Рисунок 1. Прямоугольная система координат в пространстве. Автор24 — интернет-биржа студенческих работ

Координаты точки

Теперь разберем, как определяют в такой системе координаты любой точки. Возьмем произвольную точку $M$ (рис. 2).

Рисунок 2. Произвольная точка. Автор24 — интернет-биржа студенческих работ

Построим на координатных осях прямоугольный параллелепипед, так, что точки $O$ и $M$ противоположные его вершины (рис. 3).

Рисунок 3. Построение прямоугольного параллелепипеда. Автор24 — интернет-биржа студенческих работ

«Координаты точки и координаты вектора. Как найти координаты вектора» 👇

Тогда точка $M$ будет иметь координаты $(X,Y,Z)$, где $X$ – значение на числовой оси $Ox$, $Y$ – значение на числовой оси $Oy$, а $Z$ – значение на числовой оси $Oz$.

Пример 1

Необходимо найти решение следующей задачи: написать координаты вершин параллелепипеда, изображенного на рисунке 4.

Рисунок 4. Параллелепипед. Автор24 — интернет-биржа студенческих работ

Решение.

Точка $O$ начало координат, следовательно, $O=(0,0,0)$.

Точки $Q$, $N$ и $R$ лежат на осях $Ox$, $Oz$ и $Oy$, соответственно, значит

$Q=(2,0,0)$, $N=(0,0,1.5)$, $R=(0,2.5,0)$

Точки $S$, $L$ и $M$ лежат в плоскостях $Oxz$, $Oxy$ и $Oyz$, соответственно, значит

$S=(2,0,1.5)$, $L=(2,2.5,0)$, $R=(0,2.5,1.5)$

Точка $P$ имеет координаты $P=(2,2.5,1.5)$

Координаты вектора по двум точкам и формула нахождения

Чтобы узнать, как найти вектор по координатам двух точек, необходимо рассмотреть введенную нами ранее систему координат. В ней от точки $O$ по направлению оси $Ox$ отложим единичный вектор $overline{i}$, по направлению оси $Oy$ – единичный вектор $overline{j}$, а единичный вектор $overline{k}$ нужно направлять по оси $Oz$.

Для того чтобы ввести понятие координат вектора, введем следующую теорему (здесь ее доказательство мы рассматривать не будем).

Теорема 1

Произвольный вектор в пространстве может быть разложен по трем любым векторам, которые не лежат в одной плоскости, причем коэффициенты в таком разложении будут единственным образом определены.

Математически это выглядит следующим образом:

$overline{δ}=moverline{α}+noverline{β}+loverline{γ}$

Так как векторы $overline{i}$, $overline{j}$ и $overline{k}$ построены на координатных осях прямоугольной системы координат, то они, очевидно, не будут принадлежать одной плоскости. Значит любой вектор $overline{δ}$ в этой системе координат, по теореме 1, может принимать следующий вид

$overline{δ}=moverline{i}+noverline{j}+loverline{k}$ (1)

где $n,m,l∈R$.

Определение 1

Три вектора $overline{i}$, $overline{j}$ и $overline{k}$ будут называться координатными векторами.

Определение 2

Коэффициенты перед векторами $overline{i}$, $overline{j}$ и $overline{k}$ в разложении (1) будут называться координатами этого вектора в заданной нами системе координат, то есть

$overline{δ}=(m,n,l)$

Линейные операции над векторами

Теорема 2

Теорема о сумме: Координаты суммы любого числа векторов определяются суммой их соответствующих координат.

Доказательство.

Будем доказывать эту теорему для 2-х векторов. Для 3-х и более векторов доказательство строится аналогичным образом. Пусть $overline{α}=(α_1,α_2,α_3)$, $overline{β}=(β_1,β_2 ,β_3)$.

Эти вектора можно записать следующим образом

$overline{α}=α_1overline{i}+ α_2overline{j}+α_3overline{k}$, $overline{β}=β_1overline{i}+ β_2overline{j}+β_3overline{k}$

$overline{α}+overline{β}=α_1overline{i}+α_2overline{j}+α_3overline{k}+β_1overline{i}+ β_2overline{j}+β_3overline{k}=(α_1+β_1 )overline{i}+(α_2+β_2 )overline{j}+(α_3+β_3)overline{k}$

Следовательно

$overline{α}+overline{β}=(α_1+β_1,α_2+β_2,α_3+β_3)$

Теорема доказана.

Замечание 1

Замечание: Аналогично, находится решение разности нескольких векторов.

Теорема 3

Теорема о произведении на число: Координаты произведения произвольного вектора на действительное число определяется произведением координат на это число.

Доказательство.

Возьмем $overline{α}=(α_1,α_2,α_3)$, тогда $overline{α}=α_1overline{i}+α_2overline{j}+α_3overline{k}$, а

$loverline{α}=l(α_1overline{i}+ α_2overline{j}+α_3overline{k})=lα_1overline{i}+ lα_2overline{j}+lα_3overline{k}$

Значит

$koverline{α}=(lα_1,lα_2,lα_3)$

Теорема доказана.

Пример 2

Пусть $overline{α}=(3,0,4)$, $overline{β}=(2,-1,1)$. Найти $overline{α}+overline{β}$, $overline{α}-overline{β}$ и $3overline{α}$.

Решение.

$overline{α}+overline{β}=(3+2,0+(-1),4+1)=(5,-1,5)$

$overline{α}-overline{β}=(3-2,0-(-1),4-1)=(1,1,3)$

$3overline{α}=(3cdot 3,3cdot 0,3cdot 4)=(9,0,12)$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Для начала дадим определение координат вектора в заданной системе координат. Чтобы ввести данное понятие, определим что мы называем прямоугольной или декартовой системой координат.

Определение 1

Прямоугольная система координат представляет из себя прямолинейную систему координат с взаимно перпендикулярными осями на плоскости или в пространстве.

С помощью введения прямоугольной системы координат на плоскости или в трехмерном пространстве становится возможным описывание геометрических фигур вместе с их свойствами при помощи уравнений и неравенств, то есть использовать алгебраические методы при решении геометрических задач.

Тем самым, мы можем привязать к заданной системе координат векторы. Это значительно расширит наши возможности при решении определенных задач

Прямоугольная система координат на плоскости обычно обозначается Oxy, где Ox и Oy – оси коорднат. Ось Ox называют осью абсцисс, а ось Oy – осью ординат (в пространстве появляется ещё одна ось Oz, которая перпендикулярна и Ox и Oy).

Пример 1

Итак, нам дана прямоугольная декартова система координат Oxy на плоскости если мы отложим от начала координат векторы i→ и j→ , направление которых соответственно совпадет с положительными направлениями осей Ox и Oy , и их длина будет равна условной единице, мы получим координатные векторы. То есть в данном случае i→ и j→ являются координатными векторами.

Координатные векторы

Определение 2

Векторы i→ и j→ называются координатными векторами для заданной системы координат.

Пример 2

Откладываем от начала координат произвольный вектор a→ . Опираясь на геометрическое определение операций над векторами, вектор a→ может быть представлен в виде a→=ax·i→+ay·j→ , где коэффициенты ax и ay – единственные в своем роде, их единственность достаточно просто доказать методом от противного.

Разложение вектора

Определение 3

Разложением вектора a→ по координатным векторам i→ и j→ на плоскости называется представление вида a→=ax·i→+ay·j→.

Определение 4

Коэффициенты ax и ay называются координатами вектора в данной системе координат на плоскости.

Координаты вектора в данной системе координат принято записывать в круглых скобках, через запятую, при этом заданные координаты следует отделять от обозначения вектора знаком равенства. К примеру, запись a→=(2;-3) означает, что вектор a→ имеет координаты (2;-3) в данной системе координат и может быть представлен в виде разложения по координатным векторам i→ и j→ какa→=2·i→-3·j→.

Замечание

Следует обратить внимание, что порядок записи координат, имеет важное значение, если вы запишите координаты вектора в другом порядке, вы получите совершенно другой вектор.

Опираясь на определения координат вектора и их разложения становится очевидным, что единичные векторы i→ и j→ имеют координаты (1;0) и (0;1) соответственно, и они могут быть представлены в виде следующих разложений i→=1·i→+0·j→; j→=0·i→+1·j→.

Также имеет место быть нулевой вектор 0→ с координатами (0;0) и разложением 0→=0·i→+0·j→.

Равные и противоположные векторы

Определение 5

Векторыa→иb→равны тогда, когда их соответствующие координаты равны.

Определение 6

Противоположным вектором называется вектор противоположный данному.

Отсюда следует, что координаты такого вектора будут противоположны координатам данного вектора, то есть, -a→=(-ax;-ay).

Все вышеизложенное можно аналогично определить и для прямоугольной системы координат, заданной в трехмерном пространстве. В такой системе координат имеет место быть тройка координатных векторов i→,j→,k→, а произвольный вектор a→ раскладывается не по двум, а уже по трем координатам, причем единственным образом и имеет вид a→=ax·i→+ay·j→+az·k→, а коэффициенты этого разложения (ax;ay;az) называются координатами вектора в данной (трехмерной) системе координат.

Следовательно, координатные векторы в трехмерном пространстве принимают также значение 1 и имеют координаты i→=(1;0;0) , j→=(0;1;0), k→=(0;0;1), координаты нулевого вектора также равны нулю 0→=(0;0;0) , и в таком случае два вектора будут считаться равными, если все три соответствующие координаты векторов между собой равныa→=b→⇔ax=bx, ay=by, az=bz , и координаты противоположного вектора a→ противоположны соответствующим координатам вектора a→ , то есть,-a→=(-ax;-ay; -az) .

Координаты радиус-вектора точки

Чтобы ввести данное определение, требуется показать в данной системе координат связь координат точки и координат вектора.

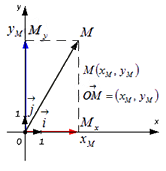
Пусть нам дана некоторая прямоугольная декартова система координат Oxy и на ней задана произвольная точка M с координатами M(xM;yM).

Определение 7

Вектор OM→ называется радиус-вектором точки M.

Определим, какие координаты в данной системе координат имеет радиус-вектор точки

Вектор OM→ имеет вид суммы OM→=OMx→+OMy→=xM·i→+yM·j→, где точки Mx и My это проекции точки М на координатные прямые Ox и Oy соответственно (данные рассуждения следуют из определения проекция точки на прямую), а i→ и j→ – координатные векторы, следовательно, вектор OM→ имеет координаты (xM;yM) в данной системе координат.

Иначе говоря, координаты радиус-вектора точки М равны соответствующим координатам точки М в прямоугольной декартовой системе координат.

Аналогично в трехмерном пространстве радиус-вектор точки M(xM;yM;zM) разлагается по координатным векторам как OM→=OMx→+OMy→+OMz→=xM·i→+yM·j→+zM·k→, следовательно, OM→=(xM;yM;zM).

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Геометрия, 11 класс

Урок № 1. Координаты в пространстве. Система координат

Перечень вопросов, рассматриваемых в теме:

Прямоугольная система координат в пространстве.
Координаты вектора, радиус-вектор.
Координаты середины отрезка, длина вектора, расстояние между точками.

Основная литература:

Гусева В.А., Куланин Е.Д. Геометрия. Профильный уровень. 10 класс – М.: Бином, 2010 – с. 130-148

Погорелов А.В. Геометрия. Учеб. для 7-11 кл. общеобразоват. Учреждение – 13-е изд-е. – М.: Просвещение, 2014. – с. 51-52

Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7-9 кл. 20-е изд-е. – М.: Просвещение, 2010. – с. 259-270.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч отрицательной полуосью. Плоскости, проходящие соответственно через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями и обозначаются Оху, Оуz, Оzх.

Прямоугольная система координат в пространстве задана, если выбрана точка – начало координат, через эту точку проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление (оно обозначается стрелкой) и задана единица измерения отрезков (рис. 121). Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат.

Координаты вектора

Зададим в пространстве прямоугольную систему координат Охуz. На каждой из положительных полуосей отложим от начала координат единичный вектор, т. е. вектор, длина которого равна единице. Обозначим через единичный вектор оси абсцисс, через – единичный вектор оси ординат и через – единичный вектор оси аппликат (рис. 124). Векторы , , – назовем координатными векторами. Очевидно, эти векторы не компланарны. Поэтому любой вектор a и можно разложить по координатным векторам, т. е. представить в виде

причем коэффициенты разложения х, у, z определяются единственным образом.

Коэффициенты х, у и z в разложении вектора по координатным векторам называются координатами вектора в данной системе координат. Координаты вектора будем записывать в фигурных скобках после обозначения вектора: {х; у; z}.

Нулевой вектор можно представить в виде так как все координаты нулевого вектора равны нулю.

Так как нулевой вектор можно представить в виде то все координаты нулевого вектора равны нулю. Далее, координаты равных векторов соответственно равны, т. е. если векторы {х₁, y₁, z₁} и {х_2, y₂, z₂) равны, то х₁ = x₂, y₁ = y₂ и z₁ = z₂

Рассмотрим правила, которые позволяют по координатам данных векторов найти координаты их суммы и разности, а также координаты произведения данного вектора на данное число.

1)Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Другими словами, если {х₁, у₁, z₁} и {х₂, у₂, z₂} — – данные векторы, то вектор + имеет координаты {х₁+х₂, у₁ + у₂, z₁ + z₂}.

2)Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Другими словами, если {х₁, y₁, z_1} и b{х₂ у₂; z₂} – данные векторы, то вектор – имеет координаты {х₁ – х₂, y₁ – y₂, z₁ – z₂}.

3)Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. Другими словами, если {х; у; х} – данный вектор, α – данное число, то вектор α имеет координаты {αх; αу; αz).

1)Признак коллинеарности векторов: Для того, чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы один из них был произведением другого на некоторое число.

Следствие: ненулевой вектор коллинарен вектору тогда и только тогда, когда существует такое число α, что =α.

Определение: Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.

2)Признак компланарности трех векторов: если вектор можно разложить по векторам и , т. е. представить в виде = x + y, где x и y — – некоторые числа, то векторы , и компланарны.