Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 сентября 2022 года; проверки требуют 2 правки.
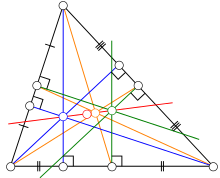
Прямая Эйлера (красная) проходит через центр описанной окружности треугольника, его ортоцентр, центр тяжести и центр окружности девяти точек

Пряма́я Э́йлера — прямая, проходящая через центр описанной окружности и ортоцентр треугольника.
Свойства[править | править код]
- Прямая Эйлера проходит через:
- На одной прямой лежат также точки пересечения прямых, содержащих стороны ортотреугольника, с прямыми, содержащими стороны треугольника. Эта прямая называется ортоцентрической осью, она перпендикулярна прямой Эйлера.

Точка Шиффлера 

- Теорема Шиффлера утверждает следующее: Если в треугольнике ABC с центром вписанной окружности I рассмотреть три треугольника BCI, CAI и ABI, то их три (первые) прямые Эйлера, а также (первая) прямая Эйлера треугольника ABC (все четыре прямые) пересекутся в одной точке — в точке Шиффлера Sp (см. рис. справа).
Вторая прямая Эйлера (прямая Эйлера — Нагеля)[править | править код]
Указанную выше прямую Эйлера иногда называют (первой) обобщённой прямой Эйлера[1]. На этой прямой лежат 4 точки:
- центроид данного треугольника (он же — центроид дополнительного треугольника, и он же — центроид антидополнительного треугольника)
- ортоцентр данного треугольника ABC
- центр описанной окружности данного треугольника ABC (он же — центр окружности Эйлера антидополнительного треугольника A”B”C”)
- центр окружности Эйлера данного треугольника ABC
- Некоторые авторы (см. рис. на сайте faculty.evansville.edu) добавляют ещё точку Лоншана L — точку зеркального отражения ортоцентра треугольника ABC относительно его центра описанной окружности (L= de Longchamps point=перевод не по правилам), введённую французским математиком Gaston Albert Gohierre. Эта точка — ортоцентр антидополнительного треугольника[2][3].
Вторую прямую Эйлера или прямую Эйлера-Нагеля определяет следующая Теорема Хузеля.
- Теорема Хузеля уточнённая(Housel). Центр тяжести (G) данного треугольника ABC (центроид), центр вписанной окружности (I), его точка Нагеля (M) и центр (S) круга, вписанного в дополнительный треугольник A’B’C’ (или в Центр Шпикера), лежат на одной прямой. Более того[4],
Указанную прямую иногда называют второй прямой Эйлера или прямой Эйлера-Нагеля. На этой прямой лежат 4 точки:
- центроид(G) данного треугольника (он же — центроид дополнительного треугольника, и он же — центроид антидополнительного треугольника).
- точка Нагеля (M) данного треугольника ABC (она же — центр круга, вписанного в антидополнительный треугольник A”B”C”)
- центр вписанной окружности (I) данного треугольника ABC
- центр (S) круга, вписанного в дополнительный треугольник A’B’C’, называемый также центром Шпикера.
- Все обобщённые прямые Эйлера обязательно проходят через центроид данного треугольника, являющегося одновременно центроидами дополнительного треугольника и антидополнительного треугольника.
Перспектор Госсарда и прямые Эйлера[править | править код]
Если брать у треугольника ABC любую пару сторон, а третьей стороной брать первую прямую Эйлера треугольника ABC, то перебором трёх вариантов можно построить три треугольника.
Их первые прямые Эйлера образуют треугольник AgBgCg, конгруэнтный треугольнику ABC
(равный ему, но повëрнутый на некоторый угол). Три пары отрезков, соединяющие сходственные вершины этих двух конгруэнтных треугольников пересекутся в точке Pg, называемой перспектором Госсарда.
Ссылка[править | править код]
Перспектор Госсарда (Gossard Perspector) http://faculty.evansville.edu/ck6/tcenters/recent/gosspersp.html
История[править | править код]
Теорема Эйлера была доказана в 1765 году Л. Эйлером.
Тогда же он обнаружил и тот факт, что середины сторон треугольника и основания его высот лежат на одной окружности — окружности Эйлера.
См. также[править | править код]
- Список объектов, названных в честь Леонарда Эйлера
- Прямая Обера
- Прямая Симсона
Примечания[править | править код]
- ↑ Зетель, 1962, с. 153.
- ↑ archive.lib.msu.edu. Дата обращения: 4 сентября 2015. Архивировано 2 июня 2013 года.
- ↑ faculty.evansville.edu. Дата обращения: 4 сентября 2015. Архивировано 10 февраля 2007 года.
- ↑ A. Bogomolny Nagel Line from Interactive Mathematics Miscellany and Puzzles (англ.). Дата обращения: 8 апреля 2019. Архивировано 10 мая 2012 года.
Литература[править | править код]
- Leonhard Euler. Solutio facilis problematum quorundam geometricorum difficillimorum // Novi Commentarii academiae scientiarum imperialis Petropolitanae. 1767, т. 11. — С. 103—123. Перепечатано в Opera Omnia, ser. I, vol. XXVI, pp. 139—157, Societas Scientiarum Naturalium Helveticae, Lausanne, 1953, MR0061061.
- Дм. Ефремов. Новая геометрия треугольника. — 1902.
- Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
- Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 96—97. — 383 с. — ISBN 5-09-001287-3..
- Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание.. — М.: Учпедгиз, 1962. — 153 с.
Прямая Эйлера
Понедельник, 16 декабря, 2019

Прямая Эйлера — это такая прямая, на которой лежат следующие точки:
- центроид треугольника (точка пересечения его медиан);
- ортоцентр треугольника (точка пересечения его высот);
- центр описанной около треугольника окружности (точка пересечения серединных перпендикуляров, проведённых к сторонам этого треугольника).
Доказательство существования прямой Эйлера
Нарисуем треугольник общего вида. Единственное, пусть он будет остроугольным. Хотя на самом деле все дальнейшие рассуждения с небольшими косметическими поправками будут справедливы и для тупоугольного треугольника. Проведём в этом треугольнике все высоты. Как известно, в треугольнике либо сами высоты, либо их продолжения пересекаются в одной точке. Назовём её точкой G. По-другому эта точка называется «ортоцентром»:
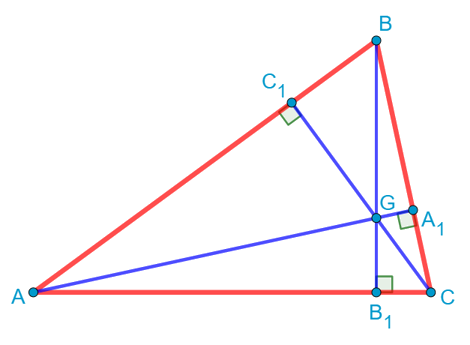
Соединим теперь основания высот A1 и C1 отрезком. И докажем, что треугольник C1BA1 подобен треугольнику ABC. Ну, действительно. У них есть общий угол B. Кроме того, если рассмотреть прямоугольный треугольник CC1B, то косинус угла B в нём равен отношению прилежащего катета BC1 к гипотенузе BC: ![]() . С другой стороны, из прямоугольного треугольника ABA1 мы получаем, что косинус того же самого угла B равен отношению прилежащего катета BA1 к гипотенузе BA:
. С другой стороны, из прямоугольного треугольника ABA1 мы получаем, что косинус того же самого угла B равен отношению прилежащего катета BA1 к гипотенузе BA: ![]() :
:
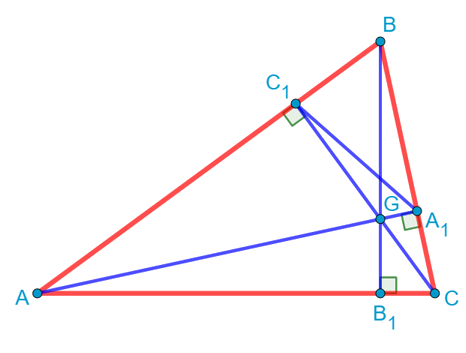
Ну и теперь мы видим, что общий угол B образован в наших треугольниках пропорциональными сторонами: ![]() . Значит, треугольники C1BA1 и ABC подобны. Причём их коэффициент подобия равен
. Значит, треугольники C1BA1 и ABC подобны. Причём их коэффициент подобия равен ![]() .
.
Обратим теперь внимание на то, что ![]() . Это означает, что сумма противоположных углов четырёхугольника GC1BA1 равна 180 градусам. Значит, вокруг него можно описать окружность:
. Это означает, что сумма противоположных углов четырёхугольника GC1BA1 равна 180 градусам. Значит, вокруг него можно описать окружность:
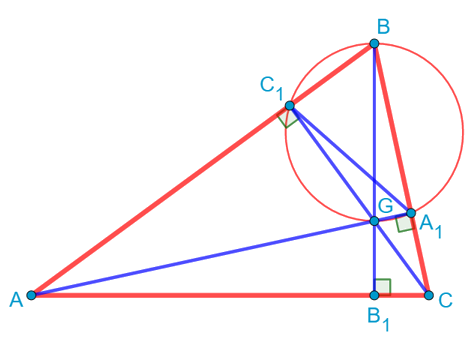
При этом отрезок BG будет являться диаметром этой окружности, поскольку на него опирается вписанный угол BA1G, который равен 90 градусов.
Проведём теперь серединные перпендикуляры к сторонам AB и AC. Они пересекутся в точке O, которая, как хорошо известно, является центром описанной около треугольника ABC окружности. То есть треугольник AOC будет равнобедренным, причём его боковые стороны по длине будут равны радиусу описанной окружности:
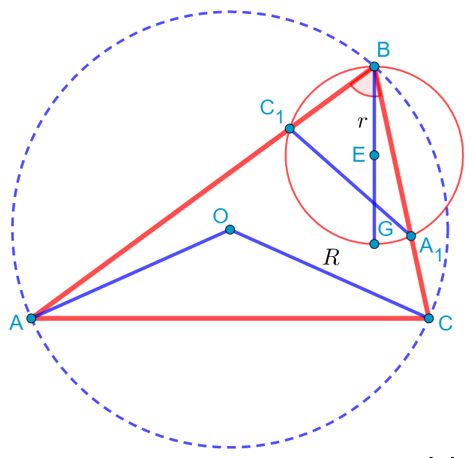
То есть мы получили, что вокруг подобных треугольников BC1A1 и ABC описаны окружности. Но коэффициент их подобия равен косинусу угла B. Но в подобных треугольниках одинаковым образом относятся все элементы, в том числе и радиусы описанных окружностей, поэтому ![]() .
.
Проведём теперь высоту OD в треугольнике AOC. Обратим внимание, что угол B является вписанным и опирается на дугу AC. Но на эту же дугу опирается и центральный угол AOC, который поэтому должен быть вдвое больше угла B. Но высота OD делит этот угол ровно пополам, так как она является одновременно и биссектрисой, проведённой к основанию равнобедренного треугольника. Значит, ∠B = ∠DOC:
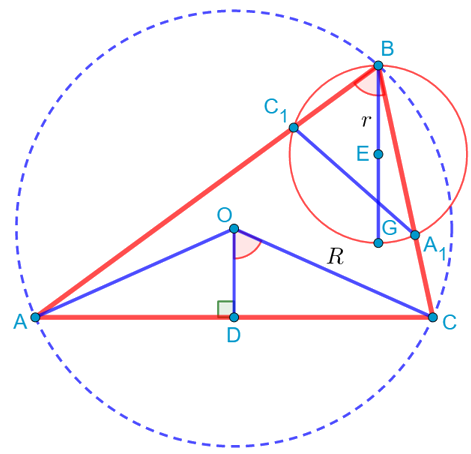
Но тогда косинус угла B мы можем расписать, используя треугольник DOC. В нём этот косинус равен отношению прилежащего катета OD к гипотенузе OC, которая равна радиусу описанной окружности R. И этот же косинус, как мы выяснили, равен отношению r к R: ![]() . Из последнего равенства получаем, что
. Из последнего равенства получаем, что ![]() или иначе
или иначе ![]() .
.
Проведём теперь отрезок BD, который будет являться медианой. Проведём также прямую через точки O и G. То есть через эти две точки проходит прямая, что, конечно, не удивительно, ведь мы знаем, что через две точки можно провести прямую, притом только одну. Эта прямая пересекает медиану BD в некоторой точке M:
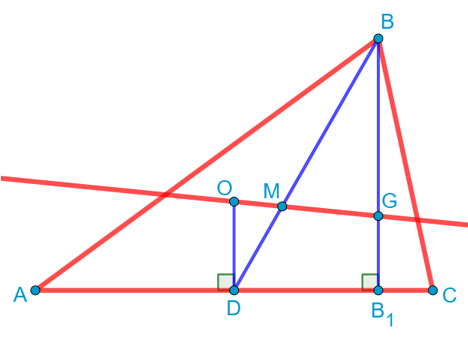
Как вы думаете, что это за точка? Уже догадались? А может быть уже знали и раньше? Если нет, то настало время удивляться! Посмотрите на треугольник OMD. Он подобен треугольнику MGB по двум углам: вертикальным и накрест лежащим при параллельных прямых. И мы даже знаем коэффициент подобия этих треугольников. Он равен 1:2. А значит, все стороны этих треугольников относятся как 1:2, в том числе и стороны DM и MB.
И что же у нас получилось? А получилось то, что точка M делит медиану BD в отношении 2:1, считая от вершины. А значит, точка M – это точка пересечения медиан треугольника или, как её по-другому называют, цетроид треугольника.
Таким образом мы доказали, что ортоцентр треугольника, центр описанной около него окружности и центроид этого треугольника лежат на одной прямой. Эта прямая и называется прямой Эйлера!
Анимация прямой Эйлера
Факт существования прямой Эйлера насколько удивителен, что даже не всегда укладывается в голове. Специально для вас я подготовил поясняющую анимацию. Посмотрите её в видео на моём Youtube-канале.
Вне зависимости от типа треугольника, как угодно можно над ним издеваться, но эти три точки всегда будут лежать на одной прямой. Возможны, правда, случаи, когда эти точки совпадают. Например, для правильного треугольника все они сливаются в одну точку. Но если мы имеем дело не с этим тривиальным случаем, то все эти точки лежат на одной прямой. Прямой Эйлера.
И у этой прямой очень много других интересных свойств. Пишите в комментариях, стоит ли написать на эту тему отдельную статью. Успехов!
Материал подготовил репетитор по математике и физике Сергей Валерьевич
В треугольнике центр описанной окружности, ортоцентр и точка пересечения медиан лежит на одной прямой, и расстояние от центра описанной окружности до ортоцентра в три раза больше расстояния от центра описанной окружности до точки пересечения медиан.
Доказательство:
Пусть Н — ортоцентр, M — точка пересечения медиан, O — центр описанной окружности.
Треугольники ABC и EFD подобны по трем сторонам с коэффициентом подобия 2.
AH/EO=2/1 (отрезки высот подобных треугольников).
AM/ME=2/1 (свойство точки пересечения медиан треугольника).
Следовательно, AH/EO=AM/ME.
Пусть G — точка пересечения отрезков AE и OH.
Треугольники OEG и HAG подобны по 2 углам. Следовательно, GH/GO=AG/GE=AH/EO=2/1.
Следовательно, M=G.
Следствие 1:
Центр окружности, описанной около треугольника DEF является серединой отрезка OH.
Следствие 2:
Расстояние от вершины треугольника до его ортоцентра в два раза больше, чем расстояние от центра его описанной окружности до середины противолежащей стороны.
Всем привет!
Продолжаем традицию воскресных текстов. В сегодняшней публикации мы разберем несколько задач и фактов, так или иначе связанных с прямой OI. Мой опыт преподавания показал, что такие задачи оказываются трудными, из-за того, что подступиться к этой прямой с геометрической точки зрения не так просто, несмотря на то, что она проходит через два важнейших центра треугольника.
Во всем нижеследующем тексте мы считаем, что треугольник ABC не является равнобедренным, а центры его вписанной и описанной окружности обозначаем традиционно символами I и O соответственно.
Когда какие-то углы вычисляются…
Когда я был классе в восьмом меня прям поразила следующая задача.
Утверждение 1. Если в треугольнике ABC угол OIA равен 30°, то один из углов B и C равен 60°.
Мне всегда казалось, что к углу OIA подобраться практически не возможно… Этим задача и оказывается сложна. Несмотря на простоту формулировки, задача ставит в тупик очень много школьников. Давайте с ней разберемся.
Тут играют очень важную роль два соображения. Первое состоит в том, что прямая OI является осью симметрии для обеих окружностей, вписанной и описанной. А второе соображение общее — если на картинке есть угол в 30 градусов, его часто полезно удвоить, сделав симметрию и заработав равносторонний треугольник.
Давайте отразим точку A относительно прямой OI, получим точку A’. Эта точка, с одной стороны, окажется на описанной окружности треугольника ABC, а с другой стороны, треугольник AIA’ будет равносторонним. Таким образом, точка A’ есть пересечение серединного перпендикуляра к отрезку AI с описанной окружностью треугольника ABC. Но по лемме от трезубце серединный перпендикуляр к отрезку AI пересекает описанную окружность треугольника ABC в серединах дуг AB и AC. Следовательно, точка A’ совпадает с одной из этих середин, пусть, скажем с серединой дуги AC. В этом случае
и задача решена. Утверждение легко обращается.
Если попытаться подумать о других величинах угла OIA, то нечто осмысленное у меня получается только для углов 0°, 180° и 90°. В первых двух случаях имеем, конечно, равнобедренный треугольник, а вот третий сам по себе интересен.
Утверждение 2. Если в треугольнике ABC угол OIA равен 90°, то 2BC=AB+AC.
Действительно, в описанном случае точка I попадает на окружность, построенную на AO как на диаметре, то есть на описанную окружность треугольника AB₁C₁, где B₁ и C₁ — середины сторон AC и AB соответственно. Раз так, заключаем, что IB₁=IC₁. Если через B₂ и C₂ обозначить точки касания вписанной окружности со сторонами AC и AB соответственно, то выводим равенство прямоугольных треугольников IB₁B₂ и IC₁C₂ и равенство отрезков B₁B₂ и C₁C₂.
Следовательно,
Утверждение легко обращается в обратную сторону.
Перпендикулярность прямой OI
Одна из моих любимых задач про прямую OI звучит так.
Утверждение 3. В треугольнике ABC на сторонах AB и AC отмечены такие точки D и E, что DB=BC=CE. Тогда прямые DE и OI перпендикулярны.
Самое простое доказательство основано на том, что отрезки OI и DE перпендикулярны тогда и только тогда, когда
при этом достаточно проверять, что выражение в левой части равенства является симметричным относительно переменных b=AC и c=AB — сторон треугольника. Давайте проделаем соответствующее вычисление. Сохраняя обозначения для середин сторон и точек касания, заведенные выше, видим, что
После понятных преобразований получаем равенство
выражение в правой части которого симметрично относительно b и c. Утверждение доказано.
Однако, все это выглядит немного таинственно. Чуть понятнее становится, когда переписываешь это решение в векторах. Ведь если посмотреть на вектор OI (здесь и далее полужирный шрифт в тексте используется для векторов) его проекции на направления AB и AC равны (b–a)/2 и (c–a)/2 соответственно. Откуда уже совсем просто выводится перпендикулярность вектору DE. Действительно, пусть e₁ и e₂ — единичные векторы, идущие по сторонам AB и AC соответственно, тогда
и
Но нет ли более геометрического решения? Конечно, есть. Одно такое решение можно придумать, проанализировать предыдущее рассуждение с векторами… Оставлю это в качестве упражнения читателям. А другое геометрическое решение основано на новом взгляде на прямую OI.
Утверждение, конечно, остается верным и в случае, когда точки D и E не лежат на сторонах, а попадают на их продолжения…
Прямая OI как прямая Эйлера
Один из довольно продвинутых способов решать задачи с прямой OI — это слегка переосмыслить ее. Давайте рассмотрим треугольник с вершинами в центрах вневписанных окружностей Ia, Ib и Ic треугольника ABC. Треугольник ABC для треугольника IaIbIc является ортотреугольником, то есть точки A, B и C — основания высот треугольника IaIbIc. Точка I является его ортоцентром, а точка O — центром окружности девяти точек. Откуда заключаем, что OI в треугольнике IaIbIc является прямой Эйлера. Таким образом верно утверждение.
Утверждение 4. Прямая OI является прямой Эйлера треугольника с вершинами в центрах вневписанных окружностей.
Утверждений про прямую Эйлера известно уже значительно больше, плюс на ней лежит довольно много известных точек, так что работать с ней куда приятнее.
Например, если хочется найти прямую, перпендикулярную прямой Эйлера, то сделать это довольно просто. Если дан треугольник KLM и X, Y и Z — основания высот треугольника из вершин K, L и M соответственно, то точки пересечения KL с XY, LM с YZ и MK с ZX лежат на одной прямой, перпендикулярной прямой Эйлера треугольника ABC. Давайте уставим этот факт.
Пусть прямые LM и YZ пересекаются в точке P, тогда
поскольку точки L, M, Y и Z лежат на одной окружности с диаметром LM. Следовательно, степени точки P относительно описанной окружности треугольника KLM и его окружности девяти точек равны. Таким образом, точки пересечения KL с XY, LM с YZ и MK с ZX лежат на радикальной оси описанной окружности и окружности девяти точек треугольника KLM, откуда и следует требуемое.
В исходных обозначениях получаем, следующее утверждение.
Утверждение 5. Основания биссектрис внешних углов треугольника ABC лежат на одной прямой перпендикулярной OI.
И если теперь, скажем, хочется устанавливать утверждение 3, то достаточно проверить, что прямая DE параллельна прямой, соединяющей основания биссектрис внешних углов. Это уже проверяется по теореме Фалеса с помощью нехитрых вычислений.
From Wikipedia, the free encyclopedia

Perpendicular lines from the side midpoints (intersect at the circumcenter)
In geometry, the Euler line, named after Leonhard Euler (), is a line determined from any triangle that is not equilateral. It is a central line of the triangle, and it passes through several important points determined from the triangle, including the orthocenter, the circumcenter, the centroid, the Exeter point and the center of the nine-point circle of the triangle.[1]
The concept of a triangle’s Euler line extends to the Euler line of other shapes, such as the quadrilateral and the tetrahedron.
Triangle centers on the Euler line[edit]
Individual centers[edit]
Euler showed in 1765 that in any triangle, the orthocenter, circumcenter and centroid are collinear.[2] This property is also true for another triangle center, the nine-point center, although it had not been defined in Euler’s time. In equilateral triangles, these four points coincide, but in any other triangle they are all distinct from each other, and the Euler line is determined by any two of them.
Other notable points that lie on the Euler line include the de Longchamps point, the Schiffler point, the Exeter point, and the Gossard perspector.[1] However, the incenter generally does not lie on the Euler line;[3] it is on the Euler line only for isosceles triangles,[4] for which the Euler line coincides with the symmetry axis of the triangle and contains all triangle centers.
The tangential triangle of a reference triangle is tangent to the latter’s circumcircle at the reference triangle’s vertices. The circumcenter of the tangential triangle lies on the Euler line of the reference triangle.[5]: p. 447 [6]: p.104, #211, p.242, #346 The center of similitude of the orthic and tangential triangles is also on the Euler line.[5]: p. 447 [6]: p. 102
Proofs[edit]
A vector proof[edit]
Let 




This follows from the fact that the absolute barycentric coordinates of 

Now, using the vector addition, we deduce that
By adding these three relations, term by term, we obtain that
In conclusion, 



In Dörrie’s book,[7] the Euler line and the problem of Sylvester are put together into a single proof. However, most of the proofs of the problem of Sylvester rely on the fundamental properties of free vectors, independently of the Euler line.
Properties[edit]
Distances between centers[edit]
On the Euler line the centroid G is between the circumcenter O and the orthocenter H and is twice as far from the orthocenter as it is from the circumcenter:[6]: p.102
The segment GH is a diameter of the orthocentroidal circle.
The center N of the nine-point circle lies along the Euler line midway between the orthocenter and the circumcenter:[1]
Thus the Euler line could be repositioned on a number line with the circumcenter O at the location 0, the centroid G at 2t, the nine-point center at 3t, and the orthocenter H at 6t for some scale factor t.
Furthermore, the squared distance between the centroid and the circumcenter along the Euler line is less than the squared circumradius R2 by an amount equal to one-ninth the sum of the squares of the side lengths a, b, and c:[6]: p.71
In addition,[6]: p.102
Representation[edit]
Equation[edit]
Let A, B, C denote the vertex angles of the reference triangle, and let x : y : z be a variable point in trilinear coordinates; then an equation for the Euler line is
An equation for the Euler line in barycentric coordinates 
Parametric representation[edit]
Another way to represent the Euler line is in terms of a parameter t. Starting with the circumcenter (with trilinear coordinates 

formed as a linear combination of the trilinears of these two points, for some t.
For example:
Slope[edit]
In a Cartesian coordinate system, denote the slopes of the sides of a triangle as 



Thus the slope of the Euler line (if finite) is expressible in terms of the slopes of the sides as
Moreover, the Euler line is parallel to an acute triangle’s side BC if and only if[9]: p.173 
Relation to inscribed equilateral triangles[edit]
The locus of the centroids of equilateral triangles inscribed in a given triangle is formed by two lines perpendicular to the given triangle’s Euler line.[10]: Coro. 4
In special triangles[edit]
Right triangle[edit]
In a right triangle, the Euler line coincides with the median to the hypotenuse—that is, it goes through both the right-angled vertex and the midpoint of the side opposite that vertex. This is because the right triangle’s orthocenter, the intersection of its altitudes, falls on the right-angled vertex while its circumcenter, the intersection of its perpendicular bisectors of sides, falls on the midpoint of the hypotenuse.
Isosceles triangle[edit]
The Euler line of an isosceles triangle coincides with the axis of symmetry. In an isosceles triangle the incenter falls on the Euler line.
Automedian triangle[edit]
The Euler line of an automedian triangle (one whose medians are in the same proportions, though in the opposite order, as the sides) is perpendicular to one of the medians.[11]
Systems of triangles with concurrent Euler lines[edit]
Consider a triangle ABC with Fermat–Torricelli points F1 and F2. The Euler lines of the 10 triangles with vertices chosen from A, B, C, F1 and F2 are concurrent at the centroid of triangle ABC.[12]
The Euler lines of the four triangles formed by an orthocentric system (a set of four points such that each is the orthocenter of the triangle with vertices at the other three points) are concurrent at the nine-point center common to all of the triangles.[6]: p.111
Generalizations[edit]
Quadrilateral[edit]
In a convex quadrilateral, the quasiorthocenter H, the “area centroid” G, and the quasicircumcenter O are collinear in this order on the Euler line, and HG = 2GO.[13]
Tetrahedron[edit]
A tetrahedron is a three-dimensional object bounded by four triangular faces. Seven lines associated with a tetrahedron are concurrent at its centroid; its six midplanes intersect at its Monge point; and there is a circumsphere passing through all of the vertices, whose center is the circumcenter. These points define the “Euler line” of a tetrahedron analogous to that of a triangle. The centroid is the midpoint between its Monge point and circumcenter along this line. The center of the twelve-point sphere also lies on the Euler line.
Simplicial polytope[edit]
A simplicial polytope is a polytope whose facets are all simplices (plural of simplex). For example, every polygon is a simplicial polytope. The Euler line associated to such a polytope is the line determined by its centroid and circumcenter of mass. This definition of an Euler line generalizes the ones above.[14]
Suppose that 


1. If 




2. If 


3. If all but one of the sides of 

[edit]
A triangle’s Kiepert parabola is the unique parabola that is tangent to the sides (two of them extended) of the triangle and has the Euler line as its directrix.[15]: p. 63
References[edit]
- ^ a b c Kimberling, Clark (1998). “Triangle centers and central triangles”. Congressus Numerantium. 129: i–xxv, 1–295.
- ^ Euler, Leonhard (1767). “Solutio facilis problematum quorundam geometricorum difficillimorum” [Easy solution of some difficult geometric problems]. Novi Commentarii Academiae Scientarum Imperialis Petropolitanae. 11: 103–123. E325. Reprinted in Opera Omnia, ser. I, vol. XXVI, pp. 139–157, Societas Scientiarum Naturalium Helveticae, Lausanne, 1953, MR0061061. Summarized at: Dartmouth College.
- ^ Schattschneider, Doris; King, James (1997). Geometry Turned On: Dynamic Software in Learning, Teaching, and Research. The Mathematical Association of America. pp. 3–4. ISBN 978-0883850992.
- ^ Edmonds, Allan L.; Hajja, Mowaffaq; Martini, Horst (2008), “Orthocentric simplices and biregularity”, Results in Mathematics, 52 (1–2): 41–50, doi:10.1007/s00025-008-0294-4, MR 2430410, S2CID 121434528,
It is well known that the incenter of a Euclidean triangle lies on its Euler line connecting the centroid and the circumcenter if and only if the triangle is isosceles
. - ^ a b Leversha, Gerry; Smith, G. C. (November 2007), “Euler and triangle geometry”, Mathematical Gazette, 91 (522): 436–452, doi:10.1017/S0025557200182087, JSTOR 40378417, S2CID 125341434.
- ^ a b c d e f Altshiller-Court, Nathan, College Geometry, Dover Publications, 2007 (orig. Barnes & Noble 1952).
- ^ a b Dörrie, Heinrich, “100 Great Problems of Elementary Mathematics. Their History and Solution”. Dover Publications, Inc., New York, 1965, ISBN 0-486-61348-8, pages 141 (Euler’s Straight Line) and 142 (Problem of Sylvester)
- ^ Scott, J.A., “Some examples of the use of areal coordinates in triangle geometry”, Mathematical Gazette 83, November 1999, 472-477.
- ^ a b Wladimir G. Boskoff, Laurent¸iu Homentcovschi, and Bogdan D. Suceava, “Gossard’s Perspector and Projective Consequences”, Forum Geometricorum, Volume 13 (2013), 169–184. [1]
- ^ Francisco Javier Garc ́ıa Capita ́n, “Locus of Centroids of Similar Inscribed Triangles”, Forum Geometricorum 16, 2016, 257–267 .http://forumgeom.fau.edu/FG2016volume16/FG201631.pdf
- ^ Parry, C. F. (1991), “Steiner–Lehmus and the automedian triangle”, The Mathematical Gazette, 75 (472): 151–154, doi:10.2307/3620241, JSTOR 3620241.
- ^ Beluhov, Nikolai Ivanov. “Ten concurrent Euler lines”, Forum Geometricorum 9, 2009, pp. 271–274. http://forumgeom.fau.edu/FG2009volume9/FG200924index.html
- ^ Myakishev, Alexei (2006), “On Two Remarkable Lines Related to a Quadrilateral” (PDF), Forum Geometricorum, 6: 289–295.
- ^ Tabachnikov, Serge; Tsukerman, Emmanuel (May 2014), “Circumcenter of Mass and Generalized Euler Line”, Discrete and Computational Geometry, 51 (4): 815–836, arXiv:1301.0496, doi:10.1007/s00454-014-9597-2, S2CID 12307207.
- ^ Scimemi, Benedetto, “Simple Relations Regarding the Steiner Inellipse of a Triangle”, Forum Geometricorum 10, 2010: 55–77.
External links[edit]
- An interactive applet showing several triangle centers that lies on the Euler line.
- “Euler Line” and “Non-Euclidean Triangle Continuum” at the Wolfram Demonstrations Project
- Nine-point conic and Euler line generalization, A further Euler line generalization, and The quasi-Euler line of a quadrilateral and a hexagon at Dynamic Geometry Sketches
- Bogomolny, Alexander, “Altitudes and the Euler Line” and “Euler Line and 9-Point Circle”, Cut-the-Knot
- Kimberling, Clark, “Triangle centers on the Euler line”, Triangle Centers
- Archived at Ghostarchive and the Wayback Machine: Stankova, Zvezdelina (February 1, 2016), “Triangles have a Magic Highway”, Numberphile, YouTube
- Weisstein, Eric W. “Euler Line”. MathWorld.


















