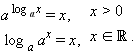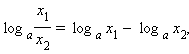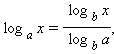Статья рассматривает понятия параллельность прямой и плоскости. Будут рассмотрены основные определения и приведены примеры. Рассмотрим признак параллельности прямой к плоскости с необходимыми и достаточными условиями параллельности, подробно решим примеры заданий.
Параллельные прямые и плоскость – основные сведения
Прямая и плоскость называются параллельными, если не имеют общих точек, то есть не пересекаются.
Параллельность обозначается «∥». Если в задании по условию прямая a и плоскость α параллельны, тогда обозначение имеет вид a∥α. Рассмотрим рисунок, приведенный ниже.
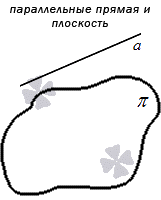
Считается, что прямая a, параллельная плоскости α и плоскость α, параллельная прямой a, равнозначные, то есть прямая и плоскость параллельны друг другу в любом случае.
Параллельность прямой и плоскости – признак и условия параллельности
Не всегда очевидно, что прямая и плоскость параллельны. Зачастую это нужно доказать. Необходимо использовать достаточное условие, которое даст гарантию на параллельность. Такой признак имеет название признака параллельности прямой и плоскости. Предварительно рекомендуется изучить определение параллельных прямых.
Если заданная прямая a, не лежащая в плоскости α, параллельна прямой b, которая принадлежит плоскости α, тогда прямая a параллельна плоскости α.
Рассмотрим теорему, используемую для установки параллельности прямой с плоскостью.
Если одна из двух параллельных прямых параллельна плоскости, то другая прямая лежит в этой плоскости либо параллельна ей.
Подробное доказательство рассмотрено в учебнике 10-11 класса по геометрии. Необходимым и достаточным условием параллельности прямой с плоскостью возможно при наличии определения направляющего вектора прямой и нормального вектора плоскости.
Для параллельности прямой a, не принадлежащей плоскости α, и данной плоскости необходимым и достаточным условием является перпендикулярность направляющего вектора прямой с нормальным вектором заданной плоскости.
Условие применимо, когда необходимо доказать параллельность в прямоугольной системе координат трехмерного пространства. Рассмотрим подробное доказательство.
Допустим, прямая а в систему координат Оху задается каноническими уравнениями прямой в пространстве , которые имеют вид x-x1ax=y-y1ay=z-z1az или параметрическими уравнениями прямой в пространстве x=x1+ax·λy=y1+ay·λz=z1+az·λ, плоскостью α с общими уравнениями плоскости Ax+By+Cz+D=0.
Отсюда a→=(ax, ay, az) является направляющим вектором с координатами прямой а, n→=(A, B, C) – нормальным вектором заданной плоскости альфа.
Чтобы доказать перпендикулярность n→=(A, B, C) и a→=(ax, ay, az), нужно использовать понятие скалярного произведения. То есть при произведении a→, n→=ax·A+ay·B+az·C результат должен быть равен нулю из условия перпендикулярности векторов.
Значит, что необходимым и достаточным условием параллельности прямой и плоскости запишется так a→, n→=ax·A+ay·B+az·C. Отсюда a→=(ax, ay, az) является направляющим вектором прямой a с координатами, а n→=(A, B, C) – нормальным вектором плоскости α.
Определить, параллельны ли прямая x=1+2·λy=-2+3·λz=2-4·λ с плоскостью x+6y+5z+4=0.
Решение
Получаем, что предоставленная прямая не принадлежит плоскости, так как координаты прямой M(1, -2, 2) не подходят. При подстановке получаем, что 1+6·(-2)+5·2+4=0⇔3=0.
Необходимо проверить на выполнимость необходимое и достаточное условие параллельности прямой и плоскости. Получим, что координаты направляющего вектора прямой x=1+2·λy=-2+3·λz=2-4·λимеют значения a→=(2, 3, -4).
Нормальным вектором для плоскости x+6y+5z+4=0 считается n→=(1, 6, 5). Перейдем к вычислению скалярного произведения векторов a→ и n→. Получим, что a→, n→=2·1+3·6+(-4)·5=0.
Значит, перпендикулярность векторов a→ и n→ очевидна. Отсюда следует, что прямая с плоскостью являются параллельными.
Ответ: прямая с плоскостью параллельны.
Определить параллельность прямой АВ в координатной плоскости Оуz, когда даны координаты A(2, 3, 0), B(4, -1, -7).
Решение
По условию видно, что точка A(2, 3, 0) не лежит на оси Ох, так как значение x не равно 0.
Для плоскости Oxz вектор с координатами i→=(1, 0, 0) считается нормальным вектором данной плоскости. Обозначим направляющий вектор прямой AB как AB→. Теперь при помощи координат начала и конца рассчитаем координаты вектора AB. Получим, что AB→=(2, -4, -7). Необходимо выполнить проверку на выполнимость необходимого и достаточного условия векторов AB→=(2, -4, -7) и i→=(1, 0, 0), чтобы определить их перпендикулярность.
Запишем AB→, i→=2·1+(-4)·0+(-7)·0=2≠0.
Отсюда следует, что прямая АВ с координатной плоскостью Оyz не являются параллельными.
Ответ: не параллельны.
Не всегда заданное условие способствует легкому определению доказательства параллельности прямой и плоскости. Появляется необходимость в проверке принадлежности прямой a плоскости α. Существует еще одно достаточное условие, при помощи которого доказывается параллельность.
При заданной прямой a с помощью уравнения двух пересекающихся плоскостей A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0, плоскостью α – общим уравнением плоскости Ax+By+Cz+D=0.
Необходимым и достаточным условием для параллельности прямой a и плоскости α яляется отсутствие решений системы линейных уравнений, имеющей вид A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0Ax+By+Cz+D=0.
Из определения следует, что прямая a с плоскостью α не должна иметь общих точек, то есть не пересекаться, только в этом случае они будут считаться параллельными. Значит, система координат Охуz не должна иметь точек, принадлежащих ей и удовлетворяющих всем уравнениям:
A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0, а также уравнению плоскости Ax+By+Cz+D=0.
Следовательно, система уравнений, имеющая вид A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0Ax+By+Cz+D=0, называется несовместной.
Верно обратное: при отсутствии решений системы A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0Ax+By+Cz+D=0 не существует точек в Охуz, удовлетворяющих всем заданным уравнениям одновременно. Получаем, что нет такой точки с координатами, которая могла бы сразу быть решениями всех уравнений A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0 и уравнения Ax+By+Cz+D=0. Значит, имеем параллельность прямой и плоскости, так как отсутствуют их точки пересечения.
Система уравнений A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0Ax+By+Cz+D=0 не имеет решения, когда ранг основной матрицы меньше ранга расширенной. Это проверяется теоремой Кронекера-Капелли для решения линейных уравнений. Можно применять метод Гаусса для определения ее несовместимости.
Доказать , что прямая x-1=y+2-1=z3 параллельна плоскости 6x-5y+13z-23=0.
Решение
Для решения данного примера следует переходить от канонического уравнения прямой к виду уравнения двух пересекающихся плоскостей. Запишем это так:
x-1=y+2-1=z3⇔-1·x=-1·(y+2)3·x=-1·z3·(y+2)=-1·z⇔x-y-2=03x+z=0
Чтобы доказать параллельность заданной прямой x-y-2=03x+z=0 с плоскостью 6x-5y+13z-23=0 , необходимо уравнения преобразовать в систему уравнений x-y-2=03x+z=06x-5y+13z-23=0.
Видим, что она не решаема, значит прибегнем к методу Гаусса.
Расписав уравнения, получаем, что 1-10230106-51323~1-102031-60113-1113~1-102031-6000-913.
Отсюда делаем вывод, что система уравнений является несовместной, так как прямая и плоскость не пересекаются, то есть не имеют общих точек.
Делаем вывод, что прямая x-1=y+2-1=z3 и плоскость 6x-5y+13z-23=0 параллельны, так как было выполнено необходимое и достаточное условие для параллельности плоскости с заданной прямой.
Ответ: прямая и плоскость параллельны.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
|
|
На
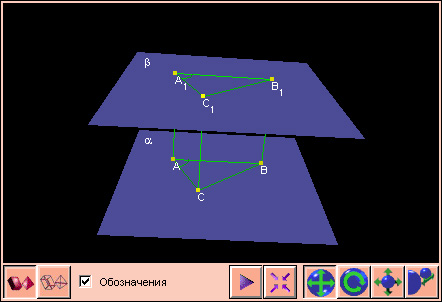
чертеже 2.3.4 показаны углы BAC и B1A1C1,
причем AB || A1B1 и AC || A1C1.
По признаку параллельности плоскостей
плоскость BAC параллельна
плоскостиB1A1C1.
Пусть
соответствующие отрезки на сторонах
угла равны: AB = A1B1 и AC = A1C1.
Проведем прямые AA1, BB1, CC1.
Четырехугольник ABB1A1 –
параллелограмм, так как AB = A1B1 и AB || A1B1,
следовательно, AA1 = BB1 и AA1 || BB1.
Аналогично докажем, что AA1 = CC1.
Отсюда следует, что BB1 = CC1 и BB1 || CC1,
следовательно, CBB1C1 –
параллелограмм и CB = C1B1.
Теперь утверждаем, что Δ ABC = Δ A1B1C1,
откуда 
BAC =
B1A1C1.
Билет
6.1
Логарифмы
по основанию 10 (обозначение: 
)
до изобретения калькуляторов широко
применялись для вычислений. Они
обладали преимуществом перед логарифмами
с иным основанием: целую часть 
логарифма
числа 
легко
определить.
Кроме
того, при переносе десятичной запятой
в числе на 
разрядов
значение десятичного логарифма этого
числа изменяется на 
Например, 
.
Отсюда следует, что достаточно составить
таблицу десятичных логарифмов для
чисел в диапазоне от 
до 
причём
привести в таблице только мантиссы (дробную
часть) логарифмов.
Связь
с натуральным логарифмом:
Поскольку
применение логарифмов для расчётов
с появлением вычислительной техники
почти прекратилось, в наши дни десятичный
логарифм в значительной степени
вытеснен натуральным. Он сохраняется
в основном в тех математических
моделях, где исторически укоренился
— например, при построении логарифмических
шкал.
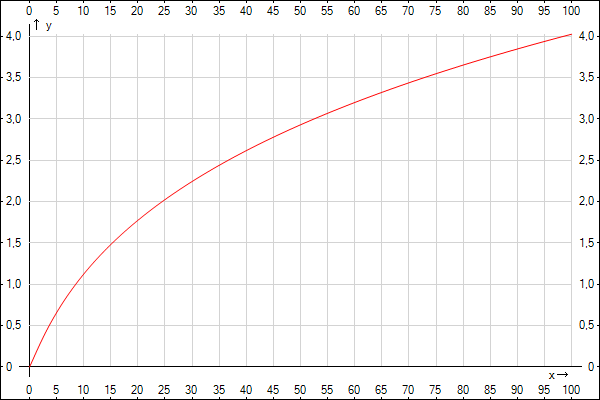
y
= lg(x) – десятичный логарифм от х
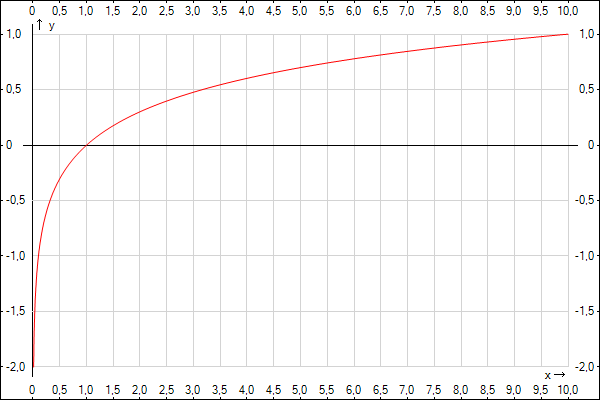
Текст
формулы:
y(x) =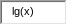 
y
= lg(1/2)(x)
– корень квадратный от десятичного
логарифма от x
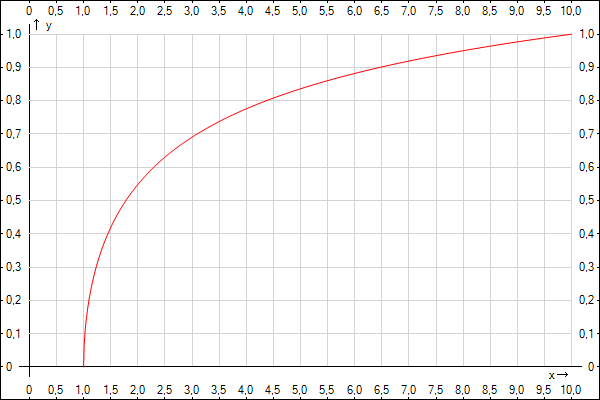
Текст
формулы:
y(x) = 
y
= lg(x+1)lg(x+2) – произведение десятичных
логарифмов
Текст
формулы:
y(x) = 
y
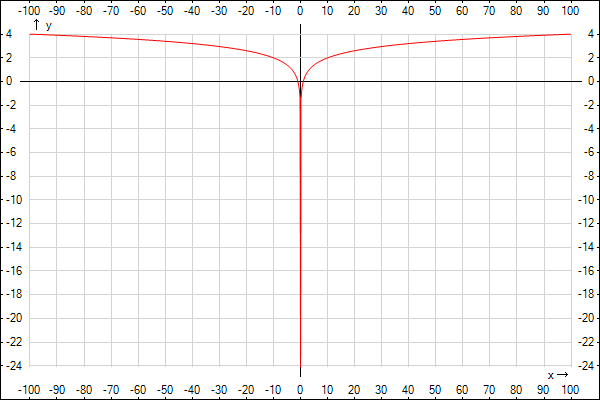
= lg(x^2) – десятичный логарифм от квадрата
x
Текст
формулы:
y(x) = 
6.2
Определение
Прямая,
пересекающая плоскость, перпендикулярна
каждой прямой, которая лежит в данной
плоскости и проходит через точку
называется перпендикулярной этой
плоскости, если она
пересечения.
Теорема
1
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ
ПРЯМОЙ И ПЛОСКОСТИ.
Если прямая,
пересекающая плоскость, перпендикулярна
двум прямым в этой плоскости, проходящим
через точку пересечения данной прямой
и плоскости, то она перпендикулярна
плоскости.
Теорема
2
1-ое
СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И
ПЛОСКОСТИ.
Если плоскость
перпендикулярна одной из двух
параллельных прямых, то она перпендикулярна
и другой
Теорема
3
2-ое
СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И
ПЛОСКОСТИ.
Две прямые,
перпендикулярные одной и той же
плоскости, параллельны.
Билет
7.1
Теорема.
Пусть 
, 
–
промежуток, функция 
непрерывна.
Тогда у функции
есть
первообразная.
Рассмотрим
функцию 
на
промежутке 
.
По предыдущей теореме, эа функция
имеет первообразную. Все первообразные
ее имеют вид 
.
Выберем из всех этих первообразных
такую, значение которой при 
равно 
.
Такая первообразная найдется (почему?).
Назовем ее натуральным
логарифмом.
Обозначение: 
.
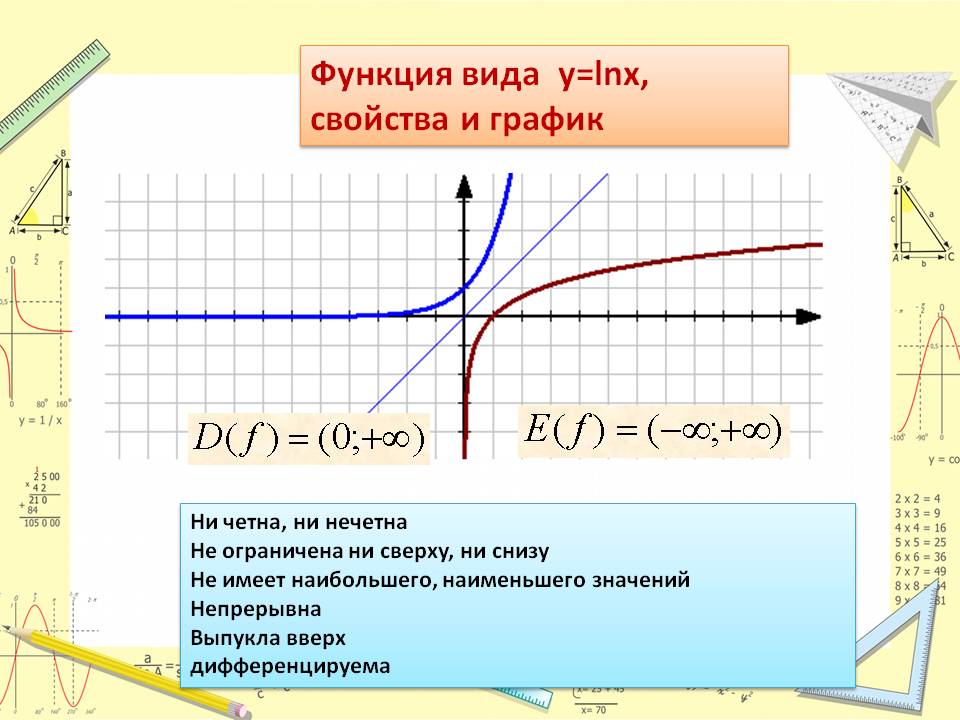
Свойства
натурального логарифма
1. Область
определения натурального логарифма
.
2. 
.
3. Натуральный
логарифм – дифференцируемая функция,
и 
, 
.
4. Натуральный
логарифм строго возрастает, так как
.
5. 
.
7.2
Расстояние
от точки до плоскости равно длине
перпендикуляра, опущенного из точки
на эту плоскость. Пусть требуется
найти расстояние от точки K до
плоскости s (АВС).
|
Алгоритм
|
Расстояние
между параллельными плоскостями
определяется длиной перпендикуляра,
опущенного из произвольной точки
одной плоскости до другой. Аналогично
находится расстояние от плоскости до
параллельной ей прямой. На прямой
берется точка и находится расстояние
до плоскости.
|
Перпендикуляром, Конец Расстоянием от |
Наклонной, Конец отрезка, |
|
Отрезок, |
Билет
8.1
При a >
0, a 
= 1,
определена функция y = a x ,
отличная от постоянной. Эта функция
называется показательной
функцией с
основанием a.
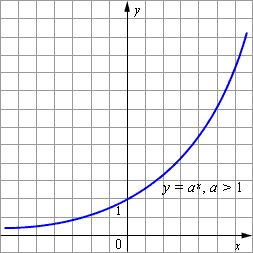
Основные
свойства показательной
функции y = a x при a >
1:
-
Область
определения функции – вся числовая
прямая. -
Область
значений функции – промежуток (0;+
). -
Функция
строго монотонно возрастает на всей
числовой прямой, то есть, если x1<
x2
, то ax1 <
ax2 . -
При x =
0 значение функции равно 1. -
Если x >
0 , то a x >
1 и если x <
0, то 0 < a <
1.
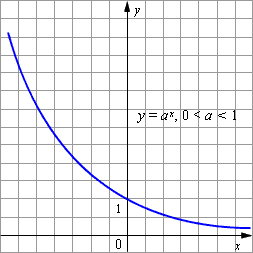
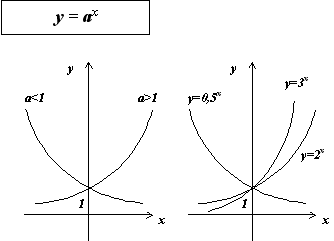
Графики
показательных функций с основанием
0 < a <
1 и a >
1 изображены на рисунке.
|
|
|
Основные
свойства показательной функции y = a x при
0 < a <
1:
-
Область
определения функции – вся числовая
прямая. -
Область
значений функции – промежуток (0;+
). -
Функция
строго монотонно возрастает на всей
числовой прямой, то есть, если x1<
x2
, то ax1 >
ax2 . -
При x =
0 значение функции равно 1. -
Если x >
0 , то 0 < a <
1 и если x <
0, то a x >
1.
К
общим свойствам показательной функции
как при 0 < a < 1, так и при a >
1 относятся:
-
ax1 ax2 = ax1+ x2,
для всех x1 и x2. -
a−x=(ax)−1=1ax для
любого x. -
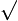
nax=axn для
любого x и
любого n
N
n
=1 . -
(ab)x = ax bx для
любых a,
b >
0; a,b
=1 . -
(ba)x=bxax для
любых a,
b >
0; a,b
=1 . -
ax1 = ax2,
то x1 = x2.
8.2
|
Теорема О Если И |
|
|
Доказательство: Пусть АВ – Проведем АНАЛОГИЧНО. |
Билет
9.1
На
промежутке (0; +∞) определена
функция, обратная к ax (a > 0, a ≠ 1).
Эта функция называется логарифмической:
|
y = loga x. |
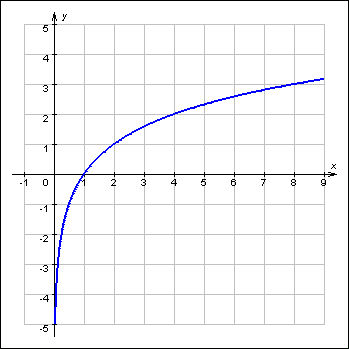
Логарифмическая
функция непрерывна и строго возрастает
(если основание a > 1) или
строго убывает (если 0 < a < 1) на
всей области определения. Множество
ее значений – все действительные
числа.
Так
как логарифмическая и показательная
функции взаимно обратны, то
при a > 0, a ≠ 1,
|
|
|
График
График |
|
|
Ниже
приведены некоторые свойства
логарифмов
(x > 0, 
a > 0, a ≠ 1, b > 0, b ≠ 1, 
).
|
9.2
Пусть
прямая пересекает плоскость, причем
не под прямым, а под каким-то
другим углом. Такая прямая
называется наклонной.
Опустим
перпендикуляр из какой-либо точки
наклонной на нашу плоскость. Соединим
основание перпендикуляра с точкой
пересечения наклонной и плоскости.
Мы получилипроекцию
наклонной на плоскость.
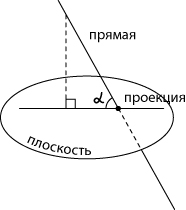
Угол
между прямой и плоскостью — это
угол между прямой и ее проекцией
на данную плоскость.
Обратите
внимание — в качестве угла между
прямой и плоскостью мы выбираем
острый угол.
Если
прямая параллельна плоскости, значит,
угол между прямой и плоскостью
равен нулю.
Если
прямая перпендикулярна плоскости,
ее проекцией на плоскость окажется
точка. Очевидно, в этом случае угол
между прямой и плоскостью равен
90°.
Прямая
перпендикулярна плоскости, если она
перпендикулярна любой прямой, лежащей
в этой плоскости.
Это
определение. Но как же с ним
работать? Как проверить, что данная
прямая перпендикулярна всем прямым,
лежащим в плоскости? Ведь их там
бесконечно много.
На практике
применяется признак
перпендикулярности прямой и плоскости:
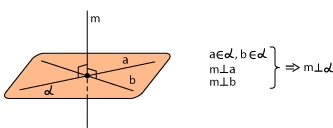
Прямая
перпендикулярна плоскости, если она
перпендикулярна двум пересекающимся
прямым, лежащим в этой плоскости.
Билет 10.1
Функция,
заданная формулой y = ax2 + bx + c
, где x и y –
переменные, а a, b, c – заданные
числа, причем a
=0 ,
называется квадратичной
функцией.
График квадратичной функции – парабола.
Если a > 0 , то ветви параболы
направлены вверх. Если a <
0 , то ветви параболы направлены вниз.
График квадратичной функции
называется параболой.
Любая
квадратичная функция представима в
виде 
.
Координаты
вершины параболы: 
.
Прямая 
является осью
симметрии графика
квадратичной функции.
При 
ветви
параболы направлены вниз, при 
—
вверх.
|
Свойство |
Дискриминант |
||
|
|
|
|
|
|
Область |
|
||
|
Множество |
|
||
|
Множество |
|
||
|
Нули |
|
|
|
|
Положительные |
|
Везде, |
Везде |
|
Отрицательные |
|
Отсутствуют |
|
|
Промежуток |
|
||
|
Промежуток |
|
||
|
Минимальное |
|
10.2
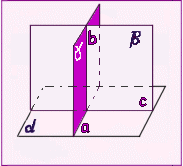
Двугранный
угол —
пространственная геометрическая
фигура,
образованная двумя полуплоскостями,
исходящими из одной прямой, а также
часть пространства, ограниченная
этими полуплоскостями
Двугранные
углы измеряются линейным углом, то
есть углом, образованным пересечением
двугранного угла с плоскостью,
перпендикулярной к его ребру. Таким
образом, чтобы измерить двугранный
угол, можно взять любую точку на его
ребре и перпендикулярно ребру провести
из неё лучи в каждую из граней. Линейный
угол между этими двумя лучами и будет
равен по величине двугранному углу.
Если один из лучей не перпендикулярен
ребру, то величина линейного угла
между лучами в общем случае будет
отлична от величины двугранного угла.
Например, в любой двугранный угол (в
том числе больший 90 градусов) можно
поместить прямой
угол так,
чтобы его вершина лежала на ребре
двугранного угла, а стороны принадлежали
его граням. В этом легко убедиться,
размещая угольник в
приоткрытой книге.
У
всякого многогранника,
правильного или неправильного,
выпуклого или вогнутого, есть двугранный
угол на каждом ребре.
Величины
двугранных углов правильных
многогранников:
|
Название |
точный |
приближённое |
|
Тетраэдр |
arccos(1/3) |
70.53° |
|
Гексаэдр или куб |
π/2 |
90°(точн.) |
|
Октаэдр |
π |
109.47° |
|
Додекаэдр |
2·arctg(φ) |
116.56° |
|
Икосаэдр |
2·arctg(φ |
138.19° |
где
φ = (1 + √5)/2 — золотое
сечение.
Билет
11.1
Справедлива
следующая теорема.
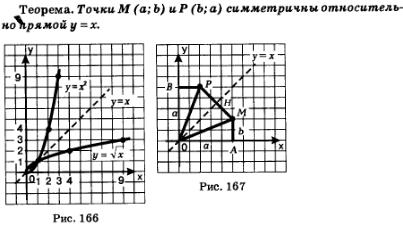
Доказательство. Будем
считать для определенности, что а и b
— положительные числа. Рассмотрим
треугольники ОАМ и ОВР (рис. 167). Они
равны, значит, ОР = ОМ и
.
Но тогда и
поскольку
прямая у = х — биссектриса угла АОВ.
Итак, треугольник РОМ — равнобедренный,
ОН — его биссектриса, а значит, и
ось симметрии. Точки М и Р симметричны
относительно прямой ОН, что и требовалось
доказать.
Итак, график
функции
можно
получить из графика функции у = х2, х>0
с помощью преобразования симметрии
относительно прямой у = х. Аналогично
график функции
можно
получить из графика функции у = х3, х>
0 с помощью преобразования симметрии
относительно прямой у=х; график
функции
можно
получить из графика функции
с
помощью преобразования симметрии
относительно прямой у = х и т.д. Напомним,
что график функции
напоминает
по виду ветвь параболы
Чем
больше п, тем круче эта ветвь устремляется
вверх на промежутке
и
тем ближе подходит к оси х в окрестности
точки х=0 (рис. 168).
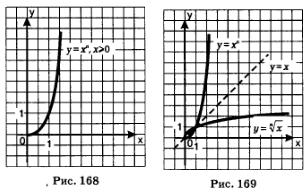
Сформулируем
общий вывод: график функции
симметричен
графику функции
,
относительно прямой у = х(рис. 169).
Свойства
функции
1)
2)
функция не является ни четной, ни
нечетной;
3) возрастает
на
4)
не ограничена сверху, ограничена
снизу;
5) не имеет наибольшего
значения;
6)
непрерывна;
7)
11.2
|
Теорема ПРИЗНАК Если |
|
|
Доказательство: Пусть Проведем |
|
Билет12.1
12.2
Параллелепипед —
это четырехугольная призма, все грани
которой — параллелограммы.
Параллелепипеды,
как и призмы, могут быть прямыми и
наклонными.
Прямой
параллелепипед,
основанием которого служит прямоугольник,
называют прямоугольным параллелепипедом.
У
прямоугольного параллелепипеда все
грани — прямоугольники.
Длины
трёх ребер прямоугольного параллелепипеда,
имеющих общий конец, называют его
измерениями.
Куб —
прямоугольный параллелепипед с равными
измерениями.
Все
шесть граней куба — равные квадраты.
Параллелепипед
симметричен относительно середины
его диагонали.
Любой
отрезок с концами, принадлежащими
поверхности параллелепипеда и
проходящий через середину его диагонали,
делится ею пополам; в частности, все
диагонали параллелепипеда пересекаются
в одной точке и делятся ею пополам.
Противолежащие
грани параллелепипеда параллельны и
равны.
Квадрат
длины диагонали прямоугольного
параллелепипеда равен сумме квадратов
трёх его измерений
В
параллелепипеде:
1)
противолежащие грани равны и
параллельны;
2)
все четыре диагонали пересекаются в
одной точке и делятся в ней пополам.
Доказательства:
1)
Для любой пары противолежащих граней
параллелепипеда имеем: соответствующие
углы равны (например,
,
и
т. д.); соответствующие стороны равны
и параллельны (
и
,
и
и
т. д. как противолежащие стороны
параллелограммов). Отсюда
и
их плоскости параллельны.
2)
и
,
поэтому
.
Через
и
проведем
плоскость, тогда
.
—
параллелограмм. Его диагонали
и
,
являющиеся диагоналями параллелепипеда,
в точке пересечения делятся пополам.
Теперь возьмем одну из этих диагоналей,
например
и
третью диагональ параллелепипеда
.
Они являются диагоналями параллелограмма
и
поэтому
проходит
через середину
,
т. е. три диагонали параллелепипеда
пересекаются в одной точке и делятся
в ней пополам. Аналогично доказывается
и для четвертой диагонали
.
Теорема
3
В
прямоугольном параллелепипеде квадрат
любой диагонали равен сумме квадратов
трех его измерений (т. е. трех ребер,
выходящих из одной вершины).
Следствие
В
прямоугольном параллелепипеде все
диагонали равны.
Билет
13.1
Простейшими
называются тригонометрические
уравнения следующих четырёх видов:
sin
x = a; cos x = a; tg x = a; ctg x = a:
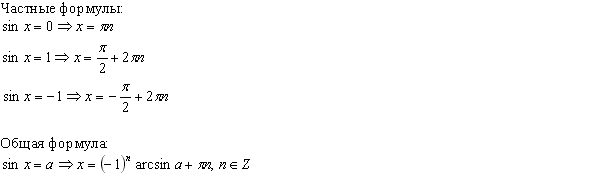
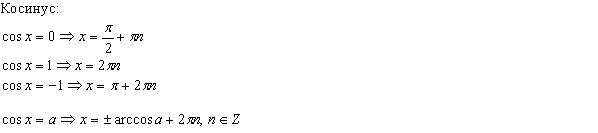
Общий
вид решения уравнения tg x = a определяется
формулой:
x = arctg(a) + pk, k Î Z
(целые числа).
Общий
вид решения уравнения ctg x = a определяется
формулой:
x = arcctg(a) + pk, k Î Z
(целые числа).
Прямая и плоскость в пространстве
§ 8.Параллельность прямой и плоскости
В пространстве прямая может лежать в плоскости, а может и не лежать в ней. При этом, если прямая не лежит в плоскости, то по аксиоме прямой и плоскости она не может иметь с этой плоскостью более одной общей точки. Это означает, что плоскость и не лежащая в ней прямая либо имеют одну общую точку, либо не имеют ни одной общей точки. Если прямая и плоскость имеют ровно одну общую точку, то они пересекаются. А если прямая и плоскость не имеют ни одной общей точки?
Определение. Прямая и плоскость, не имеющие общей точки, называются параллельными.
Если прямая a и плоскость α параллельны, то записывают a ‖ α или α ‖ a. При этом говорят, что прямая a параллельна плоскости α или плоскость α параллельна прямой a.
При решении стереометрических задач обоснование параллельности прямой и плоскости при помощи только одного определения их параллельности часто затруднительно и не приводит к желаемому результату. В таких случаях пользуются признаками параллельности прямой и плоскости, один из которых выражает следующая теорема.
Теорема 9 (признак параллельности прямой и плоскости). Если прямая, не лежащая в плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то эти прямая и плоскость параллельны.
Рис. 50
Дано: b ⊂ α, a ‖ b, a ⊄ α (рис. 50).
Доказать: a ‖ α.
Доказательство. Так как прямая b лежит в плоскости α, то (по теореме о двух параллельных прямых, одна из которых пересекает плоскость (т. 5)) прямая a, параллельная прямой b, не может пересекать плоскость α; а так как прямая a по условию не лежит в плоскости α, то прямая a параллельна плоскости α. Теорема доказана. ▼
Из этой теоремы, в частности, вытекает факт существования и способ построения прямой, параллельной данной плоскости и проходящей через данную точку, не лежащую в этой плоскости.
Теорема 10. Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то прямая пересечения этих плоскостей параллельна данной прямой.
Рис. 51
Дано: a ‖ β, a ⊂ α, α ∩ β = b (рис. 51).
Доказать: b ‖ a.
Доказательство. Прямые a и b лежат в одной плоскости α. Кроме того, прямая a не имеет общих точек с прямой b, так как прямая a по условию параллельна плоскости β, в которой лежит прямая b. Таким образом, прямые a и b лежат в одной плоскости и не имеют общих точек, следовательно, они параллельны по определению. Теорема доказана. ▼
Из этой теоремы, в частности, следует, что если прямая a параллельна плоскости α, то в плоскости α существует прямая, параллельная прямой a, и таких прямых в плоскости α бесконечно много.
Теорема 11. Если через каждую из двух параллельных прямых проведена плоскость, причём эти плоскости пересекаются, то прямая их пересечения параллельна каждой из данных прямых.
Рис. 52
Дано: a ‖ b, a ⊂ α, b ⊂ β, α ∩ β = c (рис. 52).
Доказать: c ‖ a, c ‖ b.
Доказательство. Докажем, что прямая c параллельна прямой a.
По условию теоремы прямая a параллельна прямой b, лежащей в плоскости β, а значит (по признаку параллельности прямой и плоскости), прямая a параллельна и самой плоскости β. Кроме того, плоскость α проходит через прямую a и пересекает плоскость β по прямой c. По теореме 10 прямые a и c параллельны. Тогда на основании свойства транзитивности параллельности прямых прямая b параллельна прямой c. Теорема доказана. ▼
Докажите самостоятельно ещё один признак параллельности прямой и плоскости.
Плоскость и не лежащая в ней прямая, параллельные некоторой прямой, параллельны.
Теорема 12. Если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна их линии пересечения.
Рис. 53
Дано: α ∩ β = a, b ‖ α, b ‖ β (рис. 53).
Доказать: b ‖ a.
Доказательство. По следствию из теоремы 10 в плоскостях α и β существуют соответственно прямые m и n, параллельные прямой b, а следовательно, параллельные между собой. Тогда по теореме 11 прямые m и n параллельны прямой a пересечения плоскостей α и β. На основании транзитивности параллельности прямых прямая b параллельна прямой a. Теорема доказана. ▼
ЗАДаЧа 3.005. Даны две скрещивающиеся прямые a и b. Через каждую точку прямой a проводится прямая, параллельная прямой b. Доказать, что все такие прямые лежат в одной плоскости. Как расположена эта плоскость по отношению к прямой b? Ответ обосновать.
Рис. 54
Решение. Отметим на прямой a произвольную точку B и проведём через неё прямую c (единственную!), параллельную прямой b. Через пересекающиеся прямые a и c проводим плоскость (единственную!). Обозначим её α (рис. 54). Эта плоскость (по признаку параллельности прямой и плоскости) параллельна прямой b.
Пусть M — произвольная точка прямой a, m — прямая, проходящая через точку M параллельно прямой b. Тогда прямая m параллельна прямой c (т. 7) и лежит в плоскости α (почему?). В силу произвольного выбора точки M на прямой a можно сделать вывод: все прямые пространства, параллельные прямой b и пересекающие прямую a, лежат в плоскости, которая проходит через прямую a и параллельна прямой b.
Самостоятельно докажите единственность плоскости α.
Параллельность прямых (a) и (b) обозначается так:
a∥b илиb∥a
.
Teорема 1. Через две параллельные прямые можно провести плоскость, и притом только одну.
1. так как прямые (a) и (b) параллельны, из определения следует, что через них можно провести плоскость
α
.
2. Чтобы доказать, что такая плоскость только одна, на прямой (a) обозначаем точки (B) и (C), а на прямой (b) — точку (A).
3. Так как через три точки, которые не лежат на одной прямой, можно провести только одну плоскость ((2) аксиома), то
α
является единственной плоскостью, которой принадлежат прямые (a) и (b).
Теорема 2. Через любую точку пространства вне данной прямой можно провести прямую, параллельную данной прямой, и притом только одну.
Доказательство:
1. через данную прямую (a) и точку (M), которая не лежит на прямой, проводится плоскость
α
.
2. Такая плоскость только одна (т. к. через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну).
3. А в плоскости
α
через точку (M) можно провести только одну прямую (b), которая параллельна прямой (a).
Теорема 3. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
(1 рис.)
(2 рис.)
Доказательство:
рассмотрим две параллельные прямые (a) и (b) и допустим, что прямая (b) пересекает плоскость
α
в точке (M) (1 рис.).
Из (1)-й теоремы известно, что через параллельные прямые (a) и (b) можно провести только одну плоскость
β
.
Так как точка (M) находится на прямой (b), то (M) также принадлежит плоскости
β
(2 рис.). Если у плоскостей
α
и
β
есть общая точка (M), то у этих плоскостей есть общая прямая (c), которая является прямой пересечения этих плоскостей ((4) аксиома).
Прямые (a), (b) и (c) находятся в плоскости
β
.
Если в этой плоскости одна из параллельных прямых (b) пересекает прямую (c), то вторая прямая (a) тоже пересекает (c).
Точку пересечения прямых (a) и (c) обозначим за (K).
Так как точка (K) находится на прямой (c), то (K) находится в плоскости
α
и является единственной общей точкой прямой (a) и плоскости
α
.
Значит, прямая (a) пересекает плоскость
α
в точке (K).
Теорема 4. Две прямые, параллельные третьей прямой, параллельны.
Доказательство:
выберем точку (M) на прямой (b).
Через точку (M) и прямую (a), которая не содержит эту точку, можно провести только одну плоскость
α
(через прямую и не лежащую на ней точку можно провести только одну плоскость).
Возможны два случая:
1) прямая (b) пересекает плоскость
α
; или 2) прямая (b) находится в плоскости
α
.
Пусть прямая (b) пересекает плоскость
α
.
Значит, прямая (c), которая параллельна прямой (b), тоже пересекает плоскость
α
. Так как
a∥c
, то получается, что (a) тоже пересекает эту плоскость. Но прямая (a) не может одновременно пересекать плоскость
α
и находиться в плоскости
α
. Получаем противоречие, следовательно, предположение, что прямая (b) пересекает плоскость
α
, является неверным.
Значит, прямая (b) находится в плоскости
α
.
Теперь нужно доказать, что прямые (a) и (b) параллельны.
Пусть у прямых (a) и (b) есть общая точка (L).
Это означает, что через точку (L) проведены две прямые (a) и (b), которые параллельны прямой (c). Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые (a) и (b) не имеют общих точек.
Так как прямые (a) и (b) находятся в одной плоскости
α
, и у них нет общих точек, то они параллельны.
Всё множество прямых в пространстве, которые параллельны данной прямой, называется пучком параллельных прямых.
Выводы:
1) любые две прямые пучка параллельных прямых параллельны между собой.
2) Параллельности прямых в пространстве присуща транзитивность:
еслиa∥bиb∥c,тоa∥c.
Пример:
одна сторона параллелограмма пересекает плоскость. Докажите, что прямая, которая содержит противоположную сторону параллелограмма, тоже пересекает эту плоскость.
Допустим, что у параллелограмма (ABCD) сторона (AD) пересекает плоскость
α
в точке (K).
Так как противоположные стороны параллелограмма параллельны, то, согласно третьей теореме, прямая, которая содержит сторону (BC), тоже пересекает плоскость
α
.
2) прямая и плоскость имеют только одну общую точку (прямая и плоскость пересекаются);
3) прямая и плоскость не имеют ни одной общей точки.
Теорема 5 «Признак параллельности прямой и плоскости».
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.
Геометрия, 10 класс
Урок №4. Параллельность прямых, прямой и плоскости
Перечень вопросов, рассматриваемых в теме
- Определение параллельных прямых;
- Теорема о единственности прямой, параллельной данной, проходящей через данную точку;
- лемма о двух параллельных прямых;
- теорему о параллельности трех прямых;
- определение параллельных прямой и плоскости;
- признаком параллельности прямой и плоскости.
Глоссарий по теме
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые − прямые, которые не лежат в одной плоскости.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Основная литература:
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл.– М.: Просвещение, 2014. 255 с.
Дополнительная литература:
Зив Б. Г. Дидактические материалы. Геометрия 10 кл. – М.: Просвещение, 2014. 96 с.
Глазков Ю. А., Юдина И. И., Бутузов В.Ф. Рабочая тетрадь. Геометрия 10 кл.-М.: Просвещение, 2013. 65 с.
Теоретический материал для самостоятельного изучения
Геометрия, которую мы изучаем, называется евклидовой, по имени древнегреческого ученого Евклида (3 век до нашей эры), который создал целый труд по математике под названием «Начала». В данной книге есть раздел о параллельных прямых.
В советском энциклопедическом словаре слово «параллельность» переводится с греческого языка, как «идущий рядом».
В средние века параллельность обозначалась знаком «=». В 1557 году Р. Рекордом для обозначения равенства был введен знак «=», которым мы пользуемся сейчас, а параллельность стали обозначать «║».
В книге «Начала» определение параллельных прямых звучало так «прямые, лежащие в одной плоскости и будучи бесконечно продолжены в обе стороны, ни с той, ни с другой стороны не пересекаются». Это определение почти не отличается от современного.
В области параллельных прямых работало очень много учёных: Н.И. Лобаческий (18-19 век); Аббас ал-Джаухари (работал в Багдаде в 9 веке); Фадл ал-Найризи (Богдад 10 век); Герард (Италия 12 век); Иоганн Генрих Ламберт (Берлин) и многие другие.
Каково расположение 2-х прямых на плоскости (совпадают, пересекаются, параллельны) (рис. 1 а, б, в).
Перейдем к взаимному расположению 2-х прямых в пространстве. Как и в планиметрии, две различные прямые в пространстве либо пересекаются в одной точке, либо не пересекаются (не имеют общих точек). Но второй случай допускает две возможности: прямые лежат в одной плоскости (параллельны) или прямые не лежат в одной плоскости. В первом случае они параллельны, а во втором – такие прямые называются скрещивающимися.
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.
Проиллюстрировать данные определения наглядно нам поможет куб.
Давайте укажем некоторые пары параллельных прямых:
AB||A₁B₁; AB|| CD; A₁B₁||C₁D₁; CD||C₁D₁; AD||A₁D₁; BC||B₁D₁; AD||BC; A₁D₁||B₁C₁.
А теперь рассмотрим некоторые пары скрещивающихся прямых, как мы отметили, они не должны лежать в одной плоскости:
AB A₁D₁; AB B₁C₁; CD A₁D₁; CD B₁C₁; BC C₁D₁; BC A₁B₁; AB B₁C₁; AB A₁D₁.
Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
- М и а задают плоскость α
- Прямая, проходящая через точку М параллельно прямой а, должна лежать в одной плоскости с точкой М и прямой а, т.е. в плоскости α.
- В плоскости α через точку М проходит прямая, параллельная прямой а, и притом только одна- это нам известно из кураса планиметрии.
- На чертеже эта прямая обозначена буквой b .
- Следовательно, b-единственная прямая, проходящая через точку М паралельно прямой а.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Аналогично определяется праралельность отрезка и прямой, а так же паралельность двух лучей.
Лемма. Если одна из двух паралельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
- Рассмотрим две параллельные прямые a и b и допустим, что прямая b пересекает плоскость α в точке M(а рис.).
- Мы знаем, что через параллельные прямые a и b можно провести только одну плоскость β. (теорема)
- Так как точка M находится на прямой b, то M также принадлежит плоскости β (б рис.). Если у плоскостей α и β есть общая точка M, то у этих плоскостей есть общая прямая p, которая является прямой пересечения этих плоскостей (4 аксиома).
- Прямые a, b и c находятся в плоскости β.
Если в этой плоскости одна из параллельных прямых b пересекает прямую p, то вторая прямая a тоже пересекает p.
- Точку пересечения прямых a и p обозначим за N.
Так как точка N находится на прямой p, то N находится в плоскости α и является единственной общей точкой прямой a и плоскости α.
- Значит, прямая a пересекает плоскость α в точке N.
Нам известно из курса планиметрии, что если три прямые лежат в одной плоскости и две из них параллельны третьей, то эти две прямые параллельны. Похожее утверждение имеет место и для трех прямых в пространстве.
Теорема. Если две прямые параллельны третьей прямой, то они параллельны.
Дано: a∥c и b∥c
Доказать: a∥b
Доказательство:
Выберем точку M на прямой b.
Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).
Возможны два случая:
1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.
Пусть прямая b пересекает плоскость α.
Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным. Значит, прямая b находится в плоскости α.
Теперь нужно доказать, что прямые a и b параллельны.
Пусть у прямых a и b есть общая точка L.
Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.
Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.
Если две точки прямой лежат в данной плоскости, то по аксиоме А₂ вся прямая лежит в этой плоскости. Из этого следует, что возможны три расположения прямой и плоскости:
|
|
|
|
|
|
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Обозначение: a||α.
Наглядный пример, который дает представление о прямой, параллельной плоскости- это линия пересечения стены и потолка-она параллельна плоскости пола.
Теорема (Признак параллельности прямой и плоскости)
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.
Доказательство:
Доказательство проведем от противного. Пусть a не параллельна плоскости α, тогда прямая a пересекает плоскость в некоторой точке A. Причем A не находится на b, так как a∥b. Согласно признаку скрещивающихся прямых, прямые a и b скрещивающиеся.
Мы пришли к противоречию. Так как согласно данной информации a∥b, они не могут быть скрещивающимися. Значит, прямая a должна быть параллельна плоскости α.
Существует еще два утверждения, которые используются при решении задач:
- Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
- Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо тоже параллельна данной плоскости, либо лежит в этой плоскости.
Примеры и разбор решения заданий тренировочного модуля
№1.
Тип задания: Ввод с клавиатуры пропущенных элементов в тексте
Дано: в ∆ АВС КМ − средняя линия, КМ=5; ACFE- параллелограмм.
Найти: EF
Решение: Т.к. КМ − средняя линия, то АС= 2·КМ, то АС=2·7=10
Т.к. ACFE − параллелограмм, то АС=EF=10
Ответ: EF=10
№2.
Тип задания: Единичный / множественный выбор
Точка М не лежит в плоскости ромба ABCD. На отрезке АМ выбрана точка Е так, что MЕ:ЕА=1:3. Точка F – точка пересечения прямой МВ с плоскостью CDE. Найдите АВ, если AD= 8 cм.
-
- АВ=2 см
- АВ=4 см
- АВ=5 см
- АВ=10 см
Решение:
MC 
Т.к. AD||BC||FK, следовательно, треугольники MFK и MBC- подобны (по трем углам). Значит
. BC=AD= 8 см; 
FK=BC:4=8:4=2
Ответ: 2. АВ=4 см.
