Как найти прямую пересечения плоскостей куб

Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.

Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.

Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.

1) Построить сечение куба плоскостью, проходящей через точки A, C и M.

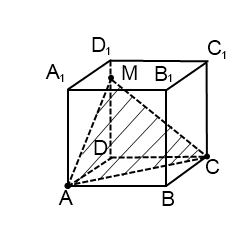
Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.

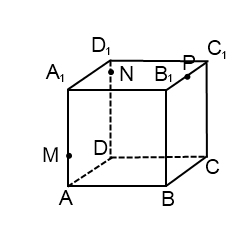
2) Построить сечение куба плоскостью, проходящей через точки M, N, P.

Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.

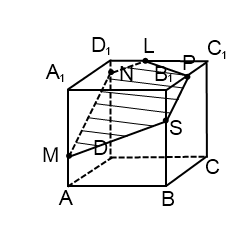Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).

Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).

Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.

Пятиугольник MNLPS — искомое сечение.

3) Построить сечение куба плоскостью, проходящей через точки M, N, P.

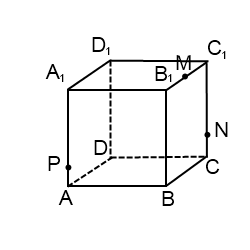
Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый). Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).

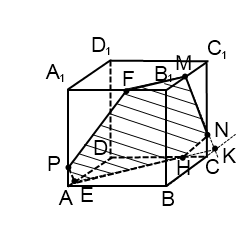
Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях. Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.

Если продолжать прямую MN, то, поскольку она лежит в плоскости (BCC1), нужно искать точку пересечения MN с одной из прямых этой плоскости. С CC1 и B1C1 точки пересечения уже есть — это M и N. Остаются прямые BC и BB1. Продолжим BC и MN до пересечения в точке K. Точка K лежит на прямой BC, значит, она принадлежит плоскости (ABC), поэтому через нее и точку E, лежащую в этой плоскости, можем провести прямую. Она пересекает ребро CD в точке H. EH -ее след (невидимый). Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).

Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.

Шестиугольник MNHEPF — искомое сечение.

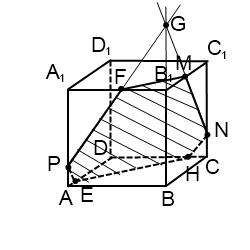
Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1). А значит, через G и P можно провести прямую, след которой PF. Далее — проводим прямые через точки, лежащие в параллельных плоскостях, и приходим к тому же результату.

Работа с прямой PE дает то же сечение MNHEPF.

4) Построить сечение куба плоскостью, проходящей через точку M, N, P.

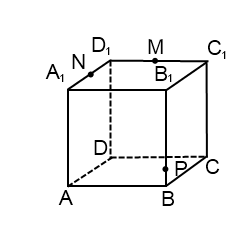Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.

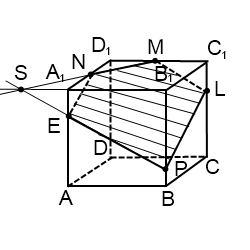Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый). В плоскости (ADD1) есть прямая NE, в параллельной ей плоскости (BCC1) — точка P. Через точку P можем провести прямую PL, параллельную NE. Она пересекает ребро CC1 в точке L. PL — след этой прямой (видимый). Точки M и L лежат в одной плоскости (CDD1), значит, через них можно провести прямую. Ее след — ML (невидимый). Пятиугольник MLPEN — искомое сечение.

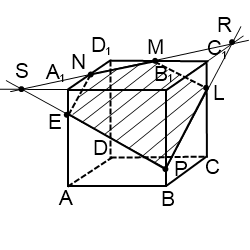Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1). В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.

Линия пересечения плоскостей онлайн

С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку “Решить”. Теоретическую часть и численные примеры смотрите ниже.

Линия пересечения плоскостей − теория, примеры и решения

Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α₁ и α₂:

α1:  A1x+B1y+C1z+D1=0,

(1)

α2:  A2x+B2y+C2z+D2=0,

(2)

где n₁={A₁, B₁, C₁} и n₂={A₂, B₂, C₂} − нормальные векторы плоскостей α₁ и α₂, соответственно.

Найдем уравнение линии пересеченя плоскостей α₁ и α₂. Для этого рассмотрим следующие случаи:

1. Нормальные векторы n₁ и n₂ плоскостей α₁ и α₂ коллинеарны (Рис.1).

Поскольку векторы n₁ и n₂ коллинеарны, то существует такое число λ≠0, что выполнено равенство n₁=λn₂, т.е. A₁=λA₂, B₁=λB₂, C₁=λC₂.

Умножив уравнение (2) на λ, получим:

α2:  A1x+B1y+C1z+λD2=0,

(3)

Если выполненио равенство D₁=λD₂, то плоскости α₁ и α₂ совпадают, если же D₁≠λD₂то плоскости α₁ и α₂ параллельны, то есть не пересекаются.

2. Нормальные векторы n₁ и n₂ плоскостей α₁ и α₂ не коллинеарны (Рис.2).

Если векторы n₁ и n₂ не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:

Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.

Так как в системе линейных уравнений (4) векторы n₁={A₁, B₁, C₁} и n₂={A₂, B₂, C₂} не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:

где x₀, y₀, z₀, m, p, l действительные числа, а t − переменная.

Равенство (5) можно записать в следующем виде:

Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α₁ и α₂. Полученное уравнение прямой можно записать в каноническом виде:

Пример 1. Найти линию пересечения плоскостей α₁ и α₂:

Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α₁ имеет нормальный вектор n₁={A₁, B₁, C₁}={1, 2, 1}. Плоскость α₂ имеет нормальный вектор n₂={A₂, B₂, C₂}={2, 9, −5}.

Поскольку направляющие векторы n₁ и n₂ неколлинеарны, то плолскости α₁ и α₂ пересекаются.

Для нахождения линии пересечения влоскостей α₁ и α₂ нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:

Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строку 2 со строкой 1, умноженной на −2:

Второй этап. Обратный ход Гаусса.

Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Получим решение:

где t− произвольное действительное число.

Запишем (11) в следующем виде:

Получили уравнение линии пересечения плоскостей α₁ и α₂ в параметрическом виде. Запишем ее в каноническом виде.

Из равентсв выше получим каноническое уравнение прямой:

Ответ. Уравнение линии пересечения плоскостей α₁ и α₂имеет вид:

Пример 2. Найти линию пересечения плоскостей α₁ и α₂:

Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α₁ имеет нормальный вектор n₁={A₁, B₁, C₁}={1, 2, 7}. Плоскость α₂ имеет нормальный вектор n₂={A₂, B₂, C₂}={2, 4, 14}.

Поскольку направляющие векторы n₁ и n₂ коллинеарны (n₁ можно получить умножением n₂ на число 1/2), то плоскости α₁ и α₂ параллельны или совпадают.

При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α₂ умножив на число 1/2:

Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α₁ и α₂ не совпадают. Следовательно они параллельны, т.е. не пересекаются.

Пример 3. Найти линию пересечения плоскостей α₁ и α₂:

Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α₁ имеет нормальный вектор n₁={A₁, B₁, C₁}={5, −2, 3}. Плоскость α₂ имеет нормальный вектор n₂={A₂, B₂, C₂}={15, −6, 9}.

Поскольку направляющие векторы n₁ и n₂ коллинеарны (n₁ можно получить умножением n₂ на число 1/3), то плоскости α₁ и α₂ параллельны или совпадают.

При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α₂ умножив на число 1/3:

Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α₁ и α₂ совпадают.

Прямая как линия пересечения плоскостей

Прямая
в пространстве может быть определена
как линия пересечения двух непараллельных
плоскостей
и,
то есть как множество точек, удовлетворяющих
системе двух линейных уравнений

(V.5)

Справедливо
и обратное утверждение: система двух
независимых линейных уравнений вида
(V.5)
определяет прямую как линию пересечения
плоскостей (если они не параллельны).
Уравнения системы (V.5)
называются общим
уравнением прямой
в пространстве
.

Пример
V.12.
Составить
каноническое уравнение прямой, заданной
общими уравнениями плоскостей

Решение.
Чтобы написать
каноническое уравнение прямой или, что
тоже самое, уравнение прямой, проходящей
через две данные точки, нужно найти
координаты каких-либо двух точек прямой.
Ими могут служить точки пересечения
прямой с какими-нибудь двумя координатными
плоскостями, например Oyz
и Oxz.

Точка
пересечения прямой с плоскостью Oyz
имеет абсциссу
.
Поэтому, полагая в данной системе
уравнений,
получим систему с двумя переменными:

Ее
решение
,вместе сопределяет точкуискомой прямой. Полагая в данной системе
уравнений,
получим систему

решение
которой
,вместе сопределяет точкупересечения прямой с плоскостьюOxz.

Теперь
запишем уравнения прямой, проходящей
через точки
и:или,
гдебудет направляющим векто-ром этой
прямой.

Пример
V.13.
Прямая задана
каноническим уравнением
.
Составить общее уравнение этой прямой.

Решение.
Каноническое
уравнение прямой можно записать в виде
системы двух независимых уравнений:



Получили
общее уравнение прямой, которая теперь
задана пересечением двух плоскостей,
одна из которых
параллельна осиOz
(),
а другая– осиОу
().

Данную
прямую можно представить в виде линии
пересечения двух других плоскостей,
записав ее каноническое уравнение в
виде другой пары независимых уравнений:



Замечание.
Одна и та же прямая может быть задана
различными системами двух линейных
уравнений (то есть пересечением различных
плоскостей, так как через одну прямую
можно провести бесчисленное множество
плоскостей), а также различными
каноническими уравнениями (в зависимости
от выбора точки на прямой и ее направляющего
вектора).

Ненулевой
вектор, параллельный прямой линии, будем
называть ее направляющим
вектором.

Пусть
в трехмерном пространстве

задана прямая l,
проходящая через точку
,
и ее направляющий вектор.

Любой
вектор
,
где,
лежащий на прямой, коллинеарен с вектором,
поэтому их координаты пропорциональны,
то есть

.
(V.6)

Это
уравнение называется каноническим
уравнением прямой. В частном случае,
когда ﻉ
есть
плоскость, получаем уравнение прямой
на плоскости

.
(V.7)

Пример
V.14.
Найти уравнение прямой, проходящей
через две точки
,.

Будем
считать вектор
направляющим, тогда уравнение искомой
прямой имеет вид

,

где
,,.

Удобно
уравнение (V.6)
записать в параметрической форме. Так
как координаты направляющих векторов
параллельных прямых пропорциональны,
то, полагая

,

получим

где
t
– параметр,
.

Расстояние от точки до прямой

Рассмотри
двухмерное евклидовое пространство ﻉ

с
декартовой системой координат. Пусть
точка
ﻉ

и
lﻉ.
Найдем расстояние от этой точки до
прямой. Положим
_,
и прямая l
задается уравнением
(рис.V.8).

Расстояние

,
вектор
,
где

– нормальный вектор прямой l,

и

– коллинеарны, поэтому их координаты
пропорциональны, то есть
,
следовательно,

,

.

Рис.
V.8

Отсюда
или умножая эти уравнения
наA
и B
соответственно и складывая их, находим
,
отсюда

или

.

Формула

(V.8)

определяет
расстояние от точки
до прямой.

Пример
V.15.
Найти уравнение прямой, проходящей
через точку
перпендикулярно прямойl:
и найти расстояние отдо прямойl.

Из
рис. V.8
имеем
,
а нормальный вектор прямойl
.
Из условия перпендикулярности имеем

или

.

Так
как
,
то

.
(V.9)

Это
и есть уравнение прямой, проходящей
через точку
,перпендикулярно
прямой
.

Пусть
имеем уравнение прямой (V.9),
проходящей через точку
,
перпендикулярна прямойl:
.
Найдем расстояние от точкидо прямойl,
используя формулу (V.8).

Для
нахождения искомого расстояния достаточно
найти уравнение прямой, проходящей
через две точки
и точку,
лежащую на прямой в основании
перпендикуляра. Пусть
,
тогда

.
(V.10)

Так
как
,
а вектор,
то

.
(V.11)

Поскольку
точка
лежит на прямойl,
то имеем еще одно равенство
или

Приведем систему
к виду, удобному для применения метода
Крамера

Ее решение имеет
вид

,

.
(V.12)

Подставляя
(V.12)
в (V.10),
получаем исходное расстояние.

Пример
V.16.
В двухмерном пространстве задана точка
и прямая.
Найти расстояние от точкидо прямой; записать уравнение прямой,
проходящей через точкуперпендикулярно заданной прямой и найти
расстояние от точкидо основания перпендикуляра к исходной
прямой.

По
формуле (V.8)
имеем

.

Уравнение
прямой, содержащей перпендикуляр, найдем
как прямую, проходящую через две точки
и,
воспользовавшись формулой (V.11).
Так как
,
то, с учетом того, что,
а,
имеем

.

Для
нахождения координат
имеем систему с учетом того, что точкалежит на исходной прямой

Следовательно,
,,
отсюда.

Рассмотрим
трехмерное евклидовое пространство ﻉ.
Пусть точка
ﻉ
и
плоскость ﻉ.
Найдем расстояние от этой точки
до плоскости,
заданной уравнением
(рис.V.9).

Рис.
V.9

Аналогично
двухмерному пространству имеем
и вектор,
а,
отсюда

.
(V.13)

Уравнение
прямой, содержащей перпендикуляр к
плоскости ,
запишем как уравнение прямой, проходящей
через две точки
и,
лежащую в плоскости:

.
(V.14)

Для
нахождения координат точки
к двум любым равенствам формулы (V.14)
добавим уравнение

.
(V.15)

Решая
систему трех уравнений (V.14),
(V.15),
найдем
,,– координаты точки.
Тогда уравнение перпендикуляра запишется
в виде

.

Для
нахождения расстояния от точки
до плоскости
вместо формулой (V.13)
воспользуемся

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Куб — свойства, виды и формулы

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

прямая призма, все грани которой есть квадраты;

прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Вершина

Точки пересечения рёбер называются вершинами. Их число равно восьми.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Диагональ куба — одна из осей симметрии.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Объем куба

Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:

Периметр куба

Сумма длин всех рёбер равна:

Площадь поверхности

Сумма площадей всех граней называется площадью поверхности куба. Она равна:

Сфера, вписанная в куб

Такая сфера имеет центр, совпадающий с центром куба.

Радиус равен половине ребра:

Сфера, описанная вокруг куба

Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:

Координаты вершин куба

В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:

Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).

Свойства куба

Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.

Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.

у куба все грани равны, являются квадратами;

у куба все рёбра равны;

один центр и несколько осей симметрии.

10 класс. Геометрия. Параллельные прямые в пространстве.

10 класс. Геометрия. Параллельные прямые в пространстве.

• Оглавление
• Занятия
• Обсуждение
• О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

1. Тема и цели урока

Мы уже изучали параллельные прямые в планиметрии. Теперь нужно дать определение параллельных прямых в пространстве и доказать соответствующие теоремы.

2. Определение параллельных прямых в пространстве

Определение: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются (Рис. 1.).

Обозначение параллельных прямых: a || b.

3. Теорема 1 и ее доказательство

Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Дано: прямая а, (Рис. 2.)

Доказать: существует единственная прямая b || a,

Через прямую а и точку , не лежащую на ней, можно провести единственную плоскость α (Рис. 3.). В плоскости α можно провести единственную прямую b, параллельную а, проходящую через точку M (из аксиомы планиметрии о параллельных прямых). Существование такой прямой доказано.

Докажем единственность такой прямой. Предположим, что существует другая прямая с, проходящая через точку M и параллельная прямой а. Пусть параллельные прямые а и с лежат в плоскости β. Тогда плоскость β проходит через точку M и прямую а. Но через точку M и прямую а проходит единственная плоскость (в силу теоремы 2). Значит, плоскости β и α совпадают. Из аксиомы параллельных прямых, следует, что прямые b и с совпадают, так как в плоскости существует единственная прямая, проходящая через данную точку и параллельная заданной прямой. Единственность доказана.

4. Лемма (о двух параллельных прямых, пересекающих плоскость) и ее доказательство

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Дано: а || b,

Доказать:

Доказательство: (Рис. 4.)

Существует некоторая плоскость β, в которой лежат параллельные прямые а и b. Точка М принадлежит и плоскости α, и прямой а, которая лежит в плоскости β. Значит, М – общая точка плоскостей α и β. А по третьей аксиоме, существует прямая MN, по которой пересекаются эти две плоскости.

Прямая MN пересекается с прямой b.(так как в противном случае, получается, что прямые MN и b параллельные, то есть a = MN, что невозможно, так как прямая а пересекается с плоскостью α в точке М по условию). То есть точка N – это точка пересечения прямой b и плоскости α..

Докажем, что N – это единственная общая точка прямой b и плоскости α. Допустим, что есть другая точка, но тогда прямая bпринадлежит плоскости α (по второй аксиоме). То есть MN = b, что невозможно, так как прямые а и bпараллельны, а прямая а должна пересекаться с прямой MN. Лемма доказана.

5. Теорема 2 и ее доказательство

Если две прямые параллельны третьей, то они параллельны.

Дано:

Доказать: .

Доказательство: (Рис. 5.)

Выберем произвольную точку К на прямой b. Тогда существует единственная плоскость α, проходящая черезточку К и прямую а. Докажем, что прямая bлежит в плоскости α.

Предположим противное. Пусть прямая bне лежит в плоскости α. Тогда прямая bпересекает плоскость α в точке К. Так как прямые bи с параллельны, то, согласно лемме, прямая с также пересекает плоскость α. Прямые а и с также параллельны, значит, по лемме, прямая а также пересекает плоскость α, но это невозможно, так как прямая а лежит в плоскости α. Получили противоречие. То есть, предположение было неверным, а значит, прямая bлежит в плоскости α.

Докажем, что прямые а и b не пересекаются. Предположим противное. Пусть прямые а и bпересекаются в некоторой точке М. Но тогда получается, что через точку М проходят две прямые а и b, параллельные прямой с, что невозможно в силу теоремы 1. Получили противоречие. Значит, прямые а и b не пересекаются.

Мы доказали, что прямые а и b не пересекаются и что существует плоскость α, в которой лежат прямые а и b. Значит, прямые а и bпараллельны (по определению), что и требовалось доказать.

6. Итоги урока

Итак, мы дали определение параллельных прямых и доказали теорему о параллельных прямых в пространстве. Также мы доказали важную лемму о пересечении параллельными прямыми плоскости и с помощью этой леммы доказали теорему: если две прямые параллельны третьей, то они параллельны. Эта теория будет использоваться дальше и для доказательства других теорем, и для решения задач.

Перечислить и указать в кубе прямые параллельные плоскости BDC1?

Геометрия | 10 – 11 классы

Перечислить и указать в кубе прямые параллельные плоскости BDC1.

Прямая, нележащая в плоскости, параллельна этой плоскости, если данная прямая параллельна хотя бы одной прямой лежащей в данной плоскости

из рисунка видно, что прямая BC1 лежит в плоскостиBDC1, а прямая АD1 параллельна ВС1 (АD1 || BC1) – так как лежат в параллельных гранях и являются равными диагоналями этих граней, значитАD1 параллельна плоскостиBDC1, то естьАD1||(BDC1)

аналогично АВ1 || C1D = > ; AB1 ||(BDC1)

B1D1 || BD = > ; B1D1 ||(BDC1)

отв : B1D1 ; АВ1 иАD1.

Две прямые одной плоскости соответственно параллельны двум прямым другой плоскости?

Две прямые одной плоскости соответственно параллельны двум прямым другой плоскости.

Можно ли утверждать что плоскости параллельны.

Верно ли утверждение, прямая параллельная плоскости, параллельна любой прямой, лежащей в этой плоскости?

Верно ли утверждение, прямая параллельная плоскости, параллельна любой прямой, лежащей в этой плоскости?

Прямая n параллельна прямой m параллельна плоскости а?

Прямая n параллельна прямой m параллельна плоскости а.

Следует ли из этого, что прямая n параллельна плоскости а.

Выберите верные утверждения?

Выберите верные утверждения.

А) Прямая, не лежащая в данной плоскости и параллельная какой либо прямой на плоскости, параллельна самой плоскости.

Б) Плоскость, проходящая через одну из двух параллельных прямых, параллельна другой прямой.

В) Через точку, не принадлежащую плоскости, можно провести бесконечное число прямых, параллельных данной плоскости.

Г) Через одну из двух параллельных прямых можно провести плоскость, параллельную другой прямой, и только одну.

Д) Если две прямые параллельны одной плоскости, то они параллельны друг другу.

Плоскости параллельны?

Прямая а лежит на плоскости.

Верно ли, что прямая а параллельна любой прямой, лежащей в плоскости.

Отметьте верные утверждения?

Отметьте верные утверждения.

1. Прямая параллельная плоскости, параллельна любой прямой, лежащей в этой плоскости.

2. Через одну из двух параллельных прямых можно провести бесконечное множество плоскостей, параллельных другой прямой.

3. Если прямая, лежащая в одной плоскости, параллельна прямой, лежащей в другой плоскости, то эти плоскости параллельны.

4. Если две плоскости параллельны одной и той же прямой, то они параллельны.

Одна из двух параллельных плоскостей перпендикулярна прямой, тогда : а)другая плоскость параллельна прямой ; б) прямая лежит в другой плоскости ; в)другая плоскость перпендикулярна прямой ; г)перямая ?

Одна из двух параллельных плоскостей перпендикулярна прямой, тогда : а)другая плоскость параллельна прямой ; б) прямая лежит в другой плоскости ; в)другая плоскость перпендикулярна прямой ; г)перямая не пресекает другую плоскость ; д) выполняются все случаи, указанные в пунктах а – г.

Докажите, что если плоскость проходит через прямую, параллельную другой прямой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна первой прямой?

Докажите, что если плоскость проходит через прямую, параллельную другой прямой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна первой прямой.

Две плоскости пересекаются по прямой а ?

Две плоскости пересекаются по прямой а .

Прямая b лежит в одной из плоскостей и не параллельна другой плоскости .

Параллельные ли прямые а и b.

Выберете верное утверждение : а)если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая лежит в данной плоскости ; б)если плоскость альфа проходит через прямую, параллельн?

Выберете верное утверждение : а)если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая лежит в данной плоскости ; б)если плоскость альфа проходит через прямую, параллельную плоскости бета, то и плоскость альфа параллельна плоскости бета ; в)если две прямые пересекают плоскость, то они параллельны ; г)прямая и плоскость называется параллельными, если они не имеют общих точек.

Перед вами страница с вопросом Перечислить и указать в кубе прямые параллельные плоскости BDC1?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 10 – 11 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Площадь боковой поверхности S = (АВ + ВС + СD + АD)·АМ = 26·АМ. По условию 26·АМ = 260. АМ = 260 / 26 = 10 см. Ответ : 10 см.

Площадь параллелограмма : S = a * b * sinα, α – угол между сторонами параллелограмма а = 3 см b = 12 см S = 18 см² 18 = 3 * 12 * sinα, sinα = 1 / 2. Α = 30° β = 180° – 30°, β = 150° (α + β = 180°. Сумма углов параллелограмма прилежащих к одной стор..

Если PL = 72°, KM = 72 * Они вертикальны. 180 – 72 = 108.

Ответ д, там получается две параллельные прямые пересечены секущей, треугольник ABN получается равнобедренный, AN = AB a AB = корень (25 – 9) = 4.

АВ = 12 см – СЕ = 4 см АВ = 8 см – СЕ = 2 см АВ = 10 см – СЕ = 2 см.

Решение – в приложении.

Остроугольный треугольник, потому что каждый угол меньше 90 градусов.

45 градусов. Так как МС биссектриса а она делит угол С пополам.

Так как мс биссектриса, то угол mca равен 1 / 2 bca ответ : 45 градусов.

[spoiler title=”источники:”]

http://www.kursoteka.ru/course/2156/lesson/6859/unit/17941/3

http://geometria.my-dict.ru/q/4790343_perecislit-i-ukazat-v-kube-pramye/

[/spoiler]