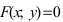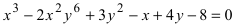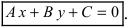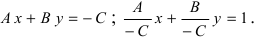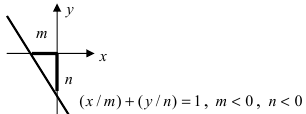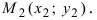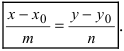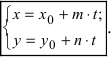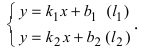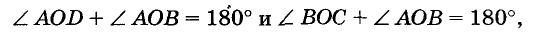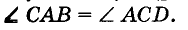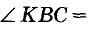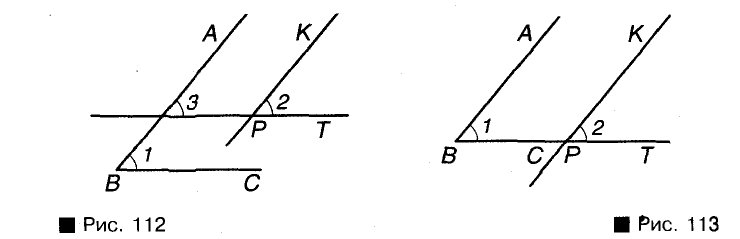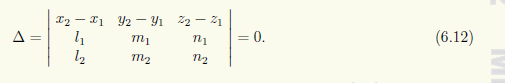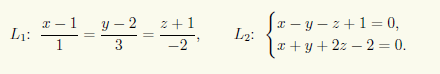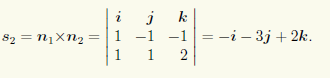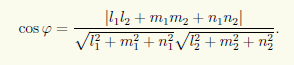Уравнения прямой в пространстве – это уравнения двух пересекающихся плоскостей
В данном разделе продолжим изучение темы уравнения прямой в пространстве с позиции стереометрии. Это значит, что мы будем рассматривать прямую линию в трехмерном пространстве как линию пересечения двух плоскостей.
Согласно аксиомам стереометрии, если две плоскости не совпадают и имеют одну общую точку, то они также имею одну общую прямую, на которой лежат все точки, которые являются общими для двух плоскостей. Используя уравнения двух пересекающихся плоскостей, мы можем определить прямую линию в прямоугольной системе координат.
По ходу рассмотрения темы приведем многочисленные примеры, ряд графических иллюстраций и развернутых решений, необходимых для лучшего усвоения материала.
Уравнения двух плоскостей, задающих прямую линию в пространстве
Пусть даны две плоскости, которые не совпадают между собой и пересекаются. Обозначим их как плоскость α и плоскость β . Разместим их в прямоугольной системе координат O х у z трехмерного пространства.
Как мы помним, любую плоскость в прямоугольной системе координат задает общее уравнение плоскости вида A x + B y + C z + D = 0 . Будем считать, что плоскости α соотвествует уравнение A 1 x + B 1 y + C 1 z + D 1 = 0 , а плоскости β уравнение A 2 x + B 2 y + C 2 z + D 2 = 0 . В этом случае нормальные вектора плоскостей α и β n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) не коллинеарны, так как плоскости не совпадают между собой и е размещаются параллельно друг другу. Запишем это условие следующим образом:
n 1 → ≠ λ · n 2 → ⇔ A 1 , B 1 , C 1 ≠ λ · A 2 , λ · B 2 , λ · C 2 , λ ∈ R
Чтобы освежить в памяти материал по теме «Параллельность плоскостей», смотрите соответствующий раздел нашего сайта.
Линию пересечения плоскостей обозначим буквой a . Т.е. a = α ∩ β . Эта прямая представляет собой множество точек, которые являются общими для обеих плоскостей α и β . Это значит, что все точки прямой линии a удовлетворяют обоим уравнениям плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . Фактически, они являются частным решением системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .
Общее решение системы линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 определяет координаты всех точек линии, по которой происходит пересечение двух плоскостей α и β . Это значит, что с его помощью мы можем определить положение прямой в прямоугольной системе координат O x y z .
Рассмотрим описанную теорию еще раз, теперь уже на конкретном примере.
Прямая O x – это прямая, по которой пересекаются координатные плоскости O x y и O x z . Зададим плоскость O x y уравнением z = 0 , а плоскость O x z уравнением у = 0 . Такой подход мы подробно разобрали в разделе «Неполное общее уравнение плоскости», так что, в случае затруднений, можно обратиться к этому материалу повторно. В этом случае координатная прямая O x определяется в трехмерной системе координат системой из двух уравнений вида y = 0 z = 0 .
Нахождение координат точки, лежащей на прямой, по которой пересекаются плоскости
Рассмотрим задачу. Пусть в трехмерном пространстве задана прямоугольная система координат O х у z . Линия, по которой пересекаются две плоскости a , задана системой уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Дана точка трехмерного пространства M 0 x 0 , y 0 , z 0 .
Давайте определим, принадлежит ли точка M 0 x 0 , y 0 , z 0 заданной прямой линии a .
Для того, чтобы получить ответ на вопрос задачи, подставим координаты точки М 0 в каждое из двух уравнений плоскости. Если в результате подстановки оба уравнения превратятся в верные равенства A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 , то точка М 0 принадлежит каждой из плоскостей и принадлежит заданной линии. Если хотя бы одно из равенств A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 окажется неверным, то точка М 0 не принадлежит прямой линии.
Рассмотрим решение примера
Прямая линия задана в пространстве уравнениями двух пересекающихся плоскостей вида 2 x + 3 y + 1 = 0 x – 2 y + z – 3 = 0 . Определите, принадлежат ли точки M 0 ( 1 , – 1 , 0 ) и N 0 ( 0 , – 1 3 , 1 ) прямой линии пересечения плоскостей.
Решение
Начнем с точки М 0 . Подставим ее координаты в оба уравнения системы 2 · 1 + 3 · ( – 1 ) + 1 = 0 1 – 2 · ( – 1 ) + 0 – 3 = 0 ⇔ 0 = 0 0 = 0 .
В результате подстановки мы получили верные равенства. Это значит, что точка М 0 принадлежит обеим плоскостям и расположена на линии их пересечения.
Подставим в оба уравнения плоскости координаты точки N 0 ( 0 , – 1 3 , 1 ) . Получаем 2 · 0 + 3 · – 1 3 + 1 = 0 0 – 2 · – 1 3 + 1 – 3 = 0 ⇔ 0 = 0 – 1 1 3 = 0 .
Как вы видите, второе уравнение системы превратилось в неверное равенство. Это значит, что точка N 0 не принадлежит заданной прямой.
Ответ: точка М 0 принадлежит прямой линии, а точка N 0 не принадлежит.
Теперь предлагаем вам алгоритм нахождения координат некоторой точки, принадлежащей прямой линии, если прямая в пространстве в прямоугольной системе координат O x y z определяется уравнениями пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .
Количество решений системы из двух линейных уравнений с темя неизвестными A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 бесконечно. Любое из этих решений может стать решением задачи.
Пусть в трехмерном пространстве задана прямая линия уравнениями двух пересекающихся плоскостей вида x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 . Найдите координаты любой из точек этой прямой.
Решение
Перепишем систему уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 ⇔ x + 0 y + 3 z = – 7 2 x + 3 y + 3 z = – 2 .
Возьмем отличный от нуля минор второго порядка в качестве базисного минора основной матрицы системы 1 0 2 3 = 3 ≠ 0 . Это значит, что z – это свободная неизвестная переменная.
Перенесем слагаемые, содержащие свободную неизвестную переменную z в правые части уравнений:
x + 0 y + 3 z = – 7 2 x + 3 y + 3 z = – 2 ⇔ x + 0 y = – 7 – 3 z 2 x + 3 y = – 2 – 3 z
Введем произвольное действительное число λ и примем, что z = λ .
Тогда x + 0 y = – 7 – 3 z 2 x + 3 y = – 2 – 3 z ⇔ x + 0 y = – 7 – 3 λ 2 x + 3 y = – 2 – 3 λ .
Для решения полученной системы уравнений применим метод Крамера:
∆ = 1 0 2 3 = 1 · 3 – 0 · 1 = 2 ∆ x = – 7 – 3 λ 0 – – 3 λ 3 = – 7 – 3 λ · 3 – 0 · ( – 2 – 3 λ ) = 21 – 9 λ ⇒ x = ∆ x ∆ = – 7 – 3 λ ∆ y = 1 – 7 – 3 λ 2 – 2 – 3 λ = 1 · – 2 – 3 λ – – 7 – 3 λ · = 12 + 3 λ ⇒ y = ∆ y ∆ = 4 + λ
Общее решение системы уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 будет иметь вид x = – 7 – 3 λ y = 4 + λ z = λ , где λ ∈ R .
Для получения частного решения системы уравнений, которое даст нам искомые координаты точки, принадлежащей заданной прямой, нам необходимо взять конкретное значение параметра λ . Если λ = 0 , то x = – 7 – 3 · 0 y = 4 + 0 z = 0 ⇔ x = – 7 y = 4 z = 0 .
Это позволяет нам получить координаты искомой точки – 7 , 4 , 0 .
Проверим верность найденных координат точки методом подстановки их в исходные уравнения двух пересекающихся плоскостей – 7 + 3 · 0 + 7 = 0 2 · ( – 7 ) + 3 · 4 + 3 · 0 + 2 = 0 ⇔ 0 = 0 0 = 0 .
Ответ: – 7 , 4 , 0
Направляющий вектор прямой, по которой пересекаются две плоскости
Давайте рассмотрим, как определить координаты направляющего вектора прямой, которая задана уравнениями двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . В прямоугольной системе координат 0хуz направляющий вектор прямой неотделим от прямой линии.
Как мы знаем, прямая перпендикулярна по отношению к плоскости в том случае, когда она перпендикулярна по отношению к любой прямой, лежащей в данной плоскости. Исходя из вышесказанного, нормальный вектор плоскости перпендикулярен любому ненулевому вектору, лежащему в данной плоскости. Эти два факта помогут нам в нахождении направляющего вектора прямой.
Плоскости α и β пересекаются по линии a . Направляющий вектор a → прямой линии a расположен перпендикулярно по отношению к нормальному вектору n 1 → = ( A 1 , B 1 , C 1 ) плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и нормальному вектору n 2 → = ( A 2 , B 2 , C 2 ) плоскости A 2 x + B 2 y + C 2 z + D 2 = 0 .
Направляющий вектор прямой a представляет собой векторное произведение векторов n → 1 = ( A 1 , B 1 , C 1 ) и n 2 → = A 2 , B 2 , C 2 .
a → = n → 1 × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2
Зададим множество всех направляющих векторов прямой как λ · a → = λ · n 1 → × n 2 → , где λ – это параметр, который может принимать любые действительные значения, отличные от нуля.
Пусть прямая в пространстве в прямоугольной системе координат O х у z задана уравнениями двух пересекающихся плоскостей x + 2 y – 3 z – 2 = 0 x – z + 4 = 0 . Найдем координаты любого направляющего вектора этой прямой.
Решение
Плоскости x + 2 y – 3 z – 2 = 0 и x – z + 4 = 0 имеют нормальные векторы n 1 → = 1 , 2 , – 3 и n 2 → = 1 , 0 , – 1 . Примем за направляющий вектор прямой линии, являющейся пересечением двух заданных плоскостей, векторное произведение нормальных векторов:
a → = n → 1 × n 2 → = i → j → k → 1 2 – 3 1 0 – 1 = i → · 2 · ( – 1 ) + j → · ( – 3 ) · 1 + k → · 1 · 0 – – k → · 2 · 1 – j → · 1 · ( – 1 ) – i → · ( – 3 ) · 0 = – 2 · i → – 2 j → – 2 k →
Запишем ответ в координатной форме a → = – 2 , – 2 , – 2 . Тем, кто не помнит, как это делается, рекомендуем обратиться к теме «Координаты вектора в прямоугольной системе координат».
Ответ: a → = – 2 , – 2 , – 2
Переход к параметрическим и каноническим уравнениям прямой в пространстве
Для решения ряда задач проще использовать параметрические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ или канонические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ . В этих уравнениях a x , a y , a z – координаты направляющего вектора прямой, x 1 , y 1 , z 1 – координаты некоторой точки прямой, а λ – параметр, принимающий произвольные действительные значения.
От уравнения прямой вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 можно перейти к каноническим и параметрическим уравнениям прямой линии в пространстве. Для записи канонических и параметрических уравнений прямой нам понадобятся навыки нахождения координат некоторой точки прямой, а также координат некоторого направляющего вектора прямой, заданной уравнениями двух пересекающихся плоскостей.
Рассмотрим написанное выше на примере.
Зададим прямую линию в трехмерной системе координат уравнениями двух пересекающихся плоскостей 2 x + y – z – 1 = 0 x + 3 y – 2 z = 0 . Напишем канонические и параметрические уравнения этой прямой.
Решение
Найдем координаты направляющего вектора прямой, который является векторным произведением нормальных векторов n 1 → = 2 , 1 , – 1 плоскости 2 x + y – z – 1 = 0 и n 2 → = ( 1 , 3 , – 2 ) плоскости x + 3 y – 2 z = 0 :
a → = n 1 → × n 2 → = i → j → k → 2 1 – 1 1 3 – 2 = i → · 1 · ( – 2 ) + j → · ( – 1 ) · 1 + k → · 2 · 3 – – k → · 1 · 1 – j → · 2 · ( – 2 ) – i → · ( – 1 ) · 3 = i → + 3 · j → + 5 · k →
Координаты направляющего вектора прямой a → = ( 1 , 2 , 5 ) .
Следующим шагом является определение координат некоторой точки заданной прямой линии, которыми является одно из решений системы уравнений: 2 x + y – z – 1 = 0 x + 3 y – 2 z = 0 ⇔ 2 x + y – z = 1 x + 3 y – 2 z = 0 .
Возьмем в качестве минорной матрицы системы определитель 2 1 1 3 = 2 · 3 – 1 · 1 = 5 , который отличен от нуля. В этом случае переменная z является свободной. Перенесем слагаемые с ней в правые части каждого уравнения и придаем переменной произвольное значение λ :
2 x + y – z = 1 x + 3 y – 2 z = 0 ⇔ 2 x + y = 1 + z x + 3 y = 2 z ⇔ 2 x + y = 1 + λ x + 3 y = 2 λ , λ ∈ R
Применяем для решения полученной системы уравнений метод Крамера:
∆ = 2 1 1 3 = 2 · 3 – 1 · 1 = 5 ∆ x = 1 + λ 1 2 λ 3 = ( 1 + λ ) · 3 – 1 · 2 λ = 3 + λ ⇒ x = ∆ x ∆ = 3 + λ 5 = 3 5 + 1 5 · λ ∆ y = 2 1 + λ 1 2 λ = 2 · 2 λ – ( 1 + λ ) · 1 = – 1 + 3 λ ⇒ y = ∆ y ∆ = – 1 + 3 λ 5 = – 1 5 + 3 5 · λ
Получаем: 2 x + y – z – 1 = 0 x + 3 y – 2 z = 0 ⇔ x = 3 5 + 1 5 y = – 1 5 + 3 5 z = λ
Примем λ = 2 для того, чтобы получить координаты точки прямой линии: x 1 = 3 5 + 1 5 · 2 y 1 = – 1 5 + 3 5 · 2 z 1 = 2 ⇔ x 1 = 1 y 1 = 1 z 1 = 2 . Теперь мы имеем достаточно данных для того, чтобы записать канонические и параметрические уравнения данной прямой в пространстве: x – x 1 a x = y – y 1 a y = z – z 1 a z ⇔ x – 1 1 = y – 1 3 = z – 2 5 x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x = 1 + 1 · λ y = 1 + 3 · λ z = 2 + 5 · λ ⇔ x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ
Ответ: x – 1 1 = y – 1 3 = z – 2 5 и x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ
Данная задача имеет еще один способ решения.
Нахождение координат некоторой точки прямой проводится при решении системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .
В общем случае ее решения можно записать в виде искомых параметрических уравнений прямой в пространстве x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ .
Получение канонических уравнений проводится следующим образом: решаем каждое из полученных уравнений относительно параметра λ , приравниваем правые части равенства.
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ λ = x – x 1 a x λ = y – y 1 a y λ = z – z 1 a z ⇔ x – x 1 a x = y – y 1 a y = z – z 1 a z
Применим данный способ к решению задачи.
Зададим положение прямой линии уравнениями двух пересекающихся плоскостей 2 x + y – z – 1 = 0 x + 3 y – 2 z = 0 . Напишем параметрическое и каноническое уравнения для этой прямой линии.
Решение
Решение системы из двух уравнений с тремя неизвестными проводится аналогично тому, как мы делали это в предыдущем примере. Получаем: 2 x + y – z – 1 = 0 x + 3 y – 2 z = 0 ⇔ x = 3 5 + 1 5 · λ y = – 1 5 + 3 5 · λ z = λ .
Это параметрические уравнения прямой в пространстве.
Канонические уравнения получаем следующим образом: x = 3 5 + 1 5 · λ y = – 1 5 + 3 5 · λ z = λ ⇔ λ = x – 3 5 1 5 λ = y + 1 5 3 5 λ = z 1 ⇔ x – 3 5 1 5 = y + 1 5 3 5 = z 1
Полученные в обоих примерах уравнения отличаются внешне, однако они эквивалентны, так как определяют одно и то же множество точек трехмерного пространства, а следовательно и одну и ту же прямую линию.
Ответ: x – 3 5 1 5 = y + 1 5 3 5 = z 1 и x = 3 5 + 1 5 · λ y = – 1 5 + 3 5 · λ z = λ
Уравнение прямой
Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
где A и B не могут быть одновременно равны нулю.
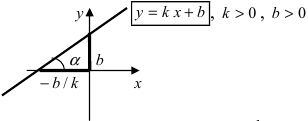
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
где k – угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.
Уравнение прямой в отрезках на осях
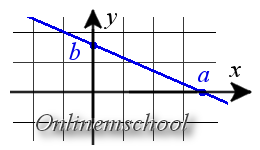
Если прямая пересекает оси OX и OY в точках с координатами ( a , 0) и (0, b ), то она может быть найдена используя формулу уравнения прямой в отрезках
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
| x – x 1 | = | y – y 1 |
| x 2 – x 1 | y 2 – y 1 |
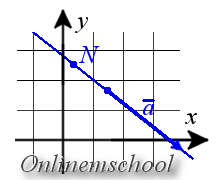
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x = l t + x 0 y = m t + y 0
где N( x 0, y 0) – координаты точки лежащей на прямой, a = < l , m >- координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки N( x 0, y 0) лежащей на прямой и направляющего вектора a = ( l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
x – 1 2 – 1 = y – 7 3 – 7
Упростив это уравнение получим каноническое уравнение прямой
Выразим y через x и получим уравнение прямой с угловым коэффициентом
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
x = t + 1 y = -4 t + 7
Решение. Так как M y – N y = 0, то невозможно записать уравнение прямой проходящей через две точки.
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
| x – x 1 | = | y – y 1 | = | z – z 1 |
| x 2 – x 1 | y 2 – y 1 | z 2 – z 1 |
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
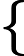 |
x = l t + x 0 |
| y = m t + y 0 | |
| z = n t + z 0 |
где ( x 0, y 0, z 0) – координаты точки лежащей на прямой, – координаты направляющего вектора прямой.
Каноническое уравнение прямой в пространстве
Если известны координаты точки M( x 0, y 0, z 0) лежащей на прямой и направляющего вектора n = , то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x – x 0 | = | y – y 0 | = | z – z 0 |
| l | m | n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
Прямая линия на плоскости и в пространстве с примерами решения
Содержание:
Общее уравнение прямой:
Пусть на плоскости дана декартова система координат. Движение точки с произвольными координатами х и у по этой плоскости порождает линию.
Определение: Любое соотношение
Определение: Порядок линии определяется по высшему показателю степени переменных х и у или по сумме показателей степени в произведении этих величин.
Пример:
а) 2х + Зу-5 = 0 – линия первого порядка; точка A(l; 1) удовлетворяет этому соотношению, а точка, например, В(1; 0) – ему не удовлетворяет;
б)
в) 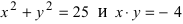
Рассмотрим другое определение линии:
Определение: Геометрическое место точек, координаты которых удовлетворяют уравнению F(x; у)=0, называется линией, а само уравнение F(x; у) = 0 – уравнением линии.
Определение: Общим уравнением прямой называется уравнение первого порядка вида
Рассмотрим частные случаи этого уравнения:
а) С = 0; 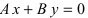
Рис. 20. Прямая, проходящая через начало координат.
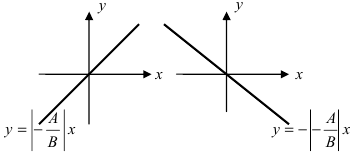
б) 5 = 0; Ах+С=0 – прямая проходит параллельно оси ординат Оу (Рис. 21):
Рис. 21. Прямая, проходящая параллельно оси ординат Оу.
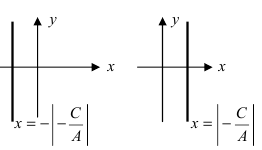
в) А = 0; Ву+С=0 – прямая проходит параллельно оси абсцисс Ох (Рис. 22):
Рис. 22. Прямая, проходящая параллельно оси абсцисс Ох.
Виды уравнений прямой
1. Уравнение прямой с угловым коэффициентом. Пусть дано общее уравнение прямой 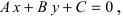
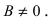
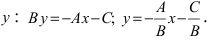
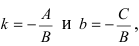
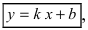
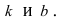
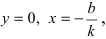
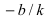
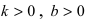
Рис. 23. Отрезки, отсекаемые прямой на координатных осях.
Из рисунка видно, что 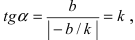
2. Уравнение прямой в отрезках.
Пусть в общем уравнении прямой параметр 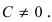
Обозначим через 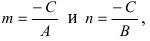
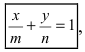
Рис. 24. Отрезки, отсекаемые прямой на координатных осях.
При у=о, х=m, т.е. прямая отсекает на оси абсцисс отрезок m. Следовательно, прямая проходит через 2 точки:
3. Уравнение прямой, проходящей через две заданные точки. Пусть дано общее уравнение прямой Ах + Ву + С = 0, которая проходит через две известные точки 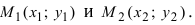
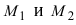
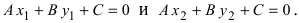
Пусть 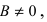
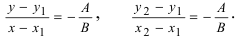
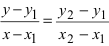
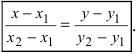
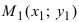
4. Уравнение прямой, проходящей через заданную точку 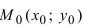
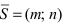
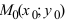
Определение: Вектор 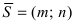
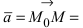
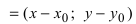
Рис. 25. Прямая, проходящая через данную точку параллельно направляющему вектору.
В силу того, что вектора 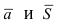
Определение: Полученное уравнение называется либо уравнением, проходящим через заданную точку параллельно направляющему вектору, либо каноническим уравнением прямой.
5. Параметрическое уравнение прямой. Если каждую дробь в каноническом уравнении прямой приравнять некоторому параметру t, то получим параметрическое уравнение прямой
Основные задачи о прямой на плоскости
1. Координаты точки пересечения двух прямых. Пусть две прямые заданы общими уравнениями 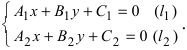
2. Угол между двумя пересекающимися прямыми. Пусть даны две пересекающиеся прямые, заданные уравнениями с угловыми коэффициентами
Требуется найти угол между этими прямыми (Рис. 26):
Рис. 26. Угол между двумя прямыми.
Из рисунка видно, что Вычислим
Наименьший угол между пересекающимися прямыми определим формулой Из полученной формулы видно:
- а) если прямые параллельны или совпадаютто Отсюда следует условие параллельности прямых: угловые коэффициенты прямых равны между собой
- б) если прямые перпендикулярныто не существует.
Отсюда следует условие перпендикулярности прямых: угловые коэффициенты прямых связаны между собой соотношением
Пример:
Определить угол между прямыми
Решение:
В силу того, что что прямые параллельны, следовательно,
Пример:
Выяснить взаимное расположение прямых
Решение:
Так как угловые коэффициенты и связаны между собой соотношением то прямые взаимно перпендикулярны.
3. Расстояние от точки до прямой. Расстояние от точки до прямой определятся вдоль перпендикуляра, опущенного из точки на прямую Если прямая задана общим уравнением, то расстояние от точки до прямой определяется формулой:
Если прямая задана уравнением прямой с угловым коэффициентом, то расстояние от точки до прямой определяется формулой:
Прямая линия на плоскости и в пространстве. Системы координат на плоскости
Рассмотрим произвольную прямую. Выберем на этой прямой начальную точку, обозначаемую буквой О, определим положительное направление, выберем некоторый отрезок в качестве линейной единицы, благодаря чему прямая станет осью. После этого условимся называть координатой любой точки М на этой оси величину отрезка . Точку О будем называть началом координат; ее собственная координата равна нулю. Так вводятся координаты на прямой.
Декартова прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком-нибудь порядке, т.е. указано, какая из них считается первой, а какая – второй. Точка пересечения осей называется началом координат и обозначается через О, а сами оси – координатными осями, причем первую из них называют также осью абсцисс и обозначают через Ох, а вторую – осью ординат, обозначаемую Оу.
Пусть М- произвольная точка плоскости. Спроектируем точку M на координатные оси, т.е., проведем через М перпендикуляры к осям Ох и Оу; основания этих перпендикуляров обозначим соответственно .
Координатами точки М в заданной системе называются числа , обозначающие величину отрезка оси абсцисс и величину отрезка оси ординат, где х – первая координата, а у- вторая координата точки М (рис.7.1). Символически это записывается в виде М(х, у).
Если задана декартова прямоугольная система координат, то каждая точка М плоскости в этой системе имеет одну вполне определенную пару координат х, у – М(х, у). И обратно, для любых х и у на плоскости найдется одна вполне определенная точка с абсциссой х и ординатой у.
На рис. 7.2 положение точки Р полностью определяется ее координатами (2;3).
Две координатные оси разделяют всю плоскость на четыре части, называемыми координатными плоскостями, определяемыми соответственно:
- первая координатная четверть: х>0, у>0;
- вторая координатная четверть: х0, у>0;
- третья координатная четверть: х0, у0;
- четвертая координатная четверть: х>0, у0.
Декартова прямоугольная система координат является наиболее употребительной. Однако, в отдельных случаях могут оказаться более удобными или косоугольная декартова или полярная системы координат.
Косоугольная система координат от прямоугольной декартовой системы координат отличается только произвольным углом между осями координат.
Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из этой точки луча OA, называемого полярной осью, масштаба для измерения длин и направления- вращения в плоскости, считаемого положительным (рис. 7.3).
Каждая точка М в полярной системе координат задается парой координат .
Декартова прямоугольная система координат связана с полярной системой формулами:
Основным инструментом аналитической геометрии служит формула для вычисления расстояния между двумя точкамии . Числа могут быть любыми действительными числами, положительными, отрицательными или 0. На рис. 7.4 все числа выбраны положительными. Проведем через точку горизонтальную прямую, а через точку – вертикальную. Пусть R -точка их пересечения. Тогда по теореме Пифагора
или (7.1.1)
Это и есть формула для вычисления расстояния между двумя точками.
Важно иметь в виду, что эта формула остается в силе независимо от того, как расположены точки . Например, если точка расположена ниже точки и справа от нес, как на рис. 7.5, то отрезок можно считать равныму .
Расстояние между точками, вычисляемое по формуле (7.1.1), от этого не изменится, так как . Заметим, что, так как величина в этом случае отрицательна, то разность больше, чем
Если обозначить через угол, образованный положительным направлением оси абсцисс и отрезком , то формулы
выражают проекции произвольного отрезка на координатные оси через его длину и полярный угол. Из формул (7.1.2) получаем формулы:
позволяющие определить полярный угол отрезка по координатам его конца и начала. Кроме того, если u – произвольная ось, а – угол наклона отрезка к этой оси, то проекция отрезка на ось равна его длине, умноженной на косинус угла наклона к этой оси:
.
Пусть на плоскости даны две произвольные точки, из которых одна считается первой, другая – второй. Обозначим их в заданном порядке через . Проведем через данные точки ось u. Пусть М- еще одна точка оси и, расположенная на ней как угодно, но не совпадает с точкой .
Определение 7.1.1. Число определяемое равенством где – величины направленных отрезков оси u, называется отношением, в котором точка М делит направленный отрезок .
Число не зависит от направления оси и от масштаба, т.к. при изменении этих параметров будут одновременно меняться величины . Кроме того, будет положительно, если Мнаходится между точками если же М вне отрезка , то -отрицательное.
Задача о делении отрезка в данном отношении формулируется следующим образом:
Считая известными координаты двух точек и и отношение в котором некоторая неизвестная точка М делит отрезок , найти координаты точки М.
Решение задачи определяется следующей теоремой.
Теорема 7.1.1. Если точка М(х, у) делит направленный отрезок в отношении то координаты этой точки выражаются формулами:
Доказательство:
Спроектируем точки на ось Ох и обозначим их проекции соответственно через (рис. 7.6). На основании теоремы о пропорциональности отрезков прямых, заключенных между параллельными прямыми (Если две прямые пересечь тремя параллельными прямыми, то отношение двух отрезков, получившихся на одной прямой, равно отношению двух соответствующих отрезков другой прямой), имеем:
Подставив в (7.1.4) величины отрезков и
, получим
Разрешая это уравнение относительно х, находим:
Вторая формула (7.1.3) получается аналогично.
Если – две произвольные точки и М(х,y) –
середина отрезка , то . Эти формулы
получаются из (7.1.3) при .
Основная теорема о прямой линии на плоскости
Предположим, что в данной плоскости задана прямоугольная система координат и некоторая прямая l.
Всякий ненулевой вектор, коллинеарный данной прямой, называется её направляющим вектором. Всякие два направляющих вектора одной и той же прямой коллинеарны между собой, т.е.
, .
Для всех направляющих векторов данной прямой, не параллельной оси ординат, отношение ординаты вектора к его абсциссе имеет одно и то же постоянное значение k, называемое угловым коэффициентом данной прямой.
Действительно, если – два направляющих вектора данной прямой /, то векторы коллинеарны, т.е.
их координаты пропорциональны: а значит
Угловой коэффициент прямой можно определить и по-другому: как тангенс угла, образованного положительным направлением оси абсцисс и заданной прямой.
Справедлива следующая теорема.
Теорема 7.3,1. Всякая прямая на плоскости определяется уравнением первой степени с двумя переменными х и у; и обратно, всякое уравнение первой степени с двумя переменными х и у определяет некоторую прямую на плоскости.
Доказательство: Пусть В = (О,b>- точка пересечения прямой L с осью у, а Р = (х,у) – любая другая точка на этой прямой. Проведем через точку В прямую, параллельную оси х, а через точку Р – прямую, параллельную оси у; проведем также прямую х = 1. Пусть k -угловой коэффициент прямой L (см. рис. 7.7). Случай к =0 не исключается.
Так как треугольники BSQ и BRP подобны, то или после упрощения
Следовательно, если точка Р принадлежит прямой L, то ее координаты удовлетворяют уравнению (7.2.1). Обратно, нетрудно показать, что если х и у связаны уравнением (7.2.1), то точка Р принадлежит прямой L, проходящей через точку (0;b) и имеющей угловой коэффициент k.
Таким образом, уравнение любой прямой можно записать в виде:
(не вертикальная прямая) , (7.2.2), х = а (вертикальная прямая) (7.2.3).
В обоих случаях мы получаем уравнение первой степени. Кроме того, каждое уравнение первой степени ио х и у можно привести к виду (7.2.2) либо (7.2.3).
Докажем обратное утверждение. Предположим, что задано произвольное уравнение первой степени:
Если , мы можем записать уравнение (7.2.4) в виде
т.е. в виде (7.2.2). При В = 0 уравнение (7.2.3) сводится к уравнению
или , т.е. к уравнению вида (7.2.3).
Таким образом, любая прямая описывается уравнением первой степени с неизвестными х и у, и обратно, каждое уравнение первой степени с неизвестными х и v определяет некоторую прямую.
Уравнение (7.2.4) называется общим уравнением прямой. Так
как , то вектор является направляющим вектором прямой (7.2.4). Вектор перпендикулярен прямой (7.2.4) и называется нормальным вектором. Возможны частные случаи:
1. или у =b, где , -это уравнсние прямой, параллельной оси Ох.
2. или х = а, где , – это уравнение прямой, параллельной оси Оу.
3. – это уравнение прямой, проходящей через начало координат.
4. А=0; С=0; Ву-0 или у = 0 – это уравнение оси абсцисс Ох.
5. В=0;С=0; Ах=0 или х = 0 – это уравнение оси ординат Оу.
Различные виды уравнений прямой на плоскости
Положение прямой на плоскости относительно системы координат можно задать различными способами. Например, прямая однозначно определяется: двумя различными точками; точкой и направляющим вектором; отрезками, отсекаемыми прямой на осях координат и др. Однако, обязательно, должна быть точка, лежащая на этой прямой.
Пусть в уравнении (7.2.4) ни один из коэффициентов А, В, С не равен нулю. Перенесем свободные члены вправо и разделим на (-С). Получим уравнение прямой в отрезках:
где -длины отрезков, отсекаемых прямой l на осях координат, взятые с соответствующими знаками (в зависимости от того, положительные или отрицательные полуоси координат пересекает прямая l).
Рассмотрим прямую l на плоскости и выберем на этой прямой какие-нибудь точки . Тогда вектор является направляющим вектором этой прямой l.
Геометрическое место концов всевозможных векторов вида где пробегает все вещественные числовые значения, определяет прямую l. Уравнение (7.3.2) называется уравнением прямой в векторной форме (векторным уравнением прямой). Записав векторное уравнение (7.3.2) в координатной форме и воспользовавшись определением равенства векторов, получим параметрические уравнения прямой:
где – координаты направляющего вектора.
Система (7.3.3) равносильна уравнению
называемым каноническим уравнением прямой на плоскости. Из системы (7.3.3) можно получить уравнение
которое называется уравнением прямой, проходящей через две данные точки
Если абсциссы точек одинаковы, т. е. то прямая параллельна оси ординат и ее уравнение имеет вид: х=а.
Если ординаты точек одинаковы, т. е. , то прямая параллельна оси абсцисс и ее уравнение имеет вид: у=b. Уравнение (7.3.5) можно преобразовать к виду:
угловой коэффициент прямой.
Уравнение (7.3.6) называется уравнением прямой, проходящей через точку и имеющей угловой коэффициент k.
Пример:
Составить уравнение прямой, проходящей через две точки
Решение:
I способ. Воспользуемся уравнением (7.3.5). Подставив известные координаты точек , получим искомое уравнение прямой:
II способ. Зная координаты точек по формуле (7.3.7) можно найти угловой коэффициент искомой прямой:
Тогда, воспользовавшись уравнением (7.3.6), найдём искомое уравнение прямой: .
Заметим, что составленное уравнение можно записать как уравнение прямой в отрезках, разделив все члены уравнения
.
Взаимное расположение двух прямых на плоскости
Пусть на плоскости заданы две прямые общими уравнениями . Угол между ними можно вычислить как угол между направляющими векторами
этих прямых:
Если прямые параллельны, то их нормальные векторы коллинеарны, а это значит, что их соответствующих координаты пропорциональны:
И обратно, если координаты при неизвестных х и у пропорциональны, то прямые параллельны. Следовательно, можно сформулировать следующую теорему:
Теорема 7.4.1. Две прямые параллельны тогда и только тогда, когда в их уравнениях коэффициенты при соответствующих переменных х и у пропорциональны.
Например, прямые параллельны,
т. к..
Если прямые перпендикулярны , то их нормальные векторы тоже перпендикулярны, а это значит, что скалярное произведение этих векторов равно нулю: , или в координатной форме
Справедливо и обратное утверждение: если скалярное произведение нормальных векторов равно нулю, то прямые /, и /2 перпендикулярны.
Теорема 7.4.2. Две прямые перпендикулярны тогда и только тогда, когда коэффициенты при переменных х и у удовлетворяют равенству .
Например, прямые перпендикулярны, так как
.
Если прямые заданы уравнениями вида и , то угол между ними находится по формуле:
Для того чтобы прямые были параллельны, необходимо и достаточно, чтобы выполнялось равенство
(7.4.5)
а для их перпендикулярности необходимо и достаточно, чтобы
(7.4.6)
Пример:
Найти проекцию точки Р (2, 3) на прямую, проходящую через точки А (4, 3) и В (6, 5).
Решение:
Проекция точки Р на прямую АВ – это точка пересечения перпендикуляра, проведенного к этой прямой из точки Р.
Вначале составим уравнение прямой АВ. Воспользовавшись уравнением (7.3.5), последовательно получаем:
Для того, чтобы составить уравнение перпендикуляра, проведенного из точки Р на прямую АВ, воспользуемся уравнением (7.3.6). Угловой коэффициент k определим из условия перпендикулярности двух прямых, т. е. из формулы (7.4.6). Поскольку ,то из равенства находим угловой коэффициент перпендикуляра . Подставляя найденное значение углового коэффициента и координаты точки Р (2, 3) в уравнение (7.3.6), получаем:
.
Решая систему уравнений, составленную из уравнений прямой АВ и перпендикуляра
найдём координаты проекции точки Р на прямую АВ: х=3 у=2, т.е.
Пример:
Издержки на производство шести автомобилей составляют 1000 млн. ден. ед., а на производство двадцати автомобилей- 15000 млн. ден. ед. Определить издержки на производство 22 автомобилей при условии, что функция К(х) издержек производства линейна, т.е. имеет вид у = ах + b .
Решение:
Обозначим через х количество автомобилей, а через y- издержки производства. Тогда из условия задачи следует, что заданы координаты двух точек- А(6; 1000) и В(20; 15000), принадлежащих линейной функции у = ах +b. Воспользовавшись уравнением (7.3.6 ), найдём искомое уравнение:
Подставив в найденную функцию х = 22, определим издержки на производство 22 автомобилей:
(млн. дсн. ед)
Пример:
Фирма продаёт свои изделия по 10 ден. ед. за единицу. Затраты на изготовление одного изделия составляют 6 ден. ед. Непроизводственные расходы фирмы равны 300 ден. ед. в год. Определить годовой выпуск продукции, необходимой для того, чтобы фирма работала с прибылью.
Решение:
Обозначим через х объём произведенной продукции. Тогда доход фирмы равен D = 10x. Затраты на производство определяются уравнением: . Найдём точку безубыточности. т.е. значение x, при котором доход фирмы равен затратам: D=K, т.е. 10x = 6x + 300. Решив это уравнение, получим значение объёма производства, при котором фирма работает без убытка: х=75. Следовательно, если объём производства то фирма будет работать с прибылью.
Прямая линия в пространстве
Системы координат в пространстве
В трехмерном пространстве система координат определяется тремя взаимно перпендикулярными осями, проходящими через начало координат О. Снабдив каждую ось единицей измерения длин, можно задать тремя упорядоченными числами (называемыми координатами) положение точки в пространстве. Например, точка Р задается упорядоченной тройкой чисел Р( 1,2,3).
Пусть задано пространство. Важнейшим понятием пространственной аналитической геометрии является понятие уравнения поверхности. Всякая же линия рассматривается как пересечение двух поверхностей. Мы остановимся на изучении поверхности первого порядка – плоскости и прямой линии.
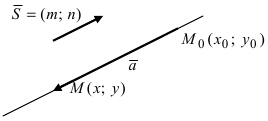
Положение прямой в пространстве вполне определяется заданием какой-либо сё фиксированной точки и вектора параллельного этой прямой.
Вектор , параллельный прямой, называется направляющим вектором этой прямой.
Итак, пусть прямая L проходит через точку , лежащую на прямой, параллельно вектору (см. рис. 7.9).
Рассмотрим произвольную точку M(x,y,z) на этой прямой. Из рисунка видно, что вектор параллельный (коллинеарный) вектору . Поскольку векторы коллинеарны, то найдётся такое число t, что , где множитель t может принимать любое числовое значение в зависимости от положения точки М на прямой.
Уравнение (7.5.1) называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки M, лежащей на прямой. Это уравнение можно записать в виде: (см. рис. 7.9). Запишем это уравнение в координатной форме. Подставив координаты векторов в уравнение (7.5.1) и воспользовавшись определением алгебраических операций над векторами и равенством векторов, получим уравнения:
Полученные уравнения называются параметрическими уравнениями прямой.
При изменении параметра t изменяются координаты х, у и z и точка М перемещается по прямой.
Разрешив уравнения (7.5.2) относительно t
и приравняв найденные значенияt получим канонические уравнения прямой:
Если прямая L в пространстве задается двумя своими точками ,то вектор
можно взять в качестве направляющего вектора и тогда уравнения (7.5.3) преобразуются в уравнения
где . (7.5.4)- это уравнение прямой, проходящей через две заданные точки
Пример:
Составить параметрические уравнения прямой, проходящей через точку, перпендикулярно плоскости Oxz.
Решение:
В качестве направляющего вектора искомой прямой можно взять единичный вектор оси Оу: • Подставив значения координат точки и значения координат направляющего вектора в уравнения (7.5.2), получаем: .
Пример:
Записать уравнения прямой в параметрическом виде.
Обозначим. Тогда ,
, откуда следует, что .
Замечание. Пусть прямая перпендикулярна одной из координатных осей, например, оси Ох. Тогда направляющий вектор
прямой перпендикулярный оси Ох, имеет координаты (о; n; р) и параметрические уравнения прямой примут вид
Исключая из уравнений параметр t, получим уравнения прямой в виде
Однако и в этом случае формально можно записывать канонические уравнения прямой в виде . Таким образом, если в знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Аналогично, канонические уравнения
определяют прямую перпендикулярную осям О х и О у или параллельную оси О z.
Пример:
Составить канонические и параметрические уравнения прямой, проходящей через точку параллельно вектору
Решение:
Подставив координаты точки , и вектора в (7.5.2) и (7.5.3), находим искомые канонические уравнения:
.и параметрические уравнения:
Пример:
Составить канонические уравнения прямой, проходящей через точку М(2, -1,4) параллельно
а) прямой ;
Решение:
а) Поскольку направляющий вектор заданной прямой
является направляющим вектором искомой прямой, то
подставив координаты точки М(2; -1; 4) и вектора в (7.5.3) получим уравнение искомой прямой:
б) Поскольку единичный вектор оси О х: будет направляющим вектором искомой прямой, то подставив в уравнение
(7.5.3) координаты точки М(2; -1; 4 ) и вектора , получаем:
в) В качестве направляющего вектора искомой прямой можно взять единичный вектор оси Оу: . В соответствии с уравнением (7.5.3), получаем или .
г) Единичный вектор оси Oz : будет направляющим вектором искомой прямой. В соответствии с уравнением (7.5.3), получаем
Пример:
Составить уравнение прямой, проходящей через две заданные точки
Решение:
Подставив координаты точек в уравнение
(7.5.4), получим:
Взаимное расположение двух прямых в пространстве
Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведенными через произвольную точку параллельно данным. Пусть в пространстве заданы две прямые:
Очевидно, что за угол между прямыми можно принять угол между их направляющими векторами и
, косинус которого находится по формуле:
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов:
Две прямые параллельны тогда и только тогда, когда пропорциональны соответствующие координаты направляющих векторов:
т.е. параллельна тогда и только тогда, когда параллелен
.
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих координат направляющих векторов равна нулю:
Пример:
Найти угол между прямыми и
Решение:
Воспользуемся формулой (7.6.1), в которую подставим координаты направляющих векторов и
. Тогда , откуда или.
Вычисление уравнения прямой
Пусть PQ — некоторая прямая на плоскости Оху (рис. 22). Через произвольную точку М0 (х0, у0) этой прямой (условно называемую «начальной точкой») проведем прямую М0х параллельную оси Ох и имеющую с ней одинаковое направление. Тогда наименьший неотрицательный угол , образованный полупрямой M0Q, лежащей выше оси М0х’ или совпадающей с ней, называется углом между данной прямой и осью Ох.
Очевидно, этот угол не зависит от выбора точки М0. Если прямая PQ пересекает ось Ох в некоторой точке А (а, 0), то ф есть обычный угол между направленными прямыми. Если PQ || Ох, то, очевидно, Ф = 0. Начальная точка М0 прямой и угол ф («направление прямой») однозначно определяют положение этой прямой на плоскости.
1) Пусть сначала . Тогда прямая PQ пересекает ось Оу в некоторой точке В (0, b), которую можно принять за начальную.
Ордината у = NM текущей точки М (х, у) прямой (рис. 23) состоит из двух частей:
из них первая постоянна, а вторая переменна. Введя угловой коэффициент tg ф = k9 из рис. 23 будем иметь
Нетрудно проверить, что формула (3) остается справедливой также и при х
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
[spoiler title=”источники:”]
http://ru.onlinemschool.com/math/library/analytic_geometry/line/
http://www.evkova.org/pryamaya-liniya-na-ploskosti-i-v-prostranstve
[/spoiler]
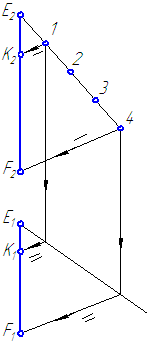
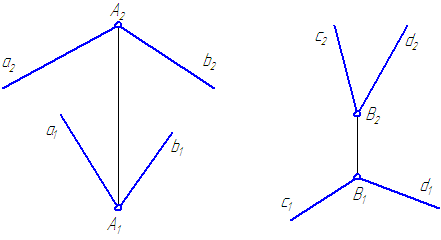
2.1. Задание прямой на эпюре
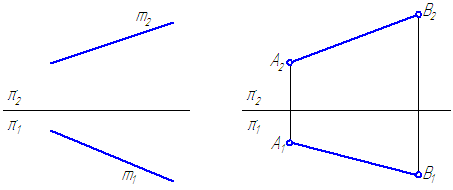
Прямая на чертеже может быть задана изображением прямой, точкой и направлением, отрезком прямой и двумя пересекающимися плоскостями.
а б
Рисунок 2.1 – Проекции прямой
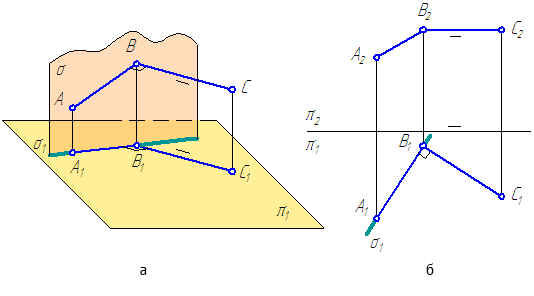
Прямоугольной проекцией отрезка в общем случае является отрезок (второе свойство центрального и параллельного проецирования). На чертеже прямая m (Рисунок 2.1, а) и отрезок АВ (Рисунок 2.1, б) произвольно наклонены к плоскостям проекций. Такие прямые называются прямыми общего положения.
Прямая, не параллельная ни одной из плоскостей проекций, называется прямой общего положения.
Длина прямоугольной параллельной проекции отрезка общего положения всегда меньше длины самого отрезка.
2.2. Прямые частного положения
Прямая, параллельная или перпендикулярная какой-либо плоскости проекций, называется прямой частного положения.
Прямые, параллельные плоскостям проекций, называются прямыми уровня.
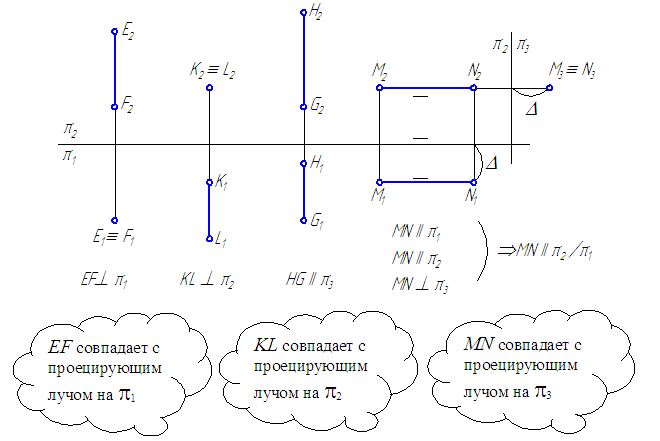
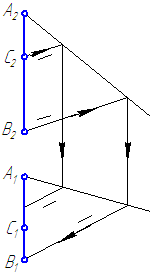
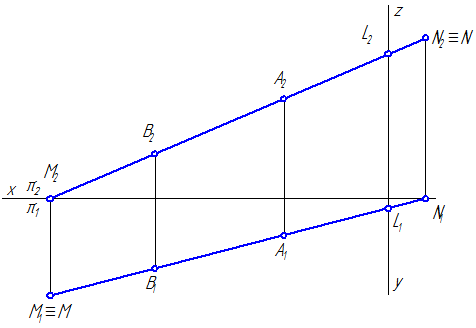
Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной прямой или горизонталью (Рисунок 2.2).
Рисунок 2.2 – Эпюр горизонтали
Если отрезок параллелен плоскости проекций π1, то его фронтальная проекция А2В2 параллельна оси проекций π1/π2, а горизонтальная проекция отрезка А1В1 определяет истинную величину АВ:
А2А0=В2В0
А2В2 || π2/π1
Прямая, параллельная фронтальной плоскости проекций, называется фронтальной прямой или фронталью (Рисунок 2.3).
Рисунок 2.3 – Эпюр фронтали
Если отрезок параллелен плоскости проекций π2, то его горизонтальная проекция параллельна оси проекций π2/π1, а фронтальная проекция отрезка C2D2 определяет истинную величину CD.
С1А0=D1D0
C1D1 || π2/π1
Прямая GH, параллельная профильной плоскости проекций, называется профильной прямой (Рисунок 2.4).
Рисунок 2.4 – Эпюр профильной прямой
Прямые, перпендикулярные плоскостям проекций, называются проецирующими.
Прямая EF, перпендикулярная горизонтальной плоскости проекций, называется горизонтально-проецирующей (Рисунок 2.4).
Прямая KL, перпендикулярная фронтальной плоскости проекций, называется фронтально-проецирующей (Рисунок 2.4).
Прямая MN, перпендикулярная профильной плоскости проекций, называется профильно-проецирующей (Рисунок 2.4).
Рисунок 2.4 – Эпюры проецирующих прямых (EF, KL, MN) и профильной прямой GH
2.3. Метод прямоугольного треугольника
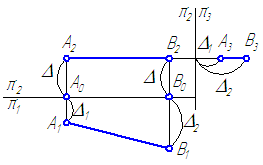
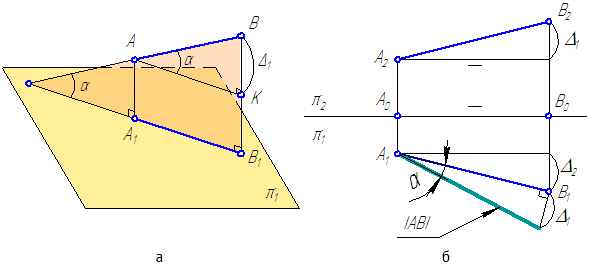
Метод прямоугольного треугольника позволяет по эпюру отрезка прямой общего положения определить его истинную величину.
Рассмотрим положение отрезка АВ относительно горизонтальной плоскости проекций π1 (Рисунок 2.5).
Рисунок 2.5 – Определение истинной величины отрезка общего положения
На рисунке 2.5, а:
АА1 – расстояние от точки А до плоскости проекций π1;
ВВ1 – расстояние от точки В до плоскости проекций π1;
А1В1 – проекция отрезка АВ на π1;
∠(AB; AK)=∠(AB; A1B1)=α – угол наклона прямой АВ к плоскости проекций π1.
ΔАКВ – прямоугольный треугольник, в котором:
АК=А1В1 – катет, равный горизонтальной проекции отрезка АВ;
ВК=ВВ1–АА1=Δ1 – второй катет, равный разности расстояний от концов отрезка АВ до плоскости π1 (то есть, разности координат Z точек А и В);
АВ – гипотенуза ΔАКВ – истинная величина.
При известных координатах концов отрезка общего положения можно на эпюре определить его истинную величину (Рисунок 2.5, б) на любой из плоскостей проекций.
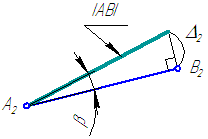
Истинная величина отрезка может быть найдена как гипотенуза прямоугольного треугольника, одним катетом которого является проекция этого отрезка на плоскость проекций (А2В2), а другим – разность координат концов этого отрезка до плоскости (Δ2), в которой ведется построение. Угол между истинной величиной (АВ) и проекцией (А2В2) определяет угол наклона (β) прямой к той плоскости проекций, в которой ведётся построение (Рисунок 2.6).Рисунок 2.6 – Определение истинной длины и угла наклона отрезка AB к плоскости проекций π2
2.4. Точка и прямая
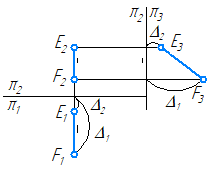
Если точка принадлежит прямой, то её проекции:
- Принадлежат одноимённым проекциям данной прямой;
- Лежат на одной линии связи.
Рисунок 2.7 – Принадлежность точки прямой
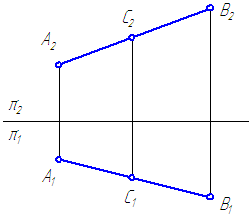
Точка С принадлежит отрезку АВ (Рисунок 2.7), так как:
- С1∈А1В1;
- С2∈А2В2;
- С1С2⊥π2/π1;
Если точка делит отрезок в каком-либо отношении, то проекции этой точки делят одноименные проекции данного отрезка в том же отношении:
{frac{A_2C_2}{C_2B_2}=frac{A_1C_1}{C_1B_1}=frac{AC}{CB}}
Справедливо и обратное утверждение.
Упражнение
Разделить точкой К отрезок EF в соотношении EK:KF=1:3 (Рисунок 2.8)
Рисунок 2.8 – Деление отрезка в заданном отношении
Решение:
-
- Проведём произвольную прямую из любого конца любой проекции отрезка, например, Е2.
- Отложим на этой прямой от точки Е2 равные отрезки, количество которых равно сумме чисел, составляющих дробь (в нашем примере 1+3=4).
- Соединим последнюю точку 4 с другим концом фронтальной проекции отрезка – точкой F2.
- Из точки 1 проведём прямую, параллельную прямой (4—F2) до пересечения с проекцией E2F2, таким образом будет найдена фронтальная проекция искомой точки К2.
- Горизонтальную проекцию точки К1 получим путём построения линии проекционной связи до пересечения её с горизонтальной проекцией отрезка.
Упражнение
Определить принадлежность точки С отрезку прямой АВ (Рисунок 2.9).
Рисунок 2.9а – Решение упражнения 2. Способ 1.
Рисунок 2.9б – Решение упражнения 2. Способ 2.Ответ: точка С не принадлежит отрезку АВ, так как не выполняется условие принадлежности точки прямой.
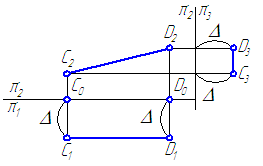
2.5. Следы прямой
След прямой – точка пересечения прямой с плоскостью проекций.
Прямая общего положения в общем случае может быть три следа:
- горизонтальный след M1– точка пересечения прямой с горизонтальной плоскостью проекций π1;
- фронтальный след N2– точка пересечения прямой с фронтальной плоскостью проекций π2;
- профильный след L3 – точка пересечения прямой с профильной плоскостью проекций π3.
След прямой является точкой частного положения, поскольку он принадлежит плоскости проекций, следовательно, след прямой всегда совпадает с одной из своих проекций:
- горизонтальный след совпадает со своей горизонтальной проекцией M≡M1,
- фронтальный – с фронтальной проекцией N≡N2,
- профильный – с профильной проекцией L≡L3 (Рисунок 2.10).
Рисунок 2.10 – Построение следов отрезка прямой АВ
Построим следы отрезка АВ с плоскостями проекций (Рисунки 2.10, 2.11).
Для построения горизонтального следа прямой АB необходимо:
- Продолжить фронтальную проекцию прямой АB до пересечения с осью X, точка пересечения М2 является фронтальной проекцией горизонтального следа;
- Из точки М2 провести линию проекционной связи до его пересечения с горизонтальной проекцией прямой АB или её продолжением. Точка пересечения М1 и будет являться горизонтальной проекцией горизонтального следа, которая совпадает с самим следом М.
Чтобы построить фронтальный след отрезка АB прямой, необходимо:
- Продолжить горизонтальную проекцию прямой АB до пересечения с осью X, точка пересечения N1 является горизонтальной проекцией фронтального следа;
- Из точки N1 провести линию проекционной связи до его пересечения с фронтальной проекцией прямой АB или ее продолжением. Точка пересечения N2 и будет являться фронтальной проекцией фронтального следа, которая совпадает с самим следом N.
Ниже приводим алгоритм построения следов отрезка прямой АВ:
A1B1 ∩ xO =N1; YN=0; N ∈ xOz (π2) ⇒ AB ∩ xOz=N
A2B2 ∩ xO =M2; ZM=0; M ∈ xOy (π1) ⇒ AB ∩ xOy=M
A1B1 ∩ yO =L1; XL=0; L ∈ yOz (π3) ⇒ AB ∩ yOz=L
A2B2 ∩ zO =L2;
Рисунок 2.11 – Эпюр построения следов отрезка прямой АВПрямая, параллельная одной из плоскостей проекций, не имеет следа на плоскости, которой она параллельна, и пересекает только две плоскости. Прямая, параллельная двум плоскостям проекций (проецирующая прямая), имеет только один след, совпадающий с проекцией прямой на плоскость, к которой она перпендикулярна.
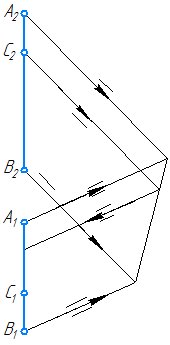
2.6. Взаимное расположение прямых
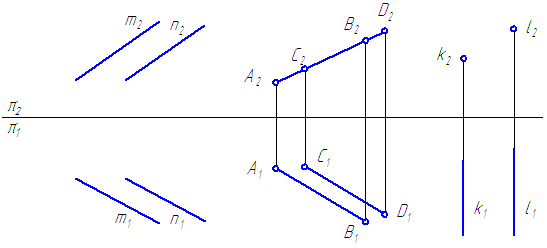
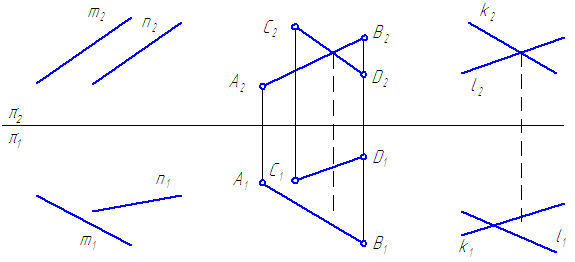
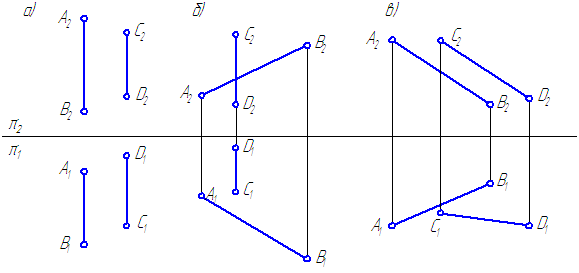
Две прямые в пространстве могут быть:
- параллельными;
- пересекающимися;
- скрещивающимися.
Параллельные прямые – прямые, пересекающиеся в несобственной точке.
Если прямые в пространстве параллельны, то их ортогональные проекции взаимно параллельны, или сливаются, или представляют собой точки, на одной из плоскостей проекций (Рисунок 2.12).
Рисунок 2.12 – Параллельные прямые
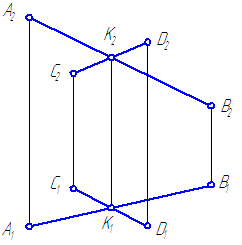
Пересекающиеся прямые – прямые, имеющие одну общую точку.Если прямые в пространстве пересекаются, то на чертеже одноименные проекции прямых пересекаются, при этом проекции точки пересечения прямых лежат на одной линии проекционной связи и делят соответствующие проекции отрезков прямых в равных отношениях (Рисунок 2.13).
{{A_2B_2}cap{C_2D_2}=K_2}
{{A_1B_1}cap{C_1D_1}=K_1}
{frac{A_2K_2}{K_2B_2}=frac{A_1K_1}{K_1B_1}}
{frac{C_2K_2}{K_2D_2}=frac{C_1K_1}{K_1D_1}}
Рисунок 2.13 – Пересекающиеся прямыеСкрещивающиеся прямые – прямые, не имеющие общих точек и не удовлетворяющие признакам параллельных и пересекающихся прямых (Рисунок 2.14).
Рисунок 2.14 — Скрещивающиеся прямые2.7. Проекции плоских углов
Угол между двумя пересекающимися прямыми проецируется в истинную величину, если плоскость этого угла параллельна плоскости проекций.
Рисунок 2.15По проекциям (Рисунок 2.15) нельзя судить о величине угла между двумя прямыми. На чертежах видно, что острый угол может проецироваться в виде тупого, а тупой – в виде острого.
Теорема о проецировании прямого угла в частном случае
Теорема. Если одна из сторон прямого угла параллельна какой-либо плоскости, а другая – этой плоскости не перпендикулярна, то на эту плоскость прямой угол проецируется в виде прямого угла (Рисунок 2.16, а и б).
Обратная теорема. Если одна из двух пересекающихся прямых параллельна некоторой плоскости проекций и проекции этих прямых на эту же плоскость пересекаются под прямым углом, то в пространстве эти прямые взаимно перпендикулярны.
Рисунок 2.16 – Проецирование прямого угла
Дано: две пересекающиеся под прямым углом прямые АВ ⊥ ВС,
причём ВС // π1 (Рисунок 2.16,б).
Доказательство:
- Проведём через отрезок АВ проецирующую плоскость – σ, σ⊥π1;
- Прямые АВ и ВВ1 лежат в плоскости σ;
- ВС⊥ВВ1 так как ВС//π1, а ВВ1⊥π1;
- Следовательно, ВС⊥σ, а значит ВС перпендикулярна и любой прямой, лежащей в плоскости σ, в частности А1В1;
- Следовательно В1С1⊥σ;
- Так как В1С1//ВС, то В1С1⊥А1В1.
2.8. Задачи для самостоятельного решения
1. Построить отрезок прямой АВ // π1, равный 35 мм и наклонённый к π2 под углом 25° (Рисунок 2.17).
Рисунок 2.172. Построить отрезок прямой CD по координатам его концов С (20; 15; 30), D (70; 40; 15) и определить истинную величину отрезка и углы наклона его к плоскостям проекций π2 и π1.
3. Постройте проекции отрезков частного положения, расположенных под углом 30° к плоскости проекций π1 и 45° — к плоскости проекций π2.
4. Определите взаимное положение прямых и постройте пересечение прямых АВ и CD прямой EF//π2/π1 (Рисунок 2.18).
Рисунок 2.18
Содержание:
Взаимное расположения прямых на плоскости:
Бывают два варианта взаимного расположения прямой и точки на плоскости: либо точка лежит на прямой в этом случае говорят, что прямая проходит через точку или точка не лежит на прямой иногда говорят, что точка не принадлежит прямой или прямая не проходит через точку.
Две прямые в плоскости могут пересекаться так как имеют общую точку или быть параллельными не имея общей точки. В пространстве может быть, когда две прямые не пересекаются, но они и не параллельны.
Определения
Два угла, на которые разбивается развернутый угол его внутренним лучом, называются смежными. Сумма мер двух: смежных углов равна 180°.
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого угла Вертикальные углы равны.
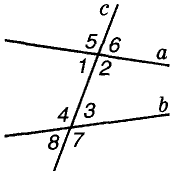
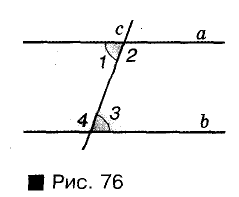
Если две прямые пересекаются, они образуют четыре угла две пары вертикальных углов. Меньший из них — угол между данными прямыми.
Две прямые называются перпендикулярными, если они пересекаются под прямым углом. Отрезки или лучи называют перпендикулярными, если они лежат на перпендикулярных прямых Две прямые на плоскости называют параллельными, ест они не пересекаются.
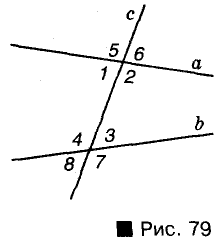
Прямая, пересекающая две другие прямые, называется и: секущей. С двумя данными прямыми она образует 8 углов, не которые пары этих углов имеют отдельные названия:
- 1 и 3, 2 и 4 — внутренние накрест лежащие;
- 1 и 4,2 и 3 — внутренние односторонние;
- 1 и 8, 2 и 7, 3 и 6, 4 и 5 — соответственные;
- 5 и 7, 6 и 8 — внешние накрест лежащие;
- 5 и 8, 6 и 7 — внешние односторонние.
Признак параллельности прямых:
Две прямые параллельны, если с секущей они образу ют равные внутренние накрест лежащие углы, или равные соответственные углы, или такие внутренние одно сторонние углы, сумма которых равна 180°.
Свойства параллельных прямых:
Секущая с двумя параллельными прямыми образуя равные внутренние накрест лежащие углы, равные ее ответственные углы, такие внутренние односторонние углы, сумма которых равна 180°.
Две прямые, параллельные третьей, параллельны.
Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой прямо» Две прямые, перпендикулярные к третьей, параллельны
Смежные и вертикальные углы
Два угла, на которые делится развернутый угол его внутренним лучом, называют смежными.
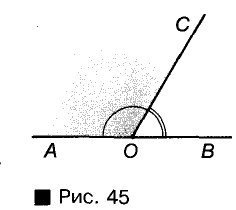
Одна сторона у смежных углов общая, а две другие — дополнительные лучи. Если точки А, О, В лежат на одной прямой, а С — произвольная точка, не принадлежащая прямой АВ, то углы АОС и СОВ — смежные (рис. 45).
Свойство смежных углов сформулируем в виде теоремы.
В математике теоремой называют каждое утверждение, истинность которого устанавливается путем логических рассуждений. Цепочку таких рассуждений называют доказательством.
В нашем учебнике теоремы напечатаны жирным шрифтом и пронумерованы.
Теорема: Сумма мер двух смежных углов равна 180°
Доказательство:
Объединение двух смежных углов является развернутым углом. Мера развернутого угла равна 180°. Значит, какими бы ни были смежные углы, сумма их мер равна 180°.
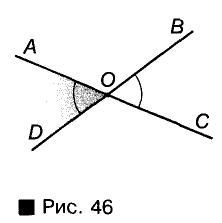
Два угла называются вертикальными, если стороны одного являются дополнительными лучами сторон другого. Например, если прямые АС и BD пересекаются в точке О, то углы AOD и ВОС — вертикальные (рис. 46). Каждый из них — смежный с углом АОВ. Углы АОВ и COD — тоже вертикальные.
Теорема: Вертикальные углы равны.
Доказательство:
Пусть AOD и ВОС — любые вертикальные углы (см. рис. 46). Каждый из них смежный с углом АОВ. По теореме о сумме смежных углов
отсюда
Правые части этих равенств одинаковые, поэтому 
Для любознательных:
Слово смежные употребляют не только применительно к углам. Смежный—это имеющий общую границу с чем-то или прилегающий к чему-то, соседний. Можно говорить о смежных комнатах, смежных полях и т. п. Относительно углов это понятие имеет особый смысл. Не каждые два угла с общей стороной называют смежными. Например, на рисунке 47 углы АОВ и ВОС имеют общую сторону ОВ, но не являются смежными.
Смежные углы — это два угла, состоящие в определенном отношении. Один угол не может быть смежным. Когда говорим, что какой-то угол смежный, то обязательно должны уточнить: смежный с каким углом? Отношение смежности углов имеет такое свойство: если угол А смежный с углом B, то и угол В смежный с углом А.
Пусть угол А смежный с углом В, а угол B смежный с углом
C. Что можно сказать об углах А и С? Они либо вертикальные, либо угол С — это тот же угол А (рис. 48).
Слово вертикальные также относится не только к углам. В основном вертикально расположенным считают продолговатый предмет, расположенный в направлении отвеса (перпендикулярно к горизонту).
Всегда верно свойство: если угол А вертикальный углу В, то и угол В вертикальный углу А.
Пример №1
Найдите меры смежных углов, если один из них на 50° больше другого.
Решение:
Пусть мера меньшего из смежных углов равна х, тогда мера большего угла х + 50°. По свойству смежных углов х + х + 50° = 180°, откуда х = 65°, а х + 50° = 115°.
Ответ. 65° и 115°.
Пример №2
Один из четырех углов, образованных пересечением двух прямых, вдвое больше другого. Найдите меру каждого из полученных углов.
Решение:
При пересечении двух прямых образуются вертикальные и смежные углы. Поскольку вертикальные углы равны, то они условие задачи не удовлетворяют. Делаем вывод: один из смежных углов вдвое больше другого, их меры х и 2х. По свойству смежных углов х + 2х = 180°, откуда х = 60°, а 2х = 120°. Соответствующие им вертикальные углы равны 60° и 120°.
Ответ. 60°, 120°, 60°, 120°.
Перпендикулярные и параллельные прямые
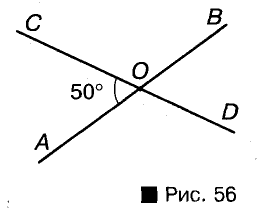
Вспомните, как могут располагаться на плоскости две прямые. Если они пересекаются, то образуют четыре угла — две пары вертикальных углов (речь идет об углах меньше развернутого). Меньший из них считается углом между данными прямыми. Например, на рисунке 56 прямые АВ И CD пересекаются под углом 50°. Говорят также, что угол между прямыми АВ и CD равен 50°. Если две прямые, пересекаясь, образуют четыре Прямых угла, говорят, что они пересекаются под прямым углом.
Две прямые, пересекающиеся под Прямым углом, называют перпендикулярными прямыми. Прямые а и б на рисунке 57 перпендикулярны одна Н другой. Записывают так: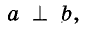
Отрезки или лучи называют перпендикулярными, если они лежат на перпендикулярных прямых.
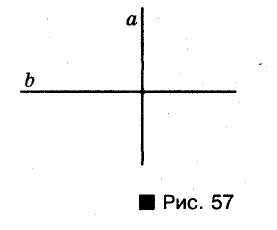
Если отрезок АВ лежит на прямой, перпендикулярной к прямой а, говорят, что отрезок АВ перпендикулярен к прямой а. Если при этом точка В принадлежит прямой о, то отрезок АВ называют перпендикуляром, проведенным из точки А к прямой а (рис. 58). Точку В называют основанием перпендикуляра, а длину Перпендикуляра АВ — расстоянием от точки А до прямой а.
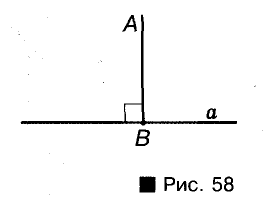
Через произвольную точку Р всегда можно провести прямую, перпендикулярную к данной прямой а. Это можно сделать с помощью угольника (рис. 59) или транспортира (рис. 60). Позже вы узнаете, как можно выполнить такое построение с помощью линейки и циркуля. Можно доказать, что существует только одна прямая, перпендикулярная к данной прямой и проходящая через данную точку.
Не каждые две прямые пересекаются. Особого внимания заслуживают прямые, которые не пересекаются и лежат в одной плоскости.
Две прямые на плоскости называются параллельными, если они не пересекаются (рис. 61). Если прямые а и b параллельные, пишут так: а || b.
Представление о параллельных прямых дают линии в тетради, линии нотного стана (рис. 62), ребра бруска.
Два отрезка или луча называют параллельными, если они лежат на параллельных прямых. Например, если ABCD — прямоугольник, то АВ || DC и ВС || AD.
Через любую точку Р, не лежащую на прямой а, можно провести прямую, параллельную прямой а (рис. 63, а). Для этого можно через точку Р провести прямую с, перпендикулярную к прямой а, а потом прямую Ь, перпендикулярную к прямой с (рис. 63, б). При таком построении всегда b || а. Можно воспользоваться линейкой и угольником.
Для любознательных:
Можно доказать (попытайтесь!),что две прямые одной плоскости, перпендикулярные к третьей прямой, параллельны. То есть, если
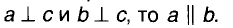
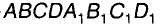
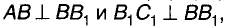
Слово параллельные происходит от греческого слова «параллелос», что в переводе означает «идущие рядом». Если говорить, что какая-либо прямая параллельна, то обязательно следует сказать, какой именно прямой она параллельна. Таким образом, параллельность прямых — это своеобразное отношение между двумя прямыми. Отношение параллельности прямых имеет такое свойство: если а || b, то и b || а. Другими отношениями являются перпендикулярность прямых, равенство углов и др. Символы этих отношений:
Позже вы узнаете о других отношениях между геометрическими объектами.
Как проводить параллельные прямые с помощью линейки и циркуля, вы узнаете позже.
Пример №3
Докажите, что биссектрисы смежных углов перпендикулярны
Решение:
Пример №4
Обозначьте на координатной плоскости точки А (2; 3) и В (-4; -3). Найдите расстояния от этих точек до осей координат, если длина единичного отрезка равна 1 см.
Решение:
Из точек А и В опустим перпендикуляры на оси координат (рис. 66). Длина отрезка AM — расстояние от точки А до оси ОХ, а длина отрезка AN — расстояние от точки А до оси OY. По рисунку видим, что AM = 3 см, a AN = = 2 см.
Аналогично определяем, что расстояние от точки В до осей координат равно 3 см и 4 см.
Ответ. От точки А — 3 см и 2 см; От точки В — 3 см и 4 см.
Признаки параллельности прямых
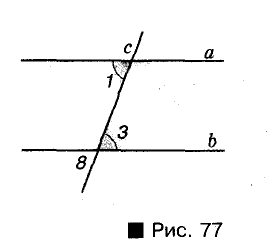
Важную роль в исследовании параллельных прямых играют понятия секущей и некоторых пар углов.
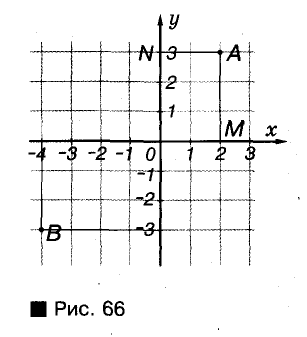
Пусть о и b – две произвольные прямые плоскости. Прямая с, пересекающая их, называется секущей прямых а и b (рис. 73).
Прямые а и b с их секущей с образуют 8 углов. На рисунке 73 они пронумерованы. Некоторые пары этих углов имеют специальные названия:
- внутренние накрест лежащие углы: 1 и 3, 2 и 4;
- внутренние односторонние углы: 1 и 4, 2 и 3;
- соответственные углы: 1 и 8, 2 и 7, 3 и 6, 4 и 5.
Обратите внимание! Если два каких-либо внутренних накрест лежащих угла равны, то также равны и внутренние накрест лежащие углы другой пары (рис. 74). Если, например, 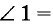
Случай, когда внутренние накрест лежащие углы равны, заслуживает особого внимания, поскольку именно при этом условии прямые а и b параллельны.
Теорема: (признак параллельности прямых).
Две прямые параллельны, если они с секущей образуют равные внутренние накрест лежащие углы.
Доказательство:
Пусть секущая АВ пересекает прямые а и b так, что образовавшиеся при этом внутренние накрест лежащие углы 1 и 3 равны. Тогда, как показано выше, углы 2 и 4 тоже равны. Допустим, что при таком условии прямые а и б пересекаются в какой-то отдаленной точке С. В результате образуется
треугольник ABC (на рисунке 75 он изображен схематически в виде пятиугольника). Представим, что этот треугольник повернули вокруг точки О — середины отрезка АВ — так, что отрезок ОА занял положение ОВ. Тогда, поскольку
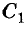
Таким образом, если 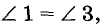
Обратите внимание на способ доказательства теоремы 3. Чтобы доказать, что прямые а и b параллельны, мы показывали, что они не могут пересекаться, то есть допускали противоречащее тому, что требовалось доказать. Такой способ рассуждения называют методом доказательства от противного.
На основе доказанной теоремы 3 нетрудно доказать и другие признаки параллельности прямых.
Теорема: Две прямые параллельны, если при пересечении с секущей они образуют внутренние односторонние углы, сумма которых равна 180°.
Доказательство:
Пусть, например, на рисунке 76 сумма внутренних односторонних углов 1 и 4 равна 180°. Сумма смежных углов 3 и 4 тоже равна 180°. Поэтому 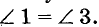
Теорема: Две прямые параллельны, если при пересечении с секущей они образуют равные соответственные углы.
Доказательство:
Пусть секущая с пересекает прямые а и b так, что образовавшиеся при этом соответственные углы 1 и 8 равны (рис. 77). Углы 8 и 3 равны, поскольку вертикальны.
Поэтому если
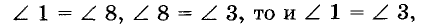
Заслуживает внимания такое следствие из теоремы 3.
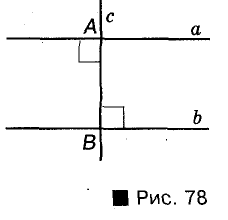
Две прямые, перпендикулярные к третьей прямой, параллельны.
Ведь если каждая из прямых а и b перпендикулярна к с, то образовавшиеся при этом внутренние разносторонние углы равны, поскольку они прямые (рис. 78). Cледовательно, а и b параллельны.
Для любознательных:
Углы 5 и 7 (а также 6 и 8) называют внешними накрест лежащими, а углы 5 и 8 (а также 6 и 7) — внешними односторонними углами (рис. 79).
Используя эти понятия, попробуйте сформулировать и доказать еще два признака параллельности прямых. Полезно также лучше понять сущность метода доказательства от противного. Если утверждение А противоречит утверждению В, то такие два утверждения называют противоречащими или противными друг другу. Из двух взаимно е противоречащих утверждений всегда одно верно, а другое ложно. Поэтому если убедимся, что утверждения А и В противоречат друг другу и, например, что утверждение В ложное, то можем быть уверены, что утверждение А верно.
Не следует путать противоречащие утверждения с противоположными. Например, когда речь идет о числовых выражениях и натуральных числах, то утверждения «выражение А положительное» и «выражение А отрицательное» или «число п простое» и «число л сложное» — противоположные, но не противоречащие, ведь каждое из них может быть неправильным. А вот утверждения «выражение А положительное» и «выражение А неположительное» или «число п простое» и «число п непростое» — взаимно противоречащие. Непростое означает составное или равное 1; неположительное — отрицательное или равное нолю.
Доказывая методом от противного, опровергать нужно не противоположное утверждение, а противоречащее данному. Опровергать что-либо — означает показать, что оно ошибочно.
Пример №5
Как построить параллельные прямые, пользуясь только линейкой и транспортиром?
Решение:
Начертим произвольный луч АВ и отложим равные углы ВАС и АСР, как показано на рисунке 80. Прямые АВ и СР параллельны, ведь углы ВАС и АСР внутренние накрест лежащие, и по построению они равны.
Через концы отрезка АВ с одной стороны от прямой АВ проведены лучи АК и ВС так, что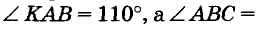
Прямую АВ можно считать секущей прямых АК и ВС (рис. 81).
Углы КАВ и ABC — внутренние односторонние. Поскольку их сумма 110° + 70° равна 180°, то прямые АК и ВС — параллельные (теорема 4). Поэтому и лучи АК и ВС — параллельные.
Ответ. Лучи АК и ВС параллельны.
Свойства параллельности прямых
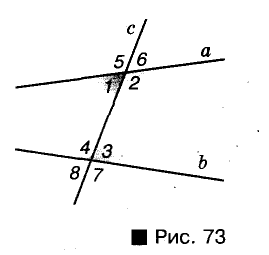
Задача:
Даны прямая а и точка Р, не принадлежащая этой прямой. Проведите через точку Р прямую, параллельную прямой а.
Решение:
С помощью линейки и угольника построение можно выполнить, как показано на рисунке 90.
Можно ли через точку Р провести две разные прямые, параллельные прямой а? Геометры издавна считали истинным такое утверждение
Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.
Древнегреческий геометр Евклид это утверждение принял без доказательства. Его назвали аксиомой Евклида, потому что все утверждения, принимаемые без доказательств, называют аксиомами. (Подробнее об аксиомах и теоремах — в следующем параграфе.)
Не все ученые считают аксиому Евклида верной. Геометрию, в которой аксиому Евклида признают верной, называют евклидовой геометрией. Вы изучаете евклидову геометрию.
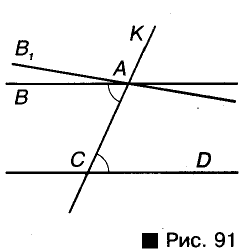
Теорема: (обратная теореме 3). Если прямые параллельны, то внутренние накрест лежащие углы, образованные ими с секущей, равны.
Доказательство:
Пусть прямые АВ и CD параллельны, а КС — их секущая, проходящая через точку А (рис. 91). Докажем, что
Допустим что 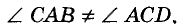
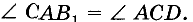
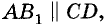
Следствие:
Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой прямой.
Действительно, если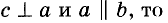
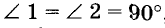
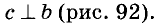
Теорема: Две прямые, параллельные третьей, параллельны.
Доказательство:
Пусть каждая из прямых а и b параллельна прямой с. Докажем, что а || b.
Допустим, что прямые а и b не параллельны (рис. 93), а пересекаются в некоторой точке Р. Получается, что через точку Р проходят две разные прямые а и Ь, параллельные с. Это противоречит аксиоме Евклида. Поскольку прямые а и b не могут пересекаться, они параллельны.
Примечание:
Доказательство теоремы верно и в случае, если прямая с лежит между а и b.
Для любознательных:
Последнюю теорему называют теоремой о транзитивности параллельности прямых (лат. transitivus — переходной), поскольку она утверждает, что параллельность двух пар параллельных прямых переходит на третью пару:
Чтобы это утверждение было верным всегда, договорились считать, что каждая прямая параллельна сама себе, то есть а || а. Ведь если
а || b и b || а, то а || а.
Отрезки одной прямой тоже считают параллельными. Например, если А, В, С, К — точки одной прямой, то каждый из отрезков АВ, АС, АК, ВС, ВК, СК параллелен любому из них (рис. 94). В целесообразности такой договоренности вы убедитесь позже, изучая параллельные переносы, параллельное проектирование и т. п. А в седьмом классе основное внимание будет обращаться на параллельность отрезков и лучей, не лежащих на одной прямой.
Существуют геометрии, в которых аксиома Евклида не считается верной. Их называют неевклидовыми геометриями. Такова, например, геометрия Лобачевского (см. с. 195).
Пример №6
Докажите, что прямые, перпендикулярные к непараллельным прямым, пересекаются.
Решение:
Пусть прямые а и b пересекаются, а прямые шип перпендикулярны к ним: 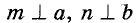
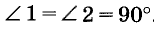
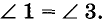
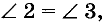
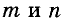
Теоремы и аксиомы
Вы уже имеете представление о теоремах. Теорема — это утверждение, в истинности которого убеждаются с помощью логических рассуждений, доказательств.
Обычно теорема содержит условие (то, что дано) и заключение (что требуется доказать). Чтобы вычленить условйе и заключение теоремы, ее удобно подать в форме «Если… , то…». Например: «Если углы вертикальные, то они равны». Здесь слова перед запятой содержат условие теоремы, а после запятой — заключение.
Часто условие теоремы записывают после слова «дано», а заключение — после слова «доказать». Например, теорему о вертикальных углах можно оформить так.
Поменяв условие и заключение теоремы местами, получим новое утверждение (истинное или ложное). Если полученное таким способом утверждение истинное, его называют обратной теоремой.
Примеры:
- «Если углы вертикальные, то они равны» — данная теорема. «Если углы равны, то они вертикальные» — обратное утверждение (ложное).
- «Если соответственные утлы равны, то прямые параллельные» — данная теорема. «Если прямые параллельные, то соответственные углы равны» — обратная теорема. Важнейшие теоремы, в которых даются критерии чего- либо, называют признаками.
Доказывая теорему, ссылаются на другие истинные утверждения. Но в самом начале изучения геометрии еще никаких других истинных утверждений» нет. Поэтому некоторые Пермью утверждения обычно принимают без доказательств. Называют их аксиомами.
Некоторые аксиомы вам уже известны. Сформулируем их еще раз.
Какой бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, ей не принадлежащие.
- Через любые две точки можно провести прямую, и только одну.
- Из трех точек прямой одна и только одна лежит между двумя другими.
- Каждый отрезок имеет определенную длину.
- Каждый угол имеет определенную меру.
- Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.
От теорем и аксиом следует отличать определения, в которых рйокрывается содержание понятия. Например: «Отрезком называется часть прямой, ограниченная двумя точками» — определение отрезка; «Острым углом называется угол, который “меньше прямого» — определение острого угла.
В определениях, аксиомах и теоремах — основное содержание геометрии. Их нужно знать, но формулировать (правильно!) можно и своими словами. Например, определение отрезка можно сформулировать так: «Отрезок — это часть прямой, ограниченная двумя ее точками», или так: «Часть прямой, ограниченная двумя ее точками, называется отрезком».
Для любознательных:
Слово аксиома греческого происхождения; сначала это слово обозначало: уважение, авторитет, неоспоримость; впоследствии словом «аксиома» начали называть утверждение, принимаемое без доказательства.
Слово теорема тоже греческого происхождения. Сначала теоремой называли зрелище, театральное представление. Первым геометрам доказанные ими теоремы казались довольно неожиданными, удивительными, словно интересные зрелища. И в самом деле удивительно: из немногих примитивных утверждений, принимаемых без доказательств, путем одних рассуждений человек может получить миллионы не очевидных следствий. Даже таких, которых в природе нигде не наблюдается. И таких, о существовании которых не догадывался ни один мыслитель.
Чтобы и вы поняли, какое удовлетворение ощущали первые геометры, открывая и доказывая все новые и новые свойства геометрических фигур с помощью одних лишь рассуждений, попробуйте ответить на один из таких вопросов.
Посмотрите на рисунок 108. На нем выделены 6 точек: середины сторон треугольника ABC и основания его высот. Кажется, все эти точки лежат на одной окружности. Действительно ли это так? В каждом треугольнике? Кто первым обнаруживал подобные закономерности и обосновывал их, тот испытывал огромное удовлетворение, словно путешественник, пришедший первым туда, где еще никто не бывал, или спортсмен, побивший мировой рекорд.
Пример №7
Биссектрисы внутренних накрест лежащих углов, образованных секущей с двумя параллельными прямыми, параллельны. Докажите. Сформулируйте обратное утверждение.
Решение:
Пусть ВС — секущая прямых АВ и CD, углы ABC и BCD — внутренние накрест лежащие, а ВК и СР — их биссектрисы (рис. 109). Покажем, что если АВ || CD, то ВК || СР.
Если АВ || CD, то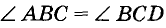
Обратное утверждение: если биссектрисы внутренних накрест лежащих углов, образованных двумя прямыми с их секущей, параллельны, то параллельны и данные прямые.
Пример №8
Два луча называют сонаправленными, если один из них является частью другого или если они параллельны и расположены по одну сторону от прямой, проходящей через их начала. Приведите примеры.
Решение:
Лучи АК и ВК (рис. 110), а также лучи АК и ВТ (рис. 111).
Пример №9
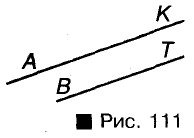
Докажите, что углы с сонаправленными сторонами равны.
Решение:
Докажем, что если лучи ВА и РК, ВС и РТ сонаправленные, то углы 1 и 2 равны.
Если данные углы расположены, как показано на рисунке 112,
Если данные углы расположены, как показано на рисунке 113, то луч РТ составляет часть луча ВС. В этом случае
- Треугольник
- Решение треугольников
- Треугольники и окружность
- Площадь треугольника
- Длина дуги кривой
- Геометрические фигуры и их свойства
- Основные фигуры геометрии и их расположение в пространстве
- Пространственные фигуры – виды, изображения, свойства
Для двух прямых в пространстве возможны четыре случая:
– прямые совпадают;
– прямые параллельны (но не совпадают);
– прямые пересекаются;
– прямые скрещиваются, т.е. не имеют общих точек и непараллельны.
Рассмотрим два способа описания прямых: каноническими уравнениями и общими уравнениями. Пусть прямые L1 и L2 заданы каноническими уравнениями:
L1: (x – x1)/l1 = (y – y1)/m1 = (z – z1)/n1, L2: (x – x2)/l2 = (y – y2)/m2 = (z – z2)/n2 (6.9)
Для каждой прямой из ее канонических уравнений сразу определяем точку на ней M1(x1; y1; z1) ∈ L1, M2(x2; y2; z2) ∈ L2 и координаты направляющих векторов s1 = {l1; m1; n1} для L1, s2 = {l2; m2; n2} для L2.
Если прямые совпадают или параллельны, то их направляющие векторы s1 и s2 коллинеарны, что равносильно равенству отношений координат этих векторов:
l1/l2 = m1/m2 = n1/n2. (6.10)
Если прямые совпадают, то направляющим векторам коллинеарен и вектор M1M2:
(x2 – x1)/l1 = (y2 – y1)/m1 = (z2 – z1)/n1. (6.11)
Это двойное равенство также означает, что точка М2 принадлежит прямой L1. Следовательно, условием совпадения прямых является выполнение равенств (6.10) и (6.11) одновременно.
Если прямые пересекаются или скрещиваются, то их направляющие векторы неколлинеарны, т.е. условие (6.10) нарушается. Пересекающиеся прямые лежат в одной плоскости и, следовательно, векторы s1, s2 и M1M2 являются компланарными. Условие компланарности этих векторов можно записать через смешанное произведение как равенство нулю определителя третьего порядка, составленного из их координат (см. 3.2):
Условие (6.12) выполняется в трех случаях из четырех, поскольку при Δ ≠ 0 прямые не принадлежат одной плоскости и потому скрещиваются.
Сведем все условия воедино:
Взаимное расположение прямых характеризуется количеством решений у системы (6.13). Если прямые совпадают, то система имеет бесконечно много решений. Если прямые пересекаются, то эта система имеет единственное решение. В случае параллельных или скрещивающихся прямых решений нет. Последние два случая можно разделить, если найти направляющие векторы прямых. Для этого достаточно вычислить два векторных произведения n1 × n2 и n3 × n4, где ni = {Ai; Bi; Ci}, i = 1, 2, 3,4. Если полученные векторы коллинеарны, то данные прямые параллельны. Иначе они скрещивающиеся.
Пример 6.4. Исследуем взаимное расположение прямых
Направляющий вектор s1 прямой L1 находим по каноническим уравнениям этой прямой: s1 = {1; 3; —2}. Направляющий вектор s2 прямой L2 вычисляем с помощью векторного произведения нормальных векторов плоскостей, пересечением которых она является:
Поскольку s1 = -s2, то прямые параллельны или совпадают. Выясним, какая из этих ситуаций реализуется для данных прямых. Для этого подставим координаты точки M0(1; 2; —1) ∈ L1 в общие уравнения прямой L2. Для первого из них получаем 1 = 0. Следовательно, точка М0 не принадлежит прямой L2 и рассматриваемые прямые параллельны.
Угол между прямыми. Угол между двумя прямыми можно найти, используя направляющие векторы прямых. Острый угол между прямыми равен углу между их направляющими векторами (рис. 6.5) или является дополнительным к нему, если угол между направляющими векторами тупой. Таким образом, если для прямых L1 и L2 известны их направляющие векторы sx и s2, то острый угол φ между этими прямыми определяется через скалярное произведение:
cosφ = |S1S2|/|S1||S2|
Например, пусть si = {li; mi; ni}, i = 1, 2. Используя формулы (2.9) и (2.14) для вычисления длины вектора и скалярного произведения в координатах, получаем
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Разновидности уравнений прямой
Канонические уравнения прямой.Пусть задана точка $M_{0} left(x_{0} ,y_{0} ,z_{0} right)$, через которую проходит прямая, а также направляющий вектор $overline{R}=mcdot overline{i}+ncdot overline{j}+pcdot overline{k}$, которому она параллельна. Уравнения $frac{x-x_{0} }{m} =frac{y-y_{0} }{n} =frac{z-z_{0} }{p}$ называются каноническими уравнениями прямой.
Параметрические уравнения прямой. Введем обозначения: $frac{x-x_{0} }{m} =t$, $frac{y-y_{0} }{n} =t$, $frac{z-z_{0} }{p} =t$. Здесь $t$ — параметр. Из этих равенств получаем: $x=x_{0} +mcdot t$, $y=y_{0} +ncdot t$, $z=z_{0} +pcdot t$. Эти уравнения называются параметрическими уравнениями прямой.
Уравнение прямой, которая проходит через две заданные точки $M_{1} left(x_{1} ,y_{1} ,z_{1} right)$ и $M_{2} left(x_{2} ,y_{2} ,z_{2} right)$. Уравнения $frac{x-x_{1} }{x_{2} -x_{1} } =frac{y-y_{1} }{y_{2} -y_{1} } =frac{z-z_{1} }{z_{2} -z_{1} } $, аналогичные каноническим, называются уравнениями прямой, проходящей через две заданные точки.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Общие уравнения прямой. Прямую линию в пространстве можно определить как линию пересечения двух не параллельных между собой плоскостей: $A_{1} cdot x+B_{1} cdot y+C_{1} cdot z+D_{1} =0$ и $A_{2} cdot x+B_{2} cdot y+C_{2} cdot z+D_{2} =0$. Решение системы уравнений, состоящей из уравнений плоскостей, называются общими уравнениями прямой.
Переход между различными видами уравнений прямой
От общих уравнений прямой можно перейти к каноническим. Для этого надо знать произвольную точку прямой и ее направляющий вектор. Выберем значение некоторой одной координаты произвольно. После этого координаты нужной точки можно найти из уравнений плоскостей, рассматривая их как систему относительно тех двух координат, которые остались. Для нахождения направляющего вектора отметим, что он должен быть перпендикулярным к нормальным векторам каждой из плоскостей. Поэтому для этого целиком подходит вектор их векторного произведения.
От канонических уравнений прямой можно перейти к общим. Для этого представим канонические уравнения как пару уравнений $frac{x-x_{0} }{m} =frac{z-z_{0} }{p} $ и $frac{y-y_{0} }{n} =frac{z-z_{0} }{p} $ и выполним преобразования.
«Взаимное расположение прямых в пространстве» 👇
Получаем: $pcdot x-mcdot z-pcdot x_{0} +mcdot z_{0} =0$ — уравнение плоскости, параллельной оси $Oy$, а $pcdot y-ncdot z-pcdot y_{0} +ncdot z_{0} =0$ — уравнение плоскости, параллельной оси $Ox$. Зная основные виды уравнений, описывающих прямые, можно более подробно рассмотреть способы расположения прямых в пространстве.
Взаимное расположение двух прямых в пространстве
Различают 3 случая взаимного расположения прямых в пространстве:
- Скрещивающиеся прямые в пространстве. Две прямых являются скрещивающимися, если они не имеют никаких общих точек и лежат в различных плоскостях. В жизни скрещивающиеся прямые — это, например, железная дорога, проходящая над автомагистралью;
- Две прямые находятся на одной плоскости и имеют одну общую точку, то есть пересекаются; Примером пересекающихся прямых в пространстве из реального мира служит обычный перекрёсток.
- Две прямые находятся на одной плоскости и не имеют общих точек, то есть параллельны друг другу. Существует частный случай параллельных прямых — это совпадающие прямые в пространстве.
Замечание 1
Вне зависимости от того, являются ли прямые пересекающимися или скрещивающимися, можно говорить об угле между ними.
Для того чтобы определить, пересекаются ли прямые в пространстве, необходимо составить систему уравнений, состоящую из уравнений этих прямых. Если эта система имеет решение, то прямые пересекаются.
Теперь рассмотрим подробнее, как определить взаимное расположение прямых в пространстве.
Пусть в пространстве заданы две прямые $L_{1} $ и $L_{2} $: $frac{x-x_{1} }{m_{1} } =frac{y-y_{1} }{n_{1} } =frac{z-z_{1} }{p_{1} } $ и $frac{x-x_{2} }{m_{2} } =frac{y-y_{2} }{n_{2} } =frac{z-z_{2} }{p_{2} } $. Выберем в пространстве произвольную точку и проведем через нее две вспомогательные прямые, параллельные данным.
Углом между прямыми $L_{1} $ и $L_{2} $ называют любой из двух сопряженных углов, образованных вспомогательными прямыми. Если величина одного из них $phi $, то величина второго $pi -phi $.
Вместо вспомогательных прямых можно взять направляющие векторы данных прямых: $overline{R_{1} }=m_{1} cdot overline{i}+n_{1} cdot overline{j}+p_{1} cdot overline{k}$ и $overline{R_{2} }=m_{2} cdot overline{i}+n_{2} cdot overline{j}+p_{2} cdot overline{k}$. Косинус одного из углов между прямыми можно найти по формуле $cos phi =frac{m_{1} cdot m_{2} +n_{1} cdot n_{2} +p_{1} cdot p_{2} }{sqrt{m_{1}^{2} +n_{1}^{2} +p_{1}^{2} } cdot sqrt{m_{2}^{2} +n_{2}^{2} +p_{2}^{2} } } $. Если значение $cos phi >0$, то получен острый угол между прямыми, если $cos phi$
Равенство $cos phi =0$ значит, что прямые перпендикулярны. Следовательно, условие перпендикулярности двух прямых в пространстве имеет вид $m_{1} cdot m_{2} +n_{1} cdot n_{2} +p_{1} cdot p_{2} =0$.
Условие параллельности двух прямых совпадает с условием коллинеарности их направляющих векторов, то есть $frac{m_{1} }{m_{2} } =frac{n_{1} }{n_{2} } =frac{p_{1} }{p_{2} }$.
Нахождение угла между прямыми частично решает также вопрос о нахождении их в одной плоскости. Имеется в виду то, что выполнение условия параллельности двух прямых одновременно означает, что они находятся в одной плоскости.
Теперь рассмотрим условие пересечения двух прямых, которое также является условием нахождения прямых в одной плоскости.
Из уравнений заданных прямых видно, что прямая $L_{1} $ проходит через точку $M_{1} left(x_{1} ,y_{1} ,z_{1} right)$, а прямая $L_{2} $ — через точку $M_{2} left(x_{2} ,y_{2} ,z_{2} right)$.
Рассмотрим вектор $overline{M_{1} M_{2} }=left(x_{2} -x_{1} right)cdot overline{i}+left(y_{2} -y_{1} right)cdot overline{j}+left(z_{2} -z_{1} right)cdot overline{k}$, который соединяет эти точки, а также направляющие векторы $overline{R_{1} }=m_{1} cdot overline{i}+n_{1} cdot overline{j}+p_{1} cdot overline{k}$ и $overline{R_{2} }=m_{2} cdot overline{i}+n_{2} cdot overline{j}+p_{2} cdot overline{k}$ прямых $L_{1} $ и $L_{2} $.
Если прямые $L_{1} $ и $L_{2} $ действительно пересекаются, то они лежат в одной плоскости $P$. В этой же плоскости $P$ лежит и вектор $overline{M_{1} M_{2} }$. Направляющий вектор $overline{R_{1} }$ коллинеарен прямой $L_{1} $, а направляющий вектор $overline{R_{2} }$ коллинеарен прямой $L_{2} $. Итак, все три вектора $overline{M_{1} M_{2} }$, $overline{R_{1} }$ и $overline{R_{2} }$ лежат в параллельных плоскостях, то есть они компланарны. Запишем условие компланарности векторов $left|begin{array}{ccc} {x_{2} -x_{1} } & {y_{2} -y_{1} } & {z_{2} -z_{1} } \ {m_{1} } & {n_{1} } & {p_{1} } \ {m_{2} } & {n_{2} } & {p_{2} } end{array}right|=0$ и получим условие пересечения двух прямых, если же это условия не выполняется, то это скрещенные прямые в пространстве.
Пример 1
Задание: Выяснить взаимное расположение прямых в пространстве:
$L_1: frac{x – 1}{1} = frac{y – 2}{3}=frac{z+1}{-2}$
$L_2: begin{cases} x-y-z+1 =0 \ x + y + 2z – 2 = 0 \ end{cases}$
Решение: Направляющий вектор первой прямой определяем по её уравнениям, он будет выглядеть как $s_1 = {1;3;-2}$.
Направляющий же вектор второй прямой определим через векторное произведение нормальных векторов, определяющих плоскости, на пересечении которых она находится:
$s_2 = n_1 × n_1 = begin{array}{|ccc|} i & j & k \ 1 & -1 & -1 \ 1 & 1 & 2 \ end{array} = – i – 3j + 2k$
В данном примере $s_1 = -s_2$, а это значит, что прямые либо параллельные, либо совпадающие.
Чтобы понять, с каким из случаев мы имеем дело, возьмём точку $M_0$с координатами $(1;2;-1)$, принадлежащую первой прямой и подставим в уравнения для второй.
В первом из них равенство не соблюдается и получается, что $1=0$. Это значит, что рассмотренная точка не лежит на второй прямой и прямые параллельны между собой.
Пример 2
Задание: провести плоскости через параллельные прямые и через прямые, которые пересекаются.
Решение каждой из этих задач начинается с того, что на нужной плоскости $P$ выбирается некоторая переменная точка $Mleft(x,y,zright)$.
Если данные прямые $L_{1} $ и $L_{2} $ — параллельны, то уравнение нужной плоскости $P$ имеет вид условия компланарности $left|begin{array}{ccc} {x-x_{1} } & {y-y_{1} } & {z-z_{1} } \ {x_{2} -x_{1} } & {y_{2} -y_{1} } & {z_{2} -z_{1} } \ {m} & {n} & {p} end{array}right|=0$ следующих трех векторов:
- $overline{M_{1} M}=left(x-x_{1} right)cdot overline{i}+left(y-y_{1} right)cdot overline{j}+left(z-z_{1} right)cdot overline{k}$ — вектор, который лежит в плоскости $P$, соединяет точку $M_{1} left(x_{1} ,y_{1} ,z_{1} right)$, принадлежещей прямой $L_{1} $, с переменной точкой $Mleft(x,y,zright)$.
- $overline{M_{1} M_{2} }=left(x_{2} -x_{1} right)cdot overline{i}+left(y_{2} -y_{1} right)cdot overline{j}+left(z_{2} -z_{1} right)cdot overline{k}$ — вектор, который лежит в плоскости $P$, соединяет точку $M_{1} left(x_{1} ,y_{1} ,z_{1} right)$, которая принадлежит прямой $L_{1} $, с точкой $M_{2} left(x_{2} ,y_{2} ,z_{2} right)$, которая принадлежит прямой $L_{2} $.
- $overline{R}=mcdot overline{i}+ncdot overline{j}+pcdot overline{k}$ — направляющий вектор одной из двух параллельных прямых, параллельный плоскости $P$.
Если данные прямые $L_{1} $ и $L_{2} $ — пересекаются, то уравнение нужной плоскости $P$ имеет вид условия компланарности $left|begin{array}{ccc} {x-x_{1} } & {y-y_{1} } & {z-z_{1} } \ {m_{1} } & {m_{2} } & {m_{3} } \ {m_{2} } & {n_{2} } & {p_{2} } end{array}right|=0$ следующих трех векторов:
- $overline{M_{1} M}=left(x-x_{1} right)cdot overline{i}+left(y-y_{1} right)cdot overline{j}+left(z-z_{1} right)cdot overline{k}$ — вектор, который лежит в плоскости $P$, соединяет точку $M_{1} left(x_{1} ,y_{1} ,z_{1} right)$, принадлежащую прямой $L_{1} $, с переменной точкой $Mleft(x,y,zright)$.
- $overline{R_{1} }=m_{1} cdot overline{i}+n_{1} cdot overline{j}+p_{1} cdot overline{k}$ — направляющий вектор прямой $L_{1} $, параллельный плоскости $P$.
- $overline{R_{2} }=m_{2} cdot overline{i}+n_{2} cdot overline{j}+p_{2} cdot overline{k}$ — направляющий вектор прямой $L_{2} $, параллельный плоскости $P$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме